组合数学(西安电子科技大学(第二版))第二章母函数_版24样版
组合数学(第二版)递推关系

递推关系
其次,证明an 是通解.若给定一组初始条件
可以仿照齐次方程通解的证明方法,证得相应于条件式 (3.2.11)的解一定可以表示为式 (3.2.10)的形式.
关于 的求法已经解决,这里的主要问题是求式(3.2.2) 的特解an * .遗憾的是寻求特 解还没有一般通用的方法.然而, 当非齐次线性递推关系的自由项f(n)比较简单时,采用 下面的 待定系数法比较方便.
递推关系 【例 3.4.2】 棋盘染色问题:给一个具有1行n 列的1×n
棋盘(见图3.4.1)的每一个 方块涂以红、蓝二色之一,要求相 邻的两块不能都染成红色,设不同的染法共有an 种,试 求an.
图 3.4.1 1×n 棋盘
递推关系
递推关系
【例3.4.3】 交替子集问题:有限整数集合Sn={1,2,…,n} 的一个子集称为交替的, 如果按上升次序列出其元素时,排列 方式为奇、偶、奇、偶、…….例如{1,4,7,8}和 {3,4,11}都是, 而{2,3,4,5}则不是.令gn表示交替子集的数目(其中包括空集), 证明
且有gn=Fn+2.
递推关系
证 显然,g1=2,对应S1 的交替子集为⌀和{1}.g2=3,对应S2 的交替子集为⌀、 {1}、{1,2}.
将Sn 的所有子集分为两部分: (1)Sn-1={1,2,…,n-1}的所有子集; (2)Sn-1的每一个子集加入元素n 后所得子集. 例如,n=4,S4={1,2,3,4}的所有子集划分为两类,即 (1)⌀、{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3}; (2){4}、{1,4}、{2,4}、{3,4}、{1,2,4}、{1,3,4}、 {2,3,4}、{1,2,3,4}.
组合数学第2章答案

组合数学第2章答案2.1 求序列{0,1,8,27,…3n …}的母函数。
解:()()++++++=++++++=nn n x n x x x x G x a x a x a x a a x G 3323322102780()46414321313=+-+--==-----n n n n n n n a a a a a n a n a左右同乘再连加:464:0464:0464:0464:4321543211123455012344=+-+-=+-+-=+-+-=+-+-----------n n n n n n n n n n n n a a a a a x a a a a a x a a a a a x a a a a a x母函数:()()42162036-+-=x x x x G2.2 已知序列()()3433{,,……()33,,n +……},求母函数。
解:1(1)nx -的第k 项为:11()k n n +-- ,对于本题,n=4, ∴母函数为:41(1)x -2.3 已知母函数G (X )=25431783x x x--+,求序列{ n a }解:G (X )=)61)(91(783x x x +-+=)61()91(x Bx A ++-从而有: ⎩⎨⎧-==⇒⎩⎨⎧=-=+4778963B A B A B A G (X )=)61(4)91(7x x +-+-G (X )=7)999x (13322 ++++x x -4))6((-6)(-6)x (13322 +-+++x xn a =7*n )6(*49n -- 2.4.已知母函数239156xx x ---,求对应的序列{}n a 。
解:母函数为239()156x G x x x -=--39(17)(18)xx x -=+- A BG(x)17x 18xA(18x)B(17x)39x=++--++=-令 A B 38A +7B =9+=⎧⎨--⎩解得:A=2 B=1所以 ii i 0i 021G(x)2*(7x)(8x)17x 18x ∞∞===+=-++-∑∑n n n a 2*(7)8=-+2.5 设n n F G 2=,其中F n 是第n 个Fibonacci 数。
组合数学(西安电子科技大学(第二版))习题3

习题三(递推关系)1.解下列递推关系:(1)120171000,1n n n a a a a a ---+=⎧⎨==⎩ (2)12016900,1n n n a a a a a --++=⎧⎨==⎩ (3)20100,2n n a a a a -+=⎧⎨==⎩ (4)120121n n n a a a a a --=-⎧⎨==⎩ (5)123012990,1,2n n n n a a a a a a a ---=+-⎧⎨===⎩ 解:(1)对应的特征方程为:27100x x -+=,解得122,5x x ==。
所以齐次递推方程的通解为:25n n n a A B =+,代入初始条件,得:00a A B =+=,1251a A B =+=,解得:11,33A B =-=, 故 112533n n n a =-+。
(2)对应的特征方程为:2690x x ++=,解得:123x x ==-,所以,齐次递推方程的通解为:()(3)n n a A Bn =+-,代入初始条件,00a A ==,1()(3)1a A B =+-=,解得:10,3A B ==-,故1(3)3n n a n =--。
(3)对应的特征方程为:210x +=,解得:12,x i x i ==-,所以,齐次递推方程的通解为:()()n n n a A i B i =+-,代入初始条件,00a A B =+=,12a A i B i =-=,解得:,A i B i =-=,故 11()()n n n a i i --=+-。
(4)对应的特征方程为:2210x x -+=,解得:121x x ==,所以,齐次递推方程的通解为:n a A Bn =+,代入初始条件,01a A ==,11a A B =+=,解得:1,0A B ==,故 1n a =。
(5)对应的特征方程为:32990x x x --+=,解得:1231,3,3x x x ===-,所以,齐次递推方程的通解为:3(3)n n n a A B C =++-,代入初始条件,00a A B C =++=,1331a A B C =+-=,2992a A B C =++=, 解得,111,,4312A B C =-==-,故 1113(3)412n n n a -=-+--2.求由A ,B ,C ,D 组成的允许重复的排列中AB 至少出现一次的排列数。
组合数学(2)

k>h Sk-Sh =39
即 ah + ah+1 +… + ak = 39
20
例8 试证在边长为 √2的正方形里任取5点,
至少有2点的距离不超过1.
如右下图所示,将边长为√2的正方形划为4
个全等的小正方形.设置相隔距离最远的点在
四个角,显然中心位置安排第五点到其他
A
1
1
E
B
四个点距离相等,而且是
最大距离,等于1。
(j – i)m= ( qj – qi)n
23
由上式可以看出,由于n与m没有除1外
的公因子,因此n是(j – i)的一个因子。然
而, 0≤i<j≤n-1, 意味着: 0 <j-i≤n-1<n,也
就是说n不可能是j - i的因子。该矛盾产生于
我们的假设: n个整数
0m+a, 1m+a, 2m+a, ….., (n-1)m+a中有两 个除以n有相同的余数r的数。因此我们断言: 这个n数中的每一个数除以n都有不同的余数。
19
S1<S2<…<S100,且 S100 = (a1 + … +a10) + (a11 + … +a20)+… + (a91 + … +a100)
根据假定有 S100≤10×16 = 160
作序列S1 , S2 , … , S100 , S1 +39, … , S100+39 . 共200项.其中最大项 S100+39≤160+39=199 由鸽巢原理,必有两项相等.而且必是前段中 某项与后段中某项相等.设 Sk = Sh + 39,
组合数学 第2章 母函数
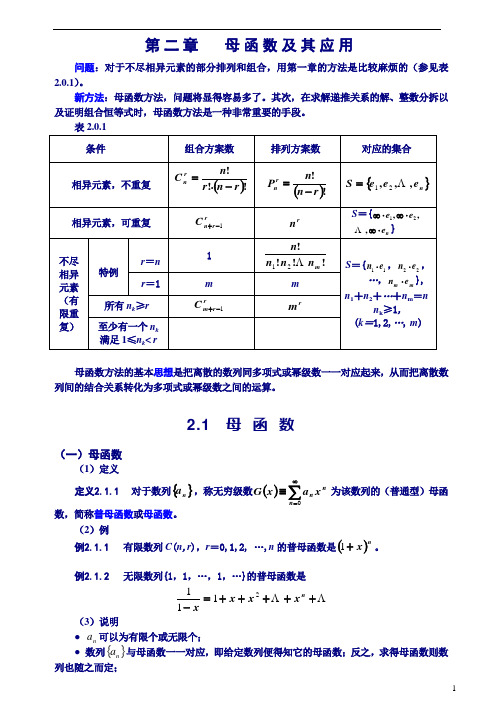
第二章 母函数及其应用问题:对于不尽相异元素的部分排列和组合,用第一章的方法是比较麻烦的(参见表2.0.1)。
新方法:母函数方法,问题将显得容易多了。
其次,在求解递推关系的解、整数分拆以及证明组合恒等式时,母函数方法是一种非常重要的手段。
母函数方法的基本思想是把离散的数列同多项式或幂级数一一对应起来,从而把离散数列间的结合关系转化为多项式或幂级数之间的运算。
2.1 母 函 数(一)母函数(1)定义定义2.1.1 对于数列{}n a ,称无穷级数()∑∞=≡0n nnxax G 为该数列的(普通型)母函数,简称普母函数或母函数。
(2)例例2.1.1 有限数列C (n ,r ),r =0,1,2, …,n 的普母函数是()nx +1。
例2.1.2 无限数列{1,1,…,1,…}的普母函数是+++++=-nxx x x2111(3)说明● n a 可以为有限个或无限个; ● 数列{}n a 与母函数一一对应,即给定数列便得知它的母函数;反之,求得母函数则数列也随之而定;例如,无限数列{0,1,1,…,1,…}的普母函数是 +++++n x x x 20=xx -1● 这里将母函数只看作一个形式函数,目的是利用其有关运算性质完成计数问题,故不考虑“收敛问题”,而且始终认为它是可“逐项微分”和“逐项积分”的。
(4)常用母函数(二)组合问题(1)组合的母函数定理2.1.1 组合的母函数:设{}m m e n e n e n S ⋅⋅⋅=,,,2211 ,且n 1+ n 2+…+ n m =n ,则S 的r 可重组合的母函数为()x G =∏∑==⎪⎪⎭⎫ ⎝⎛mi n j ji x 10=∑=n r r r x a 0 (2.1.1) 其中,r 可重组合数为rx 之系数r a ,r =0,1,2, …,n .定理2.1.1的最大优点在于:● 将无重组合与重复组合统一起来处理;● 使处理可重组合的枚举问题变得非常简单。
组合数学第二章习题解答

1+ x G(x) = (1− x)4
2.13已知
an = ∑k ,
3 k=1
n+1
1+4x+ x2 ∞ =∑ n+1 3 xn ( ) 4 (1−x) n=0
求序列{an}的母函数
G(x) =1+(1+23)x+(1+23 +33)x2 +...+(1+23 +...+(n+1)3)xn +... G(x) =(1+ x+ x2 +...) +23 x(1+ x+ x2 +...) +...(n+1)3 xn(1+ x+ x2 +...) +...
2.25 分母展开求出an的递推关系,再求出bn的递推关系 将分母展开(1-x)(1+x-x2)=1-2x2+x3 因此an满足递推关系:an-2an-2+an-3=0,a0=4,a1=-3 an-an-1+an-1-an-2-an-2+an-3 = bn+bn-1-bn-2=0 b0=4,b1=-7,母函数为:
b +(b +b )x 0 1 0 4−3x = 1+ x − x2 1+ x − x2
G x) = (
2.26 逐项展开,两边合并。
2.27 求下列递推关系的一般解
(a)an-4an-1=5n
a −4 n−1 −5 n−1 +2 a −2 = 0 a a 0 n n a −9 n−1 +2 a −2 = 0 a 0 n n 特 方 的 为和 征 程 解 4 5 一 解 : r 4n +r 5n 般 为 1 2
组合数学(第二版)波利亚(Pólya)定理

波利亚(Pólya)定理
图 6.2.3 十五子智力游戏
波利亚(Pólya)定理
波利亚(Pólya)定理
定理 6.2.6
当n≥2时,Sn 中偶置换的全体构成一个n!/2阶
的子群,称为交代群,记为An.
证 先证An 为群.
(1)封闭性:设p1,p2∈An,显然p1p2∈An,因为将二者分解的
结果相乘,仍得偶数个对换的乘积.
波利亚(Pólya)定理
6.3.3 等价类
定义 6.3.4 设G 是集S={1,2,…,n}上的置换群,若存在
i,j∈S ,满足p(i)=j, 则称i与j等价,记为i~j,S 中与i等价的元素的
全体记为Ei,称为元素i的“轨迹”或 “踪迹”.Ei 中元素的个
数称为轨迹的长度.
不难看出,元素i与j的这种等价关系满足如下三条性质:
关于普通乘法不存在单位元.而在 Z、Q、R、C中,虽然关于
普通乘法有单位元1,但数0没有逆元.
波利亚(Pólya)定理
波利亚(Pólya)定理
波利亚(Pólya)定理
6.1.2 群的性质
定理 6.1.1 群具有以下性质:
(1)单位元e唯一;
(2)逆元唯一;
(3)满足消去律:即对a,b,c∈G,若ab=ac,则b=c;若ba=ca,则
【例 6.3.3】 将S3 按共轭情况分类的结果见表6.3.1
波利亚(Pólya)定理
【例 6.3.4】 4次置换群
G={(1)(2)(3)(4),(12),(34),(12)(34)},共有3个 共轭类:
其中第2类含2个置换
波利亚(Pólya)定理
定理 6.3.1 在n 元对称群Sn 中,
证 设置换p 为(λ1,λ2,…,λn)型,将p 用轮换表示为
组合数学第二章1母函数PPT课件

若 有 两 个 色 子 , 则
( t t 2 . . . t 6 ) ( t t 2 . . . t 6 ) t 2 2 t 3 3 t 4 4 t 5 5 t 6 . . . .
中 的 t 6 的 系 数 5 显 然 相 当 于 t 1 t 5 t 6 , t 2 t 4 t 6 , t 3 t 3 t 6 , t 5 t 1 t 6 , t 4 t 2 t 6 诸 乘 积 都 产 生 t 6 这 一 项 的 方 案 数
[a 0 a 1 x a 2 x 2 ]/1 ( x ) A (x )/1 ( x )
26
2.2 母函数的性质
例. 已知
A (x ) 1 x x 2 x n 1 1 x
B (x ) 1 2 x 3 x2 4 x3 (1 1 x )2
(k1)xk
k0
(11x)2
27
2.2 母函数的性质
证
1:b0 a0a1a2 A(1)
x:b1 a1a2 A(1)a0
x2:b2
a2 A(1)a0a1
_ ) _ _ _ _ _
B (x ) A (1 )1 [x x 2 ] a 0 x (1 x x 2 ) a 1 x 2 (1 x x 2 )
30
2.2 母函数的性质
B(x)1A(1x)(a0a1x )x/1(x)
我们来看如下的例子ppt课件方法的引入我们也可以从另一角度来看要使两个色子掷出6点第一个色子除了6以外的都可选这有5种选法一旦第一个选定第二个色子就只有一种可能的选法按乘法法则有515种注意到出现15有两种选法出现24也有两种选法而出现33只有一种选法这些选法互斥且穷尽了出现6点的一切可能的选法按加法法则共有2215种不同选法
[C(n,0)C(n,1)x C(n,n)xn]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 1 x 2
n 1x n
n 0
sfsf
16
2.1母函数
例 从n双互不相同的袜子(每双袜子中的两只相同)中取出r只, 要求没有任何两只是成对的,共有多少种不同的取法?
解:生成函数为: G( x ) (1 x )
sfsf
13
2.1母函数
例 求不定方程k1+k2+k3+k4=20的解数。其中, 限制k1可取0,2,4; k2可取1,3,5; k3可取6,7;k4可取8,9。 G(x)=(1+x2+x4)(x+x3+x5)(x6+x7)(x8+x9)
= (1+x2+x4) (1+x2+x4)x(1+x)x6(1+x)x8
例 确定苹果、香蕉、橘子和梨的n-组合的个数,其中在每个n组合中要求:苹果的个数必须是偶数,香蕉的个数必须是5的倍 数,橘子的个数最多4个,梨的个数为0或1个。 解:生成函数为:
G( x) (1 x 2 x 4 ....)(x 0 x 5 ....)(1 x x 2 x 3 x 4 )(1 x)
sfsf
12
2.1母函数
例 求不定方程k1+k2+k3+k4=20的解数。其中, 限制k1可取0,2,4; k2可取1,3,5; k3可取6,7;k4可取8,9。
解:设不定方程k1+k2+k3+k4=k的解组数目为ck,本例中m=4, k=20。 注意到对ki(i=1,2,3,4)的限制,序列{ck}对应的生成函数为: G(x)=(1+x2+x4)(x+x3+x5)(x6+x7)(x8+x9)
母函数及其应用
sfsf
1
排列组合问题
sfsf
2
2.1母函数
定义2.1.1 对于数列{an},称无穷级数
G x an x n
n 0
为该数列的(普通型)母函数,简称普母函数或母函数。同时称 {an}为G(x)的生成数列。 例 有限数列C(n,r),r=0,1,2, …,n的普母函数是
n
sfsf
4
2.1母函数
sfs数
sfsf
7
2.1母函数
sfsf
8
2.1母函数
sfsf
9
2.1母函数
sfsf
10
2.1母函数
例 设有2个红球,1个黑球,1个白球,问 (1)共有多少种不同的选取方法,试加以枚举? (2)若每次从中任取3个,有多少种不同的取法? 解:设想用x,y,z分别代表红、黑、白三种球,两个红球的取 法与x0,x1,x2对应起来,即红球的可能取法与1+x+x2中x的 各次幂一一对应,亦即x0=1表示不取,x表示取1个红球,x2表 示取两个。对其它球,依此类推。则母函数 G(x,y,z) =(1+x+x2) (1+y) (1+z) =1+(x+y+z)+(x2+xy+xz+yz)+(x2y+x2z+xyz)+( x2yz) 若令x=y=z=1,就得所有不同的选取方案总数为 G(1,1,1) =1+3+4+3+1=12
g ( x) (1 x x ....)( 1 x x ...)
3 6 4 8
(1 x 2 x 4 ....)( 1 x 5 x10 ...) 1 1 1 1 3 2 4 5 1 x 1 x 1 x 1 x
sfsf
15
2.1母函数
sfsf 11
2.1母函数
例 设有2个红球,1个黑球,1个白球,问 (1)共有多少种不同的选取方法,试加以枚举? (2)若每次从中任取3个,有多少种不同的取法? 解:若只考虑每次取3个的方案数,而不需枚举,则令y=x,z =x,便有 G(x) = (1+x+x2) (1+x) (1+x) = 1+3x+4 x2+3 x3+ x4 由x3的系数即得所求方案数为3。
n
r C n , r x n 0
例 从n双互不相同的五指袜子中取出r只,要求没有任何两只是 成对的,共有多少种不同的取法?
r r C n , r 2 x 解:生成函数为: G( x ) (1 2 x)
n
n 0
sfsf
17
2.1母函数
例 某班有甲乙丙三个小组,人数分别为5,6,9。把5本相同的 书分给甲、乙、丙3个小组,再发到个人手上,每人最多发一本。 考虑将分给某组的某本书发给该组的同学A与将其发给同学B被 认为是不同的分法(每个同学最多一本),而且甲、乙两组最 少1本,甲组最多5本,乙组最多6本,丙组最少2本,最多9本, 问有多少种不同的分配方案? 解:
= (1+x2+x4)2(1+x)2x15 = (1 +x +x2 +x3 +x4 +x5)2x15 只需要多项式(1 +x +x2 +x3 +x4 +x5)2展开式中x5的系数就等于x20 的系数,由多项式定理:C20=6.
sfsf
14
2.1母函数
例 求不定方程3k1+4k2+2k3+5k4=n的非负整数解的个数。
5 6 9 4 5 6 9 5 6 9 5 6 9 5 1 1 2 x 1 1 3 1 2 2 2 1 2 x 5 6 9 20 5 6 9 x
0 1 2 2 n n Cn Cn x Cn x Cn x 1 x n
sfsf
3
2.1母函数
例 无限数列{1,1,…,1,…}的普母函数是
1 x x x
2
2
n
1 1 x
例 无限数列{1,2,…,n,…}的普母函数是
1 1 2 x 3 x (n 1) x 2 (1 x )
sfsf
18
2.1母函数
5 5 i 6 6 i 9 9 i G( x ) x x i x i i i 1 i 1 i 2
