高中数学公式大全指数与对数的幂运算与对数运算公式
方根、指数、幂、对数基本运算公式及全部推导公式

方根、指数、幂、对数基本运算公式及全部推导公式1.根式运算法则:(1) , ,;(2) ,,(ma =≥0)a =≥0,P ≠0)(5) ,0),,a m n N =≥∈其中2.指数运算法则:, , ,,,,(7)1(0)mm a aa-=≠, (8)1n a = (9)mn a =(10) d bdba c a c =⇔=3.对数运算法则:i 性质:若a >0且a≠1,则,, (3)零与负数没有对数,(4)log log 1a b b a ⨯= ⑥,(7)log log log 1a b c b c a ⨯⨯=ii 运算法则: 若a >0且a≠1,M >0,N >0,b >0且b≠1,n ∈R 则, ,, log log (,01)m n a a nb b a b m=>≠且 (4), log log n naa m m =, 1log log na a m m n=(5)换底公式 , a>0 a ≠1, b>0 b ≠1, N>0,(6)倒数公式 1log ,0,1log a b b a a a=>≠, b>0 b ≠1 (7) 十进制对数 10log lg N N = , l g 10xN x N =⇔=(8)自然对数 log e N InN = , x InN x e N =⇔= , 1lim(1) 2.71828...n n e n→∞=+≈4.指数与对数式的恒等变形:;。
5、指数方程和对数方程解题:()(1)()log ,log ()()(f x b a a a b f x b f x b f x a =⇔==⇔=定义法)()()(2)()(),log ()log ()()()0(f x g x a a a a f x g x f x g x f x g x =⇔==⇔=>转化法) ()()(3)b ()log ()log ,f x g x m m a f x a g x b =⇔=(取对数法)()(4)log log ()log ()log ()/log ,f x a b a a a g x f x g x b =⇔=(换底法)6、理解对数①两种log a b 理解方法1、表示a 的“指数”,这个指数能让a 变成b 。
新高中数学之新高考数学公式大全

焦距 离心率
焦点 长轴长:
|F1F2|=2c e=ac(0<e<1) F1(-c,0),F2(c,0)
长轴长:2a,
焦距 离心率 渐近线 实轴长
|F1F2|=2c
e=ac ( e 1)
y=±bax
2a
焦点到渐近线的距离:b
短轴长:
短轴长:2b
椭圆离心率: 常用的三角函数值
度 0°
弧度 0
sin α 0
F0,-2p
y=p2 |PF|=-y0+p2
椭圆定义 标准方程 a,b,c
|MF1|+|MF2|=2a ax22+by22=1(a>b>0)
c2=a2-b2
双曲线定义 标准方程 a,b,c
|MF1-MF2|=2a ax22-by22=1(a>0,b>0)
c2=a2+b2
结论
通径:
2b2 a
短轴到焦点的距离:a
古典概率 5分
第 4 页 (共 4 页)
公式三: sin(-α)=-sin α
公式四: sin(π-α)=sin α
公式五: 公式六:
sinπ2-α=cos α sinπ2+α=cos α
cos(α+k·2π)=cos α(k∈Z) tan(α+k·2π)=tan α(k∈Z)
cos (π+α)=-cos α
tan(π+α)=tanα
cos (-α)=cos α
sin 2α=2sinαcosα
降次公式:
cos 2α=cos2α-sin2α cos2α=1+c2os 2α
cos 2α=2cos2α-1 sin2α=1-c2os 2α
cos 2α=1-2sin2α sin αcos α=12sin 2α
指数对数和幂函数(思维导图)
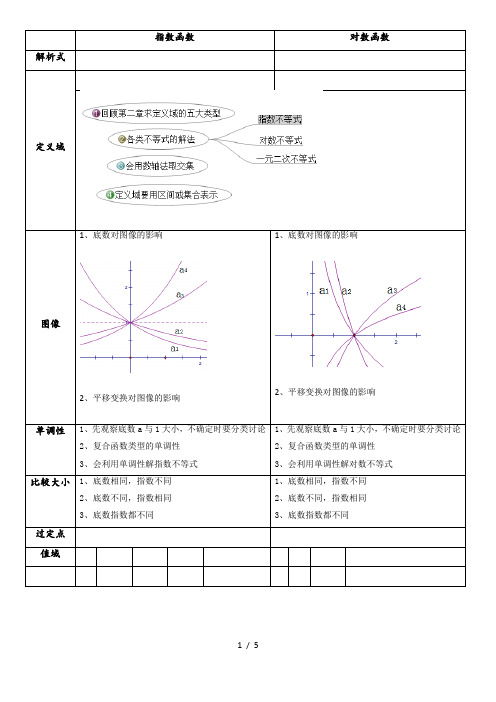
1、底数对图像的影响2、平移变换对图像的影响1、底数对图像的影响2、平移变换对图像的影响1、先观察底数a 与1大小,不确定时要分类讨论 1、先观察底数a 与1大小,不确定时要分类讨论(六)指数函数1.幂的有关概念正整数指数幂:=⋅⋅na a a a n a ; 零指数幂:0a =1( ) ;负整数指数幂:p a -= (0,a p N +≠∈);正分数指数幂:mna = (0,1a m n N n +>∈>、且);负分数指数幂:m na -=(0,1a m n N n +>∈>、且);0的正分数指数幂等于 ,0的负分数指数幂 2.幂的运算法则(0,0,a b r s Q >>∈、)r s a a = ;()r s a = ;()r ab =3.指数函数图像及性质4.指数函数()x f x a =具有性质:()()()(),1(0,1)f x y f x f y f a a a +==>≠ (七)对数函数1.定义:如果)1,0(≠>a a a 且的b 次幂等于N ,就是b a N =,那么数b 称以a 为底N 的对数,记作log a b N =,其中a 称对数的底,N 称真数.①以10为底的对数称常用对数,N 10log 记作N lg ,②以无理数( 2.71828)e e =为底的对数称自然对数,N e log 记作N ln 2.基本性质:①真数N 为正数(负数和零无对数), ②log 10a =, ③log 1a a =,④对数恒等式:log a N a N =.3.运算性质:如果,0,0,1,0>>≠>N M a a 则 ①log ()log log a a a MN M N =+; ②log log log a a a M M N N=-;③log log na a M n M =. 4.换底公式:log log log m a m NN a=(0,1,0,1,0),a a m m N >≠>≠> ①log log 1a b b a ⋅=, ②log log m n a a nb b m=.5. 对数函数x y a log =具有性质: )()()(xy f y f x f =+6.函数的图像与性质(八)幂函数:,y x =2y x =3,y x =1y x=12y x =的图像1.当0a >时,幂函数()y x R αα=∈有下列时图像为 型抛物线,图像下凸,01α<<时图像为 型抛物线,图像上凸. (2)图像都通过点 ; (3)在第一象限内,随x 的 ; 2.当a<0时,幂函数()y x R αα=∈有下列性质:(1)在第一象限内,函数图像为 型,函数值随x 的增大而 ,图像是向下凸; (2)图像都通过点 ;(3)在第一象限内,图像向上与y 轴无限地接近,向右与x 轴无限地接近;。
指数和对数的运算法则及公式推导

指数和对数的运算法则及公式推导在咱们的数学世界里,指数和对数就像是一对调皮又神奇的小伙伴,它们有着自己独特的运算法则和公式。
这些法则和公式可不是凭空出现的,而是经过了数学家们的精心推导和琢磨才得来的。
先来说说指数。
咱们假设一个指数表达式,比如说 2 的 3 次方,这表示的是 2 乘以自己 3 次,也就是 2×2×2 = 8 。
那如果是 2 的 -2 次方呢?这可就有点意思啦,它等于 1 除以 2 的 2 次方,也就是 1/4 。
再讲讲指数的运算规则。
比如同底数幂相乘,底数不变,指数相加。
就像 2 的 3 次方乘以 2 的 4 次方,等于 2 的 7 次方。
这就好比你有 3堆苹果,每堆 2 个,又有 4 堆苹果,每堆也是 2 个,加在一起不就是 7 堆,每堆 2 个嘛。
接着咱们聊聊对数。
对数其实就是指数的逆运算。
如果 2 的 3 次方等于 8 ,那么以 2 为底 8 的对数就是 3 。
就好像你知道了结果和底数,要反推出指数是多少。
说到对数的运算规则,也有不少有趣的地方。
比如对数的加法,以a 为底 M 的对数加上以 a 为底 N 的对数,等于以 a 为底 M×N 的对数。
这就好比把两个相关的东西合并起来一起计算。
还记得我上学那会,有一次数学考试,就专门考了指数和对数的运算。
当时有一道题,是让计算以 3 为底 27 的对数乘以以 3 为底 9 的对数。
我一开始有点懵,后来静下心来,想到以 3 为底 27 是 3 ,以 3 为底 9 是 2 ,那它们相乘不就是 6 嘛。
那次考试让我深刻体会到,只要把这些运算法则和公式掌握好,再难的题目也能迎刃而解。
咱们来推导一下指数和对数的一些公式。
比如说,a 的 m 次方的 n 次方,就等于 a 的 m×n 次方。
这很好理解,你想啊,m 次方表示乘 m 次,再 n 次方就是在原来的基础上再乘 n 次,那不就一共乘了 m×n 次嘛。
指数函数公式运算法则

指数函数公式运算法则指数函数是一种常见的数学函数,其公式形式为f(x) = a^x,其中a为底数,x为指数。
指数函数在数学中有着广泛的应用,因此掌握指数函数的运算法则对于解决实际问题具有重要意义。
本文将介绍指数函数的运算法则,包括指数函数的加减乘除、指数函数的幂函数、指数函数的对数函数等内容。
一、指数函数的加减乘除1. 指数函数的加法当两个指数函数相加时,如果它们的底数相同,则可以将它们的指数相加,即a^x + a^y = a^(x+y)。
例如,2^3 + 2^4 =2^(3+4) = 2^7。
2. 指数函数的减法同样地,当两个指数函数相减时,如果它们的底数相同,则可以将它们的指数相减,即a^x - a^y = a^(x-y)。
例如,3^5 - 3^3 = 3^(5-3) = 3^2。
3. 指数函数的乘法当两个指数函数相乘时,如果它们的底数相同,则可以将它们的指数相加,即(a^x) * (a^y) = a^(x+y)。
例如,2^3 * 2^4 =2^(3+4) = 2^7。
4. 指数函数的除法当两个指数函数相除时,如果它们的底数相同,则可以将它们的指数相减,即(a^x) / (a^y) = a^(x-y)。
例如,3^5 / 3^3 =3^(5-3) = 3^2。
二、指数函数的幂函数指数函数的幂函数是指数函数的一种特殊形式,其公式为f(x) = (a^x)^n,其中a为底数,x为指数,n为幂次。
当计算指数函数的幂函数时,可以将指数函数的指数与幂次相乘,即(a^x)^n =a^(x*n)。
例如,(2^3)^2 = 2^(3*2) = 2^6。
三、指数函数的对数函数指数函数的对数函数是指数函数的逆运算,其公式为y =log_a(x),其中a为底数,x为指数,y为对数。
对数函数的作用是求解指数函数的指数,即log_a(x) = y 等价于 a^y = x。
例如,log_2(8) = 3 等价于 2^3 = 8。
指数与对数的运算公式

指数与对数的运算公式一个数的指数代表把多少个这个数乘在一起。
例子: 23= 2 × 2 × 2 = 8(3个 2 乘在一起得到 8)什么是对数?对数与指数相反。
它是这个问题的答案:"什么指数会得到这个结果?":这问题的答案是:用以上的例子:•指数用 2 和 3 来得到 8(2乘3次为8)•对数用 2 和 8 来得到 3(2 成为 8,当把3个2乘在一起时)对数的意思是:用几个数与自己乘在一起会得到另一个数所以对数的答案是指数:(去这里看看指数、根和对数的关系。
)一起用指数与对数时常用在一起,因为它们的效果是"相反"的(但底"a"要相同):指数与对数互为"反函数"先做一个,然后做另一个,就还原了:但光看名字不能猜到它们是相反的……你可以这样想:a x"向上",log a(x) "向下":•向上走,然后向下走,你回到原处:向下(向上p(x)) = x,•向下走,然后向上走,你回到原处:向上(向下(x)) = x 无论如何,重点是:指数函数可以"还原"对数函数的效果。
.(反过来也一样)看这个例子:举例: log3(x) = 5,x 是什么?我们可以用以3为底的指数来"还原"对数:再来一个:对数的特性对数的其中一个强大功能是把乘变成加。
log a( m × n ) = log a m + log a n"乘的对数是对数的和"为什么是这样?看附注。
用这特性和指数定律,我们得到以下有用的特性:log a(m × n) = log a m + log a n乘的对数是对数的和log a(m/n) = log a m - log a n除乘的对数是对数的差log a(1/n) = -log a n 这是以上"除"特性的结果,因为 log a(1) = 0log a(m r) = r ( log a m )m的r次幂的对数是r 和m的对数的积记着:底 "a" 一定要相同!历史:以前没有计算器时,对数非常有用……例如,要乘两个很大的数,你可以用对数来把乘变为加(容易得多!)以前甚至有专门为此而设的对数表书。
指数与对数恒等变形公式
指数与对数恒等变形公式
摘要:
一、引言
二、指数恒等式
1.指数幂的运算法则
2.常用指数恒等式
三、对数恒等式
1.对数的性质
2.常用对数恒等式
四、指数与对数之间的关系
五、总结
正文:
一、引言
指数与对数是数学中非常基础的概念,它们在数学、物理、化学、生物等多个领域都有着广泛的应用。
理解并掌握指数与对数的恒等变形公式,对于深入研究相关领域的知识有着重要的作用。
二、指数恒等式
1.指数幂的运算法则
指数幂的运算法则主要包括:幂的乘方、积的乘方、幂的除法、幂的加法与减法等。
这些法则为指数恒等式的推导和应用提供了基础。
2.常用指数恒等式
常用的指数恒等式包括:自然指数函数的恒等式、复数指数函数的恒等式、对数函数的指数恒等式等。
这些恒等式有助于简化复杂数学问题的计算。
三、对数恒等式
1.对数的性质
对数具有以下几个基本性质:单调性、可逆性、乘法公式、除法公式、幂与对数的关系等。
这些性质为对数恒等式的推导和应用提供了基础。
2.常用对数恒等式
常用的对数恒等式包括:自然对数函数的恒等式、复数对数函数的恒等式、指数函数的对数恒等式等。
这些恒等式有助于简化复杂数学问题的计算。
四、指数与对数之间的关系
指数与对数之间有着密切的关系,它们互为反函数。
通过指数与对数的恒等变形公式,我们可以更方便地计算出指数与对数之间的转换。
五、总结
指数与对数的恒等变形公式在数学计算中有着广泛的应用。
对数指数函数公式
对数指数函数公式对数函数和指数函数是高中数学中非常重要的两类函数。
指数函数是形如y=a^x的函数,其中a为常数且a>0且a≠1,x为自变量,y为因变量;对数函数是指在指数函数y=a^x中的三个参数a、x、y中的一个固定不变的量,若固定其中的a和x,求出使得y=a^x的x,那么我们称这个x为以a为底的对数,记作x=loga y。
下面我们分别对指数函数和对数函数进行详细的介绍。
一、指数函数:指数函数是一种自变量在连续变化时,因变量按照指数规律随之变化的函数。
指数函数的一般式为y=a^x,其中a为底数,x为指数,a>0且a≠11.指数的定义和性质:指数函数中,a的取值范围与loga x存在一一对应关系,也就是a 的取值范围应该是(0,∞)。
当a=1时,指数函数简化为y=1^x=1,这是一个常值函数。
指数函数的性质如下:①当x=0时,指数函数的值为a^0=1,即指数函数在x=0处的函数值为1②当x<0时,指数函数的值为a^x=1/a^,x,即指数函数在x<0时的函数值为倒数。
③当x>0时,指数函数随着x的增大,函数值也随之增大,且增长速度越来越快。
2.指数函数的图像:指数函数的图像可以用以下性质来描述:①当a>1时,随着x的增大,函数值也随之增大,且增长速度越来越快。
这种函数的图像呈现递增趋势,且图像越来越陡峭。
②当0<a<1时,随着x的增大,函数值也随之减小,且减小速度越来越快。
这种函数的图像呈现递减趋势,且图像越来越平缓。
③当a=1时,指数函数的图像为一条水平直线,即y=1二、对数函数:对数函数是指在指数函数y=a^x中的三个参数a、x、y中的一个固定不变的量,求出使得y=a^x的x,那么我们称这个x为以a为底的对数,记作x=loga y。
1.对数的定义和性质:对数函数的定义如下:对于任意的正数a(a>0且a≠1),b(b>0),整数n,称n为以a为底的对数,记作n=loga b,当且仅当a的n次幂等于b。
指数函数与对数函数的幂次运算与对数运算
指数函数与对数函数的幂次运算与对数运算在数学中,指数函数与对数函数是重要且常见的函数类型。
它们在各个领域的应用广泛,包括科学、工程、经济等。
本文将探讨指数函数与对数函数的幂次运算与对数运算,通过详细解释和实际应用案例来阐述其重要性和应用价值。
一、指数函数的幂次运算指数函数是自变量为指数的函数,通常形式为 y = a^x,其中 a 为底数,x 为指数。
在指数函数中,幂次运算是一种常见的运算方式,旨在计算同一底数不同指数的幂次值。
举个例子,考虑指数函数 y = 2^x,我们希望计算 2 的不同指数的幂次:- 当 x = 1 时,2 的幂次为 2^1 = 2;- 当 x = 2 时,2 的幂次为 2^2 = 4;- 当 x = 3 时,2 的幂次为 2^3 = 8。
通过这些计算可以看出,随着指数 x 的增大,2 的幂次也呈现出指数级的增长趋势。
这种幂次运算在许多领域中都有广泛的应用,例如在金融领域中的复利计算、在物理学中的指数衰减等。
二、对数函数的幂次运算对数函数是指数函数的逆运算,用于求解以指数形式给出的幂次运算。
常见的对数函数有自然对数函数 ln(x) 和常用对数函数 log(x)。
对于对数函数的幂次运算,我们可以通过以下示例来说明。
- 考虑自然对数函数 ln(x),我们希望计算 ln(e^x) 这一幂次运算。
根据对数与指数函数的逆运算关系,可以得知 ln(e^x) 的结果应当为 x。
- 同样地,对于常用对数函数log(x),我们可以计算log(10^x) 的值。
根据对数与指数函数的逆运算关系,可以得知 log(10^x) 的结果同样为x。
这些示例显示了对数函数的幂次运算与指数函数的幂次运算是互为逆运算的关系。
对数函数的幂次运算在数学和工程学中具有广泛的应用,例如在信号处理中的功率计算、在经济学中的复利计算等。
三、指数运算与对数运算的应用案例1. 金融领域中的复利计算在金融领域中,指数函数与对数函数的幂次运算与对数运算被广泛用于计算复利。
指数函数与对数函数的指数运算与对数运算
指数函数与对数函数的指数运算与对数运算指数函数与对数函数是数学中常见的函数类型,它们在数学和科学领域中有广泛的应用。
本文将讨论指数函数和对数函数的指数运算与对数运算的性质和应用。
一、指数函数的指数运算指数函数是以自然常数e为底的幂函数,其一般形式为f(x) = a^x,其中a为底数,x为指数。
指数函数的指数运算有以下几个重要性质:1. 乘法性质:a^m * a^n = a^(m + n),同一底数的指数相加等于指数的乘积。
2. 除法性质:(a^m) / (a^n) = a^(m - n),同一底数的指数相减等于指数的商。
3. 幂次性质:(a^m)^n = a^(m * n),幂的幂等于指数的乘积。
4. 负指数性质:a^(-n) = 1 / (a^n),负指数等于倒数。
5. 零指数性质:a^0 = 1,任何数的0次方都等于1。
基于这些性质,我们可以进行各种复杂的指数运算。
例如,计算2^3 * 2^4,根据乘法性质,我们可以合并指数,得到2^(3+4)=2^7=128。
又如,计算(5^2)^3,根据幂次性质,我们可以进行指数的乘法运算,得到5^(2*3)=5^6=15625。
指数函数的指数运算在科学计算、金融领域、物理学等方面都有重要应用。
例如,计算复利利息、求解微分方程、描述放射性衰变等都需要运用指数函数的指数运算。
二、对数函数的对数运算对数函数是指数函数的逆运算,表示为y = logₐx,其中a为底数,x 为真数,y为对数。
对数函数的对数运算具有以下几个基本性质:1. 对数乘法性质:logₐ(x * y) = logₐx + logₐy,对数的乘法等于对数的和。
2. 对数除法性质:logₐ(x / y) = logₐx - logₐy,对数的除法等于对数的差。
3. 对数幂次性质:logₐ(x^k) = k * logₐx,对数的幂次等于指数乘以对数。
基于这些性质,我们可以进行各种复杂的对数运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学公式大全指数与对数的幂运算与对
数运算公式
数学是一门具有广泛应用的学科,不论是在学术研究还是实际生活中,数学公式都扮演着重要的角色。
在高中数学中,指数与对数是两
个重要的概念,它们的公式在解题过程中经常被用到。
本文将为您提
供高中数学公式大全,重点介绍指数与对数的幂运算与对数运算公式。
1. 指数与幂运算公式
指数与幂运算是指数函数的基本运算法则,它包括以下几个公式:
1.1 指数幂运算法则
(1)指数相同,底数相乘:a^m × a^n = a^(m+n)。
例子:2^3 × 2^4 = 2^(3+4) = 2^7。
(2)幂相同,底数相乘:a^m × b^m = (a × b)^m。
例子:2^3 × 3^3 = (2 × 3)^3 = 6^3。
(3)指数的乘方:(a^m)^n = a^(m×n)。
例子:(2^3)^4 = 2^(3×4) = 2^12。
(4)幂的乘方:(a × b)^m = a^m × b^m。
例子:(2 × 3)^4 = 2^4 × 3^4 = 16 × 81。
1.2 指数的乘法法则
(1)指数相加:a^m × a^n = a^(m+n)。
例子:2^3 × 2^4 = 2^(3+4) = 2^7。
(2)底数相乘:(a × b)^m = a^m × b^m。
例子:(2 × 3)^4 = 2^4 × 3^4 = 16 × 81。
2. 对数运算公式
对数是指数的逆运算,它有以下几个重要的运算公式:
2.1 对数幂运算法则
(1)底数相同,幂相加:loga(x × y) = loga(x) + loga(y)。
例子:log2(4 × 8) = log2(4) + log2(8)。
(2)幂的乘方:loga(x^m) = m × loga(x)。
例子:log2(4^3) = 3 × log2(4)。
2.2 对数的乘法法则
(1)底数相同,幂相乘:loga(x × y) = loga(x) + loga(y)。
例子:log2(4 × 8) = log2(4) + log2(8)。
(2)幂的乘方:loga(x^m) = m × loga(x)。
例子:log2(4^3) = 3 × log2(4)。
综上所述,指数与对数的幂运算与对数运算公式是高中数学中的重
要内容。
熟练掌握这些公式,对于解题和理解数学概念都有巨大帮助。
在学习数学的过程中,我们需要不断运用这些公式,加深理解,并能够熟练灵活地运用到实际问题中。
希望本文所提供的公式能够帮助到您的学习和应用。
