高考备考计算题规范化训练(08)
2020高考数学二轮复习80分小题精准练8理

80分小题精准练(八)(建议用时:50分钟)一、选择题:本题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知i为虚数单位,若复数z=错误!(a∈R)的实部与虚部相等,则a的值为()A.2 B.32C.错误!D.-2C[∵z=错误!=错误!=错误!+错误!i的实部与虚部相等,∴4-a=2a+2,即a=23。
故选C.]2.已知集合A={x|x2-2x>0},B={x|-2<x<3},则( )A.A∩B=B.A∪B=RC.B⊆A D.A⊆BB[A={x|x>2或x<0},B={x|-2<x<3},所以A∩B={x|-2<x<0或2<x<3},A∪B=R,故选项B正确.]3.已知矩形ABCD中,BC=2AB=4,现向矩形ABCD内随机投掷质点M,则满足错误!·错误!≥0的概率是()A。
错误! B.错误!C.π2D.错误!B[建立如图所示的直角坐标系,则B(0,0),C(4,0),A(0,2),D(4,2).设M(x,y),则错误!=(-x,-y),错误!=(4-x,-y),由错误!·错误!≥0得(x-2)2+y2≥4,由几何概型概率公式得:p=错误!=1-错误!=错误!,故选B.]4.设等差数列{a n}的前n项和为S n,若a1+a3=6,S10=100,则a5=( )A.8 B.9C.10 D.11B[设等差数列{a n}的公差为d,∵a1+a3=6,S10=100,∴2a1+2d=6 ,10a1+错误!d=100,联立解得a1=1,d=2。
则a5=1+2×4=9。
故选B.]5.根据如下样本数据x34567y 4.02。
-0.5-错误!错误!错误!错误!。
9,则x每增加1个单位,y就()A.增加1。
4个单位B.减少1。
4个单位C.增加1。
2个单位D.减少1.2个单位B[设变量x,y的平均值为:错误!,错误!,∴错误!=错误!(3+4+5+6+7)=5,错误!=错误!(4.0+2.5-0.5+0。
高中数学2008年高考真题精品解析阶段测试同步训练试题700

高中数学2008年高考真题精品解析阶段测试同步训练试题2019.091,设集合{}{}{}1,2,3,4,5,1,2,3,2,3,4U A B ===,则()U A B =ð( ) (A){}2,3(B){}1,4,5(C){}4,5(D){}1,5 2,复数()221i i +=( )(A)4-(B)4(C)4i -(D)4i3,()2tan cot cos x x x +=( )(A)tan x (B)sin x (C)cos x (D)cot x4,直线3y x =绕原点逆时针旋转090,再向右平移1个单位,所得到的直线为( )(A)1133y x =-+(B)113y x =-+(C)33y x =-(D)113y x =+5,若02,sin απαα≤≤>,则α的取值范围是:( )(A),32ππ⎛⎫ ⎪⎝⎭ (B),3ππ⎛⎫ ⎪⎝⎭ (C)4,33ππ⎛⎫ ⎪⎝⎭ (D)3,32ππ⎛⎫ ⎪⎝⎭6,从甲、乙等10个同学中挑选4名参加某项公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有( ) (A)70种(B)112种(C)140种(D)168种7,已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是( ) (A)(],1-∞- (B)()(),01,-∞+∞(C)[)3,+∞ (D)(][),13,-∞-+∞ 8,设,M N 是球心O 的半径OP 上的两点,且NP MN OM ==,分别过,,N M O 作垂线于OP 的面截球得三个圆,则这三个圆的面积之比为:( ) (A)3,5,6(B)3,6,8(C)5,7,9(D)5,8,99,设直线l ⊂平面α,过平面α外一点A 与,l α都成030角的直线有且只有:( )(A)1条(B)2条(C)3条(D)4条10,设()()sin f x x ωϕ=+,其中0ω>,则()f x 是偶函数的充要条件是( ) (A)()01f =(B)()00f =(C)()'01f =(D)()'00f =11,设定义在R 上的函数()f x 满足()()213f x f x ⋅+=,若()12f =,则()99f =( )(A)13 (B)2 (C)132 (D)21312,已知抛物线2:8C y x =的焦点为F ,准线与x 轴的交点为K ,点A 在C 上且AK =,则AFK ∆的面积为( )(A)4 (B)8 (C)16 (D)3213,设集合|0{8}x x N U =∈<≤,{1,2,4,5}S =,{3,5,7}T =,则()U S T =ð (A ){1,2,4}(B ){1,2,3,4,5,7} (C ){1,2} (D ){1,2,4,5,6,8}14,设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x ,则目标函数y x z +=5的最大值为(A )2 (B )3 (C )4 (D )515,函数1y =+04x ≤≤)的反函数是(A )2(1)y x =-(13x ≤≤) (B )2(1)y x =-(04x ≤≤) (C )21y x =-(13x ≤≤) (D )21y x =-(04x ≤≤ )16,若等差数列{}n a 的前5项和525S =,且23a =,则7a = (A )12 (B )13 (C )14 (D )1517,设b a ,是两条直线,βα,是两个平面,则b a ⊥的一个充分条件是 (A )βαβα⊥⊥,//,b a (B )βαβα//,,⊥⊥b a (C )βαβα//,,⊥⊂b a (D )βαβα⊥⊂,//,b a18,把函数sin y x =(x R ∈)的图象上所有点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是(A )sin(2)3y x π=-,x R ∈(B )sin()26x y π=+,x R ∈ (C )sin(2)3y x π=+,x R ∈ (D )sin(2)32y x π=+,x R ∈19,设椭圆22221x y m n +=(0m >,0n >)的右焦点与抛物线28y x =的焦点相同,离心率为12,则此椭圆的方程为(A )2211216x y +=(B )2211612x y += (C )2214864x y += (D )2216448x y +=20,已知函数2,0()2,0x x f x x x +⎧=⎨-+>≤⎩,则不等式2()f x x ≥的解集是(A )[1,1]- (B )[2,2]- (C )[2,1]- (D )[1,2]-试题答案1, 【解】:∵{}{}1,2,3,2,3,4A B == ∴{}2,3A B = 又∵{}1,2,3,4,5U = ∴(){}1,4,5U A B =ð 故选B 2, 【解】:∵()()222121212244i i i i i i i +=+-=⨯==- 故选A3, 【解】:∵()22222sin cos sin cos tan cot cos cos cos cos sin sin cos x x x x x x x x x x x x x +⎛⎫+=+=⋅ ⎪⎝⎭ cos cot sin xx x == 故选D4, 【解】:∵直线3y x =绕原点逆时针旋转090的直线为13y x =-,从而淘汰(C),(D )又∵将13y x =-向右平移1个单位得()113y x =--,即1133y x =-+故选A 5,【解】:∵sin αα>∴sin 0αα> ,即12sin 2sin 0223πααα⎛⎫⎛⎫-=-> ⎪ ⎪ ⎪⎝⎭⎝⎭又∵02απ≤≤ ∴5333πππα-≤-≤,∴03παπ≤-≤ ,即4,33x ππ⎛⎫∈ ⎪⎝⎭ 故选C6, 【解】:∵从10个同学中挑选4名参加某项公益活动有410C 种不同挑选方法;从甲、乙之外的8个同学中挑选4名参加某项公益活动有48C 种不同挑选方法;∴甲、乙中至少有1人参加,则不同的挑选方法共有4410821070140C C -=-=种不同挑选方法 故选C7, 【解1】:∵等比数列()n a 中21a = ∴当公比为1时,1231a a a ===,33S = ;当公比为1-时,1231,1,1a a a =-==-,31S =- 从而淘汰(A)(B)(C)故选D ;【解2】:∵等比数列()n a 中21a = ∴312321111S a a a a q q q q ⎛⎫=++=++=++⎪⎝⎭ ∴当公比0q >时,31113S q q =++≥+=;当公比0q <时,31111S q q ⎛⎫=---≤-=- ⎪⎝⎭∴(][)3,13,S ∈-∞-+∞ 故选D8, 【解】:设分别过,,N M O 作垂线于OP 的面截球得三个圆的半径为123,,r r r ,球半径为R ,则:22222222222212325182,,39393r R R R r R R R r R R R ⎛⎫⎛⎫⎛⎫=-==-==-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ∴222123::5:8:9r r r = ∴这三个圆的面积之比为:5,8,9故选D9,【解】:如图,和α成030角的直线一定是以A 为顶点的圆锥的母线所在直线,当030ABC ACB ∠=∠=,直线,AC AB 都满足条件 故选B10, 【解】:∵()()sin f x x ωϕ=+是偶函数∴由函数()()sin f x x ωϕ=+图象特征可知0x =必是()f x 的极值点, ∴()'00f = 故选D11, 【解】:∵()()213f x f x ⋅+=且()12f = ∴()12f =,()()1313312f f ==,()()13523f f ==,()()1313752f f ==,()()13925f f ==,,∴()221132n f n n ⎧⎪-=⎨⎪⎩为奇数为偶数,∴()()1399210012f f =⨯-=故选C12,【解】:∵抛物线2:8C y x =的焦点为()20F ,,准线为2x =- ∴()20K -,设()00A x y ,,过A 点向准线作垂线AB ,则()02B y -,∵AK =,又()0022AF AB x x ==--=+ ∴由222BK AK AB =-得()22002y x =+,即()20082x x =+,解得()24A ±,∴AFK ∆的面积为01144822KF y ⋅=⨯⨯= 故选B13, 解析:因为{1,2,4,6,8}T U =ð,所以(){1,2,4}U S T =ð,选A .14,解析:如图,由图象可知目标函数y x z +=5过点(1,0)A 时z 取得最大值,max 5z =,选D .15, 解析:当04x ≤≤时,[,3]11+,解1y =+12()(1)f x x -=-,选A .16, 解析:1524545()5()722a a a a S a ++==⇒=,所以4272255132a aa a d a -=+=+⋅=,选B.17, 解析:选C ,A 、B 、D 的反例如图18, 解析:选C,132sin sin()sin(2)33y x y x y x πππ=−−−−−−→=+−−−−−−−→=+向左平移个单位横坐标缩短到原来的倍.19, 解析:抛物线的焦点为(2,0),椭圆焦点在x 轴上,排除A 、C ,由12e =排除D ,选B .20, 解析:依题意得221100001122x x x x x x x x x ⎧⎧≤>≤≤<≤⇒≤≤+≥-+≥⇒--⎨⎨⎩⎩或或,选A .。
高中数学2008年高考真题精品解析阶段测试同步训练试题1080

高中数学2008年高考真题精品解析阶段测试同步训练试题2019.091,设函数32()2f x x x x =--+. (Ⅰ)求()f x 的单调区间和极值;(Ⅱ)若当[1,2]x ∈-时,3()3af x -≤≤,求a b -的最大值.2,在△ABC 中,内角,,A B C 对边的边长分别是,,a b c ,已知2222a c b +=。
(Ⅰ)若4B π=,且A 为钝角,求内角A 与C 的大小; (Ⅱ)若2b =,求△ABC 面积的最大值。
3,一条生产线上生产的产品按质量情况分为三类:A 类、B 类、C 类。
检验员定时从该生产线上任取2件产品进行一次抽检,若发现其中含有C 类产品或2件都是B 类产品,就需要调整设备,否则不需要调整。
已知该生产线上生产的每件产品为A 类品,B 类品和C 类品的概率分别为0.9,0.05和0.05,且各件产品的质量情况互不影响。
(Ⅰ)求在一次抽检后,设备不需要调整的概率;(Ⅱ)若检验员一天抽检3次,以ξ表示一天中需要调整设备的次数,求ξ的分布列和数学期望。
4,如图,一张平行四边形的硬纸片0ABC D 中,1AD BD ==,AB =它的对角线BD 把△0BDC 折起,使点0C 到达平面0ABC D 外点C 的位置。
(Ⅰ)证明:平面0ABC D ⊥平面0CBC ;(Ⅱ)如果△ABC 为等腰三角形,求二面角A BD C --的大小。
5,在数列{}n a 中,11a =,2112(1)n n a a n +=+。
(Ⅰ)求{}n a 的通项公式;(Ⅱ)令112n n nb a a +=-,求数列{}n b 的前n 项和n S 。
(Ⅲ)求数列{}n a 的前n 项和n T 。
6,已知椭圆1C 的中心和抛物线2C 的顶点都在坐标原点O ,1C 和2C 有公共焦点F ,点F 在x 轴正半轴上,且1C 的长轴长、短轴长及点F 到1C 右准线的距离成等比数列。
(Ⅰ)当2C 的准线与1C 右准线间的距离为15时,求1C 及2C 的方程; (Ⅱ)设过点F 且斜率为1的直线l 交1C 于P ,Q 两点,交2C 于M ,N 两点。
高中数学2008年高考真题精品解析阶段测试同步训练试题980
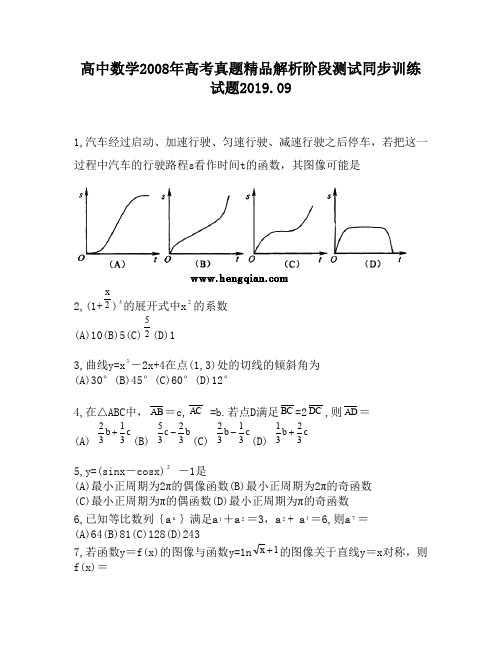
高中数学2008年高考真题精品解析阶段测试同步训练试题2019.091,汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是2,(1+2x)5的展开式中x 2的系数(A)10(B)5(C)52(D)13,曲线y=x 3-2x+4在点(1,3)处的切线的倾斜角为 (A)30°(B)45°(C)60°(D)12°4,在△ABC 中,AB =c,AC =b.若点D 满足BC =2DC ,则AD =(A) c b 3132+(B) b c 3235-(C) cb 3132-(D)c b 3231+5,y=(sinx -cosx)2-1是(A)最小正周期为2π的偶像函数(B)最小正周期为2π的奇函数 (C)最小正周期为π的偶函数(D)最小正周期为π的奇函数 6,已知等比数列{a n }满足a 1+a 2=3,a 2+ a 3=6,则a 7= (A)64(B)81(C)128(D)2437,若函数y =f(x)的图像与函数y=1n 1+x 的图像关于直线y =x 对称,则f(x)=(A)22e-x (B) x 2e (C) 12e+x (D) 22e+x8,为得到函数y=cos(x+3π)的图像,只需将函数y=sinx 的图像(A)向左平移6π个长度单位(B)向右平移6π个长度单位(C)向左平移65π 个长度单位(D)向右平移65π个长度单位9,若直线b y a x +=1与图122=+y x 有公共点,则 (A)122≤+b a (B) 122≥+b a (C)11122≤+b a (D) 11122≥+b a10,已知三棱柱ABC -111C B A 的侧棱与底面边长都相等,1A 在底面ABC 内的射影为△ABC 的中心,则A 1B 与底面ABC 所成角的正弦值等于(A)31(B)32 (C) 33(D) 3211,将1,2,3填入3×3的方格中,要求每行、第列都没有重复数字,下面是一种填法,则不同的填写方法共有(A)6种(B)12种 (C)24种(D)48种12,设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤( )A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,13,设a b ∈R ,且0b ≠,若复数3()a bi +是实数,则( )A .223b a =B .223a b =C .229b a =D .229a b =14,函数1()f x x x =-的图像关于( )A .y 轴对称B . 直线x y -=对称C . 坐标原点对称D . 直线x y =对称15,若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <c B .c <a <b C . b <a <c D . b <c <a16,设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值( )A .2-B .4-C .6-D .8-17,从20名男同学,10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为( )A .929B .1029C .1929D .202918,64(1(1-的展开式中x 的系数是( )A .4-B .3-C .3D .419,若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则MN 的最大值为( ) A .1BCD .220,设1a >,则双曲线22221(1)x y a a -=+的离心率e 的取值范围是( )A.2)B.C .(25),D.(2试题答案1, A本题主要考查了导数的几何意义即为切线斜率的几何意义。
山东省2013高考实验班备考理综物理计算题规范化训练08

2013高考备考理综计算题规范化训练(8)开始时刻:___:____日期:______姓名:____22.(15分)如图所示,在水平轨道右侧安放半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l;水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态。
小物块A静止放置在弹簧右端,A与弹簧接触但不拴接;小物块B从轨道右侧以初速度v0冲上轨道,通过圆形轨道、水平轨道后与物块A 发生对心碰且瞬间粘连,碰撞之后A、B一起运动的速度为碰撞前物块B速度的一半,之后压缩弹簧并被弹簧以原速率弹回,经水平轨道返回圆形轨道。
物块A、B均可视为质点。
已知R=0.2m,l=1.0m,v0=6m/s,物块A、B质量均为m=1kg,与PQ段间的动摩擦因数均为μ=0.2,轨道其他部分摩擦不计。
取g=10m/s2。
求:(1)物块B与物块A碰撞前速度大小;(2)物块B与物块A碰后返回到圆形轨道的高度;(3)调节PQ段的长度l,B仍以v0从轨道右侧冲上轨道,当l满足什么条件时,A、B物块能返回圆形轨道且能23.(18分)如图甲所示,水平直线MN下方有竖直向上的匀强电场,场强E10 4 N/C。
现将一重力不106 C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。
(1)求电荷进入磁场时的速度v0;(2)求图乙中t=2×10-5s时刻电荷与P点的距离;解:(1)物块B 冲上圆形轨道后回到最低点速度为v 0=6m/s与A 碰撞前,有20212121mv mv mgl -=-μ(2分)可得,物块B 与A 碰撞前速度大小s m v /241=(2分)(2)A 、B 碰后速度s m v v /222112==(1分)A 、B 整体向右经过PQ 段,有gl v v μ22223-=- (1分)得A 、B 速度s m v /23=A 、B 整体滑上圆形轨道,有2312022mgh mv -=-⨯(1分)(也可以应用 223211222222mgl mgh mv mv μ-⨯-=⨯-⨯)可得,返回到右边轨道的高度为0.2h m R ==,符合实际。
高考备考计算题规范化训练(01)

高考备考计算题规范化训练(1)开始时刻:___:____日期:______姓名:____23.(18分)研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间)t0=0.4s,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以v0=72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m。
减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动。
取重力加速度的大小g=10m/s2。
求:(1)减速过程汽车加速度的大小及所用时间;(2)饮酒使志愿者的反应时间比一般人增加了多少?(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值。
24.(20分)如图所示,在坐标系xoy的第一、第三象限内存在相同的磁场,磁场方向垂直于xoy平面向里;第四象限内有沿y轴正方向的匀强电场,电场强度大小为E。
一带电量为+q、质量为m的粒子,自y轴上的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场。
已知OP=d,OQ=2d。
不计粒子重力。
(1)求粒子过Q点时速度的大小和方向。
(2)若磁感应强度的大小为一确定值B0,粒子将以垂直y轴的方向进入第二象限,求B0的大小。
(3)若磁感应强度的大小为另一确定值,经过一段时间后粒子将再次经过Q点,且速度与第一次过Q点时相同,求该粒子相邻两次经过Q点所用的时间。
23、解:(1)设减速过程中汽车加速度的大小为a ,所用时间为t ,由题可得初速度s m v /200=,末速度0=t v ,位移m s 25=,由运动学公式得as v 220= ①av t 0=② 联立①②式,代入数据得2/8s m a = ③s t 5.2= ④(2)设志愿者反应时间为't,反应时间的增加量为t ∆,由运动学公式得s t v L +='0 ⑤ 0't t t -=∆ ⑥联立⑤⑥式,代入数据得s t 3.0=∆ ⑦(3)设志愿者所受合外力的大小为F ,汽车对志愿者作用力的大小为F 0,志愿者质量为m ,由牛顿第二定律得:ma F = ⑧由平行四边形定则得: 2220)(mg F F += ⑨ 联立③⑧⑨式,代入数据得:5410=mg F ⑩ 23、答:(1)粒子过Q 点时速度的大小 mqEd2=v ,与水平方向的夹角θ=45° (2)粒子以垂直y 轴的方向进入第二象限时2qdmE=B 0 (3)粒子相邻两次经过Q 点所用的时间 qE2mdπ)+(2=t 解析:(1)粒子在第四象限的电场中做类平抛运动,水平方向:2d=v 0t 竖直方向做匀加速直线运动,最大速度y v :t v 21=d y t mqE =at =v y ⋅ 联立以上三公式,得: m 2qEd=v =v y 0 粒子的合速度: mqEd2= v + v =v 2y 20设合速度与水平方向的夹角为θ,则: 1= v v =tan θ0y ,故θ=45°(2)粒子以垂直y 轴的方向进入第二象限,则粒子偏转的角度是135°,粒子的运动轨迹如下图所示:O 1为圆心,由几何关系可知OQ O 1∆为等腰直角三角形,则有d 22R 1=粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,即: R mv =qvB 120代人数据,整理得:2qdmE=B 0 (3)若经过一段时间后粒子能够再次经过Q 点,且速度与第一次过Q 点时相同则粒子运动的轨如图:它在磁场中运动的半径:d 2 =r 21=′R 粒子在一、三象限中运动的总时间: qE2mdπ=v R 2=t 1'π 粒子中二、四象限中运动轨迹的长度:d 2 2=s 粒子中二、四象限中运动的时间: qE2md 2= v 2s =t 2 粒子相邻两次经过Q 点所用的时间: qE2mdπ)+(2=t +t =t 21。
高中数学2008年高考真题精品解析阶段测试同步训练试题780

高中数学2008年高考真题精品解析阶段测试同步训练试题2019.091,在三角形ABC 中,5,3,7AB AC BC ===,则BAC ∠的大小为( )A .23πB .56πC .34πD .3π2,函数2()(1)1(0)f x x x =-+≤的反函数为 A.1()11)f x x -=-≥ B .1()11)f x x -=+≥ C.1()12)f x x -=-≥ D .1()12)f x x -=+≥3,设88018(1),x a a x a x +=+++则0,18,,a a a 中奇数的个数为( )A .2B .3C .4D .54,函数sin(2)3y x π=+图像的对称轴方程可能是( ) A .6x π=-B .12x π=-C .6x π=D .12x π=5,设函数1()21(0),f x x x x =+-< 则()f x ( )A .有最大值B .有最小值C .是增函数D .是减函数6,若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( )A.[B.(C.[33-D.()33-7,若A 为不等式组002x y y x ≤⎧⎪≥⎨⎪-≤⎩表示的平面区域,则当a 从-2连续变化到1时,动直线x y a += 扫过A 中的那部分区域的面积为 ( )A .34B .1C .74D .58,12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是 ( ) A . 2686C A B .2283C A C .2286C A D .2285C A9,已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合()UAB ð等于( )A .{}|24x x -<≤B .{}|34x x x 或≤≥C .{}|21x x -<-≤D .{}|13x x -≤≤10,若0.52a =,πlog 3b =,22πlog sin5c =,则( )A .a b c >>B .b a c >>C .c a b >>D .b c a >>11,“函数()()f x x ∈R 存在反函数”是“函数()f x 在R 上为增函数”的( ) A .充分而不必要条件B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件12,若点P 到直线1x =-的距离比它到点(20),的距离小1,则点P 的轨迹为( )A .圆B .椭圆C .双曲线D .抛物线13,若实数x y ,满足1000x y x y x ⎧-+⎪+⎨⎪⎩,,,≥≥≤则23x yz +=的最小值是( )A .0B .1C.914,已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于( )A .165-B .33-C .30-D .21-15,过直线y x =上的一点作圆22(5)(1)2x y -+-=的两条切线12l l ,,当直线12l l ,关于y x =对称时,它们之间的夹角为( )A .30B .45C .60D .9016,如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上.过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设BP x =,MN y =,则函数()y f x =的图象大致是( )17,若集合{|23}A x x =-≤≤,{|14}B x x x =<->或,则集合A B 等于( ) A .{}|34x x x ≤>或B .{}|13x x -<≤C .{}|34x x ≤<D .{}|21x x -≤-<18,若372log πlog 6log 0.8a b c ===,,,则( ) A .a b c >>B .b a c >> C .c a b >>D .b c a >>19,“双曲线的方程为221916x y -=”是“双曲线的准线方程为95x =±”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件20,已知ABC △中,2a =3b =60B =,那么角A 等于( ) A .135B .90C .45D .30试题答案1, 解:由余弦定理2225371cos 2532BAC +-∠==-⨯⨯,23BAC π∠=2, 解:由原函数定义域是反函数的值域,1()0f x -≤,排除B,D 两个;又原函数x 不能取1,()f x 不能取1,故反函数定义域不包括1,选C .(直接求解也容易)3, 解:由题知)8,2,1,0(8 ==i C a ii ,逐个验证知18808==C C ,其它为偶数,选A 。
高中数学2008年高考真题精品解析阶段测试同步训练试题1340

高中数学2008年高考真题精品解析阶段测试同步训练试题2019.091,设数列{}n a 中,112,1n n a a a n +==++,则通项n a = ___________。
2,已知2()2a i i -=,其中i 是虚数单位,那么实数a = . 3,已知向量a 与b 的夹角为120,且4==a b ,那么(2)+b a b 的值为 .4,若231nx x ⎛⎫+ ⎪⎝⎭展开式的各项系数之和为32,则n = ,其展开式中的常数项为 .(用数字作答)5,如图,函数()f x 的图象是折线段ABC ,其中A B C ,,的坐标分别为(04)(20)(64),,,,,,则((0))f f = ;0(1)(1)limx f x f x ∆→+∆-=∆ .(用数字作答)6,已知函数2()cos f x x x =-,对于ππ22⎡⎤-⎢⎥⎣⎦,上的任意12x x ,,有如下条件:①12x x >;②2212x x >;③12x x >.其中能使12()()f x f x >恒成立的条件序号是 .7,某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第k 棵树种植在点()k k k P x y ,处,其中11x =,11y =,当2k ≥时,111215551255k k k k k k x x T T k k y y T T --⎧⎡--⎤⎛⎫⎛⎫=+--⎪ ⎪ ⎪⎢⎥⎪⎝⎭⎝⎭⎣⎦⎨--⎛⎫⎛⎫⎪=+- ⎪ ⎪⎪⎝⎭⎝⎭⎩,.()T a 表示非负实数a 的整数部分,例如(2.6)2T =,(0.2)0T =.按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 .8,若角α的终边经过点(12)P -,,则tan 2α的值为 . 9,不等式112x x ->+的解集是 .10,已知向量a 与b的夹角为120,且4==a b ,那么a b 的值为 .11,5231x x ⎛⎫+ ⎪⎝⎭的展开式中常数项为 ;各项系数之和为 .(用数字作答)12,如图,函数()f x 的图象是折线段ABC ,其中A B C ,,的坐标分别为(04)(20)(64),,,,,,则((0))f f = ;函数()f x 在1x =处的导数(1)f '= .13,已知函数2()cos f x x x =-,对于ππ22⎡⎤-⎢⎥⎣⎦,上的任意12x x ,,有如下条件:①12x x >;②2212x x >;③12x x >.其中能使12()()f x f x >恒成立的条件序号是 .14,函数2()f x =的定义域为 .15,已知双曲线22112x y n n -=-n =16,在数列{}n a 在中,542n a n =-,212n a a a an bn++=+,*n N ∈,其中,a b 为常数,则ab =17,已知点,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB=AC =8AD =,则,B C 两点间的球面距离是18,函数2()f x =的定义域为 .19,在数列{}n a 在中,542n a n =-,212n a a a an bn++=+,*n N ∈,其中,a b 为常数,则lim n n nnn a b a b →∞-+的值是20,若A 为不等式组002x y y x ≤⎧⎪≥⎨⎪-≤⎩表示的平面区域,则当a 从-2连续变化到1时,动直线x y a += 扫过A 中的那部分区域的面积为试题答案1, 【解】:∵112,1n n a a a n +==++ ∴()111n n a a n -=+-+,()1221n n a a n --=+-+,()2331n n a a n --=+-+,,3221a a =++,2111a a =++,1211a ==+将以上各式相加得:()()()123211n a n n n n =-+-+-+++++⎡⎤⎣⎦()()()()11111111222n n n n n n n n --+⎡⎤-+⎣⎦=++=++=+ 故应填2, 【标准答案】: -1【试题分析】: a 2-2ai -1=a 2-1-2ai =2i ,a=-1 【高考考点】: 复数的运算【易错提醒】: 增根a=1没有舍去。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考备考计算题规范化训练(8)
开始时刻:___:____日期:______姓名:____23.(18分)如图所示,在高出水平地面h=1.8m的光滑平台上放置一质量M=2kg、由两种不同材料连接成一体的薄板A,其右段长度l1=0.2m且表面光滑,左段表面粗糙.在A最右端放有可视为质点的物块B,其质量m=1kg.B与A 左段间动摩擦因数μ=0.4.开始时二者均静止,现对A施加F=20N水平向右的恒力,待B脱离A(A尚未露出平台)后,将A取走.B离开平台后的落地点与平台右边缘的水平距离x=1.2m.(取g=10m/s2)求
(1)B离开平台时的速度v B.
(2)B从开始运动到刚脱离A时,B运动的时间t B和位移x B。
(3)A左端的长度l
24.(20分)如图甲所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L 的平行金属极板MN 和PQ ,两极板中心各有一小孔
1S 、2S ,两极板间电压的变化规律如图乙所示,正反向电压的大小均为0U ,周期为0T 。
在0t =时刻将一个质量为m 、电量为q -(0q >)的粒子由1S 静止释放,粒子在电场力的作用下向右运动,在0
2T t =时刻通过2S 垂直于边界进入右侧磁场区。
(不计粒子重力,不考虑极板外的电场)
(1)求粒子到达2S 时的速度大小v 和极板距离d (2)为使粒子不与极板相撞,求磁感应强度的大小应满足的条件。
(3)若已保证了粒子未与极板相撞,为使粒子在
03t T =时刻再次到达2S ,且速度恰好为零,求该过程中粒子在磁场
24 解:(1)设物块平抛运动的时间为t ,由平抛运动规律得: h=gt 2,x=v B t
联立解得v B =2m/s .
(2)设B 的加速度为a B ,B 在A 的粗糙表面滑动,受向右的滑动摩擦力做匀加速直线运动. 由牛顿第二定律,F 合=μmg=ma B ,
由匀变速直线运动规律,v B =a B t B ,x B =a B t B 2,
联立解得:t B =0.5s ,x B =0.5m .
(3)设B 刚好开始运动时A 的速度为v ,以A 为研究对象,由动能定理得Fl 1=Mv 12 设B 运动后A 的加速度为a A ,由牛顿第二定律和运动学的知识得:
F ﹣μmg=Ma A ,(l 2+x B )=v 1t B +a A t B 2,
联立解得l 2=1.5m .
答:(1)B 离开平台时的速度v B 为2m/s .
(2)B 运动的时间t B 为0.5s ,位移x B 为0.5m .
(3)A 左端的长度l 2为1.5m .
24.解:(1)粒子由1S 至2S 的过程中,根据动能定理得
2012
qU mv = ①
由①式得
v =
②
设粒子的加速度大小为
a ,由牛顿第二定律得 0U q ma d
= ③ 由运动学公式得
201()22
T d a = ④
联立③④式得
d = ⑤
(2)设磁感应强度大小为B ,粒子在磁场中做匀速圆周运动的半径为R ,由牛顿第二定律得
2
v qvB m R = ⑥
要使粒子在磁场中运动时不与极板相撞,须满足
22L
R > ⑦
联立②⑥⑦式得
B < ⑧
(3)设粒子在两边界之间无场区向左匀速运动的过程用时为1t ,有
1
d vt = ⑨
联立②⑤⑨式得 014T t = ⑩
若粒子再次达到2S 时速度恰好为零,粒子回到极板间应做匀减速运动,设匀减速运动的时间为2t ,根据运动学
公式得
22
v d t = ⑾
联立式得 022T t =
⑿
设粒子在磁场中运动的时间为t
001232
T t T t t =--- ⒀
联立⑩⑿⒀式得 0
74T t = ⒁
设粒子在匀强磁场中做匀速圆周运动的周期为T ,由式结合运动学公式得
2m
T qB π=
⒂
由题意得 T t
= ⒃
联立⒁⒂⒃式得 0
87m B qT π= ⒄。
