钟面角问题
时钟角度问题

1. 8时30分,时针和分针的夹角是多 少度?
2. 3时55分时,时针与分针的夹角是 多少度?
3. 10时26分时,时针与分针的夹角是 多少度?
已知时间求两针夹角问题时 ,先确定两针的大致位置, 根据其位置的特性找寻最简 便、准确的方法求夹角。
例2. 先将钟表的时针与分针重合在12点,转动表的指针。 (1)什么时刻分针再次与时针重合? (2)什么时刻分针与时针首次成一直线? (3)什么时刻分针与时针所成的角度首次成90o?
时钟上 的
角度问题
李倩认Βιβλιοθήκη 钟面 1小时=60分 1分=60秒 1小时=3600秒 钟面分12大格,每大格360o÷12=30o 分针60分走一圈,每分钟走360o÷60=6o 时针60分走一大格,每分钟走 30o÷60=0.5o
分针每分钟比时针多走: 6o﹣0.5o=5.5o
例1: 12点15分,时针和分针的夹角 是多少度?
看到钟表上的时针和分针 夹角也是110o,你知道张
阿姨外出了多长时间吗?
活动二
一部动画片的放映时间不足一小 时,小明发现结束时时针和分针的 位置交换了一下。
你知道动画片放映了 多长时间吗?
活动三
侦探柯南又来到了一处案发现场,死者手里拿着一张纸, 画着一个没有任何刻度的表盘,时针和分针的夹角大约是 90度,这应该是死者最后画出的案发时间。据现场观察 ,案发大约在5点与6点之间。你能推算出案发时间吗?
有人在5点半之 前见过死者
当已知两针夹角求时间时,我们可以把问 题转化为追击 问题:两针转过的角度视为路程,每分钟转过的角度视为 速度。
由 时间=路程差÷ 速度差 转化为 时间=角度差÷每分钟转过的角度差
活动一
钟面角问题

钟面角的推导及应用钟面角是指时针与分针在某一时刻所形成的角。
已知钟面数字从1到12共有12个大格,60个小格,而1周角等于360°,所以钟面每个大格对应360°÷12=30°的角,每个小格对应360°÷60=6°的角,因此时针每走1小时对应30°的角,每走一分钟对应30°÷60=0.5°的角,分针每走一分钟对应6°的角,从而可得钟面角的计算公式:1、当时针在分针的前面时钟面角=30°n+0.5°m-6°m2、当时针在分针的后面时钟面角=6°m-30°n-0.5°m这里n表示时针所指钟面时钟数,m表示分钟所指钟面分钟数,即n点m分。
1、证明:如图1,B点对O,C点对m,D点对n,A点对m,则∠BOC=6°m,∠BOD=30°n,∠DOA=0.5°m,所以∠AOC=∠COD+∠DOA=∠BOD-∠BOC+∠DOA=30°n+0.5°m-6°m2、证明:如图2:B点对O,C点对m,D点对n,A点对m,则∠BOC=6°m,∠BOD=30°n,∠AOD=0.5°m,所以∠COA=∠COB—∠AOB=∠COB—(∠AOD+∠DOB)=6°m-30°n-0.5°m。
一、求钟面角的度数例1 求5点12分的钟面角度数。
分析与解 由已知得时针在分针前面,且n=5,m=12,所以5点12分的钟面角=30°×5+0.5°×12-6°×12=150°+6°-72°=84°。
例2 求7点59分的钟面角度数。
分析与解 由已知得时针在分针的后面,且n=7,m=59,所以7点59的钟面角度数=6°×59-(30°×7+0.5°×59)=354°-210°-29.5°=144°-29.5°=114°30’。
重新认识“钟面角”

重新认识“钟面角”
日常生活中,我们几乎每天都要看钟表,然而我们对钟表表面上
的时针、分针、秒针之间的夹角(即“钟面角”)问题可能并没有在意.其实钟面角中蕴涵着丰富的数学知识,我们一起来探究一下“钟
面角”问题吧.
一、认识“钟面角”
要分析钟面角,我们首先要结合其图形特点,寻找并发现它们的
变化规律.
⑴钟表的表面特点:钟表的表面都是一个圆形,共有12个大格,每个大格间有5个小格.圆形的表面恰好对应着一个周角360°,每个大格对应30°角,每个小格对应6°角.表面一般有时针、分针、秒针三根指针.
⑵钟表时针、分针、秒针的转动情况:时针每小时转1大格,每12分钟转1小格,每12个小时转1个圆周;分针每5分钟转一大格,每1分钟转1小格,每小时转1个圆周;秒针5秒钟转1大格,每1秒钟转1小格,每1分钟转一个圆周.
⑶时针、分针、秒针的转速:有了以上的认识,我们很容易计算
出相应指针的转速:①钟表的时针转速为:30°/小时或0.5°/分钟;
②分针的转速为:6°/分钟或0.1°/秒钟;③秒针的转速为:6°/秒.
有了这些对钟面角的基本认识,我们就可以探究与钟面角有关的
问题了.。
七年级上册数学钟面问题

七年级上册数学钟面问题一、时针与分针的夹角问题。
1. 3点整时,时针与分针的夹角是多少度?- 解析:钟面一圈为360°,钟面被分成12个大格,所以每一个大格的角度为360÷12 = 30^∘。
3点整时,时针指向3,分针指向12,中间有3个大格,所以夹角为3×30 = 90^∘。
2. 4点30分时,时针与分针的夹角是多少度?- 解析:分针走30分钟,转了半圈,即180^∘。
时针每小时走一个大格,即30^∘,那么半小时时针走了30÷2=15^∘。
4点时,时针与分针夹角为4×30 = 120^∘,4点30分时,夹角为180 - (120 + 15)=45^∘。
3. 9点15分时,时针与分针的夹角是多少度?- 解析:分针15分钟转了15×6 = 90^∘(因为分针每分钟转6^∘)。
时针每小时转30^∘,15分钟是(15)/(60)=(1)/(4)小时,时针9点15分转了9×30+(1)/(4)×30 = 270 + 7.5=277.5^∘。
所以夹角为277.5 - 90=187.5^∘。
4. 5点20分时,时针与分针的夹角是多少度?- 解析:分针20分钟转了20×6 = 120^∘。
时针每小时转30^∘,20分钟是(1)/(3)小时,时针5点20分转了5×30+(1)/(3)×30=150 + 10 = 160^∘。
所以夹角为160 - 120 = 40^∘。
5. 2点40分时,时针与分针的夹角是多少度?- 解析:分针40分钟转了40×6 = 240^∘。
时针每小时转30^∘,40分钟是(2)/(3)小时,时针2点40分转了2×30+(2)/(3)×30 = 60+20 = 80^∘。
所以夹角为240 - 80 = 160^∘。
二、时针与分针重合问题。
6. 时针与分针在12点整重合,下一次重合是什么时间?- 解析:分针每分钟转6^∘,时针每分钟转0.5^∘。
【考点训练】钟面角

【考点训练】钟面角、选择题(共7小题)1在一个圆形时钟的表面,0为指针的旋转中心,0A 表示秒针,0B 表示分针,若现在的时间恰好是 12点整,当△ AOB3. ( 2007?台湾)如图,在地面上有一个钟,钟面的12个粗线刻度是整点时时针(短针)所指的位置.根据图中时针与分针(长针)的位置,该钟面所显示的时刻在下列哪范围内7. 如图,钟表8时30分时,时针与分针所成的角的度数为(、填空题(共10小题)(除非特别说明,请填准确值)& 4点到5点之间,时针和分针成直角的时间为 __________________ 9.钟表的时针在任一时刻所在的位置作为起始位置,它旋转出一个平角至少需______________ 分钟.10. _________________________________________________ 一天24小时中,时钟的分针和时针共组合成 次平角,的面积刚好达到最大值时,经过了()秒.A. 15B.C.D. 162•某同学晚上6点多钟开始做作业,他家墙上时钟的时针和分针的夹角是120°,他做完作业后还是6点多钟,且时针和分针的夹角还是 120°,此同学做作业大约用了( A. 40分钟B . 42分钟 C. 44分钟 D. 46分钟B . 6点〜7点 C. 8点〜9点D. 10点〜11点4.钟面上12: 45时,时针与分针的夹角应是()A.直角B .锐角C.钝角5•钟表上2时25分时,时针与分针所成的角是(D.不能确定D.以上答案都不对6. (2005?荆门)钟表上12时15分钟时,时针与分针的夹角为()A. 90°B . ° C. D. 60°A. 30°B . 60° C. 75 D. 90°A. 3点〜4点11.聪明一休在9点到10点之间开始解一道数学题,当时的钟面时针与分针正好成一直线,当他解完这道题时,时_____________________________________________________________ 次周角.针与分针又恰好重合,一休解这道题用了_ _ 分钟.12.钟表上分针匀速旋转一周,时针走—_ 度,钟表上8点15分时针与分针的夹角的度数为_度.13. _____________________________________________________________________________ 若时钟的时针在4点和5点之间,且与分针所夹的角为直角,则此时的时间为_________________________________________ .14.时钟的时针每小时转过的角是_ _ 度;分针每分钟转过的角是_—度,在3点和4点之间,如果时针与分针重合,则此时的时间是3点__________分.15•时针指示6点15分,它的时针和分针所夹的角是__________________ 度.点15分时,时针与分针的夹角为________________ 度.17 .钟面上9点30分时,分针与时针所成的角的度数是__________________ 度.、选择题(共7小题)1在一个圆形时钟的表面,0为指针的旋转中心,0A 表示秒针,0B 表示分针,若现在的时间恰好是 12点整,当△ AOB秒针1秒钟走6度,分针1秒针走度.6x - =90,故选C.2•某同学晚上6点多钟开始做作业,他家墙上时钟的时针和分针的夹角是时针和分针的夹角还是 120°,此同学做作业大约用了()A. 40分钟 B . 42分钟 C. 44分钟 D. 46分钟分析:根据分针每分钟转 6°,时针每分钟转°,可列方程求解. 解答:解:设开始做作业时的时间是6点x 分,•••6x - =180- 120,解得x ~ 11 ;再设做完作业后的时间是 6点y 分,•••6y - =180+120,解得y ~55,•••此同学做作业大约用了 55 - 11=44分钟. 故选C.3. ( 2007?台湾)如图,在地面上有一个钟,钟面的 12个粗线刻度是整点时时针(短针)所指的位置.根据图中时针与分针(长针)的位置,该钟面所显示的时刻在下列哪范围内()的面积刚好达到最大值时,经过了()秒.A. 15B .1吕 c 1芒459D. 16解答: 解:设秒针长 a ,分针长为b 则"pbsinC ,那么C 的度数为9°°时,面积最大.x= 1515 59120°,他做完作业后还是 6点多钟,且解答:解:方法一:设沿顺时针方向长针将遇到的整点时刻为N点,A. 3点〜4点B. 6点〜7点C. 8点〜9点D. 10点〜11点••• K N< 12贝打短针指示的时刻为N点48分.•长针应该在9: 45和10 : 50之间.•••根据图中所示,10点〜11点时,其时间约为10: 48.故选D.方法二:时针指向一小时的处,5•分针在60X上=48分处•分针下的粗刻线为50分处(即10点)•••根据图中所示,10点〜11点时,其时间约为10:48.故选D.4.钟面上12:45时,时针与分针的夹角应是()A.直角B.锐角C.钝角D.不能确定分析:12:45时刻,分针指向9,时针指向12与1之间的一处,而9与12之间的夹角就是90°, 12:45时,时4针与分针的夹角会超过90°.解答:解:由分析画出图形,可知时针与分针的夹角是钝角.故选 C.5.钟表上2时25分时,时针与分针所成的角是()A. °B. 77° 5'C. 75°解答:解:我们把时针指向2,分针指向12作为起始位置, 当分针指向25时,他转了25X 6° =150°, 此时时针转动了150°X丄=°,12则时针和3之间还有30°-° =°,故时针和分针之间夹角为30°X 2+° =°.D.以上答案都不对故选A.解答:解:方法一:设沿顺时针方向长针将遇到的整点时刻为 N 点,6. (2005?荆门)钟表上12时15分钟时,时针与分针的夹角为()A. 90° B . ° C. ° D. 60°解答:解:•••时针在钟面上每分钟转°,分针每分钟转 6°,•••钟表上12时15分钟时,时针与分针的夹角可以看成时针转过 12时°乂 15=°,分针在数字 3 上.•••钟表12个数字,每相邻两个数字之间的夹角为 30°,• 12时15分钟时分针与时针的夹角 90°-° =°. 故选B.7.如图,钟表8时30分时,时针与分针所成的角的度数为( )A. 30° B . 60° C. 75° D. 90°解答:解:T8时30分时,时针指向8与9之间,分针指向6 •钟表12个数字,每相邻两个数字之间的夹角为30°,• 8时30分时分针与时针的夹角是 2X 30° +15° =75度.故选C.、填空题(共10小题)(除非特别说明,请填准确值)分析:时针在四点与五点之间, 时针与分针有2种可能会成直角,四点与五点成30度角,时针每分钟走度, 针每分钟走6度•并且时针与分针成直角分两种情况进行讨论.解答:解:(1)时针在分针前面时,120 - 6x+=90R解得x=5=;(2)时针在分针后面时, 6x - 120 - =90 解得X =382 ;11所以在4点5十分或者4点3^分时,时针与分针成直角. 故答案为4点5「分或4点38二分.& 4点到5点之间,时针和分针成直角的时间为+分或A 点 3^ 分_而分9.钟表的时针在任一时刻所在的位置作为起始位置,它旋转出一个平角至少需360 分钟.解答:解:时针在钟面上每分钟转。
知识点236钟面角(解答)
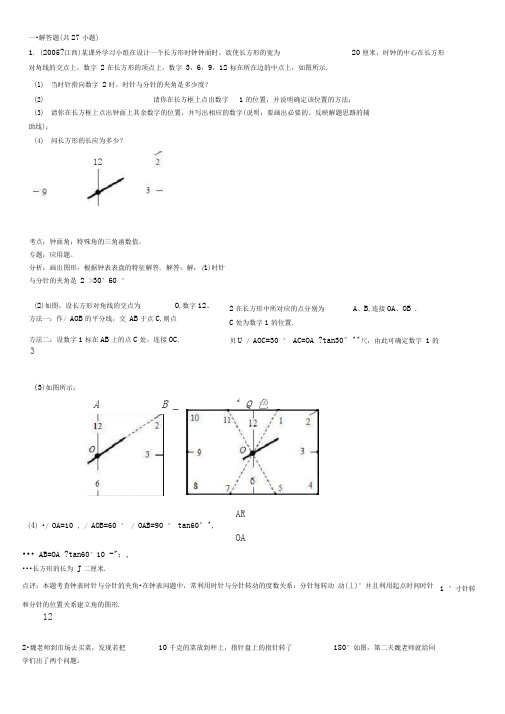
一•解答题(共27小题)1. (2005?江西)某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字 2在长方形的顶点上,数字 3,6,9,12标在所在边的中点上,如图所示. (1) 当时针指向数字 2时,时针与分针的夹角是多少度? (2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;(3) 请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、反映解题思路的辅 助线);(4) 问长方形的长应为多少?AR(4) •/ OA=10 , / AOB=60 ° / OAB=90 ° tan60°^,OA••• AB=OA ?tan60°10 -";,•••长方形的长为 J 二厘米.点评:本题考查钟表时针与分针的夹角•在钟表问题中,常利用时针与分针转动的度数关系:分针每转动 动(丄)°并且利用起点时间时针和分针的位置关系建立角的图形.122•魏老师到市场去买菜,发现若把10千克的菜放到秤上,指针盘上的指针转了 180°如图,第二天魏老师就给同学们出了两个问题:考点:钟面角;特殊角的三角函数值。
专题:应用题。
分析:画出图形,根据钟表表盘的特征解答. 解答:解:(1)时针与分针的夹角是 2 >30°60 °(2)如图,设长方形对角线的交点为 O ,数字12、方法一:作/ AOB 的平分线,交 AB 于点C ,则点 方法二:设数字1标在AB 上的点C 处,连接OC ,2在长方形中所对应的点分别为 A 、B ,连接OA 、OB .C 处为数字1的位置.贝U / AOC=30 ° AC=OA ?tan30°^^尺,由此可确定数字 1的3 (3)如图所示:A B _ _ AQ 色1 °寸针转12(1)如果把0.5千克的菜放在秤上,指针转过多少角度?(2)如果指针转了540,这些菜有多少千克?考点:钟面角。
钟面角度问题的总结
钟面角度问题的总结
角度是指两条射线之间的旋转程度,可以用度数或弧度来表示。
钟面角度问题是指与钟面上的时间相关的角度计算问题。
总结如下:
1. 钟面角度问题通常涉及到时针、分针和秒针之间的关系。
2. 一圈360度:钟面上的小时刻度一共是12个,因此每一个
小时刻度之间的夹角是360度除以12,即30度。
3. 分钟刻度的角度:钟面上的分钟刻度一共是60个,因此每
一个分钟刻度之间的夹角是360度除以60,即6度。
4. 时针角度的计算:时针每小时转动30度,分钟转动的角度
影响时针的位置。
时针的角度可以通过以下公式计算:角度 = (小时 * 30) + (分钟 / 2)。
5. 分针角度的计算:分针每分钟转动6度,秒针的角度也会影响分针的位置。
分针的角度可以通过以下公式计算:角度 = (分钟 * 6) + (秒钟 / 10)。
6. 秒针角度的计算:秒针每秒钟转动6度。
秒针的角度可以通过以下公式计算:角度 = 秒钟 * 6。
以上是钟面角度问题的一般计算方法和规律。
在具体应用中,可以根据题目给出的条件和要求,进行适当的转换和计算。
钟表面上的角度问题
钟外表上的角度问题1、魏老师到市场去买菜,发现假设把10千克的菜放到秤上,指针盘上的指针转了180°.如图,第二天魏老师就给同学们出了两个问题:〔1〕如果把0.5千克的菜放在秤上,指针转过多少角度?〔2〕如果指针转了540,这些菜有多少千克?解:〔1〕180°/ 10 =18°,0.5×18°=9°,0.5千克的菜放在秤上,指针转过9°;〔2〕540÷18=30〔〔千克〕,答:共有3千克菜.2、分别确定四个城市相应钟表上时针与分钟所成的角的度数.解:时针每小时转动360÷12=30°;巴黎时间:时针与分钟所成的角的度数为30°;伦敦时间:时针与分钟所成的角的度数为0°;北京时间:时针与分钟所成的角的度数为360°-〔8×30°〕=120°;东京时间:时针与分钟所成的角的度数为360°-〔9×30°〕=90°.3、李刚在周六下午六点多钟外出买东西时,看手表上的时针和分针的夹角是110°,下午近七点回家时,发现时针和分针的夹角又是110°,你能知道李刚同学外出用了多长时间吗?你是怎么知道的呢?解:设时针从李刚外出到回家走了x°,则分针走了〔2×110°+x°〕,由题意,得220°+x°/ 360°=x°/30°,解得x=20°,因时针每小时走30°,则20°/ 30°=2 /3 小时,即李刚外出用了40分钟时间.4、〔1〕假设时针由2点30分走到2点55分,问分针,时针各转过多大的角度?〔2〕钟表上2时15分时,时针与分针所成的锐角的度数是多少?解:〔1〕分针转过的角度:〔360°÷60〕×〔55-30〕=150°,时针转过的角度:〔360°÷60÷12〕×〔55-30〕=12.5°,∴分针,时针各转过150°、12.5°;〔2〕〔360°÷12〕-15×〔360°÷60÷12〕=30°-7.5°=22.5°,∴时针与分针所成的锐角的度数是22.5°.5、如图,在表盘上请你画出时针与分针,使时针与分针恰好互相垂直,且此时恰好为整点.〔1〕此时表示的时间是3或9点.〔2〕一天24小时,时针与分针互相垂直44次.解:〔1〕∵时针与分针恰好互相垂直,且此时恰好为整点.∴此时表示的时间是3或9点;〔2〕1-3时之间,时针在90角内移动,分针超过时针构成垂直,即时针角度加90度和270度均为垂直状态,且在360度一圈内,故每圈垂直两次;3-4时之间,从垂直开始,分针超过时针,时针加90度垂直1次,加270即超过了360度盘面,故该圈垂直1次;5-9时之间,时针超过了120度,分针先在后面和时针构成垂直,即分针角度加90度垂直一次,后分针超过时针,即时针角度加90度垂直1次,故每圈垂直2次;9-10时之间,从垂直开始,分针在后面追赶时针构成垂直1次,时针角度加90度超过360度盘面,故垂直1次;10-12时,分针在后面追赶时针时构成垂直2次.可见12小时构成垂直22次,故一昼夜构成垂直44次.6、假设时钟由2点30分走到2点50分,问时针、分针各转过多大的角度?解:在2点30时,时钟的分针指向数字6;在2点50时,时钟的分针指向数字10,因此,分针共转过“四格”,每转“一格”为30°,故分针共转过了4×30°=120°.由于时针转动的速度是分针转动速度的1 /12 ,因此,时针转动了120°×1/ 12 =10°.7、在汶川大地震后,许许多多志愿者到灾区投入了抗震救灾行列中.都江堰市志愿者小方八点多准备前去为灾民服务,临出门他一看钟,时针与分针正好是重合的,下午两点多他拖着疲惫的身体回到家中,一进门看见钟的时针与分针方向相反,正好成一条直线,问小方是几点钟去为灾民服务?几点钟回到家?共用了多少时间?在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动〔1/12 〕°依据这一关系列出方程,可以求出.解:设8点x分时针与分针重合,则:x-x /12 =40,解得:x=43.即8点43分时出门.设2点y分时,时针与分针方向相反.则:y-y /12 =10+30,解得:y=43.即2点43分时回家所以14点43分-8点43分=6点.答:共用了6个小时.8、时钟里,时针从5点整的位置起,顺时针方向转多少度时,分钟与时针第一次重合?解:在开始时,分针“落后”于时针150°.设分针与时针第一次重合时,时针转动了α角,那么,分针转动了〔150°+α〕.因为分钟转速是时针的12倍,所以150°+α=12α,a=150°/ 11 =13 7°/ 11 .即时钟里,时针从5点整的位置起,顺时针方向转13 7 /11 度时,分钟与时针第一次重合.9、同学们,闹钟都见过吧!它的时针和分针如同兄弟俩在赛跑,可你是否知道时针每分钟走多少度?分针每分针走多少度?当你弄清楚这个问题后,你能解决很多关于闹钟有趣的问题:〔1〕三点整时时针与分针所夹的角是90 度.〔2〕7点25分时针与分针所夹的角是72.5 度.〔3〕一昼夜〔0点到24点〕时针与分针互相垂直的次数有多少次?解:〔1〕3×30=90°;〔2〕2 5 /12 ×30°=72.5;〔3〕设一次垂直到下一次垂直经过x分钟,则6x-0.5x=2×905.5x=180x=360 /11 ,24×60÷360 /11=24×60×360 /11 =44〔次〕.答:一昼夜时针与分针互相垂直的次数为44次.10、观察常用时钟,答复以下问题:〔1〕早晨8时整,时针和分针构成多少度的角?〔2〕时针多长时间转一圈?它转动的速度是每小时多少度?〔3〕从8:00到8:40,分针转动了多少度?解:〔1〕8时,时针和分针中间相差4个大格.∵钟表12个数字,每相邻两个数字之间的夹角为30°,∴8时,分针与时针的夹角是4×30°=120°,答:早晨8时整,时针和分针构成120度的角;〔2〕由时钟可知时针12个小时转一圈,360°÷12=30°,答:时针12个小时转一圈,它转动的速度是每小时30度.〔3〕分针转过的角度:〔360°÷60〕×40=240°,答:分针转动了240度.11、如图,是一个时钟,过它的中心点O可以画两条相互垂直的直线,使得这两条直线经过钟面上表示时间的四个数字.〔1〕请你在图中画出符合条件的两条相互垂直的直线即可.〔2〕假设这四个数字的和是22,求出这四个数字中最小的一个数字解:〔1〕根据题意得:〔2〕设这四个数字中最小的一个数字是x,根据题意得,x+〔x+3〕+〔x+6〕+〔x+9〕=22解得:x=1,∴这四个数字中最小的一个数字是1.12、某钟楼上装有一电子报时钟,在钟面的边界上,每一分钟的刻度处,都装有一只小彩灯,晚上九时三十五分二十秒时,时针与分针所夹的角α内装有多少只小彩灯?解:晚上九时三十五分二十秒时,时针与分针所夹的角为:9×30°+35×0.5°+20×0.5°÷60-〔7×30°+20×6°÷60〕=〔75 2 /3 〕°,75 2 /3 ÷6≈12.6〔个〕.故时针与分针所夹的角α内装有12只小彩灯.1.从3时到6时,钟表的时针旋转角的度数是〔〕A.30 B.60°C.90°D.120°2.由2点15分到2点30分,时钟的分针转过的角度是〔〕A.30°B.45°C.60°D.90°3.下午2点30分时〔如图〕,时钟的分针与时针所成角的度数为〔〕A.90°B.105°C.120°D.135°4.钟表上12时15分钟时,时针与分针的夹角为〔〕A.90°B.82.5°C.67.5°D.60°5、如图是一块手表,早上8时的时针、分针的位置如下图,那么分针与时针所成的角的度数是〔c〕A.60°B.80°C.120°D.150°6、3点半时,钟表的时针和分针所成锐角是〔b〕A.70°B.75°C.85°D.90°7.在下午四点半钟的时候,时针和分针所夹的角度是〔〕A.75°B.60°C.45°D.30°8.钟表上7点20分,时针与分针的夹角为〔〕A.120°B.110°C.100°D.90°9.钟表在5点半时,它的时针和分针所成的锐角是〔〕A.15°B.70°C.75°D.90°10.3点整,钟表的时针与分针所成的角的度数为〔〕A.60°B.90°C.120°D.150°11.钟面上,3点时,时针与分针的夹角为〔〕A.90°B.80°C.70°D.75°12.甲、乙、丙、丁四个学生在判断时钟的分针和时针互相垂直的时刻,每个人说两个时刻,说对的是〔〕A.甲说3点和3点半B.乙说6点1刻和6点3刻C.丙说9点和12点1刻D.丁说3点和9点13.时钟的时针在不停的旋转,时针从上午的6时到9时,时针旋转的旋转角是〔〕A.30°B.60°C.90°D.9°14.上午9时30分,时钟的时针和分针所成的角为〔〕A.90°B.100°C.105°D.120°15.时钟钟面上的分针从12时开始绕中心旋转120°,则以下说法正确的选项是〔〕A.此时分针指向的数字为3 B.此时分针指向的数字为6C.此时分针指向的数字为4 D.分针转动3,但时针却未改变16.钟表上2时25分时,时针与分针所成的角是〔〕A.77.5°B.77°5′C.75°D.以上答案都不对17.钟面上12:45时,时针与分针的夹角应是〔〕A.直角B.锐角C.钝角D.不能确定18.钟表的分针经过40分钟,那么它转过的角度是〔〕A.120°B.240°C.150°D.160°19.时钟上的分针匀速旋转一周需要60分钟,则经过10分钟,分针旋转了〔〕A.10°B.20°C.30°D.60°20.钟表上的分针和时针经过40分钟,分针和时针旋转的角度分别是〔〕A.40°和20°B.240°和20°C.240°和40°D.40°和40°21、在火车站的钟楼上装有一个电子报时钟,在钟面的边界,每一分钟的刻度处都装有一个小彩灯,在晚上9时35分20秒时,时针与分针所夹的角内装有〔d〕个小彩灯.A.9 B.10 C.11 D.1222.小莉与小华约定周日10点整到敬老院看望老人.10点整,时钟上的时针与分针所夹的锐角是度.23、钟表上分针绕其轴心旋转,分针经过15分钟后,分针转过的角度是度,分针从12出发,转过150°,则它指的数字是.24、核对时间时,小明发现自己的闹铃比实际的时间慢了13分钟,他应该把分针顺时针旋转78度后才准确25、钟表上的分针和时针饶其轴心旋转,经过一节课40分钟后,时针转过的角度为20°26、王刚坚持在早上7:45前到学校.有一天7:20准时从家出发,以每小时3.3千米的速度匀速走向学校,到校门口一看表时针和分针刚好重合.问他家到学校有多少千米?:时针每小时转动360÷12=30°,每分钟转动30÷60=0.5°;分针每分钟转动360÷60=6°;设王刚从家到学校用了x分钟,则分针走了6x°,时针走了0.5x°,由题意得6x-0.5x=3×30+0.5×20,解得x=200 /11 .故王刚家到学校的距离为200 /11 ×3.3/60 =1 千米.27、钟表的时针在任一时刻所在的位置作为起始位置,它旋转出一个平角至少需360分钟.解:时针在钟面上每分钟转0.5°,所以它旋转出一个平角至少需180°÷0.5°=360分钟.∴它旋转出一个平角至少需360分钟.。
钟面角问题
数学实验——钟面角摘要:“钟面角” 是指时针与分针在某一时刻所成的夹角,通常情况下特指0 180 的那个角 .日常生活中,我们几乎每天都要看钟表,然而随着电子表的流行,我们对钟表表面上的时针、分针、秒针之间的夹角问题可能并没有在意 .其实钟面角中蕴含着丰富的数学知识,我们一起来探究一下“钟面角”问题吧 . 关键字: 钟面角公式 求法 追及问题一、与钟面有关的知识我们通常把研究时钟上时针与分针的问题称为时钟问题,其中包括时钟的快慢、时钟的 周期、时钟上时针与分针所成的角度等等,这里我们重点探究 “钟面角 ”问题 .要分析钟面角,我们首先要结合其图形特点,寻找并发现它们的变化规律 . ( 1)钟表的表面特点:大多数的钟表表面是一个圆,共有 12 格,每个大格间又有 5 个 小格 .圆形的表面恰好对应着一个 360°的周角,每个大格对应 30°角,而每个小格对应 6°角. 时钟表面一般有时针、分针、秒针三根指针 .( 2)钟表时针、分针、秒针的转动情况:时针每 12 小时转 1 周,每小时转 1 大格,每12 分钟转 1 小格;分针每小时转 1 周,每 5 分钟转 1 大格,每 1 分钟转 1 小格;秒针每 1 分钟转 1周,每 5秒转 1大格,每 1秒转 1小格.(3)时针、分针、秒针的转速: ①时针的转速为: 30°/小时或 0.5 °/分钟;②分针的转速为: 6°/分钟或 0.1 °/秒;③秒针的转速为 : 6°/秒 .二、建立求 “钟面角 ”的数学模型1.计算从某一时刻到另一时刻,时针(分针)转过的度数( 1)公式法:指针转过的度数 =指针转动的时间 指针的速度;( 2)观察法:从某一时刻指针转过了 a 大格 b 小格,则指针转过的度数为: (30a 6b) .例 1.从 2 点 10 分到 2 点 20 分,时针转过 _____度,分针转过 _____度? 分析:从 2 点 10 分到 2 点 20 分,经过的时间为 10 分钟 .用公式法:时针转过的角度为: 10 0.5 °=5°,分针转过的角度为: 10 6°=60°.或用观察法:时针转过格数不易观察,可知分针转过了 10 小格,分针转过的角度为:10 6°=60°.2.计算某一时刻时针与分针之间的夹角(钟面角)分 ”为了研究 “ 时n 分”(指用 12 时计时法)时针与分针所成的角,不妨规定: “ 时n mm时针所转动的角度,是指时针从“0时到 m 时 n 分 ”所 转 动 的 角 度 , 为 :(60m n) 0.5 30 m 0.5 n ,且有 0 30 m0.5n 360 ;“ 时 n 分 ”分针所转动的角度,m是指分针从 “ 时到 m 时n 分”所转动的角度,为: 6 n ,且有 0 6n 360 .所求的 “钟面角 ”m是指不超过 180°的角,则时针与分针的夹角(0180 ) 为:① 当 30 m 0. 5 n 6 n 180 时,则 30 m 0.5 n 6 n ;② 当 30 m0. 5 n 6 n 180 时,则36030 m 0.5 n 6 n .钟面角( m 时 n 分)的几种求法:例 2.分别求:(1)2 点 10 分 (2)2 点 20 分(3)2 点 45 分时钟面角的度数 .方法一:运用钟面角公式:解:(1)2 点 10 分时, m 2, n 10 ,302 0.5 10 6 10 5 180 ,故钟面角为5°1(2)2 点 20 分时,m2, n 20 ,30 2 0.5 20 6 20 50 180 ,故钟面角为50°.(3)2 点 45 分时,m2, n 45 ,30 2 0.5 45 6 45 187.5 180 ,故钟面角为 360 187.5 172.5 .方法二:观察法:解:(1)2 点 10 分时(图 1),分针指向整时点 2,此时时针与分针的夹角度数,即为时针从 2 点整到 2 点 10 分转过的度数,为: 10 0.5 °=5°,故钟面角为 5°.(2)2 点 20 分时(图 2),此时时针与分针间隔 1 个大格和若干个小格 .可知 1 大格为 30°,若干小格的度数=1 大格度数—时针从 2 点整到 2 点 20 分转过的度数,即为:30 0.5 20 20 ,故钟面角的度数为: 30 20 50.(3)2 点 45 分时(图 3),此时时针与分针间隔 6 个大格和若干个小格 .可知 1 大格为 30°,若干小格的度数=1 大格度数—时针从 2 点整到 2 点 45 分转过的度数,即为:30 0.5 45 7.5 ,夹角度数为:30 6 7.5 187.5 180 ,故钟面角为360 187.5 172.5 .12 12 1293939 36 6 6图 1 图 2 图 33.求时针、分针成特殊角时所对应的时间2 个人的同向而行的追及问题,不过这里的 2时钟问题可以看作是一个特殊的圆形轨道上个“人”分别是时钟的分针和时针.方程思想:时针、分针成特殊角时对应的时间问题,通常以整点时为基准将时针、分针所转过的角度看成一个追及问题,从而借助方程进行求解 .等量关系:整点后分针转过的角度—整点后时针转过的角度 =整点时分针、时针的夹角(分针需追赶的角度) + m时n分分针与时针的夹角(分针应多转的角度) .例 3.你能利用一元一次方程解决下列问题吗?在 3 时和 4 时之间的哪一个时刻,时钟的时针与分针:( 1)重合;(2)成直角;(3)成平角 .分析一:不妨设“这个时刻”为“3时n 分”,当3时的时候,时针与分针的夹角为30 3 90 .利用方程中追及问题的思想,可知:(1)如图4,当3 时n分“时针与分针”重合,即“分针追上了时针”,实质上是在相同的时间 n 分钟内,分针比时针多走了90°.等量关系:分针n 分钟转过的角度—时针 n 分钟转过的角度=90°.(2)如图 5,当 3 时n分“时针与分针”成直角时,分针在n分钟内不但追上了时针,而且比时针多走了90°,所以等量关系为:分针n 分钟转过的角度—时针n分钟转过的角度=90 90 180 .(3)如图 6,当 3 时n分“时针与分针”成平角时,分针在n分钟内不但追上了时针,而且比时针多走了180°,所以等量关系为:分针n 分钟转过的角度—时针n分钟转过的角度= 90 180 270 .可知 n 分钟分针转过6 n,时针转过0.5 n,解决例3问题.212 12 1293939 36 6 6图 4 图 5 图 6解法一:(1)如图 4,设 3 时n分,“时针与分针”重合,由等量关系,可得方程6 n 0.5 n 90 ,解得 n 180 .答: 3 时180分时,时钟的时针与分针重合 .11 11( 2)如图 5,设 3 时n分,“时针与分针”成直角,由等量关系,可得方程6 n 0.5 n 180 ,解得 n 360.答: 3 时360分时,时钟的时针与分针成直角 .11 11( 3)如图 6,设 3 时n分,“时针与分针”成平角,由等量关系,可得方程6 n 0.5 n 270 ,解得 n 540 .答: 3 时540分时,时钟的时针与分针成平角 .11 11分析二:不妨设“这个时刻”为“3时 n 分”,利用钟面角公式计算.(1)如图4,当时针与分针重合时,此时钟面角为 0°;(2)如图 5,当时针与分针成直角时,此时钟面角为90°;(3)如图 6,当时针与分针成平角时,此时钟面角为 180°.解法二:( 1)如图 4,设 3 时n分,“时针与分针”重合,列方程30 3 0.5 n 6 n 0 ,解得 n 180.答: 3 时180分时,时钟的时针与分针重合 .11 11(2)如图5,设 3 时n分,“时针与分针”成直角,列方程30 3 0.5 n 6 n 90 ,解得 n1 0, n2 360,其中 n1 0 不合题意,舍去;或者列方程30 3 0.5 n 6 n 270 ,解11得 n1 360, n2720(不合题意,舍去) .11 11答: 3 时360分时,时钟的时针与分针成直角 .11(3)如图 6,设 3 时n分,“时针与分针”成平角,列方程30 3 0.5 n 6 n 180 ,解得 n1 180, n2540,其中 n1180不合题意,舍去 .11 11 11答: 3 时540分时,时钟的时针与分针成平角 .11例 4.小明在晚上6点多钟出门办事,出门时看了一下钟表,此时时针与分针成90°;他于当天晚上 7 点钟之前回家,进门时又看见时针与分针成 90°.问他出去了多长时间?分析一:不妨设时刻为“6时 n 分”,时针与分针成直角.如图7、8,利用钟面角公式,此时钟面角为 90°.解法一:如图 7、8,设 6 时n分,“时针与分针”成直角,列方程30 6 0.5 n 6 n 90 ,解得 n1 180, n2540,可知出门时为 6 时180分,回家时为 6 时540分,故他外出时间为:11 11 11 113540 180 360 分钟 . 12121111 11答:他外出时间为360分钟 . 9 3 911 分析二:设他外出时间为 m 分钟,从图 7 到图 8,分针不但追上了时针,而且比时针多走了 90°.等量关系为:66分针 m 分钟转过的角度 —时针 m 分钟转过的角度 =90°+90°=180°. 图 7图 8解法二:设他外出时间为 m 分钟,可列方程 6 m 0.5 m 180,解得 m360 .11答:他外出时间为360 分钟.114.钟面角的其他应用例 5.在一个圆形时钟的表面, OA 表示秒针, OB 表示分针( O 为两针的旋转中心) .若现在时间恰好是 12 点整,经过多少秒后, AOB 的面积第一次达到最大?(设 OA 、 OB 的长度均为 r )分析:设秒针 OA 与分针 OB 所成的角为 ,应有 0 180 ,即 为秒针与分针所成 的钟面角 . 12B可知 S AOB1 OA OB sin1r 2sin ,当 AOB 的面积达到最大时,应有22sin 1,90 .12 点整,分针、秒针重合,设经过 m 秒,分针与秒针第一次9O 垂直(如图 9), AOB 的面积第一次达到最大 .等量关系为:秒针 m 秒转过的度数 — 分针 m 秒转过的度数 =90°.秒针速度为 6°/秒,分针速度为 0.1 °/秒. 6解:设经过 m 秒,分针与秒针第一次垂直 .可列方程: 6 m0.1 m 90 ,解得 图 9m 1515.59答:经过 1515秒后, AOB 的面积第一次达到最大 .595.钟面角的综合与实践活动探究:●活动 1:(1)在 3 点整的时刻,钟面上的时针与分针所成的角度为多少度?(如图 10)(2)在 3 点整后,经过多少时间两针所成的角首次等于 90°? (如图 11)(3)在问题( 2)后,经过多少时间两针所成的角第二次等于 90°?(如图 12) (4)请你计算一下:问题( 2)、( 3)中的答案各是多少?解:设经过 n 分,时针与分针成直角,由等量关系,可得方程 6 n 0.5 n 180 , 解得 n360 .11答:经过360分,时钟的时针与分针成直角 .11我们发现问题( 2)、(3)的答案都是360分钟,这一结论是必然的还是偶然的?换句话问:11如果时针与分针开始所成的角不是直角,那么间隔的时间还相同吗?33A412121212129393 9 3939366666图 10图 11图 12图 13图 14这一理性的思考,自然引出了下面的话题:(5)如果两针所成的角为任意锐角 ,那么是否也有类似的结论呢?(如图 13、图 14) (6)如果两针所成的角为任意钝角 ,或者 =0°,结论又是如何的? ●活动 2:根据以上活动,你能得到什么一般性的结论吗?设在某一时刻,时针与分针所成的角为 (其中 0 180 ) ①如果时针在分针的前面,设经过 n 分,时针与分针第一次夹角为 ,可得方程6 n 0.5 n2 , 解得 n4 ,即经过 4分钟,两针所成的角再一次为;11 11②如果分针在时针的前面,设经过 n 分,时针与分针第一次夹角为 ,可得方程6 n 0.5 n (3602 ) , 解得 n720 4 ,即经过 720 4分钟,两针所成的角再一次为.1111由这一结论不难解释问题(4)中的疑惑:( 2)、(3)的答案之所以那么巧合,仅仅是因 为当且仅当 90 时, 4 720 4 也就是说, “间隔相同时间 ”的结论对于其他情形并不1111.成立 .●活动 3:利用我们得出的结论,你还可以解决哪些与钟面角有关的问题?面对熟悉的对象,学生兴趣倍增,通过对中钟表的操作和思考,可以提出并解决更多有价值的问题,比如:①一昼夜,时钟面上时针与分针共垂直多少次?②时钟面上的时针与分针每隔多长时间重叠一次?③在同一天内的 3:00 到 4:00 之间,时钟的时针与分针何时在同一条直线上?三、文章小结通过对 “钟面角 ”问题的简单探索, 掌握关于 “钟面角 ”的知识固然重要, 但有一些关系值得我们关注 .缺乏概念的直观是空虚的, 缺乏直观的概念是盲目的 .课堂上,一味地套用公式计算钟面角,而缺乏学生实质性的智力活动,学生只能沦为做题的机器;在明白原理的基础上,寻求简便的解题思路,更值得我们表彰 .俗话说: “授人以鱼 ”不如 “授人以渔 ”, “结论 ”的真正理解、掌握必须以 “过程 ”为前提,重视 “过程 ”的教学,真正实现教学的价值 .课堂上,作为教学主导的教师,重在展示知识的产生与发展、剖析其结构与脉络,对学生作适当的指引与点拨, “导”应该牵而弗达,教师指导得过于具体或到位,就会弱化甚至干预学生 “体”、“悟”的过程,丧失了一次次独自探索的机会;而作为学习主体的学生,习惯于教师的 “喂养式 ”的教学,知识 “咀嚼 ”烂了才教给学生,学生品尝不到知识原本的滋味、体会不了咀嚼的过程;学生应通过探索,引发学习的兴趣、培养思考的习惯和创新的精神;通过交流,倾听他人、表达自我,培养团结互助的合作精神 .5。
钟面角和方位角习题课-课件
A
B
轻松一结:
我们这节课主要学习了:
1.钟面角的概念,以及关于钟面角的计算。 2.解决关于方位角的问题。
天每
开个
放孩
;子
有的
的花
孩期
子不
是一
菊样
花,
,有
选的
择孩
在子
秋是
天牡
开丹
放花
;,
而选
有择
的在
孩春
➢ He who falls today may rise tomorrow.
子天
是开
梅放
成的角是多少? 例3.时钟在4点15分时,时针与分针的夹角 为多少?
活动: 给同桌出一道关于钟面角的问题, 先独自解决,再展开讨论。
方位角 问题
D北
正东: 射线OA
E 75 °
F
西
E
30 ° H
45°
60 ° 东
正南: 正西: 正北:
射线OB 射线OC 射线OD
C
O
A 西北方向:射线OE
西南方向:射线OF
花;
,有
选的
择孩
在子
冬是
天荷
开花
放,
选
择
在
夏
我们,还在路上……
பைடு நூலகம்
分针每分钟旋转6°。
三:重要结论
时刻为m点n分的钟面角为:
|30m-5.5n|°
典型例题:
1、钟表上1时25分,时针与分针所夹的角是多少度?
30°×4-0.5°×25 =120°-12.5° =107.5° 答:时针与分针所夹的角是107.5°。
利用结论又怎样做呢?
2、3时35分,时针和分针的夹角是多少度?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
钟面角的推导及应用
钟面角是指时针与分针在某一时刻所形成的角。
已知钟面数字从1到12共有12个大格,60个小格,而1周角等于360°,所以钟面每个大格对应360°÷12=30°的角,每个小格对应360°÷60=6°的角,因此时针每走1小时对应30°的角,每走一分钟对应30°÷60=0.5°的角,分针每走一分钟对应6°的角,从而可得钟面角的计算公式:
1、当时针在分针的前面时
钟面角=30°n+0.5°m-6°m
2、当时针在分针的后面时
钟面角=6°m-30°n-0.5°m
这里n表示时针所指钟面时钟数,m表示分钟所
指钟面分钟数,即n点m分。
1、证明:如图1,B点对O,C点对m,D点对n,A点对m,则∠BOC=6°m,∠BOD=30°n,∠DOA=0.5°m,所以∠AOC=∠COD+∠DOA=∠BOD-∠BOC+∠DOA=30°n+0.5°m-6°m
2、证明:如图2:B点对O,C点对m,D点对n,
A点对m,则∠BOC=6°m,∠BOD=30°n,∠AOD=0.5°
m,所以∠COA=∠COB—∠AOB=∠COB—(∠AOD+∠
DOB)=6°m-30°n-0.5°m。
一、求钟面角的度数
例1 求5点12分的钟面角度数。
分析与解 由已知得时针在分针前面,且n=5,m=12,所以5点12分的钟面角=30°×5+0.5°×12-6°×12=150°+6°-72°=84°。
例2 求7点59分的钟面角度数。
分析与解 由已知得时针在分针的后面,且n=7,m=59,所以7点59的钟面角度数=6°×59-(30°×7+0.5°×59)=354°-210°-29.5°=144°-29.5°=114°30’。
二、时针与分针重合问题
例3 时针与分针在3点几分重合。
分析 时针与分针重合,则此时钟面角为0°,3点时时针在分针的前面,用公式1。
解 设3点x 分时针与分针重合,由1得30°× 3+0.5°x-6°x=0°。
解得x=11180=16114。
答:时针与分针在3点1611
4分重合。
例4 现在4点6分,再过几分钟时针与分针重合。
分析 显然分针在时针的后面,可设4点(6+x)分来处理或仿照例3求出时间,再减去6分。
解 设再过x 分钟时针与分针重合,由1得:30°×4+0.5°(x+6)-6°(x+6)=0°。
解得x=
11174=1511
9。
答:再过15119分钟时针与分针重合。
例5 现在6点50分,再过几分钟时针与分针重合。
分析 如图3所示,要使分针与时针重合,分针要走
45分多才能与时针重合,此时一定在7点几分。
解 设7点x 分时针与分针重合,由l 得30°×7+0.5°x-6°x=0°,得x=11
420。
所以:x+10= 11420+10=11530=48112。
答:再过4811
2分时针与分针重合。
三、时针与分针反向问题
例6 4点几分,时针与分针成一直线。
分析 显然时针在分针的后面,钟面角为180°,用公式2。
解 设4点x 分时针与分针成一直线.由2得:
6°x-30°×4-0.5°x=180°,解得x=11600
=54116。
答:4点54116
分时针与分针成一直线。
例7 10点几分时,时针与分针成一直线。
分析 显然时针在分针的前面,钟面角为180°,用公式1。
解 设10点x 分时,时针与分针成一直线。
由1得:
10×30°+0。
5°x-6°x=180°。
解得x=11240
=21119。
答:10点21119
分时针与分针成一直线。
四、时针与分针垂直问题
例8 1点几分时,时针与分针
成90°角。
分析 如图4所示:时针与分针
垂直,时针都在分针后面,钟面角为
90°或270°用公式2。
解 设1点x 分时针与分针垂直。
由2得:6°x-1×30°-0.5x °=90或6°x-1×30°-0.5x °=270°。
解得,x=11240
=21119
或x=54116。
答:在1点21119分或1点54119分时,时针与分针成90°角。
例9 4点几分,时针与分针成
90°的角。
分析 如图5所示:时针在分针
后面或在分针前面,此时钟面均为
90°,分别用公式1、2。
解 设4点x 分,时针与分针成90°,由1、2得:
4×30°+0.5°x-6°x=90°或6°x-4×30°-0.5°x=90°
解得x=
1160=5115或x=11
420=38112。
答:在4点5115分或4点3811
2分,时针与分针成90°的角。
例10 1l 点几分时针与分针
成90°角。
分析 如图6所示:时针都在
分针的前面,钟面角为90°或270°,
用公式1。
解 设11点x 分,时针与分针成直角。
由1得:11×30°+0.5°x-6°x=90°
或11×30°+0.5°x-6°x=270°。
解得x=
11
480=43117或x=11120=101110。
答:在11点43117分或11点101110分时针与分针成90°角。
五、时针与分针位置对调问题
例11 会议开始时,李老师看了一下表,会议结束时,
又看了一下表,结果分针与时针恰好对调了位置.会议是在
3点——4点之间召开,5点——6点之间结束,请问会议何
时召开,何时结束?
分析 如图7所示,会议在3点多召开,所以时针在3、
4之间,会议5点多结束,这时时针在5、6之间,即原来分
针在5、6之间,后来分针在3、4之间,所以3点几分的钟面角与5点几分的钟面角相等,但所用公式不一样,又因为3点几分至5点几分间隔的分钟数确定,所对的钟面角的度数等于6度乘以分钟数。
解 设会议在3点x 分开始,在5点y 分结束,由公式1、2得:
6°x-3×30°-0.5°x=5°30°+0.5°y-6°y=6°(x-y)
所以⎩⎨⎧-=-=-3001218012x y x y 解得⎪⎪⎩
⎪⎪⎨⎧==14329171436326y x 答:会议在3点2614363分召开,在5点17143
29分结束。
六、时针与分针构成的角度不变问题
例12 某人下午6点多外出看表上的两指针的夹角是110°,下午7点前回家发现两指针的夹角仍是110°,求这个人的外出时间。
分析 这个人外出时间在6点至7点之间,故外出时时针在前分针在后,回家时时针在后分针在前,钟面角均为110°。
解 设这人外出时间为6点x 分、回家时间为6点y 分,由公式1、2得:
⎪⎩⎪⎨⎧=-⨯-=-+⨯00000000110
5.0630611065.0630y y x x 解得⎪⎪⎩
⎪⎪⎨⎧==1158011140y x 所以y-x=11580-11140=11
440=40。
答:这人的外出时间为40分。
感谢您的阅读,祝您生活愉快。
