等积变形(附解答)
等积变形

例题讲解
练一练2:正方形ABCD、CEFG、FHIJ如图放置,已知正方形CEFG的边长是7厘米,求图中阴影 部分的面积.
例题讲解
例3:正方形ABCD、CEFG如图放置,已知三角形CEH的面积是5平方厘米,求图中阴影部分的面 积.
例题讲解
练一练3:长方形ABCD和直角梯形BCEF如图放置,已知长方形的长是5厘米,宽是3厘米,求图 中阴影部分的面积.
例题讲解
练一练5:正方形ABCD、DEFG如图放置,其边长分别是12厘米、5厘米,求图中阴影部分的面积.
例题讲解
例6:如图,正六边形ABCDEF的面积是1,求图中阴影部分的面积.
例题讲解
积.
例题讲解
例7:如图,正八边形ABCDEFGH的面积是2020,求图中阴影部分的面积.
巩固提升
作业3:如图,ABCD是边长为8厘米的正方形,梯形AEBD的对角线相交于O,三角形AOE的面积 比三角形BOD的面积小16平方厘米,求梯形AEBD的面积.
巩固提升
作业4:正方形ABCD、CEFG如图放置,已知正方形ABCD的边长是10厘米,求图中阴影部分的面 积.
巩固提升
作业5:四边形ABCD是梯形,DE//CF,已知三角形ADG、三角形BCH和三角形CDO的面积分别 是19、20和18,求五边形EFHOG的面积.
SABC SA' BC
基本要求 三角形的一条边处在平行线的一支上,与之相对的另外一个顶点在平 行线上随意移动,所得到的新三角形的面积与原三角形面积相等.
例题讲解
例题讲解
例1:正方形ABCD、CEFG如图放置,已知正方形ABCD的边长是6厘米,求图中阴影部分的面积. 分析:正方形并排放置是等积变形中最基础的题型; 第一步:找平行线,GF//AD//BE,水平方向看做一组平行线; AB//CG//EF,竖直方向看做一组平行线; 另外两组,对角线BD//CF,AC//GE; 第二步:找等积变形,三角形BDF,BD//CF,且点F在CF上,符合要求; 解析:将点F移动到点C,得到三角形BDC;
小学数学《三角形的等积变形》练习题(含答案)

三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
而四边形CEFH是它们的公共部分,
所以三角形DHF的面积=三角形BCH的面积,
进而可得阴影面积=三角形BDF的面积=三角形BCD的面积= 10×10÷2=50(平方厘米)。
法2:连接CF,那么CF平行BD,
所以,阴影面积=三角形BDF的面积=三角形BCD的面积=50(平方厘米)。
附加题目
【附1】 如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.
巩固理解结论:两个三角形等底时,面积的倍数=高的倍数
【例3】用两种不同的方法,把任意一个三角形分成四个面积相等的三角形.
分析:法1:如图(1),将BC边四等分,连接各等分点,则△ABD、△ADE、△AEF、△AFC面积相等。
法2:如图(2),D是BC的二等分点,E、F是AC、AB的中点,从而得到四个等积三角形△ADF、△BDF、△DCE、△ADE.
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
分析:
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
分析:连结AE、BF、CD(如右下图).由于三角形AEB与三角ABC的高相等,而底边EB=2BC,所以三角形AEB的面积是2.同理,三角形CBF的面积是3,三角形ACD的面积是1.
小学数学《三角形的等积变形》练习题(含答案)

内容概述
我们已经知道三角形面积的计算公式:三角形面积=底×高÷2
从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.
如果三角形的底不变,高越大(小),三角形面积也就越大(小);
如果三角形的高不变,底越大(小),三角形面积也就越大(小);
这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.
于是:三角形ABD的面积=12×高÷2=6×高
三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
【例6】如右图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
例题精讲
一元一次方程的等积变形问题

方程两边同乘或同除一个含有未知数的式子,可以消去分母,使方程化为一元一次方程。
通过这种方式,可以将方程中的某些项消去,简化方程。
方程两边同乘或同除一个含有未知数的式子
等积变形的步骤与技巧
#O3
识别等积变形的机会
观察方程 在解一元一次方程时,要时刻观察方程的形式,判断是否可以通过等积变形简化问题。 寻找等式两边的共同因子 如果等式两边有共同因子,可以通过提取共同因子简化方程。 寻找等式两边的同类项 如果等式两边有同类项,可以通过合并同类项简化方程。
03
重量不变问题
在称重过程中,当两个物体质量相等时,可以通过等积变形来求解相关问题。
01
体积不变问题
在容器中装有一定体积的水,将水倒入另一个容器,保持水的体积不变,可以通过等积变形来求解相关问题。
02
面积不变问题
在平面几何中,当两个相似图形面积相等时,可以通过等积变形来求解相关问题。
数学题目中的等积变形ຫໍສະໝຸດ 在解代数方程时,可以通过等积变形将方程转化为更易于解决的形式。
在几何图形中,可以通过等积变形将图形转化为更易于计算面积或体积的形式。
几何图形的等积变形
代数方程的等积变形
等积变形在解题中的应用
简化计算过程
通过等积变形可以将复杂的问题转化为简单的问题,从而简化计算过程。
寻找未知数
在某些问题中,可以通过等积变形来寻找未知数,从而解决问题。
解决实际问题
在解决实际问题时,等积变形可以帮助我们更好地理解问题,并找到合适的解决方案。
等积变形的注意事项与挑战
#O5
等积变形的适用范围
等积变形适用于解一元一次方程时,当方程的解为分数或根号形式时,需要进行等积变形。
小学五年级 等积变形
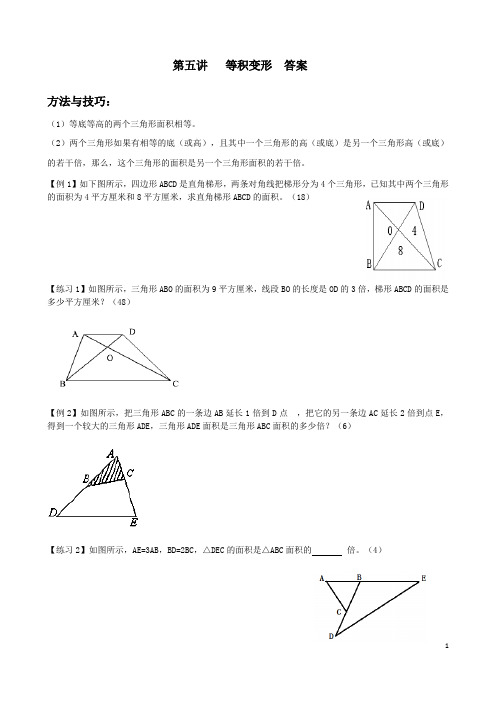
第五讲等积变形答案方法与技巧:(1)等底等高的两个三角形面积相等。
(2)两个三角形如果有相等的底(或高),且其中一个三角形的高(或底)是另一个三角形高(或底)的若干倍,那么,这个三角形的面积是另一个三角形面积的若干倍。
【例1】如下图所示,四边形ABCD是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为4平方厘米和8平方厘米,求直角梯形ABCD的面积。
(18)【练习1】如图所示,三角形ABO的面积为9平方厘米,线段BO的长度是OD的3倍,梯形ABCD的面积是多少平方厘米?(48)【例2】如图所示,把三角形ABC的一条边AB延长1倍到D点,把它的另一条边AC延长2倍到点E,得到一个较大的三角形ADE,三角形ADE面积是三角形ABC面积的多少倍?(6)【练习2】如图所示,AE=3AB,BD=2BC,△DEC的面积是△ABC面积的倍。
(4)【例3】已知三角形ABC面积为56平方厘米,是平行四边形DEFC的2倍,则阴影部分的面积是多少平方厘米?(14)【例4】如图所示,矩形ABCD的面积为24平方厘米,三角形ADM与三角形BCN的面积和为7.8平方厘米,则四边形PMON的面积是多少平方厘米?(1.8)【例5】如图所示,点M、N、P、Q分别在平行四边形ABCD的边AB、BC、CD、DA上,且PE//GM//CB,HN//QF//AB。
若平行四边形ABCD的面积为600平方厘米、阴影部分的面积为80平方厘米。
请问四边形MNPQ的面积为多少平方厘米?(340)【例6】如图所示,在正方形ABCD的BC边上取一动点E,以DE为边作矩形DEFG,且FG边通过点A。
在点E从点B移动到点C过程中,矩形DEFG的面积()(E)(A)一直变大。
(B)一直变小。
(C)先变小后变大。
(D)先变大后变小。
(E)保持不变。
【练习1】如左下图,△ABC中,D、E分别为边BC、AB的中点。
若图中阴影部分面积为1,则△ABC的面积为多少?(4)【练习2】如右上图所示,图中阴影部分的面积为多少平方厘米?(24)【练习3】如图,六角形的6个顶点恰好是一个正六边形的6个顶点。
小学五年级数学思维专题训练—等积变形(含答案解析)
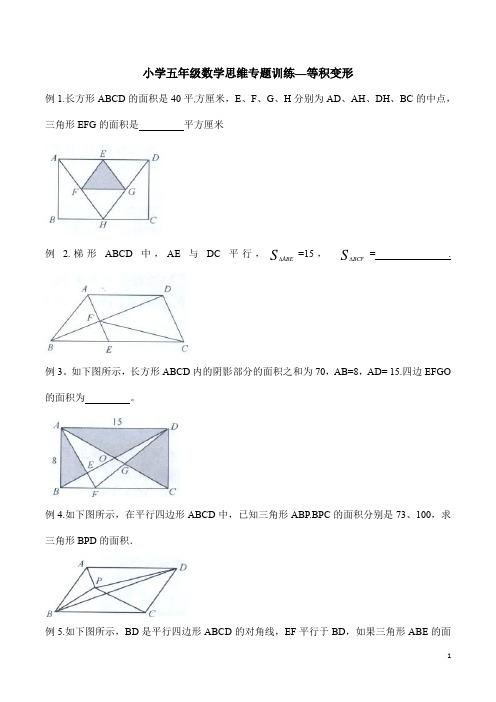
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
等积变形篇

等积变形篇丁志浩物体的形状虽然改变了,但是其面积或体积仍然保持不变.这类问题我们可以称为等积变形问题.在等积变形问题中,变化前后的体积或面积相等,往往是列方程所需的重要的相等关系.1.面积不变问题例1将图(1)三角形纸片沿虚线叠成图(2),原三角形图(1)的面积是图(2)(粗实线图形)面积的1.5倍,已知图(2)中阴影部分的面积之和为1,求重叠部分的面积.解析:首先要看清题意,其中图(2)中粗实线图形面积就是图(3)中三个角上的小三角形面积和重叠部分面积的总和,这个题目中的等量关系我们可以从图中不难看出,就是整个三角形的面积是三个角上小三角形(从图(3)中看)面积和重叠(从图(2)中看)部分面积的总和的1.5倍.如果设重叠部分面积为x,将折叠还原后,则原三角形的面积是(2x+1),图(2)中粗实线部分面积是(x+1),等量关系为:原三角形的面积=1.5粗实线部分面积解:设重叠部分面积为x.根据题意,得1.5(x+1)=2x+1.解得x=1.所以重叠部分的面积为1.例2如图2,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为7米,一个人从入口点A沿着道路走到终点B,他共走了多少米?分析:如果我们直接解这个问题,这里有重复部分,是个十分麻烦问题,现在需要对这个问题转化,可以看作用一米宽的拖把把这块区域托一遍,我们以走直线方式拖地,那么拖把走过区域是长方形,长方形的宽是一定的,是一米.而长方形的长就是拖把走过路程.长方形的面积就等于回字形面积,直接就可以算出拖把走过的路程是56米.而这正是人要走的路程.这时候我们可以看到这和拖把是否走直线没有关系了,只要拖把的宽度一定,它走过的路程就定下来,就是56米.我们也可以这样来看:所有小路连在一起可以组成一个宽1米的长长的长方形,因为长方形场地“充满”了小路,所以小路的面积等于长方形场地的面积.解:设小路的总长度为x米.根据题意,得x×1=8×7.解得x=56.所以从入口A处走到终点B,至少要走56米.2.体积不变问题例3 用直径为90mm的圆柱形玻璃杯(已装满水,且水足够多)向一个内底面积为131× 131mm2,内高为81mm的长方体铁盒倒水,当铁盒装满水时,玻璃杯中水的高度下降了多少?(结果保留π)分析:因为铁盒里水是满的,所以水的体积就等于铁盒的容积.根据长方体的体积公式可以计算出水的体积是131×131×81 mm3 ,圆柱形玻璃杯中减少的的体积为圆柱的底面积乘以水下降的高度.显然玻璃杯里倒掉的水的体积和长方体铁盒里所装的水的体积相等,所以等量关系为:玻璃杯里倒掉的水的体积=长方体铁盒的容积.解:设玻璃杯中水的高度下降了xmm.根据题意,得π·(90÷2)2x=131×131×81.解得π44.686x. 经检验,它符合题意.所以玻璃杯中水的高度下降了π44.686mm.例4将一个长、宽、高分别为15厘米、12厘米和8厘米的长方体钢块锻造成一个底面(正方形)边长为12厘米的长方体零件钢坯,试问是锻造前的长方体钢块表面积大还是锻造后的长方体零件钢坯表面积大?请你进行比较.分析:锻造前长方体钢块的体积为15×12×8cm3,锻造后长方体零件钢坯体积为12×12×它的高cm3.虽然钢块的形状发生了变化,但是钢块的体积没有变化.因此可得长方钢块体的体积=长方体零件钢坯体积,如果设长方体零件钢坯高为x厘米,得15×12×8=12×12×x.显然可以算出它的高=10厘米,但问题到此并没有结束,最终要比较它们的表面积的. 锻造前长方体钢块的表面积为为2×(12×15+15×8+12×8)平方厘米,锻造后长方体零件钢坯的表面积是2×(12×12+12×10+12×10)平方厘米.解:设锻造后的长方体零件钢坯的高为x厘米.根据题意,得5×12×8=12×12×x.解得10x=.所以锻造后的长方体零件钢坯表面积为:2(121212101210)768⨯⨯+⨯+⨯=(平方厘米).而锻造前的长方体钢块表面积为:2(1512158128)792⨯⨯+⨯+⨯=(平方厘米).所以锻造前的长方体钢块表面积比锻造后的长方体零件钢坯表面积大.例5 一种圆筒状包装的,如图3所示,其规格为“20cm×60m”,经测量这筒保鲜膜的内径、外径的长分别是3.2cm、4.0cm,则这种保鲜膜的厚度约为多少厘米?(π取3.14,结果保留两位有效数字)分析:当我们把圆筒状包装的保鲜膜展开时原来的形状可以看成长方体,根据长方体的体积公式可以计算出此时的体积为20ⅹ6000ⅹ保鲜膜的厚度,需要说明的是20 cm指展开后鲜膜的宽,也是展开前圆筒状包装的高,60 m是保鲜膜展开后的长度(单位要统一).圆筒状时可以看成圆柱体,我们要注意这个圆柱是空心的,计算时不能忘了减去空心部分.展开前后形状虽然改变了,但体积不变.即圆筒状包装体积=长方体的体积.解:设这种保鲜膜的厚度为x cm.根据题意,得223.2202060002x ⎡⎤4⎛⎫⎛⎫π-=⨯⎢⎥⎪ ⎪2⎝⎭⎝⎭⎢⎥⎣⎦.解得0.00075x≈.所以这种保鲜膜的厚度约为0.00075cm.例6 一张桌子有一个桌面和四条桌腿,做一张桌面需要木材0.03m3,做一条桌腿需要木材0.002m3,现做一批这样的桌子,恰好用去木材3.8m3,共做了多少张桌子?分析:解决这个问题关键是找出一个能表示实际问题全部意义的相等关系,我们要注意的是:一张桌子有一个桌面和四条腿,那么整张桌子所需的木材的体积是四条腿的和一个桌面的,如果设共做桌子X张,我们就容易用X表示出做桌腿所需木材的体积是4ⅹ0.002X m3 ,做桌面所需的木材的体积是0.03X m3 .因此这个问题中就有这样的相等关系:做桌面所需木材的体积+做桌腿所需木材的体积=3.8m3解:设共做了x张桌子.根据题意,得0.003x+4×0.002x=3.8.解得x=100.所以共做100张桌子.同步练习1.现有直径为0.8米的圆柱形钢坯30米,可足够锻造直径为0.4米,长为3米的圆柱形机轴多少根?2.德鑫轧钢厂要把一种底面直径6厘米,长1米的圆柱形钢锭,轧制成长4.5米,外径3厘米的无缝钢管,如果不计加工过程中的损耗,则这种无缝钢管的内径是()A. 0.25厘米 B. 2厘米C.1 厘米 D. 0.5厘米3.用直径为90 mm的圆柱形玻璃杯(已装满水)向一个由底面积为125×125 mm2内高为81mm的长方体铁盒倒水时,当倒满铁盒时玻璃杯中的水的高度下降多少?(结果保留整数π≈3.14)4.圆柱(1)的底面直径为10厘米,高为18厘米;圆柱(2)的底面直径为8厘米.已知圆柱(2)的体积是圆柱(1)的体积的1.5倍,求圆柱(2)的高.5.将内径为200毫米的圆柱形水桶中的满桶水倒入一个内部长、宽、高分别为300毫米、300毫米、80毫米的长方体铁盒,正好倒满,求圆柱形水桶的水高(精确到1毫米,≈3.14).6.一张圆桌由一个桌面和四条腿组成,如果1m三次方,木料可制作圆桌的桌面50个,或制桌腿300条,现有5m三次方,木料,请你设计一下,用多少木料.7.如图是两个圆柱体的容器,它们的半径分别是4cm和8cm,高分别为16cm和10cm,先在第一个容器中倒满水,然后将其全部倒入第二个容器中.(1)倒完后,第二个容器水面的高度是多少?(2)如右图把容器1口朝上插入容器2水位又升高多少?容器2同步练习1.现有直径为0.8米的圆柱形钢坯30米,可足够锻造直径为0.4米,长为3米的圆柱形机轴多少根?1、分析:变形前钢坯的体积等于变形后所有圆柱形机轴的总体积2.德鑫轧钢厂要把一种底面直径6厘米,长1米的圆柱形钢锭,轧制成长4.5米,外径3厘米的无缝钢管,如果不计加工过程中的损耗,则这种无缝钢管的内径是()A. 0.25厘米 B. 2厘米C.1 厘米 D. 0.5厘米3.用直径为90 mm的圆柱形玻璃杯(已装满水)向一个由底面积为125×125 mm2内高为81mm的长方体铁盒倒水时,玻璃杯中的水的高度下降多少?(结果保留整数π≈3.14)4.圆柱(1)的底面直径为10厘米,高为18厘米;圆柱(2)的底面直径为8厘米.已知圆柱(2)的体积是圆柱(1)的体积的1.5倍,求圆柱(2)的高.5.将内径为200毫米的圆柱形水桶中的满桶水倒入一个内部长、宽、高分别为300毫米、300毫米、80毫米的长方体铁盒,正好倒满,求圆柱形水桶的水高(精确到1毫米,≈3.14).6.一张圆桌由一个桌面和四条腿组成,如果1m三次方,木料可制作圆桌的桌面50个,或制桌腿300条,现有5m三次方,木料,请你设计一下,用多少木料.7.如图是两个圆柱体的容器,它们的半径分别是4cm和8cm,高分别为16cm和10cm,先在第一个容器中倒满水,然后将其全部倒入第二个容器中.(1)倒完后,第二个容器水面的高度是多少?(2)如右图把容器1口朝上插入容器2水位又升高多少?容器2。
等积变形的问题.ppt

最新课件
5
动脑筋
一个圆锥形沙堆,底面积是 25.12平方米,高是1.8米。用这 堆沙在10米宽的公路上铺3厘米 厚的路面,能铺多少米?
最新课件
6
反馈练习
1、把一个棱长是8厘米的正方体铁 块熔铸成一个底面直径是10厘米 的圆柱形铁块,这个圆柱形铁块的 高大约是多少厘米?
最新课件
1
复习:
1、圆柱、圆锥、长方体和正方体的体积 公式;
2、计算: (1)圆柱:d=4dm h=10dm v=? (2) 圆锥: v=15.7立方分米
S底=3.14平方分米 高=? (3)长方体:V=150.72立方米 宽=10米 高=3米 长=?
最新课件
2
1、理解 “等积变形”的数 学问题,并掌握其解题思路;
最新课件
7
谈一谈:
最新课件
8
最新课件
9
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
10
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
11
2、能熟练解决相关习题。
最新课件
3
例题
一个圆柱形铁块,底面半径10厘米,高5 厘米,把它熔铸成一个底面积是157平方 厘米的圆锥形铁块,圆锥的高是多少?
思考:
1、题中的变量和不变量是什么?
2、由两量可得到怎样的等量关系?
3、如何根据等量关系于 圆锥的体积
圆柱的体积:3.14×10²×5=1570(立方厘 米)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的等积变形
我们已经掌握了三角形面积的计算公式:
三角形面积=底×高÷2
这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来
角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:
①等底等高的两个三角形面积相等.
②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.
③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.
它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.
同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.
例如在图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.
例如图中,△ABC与△DBC的底相同(它们的底都是BC),△ABC的高是△DBC 高的2倍(D是AB中点,AB=2BD,有AH=2DE),则△ABC的面积是△DBC面积的2倍.
上述结论,是我们研究三角形等积变形的重要依据.
例1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.
方法2:如右图,先将BC二等分,分点D、连结AD,得到两个等积三角形,即△ABD与△ADC等积.然后取AC、AB中点E、F,并连结DE、DF.以而得到四个等积三角形,即△ADF、△BDF、△DCE、△ADE等积.
例2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1∶3∶4.
方法 1:如下左图,将BC边八等分,取1∶3∶4的分点D、E,连结AD、AE,从而得到△ABD、△ADE、△AEC的面积比为1∶3∶4.
DE,从而得到三个三角形:△ADE、△BDE、△ACD.其面积比为1∶3∶4.
当然本题还有许多种其他分法,同学们可以自己寻找解决.
例3、如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD面积相等.
证明:∵△ABC与△DBC等底等高,
∴S△ABC=S△DBC
又∵ S△AOB=S△ABC—S△BOC
S△DOC=S△DBC—S△BOC
∴S△AOB=S△COD.
例4、如图,把四边形ABCD改成一个等积的三角形.
分析本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右图,
把顶点A移到CB的延长线上的A′处,△A′BD与△ABD面积相等,从而△A′DC面积与原四边形ABCD面积也相等.这样就把四边形ABCD等积地改成了三角形△A′DC.问题是A′位置的选择是依据三角形等积变形原则.过A 作一条和DB平行的直线与CB的延长线交于A′点.
解:①连结BD;
②过A作BD的平行线,与CB的延长线交于A′.
③连结A′D,则△A′CD与四边形ABCD等积.
例5、如图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC的面积.
解法1:连结BD,在△ABD中
∵ BE=3AE,
∴ S△ABD=4S△ADE=4(平方厘米).
在△ABC中,∵CD=2AD,
∴ S△ABC=3S△ABD=3×4=12(平方厘米).
解法2:连结CE,如右图所示,在△ACE中,
∵ CD=2AD,
∴ S△ACE=3S△ADE=3(平方厘米).
在△ABC中,∵BE=3AE
∴ S△ABC=4S△ACE
=4×3=12(平方厘米).
例6、如下图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=
解:连结BG,在△ABG中,
∴ S△ADG+S△BDE+S△CFG
例7、如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF的面积.
解:连结AF、CE,∴S△ADE=S△ACE;S△CDF=S△ACF;又∵AC与EF平行,∴S△
ACE=S△ACF;
∴ S△ADE=S△CDF=4(平方厘米).
例8、如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.
解:连结BD,将四边形ABCD分成两个部分S1与S2.连结FD,有S△FBD=S △DBC=S1所以S△CGF=S△DFC=2S1.
同理 S△AEH=2S2,
因此S△AEH+S△CGF=2S1+2S2=2(S1+S2)=2×1=2.
同理,连结AC之后,可求出S△HGD+S△EBF=2所以四边形EFGH的面积为
2+2+1=5(平方单位).
例9、如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积.
解:连结AC,∵AB//CD,∴S△ADE=S△ACE
又∵AD//BC,∴S△ACF=S△ABF
而 S△ACF=S△ACE+S△AEF∶S△ABF=S△BEF+S△AEF
∴ S△ACE=S△BEF∴S△BEF=S△ADE=1.。
