第一章热力学平衡态温度
合集下载
热力学系统的平衡状态及其描述热力学

§1.1 热力学系统的平衡状态及其描述 8.2 弱简并理想Bose气体和Fermi气体
5. 热力学单位 (国际单位制)
压强:帕斯卡:
能量:焦耳:
1Pa 1N m
2
标准大气压: 1Pn 101325 Pa 10 5 Pa
1J 1N m
§1.1 热力学系统的平衡状态及其描述小结 8.2 弱简并理想Bose气体和Fermi气体
证明?
§1.3 物态方程 8.2
弱简并理想Bose气体和Fermi气体
(5)对固体、液体,要T升高而体积不变很难,故而 常测 和 T ,推知
(6)物态方程
, , T
§1.3 物态方程 8.2
弱简并理想Bose气体和Fermi气体
二、几种物态方程 1. 气体 (n摩尔)理想气体:PV nRT a (1摩尔)范氏气体:( P 2 )(v b) RT v 昂尼斯气体方程
封闭系统: 与外界可交换能量。
边界
§1.1 热力学系统的平衡状态及其描述 8.2 弱简并理想Bose气体和Fermi气体
例,气体系统
Q0 W 0
孤立系统: 粒子数 N 不变、 能量 E 不变。
Q0 W 0
封闭系统: 粒子数 N 不变、 能量 E 可变。 开放系统: 粒子数 N 可变、 能量 E 可变。
§1.1 热力学系统的平衡状态及其描述 8.2 弱简并理想Bose气体和Fermi气体
§1.1 热力学系统的平衡状态及其描述
一、热力学系统和外界 1. 系统研究对象:大量微观粒子组成的宏观系统 外界 2.系统与外界之间可能交换能量 或物质(粒子)。系统按交换类 型可分为:
系统
孤立系统:与外界无交换。 开放系统: 与外界交换能量与 粒子。
热学

第一章 温度
1.系统和外界
孤立系、封闭系、开放系。
2.平衡状态
一孤立系经过一段时间,会达到各种宏观性质不变化的状态, 又简称平衡态。
3.热力学第零定律
如果两个系统中的每一个都与第三个系统处于热平衡,它们彼 此也必定处于热平衡。
4.温度
温度是决定一个系统是否能与其他系统处于热平衡的宏观物理 性质。
5.理想气体状态方程
(D)温度相同,但但氦气的压强小于氮气的压强;
t
3 kT 2
PV= mRT/M P=RT /M
一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且它们 都处在平衡状态,则它们: (A)温度相同,压强相同;(B)温度相同,压强都不相同; (C)温度相同,但氦气的压强大于氮气的压强;
(D)温度相同,但但氦气的压强小于氮气的压强;
4. 热力学第一定律:
Q E2 E1 A
dQ dE dA
5. 循环过程:
热循环——系统从高温热源吸热,对外做功,向 低温热源放热
致冷循环——系统从低温热源吸热,接受外界 做 功,向高温热源放热 热循环:系统从高温热源吸热Q1,对外做功A,向低温热源放 热Q2,效率为 Q A = 1 2 Q1 Q1
卡诺定理:
(1).工作在两个恒温热源之间卡诺热机的效率最高。 (2).工作在两个恒温热 源之间的所有卡诺热机的效率相等, 只与温度有关,与工作物质无关。
热力学第一定律
过程
等容 等压
E
CV ,m T
CV ,m T
A
0
Q
CV ,m T
p(V2 V1 ) C p ,m T
V2 V2 RT ln RT ln V1 V1
高等工程热力学第1章
附: 华氏温标和摄氏温标
t
( C) =5 t(F ) 32 9
° °
33
☻ 压力
绝对压力 p;
表压力 pe(pg); 真空度 pv;
p=
F A
p = pb + pe ( p > pb )
p = pb - pv ( p < pb )
动压力、静压力、滞止压力和绝对压力 ?
☻ 热力学能
Uch
G = G( p, T , n1 , n2 , , nr )
热力平衡系统
其中
是驱使第i 种组分变化的势,即化学势:
12
用A表示的化学势
改变约束条件,化学势还可有其它的表达式、但是 无论如何表示,其实质都相同:
据化学势概念,定温、定容和定压、定温系统的 平衡判据:
13
四. 稳定平衡判据
力学中平衡的稳定性
+
+
1
b2
1
C)状态参数分类: 广延量 强度量 (广延量的比性质,具有强度量特性)32
► 系统两个状态相同的充要条件: 所有状参一一对应相等 简单可压缩系两状态相同的充要条件: 两个独立的状态参数对应相等
► 基本状态参数
☻ 温度
测温的基础—热力学零定律 热力学温标和国际摄氏温标
{t } C = {T }K 273.15
δ AT ,V = 0
1
δ AT , V > 0
2
定温定压系统,平衡与稳定的条件
δ GT , p = 0
1
δ GT , p > 0
2
16
过程
不同形式能量之间的转换必须通过工质的状态变化过程才 能完成。 一切过程都是平衡被破坏的结果,工质和外界有了热的、力的 或化学的不平衡才促使工质向新的状态变化,故实际过程都是不 平衡的。
t
( C) =5 t(F ) 32 9
° °
33
☻ 压力
绝对压力 p;
表压力 pe(pg); 真空度 pv;
p=
F A
p = pb + pe ( p > pb )
p = pb - pv ( p < pb )
动压力、静压力、滞止压力和绝对压力 ?
☻ 热力学能
Uch
G = G( p, T , n1 , n2 , , nr )
热力平衡系统
其中
是驱使第i 种组分变化的势,即化学势:
12
用A表示的化学势
改变约束条件,化学势还可有其它的表达式、但是 无论如何表示,其实质都相同:
据化学势概念,定温、定容和定压、定温系统的 平衡判据:
13
四. 稳定平衡判据
力学中平衡的稳定性
+
+
1
b2
1
C)状态参数分类: 广延量 强度量 (广延量的比性质,具有强度量特性)32
► 系统两个状态相同的充要条件: 所有状参一一对应相等 简单可压缩系两状态相同的充要条件: 两个独立的状态参数对应相等
► 基本状态参数
☻ 温度
测温的基础—热力学零定律 热力学温标和国际摄氏温标
{t } C = {T }K 273.15
δ AT ,V = 0
1
δ AT , V > 0
2
定温定压系统,平衡与稳定的条件
δ GT , p = 0
1
δ GT , p > 0
2
16
过程
不同形式能量之间的转换必须通过工质的状态变化过程才 能完成。 一切过程都是平衡被破坏的结果,工质和外界有了热的、力的 或化学的不平衡才促使工质向新的状态变化,故实际过程都是不 平衡的。
第一章 平衡态及状态方程

高等级公路桥梁伸 缩缝工艺研究
关于α = κβp的推导
状态方程f(T,p,V)=0
推导:以 Vm, T 为状态参量,p 为态函数: p = p(Vm ,T )
dp
=
⎜⎛ ⎝
∂p ∂T
⎟⎞ dT ⎠V
+
⎜⎜⎝⎛
∂p ∂Vm
⎟⎟⎠⎞T dVm
=
pβdT
−
1 κVm
dVm
当 p = const 时,dp=0。 pβ = 1 ⎜⎛ ∂Vm ⎟⎞ = α κVm ⎝ ∂T ⎠ p κ
2. 物质的分子、原子处于永不停息的无规则的热运动状态。
无规则运动:分子完全随机的运动,该随机性包括速度大小和
速度方向。
各项同性
热运动: 分子运动的宏观整体表现。 平均效果等于零.
典型例子:布朗运动。 1827年
英国植物学家布朗(R. Brown)
微小颗粒的无规则运动称为布朗运动。
花粉、树脂、煤、烟灰、尘埃、化石、 玻璃、矿物等
• 按照状态参量的本身性质,可以分为几何参量、 力学参量、化学参量、电磁参量以及热学特有 的热学参量—温度。
Δp→0
1 V
(
ΔV Δp
)T
=
−
1 V
(
∂V ∂p
)T
α = κβp
•理想气体 pVm = RT
α = 1 , β = 1 ,κ = 1
T
Tp
⎧α = 10−4 K −1
液 体
⎪ ⎨β
= 101~2 K −1
⎪⎩κ = 10−6atm−1
H2O 1.8×10-4 K-1 46.3 K-1
3.9×10-6 atm-1 .
体膨胀 系数
关于α = κβp的推导
状态方程f(T,p,V)=0
推导:以 Vm, T 为状态参量,p 为态函数: p = p(Vm ,T )
dp
=
⎜⎛ ⎝
∂p ∂T
⎟⎞ dT ⎠V
+
⎜⎜⎝⎛
∂p ∂Vm
⎟⎟⎠⎞T dVm
=
pβdT
−
1 κVm
dVm
当 p = const 时,dp=0。 pβ = 1 ⎜⎛ ∂Vm ⎟⎞ = α κVm ⎝ ∂T ⎠ p κ
2. 物质的分子、原子处于永不停息的无规则的热运动状态。
无规则运动:分子完全随机的运动,该随机性包括速度大小和
速度方向。
各项同性
热运动: 分子运动的宏观整体表现。 平均效果等于零.
典型例子:布朗运动。 1827年
英国植物学家布朗(R. Brown)
微小颗粒的无规则运动称为布朗运动。
花粉、树脂、煤、烟灰、尘埃、化石、 玻璃、矿物等
• 按照状态参量的本身性质,可以分为几何参量、 力学参量、化学参量、电磁参量以及热学特有 的热学参量—温度。
Δp→0
1 V
(
ΔV Δp
)T
=
−
1 V
(
∂V ∂p
)T
α = κβp
•理想气体 pVm = RT
α = 1 , β = 1 ,κ = 1
T
Tp
⎧α = 10−4 K −1
液 体
⎪ ⎨β
= 101~2 K −1
⎪⎩κ = 10−6atm−1
H2O 1.8×10-4 K-1 46.3 K-1
3.9×10-6 atm-1 .
体膨胀 系数
热学 第一章 热力学系统的平衡态与温度

例如:粒子数
箱子假想分成两相同体积 的部分,达到平衡时,两侧粒 子有的穿越界线,但两侧粒子 数相同。
三、状态参量
状态参量:描述系统平衡态宏观性质的物理量。 常用的状态参量包括以下四类:
几何参量,如体积和应变等; 力学参量,如压强和应力等; 电磁参量,如电场和磁场强度、电极化与磁化等; 化学参量,如组成系统各化学组份的质量、物质的量。 只需要体积和压强两个状态参量就能够确定热力学 系统的平衡态,这样的系统称之为简单系统。
不管是哪种气体,当
压强趋于零时,所建立的 温标都趋于相同的极限值
p
V
T lim 273.16 lim 273.16
ptr 0
ptr
ptr 0
Vtr
——理想气体温标
3、热力学温标 (不依赖于任何测温物质及其物理属性)
开尔文根据热力学第二定律建立了热力学温标。
在理想气体温标所能确定的温度范围内,理想气体
线度约为10-4---10-5 , 1cm3气体中包含1011个微粒;
二、宏观物体内的分子在不停地运动并与温度有关
1827年,布朗(英 国植物学家)
在显微镜下观察悬
浮在液体中的小颗粒
永不停息地运动着,
其中任何一个运动都 是 无 规 则 的 或 无 序 的 。 布朗粒子
--------布朗运动
布朗运动
由观察和实验总结出来的热力学规
宏观描述 律,不考虑宏观物体内大量微观粒
研
子的微观结构,从能量观点直接研
究
究宏观物体的性质与规律。——热
方
力学方法
法
从物质的微观结构出发,依据每个
微观描述 分子所遵循的力学规律,用统计的
方法研究宏观物体的性质。——统
热学教程第一章平衡态;热零律和温度;温标;理气方程

这说明:在压强极低的极限情况下,气体温度 计只取决于气体的共性,而与特定气体的特殊性 质无关。根据气体在P→0的极限情况下遵循的普 遍规律建立的温标,称为理想气体温标。
上页 下页
2.理想气体温标 P T 273.16K lim 定容:
ptr 0 P tr
定压:
V T 273.16K lim p 0V tr
上页 下页
由于气体温度计设备复杂,而且受到测温范围 的限制,不能满足科学技术上的需要.为了便于温 度的实际测量,国际上决定采用国际实用温标来逼 近热力学温标。 由于摄氏温标是历史上沿用已久的一种温标, 为了温标的统一,1960年国际计量大会规定由热 力学温标重新定义摄氏温标:
t T 273.15
三、热力学温标 完全不依赖于任何测温物质及其特殊性质的 温标。它是一种理想温标,无法直接实现(在第三章
引入)。
理想气体温标在 它所确定的测温范 围内与热力学温标 完全一致
理想气体温标在 所确定的测温范围 内实现了热力学温 标
所以:两种温标的温度都用T 表示,单位都 用K,而不再加以区分。 热力学温标所确定的温度叫热力学温度。
T T ( P ,V )
上页 下页
也可以写成隐函数的形式:
f ( P ,V , T ) 0
此即为物态方程或称为状态方程,具体形式 由试验确定。 二.理想气体状态方程: 1、气体的实验定律: (1)波意耳—马略特定律:一定质量的气体, 在T不变时,P 和V 成反比,即
PV 常量
常量由气体的质量、种类、温度决若隔板为“导热板”,则A、B两系统状态不能 独立地改变, 一个系统状态的变化会引起另一 系统状态的变化。金属板即为导热板。 两个系统通过导热板的相互接触叫热接触。 两个发生热接触的系统,经过一段时间后, 达到了温度相同的状态,我们就说这两个系统 达到了热平衡。 注意:热平衡的概念不同于平衡态。平衡态的概 念要求系统的一切宏观性质不随时间变化,需满 足热学的、力学的、化学的各种平衡条件,而满 足热平衡条件的系统,其他方面不一定满足平衡 条件。
热力学 第一章

(3)状态参量:描述热力学系统平 衡状态的宏观性质的物理量。
描述系统状态的宏观参量一般可以 直接测量。
广延量和强度量
3、均匀系与非均匀系
(1)均匀系:一个系统各部分的性质完全
一致,称为一个均匀系。(也称为一个相 —单相系) (2)非均匀系:复相系
§1.2 热平衡定律和温度
一、热平衡定律(热力学第零定律) 实验
2 3 3 6 1
如果保持温度不变,将1mol的水从1 1000 pn ,求:外界所做的功。
pn
加压到
§1.5 热力学第一定律
一、热量:系统与外界仅由于温度差,通过边界 所传递的能量。(通过分子间的碰撞来实现)
Q 过程量 热量是能量传递的另一种方式 Q 0 系统从外界吸收热量
Q 0 系统向外界放出热量
3 6 2 3
1
§1.6 热容量和焓
一、热容量
1、引入:桶的装水量(水容量)
M 水容: C h
Q 电容: C U
2、热容量:一个系统在某一过程中温度升 高1K所吸收的热量。
Q C lim T T dQ C dT
单位:焦耳/开尔文 J / K
3、系统的质量对热容量的影响:
an2 ( p 2 )(V nb) nRT V
1mol : a ( p 2 )( v b) RT v
3、简单固体和液体:
V (T , p) V0 (T0 ,0)1 (T T0 ) KT p
例1、一个简单可压缩系统,已知
nR 1 a ; KT pV p V
作业:1、1mol理想气体,在27℃的恒温下 发生膨胀,其压强由 20Pn 准静态地降到 1Pn ,求:气体所做的功和所吸取的热量。 2、在27℃,压强在0至 1000pn 之间,测得 水的体积为V (18.066 0.71510 p 0.04610 p )cm mol 如果保持温度不变,将1mol的水从1 pn 加压至 1000pn ,求:外界所做的功。
第1章 热力学系统的平衡态及状态方程

pVmol RT
对于 mol理想气体
pV RT
V Vmol
理想气体的状态方程
M
:摩尔质量,分子量
2015/3/4
37
p
V
RT
R N Ak B
p n
N A
V
k BT nk BT
气体的分子数密度
N A
V
p nk BT
理想气体的状态方程
R kB 1.380658 1023 J K NA
2015/3/4
稳定平衡
11
理解:
分子被假设为半径为r0的刚性小球 分子的大小:0.1 nm = 10-10 m = 105 fm 分子不接触时,r>>r0,其间无相互作用; 分子接触时,rr0,分子间碰撞为弹性碰撞。 (r ) 12 6 r r
Lennard-Jones Potential Model
p p0 (1 a pT )
(4) 阿伏伽德罗定律 在相同的温度和压强下,摩尔数相同的 各种气体所占的体积相同。
T0 273.16 K, p0 1 atm V0 22.4144 L/mol
2015/3/4 34
标准状况下
3.理想气体的状态方程
由玻意耳定律
pV C(T )
由温度决定的常数
热 学
第1章 热力学系统的平衡态及状态方程 第2章 热平衡态的统计分布律 第3章 近平衡态中的输运过程
2015/3/4
1
绪言
热学:研究物质的热运动、热运动对物质 宏观性质的影响及其与物质的其他运动形 式之间转换规律的物理学分支。
▲ 研究对象: 宏观物体(大量分子原子系统) 或物体系 — 热力学系统 。 ▲ 研究内容:与热现象有关的性质和规律。
对于 mol理想气体
pV RT
V Vmol
理想气体的状态方程
M
:摩尔质量,分子量
2015/3/4
37
p
V
RT
R N Ak B
p n
N A
V
k BT nk BT
气体的分子数密度
N A
V
p nk BT
理想气体的状态方程
R kB 1.380658 1023 J K NA
2015/3/4
稳定平衡
11
理解:
分子被假设为半径为r0的刚性小球 分子的大小:0.1 nm = 10-10 m = 105 fm 分子不接触时,r>>r0,其间无相互作用; 分子接触时,rr0,分子间碰撞为弹性碰撞。 (r ) 12 6 r r
Lennard-Jones Potential Model
p p0 (1 a pT )
(4) 阿伏伽德罗定律 在相同的温度和压强下,摩尔数相同的 各种气体所占的体积相同。
T0 273.16 K, p0 1 atm V0 22.4144 L/mol
2015/3/4 34
标准状况下
3.理想气体的状态方程
由玻意耳定律
pV C(T )
由温度决定的常数
热 学
第1章 热力学系统的平衡态及状态方程 第2章 热平衡态的统计分布律 第3章 近平衡态中的输运过程
2015/3/4
1
绪言
热学:研究物质的热运动、热运动对物质 宏观性质的影响及其与物质的其他运动形 式之间转换规律的物理学分支。
▲ 研究对象: 宏观物体(大量分子原子系统) 或物体系 — 热力学系统 。 ▲ 研究内容:与热现象有关的性质和规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.4 温度 描述两个或多个相互间处于热平衡的热力 学系统所具有的共同态函数。
T = g(P, V, …) Nhomakorabea 3.5 温标
温度的数值表示法
3.5.1 经验温标及其三要素
经验温标:通过测温物质的某一随温度单调变化的性质来 标度,这种温标称为经验温标。 比如:定容气体温度计,定压气体温度计
经验温标的三要素: 选择测温物质及其特性 选择固定点 规定测温物质的性质与温度的关系(如线性关系)
第一章 热力学平衡态、温度
1 热力学研究对象及其状态参量描述
1.1 热力学研究对象
包含大量(无限多)微观粒子的宏观物体的性质。
✓ 宏观物体的性质是很复杂的,多方面的
例:一块橡皮,一个铜棒 可以研究力学性质, 电学性质, 磁学性质, 化学性质
✓ 物理模型的建立
• 集中研究某种性质,忽略其它性质。
这样的做法,实际上就已经不是客观物体本身了,而是把客观物体作 了一个抽象,引进了一个假想的体系,即模型。
3.5.2 理想气体温标
当气体压强趋于零时,用不同气体温度计标度同一系统的温 度,其结果趋于一致,这一标度结果称为理想气体温标。
理想气体
TlPi m 0Tp lPi m 0TV
✓ 定义:满足波义耳-马略特定律、阿伏伽德罗定律、焦耳定律的气体。
波义耳-马略特定律:pV = C
阿伏伽德罗定律: 给定P, T,摩尔数 n V
焦耳定律: 内能U只与温度T有关 (详情见后)
✓ 气体P 0时,可看成理想气体
✓ 从微观来讲: 理想气体是忽略气体中分子之间相互作用的一个理想模型。
3.5.3 热力学温标 热力学第二定律 热力学温标(详情见后)
✓ 不依赖于测量物质 ✓ 温度值: 理想气体温标=热力学温标
3.5.4 热力学温标、摄氏温标、和华氏温标的关系
热力学平衡态的判断 力学平衡:系统各部分受力平衡 化学平衡:各组分物质无宏观定向流动 相 平 衡:各相物质无宏观定向流动 热 平 衡:热量无定向流动
✓ 主要讲 热力学平衡态,非平衡态讲一点: 实际中感兴趣的多为非平衡态; 平衡态的物理是非平衡态的物理基础。
2.3 热力学参量
• 几何参量:长度、面积、体积(V)、应变张量等 • 力学参量:压强( p)、应力张量等 • 化学参量:各组分的量:摩尔数(n)、质量、浓度等 • 电磁参量:电场强度、电极化强度、磁场强度、
• 在研究某种特定性质时,只考虑我们认为最重要最本质的 因素:建立理想模型,引进理想过程。
力学中:质点、刚体、弹性介质,理想流体,弹性碰撞 电磁学中:点电荷、电偶极子、磁偶极子 固体学中:无穷大的完美晶体 热力学中:孤立系统, 理想气体,准静态过程
✓对不同的假想体系具体考虑某一方面的性 质,就有了力学体系、电磁学体系、化学 体系,形成了物理学的不同分支,它们是 对实际的宏观系统进行不同的抽象,引进 不同的状态参量来描述。
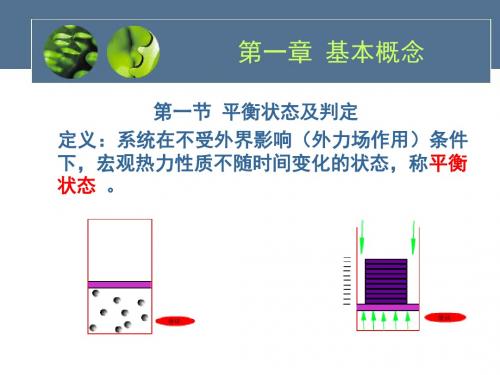
2.2 热力学平衡态
热力学平衡态 在不受外界影响的条件下,系统的宏观性质不随时间
改变(各宏观量保持恒定)的状态。
✓ 弛豫时间: 热力学平衡态是一种特殊状态。系统从初态到 达平衡态之间的状态,称为非平衡态,所需要的时间为弛 豫时间。
✓ 热力学平衡态是动态平衡,但我们一般不考虑涨落。 ✓ 热力学平衡态的概念适用于各种系统。
✓ 注意热平衡与热力学平衡的区别
3.2 热平衡定律(热力学第零定律)
如果两个热力学系统中的每一个都与第三个热力学系统处 于热平衡,则它们彼此间也一定处于热平衡。
3.3 第零定律的物理意义
1、平衡态的存在 2、一切互为热平衡的系统都具一个共同的宏观性质,即 存在一个共同的状态函数。
✓ 上述证明可推广到更复杂的系统。 ✓ 热平衡定律 温度的定义 ✓ 热平衡定律 测量温度的方法
例一 定容气体温标:
a, 水的三相点:Tt 273.16K,ppt
问题: 三相点温度与水的冰点温度的差别?
b, 温度T与压强的关系:
TV
p pt
273.16
例二 定压气体温标:
V Tp Vt 273.16
✓ 同种气体的定容与定压温度计的 测量会不同
✓ 不同气体的温度计测量会不同 ✓ 当压强趋于零时,测量则趋于一致!
热力学温标 (K) 摄氏温标 (oC) :
Tt273.15
✓ 孤立系是一个理想的极限概念 ✓ 热力学系统和外界的选择是相对的
开系 :水(或者汽) 闭系:水+汽 孤立系:水+汽+导体
• 单相系与复相系、单元系与多元系
单相系(均匀系):系统中各个部分的性质完全一样 复相系:系统可分成若干个均匀的部分
单元系:系统中只包含一种化学组分 多元系:系统中包含多种化学组分
1.2 状态参量 确定体系(或系统)状态的参量。
• 力学系统 力学参量:坐标,速度,加速度,角速度
• 电磁学体系 电磁学参量:电极化强度 P,电场 E (D), 磁化强度 M,磁场 H (B)
• 化学体系 化学参量:摩尔数
• 热力学系统 力学参量+电磁学参量+化学参量+几何参量
+ 温度!
2 热力学平衡态及其描述
2.1 热力学系统及其分类
• 热力学系统 把研究的对象视为一个系统,
称为热力学系,而系统以外的部分 则称为外界。
✓ 热力学系统是由大量的微观粒子 (分子、原子)组成的宏观系统。 ✓ 热力学系统与外界之间通过能量
和物质交换而相互联系。
• 孤立系、闭系、开系
孤立系:系统与外界无能量交换和物质交换 闭系: 有能量交换但无物质交换 开系: 有能量交换和物质交换
磁化强度等 • 温度(热力学特有的)
✓ 具体问题中并不要求把所有参量都考虑在内; ✓ 简单系统(P,V,T)。
2.4 广延量和强度量
广延量:与系统的量成正比:V、U 、S…
强度量:与系统的量无关:p、T … 注意:1、广延性的满足要求热力学极限
2、原子间的有效相互作用是短程的 长程力的能量不是广延量
3 热平衡定律和温度
3.1 热平衡
• 绝热壁及透热壁 绝热壁:两个物体通过器壁接触(无物质交换,不考虑 电磁作用),若两物体的状态可以完全独立改变,则器 壁称为绝热壁(无热量交换)。 透热壁:非绝热壁。
• 热平衡 两物体通过热接触,经过足够长的时间,将达到一个共 同的平衡态,称两物体达到了热平衡。
