华侨大学《信号与系统》证明题题库(A)
信号与系统a答案
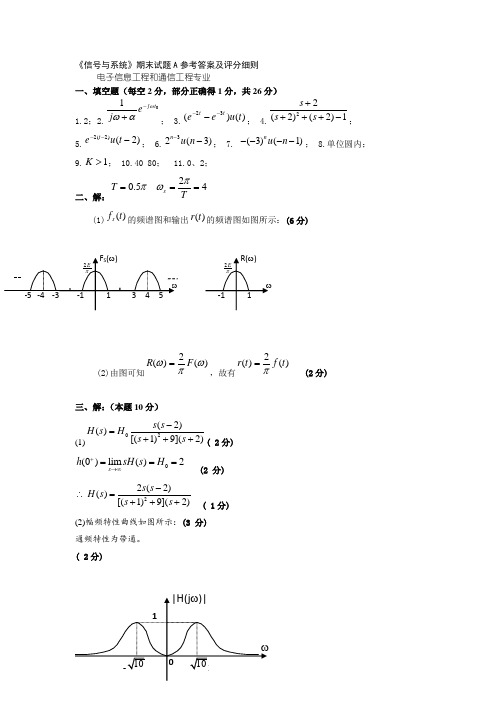
《信号与系统》期末试题A 参考答案及评分细则电子信息工程和通信工程专业 一、填空题(每空2分,部分正确得1分,共26分)1.2;2.01t j ej ωαω-+; 3.)()(32t u eett---; 4.22(2)(2)1s s s ++++-;5.)2()2(2---t u et ; 6.32(3)n u n --; 7. (3)(1)n u n ----; 8.单位圆内;9.1K >; 10.40 80; 11.0、2;二、解:425.0===TT s πωπ(1))(t f s 的频谱图和输出)(t r 的频谱图如图所示:(6分)(2)由图可知)(2)(ωπωF R =,故有)(2)(t f t r π=(2分)三、解:(本题10分)(1)2(2)()[(1)9](2)s s H s H s s -=+++( 2分)0(0)lim ()2s h sH s H +→∞=== (2 分)22(2)()[(1)9](2)s s H s s s -∴=+++ ( 1分)(2)幅频特性曲线如图所示:(3 分) 通频特性为带通。
( 2分)四、解:3212()()(2)zH z z z -=-- (1)收敛域的三种情况:2z >12z <122z << (2分)(2) 12()2z zH z z z =--- (2分)2z >时 12()[()2]()nnh n u n =- 系统因果不稳定 (2分) 12z <时 12()[()2](1)nn h n u n =-+-- 系统非因果不稳定 (2分)122z <<时12()()()2(1)nnh n u n u n =+-- 系统非因果稳定 (2分)五、求解各题1.(1)电路的S 域模型为:525)(2++=s s s H (3分)极、零点图如图所示: (2分)极点位于左半平面系统是稳定系统。
信号与系统_华侨大学中国大学mooc课后章节答案期末考试题库2023年

信号与系统_华侨大学中国大学mooc课后章节答案期末考试题库2023年1.19.已知f (t)的频谱函数为F(jw),则f (2t)cost的频谱函数为()。
答案:2. 5. 离散系统的单位响应【图片】,则该系统是(因果/非因果)的和(稳定/不稳定)。
答案:非因果、不稳定3.【图片】注意:指数函数用符号“^”表示,例如:2^k答案:2^kε(k)- 2^(k-1)ε(k-1)4.【图片】注意:用周期或者非周期回答答案:非周期5.4.若离散系统的系统函数H(z)的极点全部在单位圆内,则离散系统的频率响应就是系统函数H(z)在单位圆上的值。
答案:正确6.5.一个离散系统,只有当其系统函数H(z)的所有极点都位于左半平面时,系统才是稳定系统。
答案:错误7.6.离散系统的稳定性可由罗斯-霍尔维兹准则来判定。
答案:错误8.序列【图片】的周期为()。
答案:39.连续信号【图片】的奈奎斯特间隔为( )秒。
答案:10.能量信号与功率信号之积为能量信号;答案:正确11.非周期信号一定是能量信号;答案:错误12.【图片】。
答案:113.积分式【图片】= 。
答案:2814. 1. 线性时不变系统传输信号不失真的时域条件为单位冲激响应h(t)为()。
答案:15.离散系统的单位响应【图片】,则该系统是非因果的稳定系统。
答案:错误16.离散系统的差分方程为:y(k+2)-2y(k +1) + y (k)=2 f (k+1) + 6f (k),则系统的传输算子为()。
答案:17.【图片】不是周期信号。
答案:错误18.系统的输出y(k)和输入f(k)的关系满足:y(k)=x(2k),则该系统是时变的。
答案:正确19.系统的输出y(k)和输入f(k)的关系满足:y(k)=|x(k)|+2,则该系统是不稳定的。
答案:错误20.两个门函数(单个矩形脉冲)作卷积结果是一个三角波。
答案:错误21.周期信号的频谱具有离散性、谐波性和收敛性。
华侨大学845信号与系统08-16年真题

(1)写出电压转移函数
;
(2)画出s平面极零点分布; (3)求冲激响应和阶跃响应。
8、(12分)已知某离散时间系统的单位函数响应 。
(1)求其系统函数 ; (2)粗略绘出该系统的幅频特性; (3)画出该系统的框图。
2011年华侨大学信息科学与工程学院844信 号与系统考研真题
华侨大学2011年硕士研究生入学考试专业课试卷 (答案必须写在答题纸上)
已知其单位样值响应 的初值
。试求:
(1)系统函数 ,并说明系统是否稳定及其理由;
(2)该系统的单位样值响应 ;
(3) 写出描述系统的差分方程。 (12分)
5、已知系统函数
,分别画出直接形式和并联形式的
信号流图,并利用所画并联形式的流图建立状态空间方程。
(12分)
6、已知因果离散系统如图所示,求:
(1)系统函数 ,并画出零、极点图;
招生专业:通信与信息系统、信号与信息处理、电子与通信工程 科目名称:信号与系统 科目代码:844
第一部分、简答题(共55分)
1、请填入正确答案(共21分,每小题各3分):
(1)
。
(2)若
,则其频谱函数
。
(3)若
,则
。
(4)若
经抽样后的信号为 ,要求能从 中恢复
,则奈奎斯特角频率为 。
(5)若
,则该象函数对应的时域信号
。
(6)已知象函数
,则原序列
。
(7)某因果系统的系统函数
,要使系统稳
定,则 值的范围为 。
2、判断下述命题是否正确,并加以验证或说明(共10分,每小题 各5分):
(1)设 是系统的输入,若响应 线性,时变系统。
பைடு நூலகம்
信号与系统试题库史上最全内含答案)

信号与系统考试方式:闭卷 考试题型:1、简答题(5个小题),占30分;计算题(7个大题),占70分。
一、简答题:1.dtt df t f x e t y t )()()0()(+=-其中x(0)是初始状态,为全响应,为激励,)()(t y t f 试回答该系统是否是线性的?[答案:非线性]2.)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的,是时变的还是非时变的?[答案:线性时变的]3.已知有限频带信号)(t f 的最高频率为100Hz ,若对)3(*)2(t f t f 进行时域取样,求最小取样频率s f =?[答案:400s f Hz =]4.简述无失真传输的理想条件。
[答案:系统的幅频特性为一常数,而相频特性为通过原点的直线]5.求[]⎰∞∞--+dt t t e t )()('2δδ的值。
[答案:3]6.已知)()(ωj F t f ↔,求信号)52(-t f 的傅立叶变换。
[答案:521(25)()22j f t e F j ωω--↔]7.已知)(t f 的波形图如图所示,画出)2()2(t t f --ε的波形。
[答案: ]8.已知线性时不变系统,当输入)()()(3t e e t x t t ε--+=时,其零状态响应为)()22()(4t e e t y t t ε--+=,求系统的频率响应。
[答案:())4)(2(52)3(++++ωωωωj j j j ]9.求象函数2)1(32)(++=s s s F ,的初值)0(+f 和终值)(∞f 。
[答案:)0(+f =2,0)(=∞f ]10.若LTI 离散系统的阶跃响应为)(k g ,求其单位序列响应。
其中:)()21()(k k g k ε=。
[答案:1111()()(1)()()()(1)()()(1)222k k k h k g k g k k k k k εεδε-=--=--=--]11.已知()1 1 , 0,1,20 , k f k else ==⎧⎨⎩ ,()2 1 , 0,1,2,30 , k k f k else -==⎧⎨⎩设()()()12f k f k f k =*,求()3?f =。
华侨大学《信号与系统》证明题题库(A)答案

华侨大学信息科学与工程学院2010-2011学年二学期课程考试试卷答案(A 卷)课程名称:信号与系统 考试时间:120分钟 年级:xxx 级专业: xxx题目部分,(卷面共有50题,100分,各大题标有题量和总分) 一、证明(50小题,共100分)1.证明(1)设12112()nn i i nic c c c H p p p p p λλλλ==+++=++++∑则1()()()i nti i H p t c eu t λδ-==∑又12112()nnii nic c c c H p p p p p ααλαλαλαλ=+=+++=++++++++∑()11()()()()[()()]i nnk ttittiii i H p t c eu t ec eu t H p t e ααλααδδ----==∴+===∑∑(2)设()122()()rrc c c H p p p p λλλ=++++++则112()()()()r kr H p t c c t c t e u t δ-=+++而1221()12()()()()()()()[()()]rrr tr tc c c H p p p p H p t c c t c t eu t eH p t αλαααλαλαλαδδ----+=++++++++++=++=综合(1)(2)故[()()]()()tH p t e H p a t αδδ-=+得证2.证明[()()]()f t t t dt δϕ∞-∞''⎰{}()()[()]()()()()[()()]()[()()()()]()()[()]()()[()]()()()()[()()]()()()()[(f t t d t f t t t t f t t dtt f t t f t t dt f t t d t f t t d t f t t t t f t t dt f t t t t f ϕδϕδδϕδϕϕϕδϕδϕδδϕϕδδ∞∞∞-∞-∞-∞∞-∞∞∞-∞-∞∞∞-∞-∞''''==-'''=-+''=-+''''=--+-⎰⎰⎰⎰⎰{})()]()[()()()()]()[()()()()]t t dtt f t t f t t dt t f t t f t t dtϕδδϕδϕϕ∞∞-∞-∞∞∞-∞-∞''''''''''=+++⎰⎰⎰⎰()[()()2()()()()](0)(0)2(0)(0)(0)(0)t f t t f t t f t t dtf f f δϕϕϕϕϕϕ∞-∞''''''=++''''''=++⎰[(0)()]()[2(0)()]()[(0)()]()f t t dt f t t dt f t t dt δϕδϕδϕ∞∞∞-∞-∞-∞''''''=+-+⎰⎰⎰()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''∴=-+在这里利用了以下公式: ()()()()(0)()()(0)()()(1)(0)k k k t t dt t t dt t t dt ϕδϕδϕϕδϕϕ∞-∞∞-∞∞-∞⎧=⎪⎪''=-⎨⎪⎪=-⎩⎰⎰⎰ 3.证明2()()t t t dt δϕ∞-∞''⎰222()[()]()()()[()]t t d t t t t t t t dt ϕδϕδδϕ∞∞∞-∞-∞-∞''''==-⎰⎰2()2()()()t t t dt t t t dt δϕδϕ∞∞-∞-∞⎡⎤'''=-+⎢⎥⎣⎦⎰⎰22{2()()()[2()]}{()()()[()]}t t t t t t dt t t t t t t dt ϕδδϕδϕδϕ∞∞∞∞-∞-∞-∞-∞''''=----⎰⎰2()[2()]()2()()2()()()t t dt t t t dt t t t dt t t t dt δϕδϕδϕδϕ∞∞∞∞-∞-∞-∞-∞''''=+++⎰⎰⎰⎰2(0)[2()]()t t dt ϕδϕ∞-∞==⎰2()2()t t t δδ''∴=32()[()][2()]t t t t t t t δδδ''''===0证明()()(1)!()n n n t t n t δδ=-用归纳法()()(1)0!()t t t t δδδ==-()()()[()]()()()[()]t t t dt t t d t t t t t t t dt δϕϕδϕδδϕ∞∞∞∞-∞-∞-∞-∞''==-⎰⎰⎰()()()()()()t t t dt t t dt t t dt ϕδϕδϕδ∞∞∞-∞-∞-∞'=---⎰⎰⎰22()()(1)1!()()2()(1)2!()t t t t t t t t δδδδδδ'∴=-=-''==-⋅又33()()()[()]t t t dt t t d t δδϕδ∞∞-∞-∞'''''=⎰⎰33()()()[()]t t t t t t dt ϕδδϕ∞∞-∞-∞'''''=-⎰2()[3()()]t t t t t dt δϕϕ∞3-∞'''=-+⎰233()()()()t t t dt t t t dt δϕδϕ∞∞-∞-∞'''''=--⎰⎰(3)2()()t t dt δϕ∞-∞=-⋅⎰3()(32)()(1)3!()t t t t δδδ3'''∴=-⨯=-由归纳法可得()()(1)!()nn nt t t δδ=-4.证明:()()(3)tk r t e u t t k δ+∞-=-∞=*-∑其波形如下图所示。
华侨大学《信号与系统》证明题题库(A)

精品文档华侨大学信息科学与工程学院《信号与系统》期末考试试卷(A 卷)题 目 一 总 分 核分人 复查人 得分题目部分,(卷面共有50题,100分,各大题标有题量和总分)评卷人 得分一、证明(50小题,共100分)1.设()H p 是线性时不变系统的传输算子,且系统起始状态为零,试证明[()()]()()tH p t eH p t αδαδ-=+。
2.证明()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''=-+。
3.证明:23()2(),()0t t t t t δδδ''''==一般情况:()()(1)!()n n n t t n t δδ=- 4.设()()(3)tk r t e u t t k δ+∞-=-∞=*-∑,证明()t r t Ae -=,03t ≤≤,并求出A 值。
5.设()H p 是线性时不变系统的传输算子,且系统起始状态为零,试证明:[()()]()()t H p t e H p t βδβδ-=+6.证明()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''=-+。
7.设()()(3)tk r t e u t t k δ∞-=-∞=⋅-∑,证明(),03t r t Ae t -=≤≤,并求出A 的值。
8.若()x n 为纯虚序列,[()]()DFT x n X k =,分解为实部与虚部写做:()()r x k X k =+()i jX k ,试证明()r X k 是k 的奇函数,()i X k 是k 的偶函数。
9.已知()()N x n R n =,求()[()]X k DFT x n =,利用所得到的结果验证帕塞瓦尔定理。
<信号与系统>试卷及答案

华侨大学《信号分析与处理》期末考试B 卷答案班 级__ ______ 姓名______ ___ 学号____ _______一、填空题(1-3每空1分,后面每空2分,共20分)1.因果信号()f t 是指0t <时,()0f t =;2(1)k k ε--是_反因果_序列。
2.时域信号的展宽对应着频域信号的 压缩 。
3.在频率 Hz f m 以上没有频谱分量的带限信号,由它在均匀间隔上的抽样值唯一地决定,只要抽样间隔s T 12mf ≤。
4.⎰-=--+552)3()52(dt t t t δ 16 。
5.信号)9(2-t ε的波形为 。
6.卷积2(1)*(2)t t t e εε-+-=22(1)1(1)2t e e t ε--⎡⎤-⎣⎦-。
7.系统的输入输出方程为()(1)y t f t =-,则系统的冲激响应()h t 为(1)t δ-。
8.信号()()()f t t t πδε=+的傅立叶变换为1()j ππδωω++。
9.周期信号()cos(30)2sin(445)f t t t ππ=+++的奈奎斯特间隔为1/4。
10. 信号 )3()()(--=t t t f εε的单边拉氏变换为31se s--。
11.信号2332+++s s s 的拉氏逆变换为()22()t t e e t ε---。
二、判断题(每题1分,共8分)1、周期信号的频谱为连续谱。
( 错 )2、频域分析法只能求连续系统的零状态响应。
( 对 )3、复频域分析法中的系统函数,为时域冲激响应的单边拉氏变换。
( 对 )4、3()k k ε和3(1)kk ε---的双边Z 变换相同,其收敛域也相同。
( 错 )5、傅里叶变换不可以认为是拉普拉斯变换的一种特殊形式。
( 错 )6、()H s 的极点全部在s 平面的左半平面内,则该系统稳定。
( 对 )7、(2)k δ-的收敛域是整个z 平面。
( 错 )8、一个稳定的线性系统在任何有界的信号激励下都能得到有界的输出。
2010信号与系统(B) (答案)

h(t ) = (3e −2t + 4e −3t )ε (t )
y f (t ) = h(t ) * f (t ) = (5e − t − 3e −2 t − 2e −3t )ε ( t )
完全响应为: y( t ) = y x (t ) + y f (t ) = (5e
−t
+ 2e −2 t − 6e −3t )ε ( t )
解: (1) y A (t ) = ε (t ) − ε (t − T )
y A (t )
1 t
T
−t −2 t − ( t −T ) − e −2(t −T ) ε (t − T ) (2) y(t ) = e − e ε (t ) − e
(
)
(
)
(3)
jω
H ( jω)
ϕ (ω)
90o
-2
× ×0
[
]
y x (k ) = c1 2 k + c 2 (− 1)
k
代人初始条件有: c 1 = 2,
k
c 2 = −1 ……………2 分
∴ y x (k ) = 2 k +1 − (− 1) , k ≥ 0
…………………………………1 分
4、离散系统差分方程为 y ( n) −
3 1 1 y (n − 1) + y (n − 2) = x(n) + x(n − 1) ,求: 4 8 3
解:由系统的差分方程可得:
H (E ) = 1 + 2 E −2 E2 +2 E2 +2 = 2 = ……………………………………2 分 1 − E −1 − 2 E − 2 E − E − 2 (E − 2)(E + 1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档华侨大学信息科学与工程学院《信号与系统》期末考试试卷(A 卷)题 目 一 总 分 核分人 复查人 得分题目部分,(卷面共有50题,100分,各大题标有题量和总分)评卷人 得分一、证明(50小题,共100分)1.设()H p 是线性时不变系统的传输算子,且系统起始状态为零,试证明[()()]()()tH p t eH p t αδαδ-=+。
2.证明()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''=-+。
3.证明:23()2(),()0t t t t t δδδ''''==一般情况:()()(1)!()n n n t t n t δδ=- 4.设()()(3)tk r t e u t t k δ+∞-=-∞=*-∑,证明()t r t Ae -=,03t ≤≤,并求出A 值。
5.设()H p 是线性时不变系统的传输算子,且系统起始状态为零,试证明:[()()]()()t H p t e H p t βδβδ-=+6.证明()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''=-+。
7.设()()(3)tk r t e u t t k δ∞-=-∞=⋅-∑,证明(),03t r t Ae t -=≤≤,并求出A 的值。
8.若()x n 为纯虚序列,[()]()DFT x n X k =,分解为实部与虚部写做:()()r x k X k =+()i jX k ,试证明()r X k 是k 的奇函数,()i X k 是k 的偶函数。
9.已知()()N x n R n =,求()[()]X k DFT x n =,利用所得到的结果验证帕塞瓦尔定理。
10.证明下表中除第1行以外的其余几条性质表 DFT 的奇偶虚实性()x n()_X k()x n()X k实函数 实偶函数 实奇函数 实部为偶、虚部为奇实偶函数 虚奇函数虚函数 虚偶函数 虚奇函数实部为奇、虚部为偶虚偶函数 实奇函数11.库利—图基FFT 算法也可解释[W] 矩阵的分解简化,例如4N =可写出001010100100(0)(0)(2)100110(1)(1)(2)001100(3)(3)001010W W X X X W W X X X W W X X W W ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎣⎦⎣⎦ 试证明此矩阵表示与(976)-一致,并指出此矩阵相乘的过程与前面哪一张FFT 流程相对应。
12.函数()f t 可以表示成偶函数()e f t 与奇函数0()f t 之和,试证明:(1)若()f t 是实函数,且[()]()f t F ω=,则[()]Re[()]e f t F ω=0[()]Im[()]f t j F ω=(2)若()f t 是复函数,可表示为()()(),r i f t f t jf t =+[()]()f t F ω=则*1[()][()()],2r f t F F ωω=+-*1[()][()()],2i f t F F jωω=-- 其中*()F ω-=*[()]F t13.若已知实数有限长序列1()x n 和2()x n ,其长度为N ,且112()[()],()X k DFT x n X k ==精品文档212[()],()()(),()[()]DFT x n x n jx n x n X k DFT x n +==,试证明下列关系式成立:11()[()()]2X k X k X N k *=+- 21()[()()]2X k X k X N k j *=--14.分别利用下面几种方法证明确1[()]()u t j πδωω=+。
(1)利用符号函数11[()sgn()]22u t t =+;(2)利用矩形脉冲取极限()τ→∞;(3)利用积分定理[()()]tu t d δττ-∞=⎰(4)利用单边指数函数取极限0[()lim ,0]at a u t t -→=≥15.试证明题图所示系统可以产生单边带信号。
图中信号()g t 之频谱()G ω受限于~m m ωω-+之间,0;()sgn().m H j j ωωωω=-?设()t υ之频谱为()V ω,写出()V ω表示式,并画出图形。
16.一个理想低通滤波器的网络函数()()()j H j H j e ϕωωω=,其中0()()()()c c H j u u t ωωωωωϕωω=+--=-。
幅度响应与频率响应特性如题图所示,证明此滤波器对于()c t πδω与sin()c c t tωω的响应是一样的。
17.试证明因果系统的()R ω与()X ω被希尔伯特变换相互约束,即若因果系统的()()()H j R jX ωωω=+则 1()1()(),()X R R d X d λλωλωλπωλπωλ∞∞-∞-∞==---⎰⎰ 18.试证明对1()(0)a H s a s a=>+和22()(0)2()a s a H s a s a T π+=>⎛⎫++ ⎪⎝⎭分别用冲激不变法变换成数字滤波器的系统函数()H z ,两者具有相同的()H z ;从物理概念上解释这一结果(其中T 为抽样周期)19.一个理想低通滤波器的网络函数为()()()j H j H j e ϕωωω=其中草药 1()()0()c c H j ωωωωω-<<⎧=⎨⎩为其他值幅度响应与相移响应特性如下图所示。
证明此滤波器对于()c t πδω和sin()c c t tωω的响应是一样的。
精品文档20.若[()]()f t F ω=令()2()()Z F U ωωω=(只取单边频谱)。
试证明()Z t =1ˆ[()]()()Z f t ft ω-=+,其中()ˆ()[]jf f t d t ττπτ∞-∞=-⎰21.若()x 、()t ψ都为实函数,连续函数小波变换的定义可简写为1(,)(),x WT a b x t a ψ∞-∞=⎰[()]()t ϕω=Φ,试证明以上定义也可用下式给出。
(,)()()2j b x a WT a b X a e d ωωωωπ∞--∞=Φ-⎰(2)讨论定义式中a,b 参量的含义。
22.完整推导证明窗函数设计难则式(10100)-和式(10111)-23.试利用另一种方法证明因果系统的()R ω与()X ω被希尔伯特变换相互约束。
(1)已知()()(),()e h t h t u t h t =和0()h t 分别为()h t 的偶分量和奇分量,0()()()c h t h t h t =+,证明:00()()sgn(),()()sgn().e e h t h t t h t h t t ==(2)由傅里叶变换的奇偶虚实关系,已知()()(),H j R jX ωωω=+其中[()]()e f t R ω=0[()]()f t jX ω=。
利用上述关系证明()R ω与()X ω之间满足希尔伯特变换关系。
24.试证明对巴特沃思和切比雪夫滤波器,阻带()c Ω≤Ω衰减速度为20/NdB dec 其中N为滤波器价数。
25.试证明cos ,cos(2),,cos()t t nt ⋅⋅⋅(n 为整数)是在区间(0,2π)中的正交函数集。
26.若信号()f t 的功率谱为()f ω,试证明()df t dt信号的功率谱为2ω()fω。
27.证明:(,)(,)[(1)(1),]sal i t sal j t cal i j t =-⊕-(,)(,){[(1)]1,}sal i t cal j t sal i j t =-⊕+28.证明cos ,cos(2),cos()t t nt L (n 为整数)不是区间(0,2)π上的完备正交函数集。
29.若信号()f t 的功率谱为()f ω,试证明()df t dt信号的功率谱为2ω()fω。
30.试证明前四个勒让德多项式在(-1,1)内是正交函数集。
它是否规格化? 31.试证明cos ,cos(2),cos()t t nt L (n 为整数)是在区间(0,2)π中的正交函数集。
32.若信号12()cos(),()sin()f t t f t t ωω==,试证明两信号同时作用单位电阻时所产生的能量等于1()f t 和2()f t 分别作用时产生的能量之和,如果改为12()cos(),()cos(45)f t t f t t ωω==+o ,上述结论是否成立。
33.试证明:[](,)(,)(1)(1),sal i t sal j t cal i j t ⋅=-⊕-[]{}(,)(,)(1)1,sal i t cal j t sal i j r ⋅=-⊕+34.试证明在区间(0,2π)上,下图的矩形波与信号cos ,cos(2),,cos()t t nt ⋅⋅⋅正交(n 为整数),即此函数没有波形cos()nt 的分量。
35.试证明在区间(0,2)π,题图的矩形波与信号cos ,cos(2),cos()t t nt L 正交(n 为整精品文档数),也即此函数没有波形cos()nt 的分量。
36.已知()x n 的双边z 变换为()X z ,证明1[()]()x n X z --=37.已知[()]()x n X z =,证明0[()]()1nk zx k X z z ==-∑ 38.试证明序列相关定理,1[()()]()()m h m x m n H z X z∞=-∞-=∑其中()H z =[()],()h n X z1[()()]()()m h m x m n H z X z ∞=-∞-=∑[()]x n =℘。
39.已知线性时不变系统的状态方程和愉出方程表示为111()()()k k k k kX t A t B e t λλ⨯⨯⨯=+11()()k k r t C De t λ⨯⨯=+ 且有10,0,,0k CB CAB CA B -===L 。
证明:(1)该系统不可能同时完全可控和完全可观;(2)该系统的转移函数()()()R s H s E s ==为常数,与s 无关。
40.(1)证明:如果AB 矩阵可交换时,即AB BA =,则有()A B t At Bt e e e +=⋅。
(2)设矩阵k H 被定义为如下的k k ⨯方阵100001000010000k H ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L MM M M L L证明21212!(1)!01(2)!01kk k H t t t k te t k --⎡⎤⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦L L M M L(3)利用k J I H α=+证明21212!(1)!01(2)!01k k jk t t t t k te e t k α--⎡⎤⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦L LM M L(4)设1122100000,001000A αααα⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦求At e 41.已知两个系统有这样的关系1()()()()()t A t Be t r t C t λλλ=+⎧⎨=⎩精品文档2()()()()()T TTt A t C e t r t B t γγγ⎧=-+⎪⎨=⎪⎩ 证明:如果系统起始是静止的,则这两个系统的输出冲激响应有下列关系12()()h t h t =-42.证明周期锯齿信号的傅立叶级数裘达式为11111()[sin sin 2sin 3 (223)Af t t t t w w w p=-+++其中A 为锯齿的高度,12T p w =为锯齿波的周期。
