不规则皮件排料方案研究
不规则件优化排样的小生境遗传模拟退火算法

设 Gj ( j∈J, J 为零件集合 )为零件 j的图形 , ( X Y ( xj, yj )为该零件的给定点的坐标 , 则该零件在板材上的 定位可以表示为下述过程 :先将该零件以该定点为
轴作角度为
பைடு நூலகம்
α j
的旋转
, 然后再将定点
( xj ,
yj )在板材
作位移 (Δxj,Δyj ) 。这时零件 j在板材上的方位可
为此本文主要探讨采用求取零件最小包络矩形 的方法简化预处理 ,并且对一些形状互补的零件构 造矩形排样单元进行优化组合 ,使零件区域在最小 包络矩形中所占的比例尽可能大 ,对组合后的图形 再求取最小包络矩形 ,同时对多边形的外轮廓与包 络矩形之间产生的空白区域进行填充的预处理方 法 ;并从遗传模拟退火算法优化策略的构造出发 ,融 合小生境技术的思想 ,提出一种基于小生境技术的 遗传模拟退火算法 ( niching genetic simulated annea2 ling algorithm , GSA ) ,通过使用一种新的选择和变异 机制 ,从而提高遗传算法的稳定性和收敛速度 ,并在 此基础上开发了不规则件优化排样系统 。
件姿态时的材料利用率 ,求得材料利用率最高时的
Abstract: Firstly, we fully consider the shapes of irregular parts and convert the two2dim ensional irregular parts packing p roblem into rectangular parts packing p roblem using the com bined rectangle enclosure algorithm. W e overcome the blank area when m inimum enclosed rectangle was simp ly used to rep lace the parts packing, which re2 sults in too low utilization ratio of materials. Secondly, genetic simulated annealing algorithm and niche technique are integrated to search for the best sequence of the packed parts and each part′s angle of rotation. Finally, the lowest horizontal algorithm and filling algorithm are combined to comp lete the automatic layout. Examp les indicate that our algorithm is effective and p ractical. Key words: niche technique; genetic sim ulated annealing algorithm; combined rectangle enclosure algorithm; ir2 regular part; op tim al layout
二维不规则图形下料排样优化算法研究的开题报告

二维不规则图形下料排样优化算法研究的开题报告1、研究背景和意义二维不规则图形排样优化问题已经广泛应用于机械制造、纺织、造纸、电子元器件、板材等多个领域。
其目的是尽可能地利用原材料,并减少原材料的浪费,从而提高生产效率和降低成本。
因此,研究二维不规则图形排样优化算法具有重大的理论和实际意义。
2、研究内容与目标本文将针对二维不规则图形排样优化问题,进行深入的研究,主要包括以下内容:(1) 完成二维不规则图形排样问题的定义、模型建立及其特点分析;(2) 探究传统排样算法所存在的问题,并介绍算法改进策略;(3) 提出新的二维不规则图形排样优化算法,并与传统算法进行效果比较;(4) 通过模拟实验,分析和验证新算法的可行性和有效性。
3、研究方法和思路(1) 文献综述法:对二维不规则图形排样优化问题研究的国内外现状及发展趋势进行全面的梳理和总结,了解现有算法的优缺点,为提出新的算法奠定基础。
(2) 算法设计法:设计新的二维不规则图形排样优化算法,力求达到更高的效率和更好的效果,并通过实验来验证和分析其可行性和优越性。
(3) 实验分析法:用不同的数据集来测试新的算法的性能,并对算法进行比较和分析。
4、预期结果与创新点本文预期通过对不规则图形排样优化问题的研究,提出一种高效稳定的新算法,以解决目前排样算法在实际应用中存在的问题。
该算法可以使排样过程更好地适应实际应用需求,从而降低生产成本,提升企业效益。
本文的创新点主要体现在以下几个方面:(1) 结合不规则图形的特点,提出一种适合处理不规则图形的排样优化算法,该算法可以更好地解决不规则图形排样问题;(2) 对现有算法进行改进与优化,解决排样过程中出现多余的缝隙、分割片数过多等问题,同时提高了排样效率;(3) 通过严格的实验验证,证明该算法能够在实际生产中得到广泛应用。
青鹤真皮摄像不规则排料软件 用户手册

青鹤真皮摄像排料软件用户操作手册上海青鹤信息技术有限公司目录青鹤真皮摄像排料软件 (1)一、系统概述 (4)安装 (4)二、实例- "排料计算例" (6)三、界面概要 (9)1、整体外观 (9)另存为 (12)导入 (12)批量导出PLT (12)批量导出DXF (12)批量导出G-Code (12)排料报告 (13)导出统计报告 (13)退出 (15)自动排料 (18)量尺 (18)清除裁片 (18)导出 (19)插入照片 (20)识别材料 (22)标识瑕疵 (24)分段 (25)调整 (27)调校相机 (28)照片重构 (32)缩放 (33)视图图像 (34)视图- 查看 (35)照片区 (37)裁片区 (38)待排区 (38)状态条 (39)关于 (45)裁片属性 (59)文字高度 (60)裁片间距 (63)数据导出- G-Code (65)自动排料操作 (70)2、系统要求 (71)操作系统要求 (71)推荐硬件需求 (72)软件锁 (73)查看软件锁信息 (73)升级软件锁和Key文件 (73)设定密码 (74)一、系统概述欢迎阅读本软件使用指南。
安装管理员权限在Windows7/windows8操作系统上,安装本软件时,系统会提示需要允许安装程序管理员权限。
这是Windows7安全系统控制的标准情况,必须获得允许安装程序才能正确运行并完成安装。
欲使用本系统,请在电脑空闲的USB口上插入您获得的软件锁。
如果软件仍然提示没有找到软件锁,请联系您的分销商获取帮助。
安装目录安装程序的缺省安装路径在系统安装盘(一般是C:\craneApps)的根目录下。
没有安装到Program Files目录之下是因为新的Windows操作系统对这一目录下的访问做了限制。
而本系统的主要专业用户更习惯所谓绿色安装的策略——程序和程序将产生的运行数据都在统一目录之内。
卸载安装程序会在系统菜单中,本软件的程序组内,创建卸载链接,执行之后再删除安装目录就可以了。
零件组合排料规范方案
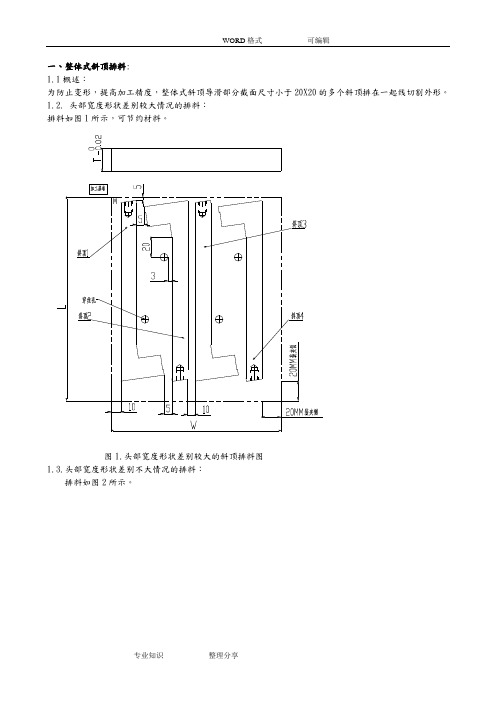
一、整体式斜顶排料:1.1概述:为防止变形,提高加工精度,整体式斜顶导滑部分截面尺寸小于20X20的多个斜顶排在一起线切割外形。
1.2. 头部宽度形状差别较大情况的排料:排料如图1所示,可节约材料。
图1.头部宽度形状差别较大的斜顶排料图1.3.头部宽度形状差别不大情况的排料:排料如图2所示。
图2. 头部宽度形状差别不大的斜顶排料图-1图3. 头部宽度形状差别不大的斜顶排料图-21.4.注意事项:⑴.斜顶排料20mm线割装夹余量留在两非基准侧,这是根据机床的装夹条件。
当斜顶排料宽度>100mm,非基准侧都要留20mm余量。
当斜顶排料宽度≤100mm,机床可以夹住一侧的余量,即可将斜顶料夹紧,这样斜顶布料时只需要留一侧面的余量20mm即可。
(即在长度方向留20mm装夹),这主要是指那种整体方斜顶。
⑵.一根斜顶对应一个穿丝孔,穿丝孔直径可为4mm、5mm、6mm……,通常情况下打∮4的穿丝孔就可以,穿丝孔位置如图1、2所示,不可以打在装夹侧。
二、镶块布料:2.1挂台式小镶块排料:在布料时,应尽量使有浇位得一面布在外边,方便电极加工。
如图4所示:图4,筋位在毛料的外部意图2.2.镶块长宽尺寸大于15×15的情况:(1)挂台两侧有胶位的镶块,如图5所示图5.挂台两侧有胶位镶块示意图此类排料镶块加工工艺:准备开料,磨料,铣挂台台阶――→NC铣挂台两侧胶位;铣头部、其余两侧面筋位开粗――→电蚀(顶面形状需要电蚀的)――→线割分开――→配入主镶打侧面开粗胶位或单独打侧面开粗筋位――→抛光。
排料方式:挂台朝一面;底部及三侧面开净料,一侧面留20mm线割装夹余量,如图6所示。
图6. 挂台两侧有胶位的镶块排料方式(2)挂台两侧无胶位的镶块,如图7所示。
图7.挂台两侧无胶位,另两侧有胶位的镶块示意图此类排料镶块加工工艺:准备开料,磨料――→NC铣挂台另两侧胶位;铣头部胶位――→电蚀(顶面形状需要电蚀的)――→线割挂台并分开镶块――→抛光。
不规则零件的加工工艺

不规则零件的加工工艺在机械加工过程中,批量加工时必须使用工装设备才能提高生产率,使产品质量稳定。
对于简单轴类、盘类、套筒类零件,使用通用夹具就能满足要求;但复杂或者不规则零件的加工,需要设计专用夹具以提高加工效率,保证加工过程的顺利进行。
因此机床夹具设计是机械制造系统的重要组成部分。
作者通过实例研究不规则工件的工艺过程,并设计专用夹具。
1不规则工件零件图图1二维零件图文中不规则工件为曲柄板零件,其二维零件图如图1所示,三维图如图2所示。
该工件材料为45号钢铸件,属于异形零件,在加工时存在一定的难度,因此一定要设计合适的夹具方能确保所有工序的完成。
图2三维零件图该零件主要由圆柱面、端面、孔系等组成。
由图1得知,该零件尺寸公差主要有:30H8的通孔;偏心外圆柱29h6,偏心距为30±0·03,长24±0·03;8的圆孔深度为59±0·05。
粗糙度公差分别为:30H8的内孔粗糙度0·8μm;5-10和5-5粗糙度均为12·5μm,在180°范围内均布;103和44圆柱断面粗糙度均为6·3μm。
在整个加工过程中要充分考虑其技术要求以保证偏心孔的位置、小孔之间的角度关系以及表面质量要求等。
在机械加工过程中,批量加工时必须使用工装设备才能提高生产率,使产品质量稳定。
对于简单轴类、盘类、套筒类零件,使用通用夹具就能满足要求;但复杂或者不规则零件的加工,需要设计专用夹具以提高加工效率,保证加工过程的顺利进行。
因此机床夹具设计是机械制造系统的重要组成部分。
(1)锻造制坯:热模锻仍然是汽车齿轮件广泛使用的毛坯锻造工艺。
近年来,楔横轧技术在轴类加工上得到了大量推广。
这项技术特别适合为比较复杂的阶梯轴类制坯,它不仅精度较高、后序加工余量小而且生产效率高。
(2)正火:这一工艺的目的是获得适合后序齿轮切削加工的硬度和为最终热处理做组织准备,以有效地减少热处理变形。
皮革下料问题

4.2 问题一 此问题涉及到皮革制造业中皮料的优化排样。排样问题是典型的 NP 难问题。因此 普通的优化排样算法是难以求解的。在工程上,通常采用遗传或者神经网络等智能优化 算法,或者是启发式的近似算法。具体到这道题,所给的牛皮原料和皮件模板都是不规 则的,沙发有 46 个模板,椅子有 10 个模板,在订单确定的情况下,设计以利用率最大 为目标的排料算法。我们提出了以下思路: 首先裁剪出两张牛皮原料最大内接矩形,并求出各个模板的包络矩形。再借鉴钢管 下料模型【1】的思想,依据利用率最大这一优化目标,设计一定的裁剪原则,从而列 举两张牛皮原料可能的几种裁剪方式,将问题简化为整数规划问题。 4.3 问题二 第二问是先用 40 张牛皮做沙发,然后用剩下的余料制作和八张新增牛皮做尽可能 多的椅子。由于题目中没有给出新增牛皮的种类,方便起见,我们假设新增的牛皮都是 小牛皮。 4.4 问题三 通过分析易得,订单数不仅仅随时间变化,而且还受到以往订单数的影响。为简化 模型,我们首先用时间序列模型,对 2010 年沙发和餐椅的订单数进行短期预测。然后, 考虑到市场因素的影响,引入“价格弹性”这一概念,得到产品销售价格与订单数的等 量关系。然后通过推导,可得到利润和折扣率或价格的关系,通过求利润的最值得到促 销价格。考虑一些实际因素可得到价格范Fra bibliotek。xi
M i, j
num j
m1
m2
m2, 2
lei
P q
x
th
ch
d
2
四、
4.1 关于题目中若干语句的理解
问题的分析
“根据制造沙发的各个部位的皮模版可以制造一把皮沙发和一把餐椅” , 即认为题目 所给的沙发模板能够制造一把沙发,餐椅模版同样可以制造一把餐椅。 “某批沙发订单确认” ,即认为生产厂家已与客户签订合同,沙发订单已经确定。此 处“订单确认”来源于“面向订单生产( MTO) ” 。 “最后一张牛皮的利用率尽可能的大” , 在我们建立的模型中, 并未对最后一张牛皮 进行单独研究,而是追求所有待裁剪的牛皮利用率最大。
板料优化排样问题
板料优化排样问题摘要、在材料加工领域,板料优化排样是实现薄板和厚板材料充分利用的一个常见问题。
该问题是典型的NP完全问题,其求解过程复杂,求解耗时大,难以获得精确解。
这不利于该问题的工程应用,为此,目前学术界提出了多种用于解决该问题的近似算法,求取在工程应用中可接受且耗时合理的优化排样方案。
该文在对板料排样问题进行阐述的基础上,对近年来国内在板料优化排样问题方面所开展的研究进行了分析,对板料排样问题的发展前景进行了展望。
关键词、优化排样问题;板料优化;算法中图分类号、TP39文献标识码、A文章编号、1009-3044(2011)20-4983-03OnPlateNestingOptimizationProblemLIWei1,LIJian2(1.AcademicAdministrationofGuizhouNormalUniversity,Gu iyang550001,China;2.SchoolofMaterialsScienceandEngine eringofJiangsuUniversity,Zhenjiang212013,China)Abstract:PlatenestingoptimizationproblemisaCommonprob lemforsheetandplatematerialstoachievefulluseinthefiel dofmaterialprocessing.TheproblemisatypicalNP-completeproblem.Theproblemsolvingprocessiscomplex,tim e-consumingtosolvelarge,difficulttoobtainexactsolutions .Thisisnotconducivetotheproblemofengineeringapplicati ons,forwhich,forthecurrentacademicmadeavarietyofappro ximationalgorithmstosolvetheproblemofstrikeintheengin eeringapplicationsandtime-consumingreasonablyacceptableoptimalnestingprogram.Thispaperdescribesthesheetmetalnestingproblems,analysis oftherecentdomesticoptimalnestinginsheetissuesresearc hcarriedout,andlookedtotheproblemofsheetmetalnestingp rospects.Keywords:optimalnestingproblems;sheetoptimization;alg orithm在材料的加工制造中,原材料的规格和目标件规格之间具有复杂的组合关系。
不规则壳体制件的模具设计
・2 1・
・
冲 模
技 术
・
/
/
厂
的] 二 艺 措施 后 , 该 制 件可 通 过 一 次落 料 拉伸 成 形 。
3 工艺计算
3 . 1 冲裁 力 的计算
/ / / 。 。
一
冲裁力F ( N) 可 由下 公 式计 算 :
, h =K Lt r
3 中问部分毛坯展开轮廓
将 该制件横截 面近似看为矩形 、 椭 圆形 , 拉 伸力
可 由下 式计 算 :
F = 0. 5 -0. 8 Lt o - ^
的经济利用率 , 还会影 响到模具结构 、 生产率 、 制件质 量、 生产操作方便 与安全等。根据参考文献[ 1 】 中排样 的原则 , 考虑 到本制 件结构 的特殊性 , 确定制件排样
得毛坯形状及尺寸如图4 所示 。 由于该制件为不规则壳体 , 难 以精确计算毛坯尺 坯尺寸 ,
①未注内圆角R 0 . 5 ; ②允许局部裂纹 , 按标 准件接收
( b )
a 一
图 1 制件图 制件二维图 b ——制件三维 图
图 2 截面选取 图
《 模 具 制造> > 2 0 1 4 年第6 期
所以, F 1 . 3 x 2 1 0 x 0 . 2 5 x 6 0 0 = 4 0 , 9 5 0 N 4 l k N
罔 4 毛 坯 最 终 形 状 及 尺 寸 图
3 . 2 拉伸 力的计 算
( 1 ) 拉 伸力 的计算 。
( 2 ) 毛坯 排 样 图 的确 定 。 排样 T作 非 常 重要 。排 样 的合 理性 , 影 响 到 材料
s h e l l s t a mp i ng d i e d e s i g n a nd t h e wo r ki n g pr o c e s s o f d i e . Ke y wor ds :i r r e g u l a r s h e l l ; a n a l y s i s o f f o r mi n g p r o c e s s ; di e s t r u c t u r e
皮料优化排样的有效方法
皮料优化排样的有效方法
张玉萍;张春丽;蒋寿伟
【期刊名称】《软件学报》
【年(卷),期】2005(16)2
【摘要】根据汽车内饰等行业需求,对皮制品加工的优化排样问题进行了研究.创新地采用离散化处理方式,同时引进边界约束,使排样过程与皮料和样片的几何信息无关,使用基于顺序的启发式底左布局将样片顺次布置到皮料上,样片的最优布置顺序和角度依靠随机优化算法来实现.设计了简洁、实用的操作算子,并提出了基于模拟退火技术的遗传算法(simulated annealing based genetic algorithm,简称SABGA),该算法在优化搜索中能自适应地控制变异率,使得优化高效地逼近全局最优解.实验及对比结果表明,提出的优化排样方式特别适用于二维不规则形体在多个二维不规则平面上的优化排样.
【总页数】8页(P316-323)
【作者】张玉萍;张春丽;蒋寿伟
【作者单位】上海师范大学,机电学院,上海,200234;上海交通大学,机械与动力学院,上海,200030;上海师范大学,机电学院,上海,200234;上海交通大学,机械与动力学院,上海,200030
【正文语种】中文
【中图分类】TP391
【相关文献】
1.近代冯秋萍“仿呢料”与“仿皮料”绒线编结技艺 [J], 王楠;张竞琼
2.近代冯秋萍“仿呢料”与“仿皮料”绒线编结技艺 [J], 王楠;张竞琼;
3.皮鞋制作过程中,皮料片边操作分为几种? [J],
4.大长径比皮料玻璃管加工工艺研究及应用 [J], 苏德坦;孙建宁;陈晓倩;毛汉祺;韩晓明;杨光;肖杰;张正君;赵慧民
5.一种皮革原皮料均匀拉伸制作机 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
皮革松面解决方案(3篇)
第1篇一、引言皮革作为一种传统的天然材料,因其独特的质感、优良的透气性和耐久性而被广泛应用于各种场合。
然而,在皮革制品的使用过程中,常常会遇到皮革松面的现象,即皮革表面出现裂纹、裂口、起泡等缺陷,这不仅影响了皮革制品的外观和品质,还可能缩短其使用寿命。
本文将针对皮革松面的成因进行分析,并提出相应的解决方案,以期为皮革行业提供参考。
二、皮革松面成因分析1. 皮革材料因素(1)皮革原料:皮革松面可能与原料皮的质量有关。
如原料皮中含有过多的油脂、蛋白质等杂质,或者在加工过程中处理不当,都会导致皮革在后期使用中出现松面现象。
(2)皮革品种:不同品种的皮革具有不同的结构特点,如粗犷的绒面革、细腻的磨砂革等。
不同品种的皮革在加工和使用过程中,松面现象的发生程度也有所不同。
2. 加工工艺因素(1)加工设备:加工设备的不合格或操作不当会导致皮革表面受损,从而引发松面现象。
(2)加工工艺:在皮革加工过程中,如涂饰、定型、烘干等环节操作不当,均可能导致皮革松面。
3. 使用环境因素(1)湿度:皮革制品在潮湿环境下容易受潮膨胀,导致表面出现裂纹、起泡等现象。
(2)温度:温度变化对皮革的影响较大,过高的温度可能导致皮革收缩、变形,进而引发松面。
(3)摩擦:皮革制品在使用过程中,表面摩擦会导致皮革表面受损,从而出现松面现象。
三、皮革松面解决方案1. 优化皮革材料(1)选用优质原料皮:确保原料皮的质量,降低皮革松面现象的发生。
(2)优化加工工艺:在皮革加工过程中,严格控制工艺参数,减少杂质含量。
2. 改进加工工艺(1)提高加工设备质量:选用合格的加工设备,确保加工过程中皮革表面不受损伤。
(2)优化加工工艺:在涂饰、定型、烘干等环节,严格控制工艺参数,降低松面现象的发生。
3. 改善使用环境(1)控制湿度:保持皮革制品存放环境的干燥,避免潮湿环境对皮革造成损害。
(2)调节温度:在温度变化较大的环境中,采取适当的调节措施,降低温度对皮革的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不规则皮件排料方案研究摘要本文针对牛皮模板的排料问题,建立了排料优化模型和组合排料优化模型,并设计了相应的排料算法,获得了牛皮利用率最大时的排料方案。
本文首先将所给牛皮、沙发和餐椅模板的图像比例尺统一化,其次将图像网格化,最后矩阵化图像,得到牛皮模板的换算矩阵和皮件模板的最小包络矩形的换算矩阵。
问题一,要求给出N张牛皮模板的排料算法,使牛皮的利用率最大化,考虑到实际生产过程中批量化生产,本文以 2.42m的牛皮模板为例,给出制作一套沙发的排料算法。
利用Matlab软件,将图像矩阵二值化为0和1的换算矩阵,将牛皮模板划分为可放置和不可放置两个区域,设包络矩形的放置方向为随机量,通过换算矩阵之间的计算,将所有沙发模板安排完全,得到了每张牛皮的利用率。
经过多次模拟,得到使牛皮利用率最大的排料方案,当使用2.42m的牛皮模板时,需要3张牛皮,每张利用率分别为87.64%,86.83%,75.52%,牛皮总的利用率为85.68%η=。
问题二,在问题一模型的基础上进行改进,仍然以2.42m的牛皮模板为例计算。
首先按照问题一的方案裁剪40张牛皮得到13套沙发,剩余1张整牛皮和额外的8张整牛皮裁剪餐椅皮板,然后采用将沙发裁剪余量和完整牛皮模板组合使用和只利用9张完整模板两种方法设计排料方案,通过Matlab软件计算,在两种情况下均可生产27把餐椅,但在余量模板和完整模板配合使用情况下可获得更多规整余量。
本文针对牛皮排料的问题,建立了排料最优化模型,给出了排料算法,得到了牛皮利用率最大时的排料方案,为皮件排料问题提供了可行方案。
关键词:排料优化模型组合优化模型换算矩阵模拟仿真Matlab软件一、问题重述在实际生产生活中裁剪是必不可少的,裁剪的好坏、利用率的高低,直接影响生产厂家的经济利益,首先定义以下三个概念:1、牛皮:整张,未裁剪的牛皮原料,经过数码取像技术转化成CAD 文件格式的二维区域;2、皮板:最终产品的模板,一般由硬纸板制成的,用于裁剪。
产品设计完后,经过数码取像技术转化成CAD 文件格式的二维区域;3、皮件:由皮革缝制成皮套,再通过其他工艺加工成的最终产品(例如皮包鞋、皮沙发等)。
根据以上定义,本问题研究的对象是数码二维区域。
附件提供了牛皮模板、沙发模板和椅子模板,根据制造沙发和椅子的各个部位的皮模板可以制造一把皮沙发和一把餐椅。
在实际生产中经常要求最后一张牛皮的利用率要尽可能大,解觉以下两个问题: 1、假设N 张牛皮的模板都和提供的两张一样,试建立数学模型,在厂家皮单确定的情况下,确定针对N 张牛皮的排料算法,要求使牛皮的利用率最大化;2、在某批沙发订单确认的情况下,在采购了40 张牛皮裁剪结束之后(发现有一定余量),插入一个餐椅皮件订单。
利用裁剪的余量,再增加8 张牛皮,计算出增加的餐椅数量。
二、基本假设1. 不考虑裁剪牛皮的刀口宽度。
2. 裁剪没有失误,牛皮无损坏。
3. 所有牛皮原料都完整。
4. 假设第二问中的40张牛皮和8张牛皮均为2.4平方米。
5.假设使用相同规格的牛皮制作沙发,不考虑套排。
三、符号说明1. j N —表示与牛皮模板j 的数量(1,2j =);2. j C —表示牛皮模板j 的实际面积(1,2j =);3. j A —表示牛皮模板j 的集合(1,2j =);4. (,)i i x y —表示沙发模板中第i 个部件的左上顶点坐标(i=1,2,3,…,46);5. i r —0-1变量,表示沙发模板中第i 个部件包络矩形的方向等于0表示横放, 等于1表示纵放(i=1,2,3,…,46);6. i L —表示沙发模板中第i 个部件包络矩形的换长(i=1,2,3,…,46);7. i W —表示沙发模板中第i 个部件包络矩形的换宽(i=1,2,3,…,46);8. i S —表示沙发模板中第i 个部件包络矩形的换面积(i=1,2,3,…,46); 9. i B —表示沙发模板中第i 个部件的占用空间集合(i=1,2,3,…,46);10. i p —0-1变量,表示沙发模板中第i 个部件是否排在当前模板(i=1,2,3,…,46); 11. j G —表示牛皮模板j 的余量部分的面积(1,2j =); 12. j D —表示牛皮模板j 的余量部分占用空间集合(1,2j =)。
四、图像与数据预处理牛皮模板及皮件各部件的几何形状都是二维不规则的,在排料中,要获取模板和各部件的几何信息,本题将信息以图像的形式给出,因此,需要对所给图像进行处理,包括图像的网格化处理和获得图像的数据矩阵。
图像处理具体过程见图4-1。
图4-1图像处理过程4.1图像网格化(1)离散化处理利用Matlab 软件[2]处理图像如下:Step 1读取灰度图像,获得灰度图像矩阵; Step 2将图像二值化,获得二进制矩阵;Step 3以20mm 为网格宽度改变二进制矩阵,将图像网格化,使边界正交化; Step 4获得图像的多边形区域。
(2)网格大小的确定如以单像素代表长度为网格基准,软件无法完全显示图像,为后续处理带来不便,再考虑到精度的要求,实际20mm 的长度为网格的宽度绘制网格。
(3)比例尺的统一将图像网格化处理之后, 根据(4.1)确定出每张图像中一单位像素对应的实际距离,进而使实际距离相同,使确定的比例尺统一化。
2=换算面积换算长度()实际面积实际长度(4.1)4.2换算数据矩阵换算数据矩阵是指将图像网格化处理之后,以单位网格的大小作为数据矩阵的元素,数据矩阵为包含0和1的二维矩阵,矩阵中1用来表示该位置包含在图像轮廓内。
4.2.1牛皮模板换算数据矩阵将牛皮网格化处理之后,通过矩阵可以表示网格化之后图像的信息,矩阵中有1元素的位置则是牛皮模板的内部位置。
所有1元素所在点组成牛皮模板的空间集合。
4.2.2皮件模板换算数据矩阵(1)最小包络矩形将沙发各部件的边界正交处理之后,各部件的几何信息已改变为多边形,首先将凹多边形转化成凸多边形,进而确定出46个凸多边形。
对于确定的46个凸多边形,因为最小包络矩形至少有一条边与该多边形的某一条边重合,具有n 个顶点的凸多边形,共有n- 1条边,所以可以作出n-1个外接矩形。
依次计算这n-1个外接矩形的面积,之后比较大小,就可以确定所有46个部件的最小包络矩形。
计算包络矩形参数的步骤如下:Step 1计算第i 条边与x 轴的夹角,可以根据连接第i 条边两端的顶点坐标求得,然后以顶点i 为中心对多边形进行旋转,使第i 条边与x 轴平行,则第i 个最小包络矩形的底边与旋转后的第i 条边重合。
Step 2多边形旋转后更新所有的顶点坐标,更新方式按式进行,然后在所有已更新坐标值的顶点中搜寻最大和最小的x 值以及最大的y 值。
''1111''k ''i cos sin sin cos k k k i i ix y x y x y x y x y x y θθθθ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥=⨯⎢⎥-⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦Step 3计算最小包络矩形的面积''''m axm in m ax m in ()()i s y y x x =-⨯-,同时记录下矩形的长''''m ax m in m ax m in m ax(,)i l y y x x =--,短边''''m ax m in m ax m in m in(,)i w y y x x =--。
依次循环执行上述步骤直到n-1个包络矩形全部求出,再逐个比较面积,最小的就是该多边形的最小包络矩形。
同时记录数据i i S s =,i i L l =,i i W w =。
利用Matlab 软件,按照Step 1- Step 3的顺序计算求得沙发各部件包络矩形的参数如表4-1所示。
2.换长与换宽的单位是20mm。
通过相同的方法,利用Matlab软件求得餐椅各部件的包络矩形参数表如表4-2所示。
表4-2 餐椅各部件包络矩形参数2. 换长与换宽的单位是20mm。
(2)包络矩形的换算矩阵包络矩形的换算矩阵为i i L W ⨯维的单位矩阵,表示皮件第i 个部件的轮廓内部空间,该矩阵决定了排料时各部件所要占用的空间。
五、问题分析5.1背景概述优化排料通常是指在一组给定尺寸的原始板材上,尽可能多地排放需要的二维零件产品,使得板材利用率最大,以减少废料。
排料是优化组合[3]的一类典型问题,在工业生产中具有较高的实用和推广价值。
提高板材利用率将会降低企业的生产成本,会给企业带来经济效益。
所以,排料问题的研究具有重要的经济价值。
从计算复杂性理论来看,排料问题属于具有较高计算复杂性的一类问题NP 完全问题,NP 是Nondeterministic Polynomial 的缩写,即为非确定型多项式的意思。
对于NP 完全问题,至今还没有找到多项式时间算法,因而,求其有效的近似解法是必由之路。
对于这类问题,以目前已经成熟的计算理论和算法,或者根本无法求解,或者其求解的计算量是爆炸性的。
所以,如何找到一种有效的排料算法具有重要的经济价值和理论价值。
5.2问题一的分析本问题为在订单确定的情况下,要求我们针对N 张牛皮,建立数学模型,确定皮件的排料算法,使牛皮的总利用率最大,这是寻找平面最优布局的优化问题[1]。
在实际生产中,工厂均是规模化生产,因此本题实际要求我们确定制作单张皮件的排料算法,以利于规模化生产。
本题要求牛皮总利用率最大化的前提下,还要求使最后一张牛皮的利用率最大,厂家要求最后一张牛皮剩余的部分尽量规整,利于再利用,则最后一张率用率最大包括剩余牛皮的面积最大即余量最大和剩余部分形状尽可能规则两个部分。
因此确定本题为双目标优化问题,使总利用率最大的目标优先于使最后一张牛皮的利用率最高的目标。
解决本题性质的双目标问题,可以通过两个阶段,建立不同的模型实现。
(1)第一阶段模型首先明确本阶段的目标是:确定制作单张皮件的排料算法,使牛皮的总利用率最大化。
牛皮的利用率为皮件总面积与牛皮总面积和牛皮余量面积之差的比值,表述为:=-皮件总面积利用率牛皮总面积牛皮余量面积其次,根据题意的要求,以皮件各部件在牛皮原料上的位置作为决策变量。
再次,根据皮件各部件必须在牛皮原料上,并且在排料中不能重叠,以及各部件均要排料一次等限制,确定排料的约束条件。
以此建立优化模型,因建立模型中包含集合等元素,普通的算法不能直接求解。
考虑将算法进行如下改进:将皮件各部件按照面积大小,从牛皮左上角开始,依次从左至右,从上至下在牛皮上排布,使用模拟仿真[4]的方法,对问题进行求解。
