数学建模 第九章 概率模型M09-2010
概率2009-2010试题及答案

[七]、 (满分 8 分) (此题仅学过 1 至 9 章的学生做;学过 1 至 9 章和 11-13 章的学生不做)
将红、白、黑三只球随机地逐个放入编号为 1,2,3,4 的四个盒内 (每盒容纳球的个数不限) ,以 X 表示有球盒子的最小号码, 试求: (1)随机变量 X 的分布律; (2) EX .
北京航空航天大学
BEIHANG UNIVERSITY
2009-2010 学年 第二学期期末
考试统一用答题册
考试课程 概率统计 (09J70040) 概率统计与随机过程 A(09J70050)
A
班 级_____________ 姓 名______________ 考场教室_________
题号 一 二 三
2、一盒内装有 5 个红球和 15 个白球,从中不放回取 10 次,每次取一个球, 则第 5 次取球时得到的是红球的概率是( (A) ) 。
1 ; 5
(B)
1 ; 4
(C)
1 1 ; (D) 3 2
。
0, x 1 0.3,1 x 3 3、已知离散型随机变量 X 的分布函数为 F ( x) 0.5,3 x 4 1, x 4
六、 (满分 12 分)
……解 (1)根据题设条件知
X
i 1
9
i
~ N (0,9 2 ) ; ………………………3 分
1
9
(2)
X
i 1
9
i
~ N (0,1) ,
Yi
~ N (0,1) ,
1
2
Y
i 1
9
2
i
9 Y ( i )2 ~ 2 (9) ;………………………6 分 i 1
数学建模-概率模型

如对均值为mu、标准差为sigma的正态分布,举例如下:
1.密度函数:p=normpdf(x,mu,sigma) (当mu=0,sigma=1时可缺省)
例 1 画出正态分布 N (0,1) 和 N (0,22 ) 的概率密度函数图形.
在MATLAB中输入以下命令: x=-6:0.01:6; y=normpdf(x); z=normpdf(x,0,2); plot(x,y,x,z)
9.1 传送系统的效率
背
传送带
景 挂钩
产品
工作台
工人将生产出的产品挂在经过他上方的空钩上运走,若 工作台数固定,挂钩数量越多,传送带运走的产品越多。
在生产进入稳态后,给出衡量传送带效 率的指标,研究提高传送带效率的途径
模型分析
• 进入稳态后为保证生产系统的周期性运转,应 假定工人们的生产周期相同,即每人作完一件产 品后,要么恰有空钩经过他的工作台,使他可将 产品挂上运走,要么没有空钩经过,迫使他放下 这件产品并立即投入下件产品的生产。 • 工人们生产周期虽然相同,但稳态下每人生产 完一件产品的时刻不会一致,可以认为是随机的, 并且在一个周期内任一时刻的可能性相同。
例:现有100个零件,其中95个长度合格,94个直径和格, 92个两个尺寸都合格。任取一个,发现长度合格,问直径 合格的概率。
设A=‘长度合格’,B=‘直径合
格’
P( A) 95 , P( AB) 92
100
100
P(B | A) P( AB) 92 P( A) 95
全概率公式和贝叶斯公式
u0 u0
L(
x)
c 2
x
0
(
x
r
)
p(r
)dr
数学建模概率模型

2
记为X ~ N(, 2 )
背景:如果决定试验结果X的是大量随机因素的总和,假设
各个因素之间近似独立,并且每个因素的单独作用相对均匀 地小,那么X的分布近似正态分布。
如:同龄人的身高、体重、考试分数、某地区年降水量等。
3、数学期望的概念和计算 描述了随机变量的概率取值中心—均值
数学期望
Y gX
E( X ) xk pk k 1
E( X ) xf ( x)dx E(Y ) EgX g( xk ) pk k 1
E(Y ) Eg( X )
g( x) f ( x)dx
4、MATLAB中相关的的概率命令
常见的几种分布的命令字符为: 正态分布:norm 指数分布:exp 泊松分布:poiss 二项分布:bino
G(n)
n
0
[(
a
b)r
(b
c)(n
r
)]
p(r
)drຫໍສະໝຸດ n(ab)np(r
)dr
dG (a b)np(n)
n
(b c) p(r)dr
dn
0
(a b)np(n) n (a b) p(r)dr
n
(b c)0 p(r)dr (a b)n p(r)dr
例3 有10台机床,每台发生故障的概率为0.08,而10台机床工作 独立,每台故障只需一个维修工人排除.问至少要配备几个维修 工人,才能保证有故障而不能及时排除的概率不大于5%。
解:随机变量X示发生故障的机床的台数,则 X ~ B(10,0.08)
即P{X n} 0.95
数学建模概率模型教案

数学建模概率模型教案教案标题:数学建模概率模型教案教学目标:1. 了解数学建模中概率模型的基本概念和应用;2. 掌握概率模型的构建方法和计算技巧;3. 培养学生的数学建模能力,能够运用概率模型解决实际问题。
教学重点:1. 概率模型的基本概念和应用;2. 概率模型的构建方法;3. 概率模型的计算技巧。
教学难点:1. 如何应用概率模型解决实际问题;2. 如何进行概率模型的计算。
教学准备:1. 教师准备:a. 熟悉概率模型的基本概念和应用;b. 准备案例或实际问题,用于演示概率模型的构建和计算;c. 准备教学PPT或其他辅助教学工具。
2. 学生准备:a. 复习概率论的基本知识;b. 准备课前作业,用于引导学生思考概率模型的应用。
教学过程:一、导入(5分钟)1. 向学生介绍今天的教学内容和目标;2. 提问:你们对概率模型有什么了解?它在数学建模中有什么应用?二、概念讲解(15分钟)1. 讲解概率模型的基本概念和定义;2. 介绍概率模型在数学建模中的应用领域;3. 通过实例解释概率模型的构建过程。
三、构建概率模型(20分钟)1. 介绍概率模型的构建方法,例如贝叶斯网络、马尔可夫链等;2. 通过案例演示概率模型的构建过程;3. 引导学生思考如何根据实际问题构建概率模型。
四、概率模型的计算(20分钟)1. 介绍概率模型的计算技巧,例如条件概率的计算、联合概率的计算等;2. 通过案例演示概率模型的计算过程;3. 练习:提供一些练习题,让学生进行概率模型的计算。
五、应用实践(15分钟)1. 提供一个实际问题,要求学生运用所学的概率模型解决;2. 学生分组讨论,提出解决方案;3. 学生展示解决方案,进行讨论和评价。
六、总结与拓展(10分钟)1. 总结概率模型的基本概念、构建方法和计算技巧;2. 拓展:介绍其他与概率模型相关的知识,如随机过程、蒙特卡洛模拟等。
教学辅助工具:1. PPT:用于呈现教学内容和案例演示;2. 黑板或白板:用于解题和学生互动;3. 实例或案例:用于演示概率模型的构建和计算;4. 练习题:用于巩固学生的概率模型应用能力。
概率模型(定稿)
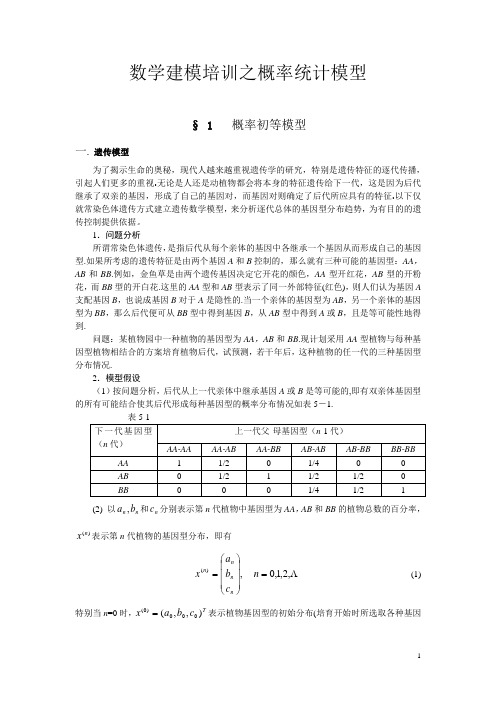
数学建模培训之概率统计模型§ 1 概率初等模型一. 遗传模型为了揭示生命的奥秘,现代人越来越重视遗传学的研究,特别是遗传特征的逐代传播,引起人们更多的重视.无论是人还是动植物都会将本身的特征遗传给下一代,这是因为后代继承了双亲的基因,形成了自己的基因对,而基因对则确定了后代所应具有的特征.以下仅就常染色体遗传方式建立遗传数学模型,来分析逐代总体的基因型分布趋势,为有目的的遗传控制提供依据。
1.问题分析所谓常染色体遗传,是指后代从每个亲体的基因中各继承一个基因从而形成自己的基因型.如果所考虑的遗传特征是由两个基因A 和B 控制的,那么就有三种可能的基因型:AA ,AB 和BB .例如,金鱼草是由两个遗传基因决定它开花的颜色,AA 型开红花,AB 型的开粉花,而BB 型的开白花.这里的AA 型和AB 型表示了同一外部特征(红色),则人们认为基因A 支配基因B ,也说成基因B 对于A 是隐性的.当一个亲体的基因型为AB ,另一个亲体的基因型为BB ,那么后代便可从BB 型中得到基因B ,从AB 型中得到A 或B ,且是等可能性地得到.问题:某植物园中一种植物的基因型为AA ,AB 和BB .现计划采用AA 型植物与每种基因型植物相结合的方案培育植物后代,试预测,若干年后,这种植物的任一代的三种基因型分布情况.2.模型假设 (1)按问题分析,后代从上一代亲体中继承基因A 或B 是等可能的,即有双亲体基因型的所有可能结合使其后代形成每种基因型的概率分布情况如表5-1.表5-1(2) 以n n b a ,和n c 分别表示第n 代植物中基因型为AA ,AB 和BB 的植物总数的百分率,)(n x 表示第n 代植物的基因型分布,即有,)(⎪⎪⎪⎭⎫⎝⎛=n n n n c b a x ,2,1,0=n (1) 特别当n =0时,T c b a x ),,(000)0(=表示植物基因型的初始分布(培育开始时所选取各种基因型分布),显然有.1000=++c b a3.模型建立注意到原问题是采用AA 型与每种基因型相结合,因此这里只考虑遗传分布表的前三列. 首先考虑第n 代中的AA 型,按上表所给数据,第n 代AA 型所占百分率为1110211---⋅+⋅+⋅=n n n n c b a a 即第n-1代的AA 与AA 型结合全部进入第n 代的AA 型,第n -1代的AB 型与AA 型结合只有一半进入第n 代AA 型,第n -1代的BB 型与AA 型结合没有一个成为AA 型而进入第n 代AA 型,故有1121--+=n n n b a a (2)同理,第n 代的AB 型和BB 型所占有比率分别为1121--+=n n n c b b (3)0=n c (4)将(2)、(3)、(4) 式联立,并用矩阵形式表示,得到,)1()(-=n n Mx x),2,1( =n (5)其中⎪⎪⎪⎭⎫ ⎝⎛=00012/1002/11M利用(5)进行递推,便可获得第n 代基因型分布的数学模型)0()2(2)1()(x M x M Mx x n n n n ====-- (6)(6)式明确表示了历代基因型分布均可由初始分布)0(x与矩阵M 确定.4.模型求解这里的关键是计算nM .为计算简便,将M 对角化,即求出可逆阵P ,使Λ=-MP P 1,即有1-Λ=P P M从而可计算 1-Λ=P P M nn),2,1( =n其中Λ为对角阵,其对角元素为M 的特征值,P 为M 的特征值所对应的特征向量.分别为,11=λ 212=λ,03=λ⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=121,011,001321p p p故有1100210111,0211-=⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎭⎫ ⎝⎛=ΛP P即得⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--=1002101110211100210111nnM ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=--00021210211211111n n n n 于是 ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛=--00011)(000212102112111c b a c b a x n nn nn n n n或写为⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=--=--0)21()21()21()21(1010010n n n n n n nc c b b c b a 由上式可见,当∞→n 时,有0,0,1→→→n n n c b a即当繁殖代数很大时,所培育出的植物基本上呈现的是AA 型,AB 型的极少,BB 型不存在.5.模型分析(1)完全类似地,可以选用AB 型和BB 型植物与每一个其它基因型植物相结合从而给出类似的结果.特别是将具有相同基因植物相结合,并利用前表的第1、4、6列数据使用类似模型及解法而得到以下结果:000021,0,,21b c c b b a a n n n +→→+→这就是说,如果用基因型相同的植物培育后代,在极限情形下,后代仅具有基因AA 与BB ,而AB 消失了.(2)本例巧妙地利用了矩阵来表示概率分布,从而充分利用特征值与特征向量,通过对角化方法解决了矩阵n 次幂的计算问题,可算得上高等代数方法应用于解决实际的一个范例.二. 传送系统的效率模型1.问题的提出在机械化生产车间里你可以看到这样的情景:排列整齐的工作台旁工人们紧张地生产同一种产品,工作台上方一条传送带在运转,带上设置着若干钩子,工人们将产品挂在经过他上方的钩子上带走,如图1.当生产进入稳定状态后,每个工人生产出一件产品所需时间是不变的,而他要挂产品的时刻却是随机的.衡量这种传送系统的效率可以看它能否及时地把工人们生产的产品带走,显然在工人数目不变的情况下传送带速度越快,带上钩子越多,效率会越高.我们要构造一个衡量传送系统效率的指标,并且在一些简化假设下建立一个模型来描述这个指标与工人数目、钩子数量等参数的关系.2.问题的分析进入稳态后为保证生产系统的周期性运转,应假定工人们的生产周期相同,即每人作完一件产品后,要么恰有空钩经过他的工作台,使他可将产品挂上运走,要么没有空钩经过,迫使他放下这件产品并立即投入下件产品的生产。
数学建模概率模型学习教案

u=1/m
p=1-(1-1/m)n
D=m[1-(1-1/m)n]/n
第18页/共43页
第十九页,共43页。
模型
(传m送óx带ín效g)率(一周期内运走 产解品释数与生产总数之比)
D m [1 (1 1 )n ]
n
m
若(一周期运行的)挂钩(guà〃gōu)数m远大于工作台数
n, 则
D
m [1 (1 n
如:同龄人的身高、体重(tǐzhòng)、考试分数、某地区年降水 量等。
第7页/共43页
第八页,共43页。
3、数学期望(qīwàng)的概念和计算
描述了随机变量的概率取值中心 (zhōngxīn)—均值
数学(shùxué) 期望
Y gX
E( X ) xk pk k 1
E( X ) xf ( x)dx E(Y ) EgX g( xk ) pk k 1
4)每人在生产完一件产品时都能且只能触到一只挂钩
,若这只挂钩是空的,则可将产品挂上运走;若该钩非 空,则这件产品被放下,退出运送系统。
第17页/共43页
第十八页,共43页。
模型 •(定m义óx传ín送g带) 效率为一周期内运走的产品(chǎnpǐn)数(记作 s建,待立定)与生产总数 n(已知)之比,记作 D=s /n
丙厂 0.03 0.05
概(2率)若;已知取到的是次品,问此次(cǐ cì)品是哪个厂生产的可能性更大?
解 设A=“取到的是一只次品”,Bi=“所取产品由第i厂提供”,
易知B1,B2,B3是样本空间的一个划分
。
3
(1)由全概率公式: p( A) P(Bi )P( A|Bi )
i 1
=0.15×0.02+0.80×0.01+0.05×0.03=0.012
概率模型

L ( x ) c 2 0 ( x r ) p ( r ) dr c 3 x ( r x ) p ( r ) dr
建模与求解 建模与求解
1)设 x<s, 求 u 使 J(u) 最小,确定S
dJ du
xu S
c 0 c 1 u L ( x u ), J (u ) L(x)
x
I ( x ) c1 x L ( x )
L ( x ) c 2 0 ( x r ) p ( r ) dr c 3 x ( r x ) p ( r ) dr
J(u)在u+x=S处达到最小
J(u)与I(x)相似 I(x)在x=S处达到最小值I(S) I(x)图形 I(S)
I(x)
I(S)+c0
I(S)
0 s S x
I ( x ) c 0 I ( S ) 的最小正根 s
2 轧钢中的浪费
背 景
随机因 素影响 轧制钢材 两道工序 粗轧 • 粗轧(热轧) ~ 形成钢材的雏形 • 精轧(冷轧) ~ 得到钢材规定的长度 粗轧钢材长 度大于规定 精轧 切掉多余 部分
钢材长度正态分布
x
u 0 u 0
L ( x ) c 2 0 ( x r ) p ( r ) dr c 3 x ( r x ) p ( r ) dr
xu
c 1 c 2 0
p ( r ) dr c 3 x u p ( r ) dr
p ( r ) dr 1
I ( x ) c0 I ( S )
不订货
记 c1 x L ( x ) I ( x )
订货点 s 是 I ( x ) c 0 I ( S ) 的最小正根
数模课件FEIM092

改为新的假定(习题8):
1.粗轧钢材长度在规定长度[l1, l]内降级使用 2.粗轧钢材长度小于规定长度l1整根报废
日常生产、生活中的类似问题: 在随机因素影响下过程有两种结果,其损失(或收益) 各有不同,综合考虑来确定应采取的决策,在统计 意义下使总损失最小(或总收益最大).
xp( x)dx
l
lp(x)dx
m
lP
直接方法
粗轧一根钢材平均浪费长度
粗轧N根 成品材 PN根 总长度mN 成品材长度l PN
共浪费长度 mN-lPN
mN lPN m lP
N
建模 选择合适的目标函数
粗轧一根钢材平均浪费长度 mN lPN m lP N
粗轧N根得成品材 PN根
得到一根成品材平均浪费长度
0.5939 0.6044 0.6150 0.6254 0.6351 0.6434 0.6492 0.6517 0.6512 0.6485 0.6445
0 0 0.0000 0.0000 0.0007 0.0066 0.0341 0.1123 0.2612 0.4630 0.6666
0 0 0 0 0 0.0000 0.0002 0.0023 0.0160 0.0650 0.1780
mN lPN PN
m l P
略去常数l, 记 J (m) m P(m)
更合适的目标函数
P(m)
l
p( x)dx,
p(x)
1
e
(
xm)
2 2
2
2
优化模型:已知l ,, 求m 使J(m) 最小.
求解 J (m) m
P(m)
y
xm,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u0 u0
L( x) c2 0 ( x r ) p(r )dr c3 x (r x) p(r )dr
建模与求解 建模与求解
1)设 x<s, 求 u 使 x J(u) 最小,确定S L( x) c2 0 ( x r ) p(r )dr c3 x (r x) p(r )dr
不订货
L( x) c0 c1 (S x) L(S ) c1 x L( x) c0 c1S L(S )
I ( x) c0 I (S )
记 c1 x L( x) I ( x)
订货点 s 是 I ( x) c0 I (S ) 的最小正根
建模与求解
I ( x) c0 I (S ) 最小正根的图解法
xp( x)dx l lp( x)dx m lP
直接方法 粗轧N根 总长度mN 成品材 PN根
粗轧一根钢材平均浪费长度
成品材长度l PN
mN lPN m lP N
共浪费长度 mN-lPN
建模
选择合适的目标函数
mN lPN 粗轧一根钢材平均浪费长度 m lP N
( z ) z ( y )dy
z ( z) / ( z)
F ( z) z F ( z ) ( z ) / ( z )
( y)
1 e 2
y2 2
求解
z
F ( z) z
问 售出一份赚 a-b;退回一份赔 b-c 题
购进太多卖不完退回赔钱
每天购进多少份可使收入最大?
分 购进太少不够销售赚钱少 析
应根据需求确定购进量. 每天需求量是随机的
存在一个合 适的购进量
每天收入是随机的
优化问题的目标函数应是长期的日平均收入 等于每天收入的期望
准 备 建 模
调查需求量的随机规律——每天 需求量为 r 的概率 f(r), r=0,1,2… • 设每天购进 n 份,日平均收入为 G(n) • 已知售出一份赚 a-b;退回一份赔 b-c
I(x)
I(S)+c0
I(S)
0 s S x
I ( x) c0 I (S ) 的最小正根 s
9.4 轧钢中的浪费
背 景
随机因 素影响
轧制钢材 两道工序 粗轧
• 粗轧(热轧) ~ 形成钢材的雏形 • 精轧(冷轧) ~ 得到钢材规定的长度 粗轧钢材长 度大于规定 精轧 切掉多余 部分
钢材长度正态分布
xsu 0
x s u 0, x u S
确定(s, S), 使目标函数——每周总费用的平均值最小 s ~ 订货点, S ~ 订货值 订货费c0, 购进价c1, 贮存费c2, 缺货费c3, 销售量 r 平均 费用
c0 c1u L( x u ), J (u ) L( x )
r n 售出r 赚(a b)r
退回n r 赔(b c)(n r )
r n 售出n 赚(a b)n
G(n) [( a b)r (b c)( n r )] f (r )
r 0 n r n 1
(a b)nf (r )
求 n 使 G(n) 最大
求解
n
将r视为连续变量
f (r ) p(r )dr(概率密度)
G(n) 0 [( a b)r (b c)( n r )] p(r )dr n (a b)np(r )dr
dG (a b)np(n) n (b c) p(r )dr 0 dn (a b)np(n) (a b) p(r )dr
n
(b c) p(r )dr (a b) p(r )dr
0 n
n
dG 0 dn
p ( r ) dr a b p ( r ) dr b c
n 0 n
结果解释
n
p ( r ) dr a b p ( r ) dr b c
n 0 n
第九章
概率模型
9.1 传送系统的效率
9.2 报童的诀窍
9.3 随机存贮策略
9.4 轧钢中的浪费 9.5 随机人口模型 9.6 航空公司的预订票策略 9.7 学生作弊现象的调查和估计
确定现象
随机现象
统计学家和赌场经理对待随机现象的态度几乎一样, 只是前者用的是随机数,后者用的是扑克牌——斯汀 • 骰子赌博的诀窍 • 敏感问题调查 调查目的:敏感问题出现的概率x有多大? 调查问卷:1.敏感问题,2.普通问题;回答:是,否 被调查人按单双学号回答问题1或2,答卷只有是或否 已知普通问题回答“是”的先验概率 p 设调查人数为n,其中回答“是”的人数为m
模型假设
1)n个工作台均匀排列,n个工人生产相互独立, 生产周期是常数; 2)生产进入稳态,每人生产完一件产品的时刻在 一个周期内是等可能的; 3)一周期内m个均匀排列的挂钩通过每一工作台 的上方,到达第一个工作台的挂钩都是空的; 4)每人在生产完一件产品时都能且只能触到一只 挂钩,若这只挂钩是空的,则可将产品挂上运走; 若该钩非空,则这件产品被放下,退出运送系统.
模型假设
• 每次订货费c0, 每件商品购进价c1, 每件商品
一周贮存费c2, 每件商品缺货损失费c3 (c1<c3). • 每周销售量 r为连续随机变量, 概率密度 p(r) .
• 周末库存量x, 订货量 u, 周初库存量 x+u.
• 每周贮存量按 x+u-r 计算 .
建模与求解
(s, S) 存贮策略
均值可以调整
方差由设备精度确定
粗轧钢材长 度小于规定
整根报废
问题:如何调整粗轧的均值,使精轧的浪费最小.
分析
设已知精轧后钢材的规定长度为 l, 粗轧后钢材长度的均方差为 .
记粗轧时可以调整的均值为 m,则粗轧得到的 钢材长度为正态随机变量,记作 x~N(m, 2).
P P( x l ) P P( x l )
xn / 2 pn / 2 m
x 2m / n p
随机模型
确定性因素和随机性因素
随机因素可以忽略 随机因素影响可以简单 地以平均值的作用出现 随机因素影响必须考虑 概率模型 统计回归模型 确定性模型
随机性模型 马氏链模型
9.1 传送系统的效率
背 景
传送带 挂钩 产品 工作台
工人将生产出的产品挂在经过他上方的空钩上运走,若工 作台数固定,挂钩数量越多,传送带运走的产品越多. 在生产进入稳态后,给出衡量传送带效 率的指标,研究提高传送带效率的途径.
求解
m J ( m) P ( m)
m l xm y , ,
J ( ) ( )
P(m) l p( x)dx p ( x)
( xm ) 1 e 2 2
2 2
( z ) z ( y )dy
( y)
u0 u0
c0 c1u L( x u ), J (u ) L( x )
x
I ( x) c1x L( x)
L( x) c2 0 ( x r ) p(r )dr c3 x (r x) p(r )dr
J(u)在u+x=S处达到最小
J(u)与I(x)相似 I(x)在x=S处达到最小值I(S) I(x)图形 I(S)
p(r )dr P , p(r )dr P
0 1 n
2
P a b 1 取n使 P2 bc
a-b ~售出一份赚的钱
b-c ~退回一份赔的钱
p
P1 0
P2 n r
(a b) n , (b c) n
9.3 随机存贮策略
问 题
以周为时间单位;一周的商品销售量为随机; 周末根据库存决定是否订货,供下周销售. (s, S) 存贮策略:下界s, 上界S,当周末库存小于s 时订货,使下周初的库存达到S; 否则,不订货. 考虑订货费、存贮费、缺货费、购进费,制订 (s, S) 存贮策略,使(平均意义下)总费用最小.
切掉多余部 分的概率
整根报废 的概率
p(概率密度)
m P , P
m P , P
存在最佳的m使总的浪费最小 0
P P P´ P´ l m m
x
建模
选择合适的目标函数 整根报废 的浪费
l
总浪费 = 切掉多余部分 + 的浪费
W l ( x l ) p( x)dx xp( x)dx
u=1/m
p=1-(1-1/m)n
D=m[1-(1-1/m)n]/n
模型解释
传送带效率(一周期内运走 产品数与生产总数之比)
m [1 (1 1 ) n ] D n m
若(一周期运行的)挂钩数m远大于工作台数n, 则
m n n( n 1) n 1 D [1 (1 )] 1 2 n m 2m 2m
定义E=1-D (一周期内未运走产品数与生产总数之比) 当n远大于1时, E n/2m ~ E与n成正比,与m成反比 若n=10, m=40, D87.5% (89.4%) 提高效率 的途径: • 增加m
• 习题1
9.2 报童的诀窍
报童售报: a (零售价) > b(购进价) > c(退回价)
x u dJ c1 c2 0 p(r )dr c3 xu p(r )dr du
c0 c1u L( x u ), J (u ) L( x )
u0 u0
xu S
p(r )dr 1
0
(c1 c2 )0 p(r )dr (c3 c1 )S p(r )dr
