迈克尔逊干涉仪实验报告数据处理
迈克尔逊干涉仪实验报告

迈克尔逊干涉仪实验报告一、实验目的1、了解迈克尔逊干涉仪的结构、原理和调节方法。
2、观察等倾干涉和等厚干涉条纹,加深对光的干涉现象的理解。
3、测量激光的波长。
二、实验原理迈克尔逊干涉仪是一种利用分振幅法产生双光束干涉的精密光学仪器。
其原理是一束光被分光板分成两束,一束经反射镜 M1 反射后沿原路返回,另一束经反射镜 M2 反射后也沿原路返回,两束光在分光板处相遇发生干涉。
当 M1 和 M2 严格垂直时,产生的是等倾干涉条纹。
此时,干涉条纹是一组同心圆环,条纹的形状取决于入射光的波长和两反射镜之间的距离 d。
当 d 增大时,条纹从中心向外“冒出”;当 d 减小时,条纹向中心“缩进”。
当 M1 和 M2 不严格垂直时,产生的是等厚干涉条纹。
此时,干涉条纹是与 M1 和 M2 交线平行的直条纹,条纹的间距与两反射镜之间的夹角以及入射光的波长有关。
三、实验仪器迈克尔逊干涉仪、HeNe 激光器、扩束镜、观察屏等。
四、实验步骤1、仪器调节调节迈克尔逊干涉仪的底座水平,使仪器稳定。
打开激光器,使激光束大致垂直入射到分光板上,调节反射镜 M1和 M2 背后的三个调节螺钉,使反射回来的两束光在观察屏上重合,此时可以看到圆形的干涉条纹。
仔细调节 M1 和 M2 背后的螺钉,使干涉条纹的圆心位于观察屏的中心。
2、观察等倾干涉条纹缓慢移动 M1 镜,观察干涉条纹的变化,记录条纹“冒出”或“缩进”的个数。
3、观察等厚干涉条纹稍微旋转 M1 镜,使 M1 和 M2 不再严格垂直,观察等厚干涉条纹。
4、测量激光波长先记录 M1 镜的初始位置 d1。
缓慢移动M1 镜,当条纹“冒出”或“缩进”一定数量(如50 个)时,记录 M1 镜的位置 d2。
重复测量多次,计算激光的波长。
五、实验数据与处理1、测量激光波长的数据记录|测量次数| M1 镜初始位置 d1 (mm) | M1 镜最终位置 d2 (mm) |条纹变化数 N ||||||| 1 | 25321 | 25875 | 50 || 2 | 26158 | 26712 | 50 || 3 | 27025 | 27580 | 50 |2、数据处理根据公式:λ =2Δd / N,其中λ为激光波长,Δd = d2 d1。
满分大物实验迈克尔逊数据处理
λ/nm602870771821662731743
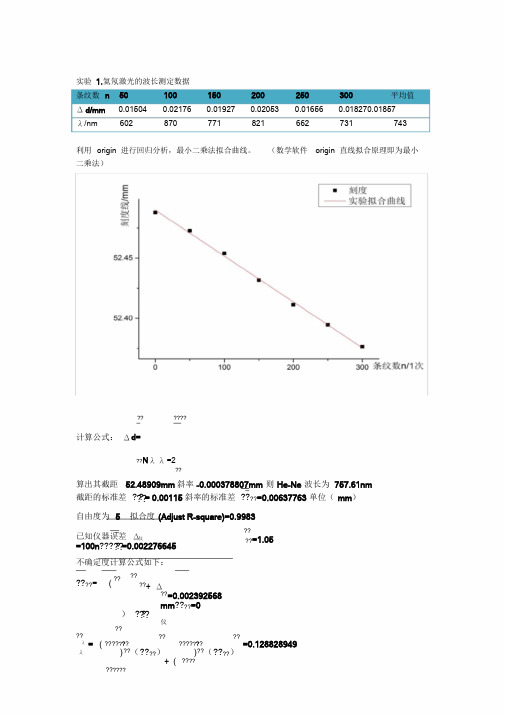
利用origin进行回归分析,最小二乘法拟合曲线。(数学软件origin直线拟合原理即为最小
二乘法)
??????
计算公式:Δd=
??Nλλ=2
实验过程虽然比较简单但是波长的测量等级达到了纳米级仪器的误差达到了100nm在测量过程中目测条纹变化数目有一定的观测误差特别是在第二个实验中通过一块反射镜来观测条纹会产生较大误差对记录人员也有一定的伤害可以采用一块放大镜方便读数
实验1.氦氖激光的波长测定数据
条纹数n50100150200250300平均值
??
算出其截距52.48909mm斜率-0.000378807mm则He-Ne波长为757.61nm截距的标准差????= 0.00115斜率的标准差????=0.00637763单位(mm)
自由度为5拟合度(Adjust R-square)=0.9983
已知仪器误差Δ仪=100n??????=0.002276645
已知仪器误差Δ仪=100n??????=0.000530346
??
=1.59
??
??Nλλ=2
??
通过对matlab绘图程序,对实验测得的六个点进行最小二乘法数据分析:
经过分析,发现有一组数据发生明显错误,故舍去该组数据进行分析。
算出其截距53.54667mm斜率-0.00030188mm则He-Ne波长为603.8nm
截距的标准差????= 0.000365斜率的标准差????=0.0000078059单位(mm)自由度为2拟合度(Adjust R-square)=0.998
迈克尔逊干涉仪实验数据处理表格

迈克尔逊干涉仪实验数据处理表格迈克尔逊干涉仪是一种用来测量光的相干性的仪器。
它的原理是利用干涉现象来测量光的波长、光速等物理量。
在实验中,我们通常会记录下一系列的实验数据,并对这些数据进行处理和分析。
下面是一个迈克尔逊干涉仪实验数据处理的表格,用于记录和处理实验数据。
在这个表格中,第一列是试验条件,包括入射角度(θ)、反射镜位移(d)和干涉条纹数(n)。
第二列到第五列是具体的实验数据,每一行代表一组实验数据。
接下来,我们可以对这些实验数据进行处理和分析。
首先,我们可以计算出每组实验数据对应的光程差(ΔL),即反射镜位移与干涉条纹数的乘积。
例如,在第一组实验中,ΔL = 0.1mm * 10 = 1mm。
同样地,我们可以计算出每组实验数据对应的波长(λ),即光程差除以干涉条纹数。
例如,在第一组实验中,λ = 1mm / 10 = 0.1mm。
然后,我们可以将所有的波长数据进行平均,得到平均波长(λ_avg)。
例如,在这五组实验中,λ_avg = (0.1mm + 0.2mm + 0.3mm + 0.4mm + 0.5mm) / 5 = 0.3mm。
接着,我们可以利用平均波长来计算光速(c)。
根据光速公式 c = λ_avg * f,其中 f 是光的频率。
假设光的频率为 5 * 10^14 Hz,则光速 c = 0.3mm * 5 * 10^14 Hz = 1.5 * 10^8 m/s。
最后,我们可以计算出每组实验数据对应的入射角度的正弦值(sinθ),即入射角度的正弦值等于反射镜位移除以干涉条纹数乘以波长。
例如,在第一组实验中,sinθ = (0.1mm / 10) * 0.1mm = 0.01。
通过以上的数据处理和分析,我们可以得到一些关于光的物理量的结果,比如平均波长和光速。
这些结果对于理解光的性质和研究光学现象非常有用。
这是一个简单的迈克尔逊干涉仪实验数据处理的表格和分析过程。
当然,在实际的实验中,可能还会有更多的数据和更复杂的处理方法。
迈克尔逊干涉仪实验报告

一、实验目的:1。
掌握迈克尔孙干涉仪的原理及调节方法。
2。
测定激光波长.二、实验原理:1.仪器的构造:图40-1为干涉仪实物图,图40—2为其光路示意图。
其中M1和M2为两平面反射镜,M1可在精密导轨上前后移动,而M2是固定的,P1是一块平行平面板,板的第二表面(靠近P2的面)涂以半反射膜,它和全反射镜M1成45度角。
P2是一块补偿板,其厚度和折射率和P1完全相同,且与P1平行,它的作用是补偿两路光的光程差,使两束光分别经过厚度和折射率相同的玻璃三次.从而白光实验中,可抵消光路中分光镜色散的影响。
放松刻度轮止动螺钉⑧,转动刻度轮⑦,可使反射镜M1沿精密导轨前后移动,当锁紧止动螺钉⑧,转动微量读数鼓轮⑨时,通过蜗轮蜗杆系统可转动刻度轮,从而带动M1微微移动,微量读数鼓轮最小格对应值为-410mm ,可估读到-510mm ,刻度轮最小分度值为-210mm ,M1的位置读数由导轨上标尺,刻度轮和微量读数鼓轮三部分组成。
反射镜M2背后有三个螺钉,用以粗调M2的倾斜度,它的下方还有两个互相垂直的微调螺丝,以便精确调节M2的方位。
2。
等倾干涉 当M1和2'M互相平行时.,得到的是相当于平行平面板的等倾干涉条纹,其干涉图样定位于无限远,如果在E 处放一块聚透镜,并在其焦平面上放一屏,则在屏上可观察到一圈圈的同心圆。
对于入射角i 相同的各束光如图所示,其光程差均为i d cos 2=∂,对于k 级亮条纹,满足 k i d ==∂cos 2,在同心圆的圆心处i=0,干涉条纹的级数最高,此时有 k d ==∂2.当移动M1使间隔d 增加,我们可以看到中心条纹一个一个向外外冒出,而当d 减小时,中心条纹将一个一个的缩进去,没冒出或缩进一个条纹,d 就增加或减少了2,如果测出M1移动的距离△d ,数出相应的冒出或缩进的条纹个数△k ,就可以计算出光源的波长:△k △d2= 。
三、实验仪器:迈克尔孙干涉仪,激光器,电源,小孔光阑,扩束镜,毛玻璃屏。
迈克尔逊干涉实验报告

迈克尔逊⼲涉实验报告迈克尔逊⼲涉实验【实验⽬的】⑴了解迈克尔逊⼲涉仪的结构、原理,学习使⽤迈克尔逊⼲涉仪产⽣⼲涉的⽅法。
⑵观察⾮定域等倾⼲涉条纹与定域等厚⼲涉条纹,巩固和加深对⼲涉理论的理解。
⑶测量 He—Ne 激光波长λ,并⽤逐差法处理数据。
⑷侧量钠光的相⼲长度 L (选做)。
【实验仪器】迈克尔逊⼲涉仪、 He—Ne、激光器、扩束镜、光栏(选做:钠光灯、⽩光光源、⽑玻璃)等。
(迈克尔逊⼲涉仪的结构与光路介绍见附页。
)1.结构迈克尔逊⼲涉仪的结构如图 7—20 所⽰,M1( 6)和M2(7)是两个精磨的平⾯反射镜。
峡固定在座上.背⾯的 3 个螺丝和在它下⾯的 2 个互相垂直的螺丝可⽤来精确地调节从镜的倾斜度。
镜可沿导轨移动,它由⼀套精密齿轮来调节。
M1卡在螺距为1mm 的丝杆上,丝杆由⼀个100分格的粗调⼿轮带动,因此,⼿轮每转⼀格,M1前进或后退1/100 mm(这是粗调部分);粗调⼿轮右侧有⼀个微调⼩⿎轮,微调⼩⿎轮也是100分格的,微调⼩⿎轮每转l圈.粗调⼿轮前进l格,M1前进或后退1/10 000mm(这是微调部分),这样,最⼩读数可估读到10-5mm 。
G1(10),G2(9)是两块折射率和厚度都相同的平⾯玻璃板,在仪器上平⾏放置,与M1和M2约成45度⾓,分别称为分光板和补偿板。
G1的⼀⾯镀有银或铝.形成半反射⾯。
2光路其光路如图7—21所⽰,从光源S来的光在G1的半反射⾯H上被分成反射光束1和透射光束l,两束光的强度近似相等。
光束l射向平⾯镜M1反射折回通过G1;光束2通过G2:射⾄G1,的半反射⾯ H 处再次反射。
最后这两束相⼲光在空间相遇产⽣⼲涉。
⽤屏E和通过望远镜等可以观察到它们的⼲涉条纹。
补偿板G2是为了消除光束1和光束2的光程不对称⽽设置的。
如果没有 G2从分光处起,光束1通过玻璃板1次,⽽光束1没有通过玻璃板;加上G2后,光束2也就通过玻璃板2次。
因⽽,光束2在光程L得到补偿,从⽽避免了因光路不对称⽽产⽣的附加光程差。
迈克尔逊干涉仪实验报告数据处理

迈克尔逊干涉仪实验报告数据处理篇一:迈克尔逊干涉仪实验报告迈克尔逊干涉仪的调整与应用1. 原始数据及处理1.1 测量钠光灯波长(?Na?589.3nm)不确定度计算:?A?2.48?x?mm, ?B?0.00004mm?U?d?mm U??U2U?d=4.4nm,Ur????100%=0.74%. ?N?1.2 双线的波长差:??Na?0.59nm 2.思考题及分析:2.1、为什么白光干涉不易观察到?答:两光束能产生干涉现象除满足同频、同向、相位差恒定三个条件外,其光程差还必须小于其相干长度。
而白光的相干长度只有微米量级,所以只能在零光程附近才能观察到白光干涉。
2.2、为什么M1和M2没有严格垂直时,眼睛移动干涉条纹会吞吐?答:因为没有严格垂直时,会形成一个披肩状的光学腔。
各处的光程差不相同,其干涉条纹的级数也会不同。
所以眼睛移动时,干涉条纹会吞吐。
2.3、讨论干涉条纹吐出或吞入时的光程差变化情况。
答:吞入时,光程差变小。
而吐出时,光程差则变大。
2.4、为什么要加补偿板?答:因为分束板的加入,使其中一路光束比另一光束附加了一定的光程。
所以加入与分束板厚度相同的补偿板来补偿这部分光程差。
2.5、如何设计一个实验,利用迈克尔逊干涉仪测玻璃的折射率?答:以白光发生干涉现象时,确定零光程处。
测定在光路中加入玻璃与否,白光产生干涉时M2镜移动的距离。
再根据所加入玻璃的厚度,计算出玻璃的折射率。
2.6、试根据迈克尔逊干涉仪的光路,说明各光学元件的作用,并简要叙述调出等倾干涉、等厚干涉和白光干涉条纹的条件及程序.答:分束板:将光束分为两路光束。
补偿板:补偿因分束板产生的光程差。
粗调螺丝:调节使其与M1镜大致垂直。
细调拉丝:精密调节M2镜的方位,使使其与M1M2镜的方位,镜严格垂直。
鼓轮:调节M2镜的位置,使光学腔的厚度改变。
等倾干涉:光学腔应严格平行。
等厚干涉:此时光学腔为披肩状。
白光干涉:零光程处附近。
2.7、如何利用干涉条纹“吞”、“吐”现象,测定单色光的波长? 答:数一定量的“吞”或“吐”,再根据公式??2?d?N计算。
迈克尔逊干涉仪实验报告
迈克尔逊干涉仪实验报告一、实验题目:迈克尔逊干涉仪二、实验目的:1. 了解迈克尔逊干涉仪的结构、原理和调节方法;2. 观察等倾干涉、等厚干涉现象;3. 利用迈克尔逊干涉仪测量He-Ne激光器的波长;三、实验仪器:迈克尔逊干涉仪、He-Ne激光器、扩束镜、观察屏、小孔光阑四、实验原理(原理图、公式推导和文字说明):在图M2′是镜子M2经A面反射所成的虚像。
调整好的迈克尔逊干涉仪,在标准状态下M1、M2′互相平行,设其间距为d.。
用凸透镜会聚后的点光源S是一个很强的单色光源,其光线经M1、M2反射后的光束等效于两个虚光源S1、S2′发出的相干光束,而S1、S2′的间距为M1、M2′的间距的两倍,即2d。
虚光源S 1、S2′发出的球面波将在它们相遇的空间处处相干,呈现非定域干涉现象,其通常将观察屏F 安放在垂直于S 1、S 2′的连线方位,屏至S 2′的距离为R ,屏上干涉花纹为一组同心的圆环,圆心为O 。
设S 1、S 2′至观察屏上一点P 的光程差为δ,则)1/)(41()2(222222222-+++⨯+=+-++=r R d Rd r R r R r d R δ (1)一般情况下d R >>,则利用二项式定理并忽略d 的高次项,于是有⎪⎪⎭⎫ ⎝⎛+++=⎪⎪⎭⎫ ⎝⎛+-++⨯+=)(12)(816)(2)(4222222222222222r R R dr r R dR r R d R r R d Rd r R δ (2)所以)sin 1(cos 22θθδRdd += (3) 由式(3)可知:1. 0=θ,此时光程差最大,d 2=δ,即圆心所对应的干涉级最高。
旋转微调鼓轮使M 1移动,若使d 增加时,可以看到圆环一个个地从中心冒出,而后往外扩;若使d 减小时,圆环逐渐收缩,最后消失在中心处。
每“冒出”(或“消失”)一个圆环,相当于S 1、S 2′的距离变化了一个波长λ大小。
如若“冒出”(或“消失”)的圆环数目为N ,则相应的M 1镜将移动Δd ,显然:N d /2∆=λ (4)从仪器上读出Δd 并数出相应的N ,光波波长即能通过式(4)计算出来。
麦克尔逊干涉仪数据处理
1姓名:吴孟杰学号:0120914430215 班级:光信科0902班麦克尔逊干涉仪数据处理一.测量激光波长数据处理过程:注:理论上钠黄光的平均波长为λ=632.8nm二.测空气的折射率实验数据的处理过程:平均波长λ=λ1+λ2+λ3+λ44×2=0.03206+0.03189+0.03189+0.031924=638.8 nm波长测量误差W=测− 理 理=0.006388−0.0063280.006328×100%=0.87%Δd 的平均值Δd =3.206+3.188+3.189+3.1924=3.194 mm钠黄光的波长差Δλ=λ 22×Δd=0.00638822×3.194=6.4 m空气折射率的测定 1=1+Nλ2l ×pΔp =1+3.5×632.8×10−62×80×10132510K =1.00014空气折射率的测定 2=1+Nλ2l ×pΔp =1+3.5×632.8×10−62×80×10132515K =1.00009 空气折射率的测定 3=1+Nλ2l ×pΔp =1+3.5×632.8×10−62×80×10132520K =1.00007 空气折射率的测定 4=1+Nλ2l×pΔp=1+3.5×632.8×10−62×80×10132525K=1.000062三.实验总结本次试验主要是应用干涉原理来测量了钠黄光的激光波长,并且测定了空气的折射率,在试验中进一步加深了对光的干涉原理有了认识,对于光形成干涉时光程差与波长的关系有了深刻认识,当是亮纹时必须时,光程差是波长的整数倍,当是暗纹时光程差是波长的(n+0.5)倍。
同时,实验测得的数据误差较小,实验中观察到了实验所要求的现象,因而实验取得了成功。
迈克尔逊干涉仪的使用实验报告
1.迈克尔逊干涉仪 图 1 是迈克尔逊干涉仪实物图。图 2 是迈克尔逊干涉仪的光路示意图,图中 M1和 M2是在相 互垂直的两臂上放置的两个平面反射镜,其中 M1是固定的;M2由精密丝杆控制,可沿臂轴前、 后移动,移动的距离由刻度转盘(由粗读和细读 2 组刻度盘组合而成)读出。在两臂轴线相交处,有 一与两轴成 45°角的平行平面玻璃板 G1,它的第二个平面上镀有半透(半反射)的银膜,以便将 入射光分成振幅接近相等的反射光⑴和透射光⑵,故 G1又称 为分光板。G2也是平行平面玻璃板,与 G1平行放置,厚度和 折射率均与 G1相同。由于它补偿了光线⑴和⑵因穿越 G1次数 不同而产生的光程差,故称为补偿板。 从扩展光源 S 射来的光在 G1处分成两部分,反射光⑴经 G1反射后向着 M2前进,透射光⑵透过 G1向着 M1前进,这两 束光分别在 M2、M1上反射后逆着各自的入射方向返回,最后 都达到 E 处。因为这两束光是相干光,因而在 E 处的观察者就 能够看到干涉条纹。 由 M1反射回来的光波在分光板 G1的第二面上反射时,如 同平面镜反射一样,使 M1在 M2附近形成 M1的虚像 M1′,因
实验步骤
1.观察扩展光源的等倾干涉条纹并测波长 ①点燃钠光灯,使之与分光板 G1等高并且位于沿分光板和 M1镜的中心线上,转动粗调手轮, 使 M1镜距分光板 G1的中心与 M1镜距分光板 G1的中心大致相等(拖板上的标志线在主尺 32 cm 位 置)。 ②在光源与分光板 G1之间插入针孔板,用眼睛透过 G1直视 M2镜,可看到 2 组针孔像。细心 调节 M1镜后面的 3 个调节螺钉,使 2 组针孔像重合,如果难以重合,可略微调节一下 M2镜后 的 3 个螺钉。当 2 组针孔像完全重合时,就可去掉针孔板,换上毛玻璃,将看到有明暗相间的干 涉圆环,若干涉环模糊,可轻轻转动粗调手轮,使 M2镜移动一下位置,干涉环就会出现。 ③再仔细调节 M1镜的 2 个拉簧螺丝,直到把干涉环中心调到视场中央,并且使干涉环中心随 观察者的眼睛左右、上下移动而移动,但干涉环不发生“涌出”或“陷入”现象,这时观察到的干涉条 纹才是严格的等倾干涉。 ④测钠光 D 双线的平均波长 。先调仪器零点,方法是:将微调手轮沿某一方向(如顺时针方 向)旋至零,同时注意观察读数窗刻度轮旋转方向;保持刻度轮旋向不变,转动粗调手轮,让读数 窗口基准线对准某一刻度,使读数窗中的刻度轮与微调手轮的刻度轮相互配合。 ⑤始终沿原调零方向,细心转动微调手轮,观察并记录每“涌出”或“陷入”50 个干涉环时,M1 镜位置,连续记录 6 次。 ⑥根据式(5-8),用逐差法求出钠光 D 双线的平均波长,并与标准值进行比较。 2.观察等厚干涉和白光干涉条纹 ①在等倾干涉基础上,移动 M2镜,使干涉环由细密变粗疏,直到整个视场条纹变成等轴双曲 线形状时,说明 M2与 M1′接近重合。细心调节水平式垂直拉簧螺丝,使 M2与 M1′有一很小夹角, 视场中便出现等厚干涉条纹,观察和记录条纹的形状、特点。 ②用白炽灯照明毛玻璃(钠光灯不熄灭),细心缓慢地旋转微动手轮,M2与 M1′达到“零程”时, 在 M2与 M1′的交线附近就会出现彩色条纹。此时可挡住钠光,再极小心地旋转微调手轮找到中央 条纹,记录观察到的条纹形状和颜色分布。 3.测定钠光 D 双线的波长差 ①以钠光为光源调出等倾干涉条纹。 ②移动 M2镜,使视场中心的视见度最小,记录 M2镜的位置;沿原方向继续移动 M2镜,使 视场中心的视见度由最小到最大直至又为最小,再记录 M2镜位置,连续测出 6 个视见度最小时 M
迈克尔逊干涉仪实验报告
迈克尔逊干涉仪(实验报告)一、实验目的1、掌握迈克尔逊干涉仪的调节方法并观察各种干涉图样。
2、区别等倾干涉、等厚干涉和非定域干涉,测定He-Ne 激光波长二、实验仪器迈克尔逊干涉仪、He-Ne 激光器及光源、小孔光阑、扩束镜(短焦距会聚镜)、毛玻璃屏等。
(图一)(图二)三、实验原理①用He-Ne 激光器做光源,使激光通过扩束镜会聚后发散,此时就得到了一个相关性很好的点光源,射到分光板P1和P2上后就将光分成了两束分别射到M1 和M2 上,反射后通过P1 、P2 就可以得到两束相关光,此时就会产生干涉条纹。
②产生干涉条纹的条件,如图2 所示,B 、C 是两个相干点光源,则到A 点的光程差δ =AB-AC=BCcosi , 若在A 点出产生了亮条纹,则δ =2dcosi=k λ (k 为亮条纹的级数) ,因为i 和k 均为不可测的量,所以取其差值,即λ =2 Δ d/ Δ k? 。
四、实验步骤1、打开激光电源,先不要放扩束镜,让激光照到分光镜P1 上,并调节激光的反射光照射到激光筒上。
2、调节M2 的位置使屏上两排光中最亮的两个光点重回,并调至其闪烁。
3、将扩束镜放于激光前,调节扩束镜的高度和偏角,使光能照在P1分光镜上,看显示屏上有没有产生同心圆的干涉条纹图案。
没有的话重复2 、3 步骤,直到产生同心圆的干涉条纹图案。
4、微调M2是干涉图案处于显示屏的中间。
5、转动微量读数鼓轮,使M1 移动,可以看到中心条纹冒出或缩进,若看不到此现象,先转动可度轮,再转动微量读数鼓轮。
记下当前位置的读数d0 ,转动微量读数鼓轮,看到中心条纹冒出或缩进30 次则记一次数据,共记录10 次数据即d0、d1 (9)6、关闭激光电源,整理仪器,处理数据。
五、实验数据处理数据记录:数据处理:Δd0=d5-d0=0.05202mm??????? Δd1=d6-d1=0.05225mmΔd2=d7-d2=0.04077mm??????? Δd3=d8-d3=0.04077mmΔd4=d9-d4=0.05071mmΔd(平均)=(Δd0+Δd1+Δd2+Δd3+Δd4)/5 =0.047304mm A类不确定度σ=5.99355*10-6mΔk=150所以λ(平均)=2Δd(平均)/Δk =630.72 nmB类不确定度:UΔB=0.5*10-7 m总不确定度:UΔd =6.01437*10-6 mUλ =2UΔd/Δk =80.1916 nm所以λ=λ(平均)+Uλ=630.72 + 80.1916 nm Eλ=(632.8-630.72)/632.8 *100% =0.329%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
竭诚为您提供优质文档/双击可除迈克尔逊干涉仪实验报告数据处理
篇一:迈克尔逊干涉仪实验报告
迈克耳逊干涉仪
一.实验目的
1.了解迈克尔逊干涉仪的结构和原理,掌握调节方法;
2.用迈克尔逊干涉仪测量钠光波长和精细结构。
二.实验仪器
迈克尔逊干涉仪、钠光灯、透镜等。
三.实验原理
迈克耳孙干涉仪原理如图所示。
两平面反射镜m1、m2、光源s和观察点e(或接收屏)四者北东西南各据一方。
m1、m2相互垂直,m2是固定的,m1可沿导轨做精密移动。
g1和g2是两块材料相同薄厚均匀相等的平行玻璃片。
g1的一个表面上镀有半透明的薄银层或铝层,形成半反半透膜,可使入射光分成强度基本相等的两束光,称g1为分光板。
g2与
g1平行,以保证两束光在玻璃中所走的光程完全相等且与入射光的波长无关,保证仪器能够观察单、复色光的干涉。
可见g2作为补偿光程用,故称之为补偿板。
g1、g2与平面镜m1、m2倾斜成45°角。
如上图所示一束光入射到g1上,被g1分为反射光和透射光,这两束光分别经m1和m2反射后又沿原路返回,在分化板后表面分别被透射和反射,于e处相遇后成为相干光,可以产生干涉现象。
图中m′2是平面镜m2由半反膜形成的虚像。
观察者从e处去看,经m2反射的光好像是从m′2来的。
因此干涉仪所产生的干涉和由平面m1与m′2之间的空气薄膜所产生的干涉是完全一样的,在讨论干涉条纹的形成时,只需考察m1和m2两个面所形成的空气薄膜即可。
两面相互平行可到面光源在无穷远处产生的等倾干涉,两面有小的夹角可得到面光源在空气膜近处形成的等厚干涉。
若光源是点光源,则上述两种情况均可在空间形成非定域干涉。
设m1和m′2之间的距离为d,则它们所形成的空气薄膜造成的相干光的光程差近似用下式表示
若m1与m′2平行,则各处d相同,可得等倾干涉。
系统具有轴对称不变性,故屏e上的干涉条纹应为一组同心圆环,圆心处对应的光程差最大且等于2d,d越大圆环越密。
反之中心圆斑变大圆环变疏。
若d增加则中心“冒出”一个条纹,反之d减小则中心“缩进”一个条纹。
故干涉条纹在
中心处“冒出”或“缩进”的个数n与d的变化量△d之间有下列关系
根据该关系式就可测量光波波长λ或长度△d。
钠黄双线的精细结构测量原理简介:
干涉条纹可见度定义为:此时干涉条纹最清晰,可见度最大;
当,时V=1,
时V=0,可见度最小。
从一视见度最低的位置开始算起,测量一次视见度最低处的位置,者其间的光程差
为,且由关系算出谱线的精细结构。
四.实验结果计与分析
其中λ=2*Δd/100,根据λ0=589.3nm;
=592.6nme=0.6%
钠光的精细结构:视见度最低的位置
d1=37.98753d2=38.29872
得
=0.5567nm
e=0.5%
误差分析及总结:
由于本实验属于较为精细的光学实验,目测读数时的误差在所难免,所以使得实验结果不准确,应注意保护眼睛,
边读书边休息,小组内交替读数。
并且仪器未调好也会造成较大误差。
五.思考题
1、在观察等倾条纹干涉时,条纹从中心“冒出”说明兼具是变大了还是变小了?条纹“缩进”又如何?调节等倾条纹时,若眼睛有左向右平移看条纹“冒出”,有右向左看是“缩进”,此时位置成什么关系?答:“冒出”时间距变大,“缩进”时间距变小。
说明m1和m2`不平行且右边间距大。
亮纹的条件:2necosγ+λ/2=kλ
干涉条纹是一组同心圆,越靠近中心,倾角i越小,折射角γ也越小,则cosγ越大,给出的k值也越大。
这说明,越靠近中心,亮环的级次越高。
当i=0°时,γ=0°,这时2e+λ/2=kλ
当增大厚度e时,会看见起初中心亮环变暗,然后变亮。
这是因为e增大,k的级次会变为k+1,因此,中心会产生一个新的亮环。
由上述可知,条纹从中心涌(:迈克尔逊干涉仪实验报告数据处理)出时,说明m2与m2之间的距离变大。
反之,则为变小。
若眼睛有左向右平移看条纹“冒出”,有右向左看是“缩进”则说明m2与m2不平行,且成的夹角的顶端在左边
2、如果实验者是高度近视眼。
不戴眼镜能看到等倾条
纹干涉或等厚条纹吗?为什么?
答:能看到,因为能够通过调节使光最终聚焦在视网膜上,因为并不是实在的物体,所以成像位置是可以调节的,而且调节并不影响m2与m2的位置关系,所以能够看到。
篇二:迈克尔逊干涉仪的使用实验报告
学生物理实验报告
实验名称迈克尔逊干涉仪的使用
学院专业班级报告人学号同组人学号
同组人学号同组人学号理论课任课教师实验课指导教
师实验日期报告日期实验成绩批改日期
篇三:迈克尔逊干涉仪实验报告
迈克尔逊干涉仪的调整与应用
1.原始数据及处理
1.1测量钠光灯波长(?na?589.3nm)
不确定度计算:
?A?2.48?x
?mm,?b?0.00004mm
?u?d?mmu??
u2
u?d=4.4nm,ur100%=0.74%.?n?
1.2双线的波长差:??na?0.59nm2.思考题及分析:
2.1、为什么白光干涉不易观察到?
答:两光束能产生干涉现象除满足同频、同向、相位差恒定三个条件外,其光程差还必须小
于其相干长度。
而白光的相干长度只有微米量级,所以只能在零光程附近才能观察到白光干涉。
2.2、为什么m1和m2没有严格垂直时,眼睛移动干涉条纹会吞吐?
答:因为没有严格垂直时,会形成一个披肩状的光学腔。
各处的光程差不相同,其干涉条纹
的级数也会不同。
所以眼睛移动时,干涉条纹会吞吐。
2.3、讨论干涉条纹吐出或吞入时的光程差变化情况。
答:吞入时,光程差变小。
而吐出时,光程差则变大。
2.4、为什么要加补偿板?
答:因为分束板的加入,使其中一路光束比另一光束附加了一定的光程。
所以加入与分束板
厚度相同的补偿板来补偿这部分光程差。
2.5、如何设计一个实验,利用迈克尔逊干涉仪测玻璃的折射率?
答:以白光发生干涉现象时,确定零光程处。
测定在光路中加入玻璃与否,白光产生干涉时
m2镜移动的距离。
再根据所加入玻璃的厚度,计算出玻璃的折射率。
2.6、试根据迈克尔逊干涉仪的光路,说明各光学元件。
