流体力学泵与风机第五版课后习题答案
流体力学泵与风机的课后习题

流体力学泵与风机的课后习题泵与风机的结构1、指出离心式风机主要部件名称2、指出轴流泵主要部件名称3、在下列热力发电厂的泵与风机序号中选择至少两个正确序号填入下面各题的空白处。
(a)锅炉给水泵 (b)汽轮机凝结水泵 (c)循环水泵(d)送风机 (e)引风机 (f)排粉风机 (g)烟气循环风机1)热力发电厂的泵与风机中 可以采用轴流式;2)热力发电厂的泵与风机中 应注意防磨、防积灰和防腐蚀;3)热力发电厂的泵与风机中 输送的是饱和热水,应采取防汽蚀措施。
4、简述热力发电厂主要有哪些风机?根据所输送的气体性质说明它们在结构上应注意哪些问题?5、轴端密封的方式有几种?它们各自是起到怎样的密封作用?各有何特点?泵与风机的叶轮理论1、转速n=1500r/min的离心风机,叶轮内径D1=480mm。
叶片进口处空气相对速度ω1=25m/s,与圆周速度的夹角为β1=60°,试绘制空气在叶片进口处的速度三角形。
答案:2、有一离心泵转速为1450r/min,其叶轮的进口尺寸为:宽度 ,直径 ,安装角 。
假设有无限多叶片且叶片为无限薄,不考虑叶片厚度对流道断面的影响。
(1)设液体径向流入叶轮,计算叶轮的理论流量。
(2)转速不变,理论流量增大20%,设进口相对流动角仍等于安装角,计算绝对速度的圆周分速度,并说明它的方向是否与圆周速度方向一致。
分析:按照题目已知条件,要计算叶轮理论流量,应想到它等于叶轮进口流道断面面积与进口径向分速度的乘积,进口流道断面面积很容易看出如何计算,进口径向分速度需根据进口速度三角形进行计算,那么就要进一步找出速度三角形的三个参数,从题意中已知了相对流动角 ,容易看出圆周速度如何计算,剩下的一个条件是什么呢?其实,“设液体径向流入叶轮”隐含了一个条件,它意味着进口绝对速度方向为径向,而径向总是与圆周速度方向垂直,所以进口绝对流动角 。
解:(1) 由题意知:、。
(m/s)画出速度三角形(图略),由图知:(m/s) 理论流量为:(m3/s)(2) 由题意知:,圆周速度不变为m/s,流量增大20%,相应的也增大20%(因为叶轮进口流道断面面积不变),即 m/s画出速度三角形(图略),由图知:m/s其方向与圆周速度的方向相反。
泵与风机课后习题参考答案(完整版)(基础教育)
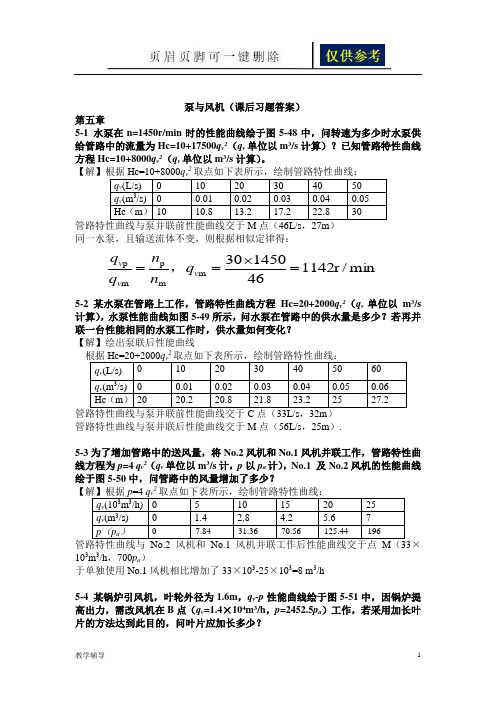
泵与风机(课后习题答案)第五章5-1 水泵在n=1450r/min 时的性能曲线绘于图5-48中,问转速为多少时水泵供给管路中的流量为Hc=10+17500q v 2(q v 单位以m 3/s 计算)?已知管路特性曲线方程Hc=10+8000q v 2(q v 单位以m 3/s 计算)。
2q v (L/s) 0 10 20 30 40 50 q v (m 3/s) 0 0.01 0.02 0.03 0.04 0.05 Hc (m ) 10 10.8 13.2 17.2 22.8 30同一水泵,且输送流体不变,则根据相似定律得:5-2 某水泵在管路上工作,管路特性曲线方程Hc=20+2000q v 2(q v 单位以m 3/s 计算),水泵性能曲线如图5-49所示,问水泵在管路中的供水量是多少?若再并联一台性能相同的水泵工作时,供水量如何变化? 【解】绘出泵联后性能曲线2q v (L/s) 0 10 20 30 40 50 60 q v (m 3/s) 0 0.01 0.02 0.03 0.04 0.05 0.06Hc (m ) 20 20.2 20.8 21.8 23.2 25 27.2 管路特性曲线与泵并联后性能曲线交于M 点(56L/s ,25m ).5-3为了增加管路中的送风量,将No.2风机和No.1风机并联工作,管路特性曲线方程为p =4 q v 2(q v 单位以m 3/s 计,p 以p a 计),No.1 及No.2风机的性能曲线绘于图5-50中,问管路中的风量增加了多少?2q v (103m 3/h) 0 5 10 15 20 25 q v (m 3/s) 0 1.4 2.8 4.2 5.6 7p (p a )0 7.84 31.36 70.56 125.44 196 ×103m 3/h ,700p a )于单独使用No.1风机相比增加了33×103-25×103=8 m 3/h5-4 某锅炉引风机,叶轮外径为1.6m ,q v -p 性能曲线绘于图5-51中,因锅炉提高出力,需改风机在B 点(q v =1.4×104m 3/h ,p =2452.5p a )工作,若采用加长叶片的方法达到此目的,问叶片应加长多少?min /r 114246145030m m p m p =⨯==v v v q n n q q ,【解】锅炉引风机一般为离心式,可看作是低比转速。
流体力学泵与风机_课后题答案详解

流体力学泵与风机部分习题答案 2-15解:(1)当1γ为空气 21p p = ()A B p h z p =++γ ()h z p p p B A +=-=∆γ 3.010008.9⨯⨯= kpa pa 94.22940== (2)当1γ为油 31p p =()z H h p p A +++=γ1 ()H h p p B γγ++=13H h z H h p p p p p B A γγγγγ--+++-=-=∆131h z h 1γγγ-+=1.090002.010008.91.010008.9⨯-⨯⨯+⨯⨯= kpa pa 04.22040== 2-16 解:21p p =()211h h H p p M +++=水γ 212h h p p a 汞油γγ++=()2121h h p h h H p a M 汞油水γγγ++=+++()2.010008.96.1378502.05.110008.998011⨯⨯⨯+⨯=++⨯⨯+-h h 26656785098002.098005.1980098011+=+⨯+⨯+-h h 1960147009802665619501--+=hm h 63.51= 2-28解:()21h h p -=γ()()()b h h h b h h h h P 02210212145sin 45sin 21-+--=γγ ()()145sin 22310008.9145sin 232310008.92100⨯-⨯⨯+⨯-⨯-⨯⨯⨯= kN N 65.343465022510008.9==⨯⨯=()()()Pbl h h h bl h h h h l D D D 2022110212145sin 45sin 21-+--=γγ m 45.222510008.9222210008.92322210008.9=⨯⨯⨯⨯⨯+⨯⨯⨯=2-32 解:b h h b h h P 02202145sin 2145sin γγ+= 2222210008.9212222110008.9⨯⨯⨯⨯⨯+⨯⨯⨯⨯=kN N 8576.1106.1108572810008.9==⨯⨯=Ph h b h h h h b h h l D 02102202102145sin 3245sin 2145sin 245sin ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=γγ 2810008.92372410008.9222410008.9⨯⨯⨯⨯⨯+⨯⨯⨯=2613= 26722613=-=p lT P G l T l P l G ⨯=⨯+⨯22672810008.9162.19⨯=⨯⨯⨯+⨯T kN T 31.10134.27481.9=+= 2-41解:245sin 0=⨯=r hb h h P x ⨯⨯⋅⋅=21γ 4212210008.9⨯⨯⨯⨯⨯=kN N 2.3939200==V P z γ=b r r r⎪⎭⎫⎝⎛⨯⨯⨯-=00245cos 45sin 2136045πγ 4212281214.310008.92⨯⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯= kN N 344.2222344==kN P 1.45344.222.3922=+=03057.0arctan 2.39344.22arctan arctan≈===x z P P α3-3解:(1)s m v d Q /0049.010025.04432323=⋅⋅=⋅=ππs kg Q /9.4=ρ(2)s m v d d v /625.032131=⎪⎪⎭⎫⎝⎛= s m v d d v /5.232232=⎪⎪⎭⎫ ⎝⎛=3-5解:s m h m Q /778.2/1000033==s m d Qv /2042≤=π所以,177.04=≥πv Qd 所以,mm m d 45045.0== 此时,s m d Q d Qv /4.1763585.0112.114422====ππ3-6解:22543212054d d A A A A A ππ======22114012021d d A A ππ=⋅="=' 22224012021d d A A ππ=⋅="='22334012021d d A A ππ=⋅="='22444012021d d A A ππ=⋅="='22554012021d d A A ππ=⋅="='2214014d d ππ=d d 1011=d r 10211= 2224034d d ππ=d d 1032= d r 10232= 2234054d d ππ=d d 1053= d r 10253= 2244074d d ππ=d d 1074= d r 10274=2254094d d ππ=d d 1035=d r 10235= ()()54321254321220240u u u u u d u u u u u d Q G ++++=++++==πρπρρ3-7解:干管前端的质量流量为:42562.2211111d A v Q πρρ⨯⨯==()s kg /128544.005.042562.22=⨯⨯⨯=πs kg Q Q Q /064272.02132===ρρρ ()s m A Q v /247.2204.043.2064272.022222=⋅⋅==πρρ()s m A Q v /05.18045.0424.2064272.023333=⋅⋅==πρρ 3-10解:将基准面建立在B 点经过的水平面上,列能量方程:gv p z gv p z 222222221111αγαγ++=++其中,m z 2.11= m p 5.11=γ s m v /21= s m v d d v /5.4122212== 121==αα gp g 25.40225.12.1222++=++γ871.125.4225.12.1222=-++=gg p γ 3-11解:将2点所在的水平面作为基准面,列能量方程: gv p z gv p z 222222221111αγαγ++=++31=z 02=zγγ21p p =s m v /31=gv p g p 2023322221++=++γγ s m gh v /2.83222=+=32.822112=⎪⎪⎭⎫ ⎝⎛=d d v v 所以,m d 12.02= 3-14解:以水面为基准面,列0-0和D-D 的能量方程:gv p z gv p z DD DD 22220000αγαγ++=++00=z00=γp02200=gv α 4-=D z0=γDpgv DD 2040002α++-=++ 所以,422=gv DD α,即,s m v D /85.88.924=⋅⋅=所以,s m v d Q D /017368.085.805.044322=⋅⋅==ππ81:1:2:24422==A D DD A A d d gv gv αα列0-0和A-A 断面的能量方程:gv p z gv p z AA AA 22220000αγαγ++=++8147000++-=++γAp 所以,8147-=γAp 所以,kpa p A 1.68= 列0-0和B-B 断面的能量方程:gv p z gv p z BB BB 22220000αγαγ++=++kpa p B 484.08.9814-=⋅-= 列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 22220000αγαγ++=++kpa p C 1.208.98142-=⨯⎪⎭⎫ ⎝⎛+-=0=D p3-18解:将基准面建在管道所在的水平面上,列能量方程:21222222111122-+++=++l h gv p z gv p z αγαγ128.998.0008.9490222+++=++g v α9.3222=gv s m v /74.82= 3-19 解:(1)(a )将基准面建在A 所在的水平面上,列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 2222000αγαγ++=++gv CC 2000042α++=++422=gv CC α s m v C /85.88.98=⨯=1:4:2:22222==B C CC B B s s gv gv αα122=gv BB α s m v /43.48.921=⨯= 且 B A v v =(b )(c )gv p z gv p z AA AA 22220000αγαγ++=++10004++=++γAp3=γAp kpa p A 4.29=(2)(a )2122000022-+++=++l CC CC h gv p z gv p z αγαγ其中,gv g v h l 2324222121+=-g v g v g v 223200004222222++++=++54222=g v 所以,s m v /96.32= s m v v /96.12121==(b )(c )gv g v p z g v p z 2222212111120000+++=++αγαγ 5300041++=++γp5341-=γp kpa p 32.331= gv g v g v p z g v p z 223242222222222220000++++=++αγαγ5423545400042⋅++++=++γp kpa p 76.112=3-20 解:()()212221221122-++=--++l a p v p z z v p ργγρs m d Qv /38.2005.014.34202.042221=⨯⨯⨯==πs m d Qv /19.1005.014.3402.04222=⨯⨯==π2423222121v v p l ρρ+=-()()242322222122212211v v v p z z v p a ρρργγρ+++=--++22214v v =()()8.930306.02.1224232300212221221⨯+---+++=v v v v p ρρρρ()()8.930306.02.12424212230022222222⨯+---+++=v v v v ρρρρ8.9606.019.1026.0133002⨯⨯-⨯⨯+= pa 16.352= mm p h 6.449.716.3521===γ3-22解:s kN h kN G /048944.0/2.176==s m GQ /1347.77.08.910048944.033=⨯⨯==γs m d Q d Qv /09.914.31347.7444222=⨯===ππ()2122221122-++=-++l a p v p H v p ργγρ其中,01≈v ,pa h p 988.9101010331=⨯⨯⨯==-γ()γgv d H H 2035.0209.97.008.97.02.1098222+⨯+=⨯⨯-++-()8.97.08.9209.9035.0209.97.008.97.02.109822⨯⨯⨯+⨯+=⨯⨯-++-H HH H 0122.19.289.498+=+-所以,m H 64.32=()212211212212-++=-++l M M a p v p H v p ργγρ()8.97.08.9209.9164.322035.0209.97.064.328.97.02.12109822⨯⨯⨯+⨯+=⨯⨯-++-M p 科技52.169.28968.7998++=+-M p 所以,pa p M 45.63-=3-263-28解:列连续性方程:s m D Qv /18.34.014.344.04221=⨯⨯==π s m d Q v /96.501.014.344.04222=⨯⨯==π列能量方程: g v p z g v p z 222222221111αγαγ++=++ g v g v p 222112221ααγ-=m 98.1318.9218.396.5022=⨯-= kpa p 404.12938.998.1311=⨯=列动量方程:()12v vQ F -=∑ρ ()12222144v v Q R d p D p -=-⨯-⨯ρππ()18.396.504.04.04404.12932-⨯=-⨯⨯R πkN R 339.14378.474.04.04404.12932=⨯-⨯⨯=π kN R 94.1112=3-33解:列能量方程:g v p z g v p z 222222221111αγαγ++=++ 其中,5321=v v 2221259v v = g v g v 209.0205.1222211αα++=++gv g v 225926.02222-= s m v /3.42= s m v /58.21=()12v v Q F -=∑ρ()1222212121v v Q R b h b h -=--ργγ 其中,s m Q /644.45.12.158.23=⨯⨯= 72.1644.410009.0108.9215.1108.9212323⨯⨯=-⨯⨯⨯-⨯⨯⨯R N R 2.480=4-2 (1) m mm d 1.0100== s kg Q /10=ρs m Q Q /01.03==ρρs m d Q v /274.11.014.301.04422=⨯⨯==π s m /10519.126-⨯=ν 8387110519.11.0274.1Re 6=⨯⨯==-νvd (紊流) (2) s kg Q /10=ρ s m Q Q /011765.0850103===ρρ s m d Q v /4987.11.014.3011765.04422=⨯⨯==π s m /1014.124-⨯=ν 13151014.11.04987.1Re 4=⨯⨯==-νvd 4-3 解:m d 3.0= C T 020= s m /107.1526-⨯=νs m d v /1067.1043.0107.152000Re 36max --⨯=⨯⋅=⋅=ν s m A v Q /103947.743.014.31067.1043323max max --⨯=⨯⨯⨯=⋅= h kg Q /9.3136002.1103947.73=⨯⨯⨯=-ρ4-4 解:212=d d 4212221==d d v v 222111Re 2214Re ===ννd v d v 所以,2Re Re 21= 4-12 紊流粗糙区,5106Re ⨯> νvd=Re ,所以,s m d v /14.325.010308.1106Re 65=⨯⨯⨯==-ν s m d v Q /154.0425.014.314.34322=⨯==π 4-13 s m s L Q /2.0/20031==s m d Q v /076433.44211==π 661107791.010308.125.0076433.4Re ⨯=⨯⨯==-νvd s L Q /202= s m v /4076433.02=4210791.7Re ⨯=s L Q /53= s m v /1019.03= 43109478.1Re ⨯=查尼氏图,得到, 5106Re ⨯=u 4104Re ⨯=l123Re Re Re Re Re <<<<u l ,所以,1Q 属于紊流粗糙区,2Q 属于紊流过渡区,3Q 属于紊流光滑区,(1) 对于1Q ,采用希弗林松公式,02326.025.0105.011.011.025.0325.01=⎪⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=-d K λm g v d l h f 888.78.92076433.425.010002326.0222111=⨯⨯⨯==λ (2) 对于2Q ,采用阿公式,02547.010791.76825.0105.011.0Re 6811.025.04325.02=⎪⎪⎭⎫ ⎝⎛⨯+⨯=⎪⎭⎫ ⎝⎛+=-d K λ m g v d l h f 086.08.924076433.025.010002547.0222222=⨯⨯⨯==λ(3) 对于3Q ,采用布公式02678.05.194773164.0Re 3164.025.025.03===λ m g v d l h f 005676.08.9244076433.025.010002678.0222333=⨯⎪⎭⎫ ⎝⎛⨯⨯==λ 4-15 5102Re ⨯=u 4000Re =lm d 05.0= m K 31025.0-⨯= s m d v u /028.405.010007.1102Re 65max =⨯⨯⨯==-νs L d v Q /905.7405.014.3028.4422max max =⨯==π 26min 10056.805.010007.14000Re --⨯=⨯⨯==d v l ν s L s m d v Q /1581.0/1001581.0405.014.310056.8432222min min =⨯=⨯⨯==--π 4-21 (1) a d d =21 2211av v = gv d l d v g v d l g v d l h f 2642Re 64221111211121111νλ=== 4212221211ad d v v h h f f == 19.1=a (2)75.425.12275.12122225.0225.0225.021125.0125.0125.021123164.023164.0a d d v v gv d l d v g v d l d v h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==νν 16.1=a (3)25.525.11222122225.0221125.01211211.0211.0a d d v v g v d l d K g v d l d K h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛= 14.1=a 4-24 解:s m Q /002742.0602329.03=⨯=s m d Q v /3972.105.014.3002742.04422=⨯⨯==π 629.022=⎪⎭⎫ ⎝⎛+g v d l ζλ ()629.08.923972.162=⨯+ζ 3151.0=ζ 4-26 解:(1) 突然缩小375.03145.7815.015.0121=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζmm m g v h j 5.760765.08.922375.022211==⨯==ζ (2)5.02=ζmm m g v h j 102102.08.9225.022222==⨯==ζ (3)1693145.781122213=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζ mm m h j 115115.08.92216923==⨯= (4)14=ζ mm m h j 204204.08.922124==⨯= 4-27 解:()()gv v g v v h h m m j j 222121-+-=''+' ()()()()02212221=-+--=''+'gv v g v v h h m m vm j j 所以,221v v v m += 此时,()j j j h gv v g v v v g v v v h h 2221222222121212211=-=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛+-=''+' 4-29 解:s m h m Q /1044.4/16333-⨯== s m d Q v /2624.205.014.31044.44423211=⨯⨯⨯==-π s m d Q v /5656.01.014.31044.44423222=⨯⨯⨯==-π m g v v p p h j 140674.08.925656.02624.28.910001739.522222121=⨯-+⨯⨯-=-+-=γ g v h j 2211ζ= 5387.01=ζ gv h j 2222ζ= 619.82=ζ5-17 解:5.6082.014.32.12.01002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 7.30422.014.32.12.05002.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 973671.014.32.11.05002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 3.101018973677.30425.608321=++=++=p p p p S S S S 22211/91.227215.03.101018m N Q S p p =⨯==22222/1.258616.03.101018m N Q S p p =⨯==5-25 解:()()⎪⎩⎪⎨⎧=++=++=1021520232322223221SQ Q Q S SQ Q Q S SQ 610=S解得,s m Q /10472.4331-⨯= s m Q /1041.2332-⨯= s m Q /1063.0333-⨯=5-27 解:94.10348.92.014.32.020002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 8.206988.91.014.31.0100025.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 78.37258.92.014.32.072002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 038035.087.14311705.321111211=+=+='S S S 所以,25.6911='S 1)()H Q S S =+'231s m S S H Q /10186.604417163331-⨯==+'=2)H SQ =2 H Q S =⎪⎭⎫ ⎝⎛'221 1325133831432=+'=-'=S S S S gd πζ ()1.25688.92.014.31325142=⨯⨯⨯=ζ 5-28 解:286.1368.93.014.383.020002.084242=⨯⨯⨯⨯==g d d l S AB AB AB AB πλ 029.1098.93.014.383.016002.084242=⨯⨯⨯⨯==g d d l S AC AC AC AC πλ 34.328.94.014.384.020002.084242=⨯⨯⨯⨯==g d d l S AD AD AD AD πλ 772.818.93.014.383.012002.084242=⨯⨯⨯⨯===g d d l S S BC BC BC CD BC πλ 5108.2⨯=A p2AB AB A Q S p γ= s m S p Q AB A AB /457868.08.91000286.136108.235=⨯⨯⨯==γ 2AD AD A Q S p γ= s m S p Q AD A AD /93993.08.9100034.32108.235=⨯⨯⨯==γ ()()222BC BC BC AC A Q S Q S p += ()s m S S p Q Q BC AC A CD BC /23488.043=+==γs m Q Q Q BC AB /69275.022=+= s m Q Q Q CD AD /17481.123=+=s m Q Q Q /86756.13321=+= 22/2.44m kN Q S p BC BC C ==γ。
第五版 流体力学习题答案完整版

《流体力学》答案1-6.当空气温度从00C 增加至020C 时,ν值增加15%,容重减少10%,问此时μ值增加多少?⎡⎤⎣⎦解0000000000(115%90%)()()0.035 3.5%gggγγννμμρνρνμρνγν⨯---====1-7.图示为一水平方向运动的木板,其速度为1m s ,平板浮在油面上,油深 1mm δ=,油的0.09807Pa s μ=,求作用于平板单位面积上的阻力?⎡⎤⎣⎦解10.0980798.070.001du Pa dy τμ==⨯= 1-9.一底面积为4045cm ⨯,高为1cm 的木板,质量为5kg ,沿着涂有润滑油的斜面等速向下运动,已知1m v s =,1mm δ=,求润滑油的动力粘滞系数?⎡⎤⎣⎦解0T GSin α-= 55255131313T GSin G g g α==⋅=⨯⨯=所以 10.400.451800.001du T A dy μμμ==⨯=但 259.8070.10513180Pa s μ⨯==⋅⨯所以1-10.一个圆锥体绕其铅直中心轴等速旋转,锥体与固定壁的间距为δ=1mm ,全部为润滑油充满,μ=0.1Pa.s ,当旋转角速度ω=16s -1,锥体底部半径R =0.3m,高H =0.5m 时,求:作用于圆锥的阻力矩。
解: 取微元体, 微元面积:阻力矩为:阻力: 阻力矩51213GVδ22cos 0dhdA r dl r du r dy dT dA dM dT rππθωτμμδτ=⋅=⋅-====⋅0333012cos 12()cos 12cos HHHM dM rdT r dAr r dh r dh r tg h tg h dhττπθωμπθδθωμπθδθ====⋅⋅=⋅⋅⋅=⋅=⋅⋅⋅⋅⎰⎰⎰⎰⎰⎰1-14.图示为一采暖系统图,由于水温升高引起水的体积膨胀,为了防止管道及暖气片胀裂,特在顶部设置一膨胀水箱,使水的体积有自由膨胀的余地,若系统内水的总体积38V m =,加热前后温度差050t C =,水的热胀系数0.0005α=,求膨胀水箱的最小容积?⎡⎤⎣⎦解因为 dV V dt α=所以 30.00058500.2dV Vdt m α==⨯⨯=2-2.在封闭管端完全真空的情况下,水银柱差250Z mm =,求盛水容器液面绝对压强1p 及测压管中水面高度1Z ?⎡⎤⎣⎦解312013.6109.80.056664a p Z p γ=+=⨯⨯⨯=11 6.6640.686809.8p Z m mm γ==== 2-6.封闭容器水面的绝对压强20107.7KNp m =,当地大气压强298.07a KNp m =,试求(1)水深0.8h m =的A 点的绝对压强和相对压强?(2)若容器水面距基准面高度5Z m =,求A 点的测压管高度和测压管水头。
流体力学泵与风机 蔡增基 第五版 下 答案讲解学习

流体力学泵与风机蔡增基第五版下答案1.描绘出下列流速场解:流线方程: yx u dy u dx = (a )4=x u ,3=y u ,代入流线方程,积分:c x y +=43直线族(b )4=x u ,x u y 3=,代入流线方程,积分:c x y +=283抛物线族(c )y u x 4=,0=y u ,代入流线方程,积分:c y =直线族(d )y u x 4=,3=y u ,代入流线方程,积分:c y x +=232抛物线族(e )y u x 4=,x u y 3-=,代入流线方程,积分:c y x =+2243椭圆族(f )y u x 4=,x u y 4=,代入流线方程,积分:c y x =-22双曲线族(g )y u x 4=,x u y 4-=,代入流线方程,积分:c y x =+22同心圆(h )4=x u ,0=y u ,代入流线方程,积分:c y =直线族(i )4=x u ,x u y 4-=,代入流线方程,积分:c x y +-=22抛物线族(j )x u x 4=,0=y u ,代入流线方程,积分:c y =直线族(k )xy u x 4=,0=y u ,代入流线方程,积分:c y =直线族(l )rc u r =,0=θu ,由换算公式:θθθsin cos u u u r x -=,θθθcos sin u u u r y +=220y x cx r xr c u x +=-=,220y x cyr y r c u y +=+=代入流线方程积分:c y x=直线族 (m )0=r u ,r c u =θ,220y x cy r yr c u x +-=-=,220y x cxr x r c u y +=+=代入流线方程积分:c y x =+22同心圆2.在上题流速场中,哪些流动是无旋流动,哪些流动是有旋流动。
如果是有旋流动,它的旋转角速度的表达式是什么?解:无旋流有:x uy u yx ∂∂=∂∂(或r ru u r∂∂=∂∂θθ)(a ),(f ),(h ),(j ),(l ),(m )为无旋流动,其余的为有旋流动对有旋流动,旋转角速度:)(21y ux u xy ∂∂-∂∂=ω(b )23=ω (c )2-=ω (d )2-=ω (e )27-=ω(g )4-=ω (i )2-=ω (k )x 2-=ω3.在上题流速场中,求出各有势流动的流函数和势函数。
流体力学泵与风机第三章一元流体动力学基础第五版

流体力学泵与风机第三章一元流体动力学基础第五版此答案仅供参考1.直径为150mm的给水管道,输水量为980.7kN/h,试求断面平均流速。
解:由流量公式Q=ρvAv=QρA注意:(kN/h→kg/s Q=ρvA)得:v=1.57m/s2.断面为300mm×400mm的矩形风道,风量为2700m3/h,求平均流速.如风道出口处断面收缩为150mm×400mm,求该断面的平均流速解:由流量公式Q=vA由连续性方程知v1A1得:v=QA=v2A2得:v2=12.5m/s3.水从水箱流经直径d1=10cm,d2=5cm,d3=2.5cm的管道流入大气中.当出口流速10m/时,求(1)容积流量及质量流量;(2)d1及d2管段的流速解:(1)由Q=v3A3=0.0049m3/s质量流量ρQ=4.9kg/s(2)由连续性方程:v1A1=v3A3,v2A2=v3A3得:v1=0.625m/s,v2=2.5m/s4.设计输水量为*****kg/h的给水管道,流速限制在0.9∽1.4m/s之间。
试确定管道直径,根据所选直径求流速。
直径应是50mm的倍数。
解:Q=ρvA将v=0.9∽1.4m/s代入得d=0.343∽0.275m∵直径是50mm的倍数,所以取d=0.3m代入Q=ρvA得v=1.18m5.圆形风道,流量是*****m3/h,,流速不超过20m/s。
试设计直径,根据所定直径求流速。
直径规定为50mm的倍数。
解:Q=vA 将v≤20m/s代入得:d≥420.5mm取d=450mm代入Q=vA得:v=17.5m/s6.在直径为d圆形风道断面上,用下法选定五个点,以测局部风速。
设想用和管轴同心但不同半径的圆周,将全部断面分为中间是圆,其他是圆环的五个面积相等的部分。
测点即位于等分此部分面积的圆周上,这样测得的流速代表相应断面的平均流速。
(1)试计算各测点到管心的距离,表为直径的倍数。
(2)若各点流速为u1,u2,u3,u4,u5,空气密度为ρ,求质量流量G。
新版流体力学泵与风机蔡增基第五版下答案-新版.pdf
xa
ux
y 2 ( y2 ( x a) 2 y 2 ( x a) 2 )
Q
y
y
uy
ห้องสมุดไป่ตู้
x 2 ( y 2 (x a)2 y 2 ( x a) 2 )
4 ydy
3xdx 2 y2 3 x2 2
(g)积分路径可以选
0,0 x,0 : dy 0, y 0
x,0 x, y : dx 0, x x
4ydy ( 4x)dx 2 y 2 2x 2
(L )积分路径可以选 0,0 x,0 : dy 0, y 0
x,0 x, y : dx 0, x x
ux ur cos u sin
1.描绘出下列流速场 解:流线方程: dx dy
ux uy
(a) u x 4 , u y 3 ,代入流线方程,积分:
3 y xc
4
直线族 (b) u x 4 , u y 3x ,代入流线方程,积分:
y 3 x2 c 8
抛物线族
(c) u x 4y , uy 0 ,代入流线方程,积分: y c
直线族 (d) u x 4 y , uy 3 ,代入流线方程,积分:
xa
6
驻点在 y 0, x
l 处,由 l 2
2,b
0.5 得椭圆轮廓方程:
x2 1
y2 (0.25) 2
1
即: x2 16 y2 1
8. 确定绕圆柱流场的轮廓线,主要取决于哪些量?已知
R 2 m ,求流函数和势函数。
解:需要流速 v0 ,柱体半径 R
v0 (r ∵R 2
R2 ) sin
r ∴ v0(r
4) sin r
R2
v0 (r
) cos
流体力学泵与风机(第五版)蔡增基课后习答案(一)
流动阻力和能量损失1.如图所示:(1)绘制水头线;(2)若关小上游阀门A ,各段水头线如何变化?若关小下游阀门B ,各段水头线又如何变化?(3)若分别关小或开大阀门A 和B ,对固定断面1-1的压强产生什么影响?解:(1)略(2)A 点阻力加大,从A 点起,总水头线平行下移。
由于流量减少,动能减少,使总水头线与测压管水头线之间的距离减小,即A 点以上,测压管水头线上移。
A 点以下,测压管水头线不变,同理讨论关小B 的闸门情况。
(3)由于1—1断面在A 点的下游,又由于A 点以下测压管水头线不变,所以开大或者关小阀门对1—1断面的压强不受影响。
对B 点,关小闸门,B 点以上测压管水头线上移,使1—1断面压强变大,反之亦然。
2.用直径的管道,输送流量为的水,如水温为mm d 100=s kg /105℃,试确定管内水的流态。
如用这样管道输送同样质量流量的石油,已知石油密度,运动粘滞系数3850m kg =ρ,试确定石油的流态。
s cm 214.1=υ解:(1)5℃时,水的运动粘滞系数sm 2610519.1−×=υ,=Av Q Q ρρ==v()231.0410110×××π20008386310519.1)1.0(41011.010Re 623>=××××××==−πυvd 故为紊流(2)200013141014.1)1.0(48501.010Re 42<=×××××=−π故为层流3.有一圆形风道,管径为300mm ,输送的空气温度20℃,求气流保持层流时的最大流量。
若输送的空气量为200kg/h ,气流是层流还是紊流?解:20℃时,空气的运动粘滞系数sm v 26107.15−−×=3205.1m kg =ρ2000Re ==υvdsm v 105.03.0107.1520006=××=−hkg s kg vA Q m 32109.83.04105.0205.132=×=×××==−πρ故,为紊流h kg 2004.水流经过一渐扩管,如小断面的直径为,大断面的直径1d 为,而,试问哪个断面雷诺数大?这两个断面的雷2d 221=d d 诺数的比值是多少?21Re Re 解:;2211A v A v Q ==4)(2122121===d dA A v v2214Re Re 221121=×==d v d v 故直径为的雷诺数大1d 5.有一蒸汽冷凝器,内有250根平行的黄铜管,通过的冷却水总流量为8L/s ,水温为10℃,为了使黄铜管内冷却水保持为紊流(紊流时黄铜管的热交换性能比层流好),问黄铜管的直径不得超过多少?解:0℃时,水的运动粘滞系数υ=1.31×10−6m 2/s24250d Q v ⋅⋅=π要使冷却水保持紊流,则4000Re ≥,4000≥υvd mm vd 61031.14000−××≤即:mmd 67.7≤若最小Re 取2000时,mmd 3.15≤6.设圆管直径,管长,输送石油的流量mm d 200=m L 1000=运动粘滞s L Q /40=系数,求沿程水头损失。
流体力学泵与风机(第五版) 蔡增基 课后习题答案(1)
64 Re
, 水 力 光 滑 区 λ = 0.3164 和粗糙区 0.25
Re
这三个公式,论证在层流中 h1 ∽ v ,光滑区 h1 ∽ v1.75 ,
粗糙区 h1 ∽ v 2 解:层流中 λ = 64 = 64υ
Re
vd
h=
λLv 2 64υ ⋅ L ⋅ v 2 = d ⋅ 2 g vd ⋅ d ⋅ 2 g
即: d ≤ 7.67mm 若最小 Re 取 2000 时, d ≤ 15.3mm 6. 设 圆 管 直 径 d = 200mm , 管 长 L = 1000m , 输 送 石 油 的 流 量
Q = 40 L / s 运动粘滞
30
系数 υ = 1.6cm 2 ,求沿程水头损失。 解:
π 2 2 ⋅d × (0.2) 4 4 Re= vd = 1.27 × 0−.2 =1588,故为层流 υ 1.6 × 10 4 λ= 64 = 64 =0.04 Re 1588
d 2 = 2 ,试问哪个断面雷诺数大?这两个断面的雷
Re 2
诺数的比值 Re1
是多少?
v2
=
解: Q = v1 A1 = v2 A2 ; v1
A1 d = ( 2 )2 = 4 A2 d1
29
vd Re1 1 = 1 1 = 4× = 2 2 Re 2 v 2 d 2
故直径为 d1 的雷诺数大 5.有一蒸汽冷凝器,内有 250 根平行的黄铜管,通过的冷却
当
在光滑区 在过渡区 在粗糙区
由h = λ l
v2 d 2g
,光滑区 λ1 = 0.3164 0.25
Re
过渡区 λ2 = 0.11( k + 68 ) 0.25
(2020年7月整理)泵与风机课后习题参考答案(完整版).doc
泵与风机(课后习题答案)第五章5-1 水泵在n=1450r/min 时的性能曲线绘于图5-48中,问转速为多少时水泵供给管路中的流量为Hc=10+17500q v 2(q v 单位以m 3/s 计算)?已知管路特性曲线方程Hc=10+8000q v 2(q v 单位以m 3/s 计算)。
2同一水泵,且输送流体不变,则根据相似定律得:某水泵5-2 在管路上工作,管路特性曲线方程Hc=20+2000q v 2(q v单位以m 3/s 计算),水泵性能曲线如图5-49所示,问水泵在管路中的供水量是多少?若再并联一台性能相同的水泵工作时,供水量如何变化?【解】绘出泵联后性能曲线2管路特性曲线与泵并联后性能曲线交于M 点(56L/s ,25m ).5-3为了增加管路中的送风量,将No.2风机和No.1风机并联工作,管路特性曲线方程为p =4 q v 2(q v 单位以m 3/s 计,p 以p a 计),No.1 及No.2风机的性能曲线绘于图5-50中,问管路中的风量增加了多少?2×103m 3/h ,700p a )于单独使用No.1风机相比增加了33×103-25×103=8 m 3/h5-4 某锅炉引风机,叶轮外径为1.6m ,q v -p 性能曲线绘于图5-51中,因锅炉提高出力,需改风机在B 点(q v =1.4×104m 3/h ,p =2452.5p a )工作,若采用加长叶片的方法达到此目的,问叶片应加长多少?【解】锅炉引风机一般为离心式,可看作是低比转速。
求切割直线:描点做切割直线vB B q p q p 06.6306.631400036005.2452K ==⨯==min /r 114246145030m m p m p =⨯==v v v q n n q q ,a A 点与B 点为对应工况点,则由切割定律得m 8.1)1114(D D )(22222==''=',D D q q v v 则应加长1.8-1.6=0.2m5.5 略5-6 8BA-18型水泵的叶轮直径为268mm ,车削后的8BA-18a 型水泵的叶轮直径为250mm ,设效率不变,按切割定律计算qv 、H 、P 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体力学泵与风机第五版课后习题答案【篇一:流体力学泵与风机习题集】习题集一、填空题1.流体力学中三个主要力学模型是(123。
2.在现实生活中可视为牛顿流体的有和等。
3.流体静压力和流体静压强都是压力的一种量度。
它们的区别在于:前者是作用在;而后者是作用在。
4.均匀流过流断面上压强分布服从于。
5.和液体相比,固体存在着、和三方面的能力。
6.空气在温度为290k,压强为760mmhg时的密度和容重分别为7.流体受压,体积缩小,密度;流体受热,体积膨胀,密度的性质,称为流体的。
8.压缩系数?的倒数称为流体的,以来表示9.1工程大气压等于千帕,等于水柱高,等于汞柱高。
10.静止流体任一边界上压强的变化,将等值地传到其他各点,只要,这就是的帕斯卡定律。
11.流体静压强的方向必然是沿着。
12.液体静压强分布规律只适用于。
13.静止非均质流体的水平面是,和。
14.测压管是一根玻璃直管或u形管,一端另一端。
15.在微压计测量气体压强时,其倾角为??30?,测得l?20cm 则。
16.作用于曲面上的水静压力p的铅直分力pz等于。
17.通过描述物理量在空间的分布来研究流体运动的方法称为。
18.流线不能相交(驻点处除外),也不能是折线,因为流线只能是一条光滑的。
19.、和之和以pz表示,称为总压。
20.液体质点的运动是极不规则的,各部分流体,这种流动状态称为。
?,21.由紊流转变为层流的临界流速vk由层流转变为紊流的临界流速vk?称为,vk称为其中vk22.对圆管来说,临界雷诺数值rek?。
23.圆管层流的沿程阻力系数仅与而和无关。
24.根据?繁荣变化特征,尼古拉兹实验曲线可分为五个阻力区,分别是;;;和。
25.紊流过渡区的阿里特苏里公式为。
26.速度的或发生变化而引起的能量损失,称为损失。
27.正方形形断面管道(边长为a),其水力半径r等于当量直径de等于28.正三角形断面管道(边长为a),其水力半径r等于de等于。
29.湿周是指和接触的周界。
滑管区与有关,在过渡区与有关,在粗糙区与有关。
31.串联管路总的综合阻力系数s等于。
32.并联管路总的综合阻力系数s与各分支管综合阻力系数的关系为。
管嘴与孔口比较,如果水头h和直径d相同,其流速比v孔口/v管嘴等于流量比q孔口/q管嘴等于33.不可压缩流体的空间三维的连续性微分方程是。
34.m?1即气流速度与相等,此时称气体处于状态。
35.淹没出流是指液体通过时的流动。
36.气体自所形成的流动,称为气体淹没射流。
37.有旋流动是指流体微团的的流动。
38.几何相似是指即线段长度保持一定的比例。
39.因次是指物理量的。
因次分析法就是通过对及因的各种性质的分析来研究现象相似性的方法。
他是一方程式的和为基础的。
40.容积泵与风机又可分为和。
41.根据流体的流动情况,可将泵和风机分为以下四种类别:;;和。
42.风机的压头(全压)p是指43.单位时间内泵或风机所输送的流体量称为风机的容积流量,特指。
44.泵或风机所提供的流量与设备本身效率之间的关系,用来表示。
45.泵或风机的工作点是与的交点。
46.泵的扬程h的定义是:泵所输送的增值。
47.安装角是指叶片与之间的交角。
48.泵和风机的全效率等于49.当泵的扬程一定时,增加叶轮转速可以相应的轮径。
50.附面层的分离发生在区。
附面层外主流区的流动属于流动。
附面层内的流动属于流动。
二、判断题1.当平面水平放置时,压力中心与平面形心重合。
2.一个工程大气压等于98kpa,相当于10m水柱的压强。
3.静止液体自由表面的压强,一定是大气压。
4.静止液体的自由表面是一个水平面,也是等压面。
5.当静止液体受到表面压强作用后,将毫不改变地传递到液体内部各点。
6.当相对压强为零时,称为绝对真空。
7.某点的绝对压强小于一个大气压强时即称该点产生真空。
8.流场中液体质点通过空间点时,所有的运动要素不随时间变化的流体叫恒定流。
9.恒定流时,流线随的形状不随时间变化,流线不一定与迹线相重合。
10.渐变流过水断面上动水压强的分布规律可近似地看作与静水压强分布规律相同。
11.流线是光滑的曲线,不能是折线,流线之间可以相交。
12.一变直径管段,a断面直径是b断面直径的2倍,则b断面的流速是a断面流速的4倍。
13.弯管曲率半径rc与管径d之比愈大,则弯管的局部损失系数愈大。
14.随流动雷诺数增大,管流壁面粘性底层的厚度也愈大。
15.水泵的扬程就是指它的提水高度。
16.管嘴出流的局部水头损失可有两部分组成,即孔口的局部水头损失及收缩断面出突然缩小产生的局部水头损失。
17.当流速分布比较均匀时,则动能修正系数的值接近于零。
18.流速分布越不均匀,动能修正系数的值越小。
19.在水流过水断面面积相等的前提下,湿周愈大,水力半径愈小。
20.圆形管的直径就是其水力半径。
21.为了减少摩擦阻力,必须把物体做成流线型。
23.水泵的安装高度取决于水泵的允许真空值、供水流量和水头损失。
24.大孔口与小孔口都可认为其断面上压强、流速分布均匀,各点作用水头可以认为是一常数。
三、简答题1.什么是粘滞性?什么是牛顿内摩擦定律?不满足牛顿内摩擦定律的流体是牛顿流体还是非牛顿流体?2.在流体力学当中,三个主要的力学模型是指哪三个?3.什么是理想流体?4.什么是实际流体?5.什么是不可压缩流体?6.为什么流体静压强的方向必垂直作用面的内法线?7.为什么水平面必是等压面?8.什么是等压面?满足等压面的三个条件是什么?9.什么是阿基米德原理?10.潜体或浮体在重力g和浮力p的作用,会出现哪三种情况?11.等角速旋转运动液体的特征有那些?12.什么是绝对压强和相对压强?13.什么叫自由表面?14.什么是流线?什么是迹线?流线与迹线的区别是什么?15.什么是流场?16.什么是欧拉法?17.什么是拉格朗日法?18.什么是恒定流动?什么是非恒定流动?19.什么是沿程损失?20.是局部损失?21.什么叫孔口自由出流和淹没出流?22.什么是有旋流动?什么是无旋流动?23.流体力学中拉格朗曰分析法和欧拉分析法有何区别?24.什么叫流管、流束、过流断面和元流?25.什么是入口段长度?对于层流、紊流分别用什么表示?26.什么是单位压能?27.什么是滞止参数?28.气流速度与断面的关系有哪几种?29.什么是几何相似、运动相似和动力相似?【篇二:许贤良_陈庆光等编著《流体力学》课后详解】1 若某种牌号的汽油的重度?为7000n/m3,求它的密度?。
7000n/m33解:由???g得,????714.29kg/mg9.8m/m2??得,?????997.0kg/m3?0.893?10?6m2/s?8.9?10?4pa?s ?1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm,可动板若以 0.25m/s的速度移动,为了维持这个速度需要单位面积上的作用力为2n/m2,求这两块平板间流体的动力黏度?。
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为duu0.25?1???500s ?3dyy0.5?10由牛顿切应力定律???du,可得两块平板间流体的动力黏度为 dy???dydu?4?10?3pa?s题1.4图解:圆盘不同半径处线速度不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r处,取增量dr,微面积,则微面积da上的摩擦力df为df??da由df可求da上的摩擦矩dtdur??2?r?dr dz?2???r3drdt?rdf?积分上式则有?1t??dt??d202??????d4?rdr?32?3题1.5图解:以d点为原点建立坐标系,设流速分布u?ay2?by?c,由已知条件得c=0,a=-625,b=50则u??625y2?50y 由切应力公式???dudu???(?1250y?50) 得???dydyy=0cm时,y=2cm时,y=4cm时,?3?0 ?1?5?10?2n/m2;?2?2.5?10?2n/m2;解:由k?lim(??v?0?v1dv)???得 v?pvdp1?v1(1000?995)?10?6m3k???????0.5?10?8pa?1 ?636262v?p995?10m2?10n/m?1?10n/m1.7 当压强增量为50000 n/m2时,某种液体的密度增长为0.02%,求此液体的体积弹性模数?。
解:由体积弹性模数公式??1dpdp?v?p?得 ?lim????v???k?v?0??v?dvd??p?p50000n/m2??????2.5?108pa?????0.02%2第2章流体静力学2.1 一潜水员在水下15m处工作,问潜水员在该处所受的压强是多少?解:由p??h得,p?1000kg/m3?9.8m/s2?15m?1.47?105pa 2.2 一盛水封闭容器,容器内液面压强po=80kn/m2。
液面上有无真空存在?若有,求出真空值。
解:pa?1.01?105pap0?0.8?105pa,即存在真空真空值pv?pa?p0?0.21?105pa2.3 如图,用u型水银测压计测量水容器中某点压强,已知h1=6cm,h2=4cm,求a点的压强。
解:选择水和水银的分界面作为等压面得pa??1(h1?h2)?pa??2h2故a点压强为pa?pa??1h1?h2(?1??2)?1.14?105pa2.4 如图示两容器底部连通,顶部空气互相隔绝,并装有压力表,p1=245kpa,p2=245kpa,试求两容器中水面的高差h。
解:由p1?p2??h得,h?p1?p2?(245?145)?103pa??10.2m 1000kg/m3?9.8m/s22.5 水压机是由两个尺寸不同而彼此连通的,以及置于缸筒内的一对活塞组成,缸内充满水或油,如图示:已知大小活塞的面积分别为a2,a1,若忽略两活塞的质量及其与圆筒摩阻的影响,当小活塞加力f1时,求大活塞所产生的力f2。
解:由p1p2fa得,f2?12 ?a2a1a2题2.3图题2.4图题2.5图2.6如图示高h=1m的容器中,上半装油下半装水,油上部真空表读数p1=4500pa,水下部压力表读数p2=4500pa,试求油的密度?。
解:由题意可得pabs?pa?p1,pabs??ghh???p2 223解得??p2?pabs??2h?836.7kg/m32.7 用两个水银测压计连接到水管中心线上,左边测压计中交界面在中心a点之下的距离为z,其水银柱高度为h。
右边测压计中交界面在中心a点之下的距离为z+?z,其水银柱高为h+?h。
(1)试求?h 与?z的关系。
(2)如果令水银的相对密度为13.6,?z=136cm时,求?h是多少?题2.6图题2.7图解:(1)分别取左边测压计中交界面为等压面得,?pa??1h??2?pa?p??(z??z)?p??(h??h)2a1?a解得?h与?z的关系为:?2?z??1?h (2)当?z=136cm时,?h? ?2?z?10cm ?12.8 给出如图所示a、b 面的压强分布图。
