原子物理课件 第4节 电子自旋与轨道运动的相互作用
电子自旋及轨道运动相互作用

电子自旋及轨道运动相互作用摘要:通过对实验事实的简单介绍,引入电子自旋的概念,并逐渐深入,对其进行进一步阐述。
说明电子自旋的特点,以及它和轨道运动之间的相互作用和能量的计算。
此外,还简要说明电子自旋与能级的分裂之间的关系,以及塞曼效应。
关键词:电子自旋轨道运动角动量能级0 引言许多实验事实证明电子具有自旋,下面叙述的斯特恩—革拉赫实验(Stern-Gerlach)实验是其中一个。
图1 斯特恩-革拉赫实验图2一个角动量为、磁矩为的陀螺在磁场中进动频率的矢量图图1中由O射出的处于s态的氢原子束通过狭缝和不均匀磁场,最后射到照相片P上,实验结果是相片上出现两条分立的线。
这说明氢原子具有磁矩,所以原子束通过非均匀磁场时受到力的作用而发生偏转;而且由分立线只有两条这一事实可知,原子的磁矩在磁场中只有两种去向,即它们是空间量子化的。
这可有下面的讨论看出。
假设原子的磁矩为M ,它在沿竖直方向z轴的外磁场B中的势能为:■式中■是原子磁矩M和外磁场之间的夹角。
原子在z方向所收到的力是:■如果原子磁矩在空间可以取任何方向的话,cos■应当可以从+1连续变化到-1,这样在照相片上应该得到一个连续的带,但实验结果只有两条分立的线,对应于cos■=+1和cos■=-1。
1 电子自旋为了说明见金属原子能级的双层结构,G.Uhlenbeck和S.A.Goudsmit在1925年首先提出,可以设想电子具有某种方式的自旋,其角动量等于(1/2)(h/2π)。
这个自旋角动量是不变的,是电子的属性之一,所以也称电子的固有矩。
电子既有某种方式的转动而电子是带负电的,因而它也具有磁矩,这磁矩的方向同上述角动量的方向相反。
每个电子具有自旋磁矩■,它和自旋角动量■的关系是:■ (1.1)式中-e是电子的电荷,μ是电子的质量。
■在空间任意方向上的投影只能取两个数值:■ (1.2)■是玻尔磁子。
由(1.1)式,电子自旋磁矩和自旋角动量之比是:■(1.3)这个比值称为电子自旋的回旋磁比率。
1.1.4原子结构第4课时-核外电子排布原理课件高二化学人教版选择性必修2

巩固练习——未成对电子数
【任务2】指出1-36号基态原子的未成对电子数。
第四周期未成对电子数规律
未成对电子数及其占据的原子轨道
4s
1
3d
4p
3d 2
4p
3d 3
4p
4
3d
5
3d
6
3d和4s
元素符号及价电子排布 K:4s1,Cu:3d104s1 Sc:3d14s2 Ga:4s24p1,Br:4s24p5 Ti:3d24s2,Ni:3d84s2 Ge:4s24p2,Se:4s24p4 V:3d34s2,Co:3d74s2 As:4s24p3 Fe:3d64s2 Mn:3d54s2 Cr:3d54s1
24Cr
3d
4s
↑↑↑↑
↑↓
只有一组全满的简并轨道
3d
4s
↑↑↑↑↑ ↑
有两组半满的简并轨道
29Cu
3d
4s
↑↓ ↑↓ ↑↓ ↑↓ ↑ ↑↓
只有一组全满的简并轨道
3d
4s
↑↓ ↑↓ ↑↓ ↑↓ ↑↓ ↑
有一组全满、一组半满的简并轨道
能量相近的简并轨道中,电子排布为全充满、半充满或全空的状 态是能量较低的稳定状态,此为洪特规则的特例。
1927年 第五届索尔维会议
第一排:欧文·朗缪尔、马克斯·普朗克、玛丽·居里、亨 得里克·洛仑兹、阿尔伯特·爱因斯坦、保罗·朗之万、Ch. E. Guye、C.T.R.威尔逊、O.W.里查森 第二排:彼得·德拜、马丁·努森、威廉·劳伦斯·布拉格、
Hendrik Anthony Kramers、保罗·狄拉克、亚瑟·康普顿、路易·德布罗意、 马克斯·波恩、尼尔斯·玻尔 第三排:奥古斯特·皮卡尔德、E. Henriot、保罗·埃伦费 斯特、Ed. Herzen、Théophile de Donder、欧文·薛定谔、E. Verschaffelt、沃尔夫冈·泡利、 沃纳·海森堡、R.H.福勒、里昂·布里渊
原子物理学第四章碱金属原子

二、碱金属原子的光谱项
R R 光谱项 : Tn *2 2 n (n )
锂:
s= 0.4 p = 0.05 d= 0.001 f =0.000 钠: s =1.35 p=0.86 d =0.001 f =0.000
三、碱金属原子能级
hcR hcR E n hcT *2 2 n (n )
第四章 碱金属原子
(讲授6学时、自学6学时)
1
§4.1 碱金属原子光谱
一、碱金属原子光谱的实验规律 二、碱金属原子的光谱项 三、碱金属原子的能量和能级
2
一、碱金属原子光谱的实验规律
1、 碱金属原子光谱具有原子光谱的一般规律性;
2、通常可观察到四个谱线系。
各种碱金属原子的光谱,具有类似的结构。 主线系(也出现在吸收光谱中); 第二辅线系(又称锐线系);
柏格曼系:
~ fn
R R , n =4,5,6… 2 2 (3 d ) (n f )
8
3、锂的四个线系
~ 2S nP 第二辅线系: ~ P nS
主 线 系:
,n = 2, 3, 4… ,n =3,4,5… ,n =3,4,5… , n =4,5,6…
第二辅 线系 主线系
s,=0
T 43484.4 16280.5 8474.1
n* 1.589 2.596 3.598
5186.9 3499.6 2535.3
4.599 5.599 6.579
T 28581.4 12559.9 7017.0 p, =1 * n 1.960 2.956 3.954 T d, =2 n* T n* 12202.5 6862.5 2.999 3.999 6855.5 4.000
原子物理学4
s
电子的自旋轨道耦合
电子围着原子核做圆周运动, 原子的总磁矩和总角动量都来 源于电子的轨道运动和电子的 自旋。 j l s 总磁矩:
总角动量: P j Pl Ps
价电子
e
Ze
由量子力学可知,Pj也是量子化的, 相应的 总角动量量子数用 j 表示,且有
§4.4 电子自旋同轨道运动的相互作用
电子的自旋
Uhlenbeck and Goudsmit 在1925年提出: 实验依据: (1)史特恩-盖拉赫实验出现偶数分裂的事实 (2)碱金属原子光谱的精细结构
P 电子具有某种方式的自旋; s s ( s 1), s 1 2
相对于外磁场方向,自旋角动量Ps在空间只能取朝上和 P 1 朝下两种取向: s B Psz ms , ms z 自旋磁矩和自旋角动量的关系是:
碱金属原子态的符号:
电子态符号:l 0 ,1, 2 , 3 ,
s, p , d , f ,
比如: n=3时,3s, 3p, 3d
原子态符号:由价电子的诸量子数来描述
L 0 ,1, 2 , 3 , S , P , D , F ,
s 1 2 L l: j ls: ,2 s 1 2 :
2
j
*
j ( j 1) l ( l 1) s ( s 1)
c
j
l
*2
l
*
2
s
*
讨论: (1) n和l相同,s不变,只有j不同,不同的j值具有不同 的能量
l 0 时, j l s l 1 / 2 l 0 时, j l s l 1 / 2,或
【精品】第2章-原子结构-电子自旋PPT课件

2.3.4 Pauli原理
2.3.4.1 原理
完全波函数
n,l,m ,m s n,l,m m s
为不使完全波函数的符号与轨道波函数的符号相 混淆,将轨道波函数改用φ表示。
i i i
全同粒子
在多电子体系中,各个电子是完全等同的,即它 们具有完全相同的静质量、电荷和自旋这些与运 动情况无关的固有性质,因此不能利用这些性质 来区分它们。由于微观粒子具有统计性质,我们 也不能通过追踪它们的运动轨迹来区分、辨认它 们,这就是全同粒子的不可区分性,在量子力学 中,这类体系为全同粒子体系。
取负号,表示两粒子交换坐标后,完全波函数绝对值 不变而符号改变,称为反对称波函数。
Pauli原理
对于包含两个或两个以上粒子的体系的完全波函数, 交换体系中任意两个粒子的坐标或自旋。
如果自旋量子数为取整数的粒子,如光子,介子,K 介子,称为玻色子(Bosons),其波函数必须是对称波 函数。
凡是自旋量子数为取半整数的粒子,如电子,质子, 中子,介子,各种超子,称为费米子(Fermions),其 波函数必须是反对称波函数。
银或碱金属的原子束通过一
个不均匀磁场射到屏幕上时,
Stern
射线束会偏转而分为对称分 布的两束。
1888~1969,美国 1943年Nobel物理奖
碱金属原子的1个s电子:l=0,m=0
l(l1)B0 zmB0
s电子不与外加磁场发生作用,原子束不应偏转 和分裂。
基态氢原子束实验也发生同样的现象。
原子中的电子除轨道运动外,还存在有其它运 动方式。
1925年,Uhlenbeck和Goudsmit提出电子自旋运动假 设:电子具有不依赖于轨道运动的、固有的磁矩。
原子物理学第4章

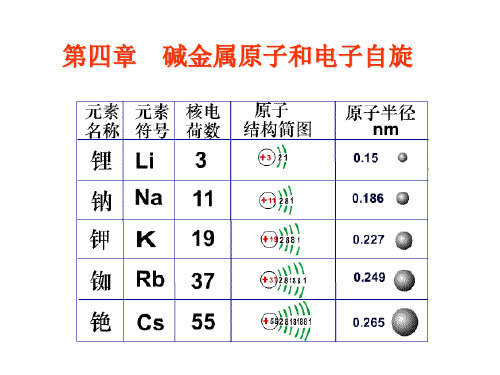
价电子的轨道:n ≥ 2
Li: Z=3=212+1 Na:Z=11=2(12+22)+1 K: Z=19=2(12+22+22)+1 Rb:Z=37=2(12+22+32+22)+1 Cs:Z=55=2(12+22+32+32+22)+1 Fr:Z=87=2(12+22+32+42+32+22)+1
3、Na原子的能级与能级跃迁
主线系:从l=1的p态→n=3, l=0的3s态, n=3,4… 锐线(二辅)系:从l=0的s态→n=3, l=1的3p态, n=4,5… 漫线 (一辅)系:从l=2的d态→n=3, l=1的3p态, n=4,5… 基线(柏格曼)系:从l=3的f态→n=3, l=2的3d态, n=4,5,6…
Rhc En 2 (n D l )
-e
●
r Rnl
●
2
2
21
20
n=2
r r1
图4-5、轨道的贯穿
0
4
r Rnl
2
2
32
31
30
n=3
r r1
0 9
l 越小,电子波 函数靠近核的概率 越大,贯穿的几率 越大,能量越低
小结:碱金属原子光谱
1、实验规律:
所有的碱金属原子的光谱,具有相仿的结构,实验观 察的谱线一般分为四个线系。
~D相同而n不同的光谱 和
R R 2、碱金属原子的光谱项: Tnl 2 n (n D l ) 2
• 量子数亏损:D l
nn
自旋与轨道运动相互作用

自旋与轨道运动相互作用
既然电子有自旋角度量,它就会与电子的轨道运动角动量合成为总角动量。
在量子力学中,角动量除了按照矢量合成的规则合成外,还有一些特别的法则。
假定用字母 j 来代表与总角动量对应的量子数,在量子力学中,角动量的合成还满足这样一个法则:
其中s=1/2是自旋量子数。
结合轨道角动量和自旋角动量的表达
式:
,
就可以求出自旋角动量和总角动量的空间
取向。
比如说,有了自旋角动量与轨道角
动量的夹角,就可以得到自旋磁矩的空间
取向:
在原子中,电子绕带正电的核运动。
从电
子上看,有正电荷绕电子转动。
有磁矩的
从本质上说,电子感受到的这个磁场起源于它绕原子核的轨道运动,因此,是自旋与轨道运动相互作用带来的结果。
这种自旋与轨道运动的相互作用使电子获得一个附加的能量:
根据前面的讨论,电子的自旋磁矩为:
由电子的轨道运动带来的等效磁场为:
Zs是价电子感受到的有效核电荷数。
利用电子做轨道运动时角动量的表达式
将与轨道运动相关的因子消掉,得到等效磁场的表达式:
以上是把电子当做非相对论粒子处理的结果,如果按相对论来处理,则附加的能量是这里的一半。
我们将采用相对论的处理结果。
另一方面,由于电子绕原子核运动的轨道是一个椭圆,因此,电子离开核的距离应该用平均值代替:
式中a₁是玻尔半径。
把这些结果凑在一起,就得到由自旋与轨道运动相互作用带来的附加能量。
原子物理学褚圣麟PPT课件

Z*e
r
H
e•
v
m
Z*e
H
r •e
轨道角动量 pl mvr sin
附加能量
Bpl
s
Els p jsB cos
p s
cos
B
0Z *ev
4πr 2
sin
p2j pl2 ps2
2 pl ps
第22页/共42页
4.4 电子自旋同轨道运动的相互作用
➢ 附加能量按相对论处理结果(1925年)
n 相同,l 不同的能级高低差别很大
第8页/共42页
4.1 碱金属原子的光谱
例 Na 原子的基态为3S,已知其共振线波长为 589.3nm, 漫线系第一条的波长为819.3nm, 基线系第 一条波长为1845.9nm, 主线系的系限波长为241.3nm, 试求 3S、3P、3D、4F 各谱项的项值。
p,l 1 n* 1.960 2.956 3.954 4.954
T
12202. 5 6862. 5 4389. 2
d,l 2 n*
2.999 3.999 5.000
f ,l
3
T
n*
6855. 5 4381. 2
4.000 5.004
3499. 6 2535. 3
5.599 6.579
3094. 4 2268. 9
V
1.85V
辅线系
~
n
~
R n*2
n*
~
n
~
E hc
第一激发 态能量
eU2
E
hc
5.6 4 8 81 019 J
U2 3.52V U U1 U2 5.38V
第27页/共42页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l 1, j 0,1 三线结构 l 1, j 0,1 三线结构
以上是量子力学对碱金属光谱精细结构的理论解释。
例 Na 原子光谱中得知其3D 项的项值T3D=1.2274×106m-1, 试计算该谱项之精细结构裂距。
已知 T3D=1.2274×106m-1 , RNa=1.0974×107m-1
§ 4.4 电子自旋同轨道的相互作用
一、施特恩—盖拉赫实验
1921年施特恩和盖拉赫用实验证明了原子具有磁矩,磁矩的数 值和取向是量子化的。
银原子的实验结果: 当B=0时,P上只有一条细痕, 磁矩不受力的作用。
当B均匀时,P上仍只有一条 细痕,磁矩不受力的作用。
当B不均匀时,P上有两条细 痕,磁矩受力的作用。
碱金属光谱的精细结构
选择定则
主线系
2P1/2 2P3/2
(第锐二线辅系线系)2S1/2
2S1/2 2P1/2 2P3/2
l 1, j 0,1 双线结构 l 1, j 0, 1 双线结构
漫线系
2D3/2
(第一辅线系) 2D5/2
基线系 2F5/2 (柏格曼系) 2F7/2
2P1/2 2P3/2 2D3/2 2D5/2
3.双层能级中,j值较大的能级较高。
3.碱金属原子态符号
2
2s+1
Lj
j=+1/2 j=-1/2
0,1, 2, 3, 4, 5, S,P, D, F, G
4. 单电子辐射跃迁的选择定则
单电子辐射跃迁的选择定则 从碱金属原子的光谱中,可以得出这样的结 论,能级的跃迁只能发生在下列条件下:
l 1, j 0,1
论文发表后,海森伯表示赞许,后经爱因斯坦等人的努力, 物理界普遍接受了自旋的概念,但泡利始终反对。
泡利认为“一种新的邪说被引进了物理学”。应当说泡利并没 有错,两年后狄拉克建立了相对论量子力学,自然地得到了电 子具有内禀角动量的重要结论。
1. 电子自旋角动量和自旋磁矩
1925年,荷兰的乌伦贝克和古德史密特提出了电子自旋的假设: 每个电子都具有自旋的特性,由于自旋而具有自旋角动量和自 旋磁矩,它们是电子本身所固有的,是电子的属性之一,又称 固有矩和固有磁矩。
2
E________ ls
hcR 2Z 4
2n3l(l 1)
2
双层能级的间隔:
E
hcR
n 3l l
2Z 4
1
讨论:
1.能级由n、j、l三个量子数决定,
当l=0时,j=s,能级不分裂;
当时l
0,j
l
1 2
,能级为双层。
2. 能级分裂的间隔由n、l决定
当n一定时,l 大,E 小,即 E4 p E4d E4 f 当l一定时,n 大,E 小,即E2 p E3 p E4 p
1 r3
p
2 j
pl2
ps2
2
3 j2
1 j2
考虑相对论效应后:
El,s
1 1
2 4 0
e Z e m mc2
1 r3
p
2 j
pl2
ps2
2
1 Z e2 h2 1 j2 l2 s2
4 0 2m2c2 4 2 r3
2
2 e2 4 0ch
R
2 2me4 (4 0 )2 ch3
r是一个变量,根据量子力学,可求得
p j pl ps (l s) j ( j l s)
电子自旋角动量引起的 能量附加值为:
Els sB cos
a图(较大的j)的能量大于 b图(较小的j)的能量,附 加能量引起双层能级。
pl
B
ps
s
a
ps
pj
pl
1 j l
2
pl
B
s
ps
b
ps
pl
pj
1 j l 2
根据量子力学角动量具有以下的形式:
Pl l(l 1) l* 其中l*为简略符号 l* l(l 1)
Ps s( s 1) s* , ( s 1/2) Pj j( j 1) j* , ( j l s或l s)
ps 和pl 就不能 平行或反平行
例如 l=1,j=1+1/2=3/2,或 j=1-1/2=1/2
pj
2 2 2
3
he
4m
1.7B
u
电子感受到的磁场:
B
0Z 4
ev r2
sin
ห้องสมุดไป่ตู้
1
4 0
Z e mc2
pl r3
Z*e B PS
r -e
B
Z*re
u
-e
m
如图,由余弦定理得:
pj
B
B
cos
p
2 j
pl2
ps2
2 pl ps
自旋—轨道相互作用能为:
pj
ps s
s
ps
El,s
sB cos
1
4 0
e Ze m mc2
1 r3
的平均值,于是:
________
hcR 2Z 4 j2 l2 s2
E l,s n3l(l 1) l 1
2
2
E________
hcR 2Z 4
ls 2n3(l 1)l 1
2
E________ ls
hcR 2Z 4
2n3l(l 1)
2
E________
hcR 2Z 4
ls 2n3(l 1)l 1
按照角动量守恒原理,总角动量的方 向不变,因此ps和pl绕pj旋进,由于pj 是个守恒量,ps和pl的夹角不变。
附加运动引起附加能量,这是碱金属 能级精细结构的原因。
pj
pl
ps 电子自旋角动量和轨道 角动量绕总角动量旋进
2.自旋—轨道相互作用能
电子自旋运动而具有自旋磁矩:
s
e m
ps
e m
13 h
怎样解释这一奇怪的现象呢?
实验装置示意图
二、电子的自旋
美国物理学家克罗尼格(R.L.Kroning)提出电子绕自 身的轴自旋的模型,并作了一番计算。并急忙去找泡 利,但遭到泡利的强烈反对,并对他说:“你的想法 很聪明,但大自然并不喜欢它”。因泡利早就想到过 这一模型,并计算出电子速度要超过光速。所以必须 放弃。 半年后,荷兰物理学家埃斯费斯特的两个学生乌仑贝克和古德 史密特(G.E.Uhlenbeck and S.A.Goudsmit)在不知上述情形下, 也提出了同样的想法,并写了一篇论文,请埃斯费斯特推荐给 “自然”杂志。并将论文寄出。接着又去找洛仑兹,洛仑兹热 情地接待了他们。但一周后,洛仑兹交给他们一叠稿纸。并告 诉他们,如果电子自旋,其表面速度将超过光速,但论文已寄 出,他们后悔不已。
从运动的相对性原理,在固定于电子的一个坐标系中,相当于 带正电的原子实绕着电子运动,电子会感受到一个磁场的存在, 其方向为原子实绕电子运动的角动量方向,因而电子自旋取向 就必须量子化,不同的取向具有不同的能量。
从实验上分析,碱金属能级是双层的,因而可以认为电子自旋 有两个取向。
设电子自旋角动量为: ps s
pl
2
1.41 ,
ps
13
22
0.87 ,
B
B
pj
pj
35 22
1.94 ,
或 pj
13
22
0.87 ,
ps s
s
ps
j3
j1
2
2
三个角动量就有如图的关系
电子自旋磁矩在轨道运动的磁场作用 下,应该绕着该磁场旋进。
从另一方面考虑,轨道运动也受到自 旋磁场的作用,也必须绕该磁场旋进。
n RNa 2.9901 T3D
Z
n n
T
RNa 2Z 2
n3l(l 1)
3.655 (m1)
电子自旋角动量的取向数为: 2s 1 2 s 1 2
电子自旋的两个取向一个顺磁场,另一个反磁场。即在磁场方
向的角动量分别为:
1 2
价电子的轨道角动量和自旋角动量合成价电子的总角动量,由 于原子实的总角动量为零(后面的课程将介绍),原子的总角 动量等于价电子的总角动量。
总角动量为: pl ps (l s) j ( j l s)
