勾股定理(4)
勾股定理知识点+对应类型
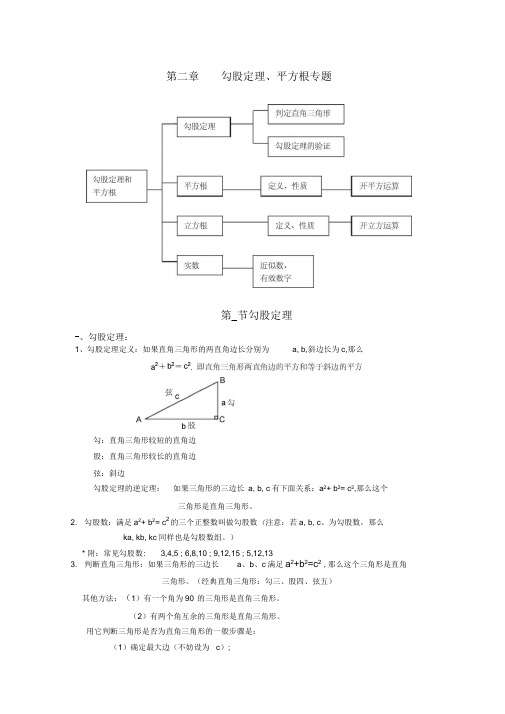
第二章勾股定理、平方根专题第_节勾股定理-、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a, b,斜边长为c,那么勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a, b, c有下面关系:a2+ b2= c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+ b2= c2的三个正整数叫做勾股数(注意:若a, b, c、为勾股数,那么ka, kb, kc同样也是勾股数组。
)* 附:常见勾股数: 3,4,5 ; 6,8,10 ; 9,12,15 ; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2) 若c2= a2+ b2,则^ ABC是以Z C为直角的三角形;若a2 + b2v c2,则此三角形为钝角三角形(其中c为最大边);若a2 + b2> c2,则此三角形为锐角三角形(其中c为最大边)4. 注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的(3) 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1) 已知直角三角形的两边求第三边。
(2) 已知直角三角形的一边,求另两边的关系。
(3) 用于证明线段平方关系的问题。
(4) 利用勾股定理,作出长为际的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a,那么这个数就叫做a的平方根。
(也称为二次方根),也就是说如果x2=a,那么x就叫做a的平方根。
勾股定理

板块一 勾股定理1.勾股定理的内容:如果直角三角形的两直角边分别是a 、b ,斜边为c ,那么a 2+b 2=c 2.即直角三角形中两直角边的平方和等于斜边的平方。
注:勾——最短的边、股——较长的直角边、 弦——斜边。
CAB cba勾股定理3.勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
即 222,,ABC AC BC AB ABC ∆+=∆在中如果那么是直角三角形。
4.勾股数:满足a 2 +b 2=c 2的三个正整数,称为勾股数.勾股数扩大相同倍数后,仍为勾股数.常用勾股数:3、4、5; 5、12、13;7、24、25;8、15、17。
板块一、勾股定理【例1】 下列说法正确的是( )A. 若a b c ,,是ABC ∆的三边,则222a b c +=B. 若a b c ,,是Rt ABC ∆的三边,则222a b c +=C. 若 a b c ,,是Rt ABC ∆的三边,90A ∠=︒,则222a b c +=D. 若 a b c ,,是Rt ABC ∆的三边,90C ∠=︒,则222a b c +=【例2】 在Rt ABC ∆中, 90C ∠=︒,(1)如果34a b ==,,则c = ; (2)如果68a b ==,,则c = ; (3)如果512a b ==,,则c = ; (4)如果1520a b ==,,则c = .【例3】 若一个直角三角形三边的长分别是三个连续的自然数,则这个三角形的周长为【例4】 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .【例5】 已知直角三角形的两边长分别为3、4,求第三边长.【例6】 已知直角三角形两边x ,y 的长满足240x -,则第三边长为______________.【例7】 一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )A .斜边长为25B .三角形周长为25C .斜边长为5D .三角形面积为20【例8】 如果梯子的底端距离墙根的水平距离是9m ,那么15m 长的梯子可以达到的高度为【例9】 如图,梯子AB 斜靠在墙面上,AC BC AC BC ⊥=,,当梯子的顶端A 沿AC 方向下滑x 米时,梯足B 沿CB 方向滑动y 米,则x 与y 的大小关系是( ) A .x y = B .x y > C .x y < D .不确定CA【例10】 如图,一个长为10米的梯子,斜靠在墙上,梯子的顶端距离地面的垂直距离为8米,如果梯子的顶端下滑1米,那么,梯子底端的滑动距离 米(填“大于”、“等于”、“小于”)68【例11】 三角形的三边长分别为6,8,10,它的最短边上的高为( )A. 6B. 4.5C. 2.4D.8【例12】 若ABC ∆的三边a b c ,,满足条件:222338102426a b c a b c +++=++,则这个三角形最长边上的高为【例13】 如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )A. 1倍B. 2倍C. 3倍D. 4倍【例14】 如图,一根高8米的旗杆被风吹断倒地,旗杆顶端A 触地处到旗杆底部B 的距离为6米,则折断点C到旗杆底部B 的距离为CBA【例15】 已知,如图所示,折叠长方形的一边AD ,使点D 落在BC 边的点F 处,•如果8cm AB =,10cm BC =,求EC 的长.【例16】 如图,有一个直角三角形纸片,两直角边6cm 8cm AC BC ==,,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,那么CD 的长为多少?EDCBA【例17】 如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC 中,边长为无理数的边数是( )A. 0B. 1C. 2D. 3CBA【例18】 如图所示,在ABC ∆中,三边a b c ,,的大小关系是( )cbaCBAA. a b c <<B. c a b <<C. c b a <<D. b a c <<【例19】 设,,,a b c d 都是正数。
勾3股4定理公式大全

勾3股4定理公式大全勾股定理公式大全勾股定理是数学中的一条基本定理,描述了直角三角形中的关系。
在三角学和几何学中,勾股定理的应用广泛且重要。
本文将为您提供勾股定理的公式大全,以帮助您深入理解和运用。
一、直角三角形及勾股定理概述在开始介绍公式之前,我们先来了解一下直角三角形和勾股定理的基本概念。
直角三角形是指其中一个角为直角(即90度),即一个角为90°的三角形。
在直角三角形中,有一条边与直角相邻,称为斜边;另外两条边称为直角边。
而勾股定理则是描述了直角三角形中三边之间的关系,即直角边的平方和等于斜边的平方。
二、勾股定理公式勾股定理的公式可以根据计算对象的不同进行分类。
下面将逐一介绍这些公式:1. 已知两直角边求斜边的长度在已知直角三角形的两条直角边的长度时,我们可以通过勾股定理求出斜边的长度。
假设直角三角形的两条直角边分别为a和b,斜边为c,则公式如下:c² = a² + b²2. 已知斜边和一直角边求另一直角边的长度当我们已知直角三角形的斜边和其中一条直角边的长度时,可以通过勾股定理求出另一条直角边的长度。
假设直角三角形的斜边为c,已知直角边为a,则公式如下:a² = c² - b²3. 已知斜边和另一直角边求第三边的长度在已知直角三角形的斜边和另一条直角边的长度时,可以通过勾股定理求出第三边的长度。
假设直角三角形的斜边为c,已知直角边为b,则公式如下:b² = c² - a²4. 已知两直角边之比求每条直角边的长度当我们已知直角三角形的两直角边之比时,可以通过勾股定理求出每条直角边的长度。
假设直角三角形的两直角边之比为m:n,直角边的长度为ma和na,则公式如下:a = n * (√(m² + n²))b = m * (√(m² + n²))三、勾股定理的应用勾股定理不仅仅是理论上的数学公式,它在实际应用中也发挥着重要的作用。
勾3股4定理公式大全

勾3股4定理公式大全勾股定理是数学中最基本的定理之一,它描述了直角三角形中直角边与斜边的关系。
而勾三股四定理,则是一种推广的勾股定理,它描述了三个直角三角形的边长之间的比例关系。
以下是勾三股四定理的三个公式及其推导过程。
一、第一个勾三股四定理公式:设直角三角形ABC,其中∠C=90°,则有AB^2=BC×AC这个公式可以通过勾股定理的推导得出。
根据勾股定理,有AC^2=AB^2+BC^2带入角C=90°,则有AB^2=AC^2-BC^2即AB^2=BC×AC。
二、第二个勾三股四定理公式:设直角三角形ABC,其中∠A=90°,则有AC^2=AB×BC这个公式可以通过将公式一中的AB和BC互换得出。
即将AB^2=BC×AC两边的AB和BC互换,得到AC^2=AB×BC。
三、第三个勾三股四定理公式:设直角三角形ABC,其中∠B=90°,则有BC^2=AB×AC这个公式可以通过将公式一中的AB和AC互换得出。
即将AB^2=BC×AC两边的AB和AC互换,得到BC^2=AB×AC。
ABCB,C在直角三角形ABC中,根据勾三股四定理公式一的推导过程,可以得到AB^2=BC×A C。
同理,根据勾三股四定理公式二和公式三的推导过程,可以得到AC^2=AB×BC以及BC^2=AB×AC。
勾三股四定理公式在解决问题时非常实用,它可以帮助我们在已知两条边后,快速求解剩余边的长度。
举个例子,假设在一个直角三角形ABC中,已知AC=5cm,BC=12cm,我们需要求解AB的长度。
根据勾三股四定理公式一,我们有AB^2=BC×AC代入已知值,即可得到AB^2 = 12cm × 5cm计算得到AB^2 = 60 cm^2再开平方根,即可得到AB的长度,约为7.746cm。
勾3股4定理公式大全

勾3股4定理公式大全1.基本形式:在直角三角形中,设直角边分别为a,b,斜边为c,则有:c²=a²+b²。
这是最基本的勾股定理形式,也是最常见的应用形式。
根据该定理,我们可以利用已知的两条边求解第三条边的长度。
2.次对边形式:在直角三角形中,设直角边为a,斜边为c,另一边为b,则有:b²=c²-a²。
这个形式是基本形式的变形,通过给出直角边和斜边,求解另一直角边的长度。
3.正弦定理:在任意三角形中,设三边分别为a,b,c,角度为A,B,C,则有:a/sin(A) = b/sin(B) = c/sin(C)。
正弦定理是三角形中的重要定理,可以用来求解三角形中的边长和角度。
它表示每个角的对边与正弦值的比例是相等的。
4.余弦定理:在任意三角形中,设三边分别为a,b,c,角度为A,B,C,则有:c² = a² + b² - 2abcos(C)。
余弦定理是另一个用于求解三角形中的边长和角度的重要定理。
它表示边的平方等于两边平方和减去两边的乘积与其夹角余弦的乘积。
5.正切定理:在任意三角形中,设三边分别为a,b,c,角度为A,B,C,则有:tan(A) = a/b,tan(B) = b/a。
正切定理表示两角的正切值相等,可以用来求解三角形中的角度。
6.角平分线定理:在任意三角形中,设三角形的内角A,内角的角平分线与边的交点与另一边的交点分别为B和C,则有:AB/AC=BD/DC。
角平分线定理表示角平分线与两边的比例相等,可以用来求解三角形中的边的比例。
7.海伦公式:在任意三角形中,设三边分别为a,b,c,半周长为s,则有:面积=√(s(s-a)(s-b)(s-c))。
海伦公式是用来计算任意三角形面积的公式,通过已知三边长度和半周长,可以求解三角形的面积。
以上是勾股定理及相关公式的简要介绍。
这些定理及公式在解决直角三角形和任意三角形的问题时非常有用,可以通过简单的数值运算求得所需的结果。
典中点勾股定理专训4巧用勾股定理判定直角的六种方法

典中点勾股定理专训4 巧用勾股定理判定直角的六种方法◐名师点金◑说明垂直的方法:1.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.2.等腰三角形中“三线合一”.3.直角三角形的判定.在几何中,我们常常先说明垂直,再利用垂直的性质来解相关问题。
典例剖析:某校把一块三角形的废地开辟为植物园,如图,测得AC=80m,BC=60m,AB=100m 。
(1)若人口E 在边AB 上,且与A,B 的距离相等.求从入口E 到出口C 的最短路线的长(提示直角三角形斜边上的中线等于斜边的一半);(2)若线段CD 是一条水渠,且点D 在边AB 上,点D 距点A 多远时,水渠最短?解题秘方:解实际生活中的问题,需先将实际问题通过建立数学模型转化为数学问题,再利用数学知识进行解答.本题中:已知△ABC 中,AC=80m,BC=60m ,AB=100m 。
(1)若AE=EB,求CE 的长; (2)若CD ⊥AB,求AD 的长。
方法1:利用三边的数量关系证明直角1.如图,在正方形ABCD 中,F 为DC 的中点,E 为BC 上一点,且CE=41BC ,求证:∠AFE 是直角.方法2:利用转化为三角形法构造直角三角形2.如图,在四边形ABCD 中,∠B=90°,AB=3,BC=4,CD=12,AD=13.求ABCD S 四边形.方法3:利用倍长中线法构造直角三角形3.如图,在△ABC 中,D 为边BC 的中点,AB=5,AD=6,AC=13.求证AB ⊥AD方法4:利用化分散为集中法构造直角三角形4.如图,在等腰直角三角形ABC 的斜边上取两点M,N,使∠MCN=45°,设AM=a,MN=x,BN=b,判断以x,a,b 为边长的三角形的形状。
方法5:利用“三线合一”法构造直角三角形5. 如图,在△ABC 中,CA=CB,∠ACB=90°,D 为AB 的中点,M,N 分别为AC,BC 上的点,且DM ⊥DN.求证:22CN CM 2AB )(+=方法6:利用轴对称的性质构造直角三角形6.如图,在Rt △ABC 中,∠B=90°,AB=3,AC=5,将△ABC 折叠,使点B 恰好落在边AC 上,与点B'重合,AM 为折痕,则MB'的长为多少?。
勾股定理

A1
B2
C3
D4
2.如图,数轴上点A所表示的数为a, 则a的值是( )
3. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使
AB边与对角线AC重合,点B落在点F 处,折痕为AE,
且EF=3,则AB的长为( )
A.3 B.4
C.5 D.6
4.如图,矩形AOBC中,点A的坐标为(0,8),点D的
二、勾股定理的证明
方法一:将四个全等的直角三角形拼成如图所示 的正方形.
方法二:将四个全等的直角三角形拼成如图(2)所 示的正方形.
方法三:如图(3)所示,将两个直角三角形拼成 直角梯形.
三、勾股定理的作用 1.已知直角三角形的任意两条边长,求第三边; 2.用于解决带有平方关系的证明问题; 3. 利用勾股定理,作出长为 的线段.
纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落
在边OB上E处,那么图中阴影部分的面积为( )
30 B.32 C.34
D.16
5.在△ABC中,AB=15,AC=13,高AD=12, 则△ABC的周长为( ) A.42 B.32 C.42或32 D.37或33
6.在直线上依次摆着7个正方形(如图),已知倾斜放置 的3个正方形的面积分别为1,2,3,水平放置的4个正 方形的面积是S1,S2,S3,S4则S1+S2+S3+S4______.
勾 股定理
一、勾股定理 直角三角形两直角边的平方和等于斜边的平方. 如果直角三角形的两直角边长分别为a、b,斜边长为c, 那么a2+b2=c2. 1.勾股定理揭示了一个直角三角形三边之间的数量关系. 2.利用勾股定理,当设定一条直角边长为未知数后,
根据题目已知的线段长可以建立方程求解,这样就将 数与形有机地结合起来,达到了解决问题的目的. 3.理解勾股定理的一些变式:a2=c2-b2,b2=c2-a2.
勾股定理(4)

蚂蚁 A C 蜂蜜
3 13
针对训练 2、如图是一个棱长为3cm正方体盒子,在盒子下 底部的A点有一只蚂蚁,它想吃到上底面B点的食 物,需爬行的最短路程是多少?
D
B
A A
C C
针对训练 3、已知长方体的长为2cm、宽为1cm、高为4cm, 一只蚂蚁如果沿长方体的表面从A点爬到B′点,那 么沿哪条路最近,最短的路程是多少?
边 l
针对训练 1、如图,从点 A 0, 发出的一束光,经 x轴反 2 射,过点 B 4, ,则这束光从点 A到点B 所经过 3 路径的长为 .
y A O D C E B
.
x
例题选讲 例2、课本P81第8题
. .
B
10
A
6
针对训练 1、如图,圆柱形玻璃杯,高为12cm,底面周长为 18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此 时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相 对的点A处,则蚂蚁到达蜂蜜的最短距离为__cm.
D’ Dˊ Aˊ B’ Bˊ
Cˊ B’
D A C
B
B
作业讲评
13m
5m
2m
C D
B
E
A
《全品》P31课时十八
1、B; 2、D; 3、A ; B; 6、B
7、 2 ; 8、7;
4、D;
5、
31 9、 ; 10、2 2
作业:
1、《全品》课时作业19;
2、练习卷;
3、预习课本P73-76,完成练习(暗线A)。
勾股定理(4) 距离最短问题
例题选讲 例1、如图,要在河边修建一个水泵站,分别向张 村A和李庄B送水,已知张村A、李庄B到河边的距 离分别为2km和7km,且张、李二村庄相距13km. (1)水泵应建在什么地方,可使所用的水管最短? (2)如果铺设水管的工程费用为每千米1500元, 为使铺设水管费用 B 最节省,请求出最 A 节省的铺设水管的 费用为多少元? 河
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理(4)
一选择题
1.已知一个Rt△的两边长分别为3和4,则第三边长的平方是()A 25 B 14 C 7 D 7或25
2.下列各组数中,以a,b,c为边的三角形不是Rt△的是()
A、a=1.5,b=2,c=3
B、a=7,b=24,c=25
C、a=6,b=8,c=10
D、a=3,b=4,c=5
3.若线段a,b,c组成Rt△,则它们的比为()A 2∶3∶4 B 3∶4∶6 C 5∶12∶13 D 4∶6∶7
4.Rt△一直角边的长为8,另两边为连续奇数,则Rt△的周长为()A 36 B 56 C 40 D不能确定
5.若Rt△两直角边的比为5∶12,则斜边上的高与斜边的比为()A 60∶13 B 5∶12 C 12∶13 D 60∶169
6.如果Rt△的两直角边长分别为n2-1,2n(n>1),那么它的斜边长是()A 2n B n+1 C n2-1 D n2+1
7.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是()
A、24cm2
B、36cm2
C、48cm2
D、60cm2
8.等腰三角形底边上的高为8,周长为32,则三角形的面积为()A、56 B、48 C、40 D、32
9.三角形的三边长为a2+b2+c2=ab+bc+ac,则这个三角形是( )
A. 等边三角形
B. 钝角三角形
C. 直角三角形
D. 锐角三角形
10.某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要() A 450a元 B 225a 元 C 150a元 D 300a元
11.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE 的面积为() A、6cm2 B、8cm2 C、10cm2 D、12cm2
12.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距()A 25海里 B 30海里 C 35海里 D 40海里
二填空题
13.在Rt△ABC中,∠C=90°,①若a=5,b=12,则c=______;②若a=15,c=25,则b=______;③若c=61,b=60,则a=_______;④若a∶b=3∶4,c=10则S Rt△ABC=________
14.有一个矩形,其面积为48m2,对角线长为10m,则这个矩形鱼池的周长_____________
15.直角三角形两直角边长分别为5和12,则它斜边上的高为__________
16.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是________m
17.已知两条线段的长为5cm和12cm,当第三条线段的长为 cm时,这三条线段能组成一个直角三角形
18.已知Rt△AB C的周长为4+23,斜边AB的长为23,则Rt△ABC•的面积为_____.
19.如图,△ABC中,∠C = 90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F 分别是垂足,且BC = 8cm,CA = 6cm,则点O到三边AB,AC和BC的距离分别等于 cm 20.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A,B,C,D的面积之和为___________cm2
21.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。
另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高_________米
22.如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.•当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯______米
三解答题
21.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,
已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D
两村到E站的距离相等,则E站应建在离A站多少km处?
22.如图,在Rt△ABC中,∠C=900,BD平分∠ABC,CD=12,AD=13,求AB的长
23.如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理
24.△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形
25.如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过的知识说明:AB2-AP2=PB×PC
26.如图,A市气象站测得台风中心在A市正东方向300千米的B处,以107千米/时的速度向北偏西60°的BF方向移动,距台风中心200•千米范围内是受台风影响的区域.(1)A市是否会受到台风的影响?写出你的结论并给予说明;(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
27.(1)国际数学家大会曾在北京召开,大会会标如图(1),它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5,求中间小正方形的面积.(2)现有一张长为6.5cm,宽为2cm的纸片,如图(2),请你将它分割成6块,•再拼合成一个正方形.(要求:先在图(2)中画出分割线,再画出拼成的正方形并标明相应数据)
部分答案
27.(1)可设直角三角形的两条直角边,根据勾股定理得到两条直角边的一个关系式,再结合已知条件联立解方程组,求出两条直角边的长.则小正方形的面积即为大正方形的面积减去4个直角三角形的面积;
(2)根据面积不变,可知要拼成的正方形的边长是.13=4+9,故可以把它分割成4个直角边分别是2和3的直角三角形和两个长宽分别是1和0.5的矩形.
解:(1)设直角三角形的两条边分别为a、b(a>b),则依题意有:,①两边平方﹣②,得ab=6,
(a﹣b)2=(a+b)2﹣4ab=1,∴a﹣b=1,故小正方形的面积为1.
(2)
(1)注意正方形的面积即为直角三角形斜边的平方;(2)注意根据图形的面积不变进行分析。
