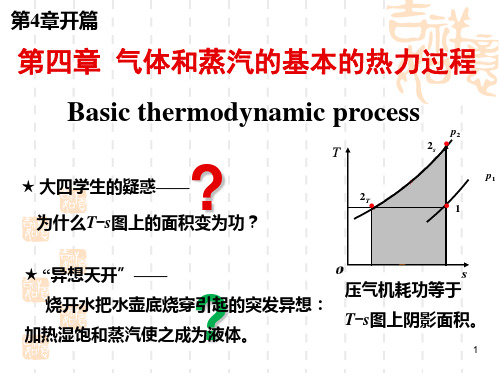
第四章 气体和蒸汽的基本的热力过程
合集下载
工程热力学 第四章 气体和蒸汽的基本热力过程.

☆注意:(1)假设上述过程都是可逆过程。(2)适 用于理想气体、闭口系统和稳定流动开口系统(即定 质量系统)
2、多变过程的过程方程式(polytropic process)
pvn 定值 ln p n ln v 定值 即多变过程在 ln p ln v 图上为直线,斜率为n 。
■初、终状态参数之间的关系
定温线在p-v图上是等轴双曲线,在T-s图上是水平线
p
2′
T
1 2
2′ 1
2
O
vO
s
1-2:吸热减压膨胀;1-2′:放热增压压缩
q du pdv pdv Tds
■热量、过程功、技术功
u cV (T2 T1) 0 h cp (T2 T1) 0
பைடு நூலகம்
qT w wt T s
■过程方程式 v 定值
如汽油机气缸中的燃烧过程。 ■初、终状态参数之间的关系
p2 / p1 T2 / T1
即定容过程压力与温度成正比。
■在p-v图和T-s图上的表示
n (p / v)v np / v
nk cn n 1 cV cV (T / s)v T / cV
/
kg
(h)v
(h)p
cp
(t 400℃
100℃ 2
t1) 310.6kJ / kg
定容过程:
s cV
400℃ 100℃
ln
T2 T1
0.4414kJ /(kg K)
q u 224.5kJ / kg
w0
wt v( p1 p2v ) 86.1kJ / kg
●可以取(, ) 之间的所有数。 n v 定值(定容过程)
2、多变过程的过程方程式(polytropic process)
pvn 定值 ln p n ln v 定值 即多变过程在 ln p ln v 图上为直线,斜率为n 。
■初、终状态参数之间的关系
定温线在p-v图上是等轴双曲线,在T-s图上是水平线
p
2′
T
1 2
2′ 1
2
O
vO
s
1-2:吸热减压膨胀;1-2′:放热增压压缩
q du pdv pdv Tds
■热量、过程功、技术功
u cV (T2 T1) 0 h cp (T2 T1) 0
பைடு நூலகம்
qT w wt T s
■过程方程式 v 定值
如汽油机气缸中的燃烧过程。 ■初、终状态参数之间的关系
p2 / p1 T2 / T1
即定容过程压力与温度成正比。
■在p-v图和T-s图上的表示
n (p / v)v np / v
nk cn n 1 cV cV (T / s)v T / cV
/
kg
(h)v
(h)p
cp
(t 400℃
100℃ 2
t1) 310.6kJ / kg
定容过程:
s cV
400℃ 100℃
ln
T2 T1
0.4414kJ /(kg K)
q u 224.5kJ / kg
w0
wt v( p1 p2v ) 86.1kJ / kg
●可以取(, ) 之间的所有数。 n v 定值(定容过程)
第四章-气体和蒸汽的基本热力过程

n k
(绝热过程)
●实际过程中,n 值是变化的,可用平均值代替;
或者把实际过程分作几段,每一段取定值。
4
4、多变过程的p-v图和T-s图 pvn 定值 ln p n ln v 定值 dp n dv 0 pv (p / v)n np / v(p-v图的斜率)
q cndT Tds
p1v1n p2v2n
T2
/ T1
(v1
/
v2 )n1
( p2
/
p )(n1)/n 1
3
3、多变指数 n (polytropic index)
n ln( p2 / p1) ln(v2 / v1)
(, )
n v 定值(定容过程)
特 n 0 p 定值(定压过程)
例 n 1 T 定值(定温过程)
(T / s)n T / cn (T-s图的斜率)
5
5、多变过程的过程功、技术功及热量
■过程功
w
2 1
pdv
p1v1n
2 1
dv vn
1( n 1
p1v1
p2v2 )
1 n 1
Rg
(T1
T2 )
k n
1 1 cV
(T1
T2 )
■技术功
2
2
2
2
wt 1 vdp
1
pdv
d ( pv)
p
2′ 1
2
T
2′
2 1
O
v
s
1-2:吸热升温膨胀 1-2′:放热降温压缩
cV cp T / cV T / cp
T
即在T-s图上,定容线比
定压线要陡一些。
定容线 1 定压线
工程热力学总复习

O
5
6
1
1
a
2
2
a
s
图11-3 初温t1对ηt的影响
优点: 循环吸热温度 , ,有利于汽机安全。
缺点: 对耐热及强度要求高,目前最高初温一般在550℃左右,很少超过600 ℃; 汽x
2a
v
t
h
2、初压p1对热效率的影响
基本状态参数,需要掌握①温标转换②压力测量(转换)③比体积与密度的转换。
04
03
01
02
系统在不受外界的影响的条件下,如果宏观热力性质不随时间而变化,这时系统的状态称为热力平衡状态,简称平衡状态。
系统内部及系统与外界之间的一切不平衡势差(力差、温差、化学势差)消失是系统实现热力平衡状态的充要条件。
k=1.3
νcr=0.577
干饱和蒸汽
k=1.135
关键:状态判断(习题8-2)
流量按最小截面(即收缩喷管的出口截面,缩放喷管的喉部截面)来计算
0
a
q m
c
b
图8-7 喷管流量qm
临界
临界 流量
喷管两种计算
设计计算
校核计算
已知
进口参数(p1、t1)、出口背压(pb)、流量qm
喷管形状、尺寸(A2、Acr)、进口参数(p1、t1)、出口背压(pb)
工 程 热 力 学
添加副标题
总复习
第一章基本概念
热力系统:人为地分割出来作为热力学分析对象的有限物质系统。 外界:系统周围物质的统称。 边界(界面):热力系与外界的分界面。 界面可以是真实,也可以是虚拟的;可以是固定,也可以是变化(运动)的。 闭口系统:与外界无物质交换,又称控制质量。 开口系统:与外界有物质交换,又称控制体积。 绝热系统:与外界无热量交换。 孤立系统:与外界无能量交换又无物质交换。可以理解成闭口+绝热,但是实际上孤立系统是不存在的。
工程热力学第四章理想气体热力过程

详细描述
03
CHAPTER
等容过程
等容过程是指气体在变化的整个过程中,其容积保持不变的过程。
定义
特点
适用场景
气体在等容过程中,气体温度和压力会发生变化,但容积保持不变。
等容过程常用于高压、高温或低温等极端条件下的气体处理。
03
02
01
等容过程定义
在等容过程中,气体吸收的热量等于气体所做的功和气体温度升高所吸收的热量之和。
多变过程的具体形式取决于气体所经历的压力和温度的变化规律。
多变过程定义热力学第一定律 Nhomakorabea热力学第二定律
理想气体状态方程
热效率
多变过程的热力学计算
01
02
03
04
能量守恒定律,用于计算多变过程中气体吸收或释放的热量。
熵增原理,用于分析多变过程中气体熵的变化。
描述气体压力、体积和温度之间的关系,可用于多变过程的计算。
衡量多变过程能量转换效率的指标,通过比较输入和输出的热量来计算。
提高热效率的方法
优化多变过程参数,如压力和温度的变化规律,以减少不可逆损失和提高能量转换效率。
热效率与熵增的关系
根据熵增原理,不可逆过程会导致熵的增加,从而降低热效率。因此,减少不可逆损失是提高多变过程热效率的关键。
热效率计算公式
$eta = frac{Q_{out}}{Q_{in}}$,其中$Q_{out}$为输出热量,$Q_{in}$为输入热量。
计算公式
通过优化气体的初态和终态,以及选择合适的加热和冷却方式,可以提高等容过程的热效率。同时,也可以通过改进设备结构和操作方式来提高热效率。
提高热效率的方法
等容过程的热效率
04
CHAPTER
03
CHAPTER
等容过程
等容过程是指气体在变化的整个过程中,其容积保持不变的过程。
定义
特点
适用场景
气体在等容过程中,气体温度和压力会发生变化,但容积保持不变。
等容过程常用于高压、高温或低温等极端条件下的气体处理。
03
02
01
等容过程定义
在等容过程中,气体吸收的热量等于气体所做的功和气体温度升高所吸收的热量之和。
多变过程的具体形式取决于气体所经历的压力和温度的变化规律。
多变过程定义热力学第一定律 Nhomakorabea热力学第二定律
理想气体状态方程
热效率
多变过程的热力学计算
01
02
03
04
能量守恒定律,用于计算多变过程中气体吸收或释放的热量。
熵增原理,用于分析多变过程中气体熵的变化。
描述气体压力、体积和温度之间的关系,可用于多变过程的计算。
衡量多变过程能量转换效率的指标,通过比较输入和输出的热量来计算。
提高热效率的方法
优化多变过程参数,如压力和温度的变化规律,以减少不可逆损失和提高能量转换效率。
热效率与熵增的关系
根据熵增原理,不可逆过程会导致熵的增加,从而降低热效率。因此,减少不可逆损失是提高多变过程热效率的关键。
热效率计算公式
$eta = frac{Q_{out}}{Q_{in}}$,其中$Q_{out}$为输出热量,$Q_{in}$为输入热量。
计算公式
通过优化气体的初态和终态,以及选择合适的加热和冷却方式,可以提高等容过程的热效率。同时,也可以通过改进设备结构和操作方式来提高热效率。
提高热效率的方法
等容过程的热效率
04
CHAPTER
工程热力学第4章气体和蒸汽的基本热力过程
n 1 pv const. 定温过程
(isothermal process; constant temperature process)
n pv const. 定熵(可逆绝热)过程
(isentropic process; reversible adiabatic process)
n v const. 定容过程
1
1
T1 p1 T2 p2
理想气体,定比热,可逆绝热过程。
13
二、过程的 p – v 图及T - s 图
p v
p v
cp cV
p v
(n 0) 0
p n p v n v
p
(n 1)
(n )
n
p v
p
v
.
n=0
n↑
n=1
n=±∞ n=κ
o
v
T T s cs
h cp
T2 T1
T2 T1
2
Tds
1
w
2
pdv
1
2 1
pvdv v
RgT1 ln
v2 v1
wt
2
vdp
1
2 1
vpdv p
RgT1
ln
p2 p1
q u w h wt q w wt 12
4–3 理想气体等比熵(可逆绝热)过程
一、过程方程
Tds δq dh vdp 0 vdp dh cpdT
4–1 研究热力过程的目的及一般方法
一、基本热力过程 (fundamental thermodynamic process)
近似直线
在ln p-lnV 图上有 ln p = -nlnV + c pvn 常数 4
(isothermal process; constant temperature process)
n pv const. 定熵(可逆绝热)过程
(isentropic process; reversible adiabatic process)
n v const. 定容过程
1
1
T1 p1 T2 p2
理想气体,定比热,可逆绝热过程。
13
二、过程的 p – v 图及T - s 图
p v
p v
cp cV
p v
(n 0) 0
p n p v n v
p
(n 1)
(n )
n
p v
p
v
.
n=0
n↑
n=1
n=±∞ n=κ
o
v
T T s cs
h cp
T2 T1
T2 T1
2
Tds
1
w
2
pdv
1
2 1
pvdv v
RgT1 ln
v2 v1
wt
2
vdp
1
2 1
vpdv p
RgT1
ln
p2 p1
q u w h wt q w wt 12
4–3 理想气体等比熵(可逆绝热)过程
一、过程方程
Tds δq dh vdp 0 vdp dh cpdT
4–1 研究热力过程的目的及一般方法
一、基本热力过程 (fundamental thermodynamic process)
近似直线
在ln p-lnV 图上有 ln p = -nlnV + c pvn 常数 4
第四章 气体和蒸汽的基本热力过程

绝热过程在 p-v 图和 T-s 图上的表示
p p = κ v v s
p p = v v T
12
3) 过程中能量的传递和转换 膨胀功: 膨胀功: q = u + w = 0
w = u = u1 u2
对于比热容为定值的理想气体, 对于比热容为定值的理想气体,
w = cV (T1 T2 ) =
q = u
定容过程吸收的热量全部用于增加工质的热力学能
6
4-3 定压过程
定压过程在 p-v 图和 T-s 图上的表示
T = T0 e
s s0 cp
T T = s p c p
7
比较
T T = s p c p
T T = s V cV
8
定压过程的功量和热量
= R (T2 T1 )
s
dp kp ( )s = dv v
dp p ( )T = dv v
p T
p
s v
T
n =0
n =1
s v
n =0
T p
n =∞
n=k
n =1
n=k
n =∞
v
s
29
理想气体基本过程的p-v, 图 理想气体基本过程的 ,T-s图
p T
p
s v
T2 p =( ) T p1 1
k 1 2 k
T
n =0
w t = c p (T1 T2 ) =
κ κ 1
Rg (T1 T2 ) wt = κ w
15
=
κ κ 1
( p1v1 p2v2 )
对于理想气体的可逆过程: 对于理想气体的可逆过程:
T2 P2 = T1 P 1
T2 v1 = T1 v2
p p = κ v v s
p p = v v T
12
3) 过程中能量的传递和转换 膨胀功: 膨胀功: q = u + w = 0
w = u = u1 u2
对于比热容为定值的理想气体, 对于比热容为定值的理想气体,
w = cV (T1 T2 ) =
q = u
定容过程吸收的热量全部用于增加工质的热力学能
6
4-3 定压过程
定压过程在 p-v 图和 T-s 图上的表示
T = T0 e
s s0 cp
T T = s p c p
7
比较
T T = s p c p
T T = s V cV
8
定压过程的功量和热量
= R (T2 T1 )
s
dp kp ( )s = dv v
dp p ( )T = dv v
p T
p
s v
T
n =0
n =1
s v
n =0
T p
n =∞
n=k
n =1
n=k
n =∞
v
s
29
理想气体基本过程的p-v, 图 理想气体基本过程的 ,T-s图
p T
p
s v
T2 p =( ) T p1 1
k 1 2 k
T
n =0
w t = c p (T1 T2 ) =
κ κ 1
Rg (T1 T2 ) wt = κ w
15
=
κ κ 1
( p1v1 p2v2 )
对于理想气体的可逆过程: 对于理想气体的可逆过程:
T2 P2 = T1 P 1
T2 v1 = T1 v2
工程热力学第四章

2、研究热力过程的一般方法
实际过程是一个复杂过程,很难确定其变化 规律,一般需要作些假设: (1) 根据实际过程的特点,将实际过程近似地概括为 几种典型过程:定容、定压、定温和绝热过程; (2)不考虑实际过程中不可逆的耗损,视为可逆过程; (3)工质视为理想气体; (4)比热容取定值。
3、分析热力过程的一般步骤
1 可知在p 由过程方程得 p ∝ κ 可知在p-v图上是一高次双曲线 v
定熵过程曲线的斜率是 ∂p = −κ p v ∂v s 定温过程曲线的斜率是
p ∂p =− v ∂v T
为什么? 为什么?
问题: 问题:定熵过程曲线 和定温过程曲线哪根 更陡? 更陡?
如
二、多变过程分析
1.多变过程的p 图和T 1.多变过程的p—v图和T-s图 p
n=+∞ n= —∞
T
n=1 n=0 n=0
n=1
n= —∞
v
s
2.内能、 2.内能、焓的变化量 内能 内能变化量 焓的变化量 3. 功和热 量 容 积 功
多变过程中容积功的计算
∆u = u2 − u1 = cv ∆T ∆h = h2 − h1 = c p ∆T
p
T2 T1
T2 > T1
pv = R T
1
2
T2 v2 = T1 v1
v
在p-v图上,等温 线的右上侧为温 度升高的方向。
4、在p-v图上熵增加的方向
p
s1
s2
s2 > s1
p2 v2 ∆s = cv ln + c p ln p1 v1 v2 ∆s = c p ln v1
1
2
v
在p-v图上,等熵 线的右上侧为熵 线的右上侧为熵增 加的方向。
工程热力学第4章

28
29
4-7 理想气体过程综述
一、各种过程在p-v图和T-s图上的相对位置
定容、定压、定温和定熵(可逆绝热)四个典型过 程都可以理解为多变过程的特例。其在p-v图上和T-s图 上的斜率如下:
( n 0)
0 p v
T cp 0 T cV
30
p p n v v n
Tc Tb
考虑过程等压 c
hc hb
a
q p ha hc 面积amnca
ha hb 面积amnca
38
p-v,T-s图练习(1)
压缩、升温、放热的过程,终态在哪个区域?
p
T
v
39
s
p-v,T-s图练习(2)
膨胀、降温、放热的过程,终态在哪个区域?
p
T
v
40
s
p-v,T-s图练习(3)
1 2
wt vdp 0
1
2
q p h wt h c
T2 p T1
T2 T1 1 Tds
2
四、Δu、 Δh、Δs和c
u c
T2 V T1
T2 T1
h c
T2 p T1
T2 T1
11
s
2
1
T2 dT cp s c p ln T T1
三、 定容过程的功量和热量
因为dv = 0,所以膨胀功为零,即
2
w pdv 0
1
注意和p-v 图对应
技术功: t vdp v( p1 p2 ) Rg (T1 T2 ) w
1
2
热量:
q Tds cV dT
29
4-7 理想气体过程综述
一、各种过程在p-v图和T-s图上的相对位置
定容、定压、定温和定熵(可逆绝热)四个典型过 程都可以理解为多变过程的特例。其在p-v图上和T-s图 上的斜率如下:
( n 0)
0 p v
T cp 0 T cV
30
p p n v v n
Tc Tb
考虑过程等压 c
hc hb
a
q p ha hc 面积amnca
ha hb 面积amnca
38
p-v,T-s图练习(1)
压缩、升温、放热的过程,终态在哪个区域?
p
T
v
39
s
p-v,T-s图练习(2)
膨胀、降温、放热的过程,终态在哪个区域?
p
T
v
40
s
p-v,T-s图练习(3)
1 2
wt vdp 0
1
2
q p h wt h c
T2 p T1
T2 T1 1 Tds
2
四、Δu、 Δh、Δs和c
u c
T2 V T1
T2 T1
h c
T2 p T1
T2 T1
11
s
2
1
T2 dT cp s c p ln T T1
三、 定容过程的功量和热量
因为dv = 0,所以膨胀功为零,即
2
w pdv 0
1
注意和p-v 图对应
技术功: t vdp v( p1 p2 ) Rg (T1 T2 ) w
1
2
热量:
q Tds cV dT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
或由
cn c p n cn cV n n 1 cn cV
等。
25
七、多变过程的能量关系w / q
w
Rg n 1
T1 T2
1
n 1
cV T1 T2
n q cV T2 T1 n 1
n
w 1 q n
3
二、研究热力过程的目的、方法—重要 ☆
1.目的 以热力学第一定律为基础,理想气体为工质,分析可逆 的基本热力过程中能量转换、传递关系,揭示过程中工质状 态参数的变化规律及热量和功量的计算。
2.方法和手段
<1>根据系统平衡的性质及过程中系统与外界热传递和功传递的特 定条件,建立过程方程式p=f(v)。 <2>借助过程方程和状态方程,找出不同状态间的参数关系,进而 相互确定之(对于实际气体,常采用图表计算)。 <3>在p-v图和T-s图中画出过程曲线,直观地描述过程中参数的变 化规律及能量转换情况。 <4>计算热力过程始、末状态间的比热力学能,比焓和比熵的变 化量(△u、△h、△s)。
第 四 章 气体和蒸汽的基本的热力过程
Basic thermodynamic process
4-1 研究热力过程的目的及一般方法
4-2 理想气体的定压、定容和定温过程 4-3 理想气体等比熵(可逆绝热)过程 4-4 理想气体多变过程 4-5 水蒸气的基本过程
1
4–1 研究热力过程的目的及一般方法
一、基本热力过程(fundamental thermodynamic process)
0
1.
1
Rg T1 T2 w
六、变比热绝热过程的计算-p113/115
w u1 u2 wt h1 h2
代替
查表
2. 用
19
3.
p2 dT s c p Rg ln 0 1 T p1 T1 T p2 1 T2 dT dT 令 0 dT ln cp cp s cp T T0 T p1 Rg T0 T T p2 1 0 0 ln s2 s1 A p1 Rg
23
Rg Rg u w cV T2 T1 T1 T2 T2 T1 n 1 1 n 1 Rg
q=
n cV T2 T1 n 1
cn T2 T1
2
1
Tds
五、比热容
n q u w cV T2 T1 c n T2 T1 n 1
p p n v v n
(n 1) (n ) n
T cp 0 T cV
T T p s cn n
v
16
三、比热容
cs 0
四、 u, h, s
u cV h c p s 2 s1
T2 T1 T2 T1
T2 V T1
2
T2 T1
h c
ห้องสมุดไป่ตู้
T2 p T1
T2 T1
9
s
1
T2 dT cV s cV ln T T1
定压过程
u cV
T2 T1
T2 T1
h c p
T2 T1
T2 T1
s
2
1
T2 dT cp s c p ln T T1
6
二、在p – v 图及T – s 图上表示
斜率
p v n
T s n
pv 常数
n
dp dv n 0 p v
p p n v v n
Tds δq cndT
T T s n cn
T2 T1 u T2 u T1 T2 T1 hT2 hT1
s 0
17
五、w,wt和q
w pdv
1
2
2
1
pv dv p1v1 v
或
w q u
0
Rg
1 RgT1 p2 v dv 1 1 p1
由于cV是温度的复杂函数,上式的积分解十分繁复,不便 于工程计算,若假设cV为定值,则cV +Rg、γ也为定值。
13
积分得到:
ln p ln v C
pv c
1
其中k为定熵指数,对于理想气体,定熵指数等于比热容比γ:
p1v1 p2v2
p1v1v1
T1 p1
定压过程
T2 V T1
T2 T1 1 Tds
2
w pv2 v1
wt 0
T2 p T1
q p h wt h c
T2 T1 1 Tds
11
2
定温过程
w pdv
1
2
2
1
v2 pv dv RgT1 ln v v1
q u w h wt
1
p2v2v2
T1v1 1 T2v2 1
1
T2 p2
1
由推导过程,上述三个过程方程式适用于: 理想气体,定比热,可逆绝热过程。 *初、终态温度变化范围在室温到600K之间时,可以将比 热容比或定熵指数作为定值。若温度变化幅度大,应用平 均定熵指数KEV。
当多变指数取不同的数值,多变过程可以化成以下4个特例:
n 0 : pv0 p C 0 C n 0 : pv p C 0 C 0 n 0 0 :: :pv pv C C T p C C 1 pv1 n C p n 1 : pv C T C k n 1 pv C C CT T C C n n 1 k :::pv pv k n k : pv pv C C kk 1 n k : n k : pv n C 1v C n : p11 p0 v C 0 n n : p v C p v C C 0 0v nn v C n : p p n : p v C p vC
定压过程 定温过程 定熵过程 定容过程
vC v C C v vC
例如:①燃气轮机燃烧室的燃烧加热过程,压力变化极微,接近定压 ②活塞压气机的汽缸套冷却足够好,压缩过程中气体温度几乎不升高,接近定温 ③燃气流过气轮机或空气流过叶轮式压气机,流速大,散热相对极少,接近绝热 ④汽油机汽缸中工质的燃烧加热过程,燃烧速度快,压力急剧上升而体积几乎不 变,接近定容。
h 0
定温过程
u 0 s
2 1
v2 v2 dT cV Rg ln s Rg ln T v1 v1
10
五、w, wt 和 q
定容过程
w pdv 0 wt vdp v p1 p2 1
1
2
2
qv u w u c
q w wt
12
4–3 理想气体等比熵(可逆绝热)过程
一、过程方程
绝热过程是任一微元过程中系统与外界都无热交换的过程,即
q cV dT pdv q c p dT vdp
c p dv dp p cV v
dp dv 0 p v
q 0
总的过程换热量也为零
2
0
定义
s ln pr Rg pr2 1 0 0 ln s2 s1 pr1 Rg
0
pr f T
( B)
比较式(A)与式(B)
pr 2 p2 p1 pr1
p2 pr 2 pr1 p1
20
4–4 理想气体多变过程
一、过程方程
p v p2v2
n 1 1
n
Tv
7
p p n v v n
T T s n cn
定容过程: n 定压过程: n 0 定温过程: n 1
p v v
T T s v cV
p 0 v p
p2 s s s Rg ln p1 T2 p2 定比热容 s c p ln Rg ln T1 p1 T2 v2 cV ln Rg ln T1 v1 p2 v2 cV ln c p ln p1 v1
0 2 0 1
22
h c p
t2 t1
T2 T1
pv 常数
n
称为多变过程,其中n为定值,称为多变指数。
*例如柴油机汽缸中的压缩过程,开始时工质 温度低于缸壁温度,边吸热边压缩而温度升高, 高于缸壁温度后则边压缩边放热,整个过程n 大约从1.6变化到1.2左右;膨胀过程,由于存 在后燃及高温时被离解气体的复合放热现象, 情况更为复杂,其散热规律的研究已不属于热 力学的范围。 2
p p v v T
T T s v c p
T T 0 s T cT
8
三、比热容
定容过程 定压过程 定温过程
cV
Rg
1
cp
1
Rg
cT
四、Δu、 Δh和Δs
定容过程
u c
n1 1 1
T2v2
n1
T1 p1
n 1 n
T2 p2
n 1 n
二、在p-v图及T-s图上表示
p p n v v n
T T T s n cn n cV
n 1
21
三、Δu, Δh和Δs t2 u cV t1 T2 T1
cn c p n cn cV n n 1 cn cV
等。
25
七、多变过程的能量关系w / q
w
Rg n 1
T1 T2
1
n 1
cV T1 T2
n q cV T2 T1 n 1
n
w 1 q n
3
二、研究热力过程的目的、方法—重要 ☆
1.目的 以热力学第一定律为基础,理想气体为工质,分析可逆 的基本热力过程中能量转换、传递关系,揭示过程中工质状 态参数的变化规律及热量和功量的计算。
2.方法和手段
<1>根据系统平衡的性质及过程中系统与外界热传递和功传递的特 定条件,建立过程方程式p=f(v)。 <2>借助过程方程和状态方程,找出不同状态间的参数关系,进而 相互确定之(对于实际气体,常采用图表计算)。 <3>在p-v图和T-s图中画出过程曲线,直观地描述过程中参数的变 化规律及能量转换情况。 <4>计算热力过程始、末状态间的比热力学能,比焓和比熵的变 化量(△u、△h、△s)。
第 四 章 气体和蒸汽的基本的热力过程
Basic thermodynamic process
4-1 研究热力过程的目的及一般方法
4-2 理想气体的定压、定容和定温过程 4-3 理想气体等比熵(可逆绝热)过程 4-4 理想气体多变过程 4-5 水蒸气的基本过程
1
4–1 研究热力过程的目的及一般方法
一、基本热力过程(fundamental thermodynamic process)
0
1.
1
Rg T1 T2 w
六、变比热绝热过程的计算-p113/115
w u1 u2 wt h1 h2
代替
查表
2. 用
19
3.
p2 dT s c p Rg ln 0 1 T p1 T1 T p2 1 T2 dT dT 令 0 dT ln cp cp s cp T T0 T p1 Rg T0 T T p2 1 0 0 ln s2 s1 A p1 Rg
23
Rg Rg u w cV T2 T1 T1 T2 T2 T1 n 1 1 n 1 Rg
q=
n cV T2 T1 n 1
cn T2 T1
2
1
Tds
五、比热容
n q u w cV T2 T1 c n T2 T1 n 1
p p n v v n
(n 1) (n ) n
T cp 0 T cV
T T p s cn n
v
16
三、比热容
cs 0
四、 u, h, s
u cV h c p s 2 s1
T2 T1 T2 T1
T2 V T1
2
T2 T1
h c
ห้องสมุดไป่ตู้
T2 p T1
T2 T1
9
s
1
T2 dT cV s cV ln T T1
定压过程
u cV
T2 T1
T2 T1
h c p
T2 T1
T2 T1
s
2
1
T2 dT cp s c p ln T T1
6
二、在p – v 图及T – s 图上表示
斜率
p v n
T s n
pv 常数
n
dp dv n 0 p v
p p n v v n
Tds δq cndT
T T s n cn
T2 T1 u T2 u T1 T2 T1 hT2 hT1
s 0
17
五、w,wt和q
w pdv
1
2
2
1
pv dv p1v1 v
或
w q u
0
Rg
1 RgT1 p2 v dv 1 1 p1
由于cV是温度的复杂函数,上式的积分解十分繁复,不便 于工程计算,若假设cV为定值,则cV +Rg、γ也为定值。
13
积分得到:
ln p ln v C
pv c
1
其中k为定熵指数,对于理想气体,定熵指数等于比热容比γ:
p1v1 p2v2
p1v1v1
T1 p1
定压过程
T2 V T1
T2 T1 1 Tds
2
w pv2 v1
wt 0
T2 p T1
q p h wt h c
T2 T1 1 Tds
11
2
定温过程
w pdv
1
2
2
1
v2 pv dv RgT1 ln v v1
q u w h wt
1
p2v2v2
T1v1 1 T2v2 1
1
T2 p2
1
由推导过程,上述三个过程方程式适用于: 理想气体,定比热,可逆绝热过程。 *初、终态温度变化范围在室温到600K之间时,可以将比 热容比或定熵指数作为定值。若温度变化幅度大,应用平 均定熵指数KEV。
当多变指数取不同的数值,多变过程可以化成以下4个特例:
n 0 : pv0 p C 0 C n 0 : pv p C 0 C 0 n 0 0 :: :pv pv C C T p C C 1 pv1 n C p n 1 : pv C T C k n 1 pv C C CT T C C n n 1 k :::pv pv k n k : pv pv C C kk 1 n k : n k : pv n C 1v C n : p11 p0 v C 0 n n : p v C p v C C 0 0v nn v C n : p p n : p v C p vC
定压过程 定温过程 定熵过程 定容过程
vC v C C v vC
例如:①燃气轮机燃烧室的燃烧加热过程,压力变化极微,接近定压 ②活塞压气机的汽缸套冷却足够好,压缩过程中气体温度几乎不升高,接近定温 ③燃气流过气轮机或空气流过叶轮式压气机,流速大,散热相对极少,接近绝热 ④汽油机汽缸中工质的燃烧加热过程,燃烧速度快,压力急剧上升而体积几乎不 变,接近定容。
h 0
定温过程
u 0 s
2 1
v2 v2 dT cV Rg ln s Rg ln T v1 v1
10
五、w, wt 和 q
定容过程
w pdv 0 wt vdp v p1 p2 1
1
2
2
qv u w u c
q w wt
12
4–3 理想气体等比熵(可逆绝热)过程
一、过程方程
绝热过程是任一微元过程中系统与外界都无热交换的过程,即
q cV dT pdv q c p dT vdp
c p dv dp p cV v
dp dv 0 p v
q 0
总的过程换热量也为零
2
0
定义
s ln pr Rg pr2 1 0 0 ln s2 s1 pr1 Rg
0
pr f T
( B)
比较式(A)与式(B)
pr 2 p2 p1 pr1
p2 pr 2 pr1 p1
20
4–4 理想气体多变过程
一、过程方程
p v p2v2
n 1 1
n
Tv
7
p p n v v n
T T s n cn
定容过程: n 定压过程: n 0 定温过程: n 1
p v v
T T s v cV
p 0 v p
p2 s s s Rg ln p1 T2 p2 定比热容 s c p ln Rg ln T1 p1 T2 v2 cV ln Rg ln T1 v1 p2 v2 cV ln c p ln p1 v1
0 2 0 1
22
h c p
t2 t1
T2 T1
pv 常数
n
称为多变过程,其中n为定值,称为多变指数。
*例如柴油机汽缸中的压缩过程,开始时工质 温度低于缸壁温度,边吸热边压缩而温度升高, 高于缸壁温度后则边压缩边放热,整个过程n 大约从1.6变化到1.2左右;膨胀过程,由于存 在后燃及高温时被离解气体的复合放热现象, 情况更为复杂,其散热规律的研究已不属于热 力学的范围。 2
p p v v T
T T s v c p
T T 0 s T cT
8
三、比热容
定容过程 定压过程 定温过程
cV
Rg
1
cp
1
Rg
cT
四、Δu、 Δh和Δs
定容过程
u c
n1 1 1
T2v2
n1
T1 p1
n 1 n
T2 p2
n 1 n
二、在p-v图及T-s图上表示
p p n v v n
T T T s n cn n cV
n 1
21
三、Δu, Δh和Δs t2 u cV t1 T2 T1
