变异概率自适应调整的遗传算法GA程序

遗传算法遗传算法

11
（5）遗传算法在解空间进行高效启发式搜索，而非盲目地穷举或完全随机搜索；
（6）遗传算法对于待寻优的函数基本无限制，它既不要求函数连续，也不要求函数可微，既可以是数学解析式所表示的显函数，又可以是映射矩阵甚至是神经网络的隐函数，因而应用范围较广；
（7）遗传算法具有并行计算的特点，因而可通过大规模并行计算来提高计算速度，适合大规模复杂问题的优化。
26
（4）基本遗传算法的运行参数有下述4个运行参数需要提前设定：
M：群体大小，即群体中所含个体的数量，一般取为 20~100； G：遗传算法的终止进化代数，一般取为100~500； Pc：交叉概率，一般取为0.4~0.99；
Pm：变异概率，一般取为0.0001~0.1。
27
10.4.2 遗传算法的应用步骤
遗传算法简称GA（Genetic Algorithms）是1962年由美国Michigan大学的Holland教授提出的模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法。
遗传算法是以达尔文的自然选择学说为基础发展起来的。自然选择学说包括以下三个方面：
1
（1）遗传：这是生物的普遍特征，亲代把生物信息交给子代，子代总是和亲代具有相同或相似的性状。生物有了这个特征，物种才能稳定存在。
18
（3）生产调度问题在很多情况下，采用建立数学模型的方法难以对生
产调度问题进行精确求解。在现实生产中多采用一些经验进行调度。遗传算法是解决复杂调度问题的有效工具，在单件生产车间调度、流水线生产车间调度、生产规划、任务分配等方面遗传算法都得到了有效的应用。
19
（4）自动控制。在自动控制领域中有很多与优化相关的问题需要求
10

GA遗传算法概述

GA遗传算法概述GA遗传算法（Genetic Algorithm）是一种受生物进化理论启发的优化算法，用于解决问题的和优化。

它模拟了自然界中生物进化的过程，通过模拟“基因”在群体中的遗传、交叉和变异等过程，逐步优化空间中的解。

1. 群体：GA遗传算法使用一个群体（population）来表示可能的解集合，每个解称为个体（individual）。

群体中的个体通过染色体（chromosome）来表示，染色体则由基因（gene）组成。

基因可以是任意类型的变量，例如二进制、整数或实数。

2. 适应度函数：GA遗传算法通过适应度函数（fitness function）来评估每个个体的优劣程度。

适应度函数将每个个体映射到一个实值，表示该个体的适应度。

适应度值越高，个体越优秀。

3.选择：在选择阶段，GA遗传算法根据个体的适应度值来选择优秀个体作为父代。

通常使用轮盘赌选择法或锦标赛选择法来进行选择。

轮盘赌选择法根据个体的适应度值来分配选择的概率，适应度值越高的个体被选中的概率越大。

锦标赛选择法则随机选择一定数量的个体，然后从中选择适应度最高的个体作为父代。

4.交叉：在交叉阶段，GA遗传算法随机选择一对父代个体，并以一定的概率对它们的染色体进行交叉操作。

交叉操作可以通过染色体的位进行交换、重组或变异，产生新的个体。

5.变异：在变异阶段，GA遗传算法以一定的概率对个体的染色体进行变异操作，以增加空间的多样性。

变异操作可以是将染色体中的位进行随机翻转、替换或插入等操作。

6.遗传进化：通过选择、交叉和变异等操作，GA遗传算法不断迭代优化个体的染色体，使得适应度值不断提高。

经过多代的演化，群体中出现了越来越优秀的个体，最终达到最优解或接近最优解。

GA遗传算法可以用于求解各种优化问题，例如函数最大化、函数最小化、组合优化、排列问题等。

它的优点在于可以在大规模空间中进行高效，并且能够找到全局最优解或接近最优解。

然而，由于遗传算法的随机性质，它无法保证每次都能找到最优解，且算法的收敛速度较慢。

遗传算法的原理及MATLAB程序实现.

1 遗传算法的原理1.1 遗传算法的基本思想遗传算法（genetic algorithms，GA）是一种基于自然选择和基因遗传学原理，借鉴了生物进化优胜劣汰的自然选择机理和生物界繁衍进化的基因重组、突变的遗传机制的全局自适应概率搜索算法。

遗传算法是从一组随机产生的初始解（种群）开始，这个种群由经过基因编码的一定数量的个体组成，每个个体实际上是染色体带有特征的实体。

染色体作为遗传物质的主要载体，其内部表现（即基因型）是某种基因组合，它决定了个体的外部表现。

因此，从一开始就需要实现从表现型到基因型的映射，即编码工作。

初始种群产生后，按照优胜劣汰的原理，逐代演化产生出越来越好的近似解。

在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样，后代种群比前代更加适应环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

计算开始时，将实际问题的变量进行编码形成染色体，随机产生一定数目的个体，即种群，并计算每个个体的适应度值，然后通过终止条件判断该初始解是否是最优解，若是则停止计算输出结果，若不是则通过遗传算子操作产生新的一代种群，回到计算群体中每个个体的适应度值的部分，然后转到终止条件判断。

这一过程循环执行，直到满足优化准则，最终产生问题的最优解。

图1-1给出了遗传算法的基本过程。

1.2 遗传算法的特点1.2.1 遗传算法的优点遗传算法具有十分强的鲁棒性，比起传统优化方法，遗传算法有如下优点：1. 遗传算法以控制变量的编码作为运算对象。

传统的优化算法往往直接利用控制变量的实际值的本身来进行优化运算，但遗传算法不是直接以控制变量的值，而是以控制变量的特定形式的编码为运算对象。

这种对控制变量的编码处理方式，可以模仿自然界中生物的遗传和进化等机理，也使得我们可以方便地处理各种变量和应用遗传操作算子。

2. 遗传算法具有内在的本质并行性。

遗传算法步骤

遗传算法（Genetic Algorithm，GA）是一种基于自然进化理论的算法，是一种可以对不同问题寻找最优解的智能算法，它可以用于优化因变
量组成的多为目标函数，使得其能够模拟自然群体中最优种群的复制
替代的演化过程。

GA的基本步骤如下：
1.初始化种群：随机选择或采用已有解法创建一个代表优化问题的群体，这一群体中包含多个个体，并对每一体对应一个可衡量适应度的值。

2.计算适应度：根据建模函数以及求解问题，计算每一体的适应度值，作为群体的适应度表示，该适应度值指示了当前群体的优劣，越高的
适应度表示越优秀的群体。

3.选择操作：通过自然选择决定种群接下来的演化趋势，选取进化最佳的个体，裁去低适应度的个体，做出自然选择的决定。

4.交叉操作：将于原始群体中优秀的体通过交叉进行基因交换，优化基因序列，达到更加精细化优化的进化效果。

5.变异操作：在交叉操作过后，某些个体的基因顺序经过一定的随机变异，添加新的基因组合，增强搜索空间的拓展能力。

6.重复上述步骤：将上述步骤重复进行，让群体在遗传进化过程中迭代优化，不断找寻最优解，最终终止整个搜索过程，达到满足目标。

以上就是GA的基本步骤，它不仅能够用于求解多种问题，而且运算
效率高，不需要事先设定初始值，使得对比其它算法更加方便和灵活。

但是，由于其随机性原因，在某些情况下可能得出的解不一定是最优解，使其在实际应用中并不尽如人意。

变异概率自适应调整的遗传算法GA程序

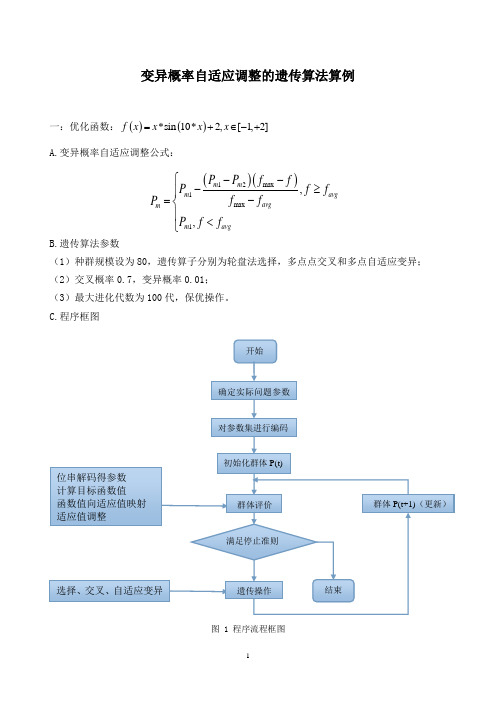
变异概率自适应调整的遗传算法算例一：优化函数：()()*sin 10*2,[1,2]f x x x x =+∈-+A.变异概率自适应调整公式：B.遗传算法参数（1）种群规模设为80，遗传算子分别为轮盘法选择，多点点交叉和多点自适应变异；（2）交叉概率0.7，变异概率0.01；（3）最大进化代数为100代，保优操作。

C.程序框图图 1 程序流程框图()()12max 1max 1,,m m m avg avg m m avg P P f f P f f f f P P f f --⎧-≥⎪-=⎨⎪<⎩ 开始确定实际问题参数对参数集进行编码初始化群体P(t) 群体P(t+1)（更新）位串解码得参数计算目标函数值函数值向适应值映射适应值调整选择、交叉、自适应变异群体评价遗传操作满足停止准则结束二：程序及运行结果（1）%变异概率自适应调整的GA程序%优化函数为f=x*sin(10*x)+2，其中，-1=<x<=2%编码长度为12位%种群规模设为80，遗传算子分别为轮盘法选择，多点点交叉和多点自适应变异。

%交叉概率0.7，变异概率0.01%最大进化代数为100代，保优操作。

%**********************%主函数*****************************************function main()global chrom lchrom oldpop newpop varible fitness popsize sumfitness %定义全局变量global pcross pmutation temp bestfit maxfit gen bestgenglobal maxgen po pp mp nplchrom=12; %染色体长度popsize=80; %种群大小pcross=0.7; %交叉概率pmutation=0.01; %变异概率maxgen=100; %最大代数po=0.1; %淘汰概率pp=0.1; %保护概率mp=floor(pp*popsize); %保护的个数np=floor(po*popsize); %淘汰的个数initpop; % 初始化种群for gen=1:maxgenobjfun; %计算适应度值pp_po; %执行保优操作select; %选择操作selfmutation; %自变异操作crossover; %交叉操作endbestbestfit % 最佳个体适应度值输出bestgen % 最佳个体所在代数输出figuregen=1:maxgen;plot(gen,maxfit(1,gen)); % 进化曲线hold on;plot(bestgen,bestfit);xlabel('Generation');ylabel('Fitness');%********************** 产生初始种群 ************************************ function initpop()global lchrom oldpop popsize chromfor i=1:popsizechrom=rand(1,lchrom); % lchrom=12 染色体长度for j=1:lchromif chrom(1,j)<0.5chrom(1,j)=0;elsechrom(1,j)=1;endendoldpop(i,1:lchrom)=chrom;end%************************%计算适应度值************************************ function objfun()global lchrom oldpop fitness popsize chrom maxfit gen varible avgfiness savgfitness % a=0;b=3;a=0;b=10;for i=1:popsizechrom=oldpop(i,:);c=decimal(chrom);varible(1,i)=a+c*(b-a)/(2.^lchrom-1); %对应变量值fitness(1,i)=varible(1,i)*sin(10*varible(1,i))+2;avgfitness=sum(fitness)/popsize;lsort; % 个体排序maxfit(1,gen)=max(fitness); %求本代中的最大适应度值maxfit%************************二进制转十进制********************************** function c=decimal(chrom)global lchrom popsizec=0;for j=1:lchromc=c+chrom(1,j)*2.^(lchrom-j);end%************************* 个体从小到大排序 ************************ function lsort()global popsize fitness oldpopfor i=1:popsizej=i+1;while j<=popsizeif fitness(1,i)>fitness(1,j)tf=fitness(1,i); % 适应度值tc=oldpop(i,:); % 基因代码fitness(1,i)=fitness(1,j); % 适应度值互换oldpop(i,:)=oldpop(j,:); % 基因代码互换fitnescs(1,j)=tf;oldpop(j,:)=tc;endj=j+1;endend%*************************保优操作*****************************function pp_po()global popsize oldpop npi=np+1; % np=floor(po*popsize); %淘汰的个数npwhile i<=popsize %将（np+1）～popsize的个体放在toldpop中，共（popsize-np）个 toldpop(j,:)=oldpop(i,:);j=j+1;i=i+1;endfor i=1:(popsize-np) %从小到大顺序排列，将前面np个淘汰oldpop(i,:)=toldpop(i,:); % 适应度是否也要互换？end%*************************转轮法选择操作********************************** function select()global fitness popsize sumfitness oldpop temp mp npsumfitness=0; %个体适应度之和for i=1:(popsize-np-mp) % 仅计算(popsize-np-mp)个个体的选择概率sumfitness=sumfitness+fitness(1,i);endfor i=1:(popsize-mp-np) % 仅计算(popsize-np-mp)个个体的选择概率p(1,i)=fitness(1,i)/sumfitness; % 个体染色体的选择概率endq=cumsum(p); % 个体染色体的累积概率（内部函数），共(popsize-np-mp)个b=sort(rand(1,(popsize-mp))); % 产生(popsize-mp)个随机数，并按升序排列。

遗传算法函数ga用法

遗传算法函数ga用法matlab 遗传算法工具箱函数gamatlab 遗传算法工具箱函数及实例讲解核心函数：(1)function[pop]=initializega(num,bounds,eevalFN,eevalOps,options)-- 初始种群的生成函数【输出参数】pop--生成的初始种群【输入参数】num--种群中的个体数目bounds--代表变量的上下界的矩阵eevalFN--适应度函数eevalOps--传递给适应度函数的参数options-- 选择编码形式( 浮点编码或是二进制编码)[precisionF_or_B],如precision--变量进行二进制编码时指定的精度F_or_B--为1 时选择浮点编码，否则为二进制编码,由precision指定精度)(2)function[x,endPop,bPop,traceInfo]=ga(bounds,evalFN,ev alOps,startPop,opts,...termFN,termOps,selectFN,selectOps,xOverFNs,xOverOps,mutFN s,mutOps)--遗传算法函数【输出参数】x--求得的最优解endPop--最终得到的种群bPop--最优种群的一个搜索轨迹【输入参数】bounds--代表变量上下界的矩阵evalFN--适应度函数evalOps--传递给适应度函数的参数startPop-初始种群opts[epsilon prob_ops display]--opts(1:2)等同于initializega 的options 参数，第三个参数控制是否输出，一般为0。

如[1e-6 1 0]termFN--终止函数的名称,如['maxGenTerm']termOps--传递个终止函数的参数,如[100]selectFN--选择函数的名称,如['normGeomSelect']selectOps--传递个选择函数的参数,如[0.08]xOverFNs-- 交叉函数名称表，以空格分开，如['arithXover heuristicXoversimpleXover'] xOverOps--传递给交叉函数的参数表，如[2 0;2 3;2 0]mutFNs-- 变异函数表，如['boundaryMutation multiNonUnifMutation nonUnifMutation unifMutation'] mutOps--传递给交叉函数的参数表,如[4 0 0;6 100 3;4 100 3;4 0 0]注意】matlab 工具箱函数必须放在工作目录下运算借过为：x =同的初始群体）一定可以得到近似最优解。

遗传算法matlab程序代码

遗传算法matlab程序代码
遗传算法（GA）是一种用于求解优化问题的算法，其主要思想是模拟
生物进化过程中的“选择、交叉、变异”操作，通过模拟这些操作，来寻
找最优解。

Matlab自带了GA算法工具箱，可以直接调用来实现遗传算法。

以下是遗传算法Matlab程序代码示例：
1.初始化
首先定义GA需要优化的目标函数f，以及GA算法的相关参数，如种
群大小、迭代次数、交叉概率、变异概率等，如下所示：
options = gaoptimset('PopulationSize',10,...
'Generations',50,...
2.运行遗传算法
运行GA算法时，需要调用MATLAB自带的ga函数，将目标函数、问
题的维度、上下界、约束条件和算法相关参数作为输入参数。

其中，上下
界和约束条件用于限制空间，防止到无效解。

代码如下：
[某,fval,reason,output,population] = ga(f,2,[],[],[],[],[-10,-10],[10,10],[],options);
3.结果分析
最后，将结果可视化并输出，可以使用Matlab的plot函数绘制出目
标函数的值随迭代次数的变化，如下所示：
plot(output.generations,output.bestf)
某label('Generation')
ylabel('Best function value')
总之，Matlab提供了方便易用的GA算法工具箱，开发者只需要根据具体问题定义好目标函数和相关参数，就能够在短时间内快速实现遗传算法。

GA遗传算法范文

GA遗传算法范文GA（Genetic Algorithm，遗传算法）是一种基于生物进化原理的优化算法，通过遗传、交叉和变异等操作来寻找最优解。

GA模拟了自然界中的进化过程，以一种更加高效的方式来解决复杂的问题。

本文将会对GA算法的原理、步骤以及应用进行详细介绍，并且分析其优势和不足之处。

GA算法的原理是受到达尔文的进化理论的启发。

在进化过程中，个体之间存在着遗传信息的交流，通过自然选择和适者生存的机制，最终会得到适应环境的个体。

GA算法也通过类似的方式来解决问题，首先定义了问题的适应度评估函数，然后通过遗传算子（如选择、交叉和变异）来产生新的解，并不断迭代，直到找到满足要求的解。

GA算法的步骤主要包括以下几个方面：1.初始化种群：生成初始的解集合，可以是随机生成的，也可以通过一些启发式算法生成。

2.确定适应度：对于每个个体，通过适应度函数来评估其适应能力。

适应度函数可以根据问题的特点进行设计，通常是一个数值来表示个体的优劣程度。

3.选择操作：根据适应度的大小，选择适应度较高的个体作为“父代”参与后续操作。

常用的选择方法有轮盘赌选择、锦标赛选择等。

4.交叉操作：选取两个父代个体，通过其中一种方式进行交叉，生成两个新的子代个体。

交叉的方式可以有很多种，如单点交叉、多点交叉等。

5.变异操作：对生成的子代个体进行变异操作，通过一定的概率进行基因的随机改变。

变异操作能够增加种群的多样性，避免陷入局部最优。

6.替换操作：将新生成的子代个体替换掉原来的父代个体，以保持种群的规模不变。

7.收敛判断：判断是否满足停止条件，如果满足则输出当前种群中的最优解，否则返回第3步。

GA算法的应用非常广泛。

例如在组合优化问题中，GA可以用来求解旅行商问题、背包问题等。

在机器学习中，GA可以用来进行特征选择、参数优化等。

在工程优化设计中，GA可以用来求解复杂的优化问题，如结构优化、布局优化等。

GA算法有一些明显的优势。

首先，GA算法具有全局能力，可以避免陷入局部最优解。

遗传算法的基本原理及流程

遗传算法的基本原理及流程遗传算法（Genetic Algorithm，简称GA）是一种通过模拟自然界进化过程来求解优化问题的算法。

它是一种群体性优化算法，最初由美国学者J. Holland提出，目前已经被广泛应用于优化、搜索、分类、数据挖掘等领域。

本文将从基本原理和流程两方面介绍遗传算法。

一、基本原理1.1 模拟自然进化过程遗传算法的灵感来源于自然界，它主要是模拟了生物进化的过程。

在遗传算法中，问题的解被表示成一个个体，每个个体都具有一定的适应度（Fitness），代表着它对问题的解决程度。

所有个体组成一个种群（Population），这个种群包含了多个可能的解决方案。

1.2 遗传操作在遗传算法中，种群经过不断的遗传操作（Cross、Mutation、Selection），产生新的个体，新个体替代原个体，直到达到最优解。

其操作的具体过程如下：（1）Cross：交叉操作，即将两个个体的某些部分进行交换，创造出新的个体。

（2）Mutation：变异操作，即对某个个体的某些部分进行修改，创造出一个新个体。

（3）Selection：选择操作，根据个体的适应度对种群进行选择，留下较优的个体，淘汰劣质的个体。

1.3 评价适应度在遗传算法中，每个个体都有一个适应度值，代表着解决问题的效果。

评价适应度通常采取如下方式：（1）目标函数：根据问题的定义，构建一个目标函数，根据该函数的值评价个体的适应度。

（2）实验法：在实际操作中，通过实验方法进行评价，得到与问题解决程度相关的数据。

二、流程介绍2.1 初始化遗传算法的第一步是初始化，首先随机生成一批个体，构成种群。

个体的生成可以采用数值或二进制方式。

在这个过程中，可以设置种群大小、交叉率、变异率等参数。

2.2 选择根据个体的适应度值，从当前种群中选择一部分个体作为下一代的种群。

选择的过程中，可以采用轮盘赌（Roulette Wheel）选择等方式。

2.3 交叉在构建新一代种群时，采用交叉操作，即两个个体随机交换某一部分基因。

基本遗传算法(GA)的算法原理、步骤、及Matlab实现

算法原理遗传算法可以用来求函数的极值。

（1）用二进制编码来离散自变量，码长根据离散精度来确定。

码长为log 2[max−min 精度+1]（2）交叉方法采用单点交叉（3）变异是根据变异概率反转子代某个位的值（4）选择策略采用轮盘赌策略，令PP i =∑p i i j=1,其中PP i 为累计概率，p i 为个体的选择概率，公式为: p i =fitness(x i )∑fitness(x i)NP i=1,其中fitness(x i )为个体的适应度，共轮转NP 次，每次轮转时，产生随机数r ,当PP i−1≤r <PP i 时选择个体i 。

算法步骤基本遗传算法的基本步骤是：1. 随机产生种群，2. 用轮盘赌策略确定个体的适应度，判断是否符合优化准则，若符合，输出最佳个体及其最优解，结束，否则，进行下一步3. 依据适应度选择再生个体，适应度高的个体被选中的概率高，适应度低的个体被淘汰4. 按照一定的交叉概率和交叉方法，生成新的个体5. 按照一定的变异概率和变异方法，生成新的个体6. 由交叉和变异产生新一代种群，返回步骤2算法的实现%基本遗传算法，一维无约束优化function [ xv,fv ] = mGA( fitness,a,b,NP,NG,Pc,Pm,eps )% 待优化的目标函数：fitness% 自变量下界：a% 自变量上界：b% 种群个体数：NP% 最大进化代数：NG% 杂交常数：Pc% 变异常数：Pm% 自变量离散精度：eps% 目标函数取最大值是的自变量值：xv% 目标函数的最小值：fvL=ceil(log2((b-a)/eps+1)); %码长x=zeros(NP,L);for i=1:NPx(i,:)=Initial(L);fx(i)=fitness(Dec(a,b,x(i,:),L));endfor k=1:NGsumfx=sun(fx);Px=fx/sumfx;PPx=0;PPx(1)=Px(1);for i=2:NP %根据轮盘赌确定父亲PPx(i)=PPx(i-1)+PPx(i);endfor i=1:NPsita=rand();for n=1:NPif sita <= PPx(n)SelFather = n;break;endendSelmother=floor(rand()*(NP-1))+1; %随机选择母亲posCut=floor(rand()*(L-2))+1; %随机确定交叉点r1=rand();if r1<=Pcnx(i,1:posCut)=x(SelFather,1:posCut);nx(I,(posCut+1):L)=x(Selmother,(posCut+1):L);r2=rand();if r2<=Pm %变异posMut=round(rand()*(L-1)+1);nx(i,posMut)=~nx(i,posMut);endelsenx(i,:)=x(SelFather,:);endendx=nx;for i=1:NPfx(i)=fitness(Dec(a,b,x(i,:),L);endendfv=-inf;for i=1:NPfitx=fitness(Dec(a,b,x(i,:),L));if fitx > fvfv=fitx;xv=Dec(a,b,x(i,:),L);endendendfunction result=Initial(length) %初始化函数for i=1:lengthr=round();result(i)=round(r);endendfunction y=Dec(a,b,x,L) %二进制转十进制base=2.^((L-1):-1:0);y=dot(base,x);y=a+y*(b-1)/(2^L-1)'end。

用Python实现遗传算法(GA)(一)

用Python实现遗传算法（GA）（一）用Python实现遗传算法（GA）（一）遗传算法（Genetic Algorithm，GA）是一种模拟生物进化过程的优化算法。

它模拟了自然界中的遗传、交叉和变异等操作，通过不断优化种群中的个体来找到问题的最优解。

在本篇文章中，我们将用Python实现一个简单的遗传算法。

首先，我们需要定义问题的适应度函数。

适应度函数用来评估每个个体的优劣程度，它决定了个体在繁殖中的概率。

在这个例子中，我们将解决一个简单的函数最小化问题，即找到函数f(x)=x^2的最小值。

我们可以定义适应度函数如下：```pythondef fitness_function(x):return x**2```接下来，我们需要定义种群的初始化函数。

种群是由一组个体组成的，每个个体都表示问题的一个解。

在这个例子中，我们将随机生成一组初始解作为种群的初始状态。

```pythonimport randomdef initialize_population(population_size, chromosome_size): population = []for _ in range(population_size):chromosome = [random.randint(0, 1) for _ inrange(chromosome_size)]population.append(chromosome)return population```然后，我们需要定义选择操作。

选择操作用来根据个体的适应度值选择出下一代的个体。

常用的选择操作包括轮盘赌选择和排名选择等。

在这个例子中，我们将使用轮盘赌选择。

```pythondef roulette_wheel_selection(population, fitness_values):total_fitness = sum(fitness_values)probabilities = [fitness / total_fitness for fitness in fitness_values]cumulative_probabilities = [sum(probabilities[:i+1]) for i in range(len(probabilities))]selected_population = []for _ in range(len(population)):random_number = random.randomfor i in range(len(cumulative_probabilities)):if random_number <= cumulative_probabilities[i]:selected_population.append(population[i])breakreturn selected_population```接下来，我们需要定义交叉操作。

遗传算法程序

遗传算法程序functionret=Mutation(pmutation,lenchrom,chrom,sizepop,pop,bound) % 本函数完成变异操作% pcorss input : 变异概率% lenchrom input : 染色体长度% chrom input : 染色体群% sizepop input : 种群规模% pop input : 当前种群的进化代数和最大的进化代数信息% ret output : 变异后的染色体fori=1:sizepop% 随机选择一个染色体进行变异pick=rand;while pick==0pick=rand;endindex=ceil(pick*sizepop);% 变异概率决定该轮循环是否进行变异pick=rand;if pick>pmutationcontinue;endflag=0;while flag==0% 变异位置pick=rand;while pick==0pick=rand;endpos=ceil(pick*sum(lenchrom)); %随机选择了染色体变异的位置，即选择了第pos个变量进行变异v=chrom(i,pos);v1=v-bound(pos,1);v2=bound(pos,2)-v;pick=rand; %变异开始if pick>0.5delta=v2*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v+delta;elsedelta=v1*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v-delta;end %变异结束flag=test(lenchrom,bound,chrom(i,:)); %检验染色体的可行性endendret=chrom;Ga优化pso%% GA 优化PSO%% 清空环境clc;clearclose all%% 参数初始化lenchrom=7; %字符串长度（个体长度），染色体编码长度pc=0.7; %设置交叉概率，本例中交叉概率是定值，若想设置变化的交叉概率可用表达式表示，或从写一个交叉概率函数，例如用神经网络训练得到的值作为交叉概率pm=0.3; %设置变异概率，同理也可设置为变化的%粒子群算法中的两个参数c1 = 1.49445;c2 = 1.49445;maxgen=20; % 进化次数popsize=30; %种群规模%粒子更新速度Vmax=1;Vmin=-1;%种群popmax=50;popmin=-50;% 变量取值范围bound=[popminpopmax;popminpopmax;popminpopmax;p opminpopmax;popminpopmax;popminpopmax;popminpopmax]; %变量范围% 优化粒子数目par_num=7;%% 产生初始粒子和速度fori=1:popsize%随机产生一个种群pop(i,:)=popmax*rands(1,par_num); %初始种群V(i,:)=rands(1,par_num); %初始化速度%计算适应度fitness(i)=fun(pop(i,:)); %染色体的适应度end%找最好的染色体[bestfitnessbestindex]=min(fitness);zbest=pop(bestindex,:); %全局最佳gbest=pop; %个体最佳fitnessgbest=fitness; %个体最佳适应度值fitnesszbest=bestfitness; %全局最佳适应度值%% 迭代寻优fori=1:maxgenifor j=1:popsize%速度更新PSO选择更新V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));V(j,find(V(j,:)>Vmax))=Vmax;V(j,find(V(j,:)< p="">%种群更新PSO选择更新pop(j,:)=pop(j,:)+0.5*V(j,:);pop(j,find(pop(j,:)>popmax))=popmax;pop(j,find(pop(j,:)< p="">% 交叉操作GAGApop=Cross(pc,lenchrom,pop,popsize,bound);% 变异操作GA变异GApop=Mutation(pm,lenchrom,GApop,popsize,[imaxgen],b ound);pop=GApop; % GA pop --> PSO pop% 适应度值-->约束条件if0.072*pop(j,1)+0.063*pop(j,2)+0.057*pop(j,3)+0.05*pop(j,4 )+0.032*pop(j,5)+0.0442*pop(j,6)+0 .0675*pop(j,7)<=264.4 if128*pop(j,1)+78.1*pop(j,2)+64.1*pop(j,3)+43*pop(j,4)+58. 1*pop(j,5)+36.9*pop(j,6)+50.5*pop(j, 7)<=69719fitness(j)=fun(pop(j,:));endend%个体最优更新if fitness(j) <fitnessgbest(j)< p="">gbest(j,:) = pop(j,:);fitnessgbest(j) = fitness(j);end%群体最优更新if fitness(j) <fitnesszbest< p="">zbest = pop(j,:);fitnesszbest = fitness(j);endendyy(i)=fitnesszbest;end%% 结果disp '*************best particle number****************' zbest %%plot(yy,'linewidth',2);grid ontitle(['适应度曲线' '终止代数＝' num2str(maxgen)]); xlabel('进化代数');ylabel('适应度');</fitnesszbest<></fitnessgbest(j)<><><>。

遗传算法（GeneticAlgorithm,GA）及MATLAB实现

遗传算法（GeneticAlgorithm,GA）及MATLAB实现遗传算法概述：• 遗传算法（Genetic Algorithm，GA）是⼀种进化算法，其基本原理是仿效⽣物界中的“物竞天择、适者⽣存”的演化法则，它最初由美国Michigan⼤学的J. Holland教授于1967年提出。

• 遗传算法是从代表问题可能潜在的解集的⼀个种群（population）开始的，⽽⼀个种群则由经过基因（gene）编码的⼀定数⽬的个体(individual)组成。

因此，第⼀步需要实现从表现型到基因型的映射即编码⼯作。

初代种群产⽣之后，按照适者⽣存和优胜劣汰的原理，逐代（generation）演化产⽣出越来越好的近似解，在每⼀代，根据问题域中个体的适应度（fitness）⼤⼩选择个体，并借助于⾃然遗传学的遗传算⼦（genetic operators）进⾏组合交叉和变异，产⽣出代表新的解集的种群。

这个过程将导致种群像⾃然进化⼀样，后⽣代种群⽐前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

• 遗传算法有三个基本操作：选择（Selection）、交叉（Crossover）和变异（Mutation）。

• （1）选择。

选择的⽬的是为了从当前群体中选出优良的个体，使它们有机会作为⽗代为下⼀代繁衍⼦孙。

根据各个个体的适应度值，按照⼀定的规则或⽅法从上⼀代群体中选择出⼀些优良的个体遗传到下⼀代种群中。

选择的依据是适应性强的个体为下⼀代贡献⼀个或多个后代的概率⼤。

• （2）交叉。

通过交叉操作可以得到新⼀代个体，新个体组合了⽗辈个体的特性。

将群体中的各个个体随机搭配成对，对每⼀个个体，以交叉概率交换它们之间的部分染⾊体。

• （3）变异。

对种群中的每⼀个个体，以变异概率改变某⼀个或多个基因座上的基因值为其他的等位基因。

同⽣物界中⼀样，变异发⽣的概率很低，变异为新个体的产⽣提供了机会。

遗传算法的基本步骤：1)编码：GA在进⾏搜索之前先将解空间的解数据表⽰成遗传空间的基因型串结构数据，这些串结构数据的丌同组合便构成了丌同的点。

3遗传算法(GA, Genetic Algorithm)

• 太多的勘察会导致早熟收敛，太多探索会使搜索变成随机搜索。
• 交叉和变异是GA中的两个重要算子，调整交叉和变异率可维护勘察/探索间的平衡，对搜索的有效性和效率有直接影响。 • 文献中的参数设定方法可分成四类：静态设定、动态确定、自主自适应和动态自适应。
静态设定
• 先通过反复试验找到一个满意的参数组合，然后应用到GA中。文献中有大量确定算子概率的指导规则，如
•
单点交叉
两点交叉
• 常见的交叉算子有：一点、两点、均匀和奇偶交叉。均匀交叉，对染色体中每一位做贝努利试验，确定其是来自父亲还是母亲。偶交叉是基因组的偶数位来自母亲，奇数位来自父亲，奇交叉刚好相反。 • 变异算子是首先对基因组的每一位做贝努利试验，确定是否要进行变异操作；然后对需要变异的位进行变异操作。 • 常见的变异操作有：翻转，针对01编码是0和1间转换；交换，从染色体中随机选择一位与需要变异的位交换基因；高斯变异是针对实数编码的，基于高斯分布从当前值的周围选择一个新值代替旧值。
• 线性定标
f, if f avg f max f ' f avg ( f f min ) /( f max f avg ), if f min (cfavg f max )/(c - 1) f [c( f f ) f f ) /( f f ), if f (cf f )/(c - 1) avg max max avg min avg max avg
incremental genetic algorithm
• 增量GA：每代拥有1-2个孩子的交叠群体 • 每代仅更新1-2个个体。 • 每代仅由1-2个孩子组成。允许定制取代方法，去定义新代应如何被集成进群体。如一个新生成的小孩可以取代他的父亲，取代群体中的随机个体，或取代最受欢迎的个体。 • 使用交叠群体，但交叠非常少，仅有1-2个个体，缺省的取代方案是最坏的。 • 取代方法规定了ga使用哪种形式的取代。取代策略确定了新个体如何插入群体，如父亲策略、随机策略、最坏策略、最好策略、自定义。

遗传算法GA

遗传算法GA遗传算法（Genetic Algorithms，GA）是⼀种全局优化⽅法，它借⽤了⽣物遗传学的观点，通过⾃然选择、遗传、变异等作⽤机制，实现种群中个体适应性的提⾼，体现了⾃然界中“物竞天择、适者⽣存”的进化过程。

遗传算法是⼀类借鉴⽣物界⾃然选择和⾃然遗传机制的随机化搜索算法，它模拟⾃然选择和⾃然遗传过程中发⽣的繁殖、交叉和基因突变现象，在每次迭代中都保留⼀组候选解，并按某种指标从解群中选取较优的个体，利⽤遗传算⼦（选择、交叉和变异）对这些个体进⾏组合，产⽣新⼀代的候选种群，并重复此过程，直到满⾜某种收敛指标为⽌。

基本遗传算法（Simple Genetic Algorithms，简称SGA，⼜称简单遗传算法或标准遗传算法），其遗传进化操作过程简单，容易理解，是其他⼀些遗传算法的雏形和基础。

基本遗传算法由编码（产⽣初始种群）、适应度函数、遗传算⼦（选择、交叉、变异）和运⾏参数组成。

1.编码问题是遗传算法有别于其他进化类算法的重要标志。

编码：由问题空间向遗传算法空间的映射。

解码：有遗传算法空间向问题空间的映射。

遗传算法通过某种编码机制把对象抽象为由特定符号按⼀定顺序排成的串。

基本遗传算法则使⽤⼆进制串进⾏编码，它采⽤随机⽅法⽣成若⼲个体的集合，该集合称为初始种群，初始种群中个体的数量称为种群规模。

个体也可称为染⾊体，⽤⼆进制串表⽰，⼆进制串中的每⼀位则称为基因。

2.遗传算法对个体的好坏⽤适应度函数值来评价，适应度函数值越⼤，个体的质量也就越好。

适应度函数是遗传算法进化过程的驱动⼒，也是进⾏⾃然选择的唯⼀标准。

适应度函数的设计直接影响到遗传算法的性能。

设计适应度函数的总体原则应使解的优劣性与适应度之间具有严格单调升的函数关系。

⼀般应将⽬标函数映射成求最⼤值形式，且适应度函数的值为⾮负数。

还可以对适应度函数进⾏定标处理。

主要⽅法有线性定标，sigma截断和乘幂标。

对于约束条件可采取惩罚操作，即把约束问题转化为⼀个附带考虑代价或惩罚的⾮约束优化问题。

变异概率自适应调整的遗传算法GA程序资料

变异概率自适应调整的遗传算法算例一：优化函数：()()*sin 10*2,[1,2]f x x x x =+∈-+A.变异概率自适应调整公式：B.遗传算法参数（1）种群规模设为80，遗传算子分别为轮盘法选择，多点点交叉和多点自适应变异；（2）交叉概率0.7，变异概率0.01；（3）最大进化代数为100代，保优操作。

C.程序框图图 1 程序流程框图()()12max 1max 1,,m m m avg avg m m avg P P f f P f f f f P P f f --⎧-≥⎪-=⎨⎪<⎩ 开始确定实际问题参数对参数集进行编码初始化群体P(t) 群体P(t+1)（更新）位串解码得参数计算目标函数值函数值向适应值映射适应值调整选择、交叉、自适应变异群体评价遗传操作满足停止准则结束二：程序及运行结果（1）%变异概率自适应调整的GA程序%优化函数为f=x*sin(10*x)+2，其中，-1=<x<=2%编码长度为12位%种群规模设为80，遗传算子分别为轮盘法选择，多点点交叉和多点自适应变异。

%交叉概率0.7，变异概率0.01%最大进化代数为100代，保优操作。

%**********************%主函数*****************************************function main()global chrom lchrom oldpop newpop varible fitness popsize sumfitness %定义全局变量global pcross pmutation temp bestfit maxfit gen bestgenglobal maxgen po pp mp nplchrom=12; %染色体长度popsize=80; %种群大小pcross=0.7; %交叉概率pmutation=0.01; %变异概率maxgen=100; %最大代数po=0.1; %淘汰概率pp=0.1; %保护概率mp=floor(pp*popsize); %保护的个数np=floor(po*popsize); %淘汰的个数initpop; % 初始化种群for gen=1:maxgenobjfun; %计算适应度值pp_po; %执行保优操作select; %选择操作selfmutation; %自变异操作crossover; %交叉操作endbestbestfit % 最佳个体适应度值输出bestgen % 最佳个体所在代数输出figuregen=1:maxgen;plot(gen,maxfit(1,gen)); % 进化曲线hold on;plot(bestgen,bestfit);xlabel('Generation');ylabel('Fitness');%********************** 产生初始种群 ************************************ function initpop()global lchrom oldpop popsize chromfor i=1:popsizechrom=rand(1,lchrom); % lchrom=12 染色体长度for j=1:lchromif chrom(1,j)<0.5chrom(1,j)=0;elsechrom(1,j)=1;endendoldpop(i,1:lchrom)=chrom;end%************************%计算适应度值************************************ function objfun()global lchrom oldpop fitness popsize chrom maxfit gen varible avgfiness savgfitness % a=0;b=3;a=0;b=10;for i=1:popsizechrom=oldpop(i,:);c=decimal(chrom);varible(1,i)=a+c*(b-a)/(2.^lchrom-1); %对应变量值fitness(1,i)=varible(1,i)*sin(10*varible(1,i))+2;avgfitness=sum(fitness)/popsize;lsort; % 个体排序maxfit(1,gen)=max(fitness); %求本代中的最大适应度值maxfit%************************二进制转十进制********************************** function c=decimal(chrom)global lchrom popsizec=0;for j=1:lchromc=c+chrom(1,j)*2.^(lchrom-j);end%************************* 个体从小到大排序 ************************ function lsort()global popsize fitness oldpopfor i=1:popsizej=i+1;while j<=popsizeif fitness(1,i)>fitness(1,j)tf=fitness(1,i); % 适应度值tc=oldpop(i,:); % 基因代码fitness(1,i)=fitness(1,j); % 适应度值互换oldpop(i,:)=oldpop(j,:); % 基因代码互换fitnescs(1,j)=tf;oldpop(j,:)=tc;endj=j+1;endend%*************************保优操作*****************************function pp_po()global popsize oldpop npi=np+1; % np=floor(po*popsize); %淘汰的个数npwhile i<=popsize %将（np+1）～popsize的个体放在toldpop中，共（popsize-np）个 toldpop(j,:)=oldpop(i,:);j=j+1;i=i+1;endfor i=1:(popsize-np) %从小到大顺序排列，将前面np个淘汰oldpop(i,:)=toldpop(i,:); % 适应度是否也要互换？end%*************************转轮法选择操作********************************** function select()global fitness popsize sumfitness oldpop temp mp npsumfitness=0; %个体适应度之和for i=1:(popsize-np-mp) % 仅计算(popsize-np-mp)个个体的选择概率sumfitness=sumfitness+fitness(1,i);endfor i=1:(popsize-mp-np) % 仅计算(popsize-np-mp)个个体的选择概率p(1,i)=fitness(1,i)/sumfitness; % 个体染色体的选择概率endq=cumsum(p); % 个体染色体的累积概率（内部函数），共(popsize-np-mp)个b=sort(rand(1,(popsize-mp))); % 产生(popsize-mp)个随机数，并按升序排列。

MATLAB中自带遗传算法函数GA的用法

MATLAB中⾃带遗传算法函数GA的⽤法ga⽤遗传算法寻找函数的最优解语法规则x = ga(fitnessfcn,nvars)x = ga(fitnessfcn,nvars,A,b)x = ga(fitnessfcn,nvars,A,b,Aeq,beq)x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)%其中fitnessfc为函数的句柄或者为匿名函数nvars,表⽰⾃变量个个数（例如⾃变量为向量X,nvars代表X中的元素个数）A，b就是表达式A*X<=b;Aeq:表⽰线性等式约束矩阵，若是没有等式约束就写为[];Beq:表⽰线性等式约束的个数Beq=length(nvars);x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon)x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)x = ga(problem)[x,fval] = ga(...)例⼦A = [1 1; -1 2; 2 1]; b = [2; 2; 3]; lb = zeros(2,1); [x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb) %lb表⽰x的下界，up表⽰上界 Optimization terminated: average change in the fitness value less than options.TolFun. x = 0.7794 1.2205 fval = -8.03916 exitflag =z=f(x,y)1、编码（解决初始化种群），先创建⼀个数组pop（popsize stringlenth）有popsize表⽰染⾊体个数列stringlenth的前⼀部分代表x的染⾊体，后⼀部分代表y的染⾊体。

GA算法和PSO算法

GA算法和PSO算法GA算法（Genetic Algorithm）是一种基于自然选择和进化论的优化算法。

它模拟了生物界的进化过程，通过选择、交叉和变异等操作来生成新的解，并逐渐优化解的质量，最终找到最优解。

GA算法的基本过程如下：1.初始化种群：随机生成一组个体（解）作为初始种群。

2.评估适应度：对每个个体进行适应度评估，根据问题的具体要求，可以定义适应度函数。

3.选择操作：根据个体适应度，利用选择操作进行个体筛选，较优秀的个体被选中用于生成下一代。

4.交叉操作：选中的个体进行交叉操作，生成新的个体。

交叉可以是单点交叉、多点交叉或均匀交叉等方式。

5.变异操作：对新生成的个体进行变异，引入一定的随机性，增加空间。

6.更新种群：将交叉、变异得到的新个体加入种群，生成下一代种群。

7.终止条件判断：判断是否达到停止迭代的条件，如找到最优解或迭代次数达到上限。

8.返回优秀个体：返回当前种群中适应度最好的个体作为最优解。

PSO算法（Particle Swarm Optimization）是一种模拟鸟群觅食行为的优化算法。

它利用群体中个体的协作和信息传递来寻找最优解。

PSO算法的基本过程如下：1.初始化粒子群：随机生成一群粒子，每个粒子表示一个解，包含位置和速度信息。

2.评估适应度：对每个粒子进行适应度评估，根据问题的具体要求，可以定义适应度函数。

3.更新粒子速度和位置：-根据粒子自身历史最优解和全局最优解，更新速度和位置。

-根据随机数和权重因子，调整速度和位置，并限定在空间范围内。

4.更新全局最优解：根据当前粒子群的适应度，更新全局最优解。

5.终止条件判断：判断是否达到停止迭代的条件，如找到最优解或迭代次数达到上限。

6.返回最优解：返回全局最优解作为最终结果。

1.都需要初始化个体或粒子群来构建初始种群。

2.都需要根据适应度函数来评估每个个体或粒子的适应度。

3.都涉及到群体的选择操作，选中优秀的个体或粒子用于后续的进化过程。

ARIMA模型--粒子群优化算法（PSO）和遗传算法（GA）

ARIMA模型--粒⼦群优化算法（PSO）和遗传算法（GA）ARIMA模型（完整的Word⽂件可以去我的博客⾥⾯下载）ARIMA模型（英语：AutoregressiveIntegratedMovingAverage model），差分整合移动平均⾃回归模型，⼜称整合移动平均⾃回归模型（移动也可称作滑动），预测分析⽅法之⼀。

ARIMA（p，d，q）中，AR是"⾃回归"，p为⾃回归项数；MA为"滑动平均"，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。

ARIMA（p，d，q）模型是（p，q）模型的扩展。

ARIMA（p，d，q）模型可以表⽰为：其中L是滞后算⼦（Lag operator），1. 平稳性：平稳性就是要求经由样本时间序列所得到的拟合曲线，在未来的⼀段时间内仍能顺着现有状态“惯性”地延续下去；平稳性要求序列的均值和⽅差不发⽣明显变化；⽅差越⼤，数据波动越⼤，⽅差计算公式如下式所⽰：⽅差等于1，那么标准差也就是1，表⽰概率函数在对称轴左右偏差1的位置导数为0，即为拐点。

期望为0，表⽰概率函数以y轴为对称轴。

平稳性分为严平稳和弱平稳严平稳：严平稳表⽰的分布不随时间的改变⽽改变，如：⽩噪声（正态），⽆论怎么取，都是期望为0，⽅差为1；弱平稳：期望与相关系数（依赖性）不变，未来某时刻的t值Xt就要依赖于它的过去信息，所以需要依赖性；2. 差分法：时间序列在t与t-1时刻的差值3. ⾃回归模型（AR）描述当前值与历史值之间的关系，⽤变量⾃⾝的历史时间数据对⾃⾝进⾏预测⾃回归模型必须满⾜平稳性的要求p阶⾃回归过程的公式定义：是当前值，是常数项，P是阶数（需要我们⾃⼰指定），是⾃相关系数，是误差4. 移动平均模型（MA）移动平均模型关注的是⾃回归模型中误差项的累加q阶⾃回归过程的公式定义：移动平均法能有效消除预测中的随机波动5. ⾃回归移动平均模型（ARMA）⾃回归与移动平均结合，公式定义如下，由下述公式我们可以得到，当拿到ARMA模型时，我们仅需要指定三个参数（p,d,q），d是阶数，d=1即为⼀阶差分，d=2为⼆阶差分，以此类推。

具有自适应交换率和变异率的遗传算法

具有自适应交换率和变异率的遗传算法袁慧梅【期刊名称】《首都师范大学学报（自然科学版）》【年(卷),期】2000(021)003【摘要】Simple genetic algorithm gets local minimization too easily and converges slowly.To solve these problems,adaptive crossover rate that has reverse hyperbolic relrnation with the numbers of iteration is designed,and adaptive mutation rate that has reverse proportion to the distances of parents and reverse exponential relatrnion to the numbers of iteration is put forward.The Practical simulation results show that the adaptive GA has greater convergence speed and larger probability ornf getting the best solution.%简单遗传算法存在着收敛速度慢、易陷入局部极小等缺陷.针对这些缺陷，本文设计出随相对遗传代数呈双曲线下降的自适应交换率，并提出与父串间的相对欧氏距离成反比、随相对rn遗传代数指数下降的自适应变异率.实例验证表明，具有自适应交换率和变异率的遗传算法在收敛速度和获得全局最优解的概率两个方面都有很大的提高.【总页数】1页(P14)【作者】袁慧梅【作者单位】首都师范大学物理系，北京，100037【正文语种】中文【中图分类】TP393【相关文献】1.双变异率自适应遗传算法研究及其应用 [J], 方咸云;方千山;王永初2.遗传算法交叉率与变异率关系的研究 [J], 黎钧琪;石国桢3.自适应变异率的遗传算法 [J], 黎明;杨小芹;周琳霞4.变异率和种群数目自适应的遗传算法 [J], 熊军;高敦堂;都思丹;沈庆宏5.一种自适应交叉率和变异率的薄膜遗传算法 [J], 李易;冯国英;马孜因版权原因，仅展示原文概要，查看原文内容请购买。