电路分析：二端口网络
电路分析-11章二端口网络
I1
(Z－21 Z12＋)I1
I2
U+1
Z11 Z12
Z12
－
Z22 Z12
+
U 2
－
上述两种等效电路适合任意二端口网络。
同样地，由Y参数方程：
I1 Y11U1 Y12U 2
I2 Y21U1 Y22U 2
可构成如下图所示的含两个受控源的等效
电路：
I1
A'
A' C'
B' D'
A"
A" C"
B" D"
I1 I1'
U1 ＋U1'
N1
－
I2 '
I1"
＋＋
U 2 ' U1"
N2
－－
I2 I2"
＋
U2 U2
－
(a)级联
根据A参数方程，有
U1
A
U 2
I1
I2
U1
A
U2
I1
I 2
由图：U1 U1 I1 I1 U2 U2 I2 I2 U2 U1 I2 I1
由于H参数中，参数有各种量纲，因此H参数又称 为混合参数。
11-2-4 A参数
若将二端口网络的 U 2,作I2 为自变量，则可建立 如下方程：
U1 AU 2 BI2 I1 CU 2 DI2
其中，A,B,C,D
称为二端口网络的
A参数。四个参数的计算方法如下：
A
U 1 U 2
I2 0
为输出端口开路时的反向转移电压比。无量纲。
《电路分析基础》：互易二端口和对称二端口
口电压均为上正下负。 1
2
Y11
I1 U1
U2
j2
Y22
Y21
I2 U1
U2 0
( 1 12
+j )
Y12
返回
X
Z11 Z22 Y11 Y22 A11 A22 H11H22 H12H21 1 H
结论：对称二端口的任意一组参数中只有两个是独立的。
例题1 求如图所示二端口网络的Y参数。假设电路角
频率为 。
12
解：该二端口是对称二端口。
假设两个端口的电流分别 1
2
从1、2端子流入，两个端 1F 1F 1F
结论：对于互易二端口，任意一组参数中只有三个 是独立的。
返回
X
2.对称二端口
如果一个互易二端口网络的两个端口可以交换，而 交换后端口电压和电流的数值不变，则称这样的二 端口网络为对称二端口网络。 结构对称的二端口一定是对称二端口，反之不然。 对称二端口的各组参数除满足互易二端口的关系外， 还具有以下关系：
§12-4 互易二端口和 对称二端口
退出 开始
内容提要
互易二端口 对称二端口
X
1.互易二端口
满足互易定理的二端口网络称为互易二端口网络。 不含受控源、仅由线性电阻、电感、电容及互感元 件组成的二端口网络通常是互易二端口。 互易二端口各组参数间的关系：
Z12 Z21 Y12 Y21 H12 H21 A11 A22 A12 A21 1 A
电路分析基础课件第13章 二端口网络
•
I
•
2I
2
+
NN
•
U2
••
I 1I 1
•+
U1
••
II2 2
++
NN
••
UU2 2
Y12
I1 U 2
U1 0
Y22
I2 U 2
U1 0
转移导纳 输入导纳
Y → 短路导纳参数
例2-1 求图示二端口的Y 参数。
解
•
I I I •
•
1 11
Yb YbYb
•
I I I •
•
2
2
2
++
•
••
UU1
1U01
第13章 二端口网络
13-1 13-2 13-3 13-4 13-5 13-6
二端口网络 二端口的方程和参数 二端口的等效电路 二端口的转移函数 二端口的连接 回转器和负阻抗转换器
重点
1. 二端口的参数和方程 2. 二端口的等效电路 3. 二端口的转移函数
13-1 二端口网络
在工程实际中，研究信号及能量的传输和 信号变换时，经常碰到如下二端口电路。
•
I1
例2-8 求二端口T 参数。 +
•
U1
解
n 0
T
0
1
n
1
2
•
I2
+
2
•
U2
A U1 U2
I2 0 1.5
B
U1 I2
U2 0
4Ω
C I1 U2
I2 0 0.5 S
D I1 I2
U2 0
2
电路分析章二端口网络
电路分析章二端口网络二端口网络是指有两个端口的电路网络。
在电路分析中，我们常常会遇到这样的问题：给定一个二端口网络，需要找到其参数，通过这些参数来描述该网络的特性。
二端口网络的参数分为两类：传输参数和散射参数。
传输参数是描述网络的输入与输出之间的关系的参数。
我们可以使用电压传输参数和电流传输参数来描述二端口网络。
电压传输参数使用开路传输参数和短路传输参数来描述。
开路传输参数是指当输入端口短路时，输出端口的电压与输入电压的比值。
短路传输参数是指当输入端口开路时，输出端口的电压与输入电压的比值。
电流传输参数使用开路传输参数和短路传输参数来描述。
开路传输参数是指当输出端口短路时，输入端口的电流与输出电流的比值。
短路传输参数是指当输出端口开路时，输入端口的电流与输出电流的比值。
散射参数是描述网络的内部反射和传输特性的参数。
散射参数包括前向散射参数和反向散射参数。
前向散射参数是指从输入端口注入的信号在网络内部发生反射后到达输出端口的比例。
反向散射参数是指从输出端口反射回到输入端口的比例。
为了求解二端口网络的参数，我们可以采用回路分析、矩阵法等方法。
回路分析方法是指通过对网络进行回路等效变换和叠加原理，将复杂的网络转换为简单的网络，然后再求解。
矩阵法是一种基于矩阵运算的方法，通过将电路网路转换为矩阵形式，然后利用矩阵的运算性质进行计算。
矩阵法可以直接求解网络的传输参数和散射参数。
除了传输参数和散射参数，我们还可以使用频率响应和零极点分析来描述二端口网络的特性。
频率响应是指输入信号的频率对输出信号的影响。
零极点分析是指通过求解网络的特征方程，找到网络的零点和极点，从而了解网络的稳定性和频率响应。
总之，在电路分析中，对于二端口网络，我们需要求解其传输参数和散射参数，并通过频率响应和零极点分析来描述其特性。
通过这些方法，我们可以更好地理解和分析二端口网络的工作原理和性能。
电路基础原理二端口网络的特性与参数分析
电路基础原理二端口网络的特性与参数分析在电路领域中，二端口网络是一个非常重要的概念。
二端口网络是指具有两个输入端口和两个输出端口的电路系统。
它可以用于各种电子设备和通信系统中，包括滤波器、放大器和传输线等。
二端口网络的特性可以通过参数来描述。
这些参数包括传输参数、散射参数、喉参数和混合参数。
传输参数描述了输入和输出之间的关系，散射参数描述了输入和输出之间的散射特性，喉参数描述了输入和输出之间的传输特性，混合参数描述了输入和输出之间的相互作用。
传输参数是描述输入和输出之间关系的一类参数。
它们包括传输增益、电压传输、电流传输和功率传输等。
传输增益是指输出电压与输入电压之间的比例关系，电压传输是指输入电压与输出电流之间的比例关系，电流传输是指输入电流与输出电压之间的比例关系，功率传输是指输入功率与输出功率之间的比例关系。
散射参数是描述输入和输出之间散射特性的一类参数。
它们包括散射系数、反射系数和传输系数等。
散射系数是指从输入端口到输出端口的散射功率与输入功率之间的比例关系，反射系数是指从输出端口返回到输入端口的反射功率与输入功率之间的比例关系，传输系数是指从输入端口到输出端口的传输功率与输入功率之间的比例关系。
喉参数是描述输入和输出之间传输特性的一类参数。
它们包括输入阻抗、输出阻抗、输入导纳和输出导纳等。
输入阻抗是指输入端口的阻抗与输入电压和输入电流之间的关系，输出阻抗是指输出端口的阻抗与输出电压和输出电流之间的关系，输入导纳是指输入端口的导纳与输入电压和输入电流之间的关系，输出导纳是指输出端口的导纳与输出电压和输出电流之间的关系。
混合参数是描述输入和输出之间相互作用的一类参数。
它们包括互阻、互导和互传等。
互阻是指输入电流与输出电压之间的关系，互导是指输入电压与输出电流之间的关系，互传是指输入功率与输出功率之间的关系。
通过对二端口网络的特性和参数进行分析，可以更好地了解电路的传输、散射、传输和相互作用特性。
电路分析之二端口网络
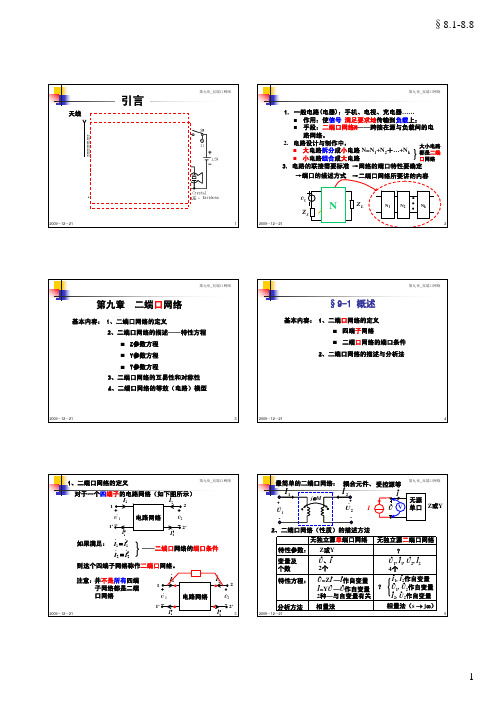
引言第九章_双端口网络§9-1 概述1、二端口网络的定义对于一个四端子的电路网络（如下图所示）2I &1I &最简单的二端口网络：受控源等I§9-2 二端口网络的开路阻抗(Z)矩阵1、Z 参数特性方程U ..无源122、各Z 参数的含义U .U 1.2N源1.U .U 1.2I N源VV3、开路阻抗矩阵或Z 矩阵特性方程还可以写成矩阵形式，有：证明：互易定理的第二种形式：激励电流源与开路端口互换位置，开路端口的响应电压不变。
例1、求图示电路的Z 参数5、例子.I 解：由各参数的定义式求例2、求图示电路的Z 参数.I 解：从特性方程来求§9-3 二端口网络的短路导纳(Y)矩阵电路的性质也可用加1、Y 参数特性方程2、各Y 参数的含义1.2.I I 1.2.I I 3、短路导纳矩阵或Y 矩阵特性方程还可以写成矩阵形式，有：Y a.I 1.I 求图示电路的Y 参数5例：Y a .I Y a例2、如图无源电阻双口网络，已知：1-1’开路时，测得U =0.5V ，U =1V§9-4 二端口网络的传输参数(T)矩阵为便于分析信号的传输情况,常以一个端口的电流、1、T(传输)参数特性方程⎪⎧2、各T 参数的意义3、传输参数矩阵或T 矩阵特性方程还可以写成矩阵形式，有：.例:写出图中T 参数1I &1Z .I 1.I1、Z与Y参数间的转换§9-6 二端口网络不同参数矩阵的互换Z2、其它各参数间的转换§9-7 二端口网络的互易和对称的条件（书§4-7）§9-8 二端口网络的等效模型（书§4-8 ）1I&&1、等效条件：I&&I&I&还可以等效为图(b)所示的T型等效模型当3、Y参数网络的∏型等效模型对一个含有公共端的用Y参数描述的二端口网络，I&&。
电路基础分析课件15二端口网络
二端口网络用于电路设计和分析，如 负反馈电路、差分放大器等。
在电力电子中的应用
电力转换和控制
在电力电子中，二端口网络用于电力转换和控制，如逆变器、整流器等。
电机控制和驱动
二端口网络用于Hale Waihona Puke 机控制和驱动，如变频器、伺服控制器等。
THANKS
感谢观看
04
CATALOGUE
二端口网络的网络分析
散射参数
定义
散射参数（Scattering Parameters）也称为S参数，用 于描述二端口网络输入端口和输 出端口之间的信号散射关系。
描述内容
S参数描述了当一个端口接收到 信号时，另一个端口如何响应，
包括幅度和相位信息。
重要性
S参数是二端口网络分析的重要 工具，广泛应用于微波、通信、
电路基础分析课件15二 端口网络
CATALOGUE
目 录
• 二端口网络概述 • 二端口网络的等效电路 • 二端口网络的连接 • 二端口网络的网络分析 • 二端口网络的应用
01
CATALOGUE
二端口网络概述
定义与分类
定义
二端口网络是指具有两个端口的电路网络，通常由电阻、电容、电感等元件组 成。
级联连接
总结词
两个二端口网络在电路中以级联的方式连接，它们共享输入和输出端，形成一个更复杂的网络结构。
详细描述
在级联连接中，一个二端口的输出端连接到另一个二端口的输入端，形成一个连续的电路路径。这种 连接方式可以构建更复杂的电路结构，实现更丰富的功能。级联连接时需要注意信号的匹配和阻抗的 连续性，以避免信号失真和反射。
在并联连接中，两个二端口的输入端和输出端分别相连，共享相同的电压源。每 个二端口网络独立处理电流，不受其他网络影响。这种连接方式常用于需要增加 元件数量或提高系统容错能力的电路中。
电路分析基础-第14章二端口网络课件
2.试用二端口网络的参数方程来证 明电阻Y-△的连接与转换中的各电阻 的表达式。
4.在学习了一端 口、二端口网络 等效的原理后， 试总结等效概念 在电路分析中的 应用。
3.已知二端口网
络 试的问Y该参二数端为口Y 能 78 73S
否等
14.4 二端口的转移函数
二端口常为完成某种功能起着耦合两部分电路的 作用，这种功能往往是通过转移函数描述或指定的。 因此，二端口的转移函数是一个很重要的概念 。
二端口转移函数
二端口的转移函数（传递函数），就是用拉氏 变换形式表示的输出电压或电流与输入电压或电流 之比 。
二. 有源二端口网络
二端口网络的输入端口与一个非理想激励源相联接， 输出
6Ω 2Ω
I1 5Ω 10Ω+15I1-
4Ω
20Ω
(a)
(b)
解：(1)因 Z12 Z21 4Ω ，故该二端口不含受控源，其
等效T形电路见图(a)。
(2)因 Z12 Z，21故该二端口含有受控源，图 (b)
为其等效电路。
应用举例
例：1二4-端6 已口知是二否端有口受的控参源数，矩并阵求为它的Y 等 效06π型42电s路，。试问
端口与一个负载相联接，这样的二端口网络称为有载二端口网络。
它起着对信号进行传递、加工、处理的作用。
I1(s)
I2(s)
ZS
+
+ U1(s)
US(s)
–
–
+
N U2(s) ZL
–
1. 输入阻抗
A[ U2(s) ] B
Zin
U1(s) AU2(s) B I2(s) I1(s) CU2(s) D I2(s)
电路分析第十章-二端口网络
双口网络参数间的相互换算
一般情况下，一个双口网络可以用以上四种参数中 的任何一种进行描述 （只要它的各组参数有意义），这 四种参数之间可以相互转换
Y参数方程
I1
I2
= =
Y11U1 Y21U1
+ Y12U 2 + Y22U 2
Z参数方程
U1 = Z11I1 + Z12I2 U 2 = Z21I1 + Z22I2
Y参数与Z参数的关系
I1 I2
=
[Y
]
UU12
UU12
=
[Z
]
II12
I1 I2
=
[Y
][Z
]
I1 I2
∴[Y][Z]=[E] [Y]=[Z]-1 [Z]=[Y]-1
例10.2-4: 求图(a) 所示电路的Z参数矩阵和Y参数矩阵。 .
3U3
.
1 I1
2Ω
+. U1
. 1 I1 Z1 +. U1 -
Z3
. I2 2
Z2
- +.
(Z21-Z12)I1
+. U2
-
1‘
2‘
图(b) 含受控源的T形等效电路
Z2 Z1
= Z12 = Z11 −
Z12
Z3 = Z 22 − Z12
U1 = Z11I1 + Z12I2 = Z11I1 + Z21I2 + (Z12 − Z21)I2 U 2 = Z21I1 + Z22 I2
1Ω
+ .2I1 2Ω
+. U3
. I2 2
+. U2
1‘
解：由Z参数方程：
(大学物理电路分析基础)第12章二端口网络
传输方程的建立基于基尔霍夫定律和元件的伏安特性，通过求解网络中电压和电流 的分布，可以得到传输方程的具体形式。
传输方程具有非线性、对称性和互易性等特点，这些特点反映了网络内部元件之间 的相互作用和网络的整体特性。
应用
用于简化电路分析过程，方便计算二端口网络的输入阻抗、输出阻抗 以及转移函数等。
04 二端口网络的连接
并联连接
01
并联连接
将两个二端口网络并联在一起，形成一个更大的二端口网络。在并联连
接中，两个二端口的端口电压相等，且都等于总电压。
02
总结词
并联连接可以增加二端口网络的电流容量，但不会改变其电压和功率。
网络函数的定义与分类
定义
二端口网络函数描述了网络内部元件 与外部端口的电压和电流之间的关系。
分类
根据电压和电流的参考方向，可以将 二端口网络函数分为阻抗、导纳、转 移和散射型函数。
网络函数的性质
线性性
二端口网络函数是线性 的，即对于多个输入和 输出信号，其响应是各 个信号响应的线性组合。
时不变性
大学物理电路分析基 础第12章二端口网络
目录
CONTENTS
• 二端口网络的定义与分类 • 二端口网络的方程与参数 • 二端口网络的等效电路 • 二端口网络的连接 • 二端口网络的网络函数
01 二端口网络的定义与分类
定义
总结词
二端口网络是指具有两个端口的电路网络，通常由两个或多个元件组成，具有 两个输入端口和两个输出端口。
二端口网络函数的特性 不随时间变化，即对于 不同时刻的输入信号， 其输出信号的特性保持 不变。
《二端口网络》课件
特性参数
电压传输系数
表示输入电压与输出电压之比，是衡量 二端口网络传输性能的重要参数。
插入衰减系数
表示在二端口网络的输出端与输入端 之间插入一个网络后引起的信号衰减
控制系统
在控制系统中，二端口网 络用于信号传输和信号处 理，如传感器、执行器、 控制器等。
02
二端口网络的基本元件
电阻器
总结词
表示电路中阻碍电流通过的元件
详细描述
电阻器是二端口网络中的基本元件之一，它对电流通过的阻力与电压成正比，具 有恒定的阻值。电阻器在电路中主要用于限制电流和调节电压。
电感器
03
二端口网络的连接与等效
串联与并联
串联
两个或多个二端口网络按照电流 方向串联在一起，总电压等于各 二端口网络的电压之和。
并联
两个或多个二端口网络并联在一 起，总电流等于各二端口网络的 电流之和。
Y-Δ等效变换
Y-Δ等效变换是一种将Y型二端口网络转换为Δ型二端口网络的方法，反之亦然。 通过改变网络端口的连接方式，可以实现电路的简化或变换。
匹配网络中的二端口网络
总结词
匹配网络中的二端口网络用于阻抗匹配，通 过调整网络的元件参数，使不同阻抗的信号 源和负载之间实现有效的能量传输。
详细描述
在匹配网络中，二端口网络通常由电阻、电 容和电感等元件组成，用于实现信号源和负 载之间的阻抗匹配。通过调整网络的元件参 数，可以减小信号传输过程中的能量损失，
信号流图的简化
在实际应用中，由于系统的复杂性和庞大性，信号流图可能会非常复杂和庞大，这 会给分析带来很大的困难。
二端口网络电路分析教程
2 21 1 Y21、Y22具有导纳性质，因此常称为导纳方程或Y方程。 当输出端口短路时，
I Y11 1 U 1
0 U 2
即Y11是输出端口短路时在输入端口处的输入导纳，称 为短路输入导纳。
1 二端口网络的一般概念
如果一个二端口网络的端口处电流与电压满足线性关系 ，则称该二端口网络为线性二端口网络，否则称为非线性 二端口网络。 如果一个二端口网络内部不含有独立电源，则称其为无 源二端口网络，如图 (a)所示；否则称为有源二端口网络 ，如图 (b)所示。本章只介绍无源线性二端口网络，在正 弦稳态下对二端口网络进行分析。
Y datY Y11Y22 Y12Y21 T datT T11T22 T12T21
3 二端口网络参数的计算
二端口网络的特性由其参数矩阵来表征。在已知二
端口网络的结构和元件参数情况下，计算不含独立源线
性二端口网络参数的基本方法是在端口外加电源，用网 络分析的任何一种方法直接建立电路方程，计算端口电
二端口网络的输入端口和输出端口的电压和电流共 、I 、U 、I 。在分析二端口网络时，通 有4个，即 U 1 1 2 2 常已知其中的两个电量，求出另外两个电量。由这4 个物理量构成的组合，共有6 组关系式，其中4 组为 常用关系式。 7.2.1 阻抗方程和Z参数 在如图所示的无源线性二端口网络中，当以电流源 、I 作为激励作用于线性无源二端口网络时，其响应 I 1 2 、I 的线性组合表示出来，即 、U 可以分别用 I U 1 2 1 2
2 21 1 22 2
当输出端口短路时，有
当输入端口开路时，有
U h11 1 I 1 I h21 2 I 1
第十六章 二端口网络
放大器
2 、二端口网络
1
i1in
1
i2 in
2
u1
1 i1out
u2
i2out 2
(1)给定一个四端网络，若 i1in i1out , i2 in i2out , 则这个四端网络构成了二端口网络。 (2)二端口网络的对外联接特性由端口电压 u1 , u2 和电流 i1 , i2 确定。端口四个变量的相互关系可 通过二端口的参数和方程来描述，参数只决定于 二端口本身的元件及联接方式。
Z1 Z 2
[Z ]
Z2
Z2 Z2 Z3
例2：若上图中加上一个受控电压源，如图所示， 求二端口网络的Z参数。 Z I I Z1
1
3
2
U1
Z2 U R
3U R
U2
Z1
Z3
Z2 U R
I1
3U R
解： 方法一：
在左边端口加电流为 I1的电流源，右端开路，则： U1 U1 ( Z1 Z 2 ) I1 Z11 Z1 Z 2 I1 U2 U2 Z 2 I1 3 Z 2 I1 Z 21 4 Z 2 I1 在右边端口加电流为 I 2 的电流源，左端开路，则： U1 U1 Z 2 I 2 Z12 Z 2 I2 U2 U2 ( Z 2 Z 3 ) I 2 3 Z 2 I 2 Z 22 4 Z 2 Z 3 I2
直接列方程
1
Yc
2
I1 YaU1 Yb (U1 U2 ) (Ya Yb )U1 YbU2 I 2 YcU2 Yb (U2 U1 ) YbU1 (Yb Yc )U2
电路基础原理概述二端口网络的特性和参数
电路基础原理概述二端口网络的特性和参数电路是现代科技中必不可少的基础，其中二端口网络是其中一种常见的电路类型。
在电路中，二端口网络是由两个输入端和两个输出端组成的电路元件，它能够传输和转换电信号。
本文将概述二端口网络的特性和参数。
一、传输特性二端口网络的传输特性是指输入电压与输出电压之间的相互关系。
传输特性可以通过观察输入和输出之间的电流和电压变化来确定。
通常，二端口网络的传输特性可以表示为一个线性的数学方程组。
这个方程组可以用来描述二端口网络的传输函数，即输入和输出之间的关系，通常表示为Vout = H Vin。
其中，H 表示传输函数，Vin 表示输入电压，Vout 表示输出电压。
二、阻抗特性阻抗是描述二端口网络响应外部电路的能力的参数。
一个二端口网络的输入阻抗和输出阻抗是反映网络与外部电路相互连接时的特性。
输入阻抗反映了二端口网络对外部电路输入信号的响应，输出阻抗反映了二端口网络对外部电路输出信号的响应。
阻抗特性的数学表示为Zin = Vin / Iin 和 Zout = Vout / Iout，其中 Zin 表示输入阻抗，Vin 表示输入电压，Iin 表示输入电流，Zout 表示输出阻抗，Vout 表示输出电压，Iout 表示输出电流。
三、特性曲线特性曲线是描述二端口网络输入和输出关系的图形，可以通过实验或者计算得到。
在特性曲线上，通常会有一些重要的特性点，例如截止点、饱和点等。
这些特性点可以用来判断二端口网络的工作状态和性能。
特性曲线可以帮助工程师了解二端口网络的行为和特点，进而进行电路设计和优化。
四、常见参数二端口网络有一些常见的参数,例如增益、带宽、相位等。
增益是指输出电压与输入电压之间的比例关系。
带宽是指在特定增益范围内的频率范围。
相位是指输入信号和输出信号之间的相对时间差。
这些参数可以帮助我们了解二端口网络的性能和应用范围。
总结：二端口网络在电路中有广泛的应用，它的特性和参数对于电路设计和分析非常重要。
二端口网络的参数与特性分析
二端口网络的参数与特性分析二端口网络是指由两个端口构成的电路网络，常见于各种电子电路中。
了解二端口网络的参数与特性对于分析电路性能、设计电路以及解决电路问题的能力至关重要。
本文将对二端口网络的参数与特性进行详细分析。
一、二端口网络的基本参数二端口网络的基本参数包括：传输函数、散射参数、混合参数、过渡参数等。
这些参数能够描述电路的输入与输出之间的关系。
1. 传输函数传输函数描述了二端口网络的输入与输出之间的传输关系。
通常用H(s)表示，其中s为复变量。
传输函数可以通过拉普拉斯变换或者其它等效方法求得。
2. 散射参数散射参数（S参数）是描述二端口网络中波的散射过程的参数。
它们包括反射系数和传输系数。
S参数可以通过测量回波系数和透射系数等实验数据计算得到。
3. 混合参数混合参数（H参数）是描述二端口网络中电流和电压关系的参数。
它们包括双端口输入电阻、输出电阻以及互阻和互导。
H参数可以通过测量电压和电流的关系得到。
4. 过渡参数过渡参数（T参数）是描述二端口网络中电流和电压关系的另一组参数。
它们包括双端口输入电阻、输出电阻以及互阻和互导。
T参数可以通过测量电压和电流的关系得到。
二、二端口网络的特性分析除了基本参数外，二端口网络还具有一些特性，这些特性可以帮助我们更好地理解二端口网络的工作原理、性能和应用。
1. 平衡与非平衡二端口网络可以分为平衡网络和非平衡网络。
在平衡网络中，输入端和输出端的特性相同；而在非平衡网络中，输入端和输出端的特性不同。
平衡与非平衡对于分析电路性能和设计电路具有重要影响。
2. 带宽与通频带带宽是指二端口网络能够传输的频率范围。
通频带是指在这个频率范围内，二端口网络的传输特性基本保持不变。
带宽和通频带决定了二端口网络的信号传输能力。
3. 稳定性与不稳定性稳定性是指二端口网络在一定条件下保持正常工作的能力。
不稳定性则指在特定条件下，二端口网络出现性能失效或者不可控的情况。
稳定性是电路设计和应用中需要考虑的一个重要因素。
二端口网络练习题及答案
二端口网络练习题及答案二端口网络是电子电路中的一个重要概念，它由两个端口组成，可以是输入端口和输出端口。
在电路分析中，二端口网络通常用来描述电路元件的电气特性，如电阻、电感和电容。
以下是一些关于二端口网络的练习题及答案：练习题1：二端口网络参数定义1. 什么是二端口网络的Z参数矩阵？2. 什么是二端口网络的Y参数矩阵？3. 什么是二端口网络的h参数矩阵？答案1：1. Z参数矩阵，也称为阻抗参数矩阵，是一个2x2的矩阵，用于描述二端口网络的输入和输出阻抗。
2. Y参数矩阵，也称为导纳参数矩阵，是一个2x2的矩阵，用于描述二端口网络的输入和输出导纳。
3. h参数矩阵，也称为混合参数矩阵，是一个2x2的矩阵，用于描述二端口网络的输入和输出混合参数。
练习题2：二端口网络参数转换1. 如何从Z参数矩阵转换到Y参数矩阵？2. 如何从Y参数矩阵转换到Z参数矩阵？答案2：1. 从Z参数矩阵转换到Y参数矩阵，可以使用以下公式：\[ Y =Z^{-1} \] 其中Z^{-1}表示Z矩阵的逆矩阵。
2. 从Y参数矩阵转换到Z参数矩阵，可以使用以下公式：\[ Z =Y^{-1} \]练习题3：二端口网络的等效电路1. 如何使用Z参数矩阵构建二端口网络的等效电路？2. 如何使用Y参数矩阵构建二端口网络的等效电路？答案3：1. 使用Z参数矩阵构建二端口网络的等效电路，可以通过将Z参数矩阵的元素视为电路元件的阻抗值来实现。
2. 使用Y参数矩阵构建二端口网络的等效电路，可以通过将Y参数矩阵的元素视为电路元件的导纳值来实现。
练习题4：二端口网络的串联和并联1. 两个二端口网络串联时，它们的Z参数矩阵如何计算？2. 两个二端口网络并联时，它们的Y参数矩阵如何计算？答案4：1. 两个二端口网络串联时，它们的Z参数矩阵可以通过矩阵加法来计算，即：\[ Z_{total} = Z_1 + Z_2 \] 其中Z_1和Z_2分别是两个二端口网络的Z参数矩阵。
电路基础原理二端口网络的参数与分析
电路基础原理二端口网络的参数与分析在电路学习的过程中，我们经常会遇到二端口网络。
什么是二端口网络呢？简单来说，二端口网络可以视为一个有两个输入端口和两个输出端口的电路系统。
它在电子设备和通信领域中有着广泛的应用，例如功率放大器、滤波器、传输线等。
在分析二端口网络之前，我们首先需要了解它的参数。
常见的二端口网络参数有四个，分别是传输函数、输入阻抗、输出阻抗和互阻。
其中，传输函数是描述输入和输出之间关系的参数，可以表示为Vout/Vin，即输出电压与输入电压的比值。
输入阻抗指的是在输入端口施加一个测试电压时，输入端口相对于这个电压的表现。
输出阻抗则是在输出端口施加一个测试电压时，输出端口相对于这个电压的表现。
而互阻则是描述输入端口和输出端口之间相互影响的参数。
接下来，我们将通过一个实例来详细分析二端口网络的参数。
假设我们要研究一个电路，输入电流为Iin，输入电压为Vin，输出电流为Iout，输出电压为Vout。
这个电路的传输函数可以表示为Vout/Vin，通过测量输入和输出的电压以及电流，我们可以得到传输函数的值。
例如，当输入电压为1V时，输出电压为2V，那么传输函数的值为2。
同样地，我们可以测量输入和输出的电流，从而获得输入阻抗和输出阻抗的数值。
假设当输入电压为1V时，输入电流为0.5A，那么输入阻抗的值为2Ω。
除了测量参数值之外，我们还可以通过二端口网络的参数来分析电路的性能。
例如，通过传输函数，我们可以确定电路的增益大小，即输出电压相对于输入电压的放大倍数。
这有助于我们评估电路的放大能力。
而输入阻抗和输出阻抗则可以告诉我们电路对外部电路的影响。
如果输入阻抗很大，也就是输入电流较小，那么它对外部电路的负载影响会较小。
同理，如果输出阻抗很小，也就是输出电流较大，那么它对外部电路的驱动能力会较强。
在分析和设计电路时，了解二端口网络的参数及其意义是非常重要的。
通过测量和计算，我们可以得到电路的性能指标，并据此进行优化和改进。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Hhh1211((ss))
h12(s) h22(s)
3、参数矩阵的求取
h1(1s)U I1 1((ss))U2(s)0， h2(1s)II1 2((ss))U2(s)0
h1(2s)U U 1 2((ss))I1(s)0， h2(2s)U I2 2((ss))I1(s)0
医学PPT
18
三、混合型参数—混合参数矩阵
方程的矩阵式：
U U1 2((ss))Z Z1 21 (1 (ss))
Z12 (s)I1(s) Z22 (s)I2(s)
医学PPT
11
一、流控型参数—开路阻抗矩阵
2、开路阻抗矩阵 ZZZ1211((ss)) 3、参数矩阵的求取
Z12(s) Z22(s)
Z1(1s)U I1 1((ss))I2(s)0， Z1(2s)U I2 1((ss))I2(s)0
U I21((ss)) hh211 (1 (ss))II11((ss)) h h2 12 2 ((ss))U U2 2((ss))
方程的矩阵式：
U I21((ss))h h1 21 1 ((ss))
h12(s)I1(s) h22(s)U2(s)
医学PPT
17
三、混合型参数—混合参数矩阵
2、混合参数矩阵
医学PPT
15
二、压控型参数—短路导纳矩阵
4、方程的矩阵形式
I(s)Y(sU ) (s)
其中 U( s)U U12((ss))，I(s)II12((ss)) 5、参数矩阵的特性
当二端口网络为线性非时变，且不含受
控源时，y12 y21
医学PPT
16
三、混合型参数—混合参数矩阵
1、对应的方程 以I1(s)、U2(s)为变量，即激励
y12 (s)U1(s) y22 (s)U2(s)
医学PPT
14
二、压控型参数—短路导纳矩阵
2、短路导纳矩阵
Yyy1211((ss))
3、参数矩阵的求取
y12(s) y22(s)
y1(1s)U I1 1((ss))U 2(s)0， y2(1s)U I2 1((ss))U 2(s)0
y2(1s)U I1 2((ss))U 1(s)0， y2(2s)U I2 2((ss))U 1(s)0
第十六章 二端口网络
医学PPT
1
本章重点与难点
❖重 点 1、二端口网络的有关基本概念 2、熟练计算二端口网络的四种参数矩阵 3、掌握分析网络参数已知的二端口网络 组成的复杂电路的分析方法
医学PPT
2
目录
16-1 概述
16-2 二端口网络参数
16-3 网络参数之间的变换关系
16-4 含二端口网络的电路分析
16-5 典型二端口元件模型
16-6 二端口网络的互联
医学PPT
3
一、N端网络与N端口网络
1．N端网络
如果一个网络有N个端子向外接
出，在分析中又并不关心电路的内部
结构及内部各个支路的情况，而只讨
论外电路的状态与变化时，称该网络
为N端网络。
医学PPT
4
2．N端口网络 如果一个网络有2N个端子向外
接出，这2N个端子又成对出现，即 端口处的输入电流等于输出电流时， 该网络可以视为一个N端口网络。
Z Z 控源时， 12
2医1学PPT
13
二、压控型参数—短路导纳矩阵
1、对应的方程 以U1(s)、U2(s)为变量，即激励
II2 1((ss)) y y1 21 1 ((ss))U U1 1((ss)) yy122(2(ss))U U22((ss))
方程的矩阵式：
II1 2((ss))yy1 21 (1 (ss))
2．二端口网络中的元件均为线性无源
非时变元件；
3．在分析中一般使用拉氏变换或相量
法进行。
医学PPT
7
四、变量与方程
1．变量
对于二端口网络，在U1(s)、U2(s)、 I1(s)、I2(s)中任选其中两个作变量，其 余两个可用这两个自变量来表示。
2．方程
线性方程组
医学PPT
8
16-2 二端口网络的参数
I2(s)U 2(s)0
I2(s)U 2(s)0
医学PPT
21
四、传输型—传输参数矩阵
4、当二端口网络为线性非时变，且不 含受控源时，AD-BC=1。
5、网络对称时，A=D。
6、注意：当以U1(s)、I1(s)为变量时，
得到的参数矩阵为逆传输参数矩阵T’。
4、当二端口网络为线性非时变，且不
含受控源时，h12h21
5、注意：当以I1(s)、U2(s)为变量时， 得到的参数矩阵为逆混合参数矩阵H’
医学PPT
19
四、传输型—传输参数矩阵
1、对应的方程 以U2(s)、I2(s)为变量，即激励
U I11((ss)) C A((ss))U U22((ss)) D B((ss)) [[II2 2((ss))]]
方程的矩阵式：
U I11((ss))C A((ss))
B(s)U2(s) D(s)I2(s)
医学PPT
20
四、传输型—传输参数矩阵
2、传输参数矩阵
TCA((ss))
B(s) D(s)
3、参数矩阵的求取
A(s)U 1(s) ， C(s)I1(s)
U2(s)I2(s)0
U2(s)I2(s)0
B(s)U 2(s) ， D (s)I1(s)
医学PPT
5
பைடு நூலகம்
二、研究的问题
1、通过定义及计算方法求二端口网络
的各种参数矩阵；（正向求解）
2、已知复杂网络中二端口网络的参数
矩阵通过模块化的思想将复杂网络等效
成为简单的单口网络及二端口网络的组
合，得出电路的解。 （反向求解）
医学PPT
6
三、研究对象的特性
1．二端口网络中不含独立源及附加电
源，也就是说动态元件的初始状态为零；
Z2(1s)U I1 2((ss))I1(s)0， Z2(2s)U I2 2((ss))I1(s)0
医学PPT
12
一、流控型参数—开路阻抗矩阵
4、方程的矩阵形式
U( sZ ) (sI)(s) 其中 U( s)U U12((ss))，I(s)II12((ss))
5、参数矩阵的特性
当二端口网络为线性非时变，且不含受
医学PPT
9
参考方向的规定
在本章的二端口网络参数中，均用以下
参考方向: (各端口均为关联方向)
I1(s)
+
U 1(s) _
线性 无源 非时变 二端口 网络
I2(s)
+
U 2(s) _
医学PPT
10
一、流控型参数—开路阻抗矩阵
1、对应的方程 以I1(s)、I2(s)为自变量，即激励
U U2 1((ss)) Z Z1 21 1 ((ss))II1 1((ss)) Z Z122(2(ss))II22((ss))