5达朗伯原理
达朗伯原理

由力系的简化理论可知: 由力系的简化理论可知 此力的作用线过 O点, 量值为惯性力系的矢量和 主矢 此 点 量值为惯性力系的矢量和( 主矢); 力偶作用在刚体上, 力偶作用在刚体上 量值为惯性力系诸力 点的力矩的代数和( 点的主矩). 对O点的力矩的代数和 对O点的主矩 点的力矩的代数和 点的主矩
F g = − ∑ mi a i = − M a C M g O = − ∑ mi ait ⋅ ri = − ∑ mi ri 2α = − J Oα (如图示)
Fg = −MaC MgC = −JCα
Fg
MgC
C
aC
注意: 有质量对称面且转轴垂直此面的 注意 刚体的定轴转动是刚体平面运动的特例, 刚体的定轴转动是刚体平面运动的特例 故刚体平面运动的惯性力系的简化方法 也适合于这样的定轴转动的刚体. 也适合于这样的定轴转动的刚体
▲: 达朗伯原理的应用 (1) 动载荷下求约束反力及加速度问题 动载荷下求约束反力及加速度问题. (2) 多自由度系统或多约束系统下求加速度及约束反力问题 多自由度系统或多约束系统下求加速度及约束反力问题.
有质量对称面且转轴垂直此面的定轴转动 的刚体, 的刚体 其上达朗伯惯性力系向对称面与 定轴的交点O简化可得一力和一力偶 简化可得一力和一力偶. 定轴的交点 简化可得一力和一力偶 其力: 其力 其力偶: 其力偶
F g
MgO
F gR = −MaC MgO = −JOα
3. 刚体平面运动 刚体有质量对称面且运动平面平行于此面 刚体平面运动( 刚体有质量对称面且运动平面平行于此面).
FS ≤ FN ⋅ f
∑Y = 0:
aA
C
mg
30° °
m Ag
FgC
B
达朗伯原理(动静法) (Principle of DAlambertMethod of 汇总

Fi N i Fgi 0
Fgi
Fi
mi Ni
ai
结论:质点系在某瞬时,其上作用的所有主动 力、约束力和惯性力组成一平衡力系
Fi N i Fgi 0
mo (Fi ) mo ( N i ) mo (Fgi ) 0
p.5
理论力学
理论力学
四、惯性力系的简化 (Simplification of Inertial Forces System) 刚体的惯性力系简化
(1) 平动刚体的惯性力系向质心的简化
Rg mi a i ac mi Mac
Rg
Fgi
ai c
ac
p.6
F v Fg m
ma F N
a
N
R
F N (ma) 0
F N Fg 0
结论:质点在某瞬时,其上作用的主动力、
约束力和惯性力组成一平衡力系
p.4
理论力学
理论力学
二、达朗伯原理(Principle of D’Alambert) 2. 质点系达朗伯原理
n 2
n
30
) 2 e 3158 ( N )
p.10
理论力学
理论力学
五、静平衡和动平衡的概念
(Static Equilibrium and Dynamic Equilibrium)
由平行力 系平衡方程求得轴承动约束力为
1 1 N A N B mg m 2 e 98 1579 1677 ( N ) 2 2
因此,高速转子还需进行动平衡试验, 使转子不出现惯性力偶,要求转子质心
《理论力学》第十四章达朗伯原理(动静法)

D d
C
mg FN
货物不滑的条件:F≤ f FN , a ≤ f g 货物不翻的条件:d ≤ b/2 , a ≤ bg/h
为了安全运送货物,应取两者中的小者作为小车的amax。
例 题7
已知:AB杆质量为m ,长为l=2r ,
r O
A
l
B
圆盘半径为r ,角速度为,角加速度为 。 求:A 端的约束反力。
FR
MIC
C
aC
FR maC M C J C
例 题5
已知:m , h , , l。
B
D
h
求:A、D处约束反力。
a
解: 取 AB 杆为研究对象
A
Fx 0 FAx F FN sin 0 Fy 0 FAy mg FN cos 0
C
n FR maC m(aC aC )
O
MIC
FR
M C J C
3、刚体作平面运动
具有质量对称平面的刚体作平面运动,并且运动平面与质量对 称平面互相平行。对于这种情形,先将刚体的空间惯性力系向质 量对称平面内简化,得到这一平面内的平面惯性力系,然后再对 平面惯性力系作进一步简化。
R
O
n FR
MIO
F R
(2)将惯性力系向质心C简化。
FR maC 2mr
n n FR maC 2mr 2
MA
A
FAy
MIC
C B
FAx
M C
1 2 J C mr 3
n FR
mg
FR
n Fx 0 FAx ( FR F ) cos 45 0 R n Fy 0 FAy mg ( FR FR ) cos 45 0 n M A( F ) 0 M A mgr ( FR F ) cos 45 r M C 0 R
《达朗贝尔原理》课件

该微分方程描述了刚体在力矩作用下的动态行为,是刚体动力学中的基本方程之 一。
达朗贝尔原理的积分方程形式
达朗贝尔原理的积分方程形式为:M(t2)-M(t1)=∫t1t2F·dr, 其中M(t2)和M(t1)分别表示刚体在时刻t2和t1的动量矩, ∫t1t2F·dr表示在时间t1到t2之间力矩的积分。
船舶工程
用于分析船舶的运动特性和稳定性。
02
达朗贝尔原理的数学表达
达朗贝尔原理的公式表达
达朗贝尔原理的公式表达为: M=∫F·dr,其中M表示刚体绕固定 点O转动的动量矩,F表示刚体上任 一点的速度矢量,dr表示矢径。
该公式描述了刚体在力矩作用下的运 动规律,是刚体动力学中的基本原理 之一。
达朗贝尔原理的微分方程形式
限制条件
达朗贝尔原理在处理复杂系统时,可能无法考虑所有 相互作用力和能量转换,导致预测精度下降。
与其他物理定律的互补性
与牛顿第三定律互补
达朗贝尔原理与牛顿第三定律互补,强调了 力和运动的相互关系。
与能量守恒定律的互补性
达朗贝尔原理在处理保守系统时,与能量守 恒定律相一致,但在非保守系统中存在差异
。
详细描述
在弹性力学中,达朗贝尔原理可以用来分析 各种复杂的力学问题,如梁的弯曲、板的变 形等。通过应用该原理,我们可以建立各种 弹性力学问题的数学模型,并进一步求解其 解析解或近似解。
05
达朗贝尔原理的局限性
适用范围和限制条件
适用范围
达朗贝尔原理主要适用于线性、保守的力学系统。对 于非线性、非保守系统,达朗贝尔原理可能不适用。
理论力学动力学部分5达朗伯原理
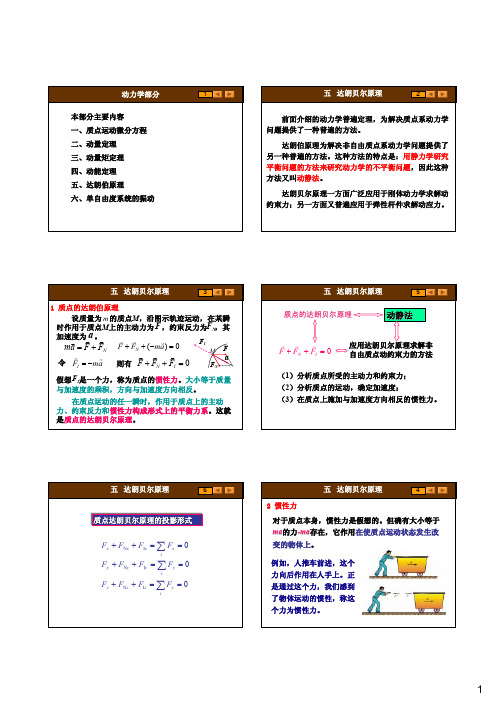
③当刚体作匀速转动且转轴通过质心C时, r FIR = 0,M IC = 0 ,惯性力系自成平衡力系。
五 达朗贝尔原理
23
3)平面运动
具有质量对称平面的刚体作平面运动,并且运 动平面与质量对称平面互相平行。
对于这种情形,先将刚体的空间惯性力系向质 量对称平面内简化,得到这一平面内的平面惯性力 系,然后再对平面惯性力系作进一步简化。
F1 FI1 FNam2m121FIiFmN1iFNFi ai
合力和外约束反力的合力,于是得
F2 a2
i
å
Mår OFr(i
+ Fi
å FrNi )+å
M+r
å FrIi O (FNi
=0 )+å
Mr O
( FIi
)
=
0
即:在质点系运动的任一瞬时,作用于质点系上的所
有主动力系,约束反力系和惯性力系构成形式上的平
五 达朗贝尔原理
24
解法1:利用达朗伯原理
取系统为研究对象,受力分析及 运动分析如图示:
运动分析:
以轮B为对象,vC = vD + wBr = wAr + wBr 求导得:aC = e Ar + e Br 由达朗伯原理:
åMO(F)
=
0,
1 2
×
P g
×r2
×eA
+
1 2
×
P g
×r2
×eB
-
P ×2r
衡力系。这就是质点系的达朗伯原理。
五 达朗贝尔原理
11
质点系达朗贝尔原理的投影形式
å Fix + FNix + FIix = Fx = 0 i
达朗伯原理

达朗伯原理
埃利斯·达朗伯(Ernst Darmbach)的原理是20世纪著名的概率统计家,也是
贝叶斯统计学诞生的催化剂。
达朗伯原理是他主要的成果,也称为达朗伯表达,是用逻辑统计学来推导事件可能性的一种方法。
达朗伯原理可以合理地推断不确定因素,包括条件及概率等,从而计算出综合结果。
基本的达朗伯原理因子包括条件独立性,事件概率和传递概率。
比如,考虑一个实验,事件A和B发生后,观察另外一个事件C的概率。
通常情况下,先考虑
条件独立性,即A和B事件发生后C事件发生的概率是确定的,比如0.5;这就是事件概率。
接下来,考虑传递概率,即A和B事件发生首先发生的概率组合。
比如,A和B事件同时发生的概率为0.3,则A和B两个条件发生后,C事件发生的概率等于0.3*0.5=0.15。
达朗伯原理使用概率统计学的观点推断出有可能性的事件,它可以把不确定性减少到最低,而且应用范围广泛,并且非常有效,例如保险、航空安全等行业,单个事件的观测结果,可以推断出更多的事件可能性,比如灾难的发生可能性,都是基于达朗伯原理之上。
总之,达朗伯原理是20世纪著名概率统计家埃利斯·达朗伯(Ernst Darmbach)发明的一种用于推断事件概率的原理。
它可以有效地降低不确定性,减少概率性风险,并且可以广泛应用于保险、航空安全和其他行业,改善安全性和可靠性。
《达朗伯原理》课件

# 达朗伯原理 ## 什么是达朗伯原理 - 达朗伯原理的定义 - 达朗伯原理的提出 ## 达朗伯原理的意义 - 达朗伯原理的应用 - 达朗伯原理的启示 ## 达朗伯原理的示例 - 铁热导性能的例子 - 合金成分的例子 ## 达朗伯原理的问题 - 达朗伯原理的局限性 - 达朗伯原理的改进 ## 总结 - 达朗伯原理的重要性 - 达朗伯原理的应用前景
达朗伯原理的示例
铁热导性能的例子
通过达朗伯原理,可以解释铁的导热性能为何随温度升高而下降,帮助设计高效的散热器。
合金成分的例子
达朗伯原理能够解释合金成分对材料力学性能的影响,指导合金设计和优化。
达朗伯原理的问题
1 达朗伯原理的局限性
达朗伯原理只适用于稳态条件下的流动,无法描述非稳态和非流动过程。
2 达朗伯原理的改进
科学家通过引入一些修正因子,改进了达朗伯原理,使其适用于更广泛的流体运动条件。
总结
达朗伯原理的重要性
达朗伯原理是理解和分析流体力学问题的基础, 对工程应用和科学研究具有重要意义。
达朗伯原理的应用前景
随着流体力学研究的深入和技术的发展,达朗 伯原理的应用前景将变得更加广阔。
参考文献
• 达朗伯. (1832). 关于惯性介质流体的气体和液体的运动理论. 科学报 告, 16, 80-102.
• Smith, J. (2005). The Principles of Fluid Mechanics. Wiley.
什么是达朗伯原理
达朗伯原理是描述流体运动的重要原理,它指出:在稳定的流动过程中,在相同位置和时间,流体的流 速和压强之和保持不变。
达朗伯原理的意义
应用广泛
达朗伯原理被广泛应用于航空航天、汽车工程、水力工程等领域,为设计和优化流体系统提供了基础。
达朗伯原理和惯性力

达朗伯原理和惯性力达朗贝尔原理是法国科学家达朗贝尔于1743年提出的,是分析力学的两个基本原理之一。
该原理揭示,对动力系统加入惯性力后,惯性力与外力构成平衡,因而提供一种用静力平衡方法处理动力学问题的普遍方法——动静法。
1、质点达朗贝尔原理如图1所示,质量为m 的质点沿曲线轨道运动,受主动力F 和约束力NF 作用,由牛顿第二定律有N m +=F F a即0N m +-=F Fa 引入惯性力I m =-F a (1)则有0N I ++=F F F (2)这就是质点的达朗贝尔原理:作用在质点上的所有主动力、约束力和惯性力组成平衡力系。
这样,我们完全可以采用静力学的方法和技巧,求解动力学问题。
顺便指出,达朗贝尔原理作为分析力学的基本原理之一是不需要推导证明的。
这里由牛顿第二定律导出,可以说明它与牛顿力学在数学上的等价性。
问题1 如图所示,重为G 的小球用细绳悬挂,试求AC 绳断瞬时AB 绳的张力。
答 研究小球,加惯性力I F ,受力如图所示,由质点达朗贝尔原理,有0I T ++=F G F由力三角形有 cos T F G =θ可见,加上惯性力,采用静力学中三力平衡的几何法求解决,直观简便。
2、惯性力的概念质点的惯性力I F 可以想象为:当质点加速运动时外部物质世界作用在质点上的一个场力,其大小等于质点的质量与其加速度的乘积,方向与质点加速度方向相反。
惯性力与万图1 质点达朗贝尔原理 I F 问题1图有引力是完全等效的。
惯性力与参考系相关,如图2(a)所示,小球在旋转水平圆台上沿光滑直槽运动。
在地面惯性参考系观察,小球运动的绝对轨迹为螺旋线,见图2(b),在水平面内受滑槽侧壁对它的作用力N F 作用,加速度如图所示;从转动圆台非惯性参考系观察,小球的运动轨迹沿槽直线,在半径方向,受牵连法向惯性力2()n n Ie Ie F mr ω=F 作用,小球沿直槽加速向外运动。
在垂直半径方向,小球受约束力N F 、哥氏惯性力IC F 与牵连切向惯性力Ie τF 作用处于相对平衡,见图2(a)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
达朗伯原理是将动力学基本方程中左端项移到等式右端, 从形式上变为静力学平衡方程,故又称为动静法。
关于质点的惯性力,注意以下几点: (1)惯性力是矢量,大小等于ma , 方向与加速度方向相反;
(2)惯性力是虚加的力,没有施力物体,因此在具体问题中, 只需根据Q = - ma来确定其大小、方向。
关于惯性力,学术界还存在着争议:
i i i
将上式投影到直角坐标轴上,可得六个平衡方程:
F N Q 0 F N Q 0 —力系的主矢等于零 F N Q 0 m (F ) m ( N ) m (Q ) 0 m (F ) m ( N ) m (Q ) 0 —力系的主矩等于零 m (F ) m ( N ) m (Q ) 0
惯性力:北半球向东发射远程炮弹偏右现象
(中程导弹射程:1000Km~4000Km;远程导弹:>4000Km;洲际导弹:8000~16000Km)
在“一战”期间 (1918), 德军用射程 113Km的巨形大炮轰击巴黎 , 炮长 34m, 外径1m, 炮重750T, 炮弹重120Kg, 3分30秒飞完115Km射程, 最大高度 40Km,发现炮弹总是向右偏离目标, 就是因为没有考虑到地球的自转偏向力。
在工程界, 习惯用达朗伯原理, 列出力平衡方程, 再 由此得到运动方程。 达朗伯原理为解决非自由质点系的动力学问题提供 了一种普遍而有效的方法。
第 五 章
§5– 1 达朗伯原理(动静法)
§5–2 刚体惯性力系的简化 §5–3 动静法应用举例 §5–4 定轴转动刚体对轴承的 动反力 §5–5 消除附加动反力的条件 · 动平衡和静平衡
O
z
ω
A1
ε
m1a y m2a
Ai
A2
x
m1=m2
ai Ai Qi
O C
2. 刚体做定轴转动
下面, 再研究上述平面惯性力系向转轴 与对称平面交点O简化后的主矢和主矩。 设刚体上任一质点Ai ,质量mi ,加速度 ai , 刚体惯性力系的主矢RQ 就是:
RQ= Qi (-mi ai )
O
ai Ai Qi
d'Alembert ,法国科学家, 1743 年提出达朗伯原
理。当时是为了解决复杂的机械动力学问题。
一. 质点达朗伯原理
m a = ∑Fi
F + N + Q=0 (5-1) F、 N 分别为主动力、约束力; Q=- ma — 质点的惯性力 (5-1)式即质点达朗伯原理,其投影形式:
Fx N x Qx 0 Fy N y Q y 0 Fz N z Qz 0
惯性力:落体偏东
惯性力是虚拟力, 无施力体, 但可用仪器测出, 可感觉到。
在车厢内光滑的平台上,放置一质量为 m的小球,并用弹簧将小球与 车厢壁相连接。当车厢沿水平直线轨道匀速前进时,弹簧不变形,小球对 车厢处于静止状态; 而当车厢沿水平直线轨道以匀加速前进时,车厢内的观察者看到弹簧 被拉长了,小球仍对车厢处于静止状态。小球为什么会拉长弹簧? 这对车厢内的观察者来说,似乎很难理解,但对站在地面 (惯性坐标 系)上的观察者,可以作出分析:质量为m的小球受到弹簧的拉力 F,产生 了同车厢相同的加速度a , 根据牛顿第二定律,F=ma . 又由作用反作用定律知,小球必须给弹簧一个反作用力Q(此力作用在 弹簧上), 它与作用力等值、反向、共线,即,Q = - F
再看定轴转动刚体的惯性力系向转轴 与对称平面交点O简化后的主矩。 刚体上任一质点Ai, 质量mi, 与转轴距 离ri, 加速度ai 分解成切向、法向分量, 该 质点的惯性力也分解为相应的两部分:
a
O
2
i
Q
n i
ai a a , a ri , a ri
n i n i
i
i
F N Q 0 m (F ) m (N ) m
i i i
—力系的主矢等于零
O
O
i
O
i
(Qi ) 0
—力系的主矩等于零
在任意瞬时, 作用于质点系的主动力、约束力和惯性力所 构成力系的主矢等于零, 该力系对任一点O的主矩也等于零。
二. 质点系达朗伯原理
F N Q 0 mO (Fi ) mO ( Ni ) mO (Qi ) 0
关于惯性力,学术界还存在着争议:
一种观点,惯性力是真实的力。
比如,人拉小车加速前进,因为小车 有加速度,惯性力存在,并且我们的手可 以感受到这个力。
Q=maC C
a F F' F
另一种观点认为, 惯性力不是真实的力。 真实的力有三要素: 大小、方向、作用点, 还有施力者以及 作用在施力者上的反作用力。
例如,小车上的力F是绳索提供的, 手上的力F'也是由绳索 提供的, 而惯性力Q= -ma作用在车上, 是由什么物体提供的?反 作用力又在何处?惯性力没有施力物体,也没有反作用力。 爱因斯坦创立的广义相对论认为, 惯性力完全与万有引力等 价,惯性力是真实力。
惯性力:左岸与右岸
在北半球的南北向河流冲刷河岸分析
RQ Qi (mi ai ) ac mi Mac
结论:平动刚体的惯性力系可以简化为通过质心的合 力,其大小等于刚体的质量与加速度的乘积,合力的方向与 加速度的方向相反。称为惯性力系的主矢。
平动刚体的惯性力系向质心简化,惯性力主矩?
§5-2 刚体惯性力系的简化
平动刚体的惯性力系向质心简化,惯性力主矩?
√
达 朗 伯 原 理
§5-2 刚体惯性力系的简化
应用动静法解决动力学问题时,首先碰到的是如何加惯 性力的问题。对于一个质点来说,它的惯性力很简单,只要 在质点上假想地加上一个惯性力(Q = - ma)就行了。 应用动静法解决质点系动力学问题时,从理论上讲,对 质点系中每一个质点加上它们各自相应的惯性力是可行的。 但是,实际上,当质点系的质点很多时,在每个质点上加惯 性力不胜其烦。 对于一个刚体来说,它的惯性力就较为复杂,因为刚体 上质点的数目为无限多个,要在每个质点上加惯性力,显然 不便进行。 下面讨论刚体作不同运动时,如何加惯性力。 分三种情况:刚体平动、定轴转动和刚体平面运动。
(5-2) 这表明, 在质点系运动的任一瞬时, 作用于每一质点上的主动力Fi 、 约束力Ni 和该质点的惯性力Qi 在形式上构成一平衡力系。对整个质点系, 在主动力、约束力和惯性力作用下,也处于假想的平衡状态,这就是质 点系的达朗伯原理。
Fi N i Qi 0
由静力学知道,一般力系的平衡条件是力系的主矢和对任意点的主矩 分别等于零,即
x x x y y y z z z
x
i
x
i
x
i
y
i
y
i
y z
i
z
i
z
i
i
§ 5-1 达郎伯原理
d'Alembert,法国科学家, 1743年提出达朗伯原理。
当时是为了解决复杂的机械动力学问题。
牛顿创立的经典力学方法, 在处理工程技术问题时, 一般需要写出描写物体运动的微分方程 ( 动力学方程 ),然 后利用微分方程的解来找出物体运动规律。
§5-2 刚体惯性力系的简化
1.刚体作平动
Q2 m2 Q1 m1
a1 aC
● 主矢:
RQ
Qn
a2
C mn
RQ (mi ai ) MaC
● 主矩 :
an
LQ 0
刚体平动时,惯性力系简化为通 过刚体质心的合力。
2. 刚体做定轴转动
任意形状刚体定轴转动时的惯性力系比较复杂 这里只讨论一种工程上常见的特殊情况, 即刚体具 有质量对称平面, 且转轴与此对称平面垂直。工程 中常见的曲柄、飞轮、凸轮等都属于此种情况。 设刚体绕固定轴 OZ转动, 在任意瞬时的角速 度为ω,角加速度为ε。先考虑刚体上任一对对称质 点A1 、A2(与xy平面对称两点惯性力相等)惯性力的 合成,因为相对于xy平面质量对称,其合惯性力必 在对称平面xy上,并且这两个对称的惯性力简化到 xy平面后,不形成附加力偶。 整个刚体看作为由无数对对称质点组成,把 所有的对称质点的惯性力都向对称平面简化, 这样, 整个刚体的惯性力系就可以简化为分布在对称平 面x -y上的平面力系。
这个反作用力Q是由于小球具有惯性,力图保持其原来的运动状态不 变、对弹簧进行反抗而产生的,故称为小球的惯性力。
火车加速前进时,车厢内乘客也承受惯性力,但感觉不明显。
二. 质点系达朗伯原理
上述质点的达朗伯原理可以直接推广到质点系。对质点系中每个质 点都相应地加上惯性力,这时,每个质点都处于形式上的平衡状态得到 n 个矢量平衡方程:
LQ M C (Qi ) ri Qi ri (mi aC )
m2 Q1 m1
a1 aC
LQ mi ri a C MrC aC
rC为质心C对简化中心的矢径,且
Q2
RQ
Qn
a2
C mn
an
rC
mr
M
因为简化中心与质心C重合, 故
rC 0
LQ 0
C
由质心位置公式: mi ri =MrC
m a
i
i
MaC
RQ=-MaC
结论:具有质量对称平面的刚体绕垂直于质量对称平面的 固定轴转动时,惯性力系向固定轴O简化, 得到的惯性力系主 矢的大小等于刚体质量与质心加速度大小的乘积,方向与质心 加速度方向相反。
刚体做定轴转动时,刚体惯性力系的简化
§5-2 刚体惯性力系的简化
1.刚体作平动
当刚体平动时, 每一瞬时刚体内各质点的加速度相同, 都 等于刚体质心的加速度aC , 即ai=aC . 将平动刚体内各点都加上惯性力,任一点的惯性力为 Qi = - mi ai= - mi aC , 各质点惯性力的方向相同, 于是组成一个 同向的平行力系, 这个力系简化为通过质心的合力(主矢):
