第4章 自变量中含有定性变量的回归分析
回归分析：探索变量之间的关系
回归分析：探索变量之间的关系引言回归分析是统计学中一种常用的数据分析方法，用于探索变量之间的关系。
它可以帮助我们理解一个或多个自变量对因变量的影响程度，并预测未来的结果。
本文将介绍回归分析的基本概念、原理和应用，以及常见的回归模型和评估方法。
第一章：回归分析的基本概念1.1 回归分析的定义回归分析是统计学中一种用于研究变量之间关系的方法。
它通过建立一个数学模型，描述自变量和因变量之间的关系，并利用数据对模型进行估计和预测。
1.2 回归分析的作用回归分析可以用于解决许多实际问题，例如预测销售额、评估市场需求、分析经济趋势等。
它可以帮助我们理解变量之间的关系，并提供决策依据。
第二章：回归分析的原理2.1 线性回归模型线性回归模型是回归分析中最常用的模型之一。
它假设自变量和因变量之间存在线性关系，并通过最小二乘法来估计模型的参数。
线性回归模型的数学表达式为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε，其中Y表示因变量，X1、X2、...、Xn表示自变量，β0、β1、β2、...、βn表示模型的参数，ε表示误差项。
2.2 模型的参数估计为了估计模型的参数，我们需要使用样本数据。
通过最小二乘法，我们可以最小化观测值与模型预测值之间的差异，从而得到最优的参数估计。
2.3 模型的拟合度模型的拟合度可以通过判定系数（R²）来评估。
判定系数表示模型预测值与实际观测值之间的相关程度，取值范围为0到1。
当判定系数接近1时，说明模型能够很好地解释观测值的变异；当判定系数接近0时，说明模型的解释能力较弱。
第三章：回归模型的应用3.1 单变量线性回归单变量线性回归是回归分析中最简单的模型。
它只包含一个自变量和一个因变量，可以用于探索两个变量之间的关系。
例如，我们可以使用单变量线性回归模型来研究温度与销售额之间的关系。
3.2 多变量线性回归多变量线性回归是回归分析中常用的模型之一。
它可以用于研究多个自变量对因变量的影响。
例解回归分析笔记(1-4章)
二、简单线性回归
只包含一个因变量 Y 和一个自变量 X 的回归为简单线性回归
Y=β0+β1X+ε
1.协方差与相关系数
对 Y 偏离其均值和 X 偏离其均值的乘积，可以计算二者的协方差，协方差会受到 度量单位的影响，因此在计算之前，先对数据进行标准化，即 Z 变换，标准化之 后的 Z 变量也称为 Z 分数，用该变量计算的协方差就是 Y 与 X 的相关系数，相关 系数具有对称性，因此相关系数矩阵也具有对称性。
7.模型的评价和选择 模型的有效性依赖于某些假设，我们需要不断地调整模型，以使模型满足这些假 设达到最优效果，整个过程是一个迭代的过程。
8.回归模型的应用 在拟合最佳模型之后，我们将应用此模型进行预测、或者评估单个变量的重要性、 了解变量之间的相互关系，总之，作为一种分析技术，大多数情况下确定回归方 程使其主要目标，但是拟合期间产生的任何结果，也都是有用的。
此外，关于自变量的取值也应注意，取值距离自变量均值越远，预测的标准误越 大，并且自变量与因变量之间的线性关系有可能不再成立，这点也需要注意。
5.模型拟合优度判断
一个回归模型的拟合优度判断可以通过以下几种方法进行，这些方法都是相关联 的，一般不会出现矛盾结果 （1）假设检验的 t 值，该值越大，说明 Y 与 X 的线性相关性就越强，拟合效果 越好 （2）观测值和预测值的散点图，这些点 （3）决定系数 R2，在简单线性回归中，其值等于相关系数的平方，这是比较重 要的判断拟合优度的指标，反映的是 Y 的总变差中能被自变量 X 所解释的比例， 值越大，说明拟合优度越好。
由于我们总能找到使铅直距离平方和达到最小的直线，因此最小二乘回归直线总 是存在的，但有时并不唯一。可以证明，最小二乘残差之和为 0。
报告中的变量选择和回归分析方法
报告中的变量选择和回归分析方法引言：报告中的变量选择和回归分析方法是数据分析和统计学中的重要内容。
在研究报告和学术论文中，合理选择变量和进行回归分析可以有效地揭示变量之间的关系，提高分析的准确性和可靠性。
本文将从六个方面对报告中的变量选择和回归分析方法进行详细论述。
一、变量选择的意义变量选择是指在进行回归分析时，从众多可能的自变量中选择出最为重要和相关的变量。
合理的变量选择可以减少冗余变量的存在，避免数据过拟合问题，并提高模型的预测能力和可解释性。
变量选择的意义在于提高研究的效率和有效性。
二、变量选择的方法1. 相关系数法：通过计算自变量与因变量之间的相关系数，选择与因变量关系最为密切的自变量。
相关系数法既简单又直观，但在多变量分析中无法考虑到变量之间的相互作用。
2. 正向选择法：从众多可能的自变量中，逐步添加具有显著影响力的变量，并根据模型的显著性检验去除不显著的变量。
正向选择法可以一步步剔除不相关的变量，但可能会错过一些有用的变量。
3. 逆向选择法：从包含所有自变量的模型开始，逐步去除不显著的变量，直到剩下的自变量都显著。
逆向选择法可以保留所有可能有用的变量，但可能出现模型过于复杂的问题。
三、回归分析的基本原理回归分析是通过建立数学模型，分析自变量对因变量的影响程度和方向。
常见的回归分析方法包括线性回归、多元回归、逻辑回归等。
回归分析需要满足一些基本的假设和前提，如线性关系、多元正态分布等。
四、回归分析的评价指标回归分析的结果需要进行评价，以判断模型的拟合程度和可靠性。
常用的评价指标包括判定系数（R平方）、均方根误差（RMSE）、残差等。
这些指标可以帮助研究者判断模型的准确性，并进行模型的改进和优化。
五、回归分析的解读和应用回归分析的结果需要进行解读，以揭示自变量与因变量之间的关系。
解读回归系数可以确定变量之间的正负相关关系，判断自变量对因变量的影响程度。
回归分析的应用广泛，可以用于预测、控制和优化等多个领域。
4-2虚拟变量回归分析汇总
平行回归模型的假定是斜率保持不变（加法类型， 包括方差分析）；
共点回归模型的假定是截距保持不变（乘法类型， 又被称为协方差分析）；
不同的回归的模型的假定是截距、斜率均为变动 的（加法、乘法类型的组合）。
当回归模型无截距项时，则可引入k个虚拟变量； 否则，就会陷入“虚拟变量陷阱
例： 分析某地区妇女的年龄、文化程度、及居住 地状况对其曾生子女数的影响。
定量变量: 年龄 定性变量:文化程度、地区
哑变量的建立
原变量编码值
文化程度=1（文盲） 文化程度=2（小学） 文化程度=3（初中） 文化程度=4（高中） 文化程度=5（大学） 地区=1（城市） 地区=2（农村）
D2 1,若X2 b D2 0,若X2 b
D1 0且D2 0, 若X2 c
有两个以上水平的虚拟自变量
Y 1 D 1 D 1 D 2 D 2 k X k
X2从c变为a的边际贡献
即从所有虚拟变量为0的状态， 变为该虚拟变量为1时的边际贡献
哑变量的建立
对于具有k类的定性变量来说，当回归模型有截 距项时，设哑变量时，我们只设k-1个哑变量。
6
3.098 32.759
Sig. .000a
Residual .851
9
.095
Total 19.438
15
a.Predictors: (Constant) , AREA, ED 3, 年 龄 , ED2, ED 4, E
b.Dependent Var iable: 生 子 女 数
SPSS输出结果
-. 39 9
第4章自变量中含有定性变量的回归分析
b. Dep enden t Vari able: 生 子 女 数
F 32.759
Si g. .000a
Coefficientsa
Unstandardized Coefficients
Model
1
(Constant)
年龄
B
Std. Error
1.409
.682
.068
.013
ED2
-1.127
.295
Sig. .087 .000 .005
引进虚拟变量时，回归方程可写为：
E(y) =0+ 1x1+ 2x2
• 女( x2=0)：E(y|女性) =0 +1x1
• 男(x2=1)：E(y|男性) =(0 + 2 ) +1x1
0的含义表示：女性职工的期望月工资收入
(0+ 2)的含义表示：男性职工的期望月工资收入
ED3
-1.309
.352
ED4 ED5 AREA
-1.576
.382
-1.569
.370
-.486
.162
a. Dep ende nt Vari able: 生 子 女 数
Standardized Coefficients
Beta
.569 -.399 -.514 -.558 -.616 -.220
则其几何图形如图2所示。
图2 不同年份消费倾向示意图
如果在模型中同时使用加法和乘法两种方式引入虚拟变量， 则回归线的截距和斜率都会改变。
例如：对于改革开放前后储蓄-收入模型，可设定为
Y
Yt 0 1Dt 1Xt 2 (Dt Xt ) t
回归分析的基本思想及其初步应用ppt
线性回归模型的评估是检验模型预测效果的重 要步骤。评估的指标包括模型的拟合优度、显 著性检验和预测精度等。
显著性检验可以通过F检验和t检验来实现，用于 检验模型的参数是否显著不为零。
03
非线性回归分析
多项式回归
04
回归分析的初步应用
经济预测
总结词
通过分析历史数据和相关经济指标，回归分 析可以预测未来的经济趋势和变化。
详细描述
回归分析在经济预测中应用广泛，例如，通 过分析历史GDP、消费、投资等数据，可以 预测未来经济增长速度、通货膨胀率等经济 指标。这种预测有助于企业和政府制定经济 政策，进行资源分配和投资决策。
结果解读
查看回归分析结果，包括系数、标 准误、显著性等。
03
02
线性回归分析
选择回归分析模块，设置自变量和 因变量。
模型评估
根据回归分析结果评估模型的性能 。
04
THANKS
感谢观看
05
回归分析的注意事项
数据质量
01
02
03
完整性
确保数据集中的所有观测 值都完整无缺，没有遗漏 或缺失的数据。
准确性
数据应准确无误，避免误 差或错误的测量和记录。
一致性
不同来源或不同时间点的 数据应具有一致的格式和 标准，以便进行比较和分 析。
过拟合与欠拟合
过拟合
模型在训练数据上表现良好，但 在测试数据上表现较差。原因是 模型过于复杂，导致对训练数据 的过度拟合。
它通过找出影响因变量的因素，并确 定这些因素对因变量的影响程度，来 预测因变量的取值。
回归分析的分类
含定性变量的回归模型
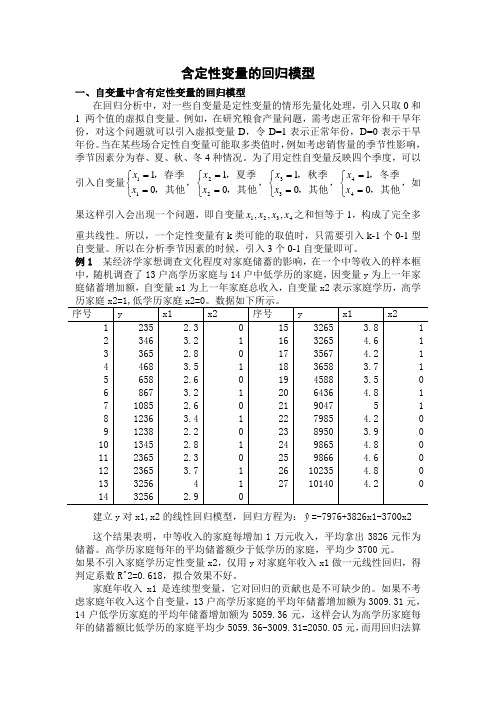
含定性变量的回归模型一、自变量中含有定性变量的回归模型在回归分析中，对一些自变量是定性变量的情形先量化处理，引入只取0和1 两个值的虚拟自变量。
例如，在研究粮食产量问题，需考虑正常年份和干旱年份，对这个问题就可以引入虚拟变量D ，令D=1表示正常年份，D=0表示干旱年份。
当在某些场合定性自变量可能取多类值时，例如考虑销售量的季节性影响，季节因素分为春、夏、秋、冬4种情况。
为了用定性自变量反映四个季度，可以引入自变量⎩⎨⎧==，其他，春季0111x x ，⎩⎨⎧==，其他，夏季0122x x ，⎩⎨⎧==，其他，秋季0133x x ，⎩⎨⎧==，其他，冬季0144x x ，如果这样引入会出现一个问题，即自变量4321,,,x x x x 之和恒等于1，构成了完全多重共线性。
所以，一个定性变量有k 类可能的取值时，只需要引入k-1个0-1型自变量。
所以在分析季节因素的时候，引入3个0-1自变量即可。
例1 某经济学家想调查文化程度对家庭储蓄的影响，在一个中等收入的样本框中，随机调查了13户高学历家庭与14户中低学历的家庭，因变量y 为上一年家庭储蓄增加额，自变量x1为上一年家庭总收入，自变量x2表示家庭学历，高学建立y 对x1,x2的线性回归模型，回归方程为：yˆ=-7976+3826x1-3700x2 这个结果表明，中等收入的家庭每增加1万元收入，平均拿出3826元作为储蓄。
高学历家庭每年的平均储蓄额少于低学历的家庭，平均少3700元。
如果不引入家庭学历定性变量x2，仅用y 对家庭年收入x1做一元线性回归，得判定系数R^2=0.618，拟合效果不好。
家庭年收入x1是连续型变量，它对回归的贡献也是不可缺少的。
如果不考虑家庭年收入这个自变量，13户高学历家庭的平均年储蓄增加额为3009.31元，14户低学历家庭的平均年储蓄增加额为5059.36元，这样会认为高学历家庭每年的储蓄额比低学历的家庭平均少5059.36-3009.31=2050.05元，而用回归法算出的数值是3824元，两者并不相等。
回归分析法概念及原理
回归分析法概念及原理回归分析是一种统计学方法，用于研究变量之间的关系，并用这些关系来预测或解释一个或多个因变量。
它可以帮助我们理解自变量与因变量之间的线性关系，并根据这种关系进行预测和解释。
回归分析的核心原理是建立一个线性方程来描述自变量和因变量之间的关系。
这个线性方程也称为回归方程。
回归方程的一般形式如下：Y=β0+β1X1+β2X2+...+βkXk+ε其中，Y表示因变量，X1、X2、..、Xk表示自变量，β0、β1、β2、..、βk表示模型的系数，ε表示误差项。
回归方程中，自变量的系数β表示因变量在自变量变化一个单位时的变化量。
例如，假设自变量为X1，系数β1为2，那么当X1增加1个单位时，因变量Y将增加2个单位。
回归分析的目标是通过拟合回归方程来估计模型的系数，并使用这些系数进行预测或解释。
常用的回归分析方法有最小二乘法和最大似然估计法。
最小二乘法是一种常用的回归估计方法。
它通过最小化实际观测值与回归方程预测值之间的误差平方和，来确定最佳的回归系数。
最小二乘法的优点是计算简单，并且能够提供估计系数的置信区间和显著性检验。
最大似然估计法是另一种常用的回归估计方法。
它通过寻找使得观测值出现的概率最大的回归系数来进行估计。
最大似然估计法的优点是可以处理更加复杂的模型，并且提供了参数的置信区间和假设检验。
在进行回归分析之前，需要满足一些基本的假设。
其中最重要的是线性性和正态性假设。
线性性假设指的是自变量和因变量之间的关系是线性的，正态性假设则指的是误差项ε服从正态分布。
在回归分析中，还需要评估模型的拟合优度。
常用的指标包括决定系数（R-squared）和调整决定系数（adjusted R-squared）。
决定系数表示回归方程对因变量变异的解释程度，取值范围从0到1，越接近1表示模型的拟合优度越好。
调整决定系数则对变量的个数进行了修正，避免过拟合。
回归分析有很多应用领域，例如经济学、社会学、生物学和工程学等。
含定性变量的回归模型
因变量是定性变量的回归模型
因变量只有两个可能结果，可用虚拟变量来表示。 定性因变量的回归方程的意义 设因变量是只取0，1两个值的定性变量，对于线性 回归模型 因变量均值 的意义 由于 是0－1型贝努利随机变量，则得概率分布
*
得
即有
由回归函数给定的因变量均值 是自 变量水平为 时 的概率。 定性因变量回归的特殊问题 离散非正态误差项 误差项 只取两个值：
*
该结果表明，中等收入的家庭每增加1万元收入，平均 拿出3826元作为储蓄。高学历家庭每年的平均储蓄额 少于低学历的家庭，平均少3701元。
两个自变量 与 的系数都是显著的，复决定系数 ，回归方程为
作 一元线性回归，得 说明拟合效果不好。 对 的一元回归残差 见表中。
*
使用虚拟变量需注意的问题
虚拟变量陷阱：若定性变量有k个类别，则引入k个虚拟变量将会产生完全多重共线性问题，避免方法： 只引入（k-1）个虚拟变量
*
自变量中含有定性变量的回归模型的应用
三.分段回归 【例9.2】用分段回归建立某工厂生产批量 与单位 成本 (美元)的回归模型。
引入虚拟自变量 ，将(2)式表示为多元线性回归 模型
记 则上式改写为
1
2
3
4
5
*
其中
由于c个自变量 之和恒等于1，存在完全共 线性。为此，剔除 ，建立回归模型
*
式回归方程显著性检验的原假设为
07
*
对定性变量数量化：只取0和1两个值的变量称 为虚拟变量。
*
虚拟变量的回归
含有一个虚拟自变量的回归
用虚拟自变量回归解决方差分析问题
因变量是定性变量的回归模型
Logistic回归模型
回归分析学习课件PPT课件
为了找到最优的参数组合，可以使用网格搜索方 法对参数空间进行穷举或随机搜索，通过比较不 同参数组合下的预测性能来选择最优的参数。
非线性回归模型的假设检验与评估
假设检验
与线性回归模型类似，非线性回归模型也需要进行假设检验，以检验模型是否满足某些统计假 设，如误差项的独立性、同方差性等。
整估计。
最大似然法
03
基于似然函数的最大值来估计参数，能够同时估计参数和模型
选择。
多元回归模型的假设检验与评估
线性假设检验
检验回归模型的线性关系 是否成立，通常使用F检 验或t检验。
异方差性检验
检验回归模型残差的异方 差性，常用的方法有图检 验、White检验和 Goldfeld-Quandt检验。
多重共线性检验
检验回归模型中自变量之 间的多重共线性问题，常 用的方法有VIF、条件指数 等。
模型评估指标
包括R方、调整R方、AIC、 BIC等指标，用于评估模 型的拟合优度和预测能力。
05
回归分析的实践应用
案例一：股票价格预测
总结词
通过历史数据建立回归模型，预测未来股票 价格走势。
详细描述
利用股票市场的历史数据，如开盘价、收盘价、成 交量等，通过回归分析方法建立模型，预测未来股 票价格的走势。
描述因变量与自变量之间的非线性关系，通过变 换或使用其他方法来适应非线性关系。
03 混合效应回归模型
同时考虑固定效应和随机效应，适用于面板数据 或重复测量数据。
多元回归模型的参数估计
最小二乘法
01
通过最小化残差平方和来估计参数，是最常用的参数估计方法。
加权最小二乘法
02
适用于异方差性数据，通过给不同观测值赋予不同的权重来调
定量分析方法之回归分析
定量分析方法之回归分析回归分析是定量分析的一种重要方法，用于研究两个或多个变量之间的关系。
它可以用来预测一个变量（因变量）如何随着其他变量（自变量）的变化而变化。
回归分析可以帮助我们理解这些变量之间的关系，以及预测未来的数据。
在本文中，我将详细介绍回归分析的原理、应用和如何进行回归分析。
回归分析的原理是建立一个数学模型来描述因变量和自变量之间的关系。
最常用的回归分析方法是线性回归分析，其中假设因变量与自变量之间存在线性关系。
也就是说，我们可以用一条直线来拟合数据，使得预测值与观察值之间的误差最小化。
我们可以用以下的数学模型来描述线性回归分析：Y=β0+β1X+ε，其中Y是因变量，X是自变量，β0和β1是回归系数，ε是误差项。
回归系数可以通过最小二乘法来估计，最小化误差平方和。
我们可以根据回归方程中的回归系数来解释自变量对因变量的影响。
回归分析可以应用于各种问题，包括经济学、金融学、市场营销、社会科学等。
例如，在经济学中，我们可以使用回归分析来研究GDP与就业率、通胀率之间的关系。
在市场营销中，我们可以使用回归分析来预测产品销售量与广告支出之间的关系。
回归分析还可以应用于预测未来的数据，例如预测股价、天气等。
进行回归分析的关键步骤包括数据收集、模型建立、模型评估和结果解释。
首先，我们需要收集数据，包括因变量和自变量的观察值。
然后，我们可以使用统计软件（如R、Python等）来建立回归模型。
在模型建立过程中，我们需要选择适当的自变量、确定回归形式（线性、非线性等）并评估模型的拟合程度。
模型评估通常包括计算回归系数、检验统计显著性和解释方差等。
最后，我们可以使用回归模型来解释结果，并进行预测和决策。
虽然线性回归是最常用的回归分析方法，但也有其他类型的回归模型可以应用于非线性关系，如多项式回归、逻辑回归、岭回归等。
这些模型在应对不同类型的数据和问题时具有更大的灵活性。
总之，回归分析是一种强大的定量分析方法，可以帮助我们理解和预测变量之间的关系。
含定性变量的回归模型-实用回归分析共78页
•
29、在一切能够接受法律支配的人类 的状态 中，哪 里没有 法律， 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律，也可以废除 法律。 ——塞·约翰逊
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
ห้องสมุดไป่ตู้
含定性变量的回归模型-实用回归分析
•
26、我们像鹰一样，生来就是自由的 ，但是 为了生 存，我 们不得 不为自 己编织 一个笼 子，然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理，即使延续时 间再长 ，也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
回归分析知识点总结
回归分析知识点总结一、回归分析的基本概念1.1 回归分析的概念回归分析是一种通过数学模型建立自变量与因变量之间关系的方法。
该方法可以用来预测数据、解释变量之间的关系以及发现隐藏的模式。
1.2 回归分析的类型回归分析主要可以分为线性回归和非线性回归两种类型。
线性回归是指因变量和自变量之间的关系是线性的，而非线性回归则是指因变量和自变量之间的关系是非线性的。
1.3 回归分析的应用回归分析广泛应用于各个领域，例如经济学、金融学、生物学、医学等。
在实际应用中，回归分析可以用于市场预测、风险管理、医疗诊断、环境监测等方面。
二、回归分析的基本假设2.1 线性关系假设线性回归分析假设因变量和自变量之间的关系是线性的，即因变量的变化是由自变量的变化引起的。
2.2 正态分布假设回归分析假设误差项服从正态分布，即残差在各个预测点上是独立同分布的。
2.3 同方差假设回归分析假设误差项的方差是恒定的，即误差项的方差在不同的自变量取值上是相同的。
2.4 独立性假设回归分析假设自变量和误差项之间是独立的，即自变量的变化不受误差项的影响。
三、回归分析的模型建立3.1 简单线性回归模型简单线性回归模型是最基础的回归分析模型，它只包含一个自变量和一个因变量，并且自变量与因变量之间的关系是线性的。
3.2 多元线性回归模型多元线性回归模型包含多个自变量和一个因变量，它可以更好地描述多个因素对因变量的影响。
3.3 非线性回归模型当因变量和自变量之间的关系不是线性的时候，可以使用非线性回归模型对其进行建模。
非线性回归模型可以更好地捕捉因变量和自变量之间的复杂关系。
四、回归分析的模型诊断4.1 线性回归模型的拟合优度拟合优度是评价线性回归模型预测能力的指标，它可以用来衡量模型对数据的拟合程度。
4.2 回归系数的显著性检验在回归分析中，通常需要对回归系数进行显著性检验，以确定自变量对因变量的影响是否显著。
4.3 多重共线性检验多重共线性是指自变量之间存在高度相关性，这可能导致回归系数估计不准确。
利用回归分析探究变量间的关系
利用回归分析探究变量间的关系回归分析是一种常用的统计方法，用于研究变量之间的关系。
通过回归分析，我们可以确定一个或多个自变量对因变量的影响程度，并建立数学模型来预测因变量的取值。
本文将介绍回归分析的基本原理，以及如何使用回归分析来探究变量间的关系。
一、回归分析的基本原理回归分析是一种建立因变量与自变量之间关系的统计模型的方法。
它基于一组观测数据，通过拟合一个数学模型来研究变量之间的关系。
回归分析的基本原理包括以下几个方面：1. 回归模型的选择：在进行回归分析之前，我们首先需要选择一个合适的回归模型。
常用的回归模型包括线性回归模型、多项式回归模型、逻辑回归模型等。
选择模型时需要考虑数据的性质和研究的目的。
2. 拟合模型：选择好回归模型后，我们需要通过计算来确定模型的参数。
拟合模型的过程通常采用最小二乘法，即寻找一组参数使得观测数据与模型预测值之间的残差平方和最小。
3. 模型评估：拟合好模型后，我们需要对模型进行评估，主要包括检验模型的显著性、拟合优度以及模型的预测能力等。
二、回归分析的应用案例回归分析在各个领域都有广泛的应用。
下面以实际案例来介绍回归分析在探究变量间关系方面的应用。
案例：销售额与广告投入之间的关系某电商平台想要了解广告投入对销售额的影响，他们收集了一段时间内的广告投入与销售额的数据。
他们使用回归分析来研究这两个变量之间的关系。
在这个案例中，广告投入是自变量，销售额是因变量。
通过回归分析，他们得到了如下的线性回归模型：销售额 = 1000 + 2 * 广告投入根据回归模型的拟合结果，可以解读出广告投入每增加1单位，销售额将增加2单位。
此外，他们还可以利用这个模型来预测不同广告投入下的销售额。
三、回归分析的局限性及注意事项尽管回归分析是一种常用的统计方法，但也存在一些局限性和注意事项，下面列举几点：1. 数据的质量：回归分析对数据的质量有一定要求，数据应当是完整、准确、可靠的。
同时还需要注意是否存在异乎寻常的离群值和异常值。
第四讲含定性自变量的回归模型与联立方程模型
第四讲含定性自变量的回归模型与联立方程模型一、含定性自变量的回归模型1、定性变量（虚拟变量）的概念一般的线性回归模型变量取值都有具体数值，然而实际问题中经常会碰到这样一些变量，如性别、职称、历史时期（计划经济或市场经济）等，它们不是用数值度量的，被称为定性变量。
含有定性变量的线性回归问题可分为自变量含定性变量和因变量含定性变量两种情况，由于后者比较复杂，有兴趣的同学可以自学。
我们这里只讨论含定性自变量的情况。
2、Eviews的操作解释变量中含有定性变量的问题比较简单。
Eviews的操作步骤与一般多元线性回归模型的建模过程基本相同，只需将定性变量看做一般数值变量操作即可。
而且含定性自变量的回归模型，其各种检验与一般线性回归模型相同。
例：为研究采取某项保险革新措施的速度Y对保险公司的规模X1和保险公司类型的关系，选取下列数据：Y是第i个公司采纳该项革新在时间上间隔的月数；X1是公司的总资产额（单位：百万美元）;X2是一个定性变量，表示公司类型，其中1表示股份公司，0表示互助公司。
数据资料见下表：二、联立方程模型 1、联立方程模型的概述联立方程模型至少含有两个待估计的方程，其一般形式为：(,,)t t t f y x βε=，1,2,,t T = 。
式中，t y 是t 时刻的内生变量向量；t x 是t 时刻的外生变量向量；β是待估计的未知参数向量，t ε是t 时刻的随机扰动项；T 表示样本的容量。
联立方程模型可能包含没有未知参数和扰动项的恒等方程，它们本身并不需要进行估计，但会作为一部分信息与其他方程一起参与整个模型的求解和分析。
联立方程模型有结构式模型与简化式模型，由于对联立方程结构模型参数直接进行OLS 估计会出现联立方程的偏倚，因此对联立方程结构模型的参数进行估计的基本思路是：把结构模型→简化模型→估计简化模型的参数→求解结构模型的参数（唯一解、多个解、无解）。
这种解的不同情况就是联立方程的识别问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
多元回归中的几种重要模型
• 第一部分：多重共线情况的处理
– 第3章 岭回归分析（ Ridge Regression ）
• 第二部分：自变量中含定性变量的处理 – 第4章 自变量中含有定性变量的回归分析 • 第三部分：因变量中含有定性变量情况的处理 – 第5章 二项Logistic回归 – 第6章 多项Logistic回归 – 第7章 有序回归（等级回归分析） – 第8章 Probit回归（概率单位回归） – 第9章 最佳尺度回归
0的含义表示：女性职工的期望月工资收入
(0+ 2)的含义表示：男性职工的期望月工资收入
1含义表示：工作年限每增加1年，男性或女性工资的平
均增加值
2含义表示：男性职工的期望月工资收入与女性职工的 期望月工资收入之间的差值 (0+ 2) - 0= 2
4.2 含多个虚拟自变量的回归
虚拟变量交互效应分析 • 当分析解释变量对变量的影响时，大多数情形只是分析了解 释变量自身变动对被解释变量的影响作用，而没有深入分析 解释变量间的相互作用对被解释变量影响。 • 前面讨论的分析两个定性变量对被解释变量影响的虚拟变量 模型中，暗含着一个假定：两个定性变量是分别独立地影响 被解释变量的 • 但是在实际经济活动中，两个定性变量对被解释变量的影响 可能存在一定的交互作用，即一个解释变量的边际效应有时 可能要依赖于另一个解释变量。 • 为描述这种交互作用，可以把两个虚拟变量的乘积以加法形 式引入模型。
a. Predi c t o rs: (Cons t a nt), AREA, ED3, 年 龄 , ED2, ED4, ED5
ANOVAb df 6 9 15 Mean Square 3.098 .095 F 32.759 Sig . .000a
Model 1
Reg ression Residual Total
Model 1 (Constant) X1 X2
ห้องสมุดไป่ตู้
ANOVAb Model 1 Sum of Squares 9000923 1475077 1.0E+07 df 2 7 9 Mean Square 4500461.300 210725.343 F 21.357 Sig. .001a
Regression Residual Total
• 本章总结
第4章 自变量中含有定性变量的回归分析
• 4.1 只有一个虚拟变量的回归
• 4.2 含有多个虚拟变量的回归
• 4.3 分段回归
第4章 自变量中含有定性变量的回归分析
• 在社会经济研究中，由许多定性变量，比如地区、民族、 性别、文化程度、职业和居住地等。 • 可以应用它们的信息进行线性回归。 • 但是，必须现将定性变量转换为虚拟变量（ (dummy variable)也称哑变量或定性变量），然后再将它们引入 方程，所得的回归结果才有明确的解释意义。 • 只取0和1两个值的变量称为虚拟变量。 • 对于具有k类的定性变量来说，设虚拟变量时，我们只 设k-1个虚拟变量。
在E(μt)=0的假定下，上述模型所表示的函数可化为: 正常年份： E(Ct X t , Dt 1) 0 (1 2 ) Xt 反常年份： E(Ct X t , Dt 0) 0 1 X t 假定2 0， 则其几何图形如图2所示。
图2 不同年份消费倾向示意图
• • 男(x=0)：E(y) =0—男学生考试成绩的期望值 女(x=1)：E(y) =0+ 1—女学生考试成绩的期望值
• •
注意：当指定虚拟变量0，1时
0 总是代表与虚拟变量值 0所对应的那个分类变量水平的
平均值
1 总是代表与虚拟变量值 1所对应的那个分类变量水平的
平均值与虚拟变量值 0所对应的那个分类变量水平的平均 值的差值，即
• 线性回归模型的基本假定
• 误差为独立正态分布的随机变量，其均值为零且方差相 等
（1）误差项的数学期望为0，表明估计的回归方程中不存在系统性 误差（Systematic Error）； （2）各误差项的方差相等； （3）各误差项之间的协方差为0；
以上三项基本假定一般又称为Gauss-Markov高斯-马尔柯夫条件。
1. 2.
回归模型中使用虚拟自变量时，称为虚拟自变量的回归 当虚拟自变量只有两个水平时，可在回归中引入一个虚 拟变量 – 比如，性别(男，女)
3.
一般而言，如果定性自变量有 k个水平/类别，需要在回 归中模型中引进k-1个虚拟变量，如果引入k个虚拟变量 将会产生完全多重共线性问题（称为虚拟变量陷阱）
建立回归方程：E(Y)=0+ 1x1+ 2x2+3x3（加法公式）
0—家电制造业投诉次数的平均值
(0+ 1)—零售业投诉次数的平均值
(0+ 2)—旅游业投诉次数的平均值
(0+ 3)—航空公司投诉次数的平均值
例：考虑个人保健支出对个人收入和教育水平的回归。教育水 平考虑三个层次：高中以下，高中，大学及其以上 • 这时需要引入两个虚拟变量：
按年龄划分为三个年龄组：6—18岁年龄组（中小学教育）；19—22岁 年龄组（大学教育）；其它年龄组。于是设定虚拟变量 D1= 1 0 6-18岁年龄组 其它 D2= 1 0 19-22年龄组 其它
则家庭教育经费支出模型可设定为 Yi 0 1 X i 2 D1i 3 D2i i 其中，Yi是第i个家庭的教育经费支出；Xi是第i个家庭的收人； 虚拟变量D1i、D2i分别表示第i家庭中是否有6—18岁和19—22岁的成员。
a. Predictors: (Constant), X2, X1
a b. Dependent Variable: Y Coefficients
dictors: (Constant), X2, X1
a.
Unstandardized Coefficients B Std. Error 930.495 466.974 387.616 62.565 1262.693 314.127
•
平均值的差值=(0+ 1) - 0= 1
【 例 2】 为
研究工资水 平与工作年 限和性别之 间的关系， 在某行业中 随 机 抽 取 10 名职工，所 得数据如右 表
Model Summary R R Square .927a .859 Adjusted Std. Error of R Square the Estimate .819 459.048
Sum of Squares 18.586 .851 19.438
a. Predic to rs: (Constant), AREA, ED3, 年 龄 , ED2, ED4, ED5 b. Dep endent Variable: 生 子女 数
Coefficientsa Unstandardized Coefficients B Std. Error 1.409 .682 .068 .013 -1.127 .295 -1.309 .352 -1.576 .382 -1.569 .370 -.486 .162 Standardized Coefficients Beta .569 -.399 -.514 -.558 -.616 -.220
4.1 只含一个虚拟自变量的回归
【例】为研究 考试成绩与性 别之间的关系 ，从某大学商 学院随机抽取 男女学生各8 名，得到他们 的市场营销学 课程的考试成 绩如右表
100
考试成绩
75
50
散点图
25
男 女
性别
考试成绩与性别的散点图
ˆ 66.875 14.875 x y
引进虚拟变量时，回归方程可写为：E(y) =0+ 1x
1 水平1 1 水平2 1 水平k 1 x1 , x2 ,, xk 1 0 其他水平 0 其他水平 0 其他水平
虚拟变量作为解释变量引入模型有两种基本方式： 加法方式和乘法方式。
（1）加法方式
引进虚拟变量
1 航空公司 1 零售业 1 旅游业 x1 , x2 , x3 0 其他行业 0 其他行业 0 其他行业
如果在模型中同时使用加法和乘法两种方式引入虚拟 变量，则回归线的截距和斜率都会改变。 例如：对于改革开放前后储蓄-收入模型，可设定为
Yt 0 1Dt 1 X t 2 ( Dt X t ) t
其中，Y为储蓄，X为收入，Dt为虚拟变量 1 改革开放以后 Dt= 0 改革开放以前
D1= 1 0 高中 其它 D2= 1 大学及其以上
0
其它
模型可设定如下：Yi 0 1 X i 2 D1i 3 D2i i
在 E(i ) =0的初始假定下，容易得到高中以下、高中、大学及其以上 教育水平个人平均保健支出的函数：
高中以下：
高中：
E(Yi|Xi，D1i=0，D2i=0)=β0+β1Xi E(Yi|Xi，D1i=1，D2i=0)=(β0+β2 )+β1Xi E(Yi|Xi，D1i=0，D2i=1)=(β0+β3 )+β1Xi
虚拟变量赋值的操作
所有EDU=0 EDU2=1,其他EDU=0 EDU3=1,其他EDU=0 EDU4=1,其他EDU=0 EDU5=1,其他EDU=0 AREA=1 AREA=0
应用SPSS建立回归方程
Model Summary Model 1 R .978a R Sq uare .956 Adjusted R Sq uare .927 Std. Error of the Estimate .30751