04-2转动定律(新)
4-2力矩转动定律转动惯量1

14
物理学
第五版
4-2 力矩 转动定律 转动惯量
练习 如图所示,圆盘的质量为m,半 径为R.求它对O’O’轴(即通过圆盘边缘且 平行于盘中心轴)的转动惯量.
O’
O
m
O’
O
第四章 刚体的转动
15
物理学
第五版
4-2 力矩 转动定律 转动惯量
4、刚体的转动惯量与以下三个因素有关: (1)与刚体的质量有关. (2)与刚体的质量分布有关. (3)与转轴的位置有关.
第四章 刚体的转动
10
物理学
第五版
4-2 力矩 转动定律 转动惯量
第四章 刚体的转动
11
物理学
第五版
4-2 力矩 转动定律 转动惯量
第四章 刚体的转动
12
物理学
第五版
4-2 力矩 转动定律 转动惯量
四 平行轴定理
质量为m 的刚体,
如果对其质心轴的转动 惯量为 JC ,则对任一与
该轴平行,相距为 d 的
第五版
4-2 力矩 转动定律 转动惯量
三 转动惯量
1、定义 J mjrj2 j
J r2dm
刚体的转动惯量等于刚体上各质点的质量 与各质点到转轴距离平方的乘积之和。
2、说明 转动惯量的单位:kg·m2
J 的意义:转动惯性的量度 .
第四章 刚体的转动
9
物理学
第五版
4-2 力矩 转动定律 转动惯量
转轴的转动惯量
d
C mO
JO JC md 2
第四章 刚体的转动
13
物理学
第五版
4-2 力矩 转动定律 转动惯量
几种均匀刚体的转动惯量
4-2力矩 转动定律 转动惯量
dm:质量元 dV :体积元
r dV
2 V
说明 刚体的转动惯量与以下三个因素有关:
(1)与刚体的体密度 有关.
(2)与刚体的几何形状(及体密度 的分 布)有关. (3)与转轴的位置有关.
例1、求长为L、质量为m的均匀细棒对图中不同轴的转动惯 量。 B A 解:取如图坐标,dm=dx X L L 2 2
m,l O
FN
θ
1 mgl sin J 2
式中
mg
1 2 J ml 3
3g sin 得 2l
由角加速度的定义
dω dω dω dθ ω dθ dt dθ dt 3g sin θdθ 有 ωdω 2l
3g 解得: ω (1 cos θ ) l
m,l O
y O Q
M 2.14 10 N m
12
二、 转动定律 (1)单个质点 m 与转轴刚性连接
z
M
O
Ft
Ft mat mr
M rF sin θ
M rFt mr
2
r
F
m Fn
M mr
2
(2)刚体 质量元受外力 Fej, 内力 Fij
M ij
rj
j
F ji
ij
O
M ji
d
iF ri
M ij M jiБайду номын сангаас
例1 有一大型水坝高110 m、长1 000 m , 水深100m,水面与大坝表面垂直,如图所 示. 求作用在大坝上的力,以及这个力对通 过大坝基点 Q 且与 x 轴平行的力矩 .
y
转动定律和转动惯量

实验一转动定律和转动惯量平动和转动是物体的两种基本的机械运动。
转动定律是描述物体定轴转动的基本定律,转动惯量是反映物体改变转动状态的惰性程度。
转动惯量是刚体转动时惯性大小的量度,是表明刚体特性的一个物理量。
刚体转动惯量除了与物体质量有关外,还与转轴的位置和质量分布(即形状、大小和密度分布)有关。
如果刚体形状简单,且质量分布均匀,可以直接计算出它绕特定转轴的转动惯量。
对于形状复杂,质量分布不均匀的刚体,计算将极为复杂,通常采用实验方法来测定,例如机械部件、电动机转子和枪炮的弹丸等。
【一】实验目的1.加深对转动惯量的感性认识和对转动定律的理解。
2.用扭摆测定几种不同形状物体的转动惯量和弹簧的扭转常数,并与理论值进行比较。
3.用实验方法学习平行轴定理。
4.巩固用作图法处理实验数据。
【二】实验原理扭摆的构造如图(1)所示,在垂直轴1上装有一根薄片状的螺旋弹簧2,用以产生恢复力矩。
在轴的上方可以装上各种待测物体。
垂直轴与支座间装有轴承,以降低磨擦力矩。
3为水平仪,用来调整系统平衡。
将物体在水平面内转过一角度θ后,在弹簧的恢复力矩作用下物体就开始绕垂直轴作往返扭转运动。
根据虎克定律,弹簧受扭转而产生的恢复力矩M与所转过的角度θ成正比,即:θKM-=(l)式中,K为弹簧的扭转常数。
根据转动定律有:图(1)图(1)βI M =式中,I 为物体绕转轴的转动惯量,β为角加速度,由上式得:IM=β (2) 令2KIω=,忽略轴承的磨擦阻力矩,由(1)、(2)得: θωθθβ222-=-==I Kdtd上述方程表示扭摆运动具有角简谐振动的特性,角加速度与角位移成正比,且方向相反。
此方程的解为:)cos(φωθ+=t A式中,A 振动的角振幅,φ为初相位角,ω为角速度。
此谐振动的周期为:22T πω==可得:224πT K I = (3)由(3)可知,只要实验测得物体扭摆的摆动周期,并在I 和K 中任何一个量己知时即可计算出另一个量。
4-2 刚体的定轴转动定律

解 (1) 用隔离法分 别对各物体作受力分析, 取如图所示坐标系.
A
FT1
PC
FC
mA
FN F T1 mA O x PA
C
FT2
mC
FT2
mB PB y
17
O
mB B
T1 mA a mB g T2 mBa
RT2 RT1 J a R
3)刚体内部的作用力对刚体的运动没有影响。 4)此公式可以推广到刚体一般的转动 M J
三、转动惯量 J 1转动惯量的物理意义 质点 F ma
质点惯性的量度
刚体
M J
因此,转动惯量是描述刚体在转动中的惯性大小的 物理量。 2 转动惯量的计算
J m r
k
2 k k
2
rk
若质量连续分布
J r dm
J r 2 dm
dm为质量元,简称质元。其计算方法如下:
质量为线分布
质量为面分布 质量为体分布
dm dl
dm ds
dm dV
面分布
其中、、分别 为质量的线密度、 面密度和体密度。
线分布
体分布
教材 表4-2 几种均匀刚体的转动惯量
21
解 细杆受重力和 铰链对细杆的约束力FN 作用,由转动定律得
m,l O
FN
θ
mg
1 mgl sin J 2
式中
1 2 J ml 3
3g sin 得 2l
22
由角加速度的定义
dω dω dθ dω ω dt dθ dt dθ
3g ωdω sin θdθ 2l
转动定理学习.pptx

即转动过程中角动量保持不变
这里可以有 J00 J11
但是 J 0 J1
在刚体碰撞等问题中,内力矩>>外力矩,角动 量保持不变。
第20页/共26页
例1 一根质量为 M ,长为l 的均匀细棒,可绕通
过棒中心的垂直轴 Z ,在 xy 平面内转 动。开始时 静止,今有质量为 m 的小球以速度 v0 垂直碰撞
撞,碰撞后与细棒一起绕
中心轴转动,求系统碰撞 v0
后的角速度
v0
•
J 1 ml2 3
解:系统的合外力矩为零,角动量守恒
mv0l mv0l 0 mvl mvl J
v l
代入上式
6v0
7l
第24页/共26页
直线运动与定轴转动规律对照
质点的直线运动
v dx dt
a
dv dt
d2 x dt2
一端固定在滑轮上(略去轮轴
处的摩檫,绳不可伸长不计质 M
量),另一端挂有一质量为m
的物体而下垂。
m
求:物体m 由静止下落h 高度 时的速度和此时轮的角速度。
h
第8页/共26页
解:①对象:刚体M、质点m
②受力分析:如图所示 ③依牛顿第二定律与转动定律列方程
(注意 T = T´ )
对物体有: mg - T = m a
量为m1和m2的物体1和2,m1< m2 如图所示。设滑轮的质量为m,
半径为r,滑轮所受的摩擦阻力矩
为M。设绳与滑轮之间无相对滑
动。试求物体的加速度和绳的张
力。
m1 m2
第11页/共26页
解:做受力分析图
m1 m2
m1< m2
4-2 力矩 转动定律 转动惯量

转动定律 转动惯量
FT1 = mA a mB g FT2 = mB a
RFT2 RFT1 = Jα a = Rα
FN
′ FT1
PC
FC
FT2
′ FT2
FT1 mB
O
mA
PA
O
x
第四章 刚体的转动
PB y
13
4-2 力矩 -
转动定律 转动惯量
解得: 解得:
mB g a= mA + mB + mC 2 mA mB g FT1 = mA + mB + mC 2
FT2 = mg ma2
第四章 刚体的转动
17
�
4-2 力矩 -
转动定律 转动惯量
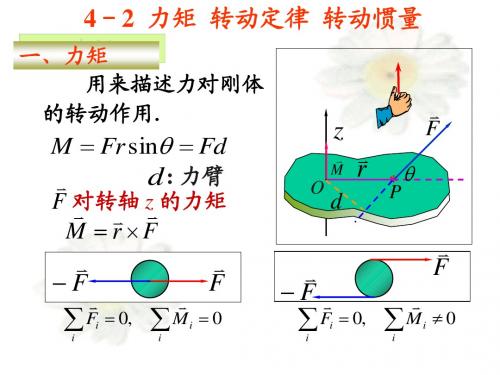
一
力矩
用来描述力对刚体 的转动作用. 的转动作用. F 对转轴 z 的力矩
z
M
F
M = r ×F M = Fr sin θ = Fd
O
r
*
d
P
θ
d : 力臂
F F
i i
∑ F = 0, ∑ M
i i
=0
F
i
F
i i
∑ F = 0, ∑ M
i
≠0
1
第四章
刚体的转动
4-2 力矩 -
9
4-2 力矩 -
转动定律 转动惯量
转动定律应用 M = Jα 说明 (1) ) 方向相同. M = Jα , α 与 M 方向相同.
(2) 为瞬时关系. ) 为瞬时关系. (3) 转动中 M = Jα与平动中F = ma ) 地位相同. 地位相同.
第四章
刚体的转动
10
4-2 力矩 -
大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量
v Fej
v Fij
2 j j
外力矩
∑M
j
+ ∑ M ij = ∑ ∆ m r α
j
Q Mij = −M ji
∴∑ Mij = 0
j
14
∑M
j
ej
= ( ∑ ∆ m j r )α
2 j
z
O
定义转动惯量
v rj ∆m j
v Fej
J = ∑ ∆m r J = r 2dm ∫
2 j j j
v Fij
转动定律 M = Jα 刚体定轴转动的角加速度与它所受的合 刚体定轴转动的角加速度与它所受的合 外力矩成正比 与刚体的转动惯量成反比. 成正比, 转动惯量成反比 外力矩成正比,与刚体的转动惯量成反比
L
9
设水深h,坝长L, 解 设水深 ,坝长 ,在坝面上取面积 元 dA = Ldy ,作用在此面积元上的力
dF = pdA = pLdy
y
y
x
h y O Q O
L
dA
dy
x
10
令大气压为 p0 ,则 p = p0 + ρg (h − y )
dF = PdA = [ p0 + ρg(h − y)]Ldy
r F
OZo ⊗
xc
θ
l
dm
xmg r
ω
α
r dm⋅ g
dω 3g cosθ α= = 2l dt dω dω dθ dω = ⋅ =ω dt dθ dt dθ
}
3g cosθ dθ ⇒ωdω = 2l
4
对刚体定轴转动: 对刚体定轴转动: 力矩M 的方向沿转轴(有正负) 力矩 的方向沿转轴(有正负) 多力作用在刚体上时的合力 的力矩: 的力矩: M = M1+M2+…+Mn 对刚体定轴转动: 对刚体定轴转动: 因力矩M 的方向沿转轴, 因力矩 的方向沿转轴,所以对转动 轴力矩矢量和变成为代数和 M2 M = M1 + M2 + … + Mn
转动定律讲解
v −F v −F
第四章 刚体的定轴转动
v F v F
v v ∑ Fi = 0 , ∑ M i = 0
圆盘静止不动
v v ∑ Fi = 0 , ∑ M i ≠ 0
圆盘绕圆心转动
力矩可以反映力的作用点的位置对物体运动的影响 力矩可以反映力的作用点的位置对物体运动的影响. 可以反映力的作用点的位置对物体运动的影响
v 铰链对细杆的约束力 F N
作用, 作用,由转动定律得
m l
v FN
l 2
1 mgl sin θ = Jα 2
第四章 刚体的定轴转动
θ
o
v P
4 – 2 力矩 转动定律 转动惯量
大学物理学
1 mgl sin θ = Jα 2 1 2 式中 J = ml 3 3g α = sin θ 得 2l 2l
第四章 刚体的定轴转动
大学物理学 4 – 2 力矩 转动定律 转动惯量 匀质细杆竖直放置, 例 一长为 l 质量为 m 匀质细杆竖直放置,其 相接,并可绕其转动. 下端与一固定铰链 O 相接,并可绕其转动 由于此竖 直放置的细杆处于非稳定平衡状态,当其受到微小扰 直放置的细杆处于非稳定平衡状态, 动时,细杆将在重力作用下由静止开始绕铰链O 转动. 动时,细杆将在重力作用下由静止开始绕铰链 转动 试计算细杆转动到与竖直线成 θ 角时的角加速度和角 速度. 速度 解 细杆受重力和
大学物理学
mg − T = ma y T ′R = Jα a y = Rα T = T ′ 2 J = m' R / 2
先文字计算求解, 文字计算求解, 带入数据求值. 后带入数据求值
m′
R o
m′
v T
m
o R
04-2转动定律(新)
F
M = r ×F M = r ×F
= r ×( F1 + F2 )
·
r
·
F2
= r × F1 + r × F2
只能引起轴的变形,而对 物体的转动效应无贡献。 在定轴转动问题中,如不讨论轴上受力,所考虑的 力矩是指力在转动平面内的分力对转轴的力矩。
如果多个外力同时作用在一个刚体上,(在此列 举三个外力)则它们的合外力矩情况如何呢? 外力F1在转动平面内进行分 解,切向分力矩 F1 r1 sin 对转动效果有贡献 同理:外力F2 .F3也能 进行矢量的分解,它 们的合外力矩为:
2
0
- f i cos i+F i cosj i )= △ m i r iω ( θ
2
负号说明与法向 加速度的方向相反
0
´ω
fi ri m △ i
切向分力:
f i sin i + F i sin j i = △ m i a i t θ
法向分力: - f i cos i - F i cosj i = △ m i r iω θ 法向分力是沿着矢径方向的 因此对刚体的转动效应无贡献
4 3 4 2
2
π
2
-
π
2
例题:计算刚体对垂直于纸面的0 轴的转动惯量(1)
半径为R、质量为M 的均匀圆盘,连接一根长为L、质量 为m 的均匀细棒(2)两根细棒长度分别为0.5L、质量 分别为m1、m2,连接在一起。
o
·
L m
Mo R
·
细棒和圆盘构成了系统 由转动惯量的可加性,转 动惯量是两部分所组成。
例题: 在图示的装置中滑轮可视作均质圆盘其半径
为r、质量为m 、滑轮两边悬挂重物质量分别为m1、m2 试求 :重物的加速度及绳子的张力。
42力矩转动定律转动惯量
dm ——质量线密度 dl
dm r dl
r1
m1
J mr 2
m2
(2)质量离散分布刚体的转动惯量 J m j rj2 m1r12 m2r22 (3)质量连续分布刚体的转动惯量
J r 2 dm
j
r2
r3m3转轴来自dm:质量元15
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
F :垂直于转轴的分力;
F F F
k
O
F
F
r
P
F
M r F 大小: M rF sin rd
方向: 右手螺旋法则
4
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
对于作定轴转动的刚体,一般规定: 如力矩使刚体沿逆时针方向转动,力矩为正; 如力矩使刚体沿顺时针方向转动,力矩为负; 讨论 1 力矩的三要素: (1)力的大小和方向; (2)力的作用点; (3)转轴位置 . 2. 若力F不在转动平面内: z
j
转动定律
M J
2 J m r jj 刚体的转动惯量:
刚体定轴转动的角 加速度与它所受的合外 力矩成正比 ,与刚体的 转动惯量成反比.
11
三 转动惯量 1. 物理意义 转动惯量与物体的惯性质量物理意义一致, 是物体转动惯性大小的量度。 2. 与转动惯量有关的因素: (3)转轴的位置; (2)质量分布; (1)刚体的总质量; 对所有质点求和:
j
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
m2
2
r3
m3
(3)质量连续分布刚体的转动惯量
J r 2 dm
转轴
dm:质量元
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M = r F sin θ
1. 力在转动平面内: ω F sin θ
0
力矩的方向判断
右手螺旋前进法则 F F cos θ
·
r
M
F r
·
θ
力矩的量值
M = r F sin θ
力矩量值的一般书写:
力矩的矢量式:
M = r ×F M = r F sin (r、 F)
2. 力不在转动平面内:
F
力矩的矢量式
点支△应设在离A 端35cm处 才能使该装置静止平衡。
二. 转动定律 研究刚体受外力矩作用时,外力矩与角加速度 之间的关系:刚体转动中的牛顿第二定律。
Fi 内力 fi 对△mi 质点进行
外力 受力分析并应用 牛顿第二定律有: 切向分力: 法向分力:
0
´ω
fi ri mi △
·
0
·j
θi
Fi
i
0
f i sinθ i + F i sin j i = △ m i a i t - f i cosθi - F i cosj i = △ m i r iω
2 2 圆盘
o
2
细棒
2
2
2
0
o
·
0.5L
m1
0.5L m2
2
同理:
J =J + J
0
杆1
杆2
L 1 m ( ) J = 3 2
杆1
1
L L 1 L +m( + ) J = m( ) 4 2 2 12
2
2 杆2
2
2
J =J + J
0
杆1
杆2
1 m L+ 7 m L = 12 12
2
1 2
2
转动定律和牛顿第二定律对照
法向分力是沿着矢径方向的 因此对刚体的转动效应无贡献 法向分力:
·
0
·
θi
ji
Fi
0
对切向分力进行数学处理:两边×
ri
ri f i sinθ i + ri F i sin j i = △ m i a i t ri
Σr f i sinθ i + Σr Fi sin j i =Σ △ m i a i t r
★
转动惯量小的刚体获 得的角加速度大,角速度改 变得快 ,保持原有转动状 态的惯性小。
决定转动惯量的三个要素:
(1)刚体的形状(2)质量分布(3)转轴的位置 见教材P95
决定转动惯量的三个要素:
(1)刚体的形状(2)质量分布(3)转轴的位置
0
·
0
ω
质量相同,但质量分布不同 转动惯量J 也不同。 ω
2 2
2
2
2
2
x = r cosj dy = r cosj dj ζ = m πr dS = 2x dy
2
y = r sin j
2
y
ω
dy
0
´
j
r
2
·x
0
y
x
1 dJ = dm( 2x ) = 1 ( ζ 2r cos j dj ) ( 2r cosj ) 12 12 2 = ζ r cos j dj 3 π 2 J = ζ r πcos j dj 3
1 2 3 4
能使它保持静止平衡?
20cm
B
m2
解:这类题目用力矩平
衡的方法就容易多了。
A
m1
m
· △
x
m3
m4
30cm
60cm
2kg 3kg 4kg 5kg
由的力矩定义
设:左端最小球处为A, 右端最大球处为B 并设:整个装置的支点△在 离细棒中心处为x 地方
画出各个小球的重力线:
M = r ×F
可列出下列方程
J = r dm
2
m ζ =π r ζ dm = 2 d r π R m m 2 r d r r d r =2 = π πR R m 2 r m d r r dr = J = R 1 mR 此结果作为经验 m 2 r = = 公式牢记! 2 R 4
2
R
设单位面积的质量为σ(面密度)
0
2
2
2
R
2
0
ω
·r
0
1 mr J= 4
2
· r
0
1 mr J= 2
2
´
´
转动惯量的计算 例题:如图所示 、求:整个装置 绕A点转动时的转动惯量。
4m
解:根据转动惯量计算的定义
ω
A
· m
L L L
L
J = mr
2m
2
J = r dm
2
本题不必用积分的形式求解 分别在3m和4m到A点 作辅助线得到r= 2 L
m x dJ = dm = x L dx m J = dJ = x L d x 1 mL = 3
2
2 L 2 0 2
dm = m dx L
线密度:单位 长度的质量
此结果作为经验 公式牢记!
例题:求质量为m 、半径为R 的均质 圆盘绕oo ´轴旋转的转动惯量。
0
´
ω
r
m dr
解:根据转动惯量计算的定义
i i
i
内力矩相互抵 消内力矩为0
外力矩之和
M
Jα
Σ r f i sinθ i +Σr Fi sin j i = Σ △ m i a i t r
i i
i
内力矩相互抵 消内力矩为0
a = rα M Σ ri f i sinθ i +Σ ri Fi sin j i = Σ △ m i a i t ri = Σ △ m i ri α
M
是矢量
物理单位: 牛顿· 米(N· m)
中学里的概念:力矩 =力×力臂 1. 力在转动平面内:
ω F sin θ
0
转动中心到力的作用 线的垂直距离。
M =Fd
F 经验告诉我们只有 切向分力对物体的 转动效应有作用。
·
r
·
θ
F cos θ
力在转动平面内 进行分解为切向 分力和法向分力
其力矩效果
Ft = F sin θ F = F cos θ
3
★当 M >0,合力矩的方向沿z 轴正方向。 ★当 M <0,合力矩的方向沿z 轴负方向。
当刚体是由n个质点所组成,它们之间内力矩情况是:
当刚体是由n 个质点 所组成,它们之间内 力矩情况是:
z
r3
· r
0
´θ 2 r2 F21
1
与F´ F´ 作为一个系统, 是一对内力,它们大小相等、方向相 反作用在一条直线上。∴ ´ = ´
2
外力矩之和
Jα
M = Jα
Jα
上式就是描述定轴转动的刚体,外力矩和角 加速度之间关系的: 转动定律
Σ
△m i ri 为一个新的物理量
2
转动惯量 J
转动定律的物理意义
M = Jα
刚体在绕定轴转动时,刚体的角加速度与它所受 的合外力矩成正比,与刚体的转动惯量成反比。 三.
转动惯量 J:
Σ △m i r
外力F 在转动平面内进行分 解,切向分力矩 F1 r1 sinθ 对转动效果有贡献。
1
z
r3
θ3
F2
θ2
·r
0
r2
1
同理:外力F .F 也能 进行矢量的分解,它 们的合外力矩为:
2 3
θ1
F3
-F1r1sin θ1
F1
M=-F r sinθ +F r sinθ +F r sinθ
1 1
1
2 2
2
3
3
2 2 2
3m
( 2 L) J = 3m +2m (2L) ( 2 L) + 4m = 22mL
2
例题:求质量为m 、长度为 L 的均质细杆绕00 ´ 轴旋转的转动惯量。
0
x
0
dx
L
解:根据转动惯量计算的定义
J = mr
2
´
ω
J = r dm
2
本题必须用积分的形式求解
取长度元dx,进而求出质量元dm。
合外力。使质点 运动状态改变。 质量。质点运动 惯性大小的量度
2
加速度。质 点运动速度 改变快慢的 一个物理量
v d r d a m m F= =m = dt dt
2
2
牛顿第二定律
ω =J d θ M =Ja = J d dt dt
合外力矩。使刚体 转动状态发生改变 转动惯量。刚体 转动惯性大小的 量度。三个要素
i
2
为一个新的物理量
单位 : Kg.m2
描述刚体在转动中转动惯性大小的量度 当物体几何形状、质量为规则 时,那么其转动惯量可写作: 当质量连续(可导)分布时:
J = mr
2
2 r = J dm
M = Jα
当以相同的力矩分别作用在 两个绕定轴转动的刚体时
★
转动惯量大的刚体获 得的角加速度小,角速度改 变得慢,保持原有转动状态 的惯性大。
ω0
0
ω
R
A
G
a0 F
f
§ 4-2 力矩 转动定律 转动惯量 刚体定轴转动的动力学: 研究刚体获得角加速度的原因和刚 体在转动过程中所遵循的牛顿第二 定律 转动定律。
一.
力矩
要使一个刚体进行绕轴转动,光有外力的 大小还不行,必须注意到外力的作用点的 位置和力的方向,即必须要有外力矩。 力矩物理符号:
20cm
A m1
m2
30cm
m
· △
