2022年中考数学压轴难题附答案

合集下载

2022届中考数学压轴题附答案

2022年中考数学压轴题1．如图1，抛物线y =14（x ﹣m ）2的顶点A 在x 轴正半轴上，交y 轴于B 点，S △OAB ＝1．（1）求抛物线的解析式；（2）如图2，P 是第一象限内抛物线上对称轴右侧一点，过P 的直线l 与抛物线有且只有一个公共点，l 交抛物线对称轴于C 点，连PB 交对称轴于D 点，若∠BAO ＝∠PCD ，求证：AC ＝2AD ；（3）如图3，以A 为顶点作直角，直角边分别与抛物线交于M 、N 两点，当直角∠MAN 绕A 点旋转时，求证：MN 始终经过一个定点，并求出该定点的坐标．解：（1）由题意和y =14（x ﹣m ）2设A （m ，0）当x ＝0时，y ═14（0﹣m ）2=m 24，即设B （0，m 24） ∴OA ＝m ，OB =m 24由S △OAB ＝1∴12•OA •OB ＝1，即m •m 24=2解得，m ＝2∴A （2，0），B （0，1）把y =14（x ﹣2）2化为一般式为，y =14x 2﹣x +1．（2）由（1）得抛物线对称轴为直线x ＝2．D 、C 两点在直线x ＝2上，则设C （2，n ），D （2，n '）如图2延长BA 交直线PC 于点Q 并设直线PC 交x 轴于点E ．∵∠BAO ＝∠PCD ，∠BOA ＝∠EAC ＝90°∴Rt △BOA ∽Rt △EAC∴∠BAO ＝∠ECA∴tan ∠BAO ＝tan ∠ECA =12∴AE AC =12 ∴AC ＝2AE又∵∠BAO ＝∠EAQ ，∠BAO ＝∠ECA∴∠ECA ＝∠EAQ又∵∠ECA +∠CEA ＝90°∴∠EAQ +∠QEA ＝90°∴BQ ⊥PC设直线AB 的解析式为y ＝kx +b ，把A （2，0），B （0，1）代入得，{0=2k +b 1=b 解得{k =−12b =1∴直线AB 的解析式为，y =−12x +1由BQ ⊥PC 设直线PC 的解析式为y ＝2x +b '．又∵过P 的直线l 与抛物线有且只有一个公共点∴令2x +b '═14（x ﹣2）2 整理得，x 2﹣12x +4﹣4b '＝0，且△＝0即144﹣4（4﹣4b '）＝0解得，b '＝﹣8∴直线PC 的解析式为，y ＝2x ﹣8．∴把点C（2，n）代入y＝2x﹣8中得，n＝2×2﹣8解得，n＝﹣4．∴C点坐标为（2，﹣4），即AC＝4由AC＝2AE得，AE＝2．把b’＝﹣8代入方程x2﹣12x+4﹣4b'＝0中得，x2﹣12x+36＝0解得，x1＝x2＝6再把x＝6代入y＝2x﹣8中得，y＝2×6﹣8解得，y＝4∴P（6，4）设直线PB解析式为y＝k'x+1把P（6，4）代入上式得，4＝6k'+1解得，k'=1 2∴直线PB的解析式为，y=12x+1又∵D（2，n'）在直线PB上，将其代入y=12x+1中得，n'=12×2+1＝2∴D点坐标为（2，2），即AD＝2∴AD＝AE∴AC＝2AD；（3）如图3中，以A为原点建立新的坐标系，则抛物线的解析式为y′=14x2，在新坐标系中设M（a，14a2），N（m，14m2）．∵AM⊥AN，∴14m 2m =−a 14a 2，∴ma ＝﹣16设直线MN 的解析式为y ′＝kx +b ，则有{ka +b =14a 2mk +b =14m2 解得：{k =14(a +m)b =−14ma ， ∵ma ＝﹣16，∴b ＝4，∴直线MN 的解析式为y ′=14（a +m ）x +4，∴直线MN 经过定点（0，4）（新坐标系中），在原来坐标系中，直线MN 经过点（2，4），∴直线MN 经过定点（2，4）．2．如图，直线y ＝﹣x +3与x 轴、y 轴分别交于B 、C 两点，抛物线y ＝﹣x 2+bx +c 经过点B 、C ，与x 轴另一交点为A ，顶点为D ．（1）求抛物线的解析式；（2）在x 轴上找一点E ，使EC +ED 的值最小，求EC +ED 的最小值；（3）在抛物线的对称轴上是否存在一点P ，使得∠APB ＝∠OCB ？若存在，求出P 点坐标；若不存在，请说明理由．解：（1）直线y ＝﹣x +3与x 轴、y 轴分别交于B 、C 两点，则点B 、C 的坐标分别为（3，0）、（0，3），将点B 、C 的坐标代入二次函数表达式得：{−9+3b +c =0c =3，解得：{b =2c =3，故函数的表达式为：y ＝﹣x 2+2x +3，令y ＝0，则x ＝﹣1或3，故点A （﹣1，0）；（2）如图1，作点C 关于x 轴的对称点C ′，连接CD ′交x 轴于点E ，则此时EC +ED 为最小，函数顶点D 坐标为（1，4），点C ′（0，﹣3），将C ′、D 的坐标代入一次函数表达式并解得：直线C ′D 的表达式为：y ＝7x ﹣3，当y ＝0时，x =37，故点E （37，0），则EC +ED 的最小值为DC ′=√1+(4+3)2=5√2；（3）①当点P 在x 轴上方时，如下图2，∵OB ＝OC ＝3，则∠OCB ＝45°＝∠APB ，过点B 作BH ⊥AP 于点H ，设PH ＝BH ＝m ，则PB ＝P A =√2m ，由勾股定理得：AB2＝AH2+BH2，16＝m2+（√2m﹣m）2，解得：m2＝8+4√2，则PB2＝2m2＝16+8√2则y P=√PB2−22=2+2√2；②当点P在x轴下方时，则y P＝﹣（2+2√2）；故点P的坐标为（1，2+2√2）或（1，﹣2﹣2√2）．3．如图，抛物线y＝ax2+bx+3√3与x轴交于A（﹣3，0），B（9，0）两点，与y轴交于点C，连接AC，BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q 沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ，过点Q作QD⊥x轴，与抛物线交于点D，连接PD与BC 交于点E．设点P的运动时间为t秒（t＞0）（1）求抛物线的表达式；（2）①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）．②在点P，Q运动的过程中，当PQ＝PD时，求t的值；（3）点M为线段BC上一点，在点P，Q运动的过程中，当点E为PD中点时，是否存在点M使得PM+12BM的值最小？若存在，请求出PM+12BM的最小值；若不存在，请说明理由．解：（1）将A（﹣3，0），B（9，0）代入y＝ax2+bx+3√3，得：{9a−3b+3√3=0 81a+9b+3√3=0，解得：{a=−√39b=2√33，∴抛物线的表达式为y=−√39x2+2√33x+3√3⋯①；（2）由题意得：∠ACO ＝∠OBC ＝30°，∠ACB ＝90°，将点B 、C （0，3√3）的坐标代入一次函数表达式并解得：直线BC 的表达式为：y =−√33x +3√3⋯②；①点P 的坐标为（﹣3+12t ，√32t ），点Q （9﹣2t ，0），将点Q 的坐标代入①式并整理得：点D [9﹣2t ，4√39（6t ﹣t 2）]； ②当PQ ＝PD 时，则DQ 中点的纵坐标＝点P 的纵坐标，即：12[4√39（6t ﹣t 2）]=√32t ，解得：t =154；（3）点P 的坐标为（﹣3+12t ，√32t ）、点D [9﹣2t ，4√39（6t ﹣t 2）]，点E 是PQ 的中点，则点E [3−34t ，√34t +2√39（6t ﹣t 2）]，将点E 的坐标代入②式并整理得：t 2﹣6t +9＝0，解得：t ＝3，即点P （−32，3√32）即点P 是AC 的中点，作点P 关于直线BC 的对称点P ′，过点P ′作P ′H ⊥x 轴、BC 于点H 、M ，过点P 作PN ⊥y 轴于点N ，则MH =12MB ，则此时，PM +12BM ＝PM +MH ＝P ′H 为最小值，∵∠ACB ＝90°，PC ＝P ′C ，∠P ′CM ＝∠NCP ，∠P ′MC ＝∠PNC ＝90°， ∴△P ′MC ≌△PNC （AAS ），∴MC ＝NC =12OC ，OM=32OC=9√32=P′H，故PM+12BM的最小值为9√32．。

2022届中考数学压轴题押题及答案解析

2022年中考数学压轴题1．如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0）、C（3，0），点B为抛物线顶点，直线BD为抛物线的对称轴，点D在x轴上，连接AB、BC．（1）如图1，若∠ABC＝60°，则点B的坐标为B（1，2√3）；（2）如图2，若∠ABC＝90°，AB与y轴交于点E，连接CE．①求这条抛物线的解析式；②点P为第一象限抛物线上一个动点，设△PEC的面积为S，点P的横坐标为m，求S关于m的函数关系式，并求出S的最大值；③如图3，连接OB，抛物线上是否存在点Q，使直线QC与直线BC所夹锐角等于∠OBD，若存在请直接写出点Q的坐标；若不存在，说明理由．解：（1）∵A（﹣1，O）、C（3，0），∴AC＝4∵直线BD为抛物线的对称轴，∴AB＝CB，BD⊥AC，AD＝CD＝2∴D（1，0），∵∠ABC＝60°，∴△ABC是等边三角形∴∠ABC＝60°，＝60°∴tan∠ABC=BDAD，即BD＝AD•tan∠ABC＝2tan60°＝2√3，∴B（1，2√3）；故答案为：B（1，2√3）；（2）①∵A（﹣1，0），C（3，0）∴AC＝4∵直线BD为对称轴∴AD＝CD=12AC＝2，AB＝BC∴D（1，0）∵∠ABC＝90°∴△ABC为等腰直角三角形∴B（1，2）设抛物线解析式为y＝a（x﹣1）2+2，图象过A（﹣1，0），则0＝a（﹣1﹣1）2+2，解得a=−1 2，∴y=−12（x﹣1）2+2，即y=−12x2+x+32；②如图2，过点P作PF⊥y轴于点F，则P（m，−12m2+m+32）∵AB＝BC，∠ABC＝90°∴∠BAC＝45°在Rt△AOE中，∠AOE＝90°，∴∠AEO＝∠EAO＝45°∴AO＝EO＝1∴E（0，1）∴S＝S四边形FPCO﹣S△PEF﹣S△CEO=12（m+3）（−12m2+m+32）−12m（−12m2+m+32−1）−12×1×3 =−34m2+2m+34=−34(m−43)2+2512∵−34＜0，∴当m=43时，S最大值=2512，∴S关于m的函数关系式为S=−34m2+2m+34，S的最大值为2512；③抛物线上存在点Q，使直线QC与直线BC所夹锐角等于∠OBD，如图3，在Rt△ABC中，∠ABC＝90°，AB＝BC，AC＝4∴△ABC是等腰直角三角形，AB＝BC＝2√2∵E（0，1）∴BE ＝AE =12BC ，即tan ∠BCE =BE BC =12∵tan ∠OBD =OD BD =12∴tan ∠BCE ＝tan ∠OBD ，即∠BCE ＝∠OBD 易求得直线CE 解析式为y =−13x +1，联立方程组{y =−13x +1y =−12x 2+x +32，解得{x 1=3y 1=0，{x 2=−13y 2=109；∴Q 1（−13，109）在直线AB 上截取BG =12BC ，∴tan ∠BCG =BG BC =12=tan ∠OBD ∴∠BCG ＝∠OBD ，过点G 作GL ⊥y 轴于L ，则△OAE ∽△LGE ∴GL OA=EL OE=EG AE=21∴GL ＝2OA ＝2，EL ＝2OE ＝2，OL ＝OE +EL ＝1+2＝3 ∴G （2，3）∴直线CG 解析式为y ＝﹣3x +9，解方程组{y =−3x +9y =−12x 2+x +32得{x 1=3y 1=0，{x 2=5y 2=−6 ∴Q 2（5，﹣6），综上所述，点Q 的坐标为：Q 1（−13，109），Q 2（5，﹣6）．2．如图，在平面直角坐标系中，抛物线y=12x2+bx+c交x轴正半轴于点A、点B，交y轴于点C，直线y＝﹣x+6经过点B、点C；（1）求抛物线的解析式；（2）点D在x轴下方的抛物线上，连接DB、DC，点D的横坐标为t，△BCD的面积为S，求S与t的函数关系式，并直接写出自变量t的取值范围；（3）在（2）的条件下，点E在x轴上方的抛物线上，过点E作EF⊥x轴，垂足为点F，连接DE，将射线ED沿直线EF折叠，得到对应射线EG，直线DF交射线EG于点H，当S＝12，EF=√5FH时，求点E的坐标．解：（1）在y＝﹣x+6中，令x＝0，得y＝6，∴C（0，6），令y＝0，得x＝6，∴B（6，0）将B（6，0），C（0，6）代入y=12x2+bx+c中，得{12×62+6b+c=0c=6，解得{b=−4c=6∴抛物线的解析式为：y=12x2−4x+6；（2）如图1，过点D作DL⊥BC于L，作DK∥y轴交BC于K，则∠DLK＝∠BOC＝90°，∵DK∥y轴∴∠DKL＝∠BCO∴∠DKL∽∠BCO∴DLDK =OBBC∴DL •BC ＝DK •OB∵D （t ，12t 2−4t +6），K （t ，﹣t +6）∴DK ＝﹣t +6﹣（12t 2−4t +6）=−12t 2+3t∴S =12DL •BC =12DK •OB =12×（−12t 2+3t ）×6=−32t 2+9t ，在y =12x 2−4x +6中，令y ＝0，得12x 2−4x +6=0，解得：x 1＝2，x 2＝6，∵点D 在x 轴下方的抛物线上，∴2＜t ＜6， ∴S =−32t 2+9t （2＜t ＜6）；（3）当S ＝12时，−32t 2+9t =12，解得：t 1＝2，t 2＝4，∵2＜t ＜6，∴t ＝4，∴D （4，﹣2）如图2，点E 在x 轴上方对称轴左侧时，过D 作DG ∥x 轴交射线EG 于G ，交EF 于R ，设E （m ，12m 2−4m +6），m ＜2，则F （m ，0），G （2m ﹣4，﹣2）∴直线DE 解析式为y =12（m ﹣4）x +6﹣2m ，直线GE 解析式为y =12（4﹣m ）x +m 2﹣6m +6 直线DH 解析式为y =2m−4x −2mm−4 ∵12（4﹣m ）×2m−4=−1∴GE ⊥DH∴∠EHG ＝∠ERD ＝90° ∵∠REG ＝∠RED ∴△EFH ∽△EDR ∴DR ER=FH EH，∵EF =√5FH ，∴EH ＝2FH∴ER ＝2DR ，即12m 2−4m +6+2＝2（4﹣m ），解得：m 1＝0，m 2＝4（舍去） ∴E 1（0，6）；如图3，点E 在x 轴上方对称轴右侧时，过D 作DG ∥x 轴交射线EG 于G ，交EF 于R ，设E （m ，12m 2−4m +6），m ＞6，与上述方法相同可得：ER ＝2DR ，即12m 2−4m +6+2＝2（m ﹣4），解得：m 1＝4（舍去），m2＝8，∴E2（8，6）；综上所述，点E的坐标为：E1（0，6），E2（8，6）．3．已知，在平面直角坐标系中，抛物线y=−12x2+2x﹣1与直线y＝﹣x﹣1相交于A，B两点，点C为顶点，连接AC．（1）如图1，连接BC，点P为线段AB上一动点，过点P作PE⊥x轴于点E，PF⊥BC 于点F，过点P作PQ∥x轴交抛物线于点Q（点Q在点P左侧），当PE•PF取得最大值时，在y轴上取一点R，连接QR，求PQ+2QR+√2RO的最小值；（2）如图2，将抛物线沿射线AC方向平移，记平移后的抛物线为y′，顶点为K，当AC＝CK时，点N为平移后的抛物线y′上一点，其横坐标为8．点M为线段AB上一点，连接CM，且CM＝BM，将△ACM绕点B顺时针旋转α度（0＜α＜180），旋转后的三角形为△A′C′M′，记直线A′C′与直线AB相交于点S，直线C′M′与直线AB相交于点T，连接NS，NT．是否存在点S和点T，使△C′ST为等腰三角形，若存在，请直接写出△NST的面积；若不存在，请说明理由．解：（1）由抛物线y =−12x 2+2x ﹣1=−12（x ﹣2）2+1得：C （2，1），解方程组{y =−12x 2+2x −1y =−x −1，得：{x 1=0y 1=−1，{x 2=6y 2=−7；∴A （0，﹣1），B （6，﹣7），过C 作CS ⊥y 轴于S ，过B 作BK ⊥y 轴于K ，则∠ASC ＝∠AKB ＝90° ∵CS ＝2，AS ＝1﹣（﹣1）＝2，BK ＝6，AK ＝﹣1﹣（﹣7）＝6 ∴AS ＝CS ，AK ＝BK∴△ACS 和△ABK 均为等腰直角三角形， ∴∠CAS ＝∠BAK ＝45°，AC ＝2√2，AB ＝6√2 ∴∠BAC ＝90°，BC =√AC 2+AB 2=4√5设P （m ，﹣m ﹣1），0≤m ≤6，则PE ＝﹣（﹣m ﹣1）＝m +1，PB =√2（6﹣m ）， ∵PF ⊥BC∴∠BFP ＝∠BAC ＝90° △BPF ∽△BCA ∴PF BP=AC BC=√24√5，∴PF =√55（6﹣m ） ∴PE •PF ＝（m +1）×√55（6﹣m ）=−√55（m −52）2+49√520，∵−√55＜0，∴当m =52时，PE •PF 取得最大值，此时，P （52，−72），∵PQ ∥x 轴∴Q （﹣1，−72），在x 正半轴上截取OG ＝OR ，连接RG ，过O 作OT ⊥RG 于T ，则RT =√22RO ，∵PQ +2QR +√2RO ＝PQ +2（QR +√22RO ）求PQ +2QR +√2RO 的最小值，即求QR +√22RO 的最小值，当Q ，R ，T 三点共线时，QR +√22RO 的值最小；∵∠ORG ＝45° ∴∠PQR ＝∠QRK ＝45° ∴QR =√2，RO =52， ∴PQ +2QR +√2RO 的最小值=52−（﹣1）+2（√2+√22×52）=7+9√22；（2）∵AC ＝CK ，∴K （4，3）∴平移后的抛物线为y ′=−12（x ﹣4）2+3， ∴N （8，﹣5）过点N 作NZ ⊥AB 于Z ，作NN ′∥x 轴交AB 于N ′，则∠NN ′Z ＝45°，N ′（4，﹣5） ∴NN ′＝8﹣4＝4，NZ =√22×4=2√2∵点M 为线段AB 上一点，且CM ＝BM ，设M （t ，﹣t ﹣1） ∴（t ﹣2）2+（﹣t ﹣1﹣1）2＝（t ﹣6）2+（﹣t ﹣1+7）2，解得：t =83∴M （83，−113）∴CM ＝BM =10√23，AM ＝AB ﹣BM =8√23∴AC ：AM ：CN ＝3：4：5，△C ′ST 为等腰三角形，可以分三种情形：①C ′T ＝ST ，如图2，作TL ⊥SC ′于L ，则∠TSC ′＝∠C ′＝∠ACM ，SL ＝LC ′=12SC ′， ∴sin ∠TSC ′＝sin ∠ACM =45，∵BA ′＝BA ＝6√2， ∴BS =BA′sin∠TSC′=6√245=15√22，∴S （−32，12），∵A′BA′S=tan ∠TSC ′＝tan ∠ACM =43，∴A ′S =34A ′B =9√22，SC ′＝A ′S +A ′C ′=13√22，SL =13√24， ∴ST =53SL =65√212∴S △NST =12ST •NZ =12×65√212×2√2=656， ②C ′S ＝C ′T ，如图3，作C ′H ⊥AB 于H ，作TL ⊥SC ′于L ，作NZ ⊥AB 于Z ，由①知AC ：AM ：CN ＝3：4：5，即：A ′C ′：A ′M ′：C ′M ′＝3：4：5， ∵TL ∥A ′M ′，∴C ′L ：LT ：C ′T ＝3：4：5，设C ′L ＝3k ，LT ＝4k ，C ′T ＝5k ∴C ′S ＝C ′T ＝5k ，LS ＝2k ，ST =√LS 2+LT 2=2√5k ，A ′S ＝5k ﹣2√2， ∵LT ∥A ′B∴A ′S ：A ′B ＝SL ：LT ＝1：2，即：2A ′S ＝A ′B ，2（5k ﹣2√2）＝6√2，解得：k =√2 ∴ST ＝2√5×√2=2√10 ∴S △NST =12ST •NZ =12×2√10×2√2=4√5； ③C ′S ＝ST ，如图4，作SB ⊥C ′T 于B ′，作TL ⊥SC ′于L ，作NZ ⊥AB 于Z ，则C ′B ′＝B ′T ，∠STC ′＝∠C ′＝∠ACM ∴SB′SC′=LT C′T =sin ∠ACM =45，设SB ′＝4t ，SC ′＝5t ，则C ′B ＝B ′T ＝3t ，ST ＝5t∴C ′L =35C ′T =185t ，SL ＝SC ′﹣C ′L =75t ，LT =245t ， ∵LT ∥BA ′ ∴SA′A′B=SL LT=724，24SA ′＝7A ′B∴24（5t ﹣2√2）＝7×6√2，解得：t =3√24 ∴ST =15√24 ∴S △NST =12ST •NZ =12×15√24×2√2=152，综上所述，△C ′ST 为等腰三角形时，△NST 的面积为：656或4√5或152．4．如图，在Rt △ABC 中，∠ACB ＝90°，D 为AB 边上的一点，以AD 为直径的⊙O 交BC 于点E ，交AC 于点F ，过点C 作CG ⊥AB 交AB 于点G ，交AE 于点H ，过点E 的弦EP 交AB 于点Q （EP 不是直径），点Q 为弦EP 的中点，连结BP ，BP 恰好为⊙O 的切线．（1）求证：BC 是⊙O 的切线．（2）求证：EF̂=ED ̂．（3）若sin ∠ABC ═35，AC ＝15，求四边形CHQE 的面积．（1）证明：连接OE ，OP ，∵AD 为直径，点Q 为弦EP 的中点，∴PE ⊥AB ，点Q 为弦EP 的中点，∴AB 垂直平分EP ，∴PB ＝BE ，∵OE ＝OP ，OB ＝OB ，∴△BEO ≌△BPO （SSS ），∴∠BEO＝∠BPO，∵BP为⊙O的切线，∴∠BPO＝90°，∴∠BEO＝90°，∴OE⊥BC，∴BC是⊙O的切线．（2）证明：∵∠BEO＝∠ACB＝90°，∴AC∥OE，∴∠CAE＝∠OEA，∵OA＝OE，∴∠EAO＝∠AEO，∴∠CAE＝∠EAO，̂=ED̂．∴EF（3）解：∵AD为的⊙O直径，点Q为弦EP的中点，∴EP⊥AB，∵CG⊥AB，∴CG∥EP，∵∠ACB＝∠BEO＝90°，∴AC∥OE，∴∠CAE＝∠AEO，∵OA＝OE，∴∠EAQ＝∠AEO，∴∠CAE＝∠EAO，∵∠ACE＝∠AQE＝90°，AE＝AE，∴△ACE≌△AQE（AAS），∴CE＝QE，∵∠AEC+∠CAE＝∠EAQ+∠AHG＝90°，∴∠CEH＝∠AHG，∵∠AHG＝∠CHE，∴∠CHE＝∠CEH，∴CH ＝CE ，∴CH ＝EQ ，∴四边形CHQE 是平行四边形，∵CH ＝CE ，∴四边形CHQE 是菱形，∵sin ∠ABC ═sin ∠ACG ═AG AC =35， ∵AC ＝15，∴AG ＝9，∴CG =√AC 2−AG 2=12，∵△ACE ≌△AQE ，∴AQ ＝AC ＝15，∴QG ＝6，∵HQ 2＝HG 2+QG 2，∴HQ 2＝（12﹣HQ ）2+62，解得：HQ =152，∴CH ＝HQ =152，∴四边形CHQE 的面积＝CH •GQ =152×6＝45．5．如图，△ABC 中，AB ＝AC ，⊙O 是△ABC 的外接圆，BO 的延长线交边AC 于点D ．（1）求证：∠BAC ＝2∠ABD ；（2）当△BCD 是等腰三角形时，求∠BCD 的大小；（3）当AD ＝2，CD ＝3时，求边BC 的长．（1）证明：连接OA．∵AB＝AC，̂=AĈ，∴AB∴OA⊥BC，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠ABD．（2）解：如图2中，延长AO交BC于H．①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC +∠C +∠BDC ＝180°，∴8∠ABD ＝180°，∴∠C ＝3∠ABD ＝67.5°．②若CD ＝CB ，则∠CBD ＝∠CDB ＝3∠ABD ， ∴∠C ＝4∠ABD ，∵∠DBC +∠C +∠CDB ＝180°，∴10∠ABD ＝180°，∴∠BCD ＝4∠ABD ＝72°．③若DB ＝DC ，则D 与A 重合，这种情形不存在．综上所述，∠C 的值为67.5°或72°．（3）如图3中，作AE ∥BC 交BD 的延长线于E ．则AE BC =AD DC =23， ∴AO OH =AE BH =43，设OB ＝OA ＝4a ，OH ＝3a ， ∵BH 2＝AB 2﹣AH 2＝OB 2﹣OH 2，∴25﹣49a 2＝16a 2﹣9a 2，∴a 2=2556，∴BH =5√24， ∴BC ＝2BH =5√22．。

2022届中考数学压轴难题押题附答案解析

2022年中考数学压轴题1．如图1，△AOB 的三个顶点A 、O 、B 分别落在抛物线F 1：y =13x 2+73x 的图象上，点A 的横坐标为﹣4，点B 的纵坐标为﹣2．（点A 在点B 的左侧）（1）求点A 、B 的坐标；（2）将△AOB 绕点O 逆时针旋转90°得到△A 'OB '，抛物线F 2：y ＝ax 2+bx +4经过A '、B '两点，已知点M 为抛物线F 2的对称轴上一定点，且点A '恰好在以OM 为直径的圆上，连接OM 、A 'M ，求△OA 'M 的面积；（3）如图2，延长OB '交抛物线F 2于点C ，连接A 'C ，在坐标轴上是否存在点D ，使得以A 、O 、D 为顶点的三角形与△OA 'C 相似．若存在，请求出点D 的坐标；若不存在，请说明理由．解：（1）当x ＝﹣4时，y =13×（﹣4）2+73×（﹣4）＝﹣4∴点A 坐标为（﹣4，﹣4）当y ＝﹣2时，13x 2+73x ＝﹣2 解得：x 1＝﹣1，x 2＝﹣6∵点A 在点B 的左侧∴点B 坐标为（﹣1，﹣2）（2）如图1，过点B 作BE ⊥x 轴于点E ，过点B '作B 'G ⊥x 轴于点G∴∠BEO ＝∠OGB '＝90°，OE ＝1，BE ＝2∵将△AOB 绕点O 逆时针旋转90°得到△A 'OB '∴OB ＝OB '，∠BOB '＝90°∴∠BOE +∠B 'OG ＝∠BOE +∠OBE ＝90°∴∠B 'OG ＝∠OBE在△B 'OG 与△OBE 中{∠OGB′=∠BEO ∠B′OG =∠OBE B′O =OB∴△B 'OG ≌△OBE （AAS ）∴OG ＝BE ＝2，B 'G ＝OE ＝1∵点B '在第四象限∴B '（2，﹣1）同理可求得：A '（4，﹣4）∴OA ＝OA '=√42+42=4√2∵抛物线F 2：y ＝ax 2+bx +4经过点A '、B '∴{16a +4b +4=−44a +2b +4=−1 解得：{a =14b =−3∴抛物线F 2解析式为：y =14x 2﹣3x +4∴对称轴为直线：x =−−32×14=6 ∵点M 在直线x ＝6上，设M （6，m ）∴OM 2＝62+m 2，A 'M 2＝（6﹣4）2+（m +4）2＝m 2+8m +20∵点A '在以OM 为直径的圆上∴∠OA 'M ＝90°∴OA '2+A 'M 2＝OM 2∴（4√2）2+m 2+8m +20＝36+m 2解得：m ＝﹣2∴A 'M =√m 2+8m +20=√4−16+20=2√2∴S △OA 'M =12OA '•A 'M =12×4√2×2√2=8（3）在坐标轴上存在点D ，使得以A 、O 、D 为顶点的三角形与△OA 'C 相似．∵B '（2，﹣1）∴直线OB '解析式为y =−12x{y =−12x y =14x 2−3x +4 解得：{x 1=2y 1=−1（即为点B '）{x 2=8y 2=−4 ∴C （8，﹣4）∵A '（4，﹣4）∴A 'C ∥x 轴，A 'C ＝4∴∠OA 'C ＝135°∴∠A 'OC ＜45°，∠A 'CO ＜45°∵A （﹣4，﹣4），即直线OA 与x 轴夹角为45°∴当点D 在x 轴负半轴或y 轴负半轴时，∠AOD ＝45°，此时△AOD 不可能与△OA 'C 相似∴点D 在x 轴正半轴或y 轴正半轴时，∠AOD ＝∠OA 'C ＝135°（如图2、图3） ①若△AOD ∽△OA 'C ，则OD A′C =OA OA′=1 ∴OD ＝A 'C ＝4∴D （4，0）或（0，4）②若△DOA ∽△OA 'C ，则DO OA′=OA A′C =4√24=√2∴OD =√2OA '＝8∴D （8，0）或（0，8）综上所述，点D 坐标为（4，0）、（8，0）、（0，4）或（0，8）时，以A 、O 、D 为顶点的三角形与△OA 'C 相似．2．四边形的一条对角线将这个四边形分成两个三角形，如果这两个三角形相似（不全等），那么我们将这条对角线叫做这个四边形的相似对角线．（1）如图1，四边形ABCD中，∠DAB＝100°，∠DCB＝130°，对角线AC平分∠DAB，求证：AC是四边形ABCD的相似对角线；（2）如图2，直线y=−√33x+4√33分别与x，y轴相交于A，B两点，P为反比例函数y=kx（k＜0）上的点，若AO是四边形ABOP的相似对角线，求反比例函数的解析式；（3）如图3，AC是四边形ABCD的相似对角线，点C的坐标为（3，1），AC∥x轴，∠BCA＝∠DCA＝30°，连接BD，△BCD的面积为√3．过A，C两点的抛物线y＝ax2+bx+c （a＜0）与x轴交于E，F两点，记|m|＝AC+1，若直线y＝mx与抛物线恰好有3个交点，求实数a的值．解：（1）如图1，设∠ACD＝α，则∠ACB＝130°﹣α，∴∠B＝180°﹣∠BAC﹣∠ACB＝180°﹣50°﹣（130°﹣α）＝α，在△ABC和△ACD中，∠B＝∠ACD，∠BAC＝∠CAD，∴△ABC∽△ACD，∴AC是四边形ABCD的相似对角线；（2）①当∠APO为直角时，当∠OAP＝30°时，过点P作PH⊥x轴于点H，设OH＝x，则HP=√3x，HA＝3x，则x+3x＝4，解得：x＝1，故点P（1，−√3），故k=−√3；当∠AOP＝30°时，同理可得：k＝﹣3√3；②当∠OAP为直角时，当∠OP A＝30°时，点P（4，﹣4√3），k＝﹣16√3；当∠AOP＝30°时，同理可得：k=−16√33（舍去）；综上，反比例函数的表达式为：y=−√3x或y=−3√3x或y=−−16√3x；（3）如图3，过点B作BH⊥CD于点H，则∠CBH＝90°﹣∠BCD＝30°，故CH=12BC，则BH=√32BC，△BCD的面积=12CD•BH=12×CD×√32CB=√3，故CD•BC＝4而△BAC∽△ACD，故CA2＝BC•CD＝4，故CA＝2，则点A（1，1），而点C（3，1），将点A、C的坐标代入抛物线表达式并解得：抛物线的表达式为：y＝ax2﹣4ax+3a+1，AC＝2，则m＝±3，故直线的表达式为：y＝±3x，直线y＝﹣3x与抛物线有两个交点，而直线y＝mx与抛物线恰好有3个交点，则直线y＝3x与抛物线有一个交点，联立直线y＝3x与抛物线的表达式并整理得：ax2﹣（4a+3）x+3a+1＝0，△＝（4a+3）2﹣4a（3a+1）＝0，解得：a=−12或−92；此外，当抛物线过原点时，直线和抛物线也有三个交点，即3a+1＝0，解得：a=−1 3；综上，a=−12或−92或−13．3．在平面直角坐标系中，抛物线y＝ax2﹣4ax+3a的最高点的纵坐标是2．（1）求抛物线的表达式；（2）将抛物线在1≤x≤4之间的部分记为图象G1将图象G1沿直线x＝1翻折，翻折后图象记为G2，图象G1和G2组成G，直线l：y＝kx+k和图象G在x轴上方的部分有两个公共点，求k的取值范围；（3）直线θ：y＝kx+k与图象G在x轴上方的部分分别交于A、M、P、Q四点，若AM ＝2PQ，求k的值．解：（1）函数的对称轴为：x＝2，将顶点坐标（2，2）代入二次函数表达式得：2＝4a﹣8a+3a，解得：a＝﹣2，故抛物线的表达式为：y＝﹣2x2+8x﹣6…①；（2）抛物线的表达式为：y＝﹣2x2+8x﹣6…②；则翻折后图象表达式为：y＝﹣2x2+2，顶点C1的坐标为（0，2），如图1，作过点A、C1直线l1，过点A作右侧图形的切线l2，直线l1：k＝2，直线l2：y＝kx+k…③，将直线l2的表达式与右侧函数表达式联立并整理得：2x2+（k﹣4）x+k+6＝0，由题意得：△＝（k﹣8）2﹣8（k+6）＝0，解得：k＝12±8√2（舍去正值），唯一符合条件的点可能在l1、l2之间（含直线），由于点A在x轴上，不属于x轴上方，故符合条件的只有l2的位置，不存在范围，即k的范围为：12﹣8√2＜k＜4；（3）设直线l于图象G交点A、M、P、Q交点的横坐标为x、x1、x3、x4，将直线l的表达式图象G2的表达式联立并整理得：2x2+kx+（k﹣2）＝0，则x+x1=−k2，则x1＝1−12k，则x 1﹣x ＝2−12k ，同理可得：x 2+x 3=8−k 2，x 3x 2=k+62，则|x 3﹣x 2|=√(x 2+x 3)2−4x 2x 3=√k 2−24k+164， ∵AM ＝2PQ ，∴x 2﹣x ＝2（x 3﹣x 2），即4（√k 2−24k+164）2＝（2−12k ）2，解得：k =44−16√73． 4．如图，半径为4的⊙O 中，弦AB 的长度为4√3，点C 是劣弧AB̂上的一个动点，点D 是弦AC 的中点，点E 是弦BC 的中点，连接DE 、OD 、OE ．（1）求∠AOB 的度数；（2）当点C 沿着劣弧AB̂从点A 开始，逆时针运动到点B 时，求△ODE 的外心P 所经过的路径的长度；（3）分别记△ODE ，△CDE 的面积为S 1，S 2，当S 12﹣S 22＝21时，求弦AC 的长度．解：（1）如图1中，过点O 作OH ⊥AB 于H ．∵OA ＝OB ＝4，OH ⊥AB ，∴AH ＝HB =12AB ＝2√3，∠AOH ＝∠BOH ，∴sin ∠AOH =AH AO =√32，∴∠AOH ＝60°，∴∠AOB＝2∠AOH＝120°．（2）如图2中，连接OC，取OC的中点P，连接DP，∵OA＝OC＝OB，AD＝DC，CE＝EB，∴OD⊥AC，OE⊥CB，∴∠ODC＝∠OEC＝90°，∴∠ODC+∠OEC＝180°，∴O，D，C，E四点共圆，∴OC是直径，∴OC的中点P是△OED的外接圆的圆心，∴OP=12OC＝2，∴点P在以O为圆心，2为半径的圆上运动，∵∠AOB＝120°，∴点P的运动路径的长=120⋅π⋅2180=4π3．（3）当点C靠近A点时，如图3中，当AC＜BC时，连接OC交AB于J，过点O作OH⊥AB于H，过点C作CK ⊥AB于K．∵AD＝CD，CE＝EB，∴DE∥AB，AB＝2DE，∴△CDE ∽△CAB ，∴S △CDES △CAB =（DE AB ）2=14， ∴S △ABC ＝4S 2，∵S △ADO ＝S △ODC ，S △OBE ＝S △OEC ， ∴S 四边形ODCE =12S 四边形OACB ，∴S 1+S 2=12（4S 2+4√3）＝2S 2+2√3， ∴S 1＝S 2+2√3，∵S 12﹣S 22＝21，∴S 22+4√3S 2+12﹣S 22＝21，∴S 2=3√34， ∴S △ABC ＝3√3=12×AB ×CK ， ∴CK =32， ∵OH ⊥AB ，CK ⊥AB ，∴OH ∥CK ，∴△CKJ ∽△OHJ ，∴CK OH=CJ OJ ， ∴CJ OJ =322=34，∴CJ =37×4=127，OJ =47×4=167， ∴JK =√CJ 2−CK 2=√(127)2−(32)2=3√1514，JH =√OJ 2−OH 2=√(167)2−22=2√157， ∴KH =√152，∴AK ＝AH ﹣KH ＝2√3−√152，∴AC =√AK 2+CK 2=(2√3−√152)2+(32)2=√18−6√5=√15−√3．当AC ＞BC 时，同法可得AC =√15+√3，同理，当点C 靠近B 点时，可知AC =(2√3+√152)2+(32)2=√15+√3．综上所述，满足条件的AC 的值为√15±√3．5．已知⊙O 1的半径为r 1，⊙O 2的半径为r 2．以O 1为圆心，以r 1+r 2的长为半径画弧，再以线段O 1O 2的中点P 为圆心，以12O 1O 2的长为半径画弧，两弧交于点A ，连接O 1A ，O 2A ，O 1A 交⊙O 1于点B ，过点B 作O 2A 的平行线BC 交O 1O 2于点C ．（1）求证：BC 是⊙O 2的切线；（2）若r 1＝2，r 2＝1，O 1O 2＝6，求阴影部分的面积．（1）证明：连接AP ，∵以线段O 1O 2的中点P 为圆心，以12O 1O 2的长为半径画弧， ∴O 1P ＝AP ＝O 2P =12O 1O 2，∴∠O 1AO 2＝90°，∵BC ∥O 2A ，∴∠O 1BC ＝∠O 1AO 2＝90°，过点O 2作O 2D ⊥BC 交BC 的延长线于点D ，∴四边形ABDO 2是矩形，∴AB ＝O 2D ，∵O 1A ＝r 1+r 2，∴O 2D ＝r 2，∴BC 是⊙O 2的切线；（2）解：∵r 1＝2，r 2＝1，O 1O 2＝6，∴O1A=12O1O2，∴∠AO2C＝30°，∵BC∥O2A，∴∠BCE＝AO2C＝30°，∴O1C＝2O1B＝4，∴BC=√O1C2−O1B2=√42−22=2√3，∴S阴影=S△O1BC −S扇形BO1E=12O1B⋅BC−60π×r12360=12×2×2√3−60×π×22360=2√3−23π．。

2022届中考数学压轴难题附答案

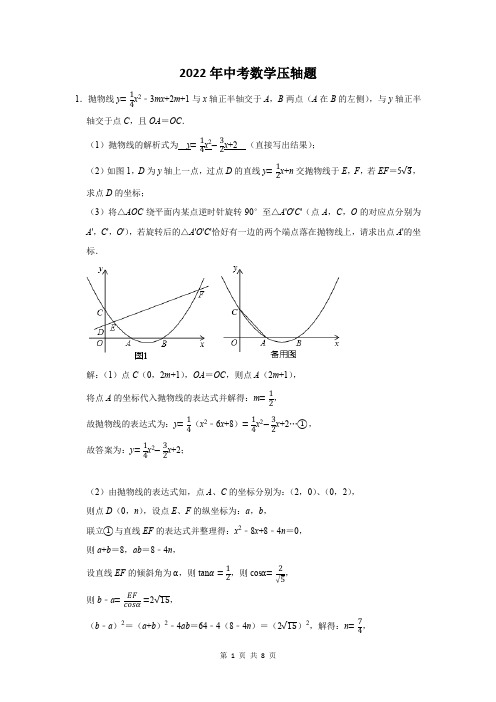
2022年中考数学压轴题1．抛物线y=14x2﹣3mx+2m+1与x轴正半轴交于A，B两点（A在B的左侧），与y轴正半轴交于点C，且OA＝OC．（1）抛物线的解析式为y=14x2−32x+2（直接写出结果）；（2）如图1，D为y轴上一点，过点D的直线y=12x+n交抛物线于E，F，若EF＝5√3，求点D的坐标；（3）将△AOC绕平面内某点逆时针旋转90°至△A'O'C'（点A，C，O的对应点分别为A'，C'，O'），若旋转后的△A'O'C'恰好有一边的两个端点落在抛物线上，请求出点A'的坐标．解：（1）点C（0，2m+1），OA＝OC，则点A（2m+1），将点A的坐标代入抛物线的表达式并解得：m=1 2，故抛物线的表达式为：y=14（x2﹣6x+8）=14x2−32x+2…①，故答案为：y=14x2−32x+2；（2）由抛物线的表达式知，点A、C的坐标分别为：（2，0）、（0，2），则点D（0，n），设点E、F的纵坐标为：a，b，联立①与直线EF的表达式并整理得：x2﹣8x+8﹣4n＝0，则a+b＝8，ab＝8﹣4n，设直线EF的倾斜角为α，则tanα=12，则cosα=√5，则b﹣a=EFcosα=2√15，（b﹣a）2＝（a+b）2﹣4ab＝64﹣4（8﹣4n）＝（2√15）2，解得：n=7 4，故点D 的坐标为：（0，74）；（3）将△AOC 绕平面内某点逆时针旋转90°至△A 'O 'C '（点A ，C ，O 的对应点分别为A '，C '，O '），若旋转后的△A 'O 'C '恰好有一边的两个端点落在抛物线上，如图所示，①当A ′C ′在抛物线上时（左侧图），设点A ′（x ，y ），则点C ′（x ﹣2，y ﹣2），将点A ′、C ′的坐标代入抛物线表达式得：y =14（x 2﹣6x +8），y ﹣2=14[（x ﹣2）2﹣6（x ﹣2）+8）]，解得：x ＝6，y ＝2，故点A ′（6，2）；②当O ′C ′在抛物线上时（右侧图），由图象可得：点A ′（4，2）；综上，点A ′的坐标为：（6，2）或（4，2）．2．已知抛物线y ＝a （x ﹣1）（x ﹣3）（a ＜0）的顶点为A ，交y 轴交于点C ，过C 作CB ∥x 轴交抛物线于点，过点B 作直线l ⊥x 轴，连结OA 并延长，交l 于点D ，连结OB ．（1）当a ＝﹣1时，求线段OB 的长．（2）是否存在特定的a 值，使得△OBD 为等腰三角形？若存在，请写出a 值的计算过程；若不存在，请说明理由．（3）设△OBD 的外心M 的坐标为（m ，n ），求m 与n 的数量关系式．解：y＝a（x﹣1）（x﹣3）＝a（x2﹣4x+3），则点C（0，3a）、函数的对称轴为：x＝2，则点B（4，3a），点A（2，﹣a），点D（4，﹣2a）；（1）点B（4，﹣3），故OB＝5；（2）OD2＝16+4a2，OB2＝16+9a2，BD2＝25a2，①当OD＝OB时，即16+4a2＝16+9a2，解得：a＝0（舍去）；②当OD＝BD时，同理可得：a=−4√2121（正值已舍去）；③当OB＝BD时，同理可得：a＝﹣1（正值已舍去）；综上，a＝﹣1或−4√21 21；（3）线段OD的函数表达式为：y=−12ax，直线OD的中点为点A（2，﹣a），则线段OD的中垂线的表达式为：y=2a x+b，将点A的坐标代入上式并解得：线段OD的中垂线的表达式为：y=2a x﹣a−4a⋯①，线段BD的中垂线的表达式为：y=12a…②，联立①②并解得：x=34a2+2＝m，y=12a＝n，故m＝3n2+2．3．如图，在平面直角坐标系中，抛物线y=13x2﹣2x经过坐标原点，与x轴正半轴交于点A，该抛物线的顶点为M，直线y=−12x+b经过点A，与y轴交于点B，连接OM．（1）求b的值及点M的坐标；（2）将直线AB向下平移，得到过点M的直线y＝mx+n，且与x轴负半轴交于点C，取点D（2，0），连接DM，求证：∠ADM﹣∠ACM＝45°；（3）点E是线段AB上一动点，点F是线段OA上一动点，连接EF，线段EF的延长线与线段OM交于点G．当∠BEF＝2∠BAO时，是否存在点E，使得3GF＝4EF？若存在，求出点E的坐标；若不存在，请说明理由．（1）解：对于抛物线y=13x2﹣2x，令y＝0，得到13x2﹣2x＝0，解得x＝0或6，∴A（6，0），∵直线y=−12x+b经过点A，∴0＝﹣3+b，∴b＝3，∵y=13x2﹣2x=13（x﹣3）2﹣3，∴M（3，﹣3）．（2）证明：如图1中，设平移后的直线的解析式y=−12x+n．∵平移后的直线经过M（3，﹣3），∴﹣3=−32+n，∴n=−3 2，∴平移后的直线的解析式为y=−12x−32，过点D（2，0）作DH⊥MC于H，则直线DH 的解析式为y ＝2x ﹣4，由{y =2x −4y =−12x −32，解得{x =1y =−2， ∴H （1，﹣2），∵D （2，0），M （3，﹣3），∴DH =√22+12=√5，HM =√12+22=√5，∴DH ＝HM ．∴∠DMC ＝45°，∵∠ADM ＝∠DMC +∠ACM ，∴∠ADM ﹣∠ACM ＝45°．（3）解：如图2中，过点G 作GH ⊥OA 于H ，过点E 作EK ⊥OA 于K ．∵∠BEF ＝2∠BAO ，∠BEF ＝∠BAO +∠EF A ，∴∠EF A ＝∠BAO ，∵∠EF A ＝∠GFH ，tan ∠BAO =OB OA =36=12，∴tan ∠GFH ＝tan ∠EFK =12，∵GH ∥EK ，∴GF EF =GH EK =43，设GH ＝4k ，EK ＝3k ，则OH ＝HG ＝4k ，FH ＝8k ，FK ＝AK ＝6k ，∴OF ＝AF ＝12k ＝3，∴k =14，∴OF ＝3，FK ＝AK =32，EK =34，∴OK =92，∴E （92，34）． 4．如图，已知抛物线：y 1＝﹣x 2﹣2x +3与x 轴交于A ，B 两点（A 在B 的左侧），与y 轴交于点C ．（1）直接写出点A ，B ，C 的坐标；（2）将抛物线y 1经过向右与向下平移，使得到的抛物线y 2与x 轴交于B ，B '两点（B '在B 的右侧），顶点D 的对应点为点D '，若∠BD 'B '＝90°，求点B '的坐标及抛物线y 2的解析式；（3）在（2）的条件下，若点Q 在x 轴上，则在抛物线y 1或y 2上是否存在点P ，使以B ′，C ，Q ，P 为顶点的四边形是平行四边形？如果存在，求出所有符合条件的点P 的坐标；如果不存在，请说明理由．解：（1）对于y 1＝﹣x 2﹣2x +3，令y 1＝0，得到﹣x 2﹣2x +3＝0，解得x ＝﹣3或1， ∴A （﹣3，0），B （1，0），令x ＝0，得到y 1＝3，∴C （0，3）．（2）设平移后的抛物线的解析式为y 2＝﹣（x ﹣a ）2+b ，如图1中，过点D ′作D ′H ⊥OB ′于H ，连接BD ′．∵D′是抛物线的顶点，∴D′B＝D′B′，D′（a，b），∵∠BD′B′＝90°，D′H⊥BB′，∴BH＝HB′，∴D′H＝BH＝HB′＝b，∴a＝1+b，又∵y2＝﹣（x﹣a）2+b，经过B（1，0），∴b＝（1﹣a）2，解得a＝2或1（不合题意舍弃），b＝1，∴B′（3，0），y2＝﹣（x﹣2）2+1＝﹣x2+4x﹣3．（3）如图2中，观察图象可知，当点P的纵坐标为3或﹣3时，存在满足条件的平行四边形．对于y1＝﹣x2﹣2x+3，令y1＝3，x2+2x＝0，解得x＝0或﹣2，可得P1（﹣2，3），令y1＝﹣3，则x2+2x﹣6＝0，解得x＝﹣1±√7，可得P2（﹣1−√7，﹣3），P3（﹣1+√7，﹣3），对于y2＝﹣x2+4x﹣3，令y2＝3，方程无解，令y2＝﹣3，则x2﹣4x＝0，解得x＝0或4，可得P4（0，﹣3），P5（4，﹣3），综上所述，满足条件的点P的坐标为（﹣2，3）或（﹣1−√7，﹣3）或（﹣1+√7，﹣3）或（0，﹣3）或（4，﹣3）．。

2022届中考数学压轴难题及答案

2022年中考数学压轴题1．如图1，矩形的边OA 在x 轴上，边OC 在y 轴上，点B 的坐标为（6，8）．D 是AB 边上一点（不与点A 、B 重合），将△BCD 沿直线CD 翻折，使点B 落在点E 处．（1）求直线AC 所表示的函数的表达式；（2）如图2，当点E 恰好落在矩形的对角线AC 上时，求点D 的坐标；（3）如图3，当以O 、E 、C 三点为顶点的三角形是等腰三角形时，求△OEA 的面积．解：（1）∵点B 的坐标为（6，8）且四边形OABC 是矩形， ∴点A 、C 的坐标分别为（6，0）、（0，8），设AC 的表达式为y ＝kx +b ，把A 、C 两点的坐标分别代入上式得{0=6k +b 8=b ，解得{k =−43b =8，∴直线AC 所表示的函数的表达式是y =−43x +8；（2）∵点A 的坐标为（6，0），点C 的坐标为（0，8）， ∴OA ＝6，OC ＝8．∴Rt △AOC 中，AC =√62+82=10， ∵四边形OABC 是矩形， ∴∠B ＝90°，BC ＝6，AB ＝8， ∵沿CD 折叠，∴∠CED ＝90°，BD ＝DE ，CE ＝6，AE ＝4， ∴∠AED ＝90°，设BD ＝DE ＝a ，则AD ＝8﹣a ，∵Rt △AED 中，由勾股定理得：AE 2+DE 2＝AD 2， ∴42+a 2＝（8﹣a ）2，解得a ＝3，∴点D 的坐标为（6，5）；（3）过点E 分别作x 、y 轴的垂线，垂足分别为M 、N ， ∵EN ⊥OC ，EM ⊥OA ，OC ⊥OA ， ∴∠ENO ＝∠NOM ＝∠OME ＝90°， ∴四边形OMEN 是矩形， ∴EM ＝ON ． ①当EC ＝EO 时， ∵EC ＝EO ，NE ⊥OC ， ∴ON =12OC ＝4＝EM ， △OEA 的面积=12×OA ×EM =12×6×4＝12； ②当OE ＝OC 时， ∵EN ⊥OC ，∴∠ENC ＝∠ENO ＝90°，设ON ＝b ，则CN ＝8﹣b ，在Rt △NEC 中，NE 2＝EC 2﹣CN 2，在Rt △ENO 中，NE 2＝EO 2﹣ON 2，即62﹣（8﹣b ）2＝82﹣b 2，解得：b =234，则EM ＝ON =234， △OEA 的面积=12×OA ×EM =12×6×234=694；故△OEA 的面积为12或694．2．直线y＝kx+8交x轴于点B，交y轴于点A，AB＝8√2．（1）如图1，求直线AB的解析式；（2）如图2，C是x轴坐标轴上一点，且OC＝OB，E是点A上方y轴上一点，CE交直线AB于点P，过点P且与BE垂直的直线交x轴于点F，设AE＝m，OF＝y，求y与m 之间的函数关系式；（3）如图3，在（2）的条件下，连接OP、EF，G是直线AB、BF的交点，H是OP上一点，连接BH、AH，若∠OPC+∠AHB＝90°，PC＝BH，求点G的坐标．解：（1）直线y＝kx+8交y轴于点A，则点A（0，8），而AB＝8√2，故OB=√(8√2)2−82=8，故点B（8，0），将点B的坐标代入一次函数表达式：y＝kx+8并解得：k＝1，故直线AB的解析式为：y＝x+8；（2）如图1，过点A作y轴的垂线交PF于N，过点N作NM⊥x轴于点M，∵OC＝OB，OE⊥BC，∴BE＝CE，∴∠EBO＝∠ECO，∵PF⊥BE，∴∠PFO+∠EBO＝90°，∴∠PFO+∠ECO＝90°，∵∠OEC+∠ECO＝90°，∴∠PFO＝∠OEC，∵AN⊥y轴，∴∠EAN＝∠EOF＝90°，∴AN∥x轴，∴∠ANP＝∠PFO，∴∠OEC＝∠ANP，∵AO＝OB，∠AOB＝90°，∴∠OAB＝∠ABO＝45°，∴∠P AE＝∠OAB＝45°，∴∠P AN＝45°，∴∠P AE＝∠P AN，∵AP＝AP，∴△P AE≌△P AN（AAS），∴AN＝AE，∵∠AOM＝∠OAN＝∠NMO＝90°，∴四边形AOMN为矩形，∴OM＝AN，MN＝OA，∴OM＝AE，∵OC＝OB＝OA，∴OC＝MN，∵∠EOC＝∠NMF＝90°，∠PFO＝∠OEC，∴△OEC≌△MFN（AAS），∴MF＝OE＝m+8，∵OM＝AE＝m，∴OF＝OM+MF＝2m+8，即y＝2m+8；（3）如图2，过点B作PO延长线的垂线，垂足为N，过点C作CM⊥OP于点M，过点O作OK⊥AB于点K，过点P作PR⊥y轴于点R，∵OB ＝OC ，∠BON ＝∠COM （AAS ），∠ONB ＝∠OMC ＝90°， ∴Rt △BHN ≌Rt △CPM （HL ）， ∴∠BHN ＝∠CPM ，PM ＝HN ， ∴PH ＝MN ＝2OM ， ∵∠AHB +∠OPC ＝90°， ∴∠AHB +∠BHN ＝90°， ∴∠AHO ＝90°， ∴∠AOH +∠OAH ＝90°， ∴∠COM ＝∠OAH ，∵OA ＝OC ，∠AHO ＝∠OMC ＝90°， ∴△AOH ≌△OCM （AAS ）， ∴AH ＝OM =12PH ， tan ∠OPK =AHPH =12， ∴OK PK=12，∴PK ＝2OK ，∵OA ＝OB ，OK ⊥AB ， ∴AK ＝BK ， ∵∠AOB ＝90°， ∴AK ＝OK =12AB ＝4√2， ∵∠P AR ＝∠OAB ＝45°， ∴∠APR ＝∠P AR ＝45°，∴PR＝AR=√22AP＝4，∴OR＝OA+AR＝12，∴P（4，12），∵C（8，0），∴直线PC的表达式为：y＝﹣3x+24，当x＝0时，y＝24，故点E（0，24），故OE＝24，∴AE＝OE﹣OA＝16，即m＝16，故y＝2m+8＝40，故OF＝40，故点F（40，0），则直线EF的表达式为：y=−35x+24，联立y=−35x+24和y＝x+8并解得：x＝10，y＝18，故点G（10，18）．3．如图，在Rt△ABC中，∠ACB＝90°，以斜边AB上的中线CD为直径作⊙O，与BC交于点M，与AB的另一个交点为E，过M作MN⊥AB，垂足为N．（1）求证：MN是⊙O的切线；（2）若⊙O的直径为5，sin B=35，求ED的长．【解答】（1）证明：连接OM，如图1，∵OC＝OM，∴∠OCM＝∠OMC，在Rt△ABC中，CD是斜边AB上的中线，∴CD=12AB＝BD，∴∠DCB＝∠DBC，∴∠OMC＝∠DBC，∴OM∥BD，∵MN⊥BD，∴OM⊥MN，∵OM过O，∴MN是⊙O的切线；（2）解：连接DM，CE，∵CD是⊙O的直径，∴∠CED＝90°，∠DMC＝90°，即DM⊥BC，CE⊥AB，由（1）知：BD＝CD＝5，∴M为BC的中点，∵sin B=3 5，∴cos B=4 5，在Rt△BMD中，BM＝BD•cos B＝4，∴BC＝2BM＝8，在Rt△CEB中，BE＝BC•cos B=32 5，∴ED＝BE﹣BD=325−5=75．4．已知∠MPN的两边分别与⊙O相切于点A，B，⊙O的半径为r．（1）如图1，点C在点A，B之间的优弧上，∠MPN＝80°，求∠ACB的度数；（2）如图2，点C在圆上运动，当PC最大时，要使四边形APBC为菱形，∠APB的度数应为多少？请说明理由；（3）若PC交⊙O于点D，求第（2）问中对应的阴影部分的周长（用含r的式子表示）．【解答】解：（1）如图1，连接OA，OB，∵P A，PB为⊙O的切线，∴∠P AO＝∠PBO＝90°，∵∠APB+∠P AO+∠PBO+∠AOB＝360°，∴∠APB+∠AOB＝180°，∵∠APB＝80°，∴∠AOB＝100°，∴∠ACB＝50°；（2）如图2，当∠APB＝60°时，四边形APBC是菱形，连接OA，OB，由（1）可知，∠AOB +∠APB ＝180°， ∵∠APB ＝60°， ∴∠AOB ＝120°， ∴∠ACB ＝60°＝∠APB ， ∵点C 运动到PC 距离最大， ∴PC 经过圆心， ∵P A ，PB 为⊙O 的切线，∴P A ＝PB ，∠APC ＝∠BPC ＝30°，又∵PC ＝PC ，∴△APC ≌△BPC （SAS ），∴∠ACP ＝∠BCP ＝30°，AC ＝BC ， ∴∠APC ＝∠ACP ＝30°， ∴AP ＝AC ，∴AP ＝AC ＝PB ＝BC ， ∴四边形APBC 是菱形；（3）∵⊙O 的半径为r ， ∴OA ＝r ，OP ＝2r ， ∴AP =√3r ，PD ＝r ，∵∠AOP ＝90°﹣∠APO ＝60°， ∴AD ̂的长度=60°π⋅r180°=π3r ， ∴阴影部分的周长＝P A +PD +AD ̂=√3r +r +π3r ＝（√3+1+π3）r ． 5．如图，P A 为⊙O 的切线，PBC 为⊙O 的割线，AD ⊥OP 于点D ，△ADC 的外接圆与BC 的另一个交点为E ．证明：∠BAE ＝∠ACB ．【解答】证明：连接OA ，OB ，OC ，BD ． ∵OA ⊥AP ，AD ⊥OP ，∴由射影定理可得：P A 2＝PD •PO ，AD 2＝PD •OD ．…（5分）又由切割线定理可得 P A 2＝PB •PC ， ∴PB •PC ＝PD •PO ，∴D 、B 、C 、O 四点共圆，…（10分）∴∠PDB ＝∠PCO ＝∠OBC ＝∠ODC ，∠PBD ＝∠COD ， ∴△PBD ∽△COD ， ∴PD CD=BD OD，…（15分）∴BD •CD ＝PD •OD ＝AD 2， ∴BD AD=AD CD．又∠BDA ＝∠BDP +90°＝∠ODC +90°＝∠ADC ， ∴△BDA ∽△ADC ， ∴∠BAD ＝∠ACD ，∴AB 是△ADC 的外接圆的切线， ∴∠BAE ＝∠ACB ．6．如图，点A 为y 轴正半轴上一点，A ，B 两点关于x 轴对称，过点A 任作直线交抛物线y =23x 2于P ，Q 两点．（1）求证：∠ABP ＝∠ABQ ；（2）若点A 的坐标为（0，1），且∠PBQ ＝60°，试求所有满足条件的直线PQ 的函数解析式．【解答】（1）证明：如图，分别过点P ，Q 作y 轴的垂线，垂足分别为C ，D ．设点A 的坐标为（0，t ），则点B 的坐标为（0，﹣t ）．设直线PQ 的函数解析式为y ＝kx +t ，并设P ，Q 的坐标分别为（x P ，y P ），（x Q ，y Q ）．由{y =kx +t y =23x 2，得23x 2−kx −t =0，于是x P x Q =−32t ，即t =−23x P x Q ．于是BC BD =y P +ty Q +t =23x P2+t 23x Q 2+t =23x P 2−23x P x Q 23x Q 2−23x P x Q =23x P (x P −x Q )23x Q (x Q −x P )=−x P x Q ．，又因为PC QD =−x Px Q ，所以BC BD =PC QD ．因为∠BCP ＝∠BDQ ＝90°，所以△BCP ∽△BDQ ，故∠ABP ＝∠ABQ ；（2）解：设PC ＝a ，DQ ＝b ，不妨设a ≥b ＞0，由（1）可知∠ABP ＝∠ABQ ＝30°，BC =√3a ，BD =√3b ，所以AC =√3a −2，AD =2−√3b ．因为PC ∥DQ ，所以△ACP ∽△ADQ ．于是PC DQ =AC AD ，即a b =√3a−22−√3b，所以a +b =√3ab ．由（1）中x P x Q =−32t ，即−ab =−32，所以ab =32，a +b =3√32，于是可求得a =2b =√3．将b=√32代入y=23x2，得到点Q的坐标（√32，12）．再将点Q的坐标代入y＝kx+1，求得k=−√3 3．所以直线PQ的函数解析式为y=−√33x+1．根据对称性知，所求直线PQ的函数解析式为y=−√33x+1或y=√33x+1．。

2022届中考数学压轴难题含答案解析

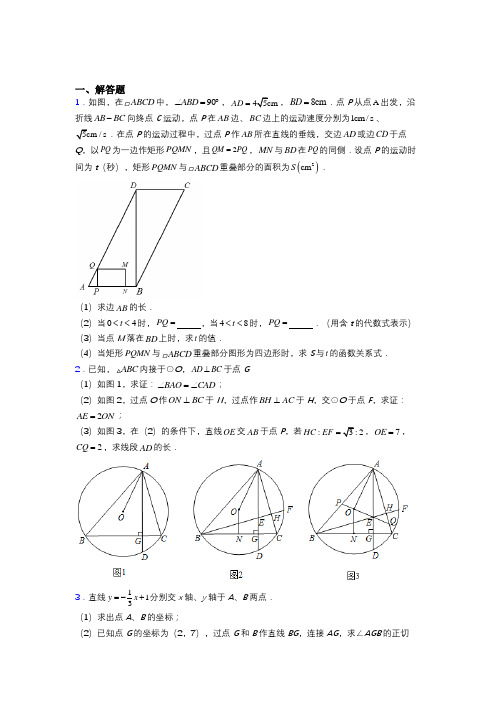
一、解答题1．如图，在ABCD中，90ABD∠=︒，45cmAD=，8cmBD=．点P从点A出发，沿折线AB BC-向终点C运动，点P在AB边、BC边上的运动速度分别为1cm/s、5cm/s．在点P的运动过程中，过点P作AB所在直线的垂线，交边AD或边CD于点Q，以PQ为一边作矩形PQMN，且2QM PQ=，MN与BD在PQ的同侧．设点P的运动时间为t（秒），矩形PQMN与ABCD重叠部分的面积为()2cmS．（1）求边AB的长．（2）当04t<<时，PQ=，当48t<<时，PQ=．（用含t的代数式表示）（3）当点M落在BD上时，求t的值．（4）当矩形PQMN与ABCD重叠部分图形为四边形时，求S与t的函数关系式．2．已知，ABC内接于⊙O，AD BC⊥于点G（1）如图1，求证：BAO CAD∠=∠；（2）如图2，过点O作ON BC⊥于N，过点作BH AC⊥于H，交⊙O于点F，求证：2AE ON=；（3）如图3，在（2）的条件下，直线OE交AB于点P，若:3:2HC EF=，7OE=，2CQ=，求线段AD的长．3．直线113y x=-+分别交x轴、y轴于A、B两点．（1）求出点A、B的坐标；（2）已知点G的坐标为（2，7），过点G和B作直线BG，连接AG，求∠AGB的正切值；（3）在（2）的条件下，在直线BG 上是否存在点Q ，使得以点A 、B 、Q 为顶点的三角形与△AOB 相似？若存在，请求出点Q 的坐标；若不存在，请说明理由．4．如图，抛物线2y ax bx c =++与x 轴交于A ，B 两点，与y 轴交于C 点，OA =1，OB =OC =3．（1）求抛物线的表达式；（2）如图1，点D 为第一象限抛物线上一动点，连接DC ，DB ，BC ，设点D 的横坐标为m ，△BCD 的面积为S ，求S 的最大值；（3）如图2，点P (0，n )是线段OC 上一点(不与点O 、C 重合)，连接PB ，将线段PB 以点P 为中心，旋转90°得到线段PQ ，是否存在n 的值，使点Q 落在抛物线上？若存在，请求出满足条件的n 的值，若不存在，请说明理由．5．已知抛物线经过()30A -,，()1,0B ，52,2C ⎛⎫⎪⎝⎭三点，其对称轴交x 轴于点H ，一次函数()0y kx b k =+≠的图象经过点C ，与抛物线交于另一点D （点D 在点C 的左边），与抛物线的对称轴交于点E ．（1）求抛物线的解析式；（2）在抛物线上是否存在点F ，使得点A 、B 、E 、F 构成的四边形是平行四边形，如果存在，求出点F 的坐标，若不存在请说明理由（3）设∠CEH=α，∠EAH =β，当αβ>时，直接写出k 的取值范围6．如图，抛物线顶点(1,4)P ，与y 轴交于点(0,3)C ，与x 轴交于点A ，B ．（1）求抛物线的解析式；（2）Q 是抛物线上除点P 外一点，BCQ △与BCP 的面积相等，求点Q 的坐标：（3）M 是线段BC 上方抛物线上一个动点，过点M 作x 轴的垂线，交线段BC 于点D ，再过点M 做MN //x 轴交抛物线于点N ，连结DN ，请问是否存在点M 使MDN △为等腰直角三角形？若存在，求出点M 的坐标；若不存在，说明理由．7．如图1所示，在等边三角形ABC 中，线段AD 为其内角平分线，过点D 的直线B 1C 1⊥AC 于点C 1，交AB 的延长线于点B 1．（1）请你探究：1111,AC DC AC CD AB BD AB DB ==是否都成立？请说明理由．（2）请你继续探究：若ABC 为任意三角形，线段AD 为其内角平分线，AC CDAB DB=一定成立吗？并证明你的判断．（3）如图2所示，在Rt ABC 中，∠ACB ＝90°，AC ＝8，AB ＝403，E 为AB 上一点且AE ＝5，CE 交内角平分线AD 于点F ，试求DFFA的值．8．“数学建模”是中学数学的核心素养，平时学习过程中能归纳一些几何模型，解决几何问题就能起到事半功倍的作用．（1）如图1，正方形ABCD中，45=；∠=︒，且DE BFEAF=，求证：EG AG（2）如图2，正方形ABCD中，45∠=︒，延长EF交AB的延长线于点G，（1）中的EAF结论还成立吗？请说明理由；⊥，垂足为点Q，交AF于点N，连结DN，求（3）如图3在（2）的条件下，作GQ AE证：45∠=︒．NDC9．如图，在Rt△AOD中，∠AOD＝90°，以点O为圆心、OA为半径作⊙O．延长AD、OD，分别交⊙O于点C、E，点B是OD延长线上一点，且有BC＝BD．（1）求证：BC是⊙O的切线；（2）若∠OAD＝30°，CD＝3，求弧CE长．（3）若OD＝3，DE＝1，求BE．10．已知在菱形ABCD中，8∠=︒，点P是直线AB上任意一点，联结BADAB=，120PC．在PCD∠内部作射线CQ与对角线BD交于点Q（与B、D不重合），且30PCQ∠=︒，联结PQ．（1）如图1，当点P在边AB上时，如果6BP=，求线段PC的长；（2）求证：△PCQ是等腰三角形（3）直线PQ与直线BC交于点E，如果QCE∆与BCP∆相似，求线段BP的长．11．如图，已知正方形ABCD，直线BC上任意一点E，连接AE，将△ABE绕点A逆时针旋转α（0°＜α＜360°）得到△AFG，直线BF、EG交于点M．（1）如图1，当点E在线段BC上，α＝90°时，求证：M为GE的中点；（2）如图2，当点E在射线BC上，（1）中的结论是否发生变化，说明理由．（3）当AB＝4，BE＝5，BM＝41时，求DM的长（直接写出结果）．12．如图1，二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A（﹣1，0）、B（3，0），与y轴交于点C，连接AC和BC，∠OAC＝60°．（1）求二次函数的表达式．（2）如图2，线段BC上有M、N两动点（N在M上方），且MN 3P是直线BC下方抛物线上一动点，连接PC、PB，当△PBC面积最大时，连接PM、AN，当MN运动到某一位置时，PM+MN+NA的值最小，求出该最小值．（3）如图3，在（2）的条件下，连接AP，将AP绕着点A逆时针旋转60°至AQ．点E为二次函数对称轴上一动点，点F为平面内任意一点，是否存在这样的点E、F，使得四边形AEFQ 为菱形，若存在，请直接写出点E 的坐标，若不存在，请说明理由．13．将矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ，其中点E 与点B ，点G 与点D 分别是对应点，连接BG ．(1)如图，若点A ，E ，D 第一次在同一直线上，BG 与CE 交于点H ，连接BE ． ①求证：BE 平分∠AEC ．②取BC 的中点P ，连接PH ，求证：PH ∥CG ． ③若BC ＝2AB ＝2，求BG 的长．(2)若点A ，E ，D 第二次在同一直线上，BC ＝2AB ＝4，直接写出点D 到BG 的距离． 14．预备知识：(1)在一节数学课上，老师提出了这样一个问题：随着变量t 的变化，动点在平面直角坐标系中的运动轨迹是什么？一番深思熟虑后，聪明的小明说：“是一条直线”，老师问：“你能求出这条直线的函数表达式吗？”小明的思路如下：设这条直线的函数表达式为()0y kx b k =+≠，将点代入得：，整理得∵t 为任意实数，等式恒成立， ∴，∴，2b =∴这条直线的函数表达式为请仿照小明的做法，完成问题：随着变量t 的变化，动点在平面直角坐标系中的运动轨迹是直线l ，求直线l 的函数表达式．问题探究：(2)如图1，在平面直角坐标系中，已知，，且，AB AC =，则点C 的坐标为_________．结论应用：(3)如图2，在平面直角坐标系中，已知点()1,0P ，Q 是直线122y x =-+上的一个动点，连接PQ ，过点P 作，且，连接，求线段的最小值．15．定义：在平面直角坐标系中，对于任意两点()11,A x y ，()22,B x y ，如果点(),M x y 满足122x x x -=，122y y y -=，那么称点M 是点A 、B 的“双减点”．例如：()4,5A -，()6,1B -、当点(),T x y 满足4652x --==-，()5132y --==，则称点()5,3M -是点A 、B 的“双减点”．(1)写出点()1,3A -，()1,4B -的“双减点”C 的坐标；(2)点()6,4E -，点4,43F m m --⎛⎫⎪⎝⎭，点(),M x y 是点E 、F 的“双减点”．求y 与x 之间的函数关系式；(3)在（2）的条件下，y 与x 之间的函数图象与y 轴、x 轴分别交于点A 、C 两点，B 点坐标为3,0，若点E 在平面直角坐标系内，在直线AC 上是否存在点F ，使以A 、B 、E 、F 为顶点的四边形为菱形？若存在，请求出F 点的坐标；若不存在，请说明理由． 16．如图，抛物线2=y ax bx +的对称轴为y a 19），P 为抛物线上一点，A （0，32）．(1)求抛物线解析式；(2)Q 为直线AP 上一点，且满足AQ ＝2AP ．当P 运动时，Q 在某个函数图象上运动，试写出Q 点所在函数的解析式；(3)如图2，以PA 为半径作⊙P 与x 轴分别交于M （x 1，0），N （x 2，0）（x 1＜x 2）两点，当△AMN 为等腰三角形时，求点P 的横坐标．17．如图1，在直角坐标系中，O 是坐标原点，点A 在y 轴正半轴上，二次函数y =ax 2+16x +c 的图象F 交x 轴于B 、C 两点，交y 轴于M 点，其中B （﹣3，0），M （0，﹣1）．已知AM =BC ．(1)求二次函数的解析式；(2)证明：在抛物线F 上存在点D ，使A 、B 、C 、D 四点连接而成的四边形恰好是平行四边形，并请求出直线BD 的解析式；(3)在（2）的条件下，设直线l 过D 且l ⊥BD ，分别交直线BA 、BC 于不同的P 、Q 两点，AC 、BD 相交于N ，求11BP BQ+的值； 18．如图，抛物线26y ax bx =++经过点()2,0A -、()4,0B 两点，与y 轴交于点C ，点D 是抛物线上一个动点，设点D 的横坐标为()14m m <<．连接AC 、BC 、DB 、D C ．(1)求抛物线的函数表达式；(2)BCD△的面积等于AOC△的面积的34时，求m的值；(3)在（2）的条件下，若点M是x轴上的一个动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B、D、M、N为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由．19．如图，在平面直角坐标系中，直线343y x=+与x轴、y轴分别交于A、B两点，点C在x轴上，且60ABC∠=︒．（1）点C的坐标为；（2）若动点P从点A出发，沿AC向点C运动，同时动点Q从点C出发，沿C B A→→方向向点A运动，动点P的运动速度是每秒1个单位长度，动点Q的运动速度是每秒2个单位长度，设APQ∆的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，并写出自变量t的取值范围；（3）在（2）的条件下，当APQ∆的面积最大时，y轴上有一点M，则平面内是否存在一点N使得以A，Q，M，N为顶点的四边形构成以AQ为边的菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．20．如图1，抛物线y12=-x2+bx+c与x轴交于A（﹣1，0）和B点，与y轴交于点C（0，2）．（1）求这个抛物线的解析式；（2）若点P在抛物线上，且满足∠PAB＝∠ACO，求点P的坐标；（3）如图2，若点D是在直线BC上方的抛物线的一点，作DE⊥BC于点E，求线段DE的最大值．【参考答案】参考答案**科目模拟测试一、解答题1．（1）4；（2）2,162t t -；（3）0.8或7.2；（4）()()()222800.8814,4781285127.28t t S t t t t t t t ⎧<≤⎪=-+≤<<≤⎨⎪-+≤<⎩【解析】【分析】（1）利用勾股定理直接计算即可；（2）先求解25tan 2,sin 45BD BD A A AB AD =====再用含t 的代数式表示,,,AP PB PC 再利用三角函数建立方程求解两种情况下的PQ 即可；（3）分两种情况讨论：如图，当P 在AB 上，M 落在BD 上，如图，当P 在BC 上，M 落在BD 上，则,M D 重合，再利用矩形的性质结合三角函数可得结论；（4）如图，当M 第一次落在BD 上，即00.8t时，此时重叠部分的面积为四边形，当14t ≤<时，重叠部分为四边形，如图，当47t <≤时，此时重叠部分的面积为四边形，如图，当M 第2次落在BD 上时，7.2,t当7.28t 时，此时重叠部分的面积为四边形，再利用图形的性质列面积函数关系式即可.【详解】解：（1） 90ABD ∠=︒，5cm AD =，8cm BD =， ()2222458 4.AB AD BD ∴=-=-=（2）当04t <<时，P 在AB 上，,AP t =90,4,8,45,ABD AB BD AD ∠=︒===825tan 2,sin ,545BD BD A A AB AD ∴===== 而四边形PQMN 为矩形， 90,,,QPN QPA PQ MN PN MQ ∴∠=︒=∠==2,PQ AP∴= 2,PQ t ∴=当48t <<时，P 在BC 上，如图，此时()54,PB t =-，ABCD ，,,A C AD BC ∴∠=∠= 45545855,PC BC PB t t =-=-+=-25sin 5855PQ PQ C PC t∴∠===-， 162.PQ t ∴=-故答案为：2,162t t -（3）如图，当P 在AB 上，M 落在BD 上，此时4,,AP PN AP PB QM PB +=+==2,QM PQ24,PB PQ t54,t 解得：0.8,t如图，当P 在BC 上，M 落在BD 上，则,M D 重合，4,CQ DQ CQ MQ162,PQ t 同理可得：18,2CQ PQ t 2324,MQ PQ t32484,t t解得：7.2.t（4）当M 第一次落在BD 上，即00.8t时，此时重叠部分的面积为四边形，如图，此时,2,24,AP t PQ t QM PQ t2248,S t t t当M 落在BC 上时，如图，同理可得：1,2,,4,24,2AP t PQ t MN BN MN t PB t QM PN PQ t AB ======-====44,t 解得：1,t =当14t ≤<时，重叠部分为四边形，如图，同理可得：,2,4,4,AP t PQ t PB t HQ ===-= ()2144?28,2S t t t t =-+=-+ 如图，当N 落在AD 上时，同理可得：162,8,2324,PQ t CQ t MQ PN PQ t 而4,PN CD3244,t 解得：7,t =当47t <≤时，此时重叠部分的面积为四边形，如图，此时44,DQ CQ t()()2144?1628,2S t t t t =-+-=-+ 当M 第2次落在BD 上时，7.2,t当7.28t 时，此时重叠部分的面积为四边形，如图，同理可得：162,22162,PQ t MQ PQ t2221628128512.S t t t综上：()()()222800.8814,4781285127.28t t S t t t t t t t ⎧<≤⎪=-+≤<<≤⎨⎪-+≤<⎩【点睛】本题考查的是平行四边形的性质，矩形的判定与性质，列面积函数关系式，锐角三角函数的应用，清晰的分类讨论是解题的关键.2．（1）见解析；（2）见解析；（37137【解析】【分析】（1）连接,BO BD ，根据圆周角定理以及三角形的内角和，以及AD BD ⊥，即可证明BAO CAD ∠=∠；（2）延长CO 交O 于点M ，连接BM 、AM ，依垂径构造中位线，得2BM ON =，证明四边形AEBM 是平行四边形，得AE BM =结论可证；（3）连接OE 并延长交AC 于点Q ,连接,,AF OB OC ，CD ，,AD BC AH BF ⊥⊥，证EH HF =结合边比得60HFC ∠=︒，证AOP ≌AEQ △，得APQ 是等边等边三角形，PBO ≌QOC ，得等边边长13，得半径3BO =AEH △，求得1cos 7AEH ∠=继续解形计算，可得7137AD =【详解】（1）如图，连接,BO BD ，AD BC ⊥90DAC C ∴∠+∠=︒AO BO =AOB ABO ∠=∠2180AOB BAO ∴∠+∠=︒即2AOB BAO ∠+∠()2DAC C =∠+∠=AB AB2AOB C ∴∠=∠BAO DAC ∴∠=∠（2）如图，延长CO 交O 于点M ，连接BM 、AMON BC ⊥NB NC ∴=OM OC =2ON BM ∴= MC 为O 的直径，90MBC ∴∠=︒，90MAC ∠=︒MB BC ∴⊥,MA AC ⊥AD BC ⊥,BH AC ⊥∴//MB AE ，//MA BH∴四边形AMBE 是平行四边形AE MB ∴=∴2AE ON =（3）如图，连接OE 并延长交AC 于点Q ,连接,,AF OB OC ，CD ，,AD BC AH BF ⊥⊥,90,90GBH BEG HAE AEH ∴∠+∠=︒∠+=︒,BEG AEH ∠=∠,GBH HAE ∴∠=∠,即CAD CBF ∠=∠CF CF =CAF CBF ∴∠=CAD CAF ∴∠=∠AH BF ⊥AHE AHF ∴∠=∠又AH AH =AHE AHF ∴△≌△HE HF ∴=:32HC EF =3HC HF ∴=tan 3HC HFC HF∠==60HFC ∴∠=︒设ON k =，由（2）可得2AE ON =2k =,60,HFC CB CB ∠=︒=120BOC ∴∠=︒,60BAC BFC ∠=∠=︒ON BC ⊥1602BON BOC ∴∠=∠=︒ 22cos ON OB ON k BON∴===∠ 2OA OB OC k ∴===AO AE ∴=AOE AEO ∴∠=∠AOP AEQ ∴∠=∠由（1）可得BAO CAD ∠=∠，在AOP 和AEQ △中，BAO CAD AO AEAOP AEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AOP ≌AEQ △∴=AP AQ ，OP EQ =60BAC ∠=︒APQ ∴△是等边三角形，60APQ AQP ∴∠=∠=︒120BPO OQC ∴∠=∠=︒120BOC ∠=︒18060BOP COQ BOC ∴∠+∠=︒-∠=︒180********BOP PBO OPB ∠+∠=︒-∠=︒-︒=︒COQ PBO ∴∠=∠在PBO 与QOC 中COQ OBP OQC BPO BO OC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴PBO ≌QOCOQ BP ∴=，OP QC =OP EQ =2EQ QC ∴==7OE =27211PQ AP AQ PO OE EQ ∴===++=++=在Rt EHQ 中，60AQP ∠=︒,2EQ =sin 2EH EQ EQH ∴=⨯∠==1cos 12HQ EQ EQA EQ =⋅∠==EF EH ∴=在Rt HCF △中，cos 2HF CF HFC===∠在Rt AEH 中,12AH AQ HQ =-=AE ∴=AO AE ∴==在Rt AEH △中，1cos 7EH AEH AE ∠=== ,AH BF AD BC ⊥⊥∴AEH GAC GAC GCA ∠+∠=∠+∠AEH ACG ∴∠=∠在Rt AGC 中，13215AC AQ QC =+=+=115cos cos 77CG AC ACG AC AEH AC ∴=⋅∠=⋅∠==AG ∴=DAC CAF ∠=∠DC CF ∴=GD ∴=AD AG GD ∴=+=+∴AD = 【点睛】本题考查了圆与三角形的综合，三角形全等的性质与证明，中位线定理，平行四边形的性质与判定，勾股定理，解直角三角形，圆周角定理，添加辅助线是解题的关键．3．（1）()3,0A ，()0,1B ；（2）1tan 2AGB ∠=；（3）存在，11,23Q ⎛⎫ ⎪⎝⎭，21,03Q ⎛⎫- ⎪⎝⎭，()33,10Q ，()43,8Q -- 【解析】【分析】（1）对于113y x =-+，令x ＝0，则y ＝1，令y ＝0，即113x -+＝0，解得x ＝3，即可求解；（2）证明AG 2＝AB 2＋BG 2，则△ABG 为直角三角形，即可求解；（3）分△ABQ ∽△AOB 、△ABQ ∽△BOA 两种情况，利用三角形相似边的比例关系，即可求解．【详解】解：（1）对于113y x =-+，令x ＝0，则y ＝1，令y ＝0，即113x -+＝0，解得x ＝3，故点A 、B 的坐标分别（3，0）、（0，1）；（2）由A 、B 、G 的坐标知，BG 2＝22＋（7−1）2＝40，同理AB 2＝10，AG 2＝50，故AG 2＝AB 2＋BG 2，故△ABG 为直角三角形，则tan ∠AGB ＝101240ABBG ==；（3）设直线BG 的表达式为y ＝kx ＋b ，则721k bb =+⎧⎨=⎩，解得31k b =⎧⎨=⎩故直线BG 的表达式为y ＝3x ＋1，设点Q （m ，3m ＋1），①当△ABQ ∽△AOB 时，则AB BQ AO OB =，即()223111031m m ++-=，解得m ＝±13，∴11,23Q ⎛⎫ ⎪⎝⎭，21,03Q ⎛⎫- ⎪⎝⎭②当△ABQ ∽△BOA 时，ABBQ OB AO =，即()223111013m m ++-=解得：m ＝±3，∴()33,10Q ，()43,8Q --故点P 的坐标为（13，2）或（−13，0）或（3，10）或（−3，−8）．【点睛】本题考查的是一次函数综合运用，涉及到一次函数的性质、解直角三角形、三角形相似等，其中（3），要注意分类求解，避免遗漏．4．（1）2y x 2x 3=-++；（2）278；（3）存在，n =1或n =3+332- 【解析】【分析】（1）通过待定系数法求解函数解析式即可；（2）作DF ⊥x 轴于点F ，交BC 于点E ，根据12S DE OB =⋅求得S 关于m 的解析式，根据二次函数的性质求解即可；（3）过点P 作PB 的垂线，交抛物线于点1Q 和2Q ，作1Q M y ⊥轴于点M ，2Q N y ⊥轴于点N ，利用全等三角形的性质求解即可．【详解】解：(1)设函数关系式为2y ax bx c =++由题意，得A (－1，0)，B (3，0)，C (0，3)∴(1)(3)y a x x =+-把C (0，3)代入得，1a =-∴2y x 2x 3=-++(2)作DF ⊥x 轴于点F ，交BC 于点E设直线BC 关系式为y =kx ＋b ，代入(3，0)，(0，3)得k =－1，b =3，∴y =－x ＋3∵点D 的横坐标为m ，则DF =223m m -++，EF =－m ＋3∴DE =23m m -+22133327(3)()22228S DE OB m m m =⋅=-+=--+∵302-<，∴S 的最大值是278(3)过点P 作PB 的垂线，交抛物线于点1Q 和2Q ，作1Q M y ⊥轴于点M ，2Q N y ⊥轴于点N∴1290Q MP Q NP BOP ∠=∠=∠=︒∵1190Q PM PQ M ∠+∠=︒，190Q PM BPO ∠+∠=︒，∴1PQ M BPO ∠=∠又∵1BP PQ =，∴1Q PM PBO △≌△∴1MQ OP n ==，3MP OB ==，∴1()3Q n n +，代入抛物线，得2323n n n +=-++解得11n =，20n =(舍去)同理，2PN Q PBO ≌，∴2Q (－n ，n －3)代入抛物线，得2323n n n =-+－－解得13+33n -=2333n --=舍去) 综上，存在n 的值，n =1或n 3+33-【点睛】此题考查了二次函数与几何的综合应用，涉及了待定系数法求解析式，二次函数的性质，全等三角形的判定与性质，解题的关键是熟练掌握二次函数以及全等三角形的判定与性质．5．（1）y ＝12x 2＋x −32；（2）（3，6）或（-5，6）或（−1，-2）；（3）−12＜k ＜56且k ≠0或56＜k ＜43【解析】【分析】（1）把A（−3，0），B（1，0），52,2C⎛⎫⎪⎝⎭代入y＝ax2＋bx＋c，解方程组即可；（2）把C点坐标代入直线CD，得2k＋b＝52，分两种情况：①若AB为平行四边形的边时，②若AB为平行四边形的对角线时，得关于k、b的方程组，解方程组即可求解；（3）分两种情况：①当E点在x轴上方时，②E点在x轴下方时，根据当α＝β时，列方程，可求出k的值，进而求出k的取值范围．【详解】解：（1）设抛物线的解析式为y＝ax2＋bx＋c，∵抛物线经过A（−3，0），B（1，0），C（2，52）三点，∴9305 422a b ca b ca b c⎧⎪-+=⎪++=⎨⎪⎪++=⎩，∴12132abc⎧⎪⎪⎨⎪⎪-⎩＝＝＝，∴抛物线的解析式为y＝12x2＋x−32；（2）如图1所示，将C点坐标代入直线CD，得2k＋b＝52，当x＝−1时，y＝−k＋b，即E（−1，−k＋b）．①若AB为平行四边形的边时，则F（-1+4，−k＋b）或F（-1-4，−k＋b），即：F（3，−k＋b）或F（-5，−k＋b），把F（3，−k＋b）代入y＝12x2＋x−32，得−k＋b=6，把F （-5，−k ＋b ），代入y ＝12x 2＋x −32，得−k ＋b =6，又∵2k ＋b ＝52， ∴k =76-，b =296 ∴F （3，6）或（-5，6）；②若AB 为平行四边形的对角线时，则F 和E 关于x 轴对称，∴F （−1，k -b ），∴k -b =-2，又∵2k ＋b ＝52， ∴k =16，b =136，∴F （−1，-2），综上所述：F 的坐标为（3，6）或（-5，6）或（−1，-2）；（3）如图2所示，①当E 点在x 轴上方时，如图2所示，当α＝β时，∵∠EHA ＝90°，∴∠AEC ＝90°，∴∠AEH =∠EGH ，∵∠AHF =∠FHG =90°，∴AHF FHG ∽，∴AEAHEG EH =，∵A （−3，0），E （−1，−k ＋b ），G （bk -，0），()()2222221k b k b b k b k +-+=-+⎛⎫-++-+ ⎪⎝⎭，∴k 2−bk −2＝0，联立方程220522k bkk b⎧--=⎪⎨+=⎪⎩，解得k＝−12（k＝43舍去），随着E点向下移动，∠CEH的度数越来越大，∠EAH的度数越来越小，当E点和H点重合时（如图3所示），α和β均等于0，此时联立方程522k bk b⎧+⎪⎨⎪-+⎩＝＝，解得5656kb⎧=⎪⎪⎨⎪=⎪⎩，因此当−12＜k＜56且k≠0时，α＞β；②E点在x轴下方时，如图4所示，当α＝β时，∵∠EHA＝90°，∴∠AEC＝90°，根据①可得此时k＝43（k＝−12舍去），随着E点向下移动，∠CEH的度数越来越小，∠EAH的度数越来越大，因此当56＜k＜43时，α＞β．综上所述可得，当α＞β时，k取值范围为−12＜k＜56且k≠0或56＜k＜43．【点睛】本题考查的是一次函数、二次函数和相似三角形的判定和性质的综合应用，掌握待定系数法求函数解析式和数形结合思想方法是解题的关键．6．（1）2y x 2x 3=-++；（2）1(2,3)Q ，2317117(,)22Q +--，3317117(,)22Q --+；（3）存在，(2,3)M 或5175317(,)22--+ 【解析】【分析】（1）设2(1)4(0)y a x a =-+≠，把C(0,3)代入求出a ，即可得出答案；（2）①过P 作PQ //BC ，交抛物线于点Q ，如图1所示；②求出点G 坐标，可得2PG GH ==，过H 作直线23Q Q //BC ，交x 轴于点H ，分别求出Q 的坐标即可；（3）MDN △为等腰直角三角形，则MN MD =，求出MN 、MD 的长度即可列出等量关系式，从而得出答案．【详解】（1）设2(1)4(0)y a x a =-+≠，把C(0,3)代入抛物线解析式得：43a +=，即1a =-，则抛物线解析式为22(1)423 y x x x =--+=-++；（2）由(3,0)B ，C(0,3)，得到直线BC 解析式为3y x =-+，①过P 作1PQ //BC ，交抛物线于点1Q ，如图1所示，(1,4)P ，∴直线PQ 解析式为5y x =-+，联立得：2235y x x y x ⎧=-++⎨=-+⎩，解得：14x y =⎧⎨=⎩或23x y =⎧⎨=⎩，即1(2,3)Q ；②过P 作PH x ⊥轴，交BC 于点G ，交x 轴于点H ，令1x =，代入3y x =-+，得2y =，(1,2)G ∴，2PG GH ∴==，过H 作直线23Q Q //BC ，则直线23Q Q 解析式为1y x =-+，联立得：2231y x x y x ⎧=-++⎨=-+⎩，解得：x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧⎪⎪⎨⎪=⎪⎩2Q ∴，3Q ，综上所述：点Q 的坐标为1(2,3)Q，2Q，3Q ；（3）MDN △为等腰直角三角形，则MN MD =，点()2,23M m m m -++，令x m =，代入3y x =-+得：3y m =-+，(,3)D m m ∴-+，函数的对称轴为：1x =，则点N 的横坐标为：2m -，则|22|MN m =-，2223(3)3MD m m m m m =-++--+=-+，2223m m m ∴-=-+，2223m m m -=-+或2223m m m -+=-+，解得：12m =或21m =-（舍）或3m =4m = 当2m =时，2233m m -++=，当m =223m m -++= 故点M 的坐标为：(2,3)或．【点睛】本题考查了二次函数综合题，设计知识有：用待定系数法求函数解析式、同底等高的面积计算、等腰直角三角形的性质，一次函数与二次函数交点问题，熟练掌握相关知识点是解决本题的关键．7．（1）都成立，理由见解析；（2）结论依然成立，理由见解析；（3）58【解析】【分析】（1）利用等边三角形的性质和含30直角三角形的性质，求得对应边的比值，即可求解；（2）过点B 作BE AC ∥交AD 延长线于点E ，利用等腰三角形的性质可得AB BE =，再利用相似三角形的性质即可求解；（3）连接DE ，由（2）可得，35CD AC DB AB ==，58EF AE FC AC ==，利用相似三角形的性质求解即可．【详解】（1）两个等式都成立，理由如下：∵ABC 为等边三角形，AD 为角平分线∴AD 垂直平分BC ，30CAD BAD ∠=∠=︒，AB AC = ∴CD BD =∴AC CD AB DB= ∵60CAB ∠=︒，11B C AC ⊥∴130B ∠=︒∴112AB AC =，即1112AC AB = 又∵130DAB B ∠=︒=∠∴1AD DB =在1Rt ADC 中，130C AD ∠=︒，∴112DA DB DC ==，1112C D DB = ∴1111AC C D AB DB = （2）结论依然成立，理由如下：如下图：过点B 作BE AC ∥交AD 延长线于点E∴E CAD BAD ∠=∠=∠∴AB BE =∵BE AC ∥∴ACD EBD △△∽∴AC CD EB DB= 又∵AB BE =∴AC CD AB DB=（3）如图，连接DE∵AD平分CAB∠∴AD为ABC和ACE的内角角平分线由（2）的性质可得，834053CD ACDB AB===，58EF AEFC AC==又∵5340553AEEB==-∴CD AE DB EB=∴BD BE BC AB=又∵B B∠=∠∴BDE BCA∽∴BED BAC ∠=∠∴DE AC∥∴DEF ACF∽∴58 DF EFAF FC==【点睛】此题考查了相似三角形的判定与性质，涉及了等边三角形的性质，等腰三角形的性质以及含30直角三角形的性质，解题的关键是灵活利用相关性质，构造出相似三角形，再利用相似三角形的性质求解即可．8．（1）见解析；（2）结论依然成立，理由见解析；（3）见解析【解析】【分析】（1）根据半角旋转模型，把△ABF逆时针旋转90°，则AB与AD重合，设F对应的点为M，即可证明AME AFE≅，得到AEM AEF∠=∠，再结合AEM EAG∠=∠，可得AEM AEF∠=∠，可得EG AG=；（2）结论依然成立，证明方法与（1）一样；（3）又等腰三角形三线合一的性质可得GQ垂直平分EA，可得△ANE是等腰直角三角形，可得A、D、E、N四点共圆，根据圆周角45NDC EAN∠=∠=︒【详解】（1）把△ABF 逆时针旋转90°，则AB 与AD 重合，设F 对应的点为M ，∴AMD AFB ≅∴90,,MDA FBA AM AF MAD FAB ∠=∠=︒=∠=∠ ∴M 、D 、C 三点共线∵45EAF ∠=︒∴45EAD FAB EAD MAD MAE ∠+∠=∠+∠=∠=︒ ∴()AME AFE SAS ≅∴AEM AEG ∠=∠∵AB ∥CD∴AEM EAG ∠=∠∴AEG EAG ∠=∠∴EG AG =（2）结论依然成立，EG AG =把△ABF 逆时针旋转90°，则AB 与AD 重合，设F 对应的点为M ， ∴AMD AFB ≅∴90,,MDA FBA AM AF MAD FAB ∠=∠=︒=∠=∠ ∴M 、D 、C 三点共线∵45EAF ∠=︒∴45EAD FAB EAD MAD MAE ∠+∠=∠+∠=∠=︒ ∴()AME AFE SAS ≅∴AEM AEG ∠=∠∵AB∥CD∴AEM EAG∠=∠∴AEG EAG∠=∠∴EG AG=（3）连接EN由（2）得EG AG=∵GQ AE⊥∴GQ垂直平分AE∴EN=AN∵45EAF∠=︒∴90ANE ADE∠=︒=∠∴A、D、E、N四点在以AE为直径的同一个圆上，∴45NDC EAN∠=∠=︒．【点睛】本题考查半角旋转模型，熟练根据模型做出辅助线是解题的关键．第（3）问根据四点共圆证明是本题的难点．9．（1）见详解；（2）12π；（3）16【解析】【分析】（1）连接CO，先证∠BCD=∠ADO，由∠A+∠ADO=90°，可得∠OCA+∠BCD=90°，进而即可得到结论；（2）先证BCD△是等边三角形，∠BOC=30°，求出OC=3，利用弧长公式即可求解；（3）过点O作ON⊥AD，过点B作BM⊥CD，利用勾股定理和面积法求出ON=125，AN=165，结合垂径定理和等腰三角形的性质得DM=710，最后利用锐角三家函数即可求解．【详解】解：（1）连接CO，∵BC＝BD，∴∠BDC=∠BCD，∵∠BDC=∠ADO，∴∠BCD=∠ADO，∵OA=OC，∴∠A=∠OCA，∵∠AOD＝90°，∴∠A+∠ADO=90°，∴∠OCA+∠BCD=90°，即OC⊥BC，∴BC是⊙O的切线；（2）∵∠OAD＝30°，∴∠OCA=∠OAD＝30°，∠AOC=180°-30°-30°=120°，∠ADO=∠BDC=90°-30°=60°，∴∠BOC=120°-90°=30°，又∵BC＝BD，∴BCD△是等边三角形，∴CB=CD＝3，∵OC⊥BC，∴OC=3×3=3，∴30311802CEππ⨯==；（3）过点O作ON⊥AD，过点B作BM⊥CD，∵OD＝3，DE＝1，∴AO=EO=3+1=4，∴AD5=，∴ON=125 OD OAAD⨯=，∴AN165 =，∴AC=2AN=325，∴CD=325-5=75，∵BD=BC，∴DM=75÷2=710，∵∠BDM=∠ADO，∴cos∠BDM=cos∠ADO，即：35 DM ODBD AB==，∴BD=53DM=710×53=76，∴BE=76-1=16．【点睛】本题主要考查圆和三角形的综合，掌握勾股定理，切线的判定定理，垂径定理，锐角三角函数的定义是解题的关键．10．（1）PC=2）见解析；（3）满足条件的PB的值为4+4．【解析】【分析】（1）如图1中，作PH⊥BC于H，．解直角三角形求出BH，PH，在Rt△PCH中，理由勾股定理即可解决问题；（2）根据菱形性质以及∠BAD=120°得∠PBQ=30°，再由∠PCQ=30°证明△POB∽△QOC 以及△POQ∽△BOC，即可得到∠PCQ=∠CPQ；（3）分两种情形：①如图2中，若直线QP交直线BC于B点左侧于E，②如图3中，若直线QP交直线BC于C点右侧于E，分别求解即可．【详解】解：（1）如图1中，作PH BC⊥于H．四边形ABCD 是菱形，8AB BC ∴==，//AD BC ，180A ABC ∴∠+∠=︒，120A ∠=︒，60PBH ∴∠=︒，6PB =，90PHB ∠=︒，cos603BH PB ∴=︒=，sin 6033PH PB =︒=，835CH BC BH ∴=-=-=，2222(33)5213PC PH CH ∴=+=+=．（2）设PC 交BD 于O ．四边形ABCD 是菱形，30ABD CBD ∴∠=∠=︒，30PCQ ∠=︒，PBO QCO ∴∠=∠，POB QOC ∠=∠，POB QOC ∴∆∆∽，∴PO BO QO CD =， ∴OP QO BO CD=， POQ BOC ∠=∠，POQ BOC ∴∆∆∽，30OPQ OBC PCQ ∴∠=∠=︒=∠，∴△PCQ 是等腰三角形；（3）①如图2中，若直线QP 交直线BC 于B 点左侧于E ．此时120CQE ∠=︒，60PBC ∠=︒，PBC ∴∆中，不存在角与CQE ∠相等，此时QCE ∆与BCP ∆不可能相似．②如图3中，若直线QP 交直线BC 于C 点右侧于E ．则60CQE B QBC QCP CBP ∠=∠=+∠=︒=∠，PCB E ∠>∠，∴只可能75BCP QCE ∠=∠=︒，作CF AB ⊥于F ，则4BF =，43CF =，45PCF ∠=︒，43PF CF ∴==，此时443PB =+，③如图4中，当点P 在AB 的延长线上时，QCE ∆与BCP ∆相似，120CQE CBP ∴∠=∠=︒，15QCE PCB ∴∠=∠=︒，作CF AB ⊥于F ．30FCB ∠=︒，45FCP ∴∠=︒，142BF BC ∴==，43CF PF ==， 434PB ∴=-．综上所述，满足条件的PB 的值为443+或434-．【点睛】本题考查了菱形的性质，解直角三角形，相似三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．11．（1）见解析；（2）不发生变化，理由见解析；（3）1【解析】【分析】（1）将△ABE 绕点A 逆时针旋转α 得到△AFG ，当点E 在线段BC 上，α＝90°时，过E 作EH BC ⊥，证明四边形HEDG 是平行四边形，即可得M 是GE 的中点；（2）过点E 作//EN GF ,交BM 的延长线于点N ，连接GN ,EF ，方法同（1）证明四边形FEGN 是平行四边形即可；（3）根据勾股定理求得AE ，①当E 在射线BC 上时，根据（2）的结论，取AE 的中点P ，连接,BP MP ，根据直角三角形斜边上的中线等于斜边的一半，三角形中位线定理，可得AE BM =，进而证明ABEM 是矩形，进而求得DM ，②当E 在射线CB 上时，可得此情况不符合题意，综合①②可得结果．【详解】（1）过E 作EH BC ⊥,如图，四边形ABCD 是正方形，45DBC ∴∠=︒//AB CDHE BC ⊥45BHE ∴∠=︒将△ABE绕点A逆时针旋转α得到△AFG，,∴=BE GD∴=HE GD⊥⊥,GF AD AD DC∴三点共线,,G D C∴⊥GC BC∴GD HE//∴四边形HEDG是平行四边形∴为GE的中点；M（2）（1）中的结论，M是GE的中点，仍然成立，理由如下：如图，过点E作//EN GF,交BM的延长线于点N，连接GN,EF将△ABE绕点A逆时针旋转α得到△AFG，,=∴=,BE FGAB AF∠=设ABFβ∴∠=∠=ABF AFBβ四边形ABCD是正方形，90∴∠=∠=︒ABC AFG∴∠=︒-,18090∠=︒-∠-∠=︒-GFN AFB AFGβEBNβ90EN GF//BNE GFNβ∴∠=∠=︒-90∴∠=∠EBN ENB∴=EB EN=BE FG∴四边形FEGN 是平行四边形∴M 是GE 的中点（3）AB ＝4，BE ＝5，BM ＝41 四边形ABCD 是正方形，90ABC AFG ∴∠=∠=︒,4AD AB BC ===Rt ABE △中，22224541AE AB BE =+=+=AE BM ∴=将△ABE 绕点A 逆时针旋转α得到△AFG ,AB AF ∴=,BE FG =,AE AG =①当E 在射线BC 上时，如图，取AE 的中点P ，连接,BP MP则PA PE =∴114122BP AE ==由（2）可知M 为GE 的中点， ∴114122PM AG == BP PM ∴=PA PE =∴四边形ABEM 是平行四边形41BP PM AE BM ∴+===即AE BM =∴四边形ABEM 是矩形即,,B P M 三点共线，如图，541DM AM AD BE BC ∴=-=-=-=②当E 在射线CB 上时，，由已知，AE 41BM 41由题意，AE ≠BM 故此情况不存在综上所述，1DM =【点睛】本题考查了正方形的性质，平行四边形的性质与判定，矩形的性质与判定，勾股定理，等腰三角形的性质，等边对等角，三线合一，旋转的性质，综合运用以上知识，并能正确的添加辅助线是解题的关键．12．（1）23233y =221733）存在，111⎛ ⎝⎭或1111,⎛ ⎝⎭ 【解析】【分析】（1）由已知可设抛物线的解析式为(1)(3)y a x x =+-，由已知条件可求得点C 的坐标，把点C 的坐标代入解析式中即可求得a 的值，从而可得二次函数的表达式；（2）过点P 作PD ⊥x 轴于点D ，连接PO ，设点P 的坐标为23233m ⎛ ⎝，则由题意可得OD 、PD 的长度，由PBC POC POB BOC S S S S =+-可得关于m 的二次函数，即可求得此时函数的最大值，从而可得点P 的坐标；过点A 作BC 的平行线，且在位于x 轴下方的直线上取AG =NM ，过G 作GH 垂直x 轴于点H ，连接GP ，则可求得点G 的坐标，当点M 在线段GP 上时，PM +NA 最小，从而PM +MN +NA 最小，可求得其最小值．（3）当四边形AEFQ 是菱形时，△AEQ 是等腰三角形，由点E 在抛物线的对称轴上，故设点E (1，n )，由旋转的性质则可得AE =AQ =AP ，可得关于n 的方程，解方程即可求得n ，从而求得点E 的坐标．【详解】（1）∵抛物线交x 轴于A （﹣1，0）、B （3，0）两点∴设抛物线的表达式为(1)(3)y a x x =+-，且OA =1∵∠OAC =60゜，OA ⊥OC∴∠OCA =30゜∴AC =2OA =2∴OC∴(0,C把点C 的坐标代入(1)(3)y a x x =+-中，得3a -=∴a =∴1)(3)y x x =+-展开得：2y =-即二次函数的表达式为2y x x =-（2）过点P 作PD ⊥x 轴于点D ，连接PO ，如图2—1设点P 的坐标为2m ⎛ ⎝ ∵点P 位于第四象限内∴OD =m ，22PD =-=+⎝∵B (3，0)∴OB =3∵PBC POC POB BOC S S S S =+-111222OC OD PD OB OC OB =⨯+⨯-⨯232⎛=++ ⎝2= 232m ⎫=-⎪⎝⎭ ∴当32m =时，△PBC 的面积有最大值当当32m =2=此时点P 的坐标为3,2⎛ ⎝⎭∵MN =为定值 ∴PM +MN +NA 的最小值就是求PM +NA 的最小值过点A 作BC 的平行线，且在位于x 轴下方的直线上取AG =NM ，过G 作GH 垂直x 轴于点H ，连接GP ，如图2-2 ∵AG ∥NM ，AG =NM ∴四边形AGMN 是平行四边形 ∴GM =AN∴PM +NA =PM +GM ≥GP∴当点M 在线段GP 上时，PM +NA 最小，且最小值为线段GP 的长，从而PM +MN +NA 最小在Rt △COB 中，由勾股定理得BC ∴BC =2OC ∴∠CBO =30゜ ∵AG ∥BC∴∠HAG =∠CBO =30゜ ∵GH ⊥x 轴∴12HG AG ==由勾股定理得34AH == ∴37144OH OA AH =+=+=∴G 点坐标为7,4⎛- ⎝⎭由勾股定理得GP =即PM +NA 的最小值为2174∴PM +MN +NA 的最小值为217342+（3）存在；理由如下：由于四边形AEFQ 是菱形，则△AEQ 是等腰三角形，且AE =AQ ∵抛物线的对称轴为直线x =1，点E 在抛物线的对称轴上 ∴设点E (1，n )则2222(11)4AE n n =++=+ ∵AP 绕点A 旋转后得到AQ ∴AP =AQ ∴AE =AQ =AP∵2223531751216AP ⎛⎫=++= ⎪⎝⎭⎝⎭∴由AE =AP 得：2175416n += 解得：111n =∴点E 的坐标为111⎛ ⎝⎭或1111,⎛ ⎝⎭【点睛】本题是二次函数的综合题，考查了用待定系数法求二次函数的解析式及二次函数的性质，图形的面积，菱形的性质，直角三角形的性质等，综合性强，考查的知识点多，运算量大，是中考常考的压轴题．就数学思想方法而言有：割补思想，转化思想（三线段和的最小值转化为两线段和的最小值），方程思想，数形结合等．13．(1)757221【解析】【分析】（1）①根据旋转的性质得到CB CE =，求得EBC BEC ∠=∠，根据平行线的性质得到EBC BEA ∠=∠，于是得到结论；②如图1，过点B 作CE 的垂线BQ ，根据角平分线的性质得到AB BQ =，求得=CG BQ ，根据全等三角形的性质得到BH GH =，根据三角形的中位线定理即可得到结论； ③如图2，过点G 作BC 的垂线GM ，解直角三角形即可得到结论．（2）如图3，连接DB ，DG ，过G 作GP BC ⊥交BC 的延长线于P ，GN DC ⊥交DC 的延长线于N ，根据旋转的性质得到4==CE BC ，2CD AB ==，解直角三角形得到1NG =，3PG =(1)解：①证明：矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ，CB CE ∴=，EBC BEC ∴∠=∠，又//AD BC ，EBC BEA ∴∠=∠， BEA BEC ∴∠=∠，BE ∴平分AEC ∠；。

2022届中考数学压轴难题及答案解析

一、解答题1．如图①，二次函数2y ax bx c =++（a ≠0）的图象经过点A （1-，0），并且与直线122y x =-相交于坐标轴上的B 、C 两点，动点P 在直线BC 下方的二次函数的图象上．（1）求此二次函数的表达式；（2）如图①，连接PC ，PB ，设△PCB 的面积为S ，求S 的最大值；（3）如图②，过点A ，C 作直线，求证AC ⊥BC ；（4）如图②，抛物线上是否存在点Q ，使得∠ABQ ＝2∠ABC ？若存在，则求出直线BQ 的解析式；若不存在，请说明理由．2．如图，直线3y kx =+交x 轴于A 点，交y 轴于B 点，过A 、B 两点的抛物线的顶点坐标(1，4)．（1）求k 的值和抛物线的解析式；（2）在抛物线的对称轴上求一点P ，使得PAB 的周长最小，并求出最小值；（3）在抛物线的对称轴上是否存在点Q ，使ABQ 是等腰三角形？若存在，求出符合条件的Q 点坐标；若不存在，请说明理由．3．已知：如图，在平面直角坐标系中，点O 为坐标原点，直线y ＝﹣x +b （b ＞0）交x 轴于点A ，交y 轴于点C ，以OA ，OC 为边作矩形ABCO ，矩形ABCO 的面积是36．（1）求直线AC 的解析式．（2）点P 为线段AB 上一点，点Q 为第一象限内一点，连接PO ，PQ ，∠OPQ ＝90°，且OP ＝PQ ，设AP 的长为t ，点Q 的横坐标为d ，求d 与t 的函数关系式．（不要求写出自变量t 的取值范围）（3）在（2）的条件下，过点Q 作QE ∥PO 交AB 的延长线于点E ，作∠POC 的平分线OF 交PE 于点F ，交PQ 于点K ，若KQ ＝2EF ，求点Q 的坐标． 4．在ABC 中，AB BC =，45B ∠=︒，AD 为BC 边上的高．（1）如图1，若1AD =，求线段CD 的长度；（2）如图2，点E ，点F 在AB 边上，且满足AE BF =，连接CE ，CF 分别交线段AD 于点M ，点N ，若点M 为线段CE 的中点，求证：2AN CD AB +=；（3）在（2）问条件下，若2AC =，点K 为AC 边上一动点，点Р为ACF 内一点且满足ACP CAD ∠=∠，当PK PA +取最小值时，请直接写出CPK S △的值．5．已知有理数a ，b ，c 在数轴上对应的点分别为A ，B ，C ，其中b 是最小的正整数，a ，c 满足()2250a c ++-=．（1）填空：=a ______，b =______，c =______；（2）点A ，B ，C 分别以每秒4个单位长度，1个单位长度，1个单位长度的速度在数轴上同时向右运动，设运动时间为t 秒．①当AC 长为6时，求t 的值；②当点A 在点C 左侧时（不考虑点A 与B ，C 重合的情况），是否存在一个常数m 使得2AC m AB +⋅的值在某段运动过程中不随t 的改变而改变？若存在，求出m 的值；若不存在，请说明理由．6．问题提出：（1）如图①，在ABC 中，90BAC ∠=︒，AH BC ⊥，垂足为点H ，若4AB =，3AC =，则线段CH 的长度为___________；问题探究：（2）如图②，在四边形ABCD 中，90BAD C ∠=∠=︒，AB AD =，点F 为CD 边的中点，点E 是BC 边上的一点，连接AE ，AF ，EF ．若45EAF ∠=︒，6BC =，2CD =，求线段EF 的长；问题解决：（3）如图③，在四边形ABCD 中，AD BC ∥，AB AD =，60ABC ∠=︒，90C ∠=︒，点M ，N 是BC 边上的两点，连接AM ，AN ，BD ，BD 交AM 于点E ，交AN 于点F ．若30MAN ∠=︒，4BE =，6DF =，求AMN 的面积．7．如图抛物线2y ax bx c =++经过点()1,0A -，点()3,0B ，点()0,3C ．（1）求抛物线的解析式及其对称轴；（2）点P 为抛物线上一点，连接CP ，若直线CP 分四边形CBPA 的面积为1:3的两部分，求点P 的坐标．（3）点D 、E 是直线1x =上的两个动点，且1DE =，点D 在点E 的上方，求四边形ACDE 的周长的最小值及此时点D 的坐标．8．问题提出（1）如图①，在△ABC 中，BC ＝2，将△ABC 绕点B 顺时针旋转60°得到△A ′B ′C ′，则CC ′＝；问题探究（2）如图②，在△ABC 中，AB ＝BC ＝3，∠ABC ＝30°，点P 为△ABC 内一点，连接PA 、PB 、PC ，求PA ＋PB ＋PC 的最小值，并说明理由；问题解决（3）如图③，在四边形ABCD 中，AD ∥BC ，AB ＝6，AD ＝4，∠ABC ＝∠BCD ＝60°．在四边形ABCD 内部有一点，满足∠APD ＝120°，连接BP 、CP ，点Q 为△BPC 内的任意一点，是否存在一点P 和一点Q ，使得PQ ＋BQ ＋CQ 有最小值？若存在，请求出这个最小值；若不存在，请说明理由．9．如图，在ABC 中，45A ∠=︒．（1）如图1，若62AC =13BC =ABC 的面积；（2）如图2，D 为ABC 外的一点，连接CD ，BD 且CD CB =，ABD BCD ∠=∠．过点C 作CE AC ⊥交AB 的延长线于点E ．求证：22BD AB +=．（3）如图3，在（2）的条件下，作AP 平分CAE ∠交CE 于点P ，过E 点作EM AP ⊥交AP 的延长线于点M ．点K 为直线AC 上的一个动点，连接MK ，过M 点作'MK MK ⊥，且始终满足'MK MK =，连接'AK ．若4AC =，请直接写出''AK MK +取得最小值时()2''AK MK +的值．10．如图1，抛物线y ＝ax 2﹣94x +c 与x 轴交于A （﹣1，0）和B 两点，与y 轴交于C （0，﹣3），E 为抛物线顶点，抛物线的对称轴交x 轴于点H ．（1）求抛物线的解析式；（2）已知点3(0,2)2F -，点P 在对称轴右侧的抛物线上运动，连接PO ，PO 与对称轴交于点D ，连接DF ．当DF 平分∠ODE 时，求点P 的坐标；（3）如图2，平移对称轴EH 交抛物线于M ，交直线BC 于N ．以N 为圆心，NM 为半径作⊙N ．当⊙N 与坐标轴相切时，请直接写出⊙N 的半径长．11．已知，如图，抛物线y ＝14-x 2+bx +c 与x 轴正半轴交于A 、B 两点，与y 轴交于点C ，直线y ＝x ﹣2经过A 、C 两点．（1）直接写出抛物线的解析式；（2）P 为抛物线上一点，若点P 关于直线AC 的对称点Q 落在y 轴上，求P 点坐标；（3）现将抛物线平移，保持顶点在直线y ＝x ﹣114，若平移后的抛物线与直线y ＝x ﹣2交于M 、N 两点．①求证：MN 的长度为定值；②结合（2）的条件，直接写出△QMN 的周长的最小值12．如图，抛物线y ＝ax 2+bx +6与x 轴交于A （2，0），B （8，0）两点，与y 轴交于点C．（1）求抛物线的解析式；（2）点P是抛物线上一动点，当∠PCB12∠BCO时，求点P的横坐标．13．【探究发现】(1)如图①，已知四边形ABCD是正方形，点E为CD边上一点（不与端点重合），连接BE，作点D关于BE的对称点D'，DD'的延长线与BC的延长线交于点F，连接BD′，D'E．①小明探究发现：当点E在CD上移动时，△BCE≌△DCF．并给出如下不完整的证明过程，请帮他补充完整．证明：延长BE交DF于点G．②进一步探究发现，当点D′与点F重合时，∠CDF＝°．【类比迁移】(2)如图②，四边形ABCD为矩形，点E为CD边上一点，连接BE，作点D关于BE的对称点D'，DD′的延长线与BC的延长线交于点F，连接BD'，CD'，D'E．当CD'⊥DF，AB＝2，BC＝3时，求CD'的长；【拓展应用】(3)如图③，已知四边形ABCD为菱形，AD3AC＝2，点F为线段BD上一动点，将线段AD绕点A按顺时针方向旋转，当点D旋转后的对应点E落在菱形的边上（顶点除外）时，如果DF＝EF，请直接写出此时OF的长．14．某一种蜜桔在农贸水果市场的需求量y1（万斤）、市场供应量y2（万斤）与市场价格x（元/斤）分别满足下列关系：y1=-0.2x + 2.8 ，y2= 0.4x - 0.8．当y1=y2 时的市场价格称为市场平衡价格，此时的需求量称为平衡需求量．(1)求平衡价格和平衡需求量．(2)若该蜜桔的市场销售量y（万件）是市场需求量y1和市场供应量y2两者中的较小者，该蜜桔的市场销售额P（万元）等于市场销售量y 与市场价格x 的乘积．当市场价格x 取何值时，市场销售额P 取得最大值？(3)蜜桔的每斤进价为m 元，若当3≤x≤10 时，随着x 的增大，蜜桔的销售利润（万元）会经历先减小后增大再减小的变化，请直接写出m 的取值范围．15．已知，AB是O的直径，P为AB延长线上一点，点C在O上，连接PC交O于点D，(1)如图1：求证：；图1(2)如图2：E为O上一点，连接CE、AD交于点F，若，求证：；图2(3)如图3：在（2）的条件下，AB交CE于点G，GM⊥CP于M，若，，求线段AB的长．图316．如图，在正方形ABCD 中，点E 是BC 边上的一点，∠AEP=90°，且EP 交正方形外角的平分线CP 于点P．(1)求∠ECP 的度数；(2)求证：∠BAE=∠CEP；(3)求证：AE=EP；(4)在AB 边上是否存在点M，使得四边形DMEP 是平行四边形？若存在，请画出图形并给予证明；若不存在，请说明理由．17．在△ABC中，AB=AC，点D为AB边上一动点，∠CDE=∠BAC=α，CD=ED，连接BE，EC．(1)问题发现：如图①，若α=60°，则∠EBA= ，AD与EB的数量关系是；(2)类比探究：如图②，当α=90°时，请写出∠EBA 的度数及AD 与EB 的数量关系并说明理由； (3)拓展应用：如图③，点E 为正方形ABCD 的边AB 上的三等分点，以DE 为边在DE 上方作正方形DEFG ，点O 为正方形DEFG 的中心，若OA =2，请直接写出线段EF 的长度18．问题提出：如图①所示，在矩形AOCB 和矩形ODEF 中，CO FOk AO DO==，点A ，O ，D 不在同一直线上，连接,AD CF ．HO 是AOD △的中线，那么,HO CF 之间存在怎样的关系？(1)问题探究：先将问题特殊化，如图②所示，当1k =且90AOD ∠=︒时，,HO CF 的数量关系是________，位置关系是________．(2)问题拓展：再探究一般情形如图③所示，当1k =，90AOD ∠≠︒时，证明（1）中的结论仍然成立．(3)问题解决：回归图①所示，探究,HO CF 之间存在怎样的关系（数量关系用k 表示）？ 19．已知：如图1，点A （a ，b ），AB x ⊥轴于点B ，并且满足224(8)0a b a b +++-+=．（1）试判断△AOB 的形状，并说明理由；（2）如图2，若点C 为线段AB 的中点，连OC 并作OD OC ⊥，且OD OC =，连AD 交x 轴于点E ，试求点E 的坐标；（3）如图3，若点M 为点B 的左边x 轴负半轴上一动点，以AM 为一边作45MAN ∠=︒交y 轴负半轴于点N ，连MN ，在点M 运动过程中，试猜想式子OM MN ON +-的值是否发生变化？若不变，求这个不变的值；若发生变化，试求它变化的范围．20．如图，已知AB 是⊙O 的直径．BC 是⊙O 的弦，弦ED 垂直AB 于点F ，交BC 于点G ．过点C 作⊙O 的切线交ED 的延长线于点P（1）求证：PC ＝PG ；（2）判断PG 2＝PD ·PE 是否成立？若成立，请证明该结论；（3）若G 为BC 中点，5OG 5sin B =，求DE 的长．【参考答案】**科目模拟测试一、解答题 1．（1）213222y x x =--；（2）4；（3）见解析；（4）存在，41633y x =-和41633y x =-+.【解析】【分析】（1）根据题意先求出点B 、C 的坐标，进而利用待定系数法即可求解；（2）由题意过点P 作PD ⊥x 轴于D ，交BC 于点E ，并设点P （x ，12x 2﹣32x ﹣2），进而根据S △CPB ＝S △CPE +S △BPE =111222OD PE BD PE PE OB ⋅+⋅=⋅，进行计算即可求解；（3）根据点C （0-，2），点B （4，0），点A （1-，0），得出OB ＝4，OC ＝2，OA ＝1，在Rt △OBC 中，根据勾股定理BC 22+16425OB OC +Rt △OAC 中，AC 22+4+15OC OA =AB =OA +OB =4-（-1）=5，根据勾股定理逆定理22+BC AC=2222255AB +===，即222BC AC AB +=即可；（4）根据题意分点Q 在BC 下方、在AC 的延长线上取一点F ，使CF ＝AC ，作出∠ABQ ＝2∠ABC ，连接BF ，设BF 与抛物线交于点Q ，过点F 作FN ⊥y 轴于N ，FH ⊥x 轴于H ，点Q 在BC 上方，延长FH 到M ，使HM ＝HF ，连接BM 并延长BM 交y 轴于G ，作出∠MBH ＝∠FBH ＝2∠ABC ，两种情况求出点F ，和点M 的坐标，进而利用待定系数法求BQ 解析式即可求解．【详解】解：（1）∵122y x =-交坐标轴于B ，C 两点，当x =0时，y =-2,点C （0-，2），当y =0时，1202x -=，解得4x =，点B （4，0），∵A （1-，0），∴2y ax bx c =++16420202a b a b c +-=⎧⎪--=⎨⎪=-⎩，解得12322a b c ⎧=⎪⎪⎨=-⎪⎪=-⎩， ∴二次函数解析式为：213222y x x =--；（2）过点P 作PD ⊥x 轴于D ，交BC 于E ，设P 点的横坐标为m ，则 P （m ，213222m m --），E （m ，122m -）， ∴PE ＝2113(2)(2)222m m m ----＝2122m m -+， ∵OB ＝4，∴S △CPB ＝S △CPE +S △BPE =()11112222OD PE BD PE PE OD BD PE OB ⋅+⋅=+=⋅， =21142)22m m ⨯+（- ， ∴S △CPB ＝()22424m m m -+=--+，当2m =时，4PCB S ∆=最大， ∴S 的最大值为4；（3）证明：点C （0-，2），点B （4，0），点A （1-，0），∴OB ＝4，OC ＝2，OA ＝1，∵∠AOC ＝∠COB ＝90°，在Rt △OBC 中，根据勾股定理BC 22+16425OB OC +在Rt △OAC 中，AC 22+4+15OC OA =AB =OA +OB =4-（-1）=5，∵22+BC AC =2222(25)(5)255AB +===，即222BC AC AB +=，∴∠ACB=90°，∴AC ⊥BC ；（4）存在点Q，使∠ABQ＝2∠ABC．当点Q在x轴下方的抛物线上时：在AC的延长线上取一点F，使CF＝AC，连接BF，若BF与抛物线有交点，设BF与抛物线交于点Q，过点F作FN⊥y轴于N，FH⊥x轴于H.∵∠FNC＝∠AOC＝90°，∠FCN＝∠ACO，AC＝CF，∴△FNC≌△AOC，∴FN＝AO＝1，∵FH⊥x轴，∴OH＝NF＝1，∵BC⊥AC，AC＝CF，∴∠ABF ＝2∠ABC ，∵AC ＝CF ，AO ＝OH ，∴HF ＝2OC ＝4，∴F （1，4-），设BQ 的解析式为：y kx b =+，∴440k b k b +=-⎧⎨+=⎩，解得：43k =，163b =-， ∴BQ 的解析式为：41633y x =-． ∵24163313222y x y x x ⎧=-⎪⎪⎨⎪=--⎪⎩ ， 21341622233x x x --=- ， 2317200x x -+= ，=289240490∆-=＞，∴方程组有两个不同的解，直线BF 与抛物线有两个不同的交点，Q 存在．当点Q 在x 轴上方的抛物线上时：延长FH 到M ，使HM ＝HF ，连接BM 并延长BM 交y 轴于G ，若BG 与抛物线有交点，设BG 交抛物线于点Q ，∵FH ⊥x 轴，FH ＝MH ，∴∠MBH ＝∠FBH ＝2∠ABC ，M （1,4），∴BM 的解析式为：41633y x =-+． ∵24163313222y x y x x ⎧=-+⎪⎪⎨⎪=--⎪⎩， 21341622233x x x --=-+ ， 23440x x --= ，=1+528=5290∆＞，∴方程组有两个不同的解，直线BM 与抛物线有两个不同的交点，Q 存在．∴存在抛物线上点Q ，使∠ABQ ＝2∠ABC ，直线BQ 的解析式有两个，它们是： 41633y x =-和41633y x =-+．【点睛】本题考查待定系数法求二次函数解析式和性质，一次函数解析式，三角形面积的最值，直线的位置关系，二倍角的函数解析式，一元二次方程，三角形全等判定与性质，勾股定理与勾股定理逆定理，本题综合性强，难度大，是中考压轴题，利用辅助线作出准确图形，熟练掌握所需知识是解题关键．2．（1）k =3，抛物线的解析式为2y x 2x 3=-++；（2）△PAB 周长的最小值为P 坐标为（1，2）；（3）存在，点Q 坐标分别为Q 1（1），Q 2（1，Q 3（1，0），Q 4（1，1）．【解析】【分析】（1）令x =0，可得点B 坐标，根据顶点坐标可设设抛物线解析式为2(1)4y a x =-+，把点B 坐标代入可求出a 值，即可得抛物线解析式，令y =0可得点A 坐标，代入3y kx =+即可得k 值；（2）如图连接BC ，交对称轴于P ，根据抛物线解析式可得对称轴为直线x =1，点C 坐标为（3，0），根据二次函数得对称性可得PA =PC ，即可得出PA +PB =BC ，可得△PAB 得周长的最小值为BC +AB ，利用勾股定理即可得△PAB 周长的最小值，根据点B 、C 坐标，利用待定系数法可得直线BC 解析式，令x =1即可得点P 坐标；（3）设点Q 坐标为（1，m ），分QA =AB ，QB =AB ，QA =QB ，三种情况，根据两点间距离公式求出m 的值即可得答案．【详解】（1）当x =0时，y =3，∴点B 坐标为（0，3），∵过A 、B 两点的抛物线的顶点坐标(1，4)，∴设抛物线的解析式为2(1)4y a x =-+，∴2(01)43a -+=，解得：1a =-,∴抛物线的解析式为2(1)4y x =--+，即2y x 2x 3=-++，当y=0时，2230x x -++=，解得：11x =-，23x =，∵点A 在x 轴负半轴，∴A （-1，0），C （3，0），把A （-1，0）代入3y kx =+得：-k +3=0，解得：k =3．（2）如图，连接BC ，交对称轴于点P ，∵抛物线的解析式为2y x 2x 3=-++，∴对称轴为直线x =212(1)-=⨯-， ∵抛物线与x 轴交于点A 、C ，∴A 、C 关于对称轴对称，∴PA =PC ，∴PA+PB=PB+PC=BC，∴△PAB的周长的最小值为AB+BC，∵A（-1，0），B（0，3），C（3，0），∴OA=1，OB=3，OC=3，∴AB+BC=2222OA OB OB OC+++=1032+，设直线BC的解析式为y=kx+b，∴330bk b=⎧⎨+=⎩，解得：k=-1，∴直线BC的解析式为y=-x+3，当x=1时，y=-1+3=2，∴点P坐标为（1，2）．∴△PAB周长的最小值为1032+，点P坐标为（1，2）．（3）设点Q坐标为（1，m），∵A（-1，0），B（0，3），∴AB22(10)(03)--+-10，QA22(11)(0)m--+-24m+ QB22(10)(3)m-+-2(3)1m-+①当QA=AB时，24m+10解得：m=6∴Q1（16），Q2（1，6-②当QB=AB时，2(3)1m-+10，解得：m=6或m=0，∵直线AB的解析式为y=3x+3，∴x=1时，y=6，∴点（1，6）在直线AB上，与A、B不能构成三角形，∴Q3（1，0），③当QA=QB时，解得：m=1，∴Q4（1，1），综上所述：存在点Q，使ABQ是等腰三角形，点Q坐标分别为Q 1（1），Q2（1，Q3（1，0），Q4（1，1）．【点睛】本题考查二次函数与一次函数的综合，熟练掌握待定系数法求函数解析式、二次函数得对称性并灵活运用分类讨论得思想是解题关键．3．（1）直线AC的解析式为y＝﹣x+6；（2）d=4-t；（3）Q（212，1）．【解析】【分析】（1）先由解析式求出得A、C点的坐标，得OA=OC，得四边形ABCO为正方形，再根据正方形的面积求得边长，便可得b的值；（2）过点Q作QG⊥AB交AB延长沿于点G，证明Rt△AOP≌Rt△GPQ（AAS），得到AP=GQ，进而求得结论便可；（3）过点P作PH⊥OF于点H，延长PH交EQ的延长线于点R，EQ的延长线与x轴交于点N，过Q作QM⊥x轴于点M．证明Rt△AOP≌Rt△GPQ（CCS），得PK=QR，∠R=∠OKP，再证明∠R=∠FPR，得EP=ER，再证FE=NR，设FE=NR=k，NQ=m，在Rt△PQE中，由勾股定理列出方程，得到k与m的关系，解Rt△PQE得tan∠PEQ，进而把这个函数值运用到△OAP中，求得t的值，再运用（2）中结论得Q的纵坐标d的值，再运用到△QNM中求得NM，NQ的值，进而求得ON，便可得Q的横坐标的值．【详解】解：（1）∵直线y＝﹣x+b（b＞0）交x轴于点A，交y轴于点C，∴(,0),(0,)A b C b，∴OA=OC=b，∴矩形ABCO为正方形，∵矩形ABCO的面积是36．∴b=6，即直线AC的解析式为y＝﹣x+6；（2）如图，过点Q作QG⊥AB交AB延长沿于点G，∵∠OPQ=90°，∴∠APO+∠GPQ=90°，∵∠APO+∠AOP=90°，∴∠AOP=∠GPQ，∵在矩形ABCO，∠OAP=90°，QG⊥AB,∴∠QGP=∠OAP=90°，∵PQ=OP，∴Rt△AOP≌Rt△GPQ（AAS），∴AP=GQ，∵AP=t，∴GQ=t，∴d=4-t；（2）过点P作PH⊥OF于点H，延长PH交EQ的延长线于点R，EQ的延长线与y轴交于点N，过Q作QM⊥y轴于点M．则AP=t，QM=d，且d=6-t．∵OF 平分∠POC ，∴∠POF =∠COF =∠PFO ，∴PF =PO ，∵PH ⊥OF ，∠OPQ ＝90°，∴∠OPH =∠FPH ，∠KPH =∠POH ，在△OPK 和△PQR 中，90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩＝＝＝＝， ∴△OPK ≌△PQR （ASA ）， ∴PK =QR ，∠R =∠OKP ，∵∠OKP +∠POK =∠POK +∠OPH =90°， ∴∠OKP =∠OPH ，∴∠R =∠OPH ，∵PO =PF ，PH ⊥OF ，∴∠OPH =∠FPH ，∴∠R =∠FPR ，∴EP =ER ，∵PE ∥ON ，OP ∥EN ，∴四边形OPEN 是平行四边形， ∴EN =PO =PF ，∴PE -PF =ER -EN ，∴FE =NR ，设FE =NR =k ，则KQ =2FE =2k ，又设NQ =m ，∴PK =QR =m +k ，∴PQ =m +3k ，∴PO =EN =PF =m +3k ，∴QE =EN -QR =m +3k -m =3k ， PE =PF +FE =4k +m ，在Rt △PQE 中，∵PE 2=PQ 2+QE 2，∴（4k +m ）2=（3k +m ）2+（3k ）2， ∴k 1=0（舍去），k 2=m ，∴PQ =4m ，QE =3m ，∴tan ∠PEN =43PQ QE =， ∵OP ∥EN ，∴∠OPA =∠PEN ，∴tan ∠APO =43， ∵AO =6，∴AP =4.5，∴t =4.5，∴QM =d =6-t =1.5，∵PE ∥OC ，∴∠QNM =∠PEN ，∴tan ∠QNM =tan ∠PEN =43， ∴NM =9tan 8QM QNM =∠，∴m =NQ 158=， ∴PE =ON =4k +m =5m =758， ∴OM =ON +NM =212， ∴Q （212，1）．【点睛】本题是一次函数与四边形的综合题，主要考查了一次函数的图象与性质，全等三角形的性质与判定，正方形的性质，旋转的性质，解直角三角形的应用，等腰三角形的性质与判定，平行四边形的性质与判定，是一道综合性极强的题目，解决这类问题常用到数形结合、方程和转化等数学思想方法．构造全等三角形是解题的关键，也是问题的突破口．4．（11；（2）证明见解析；（3 【解析】【分析】（1）证明,AD BD = 再利用勾股定理求解,,AB BC 从而可得答案；（2）如图，过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥ 证明,EHM CDM ≌ 可得,AE == 同理：,BF == 而,AE BF = 再证明,FQC DCA ≌ 可得,FCQ CAD ∠=∠ 再证明,AF AN = 从而可得结论；（3）如图，记CP 与AB 的交点为,L 由（2）得：45,ACF BAD ∠=∠=︒ 证明,22.5,CF CA CAD =∠=︒ 可得CP 平分,ACF ∠ 则,A F 关于直线CP 对称，,PF PA = 过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+= 所以PA PK +最短，设,PK n = 则1,1,PF PA n AK ==-= 再利用勾股定理求解,n 即可得到答案.【详解】解：（1）45B ∠=︒，AD 为BC 边上的高，90,45,ADB B BAD ∴∠=︒∠=∠=︒ 221,112,AD BD AB ∴===+=AB BC =，2,2 1.BC CD BC BD ∴==-=-（2）如图，过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥则90,EHM CDM ∠=∠=︒M 为CE 的中点，,HME DMC ∠=∠,EM CM ∴=,EHM CDM ∴≌,EH CD ∴=45,90,BAD AHE EHM ∠=︒∠=∠=︒ 22,AE EH CD ∴==同理：22,BF FQ BQ == 而,AE BF =,FQ BQ CD EH ∴===,BD CQ AD ∴==90,ADC CQF ∠=∠=︒,FQC DCA ∴≌,FCQ CAD ∴∠=∠,AB BC =,BAC BCA ∴∠=∠,BAD ACF ∴∠=∠ 而,B BAD ∠=∠,,B FCQ AFN ANF ACF CAD ∠+∠=∠∠=∠+∠,AFN ANF ∴∠=∠,AF AN ∴=2.AN CD AF AE AF BF AB ∴=+=+=（3）如图，记CP 与AB 的交点为,L 由（2）得：45,ACF BAD ∠=∠=︒,45,BA BC B =∠=︒67.5,BAC BCA ∴∠=∠=︒67.5,CFA BAC ∴∠=︒=∠,22.5,CF CA CAD ∴=∠=︒22.5,ACP CAD ∠=∠=︒CP ∴平分,ACF ∠,,CP AF AL FL ∴⊥=则,A F 关于直线CP 对称，,PF PA =过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+=所以PA PK +最短，2,AC ∴= 则2,CF = 而45,ACF ∠=︒1,CK FK ∴==设,PK n = 则1,21,PF PA n AK ==-=())222121,n n ∴-=+ 解得：21,n = )121121.22CPK S ∴=⨯⨯= 【点睛】本题考查的是全等三角形的判定与性质，等腰直角三角形的判定与性质，等腰三角形的判定与性质，勾股定理的应用，本题综合性较强，是压轴题，知识的系统化是解题的关键.5．（1）2,1,5-；（2）①13或133；②存在，m 的值为2-或2．【解析】【分析】（1）根据正整数的定义、绝对值的非负性、偶次方的非负性分别可求出,,b a c 的值；（2）①先求出运动t 秒后，点,A C 所表示的数，再分点A 在点C 左侧和点A 在点C 右侧两种情况，然后根据数轴的定义建立方程，解方程即可得；②先求出运动t 秒后，点,,A B C 所表示的数，从而可得AC 的长，再分点A 在点B 左侧和点A 在点B 右侧两种情况，分别求出AB 的值，代入化简，然后根据整式的无关型问题求解即可得．【详解】解：（1）b 是最小的正整数，1b ∴=，()2250a c ++-=，20,50a c ∴+=-=，解得2,5a c =-=，故答案为：2,1,5-；（2）①由题意，运动t 后，点A 所表示的数是42t -，点C 所表示的数是5t +，当点A 在点C 左侧时，5(42)6AC t t =+--=，解得13t =，当点A 在点C 右侧时，42(5)6AC t t =--+=，解得133t =，综上，t 的值为13或133； ②由题意，运动t 后，点A 所表示的数是42t -，点B 所表示的数是1t +，点C 所表示的数是5t +，当421t t -=+时，13t =，当425t t -=+时，73t =，因为点A 在点C 左侧，所以5(42)73AC t t t =+--=-，当点A 在点B 左侧，即01t <<时，1(42)33AB t t t =+--=-，则22(73)(33)314(36)AC m AB t m t m m t +⋅=-+-=+-+，由360m +=得：2m =-，即在01t <<运动时间内，当2m =-时，2AC m AB +⋅的值不随t 的改变而改变；当点A 在点B 右侧，即713t <<时，42(1)33AB t t t =--+=-，则22(73)(33)143(36)AC m AB t m t m m t +⋅=-+-=-+-，由360m -=得：2m =，即在713t <<运动时间内，当2m =时，2AC m AB +⋅的值不随t 的改变而改变；综上，存在一个常数m 使得2AC m AB +⋅的值在某段运动过程中不随t 的改变而改变，m 的值为2-或2．【点睛】本题考查了数轴、一元一次方程的应用、绝对值和偶次方的非负性、整式等知识点，较难的是题（2）②，正确分两种情况讨论是解题关键．6．（1）95；（2）257；（3）【解析】【分析】（1）利用勾股定理求出BC 的长，证明△AHC ∽△BAC ，推出AC CH BC AC =，即353CH =，求解即可；（2）过点A 作AM ⊥AE ，交CD 的延长线于M ，证明△BAE ≌△DAM ，推出BE=DM ，AE=AM ，再证明△EAF ≌△MAF ，得到EF=MF ，设BE=x ，则DM=x ，CE =6-x ，求得EF=MF=x +1，利用勾股定理得到222CE CF EF +=，222(6)1(1)x x =+-+，求出x 即可得到答案；（3）过点A 作AO BD ⊥，设AO x =，根据勾股定理列方程求得x ，分别讨论，求得ABN 为等边三角形，AM 为ABN 的角平分线，可得AMN 的面积为ABN 面积的一半，即可求解．【详解】解：（1）在ABC 中，90BAC ∠=︒，4AB =，3AC =，∴5BC ==，∵AH BC ⊥，∴∠AHC =90BAC ∠=︒，∵∠C=∠C，∴△AHC ∽△BAC ， ∴AC CH BC AC =，即353CH =， ∴95CH =，故答案为：95；（2）过点A 作AM ⊥AE ，交CD 的延长线于M ，∴∠EAM =90BAD ∠=︒，∴∠BAE=∠DAM ，∵90BAD C ∠=∠=︒，∴∠B +∠ADC =180°，∵∠ADM +∠ADC =180°，∴∠B =∠ADM∵AB=AD∴△BAE ≌△DAM∴BE=DM ，AE=AM ，∵45EAF ∠=︒，∴∠MAF =45EAF ∠=︒，又∵AF=AF ，∴△EAF ≌△MAF ，∴EF=MF ，设BE=x ，则DM=x ，CE =6-x ，∵点F 为CD 边的中点，2CD =，∴CF=DF =1，∴EF=MF=x +1，∵222CE CF EF +=，∴222(6)1(1)x x =+-+，解得187x =，∴EF=x +1=1825177+=；（3）过点A 作AO BD ⊥，如下图：∵AB AD =，AD BC ∥，AO BD ⊥∴1302ABD ADB DBC ABC ∠=∠=∠=∠=︒，BO OD =，180BAD ABC ∠+∠=︒∴120DAB ∠=︒设AO x =，则2AB x =，cos303OD BO AB x ==⨯︒=∴10EF BO BE OD DF =-+-=-6OF =-，6BF BO OF =+=-，又∵30EAF ABF ∠=∠=︒，AFE BFA ∠=∠∴FAE FBA △∽△ ∴AF FE BF FA=，∴226)1260AF EF BF x =⨯=--=-+由勾股定理得：2222226)436FA AO OF x x =+=+-=-+∴224361260x x -+=-+，即2260x -+=解得x =x当x =6BO OD ==，点O 与点F 重合，∴AF BD ⊥，6BF DF ==，AF AO ==∴AD AB ===又∵30ADB ∠=︒∴60DAN ∠=︒∴60BAN ∠=︒∴ABN 为等边三角形30MAN ∠=︒∴AM 平分BAN ∠cos306AM AB =⨯︒=111222AMN ABN S S BN AM ==⨯⨯⨯=△△当x 6AD =，32OB OD ==，310BD BE DF =<+=，不符合题意，综上，AMN 的面积为【点睛】此题考查了四边形的综合应用，涉及了全等三角形的判定与性质，相似三角形的判定与性质，勾股定理以及一元二次方程的求解，解题的关键是熟练掌握相关基本性质，构造出全等三角形和直角三角形．7．（1）2y x 2x 3=-++；1x =；（2）79(,)24-；（3＋17(1,)3D 【解析】【分析】（1）根据待定系数法求出函数解析式，然后根据二次函数一般式对称轴为2b x a=-解答即可；（2）设直线CP 与x 轴交于点E ，然后根据11:():():22PCB PCA C P C P S S EB y y AE y y BE AE =⨯-⨯-=，求解即可；（3）CD ＋AE ＝A ′D ＋DC ′，则当A ′、D 、C ′三点共线时，CD ＋AE ＝A ′D ＋DC ′最小，周长也最小，即可求解．【详解】解：（1）∵抛物线2y ax bx c =++经过点()1,0A -，点()3,0B ，点()0,3C ，∴00933a b c a b c c =-+⎧⎪=++⎨⎪=⎩，解得：123a b c =-⎧⎪=⎨⎪=⎩， ∴抛物线解析式为：2y x 2x 3=-++，则对称轴为：2122(1)bx a ；（2）如图：设直线CP 与x 轴交于点E ，直线直线CP 分四边形CBPA 的面积为1:3的两部分，又∵11:():():22PCB PCA C P C P S S EB y y AE y y BE AE =⨯-⨯-=，则:1:3BE AE =或3:1，令2230y x x =-++=，解得：123,1x x ==-，∴(1,0),(3,0)A B -，∴4AB =，∴1AE =或3，即点E 的坐标为(0,0)或(2,0)，当点E 的坐标为(0,0)时，直线CP 与y 轴重合，与抛物线只有一个交点C ，不符合题意；∵直线CP 经过(0,3)C ，点E (2,0)，∴设直线CP 的解析式为：y mx n =+，则302nk n=⎧⎨=+⎩，解得：323mn⎧=-⎪⎨⎪=⎩，∴直线CP的解析式为：332y x=-+，联立一次函数与二次函数解析式得：223332y x xy x⎧=-++⎪⎨=-+⎪⎩，解得：7294xy⎧=⎪⎪⎨⎪=-⎪⎩或3xy=⎧⎨=⎩（舍），∴点P的坐标为：79 (,) 24-；（3）四边形ACDE的周长＝AC＋DE＋CD＋AE，其中AC＝221310+=，DE＝1是常数，故CD＋AE最小时，周长最小，取点C关于直线x＝1对称点C′（2，3），则CD＝C′D，取点A′（−1，1），则A′D＝AE，故：CD＋AE＝A′D＋DC′，则当A′、D、C′三点共线时，CD＋AE＝A′D＋DC′最小，周长也最小，223213A C''=+=，四边形ACDE的周长的最小值＝AC＋DE＋CD＋AE101＋A′D＋DC101＋A′C′10113设直线A C''的解析式为：y dx e=+，则132d ed e=-+⎧⎨=+⎩，解得：2353de⎧=⎪⎪⎨⎪=⎪⎩，∴直线A C''的解析式为：2533y x=+，当1x=时，257333y=+=，∴点D的坐标为：7 (1,)3．【点睛】本题考查了二次函数综合，涉及到一次函数，图像面积，点的对称，勾股定理等，其中确定出点A 来求最小值，是本题的难点．8．（1）2；（2）32；（3）存在，223 3【解析】【分析】（1）如图①，根据等边三角形的判定和性质解决问题即可．（2）如图②，将△ABP绕点B逆时针旋转60°得到△BFE，连接PF，EC．易证PA＋PB＋PC＝PC＋PF＋EF，因为PC＋PF＋EF≥EC，推出当P，F在直线EC上时，PA＋PB＋PC的值最小，求出EC的长即可解决问题．（3）如图③−1中，将△PBQ绕点B逆时针旋转60°得到△EBG，则PQ＝EG，△BQG是等边三角形，易知PQ＋BQ＋CQ＝EG＋GQ＋QC≥EC，推出EC的值最小时，QP＋QB＋QC的值最小，如图③−2中，延长BA交CD的延长线于J，作△ADJ的外接圆⊙O，将线段BO，BP绕点B逆时针旋转60°得到线段BO′，BE，连接EO′，OB，OP．易证△BEO′≌△BPO（SAS），推出EO′＝OP＝433，推出点E的运动轨迹是以O′为圆心，433为半径的圆，推出当点E在线段CO′上时，EC的值最小，最小值＝CO′−EO′．【详解】（1）如图①，由旋转的性质可知：△BCC′是等边三角形，∴CC′＝BC＝2，故答案为2．（2）如图②，将△ABP绕点B逆时针旋转60°得到△BFE，连接PF，EC．由旋转的性质可知：△PBF 是等边三角形，∴PB ＝PF ，∵PA ＝EF ，∴PA +PB +PC ＝PC +PF +EF ，∵PC +PF +EF ≥EC ，∴当P ，F 在直线EC 上时，PA +PB +PC 的值最小，根据旋转以及翻折的性质可得BC ＝BE ＝BA ＝3，∵,30EBF ABP ABP PBC ∠=∠∠+∠=︒，∴90FBP EBF PBC ∠+∠+=︒,∵EB ⊥BC ，∴EC ＝2BC ＝32，∴PA +PB +PC 的最小值为32．（3）如图③﹣1中，将△PBQ 绕点B 逆时针旋转60°得到△EBG ，则PQ ＝EG ，△BQG 是等边三角形，∴BQ ＝QG ，PQ ＝EG ，∴PQ +BQ +CQ ＝EG +GQ +QC ≥EC ，∴EC 的值最小时，QP +QB +QC 的值最小，如图③﹣2中，延长BA 交CD 的延长线于J ，作△ADJ 的外接圆⊙O ，将线段BO ，BP 绕点B 逆时针旋转60°得到线段BO ′，BE ，连接EO ′，OB ，OP ．∵,,BO BO BE BP O BE OBP ==∠=∠''，∴△BEO ′≌△BPO （SAS ），∴EO ′＝OP ，∵∠APD +∠AJD ＝180°，∴A ，P ，D ，J 四点共圆，∴OP 43 ∴EO 43， ∴点E 的运动轨迹是以O 43为半径的圆， ∴当点E 在线段CO ′上时，EC 的值最小，最小值＝CO ′﹣EO ′，连接OO ′，延长OO ′到R ，使得O ′R ＝OO ′，连接BR ，则∠OBR ＝90°，作RH ⊥CB 交CB 的延长线于H ，O ′T ⊥CH 于T ，OM ⊥BC 于M ．在Rt △OBM 中，BM ＝5，OM 113 ∴OB 22OM BM +113 ∴BR 3＝14，由△BHR ∽△OMB ， ∴RH BM ＝BR OB， ∴RH ＝3∵HR ∥O ′T ∥OM ，OO ′＝RO ′，∴TM ＝TH ，∴O ′T ＝2RH OM +133 ∴BT 22O B O T -''3，∴CO，∴CO′﹣EO∴QP+QB+QC【点睛】本题属于四边形综合题，考查了旋转变换，全等三角形的判定和性质，等边三角形的判定和性质，解直角三角形等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．9．（1）6；（2）证明见解析；（3）48+【解析】【分析】（1）通过作辅助线构造等腰直角三角形，利用勾股定理求出AB边上的高和AB，再利用三角形面积公式求解；（2）通过在BE上截取BF=BD，构造出两组全等三角形，即可完成求证；（3）先通过延长ME，构造全等三角形，得出''AK MK FK MK+=+，利用轴对称，得出''AK MK+的最小值等于'FM，最后利用直角三角形的性质与勾股定理进行计算求解即可．【详解】解：（1）如图，过C点作CD⊥AB，垂足为点D，∵45A∠=︒，∴45A ACD∠=∠=︒，∴AD=CD，∵AC=222 AC AD CD=+，∴==6AD CD，∵BC=，∴4 BD=，∴AB=AD-BD=6-4=2,∴11==26=622ABCS AB CD⨯⨯⨯⨯，∴ABC的面积为6．（2）如图所示，在BE 上截取BF =BD ，∵∠D +∠DCB +∠DBC =180°，∠1+∠DBC +∠2=180°，且∠1=∠BCD ，∴∠D =∠2，∵CD CB =，∴△CDB ≌△CBF （SAS ），∴CB =CF ，∴∠2=∠3，∴∠ABC =∠EFC ，∵∠A =45°，AC ⊥CE ，∴∠E =45°，∴∠A =∠E ，∴△ABC ≌△EFC （AAS ），∴AC=CE ,AB =EF ，∴AE =AB +BF +EF =2AB +BD ,∵222AE AC CE =+, ∴2AE AC =,∴22BD AB AC +=；（3）如图3，延长ME 至F ，使MF =MA ，连接KF ，∵'90KMK AMF ︒∠=∠=，∴'AMK FMK ∠=∠，又∵'MK MK =，∴()'AMK FMK SAS ≌，∴'=F AK K ，∴''AK MK FK MK +=+，作M 点关于AC 的对称点'M ，则'=M K MK ，∴''=F =F 'AK MK K MK K M K +++，连接'M K ，则''M K FK M F +≥，∴当'M K F 、、共线时F 'K M K +的值最小，等于'M F ，∴''AK MK +取得最小值时()2''AK MK +的值即为2'M F 的值，连接'M A AF 、，由轴对称的性质可得：'=M AC MAC ∠∠，'=AM AM ，∵45CAE ∠=︒，AM 平分CAE ∠，∴22.5CAM ∠=︒，∴'22.5M AC CAM ∠=∠=︒，∴'45M AM ∠=︒，∵M A MF =，且90AMF ︒∠=，∴45MAF ∠=︒，∴'90M AF ∠=︒，∴222'='M F AM AF +，∵2222AM MF AM +=∴222222'='=23M F AM AF AM AM AM ++=，如图4，取AE 中点O 点，连接OC ，OM ，作MH AE ⊥于H ，∵=4AC ，∴=CE=4AC ，∴AE由直角三角形斜边上的中线等于斜边的一半，得OA OC OE OM ==== ∴22.5AMO MAO ∠=∠=︒，∴45MOH AMO MAO ∠=∠+∠=︒，∴45MOH OMH ∠=∠=︒，∴OH MH =，∵(2222=OM 8OH MH +==, ∴=2OH MH =，∴2AH =，∴222=16AM AH MH =++∴()22''=3=48AK MK AM ++∴()2''AK MK +的值为48+【点睛】本题综合考查了全等三角形的判定与性质、勾股定理、直角三角形的性质、轴对称、等腰三角形的性质与判定等内容，解决本题的关键是正确作出辅助线构造全等三角形或等腰直角三角形等，本题较为综合，要求学生有较强的理解能力与分析能力．10．（1）y ＝239344x x --；（2）点P 的坐标为：13313-13313-或(3，3)；（3）⊙N 的半径为163或83或1．【解析】【分析】（1）代入点A 、C 的坐标求出解析式；（2）先求出直线OD 的解析式，再和二次函数为的解析式y ＝239344x x -+联立即可求解；（3）先求出直线BC 的解析式，设N (m ，3m 34-)，则M (m ，239344m m --)，求出MN 的距离，最后利用“当⊙N 与y 轴相切时，MN =m ”，得出结果．【详解】解：（1）将点A （-1，0），C （0，3）代入抛物线的解析式得，9043a c c ⎧++=⎪⎨⎪=-⎩，解得343a c ⎧=⎪⎨⎪=-⎩，故二次函数的解析式为y ＝239344x x --；（2）∵抛物线y ＝239344x x --=23325()423x --， ∴抛物线的顶点E 的坐标为(325,23-)， ∵DF 平分∠ODE ，∴∠ODF =∠FDE ，∵EH ∥y 轴，∴∠FDE =∠OFD ，∴OD =OF ，∵(0,F ， ∴OD =OF设D (32，m )，则OD ²=223()2m +，即2(=223()2m +，解得：m =-32或32， ∴D (32，32-)或(32，32)，设直线OD 的解析式为y =kx ， ∴32-=32k 或32=32k ，解得：k =-1或k =1， ∴直线OD 的解析式为：y =x 或y =－x ，联立239344y x y x x =⎧⎪⎨=--⎪⎩或239344y x y x x =-⎧⎪⎨=--⎪⎩，解得：x舍去)；或x =3或43-(舍去)； ∴y3， ∴点P 的坐标为：或(3，3)；（3）由（1）得二次函数为：y ＝239344x x --，当y =0时，239344x x --=0，解得：121,4x x =-=， ∴B (4，0)，设直线BC 为：y =kx +b ，经过点C (0，-3)，则有043k b b =+⎧⎨=-⎩，解得：343k b ⎧=⎪⎨⎪=-⎩ ， ∴直线BC 为：y=334x -，设N (m ，3m 34-)，则M (m ，239344m m --)， ∴MN =M N y y -=239333444m m m ---+=2334m m - 当⊙N 与y 轴相切时，MN =m ， ∴2334m m -=m ，解2334m m -=m ，得m =163或0(舍去)，解2334m m -=-m ，得m =83或0(舍去)， ∴⊙N 的半径为163或83；当⊙N 与x 轴相切时，MN =334m -+， ∴2334m m -=334m -+，解2334m m -=334m -+，得m =4(舍去)或-1(舍去)，解2334m m -=3m 34-，得m =4(舍去)或1， ∴⊙N 的半径为1；综上，⊙N 的半径为163或83或1．【点睛】本题考查了待定系数法求二次函数及一次函数的解析式，两点之间的距离公式，圆的切线的性质，解本题的关键用方程的思想解决问题．11．（1）213y x x 242=-+-；（2）P 点坐标为(6，2)；（3）①2252 【解析】【分析】（1）求出A 、C 点的坐标，再将点代入y ＝14-x 2+bx +c ，即可得解；（2）先求∠OCA =45º，再由对称性可知PC ⊥y 轴，即可求出点P 的纵坐标，最后利用二次函数的解析式求出结果；（3）①先求出平移后的抛物线，再利用2111()44x m m --+-=x -2，得出2121224,43x x m x x m m +=-⋅=-+，最后利用两点之间的距离公式求解；②作KQ ⊥MN ，连接MK ，MP ，先得出KM =QN 即求KM +MP 的最小值，即KP 的长，最后根据△QMN 的周长的最小值即KQ +KP ，得解．【详解】解：（1）在y ＝x ﹣2中，令y =0，x =2；令x =0，y =-2；∴A (2，0)，C (0，-2)，代入y ＝14-x 2+bx +c 得104242b c c⎧=-⨯++⎪⎨⎪-=⎩，。

2022年中考数学压轴大题含答案

2022年中考数学压轴题1．如图，抛物线y ＝ax 2+bx +4交x 轴于A （﹣3，0），B （4，0）两点，与y 轴交于点C ，连接AC ，BC ．点P 是第一象限内抛物线上的一个动点，点P 的横坐标为m ．（1）求此抛物线的表达式；（2）过点P 作PM ⊥x 轴，垂足为点M ，PM 交BC 于点Q ．试探究点P 在运动过程中，是否存在这样的点Q ，使得以A ，C ，Q 为顶点的三角形是等腰三角形．若存在，请求出此时点Q 的坐标，若不存在，请说明理由；（3）过点P 作PN ⊥BC ，垂足为点N ．请用含m 的代数式表示线段PN 的长，并求出当m 为何值时PN 有最大值，最大值是多少？解：（1）由二次函数交点式表达式得：y ＝a （x +3）（x ﹣4）＝a （x 2﹣x ﹣12）＝ax 2﹣ax ﹣12a ，即：﹣12a ＝4，解得：a =−13，则抛物线的表达式为y =−13x 2+13x +4；（2）存在，理由：点A 、B 、C 的坐标分别为（﹣3，0）、（4，0）、（0，4），则AC =√32+42=5，AB ＝4﹣（﹣3）＝7，BC ＝4√2，∠OBC ＝∠OCB ＝45°，设BC 的解析式为y ＝kx +b ，将点B 、C 的坐标代入解得：{4k +b =0b =4，解得{k =−1b =4， ∴y ＝﹣x +4…①，设直线AC 的解析式为y ＝k ′x +b ′，则有{−3k +b′=0b′=4，解得{k′=43b′=4∴直线AC 的表达式为：y =43x +4，设线段AC 的中点为K （−32，2），过点M 与CA 垂直，直线的表达式中的k 值为−34，同理可得过点K 与直线AC 垂直，直线的表达式为：y =−34x +78⋯②，①当AC ＝AQ 时，如图1，则AC ＝AQ ＝5，设：QM ＝MB ＝n ，则AM ＝7﹣n ，由勾股定理得：（7﹣n ）2+n 2＝25，解得：n ＝3或4，∵点Q 在点B 的左侧，∴n ＝3故点Q （1，3）；②当AC ＝CQ 时，如图1，CQ ＝5，则BQ ＝BC ﹣CQ ＝4√2−5，则QM ＝MB =8−5√22，故点Q （5√22，8−5√22）；③当CQ ＝AQ 时，联立①②并解得：x =252（舍去）；故点Q 的坐标为：Q （1，3）或（5√22，8−5√22）；（3）设点P （m ，−13m 2+13m +4），则点Q （m ，﹣m +4），∵OB ＝OC ，∴∠ABC ＝∠OCB ＝45°＝∠PQN ，∴PN ＝PQ sin ∠PQN =√22（−13m 2+13m +4+m ﹣4）=−√26（m ﹣2）2+2√23，∵−√26＜0，∴PN 有最大值，当m ＝2时，PN 的最大值为：2√23．2．如图，边长为8的正方形OABC 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，点P 是抛物线上点A 、C 间的一个动点（含端点），过点P 作PF ⊥BC 于点F ，点D 、E 的坐标分别为（0，6），（﹣4，0），连接PD ，PE ，DE ．（1）求抛物线的解析式；（2）小明探究点P 的位置时发现：当点P 与点A 或点C 重合时，PD 与PF 的差为定值，进而猜想：对于任意一点P ，PD 与PF 的差为定值，请你判定该猜想是否正确，并说明理由；（3）请直接写出△PDE 周长的最大值和最小值．解：（1）∵边长为8的正方形OABC 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，∴C （0，8），A （﹣8，0），设抛物线解析式为：y ＝ax 2+c ，则 {c =864a +c =0，解得：{a =−18c =8． ∴抛物线解析式为y =−18x 2+8．（2）设P （x ，−18x 2+8），则F （x ，8），则PF ＝8﹣（−18x 2+8）=18x 2．PD 2＝x 2+[6﹣（−18x 2+8）]2=164x 4+12x 2+4＝（18x 2+2）2 ∴PD =18x 2+2，∴d ＝|PD ﹣PF |＝|18x 2+2−18x 2|＝2 ∴d ＝|PD ﹣PF |为定值2；（3）如图，过点E 作EF ⊥x 轴，交抛物线于点P ，由d ＝|PD ﹣PF |为定值2，得C △PDE ＝ED +PE +PD ＝ED +PE +PF +2＝ED +2+（PE +PF ），又∵D （0，6），E （﹣4，0）∴DE =√62+42=√52=2√13．∴C △PDE ＝2√13+2+（PE +PF ），当PE 和PF 在同一直线时PE +PF 最小，得C △PDE 最小值＝2√13+2+8＝2 √13+10．设P 为抛物线AC 上异于点A 的任意一点，过P 作PM ∥x 轴，交AB 于点M ，连接ME ，如图2．由于E 是AO 的中点，易证得ME ≥PE （当点P 接近点A 时，在△PME 中，显然∠MPE 是钝角，故ME ≥PE ，与A 重合时，等号成立），而ME ≤AE +AM ，所以PE ≤AE +AM ．所以当P 与A 重合时，PE +PF 最大，AE ＝8﹣4＝4，PD =√AO 2+DO 2=√82+62=10．得C △PDE 最大值＝2√13+4+10＝2√13+14．综上所述，△PDE 周长的最大值是2√13+14，最小值是2 √13+10．3．如图，抛物线y ＝﹣x 2+bx +c 与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点N ，过A 点的直线l ：y ＝kx +n 与y 轴交于点C ，与抛物线y ＝﹣x 2+bx +c 的另一个交点为D ，已知A （﹣1，0），D （5，﹣6），P 点为抛物线y ＝﹣x 2+bx +c 上一动点（不与A 、D 重合）．（1）求抛物线和直线l 的解析式；（2）当点P 在直线l 上方的抛物线上时，过P 点作PE ∥x 轴交直线l 于点E ，作PF ∥y 轴交直线l 于点F ，求PE +PF 的最大值；（3）设M 为直线l 上的点，探究是否存在点M ，使得以点N 、C ，M 、P 为顶点的四边形为平行四边形？若存在，求出点M 的坐标；若不存在，请说明理由．解：（1）将点A 、D 的坐标代入直线表达式得：{−k +n =05k +n =−6，解得：{k =−1n =−1，故直线l 的表达式为：y ＝﹣x ﹣1，将点A 、D 的坐标代入抛物线表达式，同理可得抛物线的表达式为：y ＝﹣x 2+3x +4；（2）直线l 的表达式为：y ＝﹣x ﹣1，则直线l 与x 轴的夹角为45°，即：则PE ＝PF ，设点P 坐标为（x ，﹣x 2+3x +4）、则点F （x ，﹣x ﹣1），PE +PF ＝2PF ＝2（﹣x 2+3x +4+x +1）＝﹣2（x ﹣2）2+18，∵﹣2＜0，故PE +PF 有最大值，当x ＝2时，其最大值为18；（3）NC ＝5，①当NC 是平行四边形的一条边时，设点P 坐标为（x ，﹣x 2+3x +4）、则点M （x ，﹣x ﹣1），由题意得：|y M ﹣y P |＝5，即：|﹣x 2+3x +4+x +1|＝5，解得：x ＝2±√14或0或4（舍去0），则点M 坐标为（2+√14，﹣3−√14）或（2−√14，﹣3+√14）或（4，﹣5）； ②当NC 是平行四边形的对角线时，则NC 的中点坐标为（0，32），设点P 坐标为（m ，﹣m 2+3m +4）、则点M （n ，﹣n ﹣1），N 、C ，M 、P 为顶点的四边形为平行四边形，则NC 的中点即为PM 中点，即：{m +n =0−m 2+3m +4−n −1=3，解得：{m =4n =−4，故点M （﹣4，3）；故点M 的坐标为：（2+√14，﹣3−√14）或（2−√14，﹣3+√14）或（4，﹣5）或（﹣4，3）．。

2022年中考数学压轴题(附答案)

一、解答题1．如图，在平面直角坐标系中，一抛物线的对称轴为直线x＝1，且该抛物线与y轴负半轴交于C点，与x轴交于A，B两点，其中B点的坐标为（3，0），且OB＝OC．(1)求此抛物线的函数表达式；(2)若平行于x轴的直线与该抛物线交于M、N两点（其中点M在点N的右侧），在x轴上是否存在点Q，使△MNQ是以MN为一直角边的等腰直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．2．直线y＝﹣x+6与x轴、y轴分别交于点A，点B．点P为线段AB上一动点（与点A，B不重合）．过点P作PM⊥OA于点M，以OB，OM为邻边作矩形BOMN．点Q在直线BN上，且PQ⊥OP．（1）如图1，①判断△APM的形状，并说明理由；②求证：△PNQ≌△OMP；③若∠PQN＝22.5°，直接写出点P的坐标．（2）作射线OQ交直线AB于点K，∠OPQ的角平分线交边OB于点G．若BGOG＝35，①当∠PKQ为钝角时，直接写出线段PK的长；②当∠PKQ为锐角时，直接写出BK2+AP2的值．3．已知抛物线29 4y ax x c=++与x轴交于A、B两点，与y轴交于C点，且点A的坐标为1,0、点C 的坐标为()0,3．（1）求该抛物线的函数表达式；（2）如图1，若该抛物线的顶点为P ，求PBC 的面积；（3）如图2，有两动点D 、E 在COB △的边上运动，速度均为每秒1个单位长度，它们分别从点C 和点B 同时出发，点D 沿折线COB 按C →O →B 方向向终点B 运动，点E 沿线段BC 按B →C 方向向终点C 运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t 秒，在点D 、E 运动过程中，该抛物线上存在点F ，使得依次连接AD 、DF 、FE 、EA 得到的四边形ADFE 是平行四边形，请直接写出所有符合条件的点F 的坐标．4．如图，在平面直角坐标系中，抛物线264y ax ax =-+与x 轴的一个交点为()2,0A -，与y 轴的交点为C ，点B 为抛物线对称轴上一动点．（1）抛物线的函数表达式为________，抛物线的对称轴为________．（2）线段BC 绕点B 顺时针旋转90︒得到BP ，当点P 落在抛物线上时，求出点B 坐标．（3）当点B 在x 轴上时，M ，N 是抛物线上的两个动点，M 在N 的右侧，若以B ，C ，M ，N 四点为顶点的四边形是平行四边形，求出此时点M 的横坐标．5．如图，抛物线顶点(1,4)P ，与y 轴交于点(0,3)C ，与x 轴交于点A ，B ．（1）求抛物线的解析式；（2）Q 是抛物线上除点P 外一点，BCQ △与BCP 的面积相等，求点Q 的坐标：（3）M 是线段BC 上方抛物线上一个动点，过点M 作x 轴的垂线，交线段BC 于点D ，再过点M 做MN //x 轴交抛物线于点N ，连结DN ，请问是否存在点M 使MDN △为等腰直角三角形？若存在，求出点M 的坐标；若不存在，说明理由．6．已知二次函数y ＝x 2+bx +b ﹣1，其中b 为常数．（1）当y ＝0时，求x 的值；（用含b 的式子表示）（2）抛物线y ＝x 2+bx +b ﹣1与x 轴交于A ，B 两点（点A 在点B 的左侧），过点E （4，2）作直线交抛物线于P ，Q 两点，其中点P 在第一象限，点Q 在第四象限，连接AP ，AQ 分别交y 轴于点M （0，m ），N （0，n ）．①当b ＜2时，求点P 的横坐标xP 的值；（用含m ，b 的式子表示）②当b ＝﹣3时，求证：OM •ON 是一个定值．7．如图，抛物线y ＝－x 2＋bx ＋c 与x 轴交于A ，B 两点，其中A （3，0），B （－1，0），与y 轴交于点C ，抛物线的对称轴交x 轴于点D ，直线y ＝kx ＋b 1经过点A 、C ，连接CD ．（1）分别求抛物线和直线AC 的解析式；（2）在直线AC 下方的抛物线上，是否存在一点P ，使得△ACP 的面积是△ACD 面积的2倍，若存在，请求出点P 的坐标；若不存在，请说明理由；（3）在抛物线的对称轴上是否存在一点Q ，使线段AQ 绕Q 点顺时针旋转90°得到线段QA 1，且点A 1恰好落在该抛物线上？若存在，求出点Q 的坐标；若不存在，请说明理由．8．如图1，在ABC 中，90,ACB CD ∠=︒平分ACB ∠，且AD BD ⊥于点D ．（1）判断ABD △的形状；（2）如图2，在（1）的结论下，若22,3,75BQ DQ BQD ==∠=︒，求AQ 的长；（3）如图3，在（1）的结论下，若将DB 绕着点D 顺时针旋转()090αα︒<<︒得到DP ，连接BP ，作DE BP ⊥交AP 于点F ．试探究AF 与DE 的数量关系，并说明理由．9．如图1，已知数轴上的点A 、B 对应的数分别是﹣5和1．（1）若P 到点A 、B 的距离相等，求点P 对应的数；（2）动点P 从点A 出发，以2个单位/秒的速度向右运动，设运动时间为t 秒，问：是否存在某个时刻t ，恰好使得P 到点A 的距离是点P 到点B 的距离的2倍？若存在，请求出t 的值；若不存在，请说明理由；（3）如图2在数轴上的点M 和点N 处各竖立一个挡板（点M 在原点左侧，点N 在原点右侧且OM ＞ON ），数轴上甲、乙两个弹珠同时从原点出发，甲弹珠以2个单位/秒的速度沿数轴向右运动，乙弹珠以5个单位/秒的速度沿数轴向左运动．当弹珠遇到挡板后立即以原速度向反方向运动，若甲、乙两个弹珠相遇的位置恰好到点M 和点N 的距离相等，试探究点M 对应的数m 与点N 对应的数n 是否满足某种数量关系，请写出它们的关系式，并说明理由．10．如图，在平面直角坐标系xOy 中，△ABC 是等腰直角三角形，∠BAC ＝90°，A （1，0），B （0，2），二次函数y ＝x 2+bx ﹣2的图象经过C 点．（1）求二次函数的解析式；（2）若点P是抛物线的一个动点且在x轴的下方，则当点P运动至何处时，恰好使△PBC 的面积等于△ABC的面积的两倍．（3）若点Q是抛物线上的一个动点，则当点Q运动至何处时，恰好使∠QAC＝45°？请你求出此时的Q点坐标．11．已知，如图，抛物线y＝14x2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y＝x﹣2经过A、C两点．（1）直接写出抛物线的解析式；（2）P为抛物线上一点，若点P关于直线AC的对称点Q落在y轴上，求P点坐标；（3）现将抛物线平移，保持顶点在直线y＝x﹣114，若平移后的抛物线与直线y＝x﹣2交于M、N两点．①求证：MN的长度为定值；②结合（2）的条件，直接写出△QMN的周长的最小值12．已知二次函数经过点A（﹣3，0）、B（1，0）、C（0，3）．(1)求该抛物线解析式；(2)如图1，点M 为抛物线上第二象限内一动点，BM 交y 轴于点N ，当BM 将四边形ABCM 的面积分为1：2两部分时，求点M 的坐标；(3)如图2，点P 为对称轴上D 点下方一动点，点Q 为直线y ＝x 第一象限上的动点，且DP ＝2OQ ，求BP +2BQ 的最小值并求此时点P 的坐标．13．如图，在平面直角坐标系中，函数的图象分别交x 轴、y 轴于A 、B 两点，过点A 的直线交y 轴的正半轴于点M ，且点M 为线段OB 的中点．(1)求直线AM 的函数解析式．(2)如果在直线AM 上有一点P ，使得，请求出点P 的坐标．(3)在坐标平面内是否存在点N ，使以A 、B 、M 、N 为顶点的四边形是平行四边形？若存在，请直接写出所有点N 的坐标；若不存在，请说明理由．14．定义：在平面直角坐标系中，对于任意两点()11,A x y ，()22,B x y ，如果点(),M x y 满足122x x x -=，122y y y -=，那么称点M 是点A 、B 的“双减点”．例如：()4,5A -，()6,1B -、当点(),T x y 满足4652x --==-，()5132y --==，则称点()5,3M -是点A 、B 的“双减点”．(1)写出点()1,3A -，()1,4B -的“双减点”C 的坐标；(2)点()6,4E -，点4,43F m m --⎛⎫ ⎪⎝⎭，点(),M x y 是点E 、F 的“双减点”．求y 与x 之间的函数关系式；(3)在（2）的条件下，y 与x 之间的函数图象与y 轴、x 轴分别交于点A 、C 两点，B 点坐标为3,0，若点E 在平面直角坐标系内，在直线AC 上是否存在点F ，使以A 、B 、E 、F 为顶点的四边形为菱形？若存在，请求出F 点的坐标；若不存在，请说明理由． 15．如图，拋物线24832999y x x =-++与x 轴交于A ，B 两点（点A 在点B 的左侧），顶点为D ．点P 为对称轴右侧抛物线上的一个动点，其横坐标为m ，直线AD 交y 轴于点C ，过点P 作PF ∥AD 交x 轴于点．F ，PE ∥x 轴，交直线AD 于点E ，交直线DF 于点M ．(1)求直线AD 的表达式及点C 的坐标；(2)当DM ＝3MF 时，求m 的值；(3)试探究点P 在运动过程中，是否存在m ，使四边形AFPE 是菱形，若存在，请直接写出点P 的坐标；若不存在，请说明理由．16．如图（1），抛物线y ＝﹣x 2+bx +c 与x 轴交于A 、B 两点，与y 轴交于点C ，已知点B 坐标为（2，0），点C 坐标为（0，2）．(1)求抛物线的表达式；(2)如图（1），点P 为直线BC 上方抛物线上的一个动点，当△PBC 的面积最大时，求点P 的坐标；(3)如图（2），过点M（1，3）作直线MD⊥x轴于点D，在直线MD上是否存在点N，使点N到直线MC的距离等于点N到点A的距离？若存在，求出点N的坐标；若不存在，请说明理由．17．在平面直角坐标系中，抛物线y12=-x22x+3与x轴交于A、B两点（A在B左侧），与y轴交于点C，抛物线的顶点为D，过点B作BC的垂线，交对称轴于E．(1)如图1，点P为第一象限内的抛物线上一动点，当△PAE面积最大时，在对称轴上找一点M，在y轴上找一点N，使得OM+MN+NP最小，求此时点M的坐标及OM+MN+NP 的最小值；(2)如图2，平移抛物线，使抛物线的顶点D在射线AD上移动，点D平移后的对应点为D'，点A的对应点A'，设原抛物线的对称轴与x轴交于点F，将△FBC沿BC翻折，使点F 落在点F′处，在平面上找一点G，使得以A'、D'、F'、G为顶点的四边形为菱形．直接写出D′的坐标．18．如图，在矩形ABCD中，6cmAB=，12cmBC=，点P从点A出发沿AB以1cm/s的速度向点B移动；同时，点Q从点B出发沿BC以2cm/s的速度向点C移动．（1）几秒钟后DPQ的面积等于228cm；（2）在运动过程中，是否存在这样的时刻，使点D恰好落在以点Q为圆心，PQ为半径的圆上？若存在，求出运动时间；若不存在，请说明理由．（3）在点P、Q的运动过程中，几秒后DPQ是直角三角形？请直接写出答案．19．已知AB、CD为O的两条弦，//AB CD．（1）如图1，求证弧AC=弧BD；（2）如图2，连接AC、BC、OA、BD，弦BC与半径OA相交于点G，延长AO交CD于点E，连接BE，使BE BD=，若OA BC⊥，求证：四边形ABEC为菱形；（3）在（2）的条件下，CH与O相切于点C，连接CO并延长交BE于点F，延长BE交CH于点H，11OF=，24sin25BDC∠=，求CH长．20．如图1和图2，在△ABC中，AB＝AC＝5，sinC＝35．点K在AC边上，点M，N分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；（3）设点P移动的路程为x，当0≤x≤3及3≤x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝94，请直接写出点K被扫描到的总时长．【参考答案】**科目模拟测试一、解答题1．(1)y＝x2﹣2x﹣3(2)0）或（20）或（00）【解析】【分析】（1）根据线段相等、对称轴求出A，C两点的坐标，设出抛物线的函数表达式，并代入A，B，C三点坐标，得方程组，解出未知数的值，即可得到函数表达式；（2）根据题意，设出M点的坐标，表示出MN的长度，再分类讨论，当点M、N在x轴下方和下方时，分别根据MN＝MQ、MN＝NQ列出方程，解方程即可．(1)∵B点的坐标为（3，0）且OB＝OC∴C点的坐标为（0，﹣3）∵抛物线的对称轴为直线x＝1，B点的坐标为（3，0）∴A点的坐标为（﹣1，0）设抛物线的函数表达式为y＝a（x+1）（x﹣3）（a≠0）将C（0，﹣3）代人y＝a（x+1）（x﹣3）中解得：a＝1∴抛物线的函数表达式为y＝（x+1）（x﹣3）＝x2﹣2x﹣3．(2)∵MN∥x轴，且M、N在抛物线上∴M、N关于直线x＝1对称设点M（m，m2﹣2m﹣3）且m＞1则MN＝2（m﹣1）①当点M、N在x轴下方时，若∠QMN＝90°且MN＝MQ时，△MNQ为等腰直角三角形∴MQ⊥MN即MQ⊥x轴∴2（m﹣1）＝﹣（m2﹣2m﹣3）解得：m1m2∴点M2﹣Q10）由MQ1＝MN可得﹣（2﹣xN解得：xN＝2∴点N为（22﹣故当∠MNQ2＝90°，MN＝NQ2时，点Q2的坐标为（2﹣5，0）②当点M、N在x轴上方时，若∠QMN＝90°且MN＝MQ时，△MNQ为等腰直角三角形∴MQ⊥MN，即MQ⊥x轴∴2（m﹣1）＝m2﹣2m﹣3解得：m1＝2+5，m2＝2﹣5（舍去）∴点M为（2+5，2+25），点Q3为（2+5，0）由MQ3＝MN，可得2+25＝2+5﹣xN，解得xN＝﹣5∴点N为（﹣5，2+25）当∠MNQ4＝90°，MN＝NQ4时，点Q4的坐标为（﹣5，0）综上所述，存在满足条件的点Q，其坐标分别为（5，0）或（2﹣5，0）或（2+5，0）或（﹣5，0）．,【点睛】本题是二次函数的综合题目，涉及等腰直角三角形的存在性问题，主要考查了待定系数法求二次函数解析式、二次函数的性质、等腰三角形的性质及判定，熟练运用上述知识是解题的关键．2．（1）①等腰直角三角形，理由见解析，②证明见解析，③(63232)，，（2）52，②225 2【解析】【分析】（1）①求出直线y＝﹣x+6与x轴、y轴交点坐标，得出∠BAO＝45°即可证明；②由①得出BN＝PN＝OM，再根据PQ⊥OP得出∠PQB=∠OPM，即可证明△PNQ≌△OMP；③∠PQN＝22.5°，可得BQ＝PB，设点P坐标为（a，-a+6），列出关于a的方程求解即可；（2）①证△OPG∽△OBP，求出OP长，得出P点坐标，再证△OPB∽△KPO，求出PK 的长即可；②类似①得出P点坐标，求出PK的长即可．【详解】解：（1）①△APM是等腰直角三角形，理由如下：y＝﹣x+6与x轴、y轴分别交于点A，点B．当x＝0时，y＝6，当y＝0时，x＝6，则点A（6，0）点B（0，6）；∴OA=OB，∴∠BAO＝45°，∵PM⊥OA，∴∠BAO＝∠MPA＝45°，∴PM＝PA，∴△APM是等腰直角三角形；②由①同理可得BN＝PN，∵BN＝OM，∴PN＝OM，∵PQ⊥OP，∴∠QPN+∠OPM＝90°，∵∠POM+∠OPM＝90°，∴∠POM＝∠QPN，∵∠PMO＝∠PNQ＝90°，∴△PNQ≌△OMP；③设点P坐标为（a，-a+6），∵∠PQN＝22.5°，∠PBN＝45°，∴∠PQN＝∠BPQ＝22.5°，∴BQ＝PB，∵△PNQ≌△OMP；∴QN＝PM=-a+6，6a a+=-+，解得，6a=-则点P坐标为(6-；（2）∵BGOG＝35，OB=6，∴94BG=，154OG=，①∵∠OPQ 的角平分线交边OB 于点G ,∴∠OPG ＝∠OBA ＝45°，∵∠PGO ＝45°+∠BPG ，∠BPO ＝45°+∠BPG ，∴∠PGO ＝∠BPO ，∴△OPG ∽△OBP ， ∴OP OG OB OP =，即1546OP OP =，解得3102OP =（负值舍去），设点P 坐标为（a ，-a +6），222310(6)()2a a +-+=，解得，132a =，292a =；当∠PKQ 为钝角时，92a =，P 坐标为93()22，，则322AP =，922BP =， ∵∠POK ＝∠OBA ＝45°，∠BPO ＝∠BPO ，∴△OPB ∽△KPO ，∴OP PB KP OP =，即31092223102KP =，解得522KP =；②当∠PKQ 为锐角时，32a =，P 坐标为39()22，，则92AP =32BP = 由①得，310OP =OP PB KP OP =即31032223102KP =，1522KP =， 152326222BK =-=， BK 2+AP 2=229222562+=22（）（）．【点睛】本题考查了一次函数与图形，全等三角形的判定与性质，相似三角形的判定与性质，解题关键是熟练运用相关定理进行推理证明．3．（1）239344y x x =-++；（2）458；（3）1013,36⎛⎫ ⎪⎝⎭或()3,3．【解析】【分析】（1）把A 、C 两点代入抛物线294y ax x c =++解析式，即可得表达式．（2）把解析式配方得顶点式，即可得顶点坐标，令y=0，得B 点的坐标，连接OP ，可求得PBC OPC OPB OBC S S S S =+-=111••••••222p p OC x OB y OB OC +-，即得结果．（3）在△OBC 中，BC ＜OC +OB ，当动点E 运动到终点C 时，另一个动点D 也停止运动，由勾股定理得BC =5，当运动时间为t 秒时，BE =t ，过点E 作EN ⊥x 轴，垂足为N ，根据相似三角形的判定得△BEN ∽△BCO ，根据相似三角形的性质得，点E 的坐标为43(4,)55t t -，分两种情形讨论当点D 在线段CO 上运动时，0＜t ＜3，此时CD =t ，点D 的坐标为（0，3-t ），当点D 在线段OB 上运动时，3≤t ≤5，BD =7-t ，根据平行四边形ADFE 的性质得出坐标．【详解】解：（1）∵抛物线294y ax x c =++经过A （-1，0），C （0，3）两点， ∴9043a c c ⎧-+=⎪⎨⎪=⎩，解得343a c ⎧=-⎪⎨⎪=⎩， ∴该抛物线的函数表达式为239344y x x =-++；（2）∵抛物线223933753()444216y x x x =-++=--+， ∴抛物线的顶点P 的坐标为375(,)216， ∵239y 344x x =-++，令y=0，解得：x 1=-1，x 2=4，∴B 点的坐标为（4，0），OB =4，如图，连接OP ，则PBC OPC OPB OBC S S S S =+-，=111222p p OC x OB y OB OC ⋅⋅+⋅⋅-⋅⋅ =1317513443222162⨯⨯+⨯⨯-⨯⨯ =975648+- =458∴△PBC 的面积为458；（3）∵在△OBC 中，BC ＜OC +OB ，∴当动点E 运动到终点C 时，另一个动点D 也停止运动，∵OC =3，OB =4，∴在Rt △OBC 中，225BC OB OC =+=∴0＜t ≤5，当运动时间为t 秒时，BE =t ，如图，过点E 作EN ⊥x 轴，垂足为N ，则△BEN ∽△BCO ，∴5BN EN BE t BO CO BC === 43BN ,,55t EN t == ∴点E 的坐标为43(4,)55t t -，下面分两种情形讨论：Ⅰ、当点D 在线段CO 上运动时，0＜t ＜3，此时CD =t ，点D 的坐标为（0，3-t ），设点239,344F a a a ⎛⎫-++ ⎪⎝⎭根据平行四边对角线互相平分，得，2414533933544a t t t a a ⎧-=-⎪⎪⎨⎪-+=-++⎪⎩，消去t 得，237100a a --= ，解得1210,13a a ==- （舍去）当1103a =时，239163443a a -++=， ∴ F 坐标为1013(,)36Ⅱ、如图，当点D 在线段OB 上运动时，3≤t ≤5，BD=7-t ，()473OD t t =--=- ()3,0D t ∴-根据平行四边的性质，AD DF = ，AE DF =，243(1)(4)53933445t a t a a t ⎧---=--⎪⎪∴⎨⎪-++=⎪⎩，消去t 得，2120a a +-=，解得14a =-（舍去），23a =当3a =时，2393344a a -++= ∴ F 坐标为（3，3），综上所述：F 坐标为1013(,)36或（3，3）．【点睛】本题考查了抛物线的综合运用，本题涉及到抛物线的求解，勾股定理，二次函数的性质，相似三角形的判定与性质，正确运用分类讨论思想是解题的关键．4．（1）20.25 1.54=-++y x x ，直线3x =；（2）12(3,3),(3,1)B B ；（3）M 的横坐标为3259±或436 【解析】【分析】（1）把()2,0A -代入函数解析式，求出a 的值即可得函数关系式，再进行配方可得函数的对称轴；（2）设(3,)B t ，过B 作BE y ⊥轴垂足为E ，过点P 作PF BE ⊥垂足为F ，证明≌CEB BFP 得3,4PF BE BF CE t ====-，可得(7,3)P t t -+，代入抛物线解析式得方程，求解即可；（3）分两种情况，根据平行四边形的判定与性质求解即可．【详解】解：（1）把()2,0A -代入264y ax ax =-+得，4+124=0a a +解得，a=-0.25∴抛物线的函数表达式为20.25 1.54=-++y x x ，由220.25 1.54=0.25(3) 6.25y x x x =-++-⨯-+∴抛物线的对称轴为直线3x =，故答案为：20.25 1.54=-++y x x ，直线3x =；（2）∵点B 为抛物线对称轴上一动点∴设(3,)B t过B 作BE y ⊥轴垂足为E ，过点P 作PF BE ⊥垂足为F∵90CBP ∠=︒，∴CBE BPF ∠=∠，∵,90=∠=∠=︒BC BP CEB BFP ， ∴≌CEB BFP∴3,4PF BE BF CE t ====-∴(3,7)+-P t t ，∵点P 落在抛物线上，∴把(7,3)P t t -+代入20.25 1.54=-++y x x ，整理得2430t t -+=得121,3t t ==所以12(3,3),(3,1)B B（3）①如图，当BC 为边时，∵四边形BCNM 是平行四边形，∴//,=BC MN BC MN∵点B 向左平移3个单位，再向上平移4个单位得到点C ∴设点23,442⎛⎫-++ ⎪⎝⎭m m M m ，则N 坐标为233,842⎛⎫--++ ⎪⎝⎭m m m ∵点N 在抛物线上，∴把233,842⎛⎫--++ ⎪⎝⎭m m N m 代入23442=-++x x y 得223(3)3(3)844242---++=-++m m m m ，解得436=m ②如图，当BC 为对角线时，∵四边形BNCM 是平行四边形，∴,==CQ BQ NQ MQ∵(3,0),(0,4)B C ，∴(1.5,2)Q ，∴设点23,442⎛⎫-++ ⎪⎝⎭m m M m ，则N 坐标为233,42m m m ⎛⎫-- ⎪⎝⎭∵点N 在抛物线上，∴把233,42m m N m ⎛⎫-- ⎪⎝⎭代入23442=-++x x y 得()()22333344242m m m m ---=-++，解得32592m ±= 所以点M 的横坐标为32592±或436．【点睛】本题是二次函数综合题目，考查了二次函数解析式的求法、平行四边形的性质、平移的性质、解方程等知识；本题综合性强，有一定难度．5．（1）2y x 2x 3=-++；（2）1(2,3)Q ，2317117(,)22Q +--，3317117(,)22Q --+；（3）存在，(2,3)M 或5175317(,)22--+ 【解析】【分析】（1）设2(1)4(0)y a x a =-+≠，把C(0,3)代入求出a ，即可得出答案；（2）①过P 作PQ //BC ，交抛物线于点Q ，如图1所示；②求出点G 坐标，可得2PG GH ==，过H 作直线23Q Q //BC ，交x 轴于点H ，分别求出Q 的坐标即可；（3）MDN △为等腰直角三角形，则MN MD =，求出MN 、MD 的长度即可列出等量关系式，从而得出答案．【详解】（1）设2(1)4(0)y a x a =-+≠，把C(0,3)代入抛物线解析式得：43a +=，即1a =-，则抛物线解析式为22(1)423 y x x x =--+=-++；（2）由(3,0)B ，C(0,3)，得到直线BC 解析式为3y x =-+，①过P 作1PQ //BC ，交抛物线于点1Q ，如图1所示，(1,4)P ，∴直线PQ 解析式为5y x =-+，联立得：2235y x x y x ⎧=-++⎨=-+⎩，解得：14x y =⎧⎨=⎩或23x y =⎧⎨=⎩，即1(2,3)Q ；②过P 作PH x ⊥轴，交BC 于点G ，交x 轴于点H ，令1x =，代入3y x =-+，得2y =，(1,2)G ∴，2PG GH ∴==，过H 作直线23Q Q //BC ，则直线23Q Q 解析式为1y x =-+，联立得：2231y x x y x ⎧=-++⎨=-+⎩，解得：x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧⎪⎪⎨⎪=⎪⎩2Q ∴，3Q ，综上所述：点Q 的坐标为1(2,3)Q，2Q，3Q ；（3）MDN △为等腰直角三角形，则MN MD =，点()2,23M m m m -++，令x m =，代入3y x =-+得：3y m =-+，(,3)D m m ∴-+，函数的对称轴为：1x =，则点N 的横坐标为：2m -，则|22|MN m =-，2223(3)3MD m m m m m =-++--+=-+，2223m m m ∴-=-+，2223m m m -=-+或2223m m m -+=-+，解得：12m =或21m =-（舍）或3m =4m =当2m =时，2233m m -++=，当m =223m m -++= 故点M 的坐标为：(2,3)或．【点睛】本题考查了二次函数综合题，设计知识有：用待定系数法求函数解析式、同底等高的面积计算、等腰直角三角形的性质，一次函数与二次函数交点问题，熟练掌握相关知识点是解决本题的关键．6．（1）x 1=-1，x 2=1-b ；（2）①xP =m -b +1；②OM •ON =2．【解析】【分析】（1）令y =0可得x 2+bx +b -1=0，然后解一元二次方程即可解答；（2）①当b <2时，由不等式性质可得：1-b >-1，根据点A 在点B 的左侧，可得A （-1，0），再利用待定系数法求得直线AM 的解斤式为y =mx +m ，联立方程组可得：x 2+（b -m ）x +b -m -1=0，由根与系数关系可得xA +xP =-（b -m ）=m -b ，进而确定xP ；②当b =-3时，二次函数解析式为y =x 2-3x -4，由题意可得P （m +4，m 2+5m ），Q （n +4，n 2+5），再根据直线PQ 过点E （4，2），可推出（mn +2）m -n ）=0，再由P 、Q 不重合，即mn ，得出mn =-2即可．【详解】解：（1）当y =0时，x 2+bx +b -1=0，即（x +1）（x +b -1）=0， ∴x +1=0或x +b -1=0，即x 1=-1，x 2=1-b ；（2）①当b <2时，由（1）可知：x 1=-1，x 2=1-b ， ∵b <2， ∴-b >-2， ∴1-b >-1，∵点A 在点B 的左侧， ∴A （-1，0），设直线AM 的解析式为y =kx +a ， ∵A （-1，0），M 0，m ），∴0k a a m -+=⎧⎨=⎩，解得k m a m =⎧⎨=⎩∴直线AM 的解析式为y =mx +m ，联立方程组，得：2,1y mx my x bx b =+⎧⎨=++-⎩消去y 可得：x 2+（b -m ）x +b -m -1=0，由根与系数关系，得xA +xP =-（b -m ）=m -b ， ∴xP =m -b +1；②证明：当b =-3时，二次函数解析式为y =x 2-3x -4， ∴A （-1，0），B （4，0）， ∵xP =m +4，∴yP =m +4）2-3（m +4）-4=m 2+5m ， ∴P （m +4，m 2+5m ）， ∴直线AN 的解析式为：(1)01ny x nx n =+=++，联立方程组可得：234,y x x y nx n ⎧=--⎨=+⎩∴x 2-（3+n ）x -4-n =0∴xQ =4+n ，yQ =n 2+5n ，即Q （n +4，n 2+5n ）， ∵直线PQ 过点E （4，2）， ∴kEP =kEQ ，∴2225254444m m n n m n ++=+-+-，即mn 2+5mn -2m =m 2n +5mn -2n ，即（mn +2）（m -n ）=0， ∵P 、Q 不重合，即m ≠n ， ∴mn =-2，∴OM ·ON =|mn |=2为定值．【点睛】本题主要考查了二次函数的性质、待定系数法、一次函数图象和性质、一元二次方程根与系数关系等知识点，本题综合性较强，熟练掌握二次函数的图象及性质、灵活应用根与系数的关系成为解答本题的关键．7．（1）y ＝－x 2+2x +3，y ＝-x +3；（2）存在，（－1，0）或（4，－5）；（3）存在，（1，2）或（1，－3）【解析】【分析】（1）将点A ，B 坐标代入抛物线解析式中，求出b ，c 得出抛物线的解析式，进而求出点C 的坐标，再将点A ，C 坐标代入直线AC 的解析式中，即可得出结论；（2）利用抛物线的对称性得出BD AD =，进而判断出ABC 的面积和ACP △的面积相等，即可得出结论；（3）分点Q 在x 轴上方和在x 轴下方，构造全等三角形即可得出结论．【详解】（1）把(30)A ，、(10)B -，代入2y x bx c =-++，解得2b =、3c =∴抛物线的解析式为2y x 2x 3=-++则C 点为（0，3），又(30)A ，，代入1y kx b =+，得1k =-，13b =， ∴直线AC 的解析式为3y x =-+，（2）如图，连接BC ，∵点D 是抛物线的对称轴与x 轴的交点， ∴AD BD =， ∴2ABCACDSS=，∵2ACP ACD S S =△△，∴ACP ABC S S =△△，此时，点P 与点B 重合，即：(10)P -，，过B 点作PB AC ∥交抛物线于点P ，则直线BP 的解析式为1y x =--①， ∵抛物线的解析式为2y x 2x 3=-++②，联立①②解得，10x y =-⎧⎨=⎩或45x y =⎧⎨=-⎩，∴P （4，﹣5），∴即点P 的坐标为（﹣1，0）或（4，﹣5）；（3）由（1）可知，抛物线解析式为()214y x =--+ 把1x =代入直线AC 解析式3y x =-+得AC 与抛物线对称轴的交点(1,2)M ，如下图所示：22222BM AM ==+，4AB =即222BM AM AB +=则MAB △是等腰直角三角形，符合题意，M 点即为所求Q 点的一种情况，当Q 点在x 轴下方时，设Q 为(1,)m ，0m ＜，因为线段AQ 绕Q 点顺时针旋转90°得到线段1QA 过A1作直线DQ 的垂线于E 点，则1ADQ QEA ≌ ∴2AD QE ==，1DQ EA m ==- ∴12(1)A m m --，∵点A1恰好落在抛物线2y x 2x 3=-++上，代入，解得m=－3或2m = (舍去) ∴Q （1，－3）综上，Q 点坐标为（1,2）或（1，－3），【点睛】本题考查的是二次函数的综合题，涉及解析式的求解，与三角形面积有关的问题，全等三角形的判定与性质，解题的关键是利用数形结合的思想，设点坐标并结合几何图形的性质列式求解．8．（1）ABD △是等腰直角三角形，证明见解析；（2）38；（3）2,AF DE =证明见解析【解析】【分析】（1）先求解45,ACD BCD ∠=∠=︒取AB 的中点,G 连接,,CG DG 再证明,,,A C B D 在以G 为圆心，GC 为半径的同一个圆上，从而可得答案.（2）如图，把ADQ △顺时针旋转90︒得到,BDQ ' 连接,QQ ' 过Q '作,Q F BQ '⊥ 交BQ 的延长线于,F 证明45,32,DQQ QQ ∠=︒='' 证明120,60,BQQ FQQ ∠=︒∠='︒' 求解3236·cos 60,?sin 60,22QF QQ FQ QQ =︒==︒=''' 再利用勾股定理可得答案；（3）如图，连接,BF 证明 ,DPE ABF ∽ 可得,DP DEAB AF= 结合（1）问的结论可得答案. 【详解】解：（1） 90,ACB CD ∠=︒平分ACB ∠， 45,ACD BCD ∴∠=∠=︒取AB 的中点,G 连接,,CG DG90,ACB ADB ∠=∠=︒ ,CG AG BG DG ∴===,,,A C B D ∴在以G 为圆心，GC 为半径的同一个圆上， 45,ABD ACD ∴∠=∠=︒ABD ∴为等腰直角三角形.（2）如图，,90,AD BD ADB =∠=︒把ADQ △顺时针旋转90︒得到,BDQ ' 连接,QQ ' 过Q '作,Q F BQ '⊥ 交BQ 的延长线于,F3,90,,DQ DQ QDQ AQ BQ ''∴∠=︒='==2245,3332,DQQ QQ ''∴∠=︒=+=75,BQD ∠=︒120,60,BQQ FQQ ∴∠=︒∠='︒'3236·cos 60?sin 60QF QQ FQ QQ ∴=︒==︒=''' 327222BF BQ QF ∴=+== 22723638,22BQ ⎛⎫⎛⎫∴=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭' 38.AQ BQ '∴==（3）2,AF DE =理由如下：如图，连接,BF2,90,45,BD AD BD ADB ABD BAD AB =∠=︒∠=∠=︒= ,,,DB DP BDP DE BP α=∠=⊥11,,90,,22BE PE BDE PDE DBE FB FP αα∴=∠=∠=∠=︒-=,90,AD DP ADP α=∠=︒+145,2DAP DPA α∴∠=∠=︒-114545,22BAP PDE αα⎛⎫∴∠=︒-︒-==∠ ⎪⎝⎭11180459045,22APB αα⎛⎫∴∠=︒--︒-︒-=︒ ⎪⎝⎭,FB FP =45,90,FBP FPB BFP BFA ∴∠=∠=︒∠=︒=∠ 90,BFA DEP ∴∠=∠=︒ ,DPE ABF ∴∽,DP DEAB AF∴= 2DE DB AF AB ∴== 即2.AF DE = 【点睛】本题考查的是等腰直角三角形的判定与性质，旋转的性质，相似三角形的判定与性质，圆的确定，圆周角定理的应用，是典型的综合题，熟练的运用图形的性质，作出恰当的辅助线是解本题的关键.9．（1）点P 对应的数为-2；（2）当t =2或6时，恰好使得P 到点A 的距离是点P 到点B 的距离的2倍；（3）m +13n =0．【解析】【分析】（1）设点P 对应的数为x ，表示出BP 与PA ，根据BP =PA 求出x 的值，即可确定出点P 对应的数；（2）表示出点P 对应的数，进而表示出PA 与PB ，根据PA =2PB 求出t 的值即可；（3）因为OM ＞ON ，只有甲乙均反弹之后在中点相遇一种情况，设点M 对应的数为m ，点N 对应的数为n ，时间为t ，则M 、N 的中点对应的数为2m n+，根据甲、乙两个弹珠相遇的位置恰好到点M 和点N 的距离相等列出关系式即可．【详解】解：（1）点A 、B 对应的数分别是﹣5和1，设点P 对应的数为x ，则BP =1-x ，PA =x +5， ∵BP =PA ， ∴1-x =x +5，解得：x =-2， ∴点P 对应的数为-2；（2）P 对应的数为-5+2t ， ∴PA =2t ，PB =|-5+2t -1|=|2t -6|， ∵PA =2PB ， ∴2t =2|2t -6|，当t =2t -6时，t =6；当t +2t -6=0时，t =2；答：当t =2或6时，恰好使得P 到点A 的距离是点P 到点B 的距离的2倍；（3）设点M 对应的数为m ，点N 对应的数为n ，时间为t ，则M 、N 的中点对应的数为2m n+， ∴MN =n -m ，OM =-m ，ON =n ，∴()()252502t t n m m n t m m ⎧+=-⎪+⎨⎛⎫=-+- ⎪⎪⎝⎭⎩，即()()351073352t n m n m t ⎧=-⎪⎨-=⎪⎩，化简得m +13n =0．【点睛】本题考查了二元一次方程的应用，数轴，两点间的距离，运用分类讨论思想、方程思想及数形结合思想是解题的关键．10．（1）；（2）当点P运动至坐标为或时，恰好使△PBC的面积等于△ABC的面积的两倍；（3）或【解析】【分析】（1）如图，过C作于先证明可得再代入二次函数y＝x2+bx﹣2中，再利用待定系数法求解b即可；H再求解直线BC （2）先求解过P作轴交BC于,为：设则再利用再解方程即可；（3）分两种情况讨论：如图，作B关于AC的对称点,N连接作的角平分线H交抛物线于,Q由则再求解的交CN于,解析式，再求解与抛物线的交点坐标即可，如图，同理可得：当平分BAC时，射线与抛物线的交点Q满足按同样的方法可得答案.【详解】解：（1）如图，过C作于则而而二次函数y＝x2+bx﹣2的图象经过C点，解得：∴ 二次函数的解析式为：（2）过P 作轴交BC 于,H设直线BC 为,y mx n =+解得：所以直线BC 为：设则整理得：解得：当2x =时，当时，或所以当点P 运动至坐标为或时，恰好使△PBC 的面积等于△ABC 的面积的两倍．（3）如图，作B 关于AC 的对称点,N 连接作的角平分线交CN 于,H 交抛物线于,Q由则平分则同理可得直线的解析式为：解得：或（不合题意，舍去）如图，同理可得：当平分BAC时，射线与抛物线的交点Q满足同理：直线为：解得：或（不合题意舍去）【点睛】本题考查的是利用待定系数法求解一次函数，二次函数关系式，全等三角形的性质与判定，等腰直角三角形的性质，一元二次方程的解法，清晰的分类讨论是解本题的关键.11．（1）213y x x 242=-+-；（2）P 点坐标为(6，2)；（3）①【解析】【分析】（1）求出A 、C 点的坐标，再将点代入y ＝14-x 2+bx +c ，即可得解；（2）先求∠OCA =45º，再由对称性可知PC ⊥y 轴，即可求出点P 的纵坐标，最后利用二次函数的解析式求出结果；（3）①先求出平移后的抛物线，再利用2111()44x m m --+-=x -2，得出2121224,43x x m x x m m +=-⋅=-+，最后利用两点之间的距离公式求解；②作KQ ⊥MN ，连接MK ，MP ，先得出KM =QN 即求KM +MP 的最小值，即KP 的长，最后根据△QMN 的周长的最小值即KQ +KP ，得解．【详解】解：（1）在y ＝x ﹣2中，令y =0，x =2；令x =0，y =-2；∴A (2，0)，C (0，-2)，代入y ＝14-x 2+bx +c 得104242b c c⎧=-⨯++⎪⎨⎪-=⎩，解得322b c ⎧=⎪⎨⎪=-⎩， ∴抛物线的解析式为：213y x x 242=-+-；（2）如图，∵OA =OC =2，∴∠OCA =45°，∵点P 关于直线AC 的对称点Q 在y 轴上，∴∠OCA =∠PCA =45°，∴PC ⊥y 轴，∴P 的纵坐标为-2，由2132242x x -=-+-；解得16x =，20x =(舍去)，∴P 点坐标为(6，2)；（3）①设顶点为(m ，m ﹣114)，平移后抛物线解析式为2111()44y x m m =--+-，则2111()44x m m --+-=x -2， 22(42)430x m x m m +-+-+=，设1122(,),(,)M x y N x y ，则2121224,43x x m x x m m +=-⋅=-+，∴MN 22222121212121212()()()(22)2()8x x y y x x x x x x x x -+--+--++-22= ∴MN 的长度为定值22②如图，作KQ ⊥MN ，连接MK ，MP ，由题知P (6，2)，Q (0，4)，KQ =MN 2，则只需求QM +QN 的最小值即可，∵//,,KQ MN KQ MN =∴KM =QN 即求KM +MP 的最小值，即KP 的长，∵Q (0，4)，KQ 2 ∴K (-2，2)，∴KP 228445+=∴△QMN 的周长的最小值为52【点睛】本题考查了二次函数的综合应用，算了掌握二次函数的图象及性质，轴对称的性质，正确作出图形是解题的关键．12．(1)y＝﹣x2﹣2x+3．(2)M（﹣2，3）或（，119）．(3)最小值为AC＝32P（﹣1，2）．【解析】【分析】（1）根据A、B点的坐标设出抛物线的交点式，再将C点的坐标带图求解，即可得出结论．（2）过A点作AG⊥x轴交BM的延长线于G，则，设ON＝t，则AG＝4t，CN＝3﹣t，进而得出或2，进而建立方程求解，即可得出结论．（3）先判断出△PCD∽△OBQ，进而得出PC2OQ，在判断出A、P、C在同一条直线上时，BP2的最小值，在求出直线AC的解析式，即可得出结论．(1)解：∵二次函数经过点A（﹣3，0）、B（1，0），∴设抛物线的解析式为y＝a（x+3）（x﹣1），∵点C（0，3）在抛物线上，∴﹣3a＝3，∴a＝﹣1，∴抛物线的解析式为y＝﹣（x+3）（x﹣1）＝﹣x2﹣2x+3；(2)解：如图1，过点A作AG⊥x轴交BM的延长线于G，由（1）知，抛物线的解析式为y＝﹣x2﹣2x+3，设点M（m，﹣m2﹣2m+3）（﹣3＜m＜0），∴S△BCM＝12CN（1﹣m），S△ABM＝S△ABG﹣S△AMG＝12AG[（1+3）﹣（m+3）]＝12AG（1﹣m），∴，∵，∴＝14，设ON＝t，则AG＝4t，CN＝3﹣t，∵BM将四边形ABCM的面积分为1：2两部分时，∴＝12或2，∴，或2，∴或2，∴t＝1或13t ，∴N（0，1）或N（0，13），当N（0，1）时，∵B（1，0），∴直线BM的解析式为y＝﹣x+1①，由（1）知，抛物线的解析式为y＝﹣（x+3）（x﹣1）②，联立①②解得，或，∴M（﹣2，3）；当N（0，13）时，∵B（1，0），∴直线BM的解析式为y＝﹣13x+13③，联立②③解得，或，∴M（，119）；即M（﹣2，3）或（，119）；(3)解：如图2，连接PC，CD，过点C作CH⊥DP于H，由（1）知，抛物线的解析式为y＝﹣x2﹣2m+3＝﹣（m﹣1）2+4，∴D（﹣1，4），∵C（0，3），∴CD2，DH＝1，CH＝1，∴DH＝CH，∴∠CDP＝45°，∵点Q为直线y＝x第一象限上的动点，∴∠BOQ＝45°＝∠CDP，∵DP2OQ，∴2，∵2∴＝2∴△PCD∽△OBQ，∴，∴PC2OQ，∴BP2＝BP+PC，连接AP，∵点P是抛物线的对称轴上的点，∴PB＝PA，∴BP+2OQ＝BP+PC＝PA+PC，∴当点A，P，C在同一条直线上时，BP+2OQ最小，最小值为AC＝＝32，∵A（﹣3，0），C（0，3），∴直线AC的解析式为y＝x+3，当x＝﹣1时，y＝2，∴点P（﹣1，2）．【点睛】本题考察了二次函数解析式的求法，抛物线的性质，三角形面积公式，相识三角形等问题，需要数形结合解答问题．13．(1)443y x=-+(2)(0，4)或(6，-4)(3)(-3，12)，(3，-4)或(3，4).【解析】【分析】利用一次函数图象上点的坐标特征可求得点A，B的坐标，由点M是线段OB的中点可得出点M的坐标，根据A、M的坐标，利用待定系数法即可求得直线AM的解析式；设点P的坐标为，利用三角形的面积公式结合，即可得到关于x的含绝对值符号的一元一次方程，解之即可求得点P的坐标；设点N的坐标为，分别以△ABM的三边为对角线，利用平行四边形的对角线互相平分即可得到关于m，n的方程，解之即可求解.(1)解：当x=0时，，。

2022年中考数学压轴难题附答案解析

2022年中考数学压轴题1．抛物线y＝﹣x2+2x+3与x轴交于点A，B（点A在点B的左边），与y轴交于点C．（1）如图1，点P，Q都在直线BC上方的抛物线上，且点P的横坐标比点Q的横坐标小1，直线PQ与x轴交于点D，过点P，Q作直线BC的垂线，垂足分别为点E，F．当PE+QF的值最大时，将四边形PEFQ沿射线PQ方向平移，记平移过程中的四边形PEFQ为P1E1F1Q1，连接CP1，P1F1，求CP1+P1F1+√22Q1D的最小值，并求出对应的点Q1的坐标．（2）如图2，对于满足（1）中条件的点Q1，将线段AQ1绕原点O顺时针旋转90°，得线段A1Q2，点M是抛物线对称轴上一点，点N是坐标平面内一点，点N1是点N关于直线A1Q2的对称点，若以点A1，Q1，M，N1为顶点的四边形是一个矩形，请直接写出所有符合条件的点N的坐标．解：（1）如图1，过P作PL∥y轴交直线BC于L，过Q作QS∥y轴交BC于S，抛物线y＝﹣x2+2x+3与x轴交于点A，B（点A在点B的左边），与y轴交于点C．∴A（﹣1，0），B（3，0），C（0，3）；∴直线BC的解析式为y＝﹣x+3，设P（t，﹣t2+2t+3），则L（t，﹣t+3），Q（t+1，﹣t2+4），S（t+1，﹣t+2），PL＝﹣t2+2t+3﹣（﹣t+3）＝﹣t2+3t，QS＝﹣t2+4﹣（﹣t+2）＝﹣t2+t+2，∵PE⊥BC，QF⊥BC，PL∥y轴，QS∥y轴∴∠PEL＝∠QFS＝∠BOC＝90°，∠PLE＝∠QSF＝∠BCO＝45°∴PE=√22PL=√22(−t2+3t)，QF=√22QS=√22(−t2+t+2)，∴PE+QF=√22(−t2+3t)+√22（﹣t2+t+2）=−√2(t−1)2+2√2∵−√2＜0，0＜t＜3，∴当t＝1时，PE+QF有最大值为2√2，此时P（1，4），Q（2，3），∴直线PQ解析式为y＝﹣x+5，PQ=√(1−2)2+(4−3)2=√2．H（0，5），D（5，0）∴BD＝2如图2，过B作BB′⊥PQ于B′，在Rt△BB′D中，BB′＝BD•sin∠BDB′＝2sin45°=√2，∴PE＝QF＝P1E1＝Q1F1＝BB′=√2（平行线间距离相等）∴PQ＝QF∵QF⊥BC，BC∥PQ，∴QF⊥PQ，∴四边形PEFQ是正方形，∵∠QEP＝∠EPQ＝45°，∴E点与C点重合，F点坐标为（1，2）由平移知P1E1F1Q1与正方形PEFQ是全等形，∴P1F1＝PF＝2．易证Rt△CPP1≌Rt△FQQ1，∴CP1＝FQ1作D（5，0）作DH⊥x轴，过Q1作Q1H⊥DH，∵∠HDQ1＝45°，∴Q1H=√22Q1D，当点F、Q1、H三点在同一直线上，FQ1H⊥DH轴时，FQ1+Q1H最小，即CP1+P1F1+√22Q1D 的值最小，∵此时，F点坐标为（1，2），Q1（3，2），H（5，2），FH＝4．∴CP1+P1F1+√22Q1D的最小值＝4+2＝6，Q1（3，2）．（2）如图3，将线段AQ1绕原点O顺时针旋转90°得线段A1Q2，根据旋转90°点坐标变化规律可知A1（0，1），Q2（2，﹣3）．∵抛物线对称轴为x=−22×(−1)=1，设M（1，m），∴A1M2＝（1﹣0）2+（m﹣1）2＝m2﹣2m+2A1Q12＝（0﹣3）2+（1﹣2）2＝10MQ12＝（1﹣3）2+（m﹣2）2＝m2﹣4m+8若A1M为斜边，则由题意得：A1Q22+MQ22=A1M2，10+m2﹣4m+8＝m2﹣2m+2解得：m＝8，M1（1，8）若Q1M为斜边则由题意得：A1M2+A1Q22=Q2M2，m2﹣2m+2+10＝m2﹣4m+8m＝﹣2，∴M2（1，﹣2）若A1Q1为斜边，则由题意得：A1M2+MQ12=A1Q22，即：（m2﹣2m+2）+（m2﹣4m+8）＝10．解得m＝0或m＝3，即∴M3（1，0）或M4（1，3）．∵四边形A1MQ1N1是矩形，∴根据点的平移可知N1坐标为（﹣2，7）或（4，﹣1）或（2，0）或（2，3），∵N'1与N'关于直线A1Q1对称，∴N'1N'⊥A1Q1，T为N'1N'中点，由点坐标可求直线A1Q1解析式为：y＝﹣2x+1，直线N'1N'解析式为：y=12x+8，故T坐标为（−145，335），∴N'坐标为（−185，315）同理可得其他N'为（−45，−175），（−25，−65）或（−145，35）综上所述：N为（−185，315）或（−45，−175），（−25，−65）或（−145，35）．2．如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c 与x 轴交于点A （﹣2，0），点B （4，0），与y 轴交于点C （0，8），连接BC ．又已知位于y 轴右侧且垂直于x 轴的动直线l ，沿x 轴正方向从O 运动到B （不含O 点和B 点），且分别交抛物线、线段BC 以及x 轴于点P ，D ，E ．（1）求抛物线的表达式；（2）连接AC ，AP ，当直线l 运动时，求使得△PEA 和△AOC 相似的点P 的坐标；（3）作PF ⊥BC ，垂足为F ，当直线l 运动时，求Rt △PFD 面积的最大值．解：（1）将点A 、B 、C 的坐标代入二次函数表达式得：{4a −2b +c =016a +4b +c =0c =8，解得：{a =−1b =2c =8，故抛物线的表达式为：y ＝﹣x 2+2x +8；（2）∵点A （﹣2，0）、C （0，8），∴OA ＝2，OC ＝8，∵l ⊥x 轴，∴∠PEA ＝∠AOC ＝90°，∵∠P AE ≠∠CAO ，∴只有当∠P AE ＝∠ACO 时，△PEA ∽△AOC ，此时AE CO =PE AO ，即：AE 8=PE 2，∴AE ＝4PE ，设点P 的纵坐标为k ，则PE ＝k ，AE ＝4k ，∴OE ＝4k ﹣2，将点P 坐标（4k ﹣2，k ）代入二次函数表达式并解得：k ＝0或2316（舍去0），则点P （154，2316）；（3）在Rt △PFD 中，∠PFD ＝∠COB ＝90°，∵l ∥y 轴，∴∠PDF ＝∠OCB ，∴Rt △PFD ∽Rt △OCB ，∴S △PFDS △BOC =(PD BC )2，∴S △PDF =(PD BC )2•S △BOC ，而S △BOC =12OB •OC =12×4×8=16，BC =√CO 2+BO 2=4√5，∴S △PDF =(PD BC )2•S △BOC =15PD 2，即当PD 取得最大值时，S △PDF 最大，将B 、C 坐标代入一次函数表达式并解得：直线BC 的表达式为：y ＝﹣2x +8，设点P （m ，﹣m 2+2m +8），则点D （m ，﹣2m +8），则PD ＝﹣m 2+2m +8+2m ﹣8＝﹣（m ﹣2）2+4，当m ＝2时，PD 的最大值为4，故当PD ＝4时，∴S △PDF =15PD 2=165．3．已知一次函数y1＝kx+n（n＜0）和反比例函数y2=mx（m＞0，x＞0）．（1）如图1，若n＝﹣2，且函数y1、y2的图象都经过点A（3，4）．①求m，k的值；②直接写出当y1＞y2时x的范围；（2）如图2，过点P（1，0）作y轴的平行线l与函数y2的图象相交于点B，与反比例函数y3=nx（x＞0）的图象相交于点C．①若k＝2，直线l与函数y1的图象相交点D．当点B、C、D中的一点到另外两点的距离相等时，求m﹣n的值；②过点B作x轴的平行线与函数y1的图象相交于点E．当m﹣n的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．解：（1）①将点A的坐标代入一次函数表达式并解得：k＝2，将点A的坐标代入反比例函数得：m＝3×4＝12；②由图象可以看出x＞3时，y1＞y2；（2）①当x＝1时，点D、B、C的坐标分别为（1，2+n）、（1，m）、（1，n），当B为中点时，则BD＝BC，即2+n﹣m＝m﹣2，则 m ﹣n ＝1；当D 为中点时，则 DB ＝DC ，即m ﹣（2+n ）＝2+n ﹣n ，故m ﹣n ＝4，当C 为中点时，则 CB ＝CD ，即m ﹣n ＝n ﹣（2+n ），则 m ﹣n ＝﹣2 （不符合题意舍去），∴m ﹣n ＝1或4．②点E 的横坐标为：m−n k ，当点E 在点B 左侧时，d ＝BC +BE ＝m ﹣n +（1−m−n k ）＝1+（m ﹣n ）（1−1k ）， m ﹣n 的值取不大于1的任意数时，d 始终是一个定值，当1−1k=0时，此时k ＝1，从而d ＝1．当点E 在点B 右侧时，同理BC +BE ＝（m ﹣n ）（1+1k ）﹣1，当1+1k =0，k ＝﹣1时，（不合题意舍去）故k ＝1，d ＝1．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2022年中考数学压轴题1．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c经过原点，与x轴交于另一点A，对称轴x＝﹣2交x轴于点C，直线l过点N（0，﹣2），且与x轴平行，过点P作PM⊥l 于点M，△AOB的面积为2．（1）求抛物线的解析式；（2）当∠MPN＝∠BAC时，求P点坐标；（3）①求证PM＝PC；②若点Q坐标为（0，2），直接写出PQ+PC的最小值．解：（1）∵抛物线y＝ax2+bx+c经过原点，且对称轴为x＝﹣2，∴c＝0，OA＝4，又△AOB的面积为2，∴BC＝1，即顶点B的坐标为（﹣2，﹣1），∴−b2a=−2，−b24a=−1，解得a=14，b＝1，∴抛物线的解析式为y=14x2+x；（2）∵BC＝1，AC＝2，∴tan∠BAC=12，设P点坐标为（x，14x2+x），如图1，当点P在y轴右侧，PM=14x2+x−（﹣2）=14x2+x+2，MN＝x，∴tan∠MPN=MNPM=x14x2+x+2=12，即x2﹣4x+8＝0，此方程无解；如图2，当点P在y轴左侧，此时PM=14x2+x+2，MN＝﹣x，∴tan∠MPN=MNPM=−x14x2+x+2=12，即x2+12x+8＝0，解得x1=−6+2√7，x2=−6−2√7，则y1=10−4√7，y2=10+4√7，∴点P坐标为（−6+2√7，10−4√7）或（−6−2√7，10+4√7）；（3）①如图3，过点P作PD⊥BC于点D，则PD＝x+2，DC=14x2+x，由（2）知PM =14x 2+x +2，在Rt △PCD 中，PC 2=(x +2)2+(14x 2+x)2=116x 4+12x 3+2x 2+4x +4=PM 2， ∴PM ＝PC ；②由①知，PM ＝PC ，∴PQ +PC 的最小值为PQ +PM 的最小值，当Q 、P 、M 三点共线时，PQ +PM 有最小值为4．∴PQ +PC 的最小值为4．2．如图，抛物线y =−√33x 2−√3x +4√33与x 轴交于A ，B 两点（A 点在B 点的左侧），与y 轴交于点C ，顶点为D ，连接AC ．（1）求顶点D 的坐标及直线AC 的解析式；（2）如图，P 为直线AC 上方抛物线上的一动点，连接PC 、P A ，当△P AC 面积最大时，过P 作PQ ⊥x 轴于点Q ，M 为抛物线对称轴上的一动点，过M 作y 轴的垂线，垂足为点N ．连接PM ，NQ ，求PM +MN +NQ 的最小值．解：（1）y =−√33x 2−√3x +4√33，令y =−√33x 2−√3x +4√33=0，解得：x ＝﹣4或1，故点A 、B 的坐标分别为：（﹣4，1）、（1，0），点C （0，4√33），由抛物线的表达式知，顶点D （−32，25√312）；将点A 、C 的坐标代入一次函数：y ＝kx +b 得：{−4k +b =0b =4√33，解得{k =√33b =4√33，则直线AC 的表达式为：y =√33x +4√33；（2）设直线PQ 交AC 于点H ，设点P （x ，−√33x 2−√3x +4√33），则点H （x ，√33x +4√33），则△P AC 面积＝S △PHC +S △PHA =12×PH ×OA ＝2×[−√33x 2−√3x +4√33−（√33x +4√33）]=−√36（x 2+4x ），∵−√36＜0，故△P AC 面积存在最大值，此时x ＝﹣2，故点P （﹣2，2√3），则点Q （﹣2，0）；将点P 向右平移32个单位得到点P ′（−12，2√3），作点P ′关于y 轴的对称点P ″（12，2√3），连接P ″Q 交y 轴于点N ，过点N 作NM 垂直于函数的对称轴于点M ，则点M 、N 为所求点，理由：连接PM 、P ′N ，∵PP′∥MN，PP′＝MN=32，故四边形PPNM为平行四边形，故PM＝P′C＝P″C，则PM+MN+NQ＝P″C+MN+NQ＝MN+P″Q为最小，∴PM+MN+NQ最小值＝MN+P″Q=32+√(12+2)2+(2√3)2=3+√732．3．如图1，在平面直角坐标系中，抛物线y=−√33x2+2√33x+√3与x轴交于A、B两点（A 在B的左侧），与y轴交于点C，顶点为D．（1）求△BCD的周长；（2）如图2，点P是第一象限内对称轴右侧抛物线上一点，过P作PM∥y轴交BC于M，交x轴于E，过D作DN∥y轴交BC于N，当PM+MN最大时，将线段PM绕P点旋转得线段PM′，连接BM′，取BM′的中点F，求EF的最小值及PM+MN的最大值；（3）如图3，在（2）的条件下，当PM+MN最大时，将△BME沿射线BC方向平移(10−5√3)个单位得△B′M′E′，作射线OE′，点G是射线OE′上一动点，连接BG，将△BOG 沿直线BG翻折得△BO′G，在y轴上有一点T（0，2），连接TO′、OO′，△TOO′能否构成等腰三角形？若能，求出点G的坐标；若不能，请说明理由．解：（1）如图1，过D作DS⊥x轴于S，过C作CT⊥DS于T，令x＝0，得y=√3，∴C（0，√3）令y ＝0，−√33x 2+2√33x +√3=0，解得：x 1＝﹣1，x 2＝3，∴A （﹣1，0），B （3，0）， ∵y =−√33x 2+2√33x +√3=−√33（x ﹣1）2+4√33，∴D （1，4√33）有勾股定理可得：BC =√OB 2+OC 2=√32+(√3)2=2√3，BD =(4√33)2+22=2√213，CD =12+(4√33−√3)2=2√33 ∴△BCD 的周长＝BC +BD +CD ＝2√3+2√213+2√33=2√21+8√33；（2）设直线BC 的解析式为y ＝kx +b ，将B （3，0），C （0，√3）分别代入并解方程组得：y =−√33x +√3，∴N （1，2√33）设P （m ，−√33m 2+2√33m +√3），则M （m ，−√33m +√3），过M 作MK ⊥DN 于K ， ∴PM =−√33m 2+2√33m +√3−（−√33m +√3）=−√33m 2+√3m ， ∵MK ⊥DN ，DS ⊥OB ，∴MK ∥OB ，∠MKN ＝∠BOC ＝90° ∴∠NMK ＝∠CBO ， ∴△MKN ∽△BOC ∴MN MK=BC OB，即：MN •OB ＝BC •MK ，3MN ＝2√3（m ﹣1）∴MN =2√3(m−1)3， ∴PM +MN =−√33m 2+√3m +2√3(m−1)3=−√33(m −52)2+17√312， ∵−√33＜0∴当x =52时，PM +MN 的最大值=17√312，PM =5√312， ∴P （52，7√312），以P 为圆心，PM 为半径作⊙P ，作点B 关于直线PE 的对称点B ′，连接PB ′交⊙P 于点M ′，连接BM ′，F 为BM ′中点，连接EF ， ∵BE ＝B ′E ，BF ＝M ′F ∴EF =12BM ′，∵PB ′＝PB =(3−52)2+(7√312)2=√18312， ∵P 、M ′、B ′三点共线时，B ′M ′最小值=√183−5√312，∴此时，EF 最小，且EF 的最小值=12B ′M ′=√183−5√324．（3）△TOO ′能构成等腰三角形．如图3，∵E （52，0），将△BME 沿射线BC 方向平移(10−5√3)个单位得△B ′M ′E ′，连接EE ′，过E ′作E ′N ⊥OB 于N ， ∴E ′E ∥BC∴∠E ′EN ＝∠CBO ，∠E ′NE ＝∠COB ＝90° ∴△E ′EN ∽△CBO ∴E′N OC=EN OB=EE′BC，即：√3=EN 3=√32√3∴E ′N =10−5√32，EN =10√3−152∴ON ＝OE ﹣EN =52−10√3−152=10﹣5√3， ∴E ′（10﹣5√3，10−5√32） ∴直线OE ′的解析式为y =12x ， ∵△TOO ′为等腰三角形，∴TO ＝TO ′＝2或OO ′＝OT ＝2或O ′T ＝O ′O ①若TO ＝TO ′＝2时，由翻折得：BO ′＝BO ∴BT 垂直平分OO ′，即B 、G 、T 三点共线易求得直线BT 解析式为：y =−23x +2 解方程组{y =−23x +2y =12x 得：{x =127y =67∴G （127，67）；②若OO ′＝OT ＝2时，∵BO ′＝BO ，∠OBG ＝∠O ′BG ∴BG 垂直平分OO ′，设BG 交OO ′于点Q ，则易求得Q （13，2√23）， ∴待定系数法可求得直线BG 的解析式为：y =−√24x +3√24∴G （3√2−3，3√2−32）；易求得点O ′（3﹣2√2，1），直线BQ 解析式为：y ＝（2√2−3）x +9﹣6√2∴G （30−12√217，15−6√217）；综上所述，点G 的坐标为：G （127，67）或G （3√2−3，3√2−32）或G （30−12√217，15−6√217）．4．如图，AB 是⊙O 的直径，点C 是⊙O 上一点（与点A ，B 不重合），过点C 作直线PQ ，使得∠ACQ ＝∠ABC ．（1）求证：直线PQ 是⊙O 的切线．（2）过点A 作AD ⊥PQ 于点D ，交⊙O 于点E ，若⊙O 的半径为2，sin ∠DAC =12，求图中阴影部分的面积．解：（1）证明：如图，连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵OA＝OC，∴∠CAB＝∠ACO．∵∠ACQ＝∠ABC，∴∠CAB+∠ABC＝∠ACO+∠ACQ＝∠OCQ＝90°，即OC⊥PQ，∴直线PQ是⊙O的切线．（2）连接OE，∵sin∠DAC=12，AD⊥PQ，∴∠DAC＝30°，∠ACD＝60°．∴∠ABC＝∠ACD＝60°，∴∠CAB＝90°﹣60°＝30°，∴∠EAO＝∠DAC+∠CAB＝60°，又∵OA＝OE，∴△AEO为等边三角形，∴∠AOE＝60°．∴S阴影＝S扇形﹣S△AEO＝S 扇形−12OA •OE •sin60° =60π360×22−12×2×2×√32 =2π3−√3．∴图中阴影部分的面积为2π3−√3．5．如图，在△ABC 中，∠ACB ＝90°，将△ABC 沿直线AB 翻折得到△ABD ，连接CD 交AB 于点M ．E 是线段CM 上的点，连接BE ．F 是△BDE 的外接圆与AD 的另一个交点，连接EF ，BF ．（1）求证：△BEF 是直角三角形；（2）求证：△BEF ∽△BCA ；（3）当AB ＝6，BC ＝m 时，在线段CM 上存在点E ，使得EF 和AB 互相平分，求m 的值．（1）证明：∵∠ACB ＝90°，将△ABC 沿直线AB 翻折得到△ABD ， ∴∠ADB ＝∠ACB ＝90°，∵∠EFB ＝∠EDB ，∠EBF ＝∠EDF ，∴∠EFB +∠EBF ＝∠EDB +∠EDF ＝∠ADB ＝90°， ∴∠BEF ＝90°， ∴△BEF 是直角三角形．（2）证明：∵BC ＝BD ， ∴∠BDC ＝∠BCD ， ∵∠EFB ＝∠EDB ， ∴∠EFB ＝∠BCD ，∵AC ＝AD ，BC ＝BD ， ∴AB ⊥CD ， ∴∠AMC ＝90°，∵∠BCD +∠ACD ＝∠ACD +∠CAB ＝90°， ∴∠BCD ＝∠CAB ， ∴∠BFE ＝∠CAB ， ∵∠ACB ＝∠FEB ＝90°， ∴△BEF ∽△BCA ．（3）解：设EF 交AB 于J ．连接AE ． ∵EF 与AB 互相平分， ∴四边形AFBE 是平行四边形， ∴∠EF A ＝∠FEB ＝90°，即EF ⊥AD ， ∵BD ⊥AD ， ∴EF ∥BD ， ∵AJ ＝JB ， ∴AF ＝DF ， ∴FJ =12BD =m 2， ∴EF ＝m ，∵△ABC ∽△CBM ， ∴BC ：MB ＝AB ：BC ，∴BM =m 26，∵△BEJ ∽△BME ， ∴BE ：BM ＝BJ ：BE ， ∴BE =m √2， ∵△BEF ∽△BCA ， ∴AC EF=BC BE，第 11 页共 11 页即√36−m 2m =m m √2，解得m ＝2√3（负根已经舍弃）．。