定积分在几上的应用
定积分运算法则
• 通过定积分求解经济学中的边际产量、边际消费等边际问题
求解经济学中的总量问题
• 通过定积分求解经济学中的总产量、总消费等总量问题
求解经济学中的平均问题
• 通过定积分求解经济学中的平均产量、平均消费等平均问题
谢谢观看.
Thank you for watching.
Docs
⌛️
06
定积分的数值计算方法
数值积分的基本原理与方法
数值积分的定义
数值积分的方法
• 通过数值方法近似求解定积分的值
• 辛普森法
• 龙贝格法
• 高斯积分法
数值积分的误差分析与控制
误差分析
误差控制
• 分析数值积分方法的误差来源
• 选择合适的数值积分方法
• 估计数值积分方法的误差范围
• 控制积分区间的长度
求解物体的速度
• 通过定积分求解物体在变力作用下的速度
求解物体的加速度
• 通过定积分求解物体在变力作用下的加速度
定积分在工程学中的应用
求解工程问题的面积
求解工程问题的体积
求解工程问题的质心位置
• 通过定积分求解曲线围成的面积
• 通过定积分求解曲面围成的体积
• 通过定积分求解物体的质心位置
定积分在经济学中的应用
积分问题
换元积分法的原理
• 利用换元公式将原积分变量变换为新变量，从而简化积分过程
换元积分法的常见类型与方法
01
幂函数换元法
• 将复杂的幂函数积分问题转化为简单的指数函数积分问
题
02
三角函数换元法
• 将复杂的三角函数积分问题转化为简单的指数函数积分
问题
03
定积分在几何学上的应用研究报告
8 2a 3
2 sin2 udu
0
0
4 3a 3
8 2a 3
1 2
2
6 3a 3
第六章 定积分的应用
16
说明：Vy 也可按柱壳法求出
Vy
2a 2 xydx 2 2 a t sin t
0
0
a2 1 cost 2 dt
8 a3
2 0
t
sint
sin4 t dt 2
16 a3 2u 0
23
例 13 求阿基米德螺线 a a 0相应于0 2 一段的弧长。
解：
弧长元素为
从而，所求弧长
ds 2 2 d
a 2 2 a 2d a 1 2d
s 2 a 1 2d 0
a
2
1 2
1 2
ln
1
2
2 0
a
2
2
1 4 2
ln
2
1
4 2
第六章 定积分的应用
x t y t
给出时，按顺时针方向规定起点和终点的参数值t1 和t2 。
Y
t 1
对应
x
a
Y a
O
bX
O
a
bX
则曲边梯形面积 A
t2
t1
t t dt
t1 对应x b
第六章 定积分的应用
5
例 求由摆线x a t sint ，y a 1 cost a 0 的一拱与x 轴所围
s b 1 y 2dx b 1 f 2 x dx
a
a
第六章 定积分的应用
20
2.曲线弧由参数方程
x y
t t
t
给出
弧长元素（即弧微分）为ds 2 t 2 t dt ，因此
高等数学(上册)-第5章第6讲(定积分的几何应用)[22页]
![高等数学(上册)-第5章第6讲(定积分的几何应用)[22页]](https://img.taocdn.com/s3/m/9c36fcd0783e0912a2162ad6.png)
5
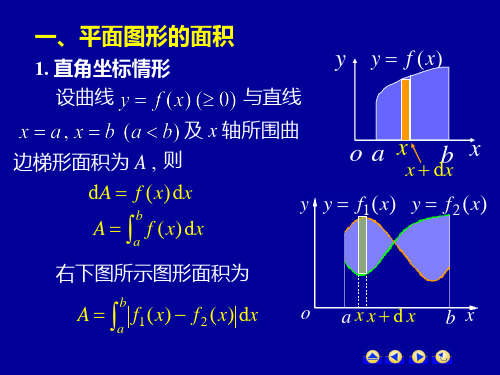
二、 平面图形的面积
1. 直角坐标系中的平面图形的面积
在平面直角坐标系中求由曲线y f (x)，y g(x)和直线x a，x b围成图
形的面积A，其中函数f (x)，g(x)在区间[a,b]上连续，且f (x) g(x)，如图所示.
在区间[a,b] 上任取代表区间[x, x dx]，在区间两个端点处做垂直于x 轴的
A 1 r2 ( )d.
2
β
O
α
ρ 10
本讲内容
01 微元法 02 平面图形的面积 03 体积 04 平面曲线的弧长
11
三、 体积
1.旋转体的体积.
由一个平面图形绕这平面内一条直线旋转一 y 周而成的立体称为旋转体，这条直线称为旋转轴.
如圆柱、圆锥、圆台、球体都是旋转体. 设一旋转体由连续曲线 y f (x)，直线x a， O a
直线，由于 dx 非常小，这样介于两条直线之间的图形可以近似看成矩形，因
此面积微元可表示为
[ f (x) g(x)]dx,
于是，所求面积A为
b
A a [ f (x) g(x)]dx.
若f (x) g(x)，则有
A
b
[ f (x) g(x)]dx.
a
综合以上两种情况，由曲线 y f (x)，y g(x)
y x 1(y)
d
c O
x 2(y) x
7
二、 平面图形的面积 例 1 求由两抛物线y x2与x y2 所围成图形的面积A .
解
解方程组
y x
x2，得到两抛物线的交点为(0，0)，(1，1)， y 2，
y
两抛物线围成的图形如图所示.
则所求面积 A 为
A
高中数学 1.7 1定积分的应用教案 新人教A版选修2-2
2013年高中数学 1.7 1定积分的应用教案新人教A版选修2-2一、主要内容：1．面积：了解定积分的元素法，掌握用两条、三条、四条简单曲线所围平面图形的面积，并能根据图形选用以y作积分变量以简化计算过程；会用参数方程求解常用图形（圆、星形线）的面积，能用极坐标求用极坐标表示的圆、阿基米德螺线的图形的面积2．体积：掌握简单图形分别绕x轴、y轴旋转所得旋转体体积，能在平行截面面积为已知时求立体的体积3．弧长：掌握用参数方程所表示的常用曲线（圆、星形线等）的弧长4．功：会求在变力沿直线所作的功5．习题课2学时二、具体的内容分配如下：习题6－1：定积分的元素法，平面图形的面积, 旋转体体积(1)习题6－2：旋转体体积(2)，平面曲线的弧长，变力沿直线所作的功总习题六：三、习题内容：习题6—1一、填空题1、曲线x e y =，x 轴及直线()ln ,ln 0.x a x b b a ==，围成图形面积 是_____2、由曲线θcos 2a r =所围成图形的面积是 二、选择题1、曲线3x y =与直线1,0==y x 围成的面积是（ ） A ．43 B ．1 C ．34 D ．32 2、由x 轴、曲线2x y =和直线32=x 围成的图形面积被直线k x =分成两个相等的面积，则 k 应为（ ）A ．322- B ．612 C ．1 D ．312-三、求解题1、用定积分计算下列图形的面积 （1）由曲线222,1x y x y =+=围成（2）由曲线21y x=与直线4,==y x y 围成（3）由曲线x y 42=与圆()4122=+-y x 围成2、求星形线｛33cos sin x a ty a t==所围成0.的面积 3、求以下极坐标所表示的图形的面积 （1）心形线()θcos 1-=a r 围成（2）对数螺线a r e θ=对应θ从0到2π的一段与极轴所围成 （3）伯努利双纽线θ2cos 22a r =右边一支（即对应θ从4π-到4π的一段）习题 6—2 一、填空题1、连续曲线()x f y = ()()0≥x f ，直线b x a x ==,()b a 及x 轴所围成图形绕x 轴旋转而成的旋转体的体积是______2、曲线2x y =及直线1=y 所围成图形绕y 轴旋转而成的旋转体的体积是_______ 二、选择题1、由曲线2x y =与直线x y =围成平面图形绕y 轴旋转所得的旋转体的体积是（ ）A ．()dx x x ⎰-102π Ｂ．)21d y y π-⎰Ｃ．()⎰-1042dx x x π Ｄ．()dy y y ⎰-102π2、底面为圆422=+y x ，垂直于x 轴的所有截面都是正方形的立体体积为（ ）A. 3121 B. 3210 C. 3242 D. 3185 三、解答题1、求下列旋转体的体积（1）曲线x y sin = ()π≤≤x 0与x 轴所围成的图形分别绕x 轴、y 轴旋转（2）曲线x y =与直线2-=x y ，0=y 所围成的图形分别绕x 轴、y轴旋转（3）星形线｛ta y t a x 33sin cos == ()π≤≤t 0绕x 轴旋转2、求底面为园222R y x =+，而垂直于x 轴的所有截面都是等边三角形的立体的体积习题6—3一、求下列弧线段的长度1、星形线｛ta y ta x 33sin cos ==的全长 2、抛物线x y 2= 从()2,1到()4,4的一段二、根据虎克定律，弹簧的倔强系数为k ，把弹簧拉长x 的拉力为kx f =，求将一根弹簧从原长拉伸x 的长度，外力做的功三、在一个半径为R 的半球形容器里盛放着密度为ρ的液体，求为将液体吸出容器至少应做多少功四、水渠的截面为一等腰梯形，上、下底分别为2m 和1m ，深为2m ，水渠上有一闸门，求渠水满时对闸门的压力（水的密度31000m kg=ρ）。
高中数学同步教学 第4章 §3 定积分的简单应用
0
0
＝π(12x2－15x5)|01＝π(12－15)＝π×130＝130π.
• 4．由曲线y＝x2,直线x＝1,x＝2与x轴所围成的平面图形绕x
31π 5
轴[解旋析转] 一设周所得所旋得转旋体的转体体积的为 体V，积为________.
则 V＝2π(x2)2dx＝2πx4dx＝5πx5|12＝315π.
1
1
互动探究学案
命题方向1 ⇨不分割型平面图形面积的求解
• 典例 1 曲线y＝x2与直线y＝x所围成的封闭图形16 的面积 为____.
• [思路分析] 从图形上可以看出,所求图形的面积可以转化 为一个三角形与一个曲边三角形面积的差,进而可以用定积 分求出面积．为了确定出积分的上、下限,我们需要求出直 线[解和析抛] 物解线方程的组交yy点＝＝xx的，2，横坐标．
第四章 定积分
• 本章知识概述：本章的主要内容是定积分的概念,计算和简 单应用．
• 教科书通过曲边梯形面积问题,变速直线运动物体的路程问 题,变力做功等问题,充分演示了定积分概念产生的背景以 及定积分概念形成过程中的思路．微积分基本定理为我们 处理积分的计算问题提供了有力工具,教科书主要介绍了求 简单图形的面积和求简单旋转体的体积．
1．平面图形的面积 如果函数 y＝f(x)在区间[a，b]上连续且恒有 f(x)≥0，那么定积分b f(x)dx 表
a
示由__直__线__x_＝__a_,x_＝__b_(_a_≠_b_)_,y_＝__0_和__曲__线__y_＝__f_(_x)_______所围成的曲边梯形的面积． 2．简单几何体的体积
得 x1＝0，x2＝1. 故所求图形的面积为
S＝1xdx－1x2dx
0
0
高中数学人教A版选修2-2课件 1-7 定积分的简单应用 第13课时《定积分的简单应用》
解析：(1)由v(t)＝8t－2t2≥0，得0≤t≤4，
即当0≤t≤4时，P点向x轴正方向运动，
当t＞4时，P点向x轴负方向运动．
故t＝6时，点P离开原点的路程为
s1＝4(8t－2t2)dt－6(8t－2t2)dt
0
4
＝4t2－23t3|40－4t2－23t3|64＝1328.
a
成的曲边梯形的面积．
【练习1】 曲线y＝cosx0≤x≤32π与坐标轴所围成的图形面积是
() A．2
B．3
5 C.2
D．4
3
3
解析：S＝ 2 a
cosxdx＋|
2
cosxdx|＝
2
0
cosxdx－
2
cosxdx＝sinx|
2 0
－
(2)路程是位移的绝对值之和，因此在求路程时，要先判断速度 在区间内是否恒正，若符号不定，应求出使速度恒正或恒负的区间， 然后分别计算，否则会出现计算失误．
变式探究2 (1)一物体沿直线以v＝3t＋2(t单位：s，v单位：m/s)
的速度运动，则该物体在3 s～6 s间的运动路程为( )
A．46 m
3
(3t2－2t＋4)dt＝()－(8
2
－4＋8)＝18.
答案：(1)B (2)D
考点三 利用定积分计算变力做功 例3 设有一长25 cm的弹簧，若加以100 N的力，由弹簧伸长到
30 cm，又已知弹簧伸长所需要的拉力与弹簧的伸长量成正比，求使 弹簧由25 cm伸长到40 cm所做的功．
∴W＝∫00.1250xdx＝25x2|00.12＝0.36(J)． 答案：0.36 J
高数课件第六章定积分的应用：第二节定积分的几何应用
y
c
b O
x
bx
x
x x 1 sh dx ch dx c c b x xb s 2 ch dx 2c sh 0 c c 0 x b 1 x 2c sh ( c ch ) c sh c c c c
2
e e ch x 2 x x e e sh x 2 (ch x) sh x
Hale Waihona Puke 2 (t ) 2 (t ) d t
因此所求弧长
s
2 (t ) 2 (t ) d t
(3) 曲线弧由极坐标方程给出:
令 x r ( ) cos , y r ( ) sin , 则得
dx [r ( ) cos r ( ) sin ]d dy [r ( ) sin r ( ) cos ]d
2
选 x 为积分变量 (1) x [2, 0], dA1 ( x 3 6 x x 2 )dx 于是所求面积 A A1 A2
特别注意:
各积分区间 A ( x 3 6 x x 2 )dx 0 (x x 6 x)dx 上被积函数的 2 253 形式不同． . 12
0
3
2
3
x2 1 练习：1.求曲线 y , y 与直线 x 3 2 1 x 2
x 3 所围成的图形的面积。
2.求曲线 xy 1 与直线
x y 0 y 2
x y 2
P1
2
所围成的图形的面积。 2014考研题
提示：1
P2
y
1
32 1 0 2 1 1 3 x 1 x 1 1 s 2[ ( )d x ( ( 3 3 2) ) d x ] 2 0 1 x 1 3 2 2 1 x2
高等数学第六章第二节定积分在几何学上的应用课件.ppt
解:
cos x 0,
2
x
2
s
2
2
2 2 0
1 y2 dx 1 ( cos x)2 dx
2 2
2 cos x dx
0
2
2
2
2
sin
x 2
2
0
4
的弧长.
例11. 计算摆线
一拱
的弧长 .
y
解: ds
(dd
x t
)2
(
d d
y t
)
2
d
t
o
a2 (1 cos t)2 a2 sin2 t d t
1 y2 dx
因此所求弧长
s b 1 y2 dx a
b
a
1 f 2(x) dx
y
y f (x)
ds
o a xxdxb x
(2) 曲线弧由参数方程给出:
弧长元素(弧微分) :
ds (dx)2 (dy)2
2 (t) 2 (t) dt
因此所求弧长
s
2 (t) 2 (t) d t
(3) 曲线弧由极坐标方程给出:
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
方法2 利用椭圆参数方程
则 V 20a y2 dx 2 ab2 sin3t d t
2 ab2 2 1
3
4 ab2
3
特别当b
=
a
第一节 定积分在几何上的应用6-1
所围图形绕 x 轴旋转
而成的椭球体的体积. 解: 方法1 利用直角坐标方程
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
方法2 利用椭圆参数方程
则 V 20a y2 dx 2 ab2 sin3t d t
2
0
4 3 a2
3
对应 从 0 变
2 a
o
x
d
例6. 计算心形线
与圆
所围图形的面积 .
1 2cos cos 2
解: 利用对称性 , 所求面积
A
1a2 2
2
1 a2 (1 cos )2 d
2
1 2
(1
cos
2
)
1 a2 a2 (3 2cos 1 cos 2 )d
b
b
A a dA( x) a f ( x)dx.
y
妨此可得（图1）的面积： d
A
d
dA( y)
d
f ( y)dy.
y
c
c
c
（图2）的面积：
y
O
y f2(x)
y f1( x)
oa
x bx
（图2）
A
b[ a
f2(x)
f1( x)]dx
A
x=f(y)
（图1）
及 y 轴所围曲边梯形绕 y 轴的旋转体的体积计算公式
定积分的应用
b
S a [ f (x)-g(x)]dx
y
a
O
y = f (x)
bx y = g(x)
例1 计算由曲线 y x2 及直线 y x 所围成的平面图形
的面积。
例1 计算由曲线 y x2 及直线 y x 所围成的平面图形
的面积。
解：作出所围成的平面图形
解：在弹性限度内，拉伸（或压
缩）弹簧所需的力Ｆ（x）与弹
簧拉伸（或压缩）的长度x成正
比．
即：F(x)=kx
所以据变力作功公式有
W
L
F(x)dx
0
L 0
kxdx
1kx2 2
|0L
1 2
kL2
作业：
课本58页练习（1）（2） 课本59页练习1,2
的面积为 （ ）
(A) 2 (C) 2 2
e
(B) 2 e (D) e 1 2
e
二、物理中的应用
1、变速直线运动的路程
设物体运动的速度vv(t)，则此物体在时 间间[a, b]内运动的路程s为
b
s a v(t)dt
例 1 一辆汽车的速度一时间曲线如图所示，求
汽车在这 1 min 行驶的路程。
y x
y
x2
解方程组，得交点的横坐标为x=0
和x=1, 即区间为[0，1]。于是，
平面图形的面积
A
1(x x2)dx
0
(1 2
x2
1 3
x3)
1 0
1 6
例 2 求 y = sinx， y = cos x， x 0, x
2
所围成的平面图形的面积。
定积分的意义及其在几何中的应用
定积分的意义及其在几何中的应用定积分是微积分中的一种重要概念，它是反映了函数在一些区间上面积的大小。
定积分的含义非常丰富，不仅可以用于求函数的面积、周长、体积等几何问题，还广泛应用于物理学、经济学、生物学等领域的计算与分析中。
首先，定积分的最基本的含义是求函数在一些区间上的面积。
对于非负连续函数f(x)，可以将其图像以下方的函数图形为界，通过分割区间，构造出一系列较窄的矩形，然后求出这些矩形的面积之和，即可近似地得到曲线下面积的值。
随着分割区间的无穷细小，这个近似的面积将趋近一个确切的值，即定积分。
如果函数是负值或者非连续的情况，面积的计算则需要对函数图像进行分段处理，并分别计算每个部分的面积。
所以，定积分在几何中的应用可以明确地用于求曲线与坐标轴之间的面积。
其次，定积分也可以用于求曲线的弧长。
由于曲线的形状较为复杂，无法直接计算其弧长，但通过将曲线分成许多较小的线段，并每个线段用直线段来代替，再对这些直线段进行求和的方式，可以用定积分来近似计算曲线的长度。
当分割的线段无限细小时，这个近似的弧长将趋近于曲线的实际弧长。
这种方法虽然只能得到近似值，但对于一些无法获得解析解的复杂曲线来说，这种近似是非常有用的。
此外，在三维几何中，定积分可以应用于计算旋转体的体积。
对于一个曲线沿着坐标轴旋转形成的立体，可以将其分成许多非常薄的盘状元素，并计算每个盘状元素的体积，然后通过定积分将这些体积相加，即可得到整个旋转体的体积。
这个方法适用于各种形状的旋转体，能够有效地求解这些体积。
除了在几何中的应用，定积分在物理学、经济学、生物学等领域也有广泛的应用。
在物理学中，定积分可以用于计算各种形状物体的质心、重心等。
在经济学中，定积分常用于求解定量经济模型中的微积分方程，如求解需求曲线、利润函数等。
在生物学中，定积分可以用于计算生物体的体积、质量、功率等。
总之，定积分是微积分中一个重要的概念，不仅在几何中用于求解曲线的面积、弧长、旋转体的体积等问题，还在许多学科中都有广泛的应用。
定积分在几何上的应用
2
a
y x2 y 2 2 1 2 b a b
4ab sin tdt ab.
2 0
2019/4/7 第六章 定积分的应用
2
o
图6-2-5
a x
8
2.极坐标情形
设由曲线 ( ) 及射线
d
()
d 、 围成一曲边扇 ( ) 形，求其面积．这里， 在[ , ]上连续，且 ( ) 0 ． 1 o 面积元素 dA [ ( )]2 d x 2 图6-2-6
3
a
o
a x
旋转体的体积
V a x a
2 3
图6-2-12
2019/4/7
第六章 定积分的应用
32 3 dx a . 105
16
类似地，如果旋转体是由连续曲线
x ( y ) 、直线 y c 、 y d 及y 轴所围 成的曲边梯形绕y 轴旋转一周而成的立体，
第六章 定积分的应用
1
b
例 1 计算由两条抛物线y 2 x 和 y x 2 所围成的 图形的面积.
解
两曲线的交点
(0,0) (1,1)
选 x 为积分变量 x [0,1]
面积元素 dA ( x x 2 )dx
2 3 x 1 2 A 0 ( x x )dx x . 3 0 3 3
R 2 2
1 2 R x dx R h. 2
23
第六章 定积分的应用
三、平面曲线的弧长
设 A、 B 是曲线弧上的两 个端点，在弧上插入分点
y
M2
M1
A M0
M n1
高中数学(新课标)选修2课件1.7.1-2定积分的应用
a
a
＝b[f(x)－g(x)]dx.
a
③如图(6)所示，所求面积 S＝S1＋S2＝ac[f(x)－g(x)]dx＋cb[g(x)－f(x)]dx
＝b|f(x)－g(x)|dx.
a
知识点二 定积分在物理中的应用 1．变速直线运动的路程 我们知道，做变速直线运动的物体所经过的路程 s，等于其速 度 函数 v＝ v(t)(v(t)≥0)在 时间 区间 [a， b] 上的定 积分 ，即 s ＝ ____b_v_(_t)_d_t ___.
【解析】 (1)由 v(t)＝8t－2t2≥0 得 0≤t≤4，即当 0≤t≤4 时， P 点向 x 轴正方向运动，t>4 时，P 点向 x 轴负方向运动．
故 t＝3 时，点 P 离开原点的路程
s1＝03(8t－2t2)dt＝4t2－23t330 ＝18. (2)当 t＝5 时，点 P 离开原点的位移 s2＝5(8t－2t2)dt
解析：由题意 v＝x′＝8t，t＝12 x，所以 v＝4 x.
又 F＝kv(k 是比例系数)，且当 v＝10 米/秒时 F＝2 牛，
所以 2＝10k，所以 k＝15，所以 F＝45 x，
又 F 与物体运动的方向相反，
所以 W＝－245 0
xdx＝－185x3220
＝－1165
2(焦耳)．
所以物体从 x＝0 到 x＝2 阻力所做的功为－1165 2焦耳．
解得 t＝0 或 t＝6，
t＝0 对应于 P 点刚开始从原点出发的情况，
∴t＝6 是所求的值．
状元随笔 首先要确定的是所需求的是路程还是位移，然后 用相应的方法求解．
方法归纳
(1)用定积分解决变速直线运动的位移和路程问题时，将物理问 题转化为数学问题是关键．
高数第五章 定积分的应用
第五章 定积分的应用在本章中，我们将利用学过的定积分理论来解决一些实际问题.首先介绍建立定积分数学模型的方法——微分元素法；再利用这一方法求一些几何量(如面积、体积、弧长等)和一些物理量(如功、液体静压力、引力等)；并介绍定积分在经济学中的简单应用.第一节 微分元素法实际问题中，哪些量可用定积分计算？如何建立这些量的定积分表达式？本节中我们将回答这两个问题.由定积分定义知，若（）f x 在区间,a b ⎡⎤⎣⎦上可积，则对于,a b ⎡⎤⎣⎦的任一划分：1＜＜＜0n a x x x b == ，及1,i i x x -⎡⎤⎣⎦中任意点i ξ,有d Δ01()lim()nb i i aλi f x x f ξx →==∑⎰，(5-1-1)这里()-=-= 11,2,,i i i Δx x x i n ,}{≤≤=1m ax i i nλΔx . (5-1-1)式表明定积分的本质是一类特定和式的极限，此极限值与,a b ⎡⎤⎣⎦的分法及点i ξ的取法无关，只与区间,a b ⎡⎤⎣⎦及函数（）f x 有关.基于此，我们可以将一些实际问题中有关量的计算归结为定积分来计算.例如，曲边梯形的面积、变速直线运动的位移等均可用定积分来表达.由上一章中分析曲边梯形面积用定积分来表示的过程，我们可概括地将此过程描述为“划分找近似，求和取极限”.也就是说，将所求量整体转化为部分之和，利用整体上变化的量在局部近似于不变这一辩证关系，局部上以“不变”代替“变”，这是利用定积分解决实际问题的基本思想.根据定积分的定义，如果某一实际问题中所求量U 符合下列条件:(1)建立适当的坐标系和选择与U 有关的变量x 后，U 是一个与定义在某一区间,a b ⎡⎤⎣⎦上的可积函数（）u x 有关的量； (2)U 对区间,a b ⎡⎤⎣⎦具有可加性，即如果把,a b ⎡⎤⎣⎦任意划分成n 个小区间()-=-= 11,2,,i i i Δx x x i n ，则U 相应地分成n 个部分量i ΔU ，且1nii U U Δ==∑；(3) 部分量i ΔU 可近似地表示成()()1,i i i i i u ξΔx ξx x -∈⎡⎤⎣⎦，且i ΔU 与()i i u ξΔx 之差是iΔx 的高阶无穷小，即()()i i i i ΔU u ξΔx o Δx -=,那么，我们可得到所求量U 的定积分数学模型d ()b au x U x =⎰. (5-1-2)在实际建模过程中，为简便起见，通常将具有代表性的第i 个小区间1,i i x x -⎡⎤⎣⎦的下标略去，记为［,d ］x x x +，称其为典型小区间，相应于此小区间的所求量的部分量记作ΔU .因此，建立实际问题的定积分模型可按以下步骤进行：(1) 建立坐标系，根据所求量U 确定一个积分变量x 及其变化范围,a b ⎡⎤⎣⎦；(2) 考虑典型小区间［,d ］x x x +,求出U 相应于这一小区间的部分量ΔU ，将ΔU 近似地表示成,a b ⎡⎤⎣⎦上的某个可积函数（）ux 在x 处的取值与小区间长度d Δx x =的积，即 d （d ）()ΔU u x x o x =+， (5-1-3)我们称d ()u x x 为所求量U 的微分元素(简称微元或元素)，记作d d ()U u x x=；(3) 计算所求量U ，即d =d ()b b aau x U x =⎰⎰U .上述建立定积分数学模型的方法称为微分元素法，这一方法的关键是步骤(2)中微分元素d U 的取得.第二节 平面图形的面积在上一章开头讨论过由连续曲线()()()0y =f x f x ≥,以及直线()x=a ,x =b a <b 和x 轴所围成的曲边梯形的面积()d baA f x x =⎰.如果()f x 在,a b ⎡⎤⎣⎦上不都是非负的，由定积分对区间的可加性，则所围图形的面积为()d b aA f x x =⎰.本节将讨论一般平面图形的问题，如果其边界曲线是由两条连续曲线()1y f x =, ()2y f x =()()21f x f x ⎡⎤≥⎣⎦及直线x =a ,x =b 所围成的平面图形，其面积便可用定积分来计算.下面我们运用定积分的微分元素法，建立不同坐标系下平面图形的面积计算公式.一、 直角坐标情形设一平面图形由曲线()()12,y f x y f x ==及直线x =a 和()x =b a b <围成(见图5-1).图5-1为求其面积A ，我们在,a b ⎡⎤⎣⎦上取典型小区间［,d ］x x x +，相应于该小区间的平面图形面积ΔA 近似地等于高为()()12f x f x -、宽为d x 的窄矩形的面积，从而得到面积微元()()d d 12A f x f xx =-.所以，此平面图形的面积为()()d 12b aA f x f xx =-⎰. (5-2-1)类似地，若平面图形由12（），（）x φy x φy ==及直线y c =和()y d d c =>围成(见图5-2)，则其面积为()()d 12d cA φy φy y =-⎰. (5-2-2)图5-2例1 计算由抛物线21y x =-+与2y x =所围图形的面积A . 解 解方程组221y x y x⎧=-+⎪⎨=⎪⎩得两抛物线的交点为122⎛⎫ ⎪⎝⎭和122⎫⎪⎝⎭，于是图形位于2x =-与2x =之间，如图5-3所示，取x 为积分变量，由(5-2-1)式得d 22222)A xxx x=--=-32022()3x x =-=图5-3例2 计算由直线4y x =-和抛物线22y x =所围平面图形的面积A . 解 解方程组224y xy x ⎧=⎪⎨=-⎪⎩得两线的交点为(2，-2)和(8，4)，平面图形，如图5-4所示，位于直线2y =-和4y =之间，于是取y 为积分变量，由(5-2-2)式得d 24242yA y y -=+-⎰3242(4)26yyy -=+-18=.图5-4注意：若在例1中取y 为积分变量，在例2中取x 为积分变量，则所求面积的计算会较为复杂.例如在例2中，若选x 为积分变量，则积分区间是［0，8］.当（，2）0x ∈时，典型小区间（,d ）x x x +所对应的面积微元是(d d A x=⎤⎦；而当（2，8）x ∈时，典型小区间所对应的面积微元是()d d 4A x x ⎤-⎦=. 故所求面积为(()d d 28024A x x x⎤⎤+-⎦=⎦⎰⎰.显然，上述做法较例2中的解法要复杂.因此，在求平面图形的面积时，恰当地选择积分变量可使计算简便.当曲边梯形的曲边为连续曲线，其方程由参数方程(),(),x φt y ψt =⎧⎨=⎩12t t t ≤≤ 给出时，若其底边位于x 轴上，（）φt 在12［，］t t 上可导，则其面积微元为 ()()d d d A y x ψt φt t ==' d (0)t >. 从而面积为()()d 21t t A ψt φt t ='⎰. (5-2-3)同理，若其底边位于y 轴上，且（）ψt 在12［，］t t 上可导，则其面积微元为 ()()d d d A x y φt ψt t ==' d (0)t > 从而面积为()()d 21t t A φt ψt t ='⎰. (5-2-4)例3 设椭圆方程为12222y x ab+= (,a b 为正的常数)，求其面积A .解 椭圆的参数方程为cos ,sin ,x a t y b t =⎧⎨=⎩20t π≤≤. 由对称性知d 204sin (cos )A b t a t tπ'=⋅⎰d d 22201cos 24sin 42ta b t t a b t ππ-==⎰⎰a b=π.二、 极坐标情形设一平面图形，在极坐标系下由连续曲线（）r r θ=及射线，θαθβ==所围成(称为曲边扇形，如图5-5所示.)为求其面积，我们在θ的变化区间［，］αβ上取一典型小区间［，d ］θθθ+，相应于此区间上的面积近似地等于中心角为d θ、半径为（）r θ的扇形面积，从而得到面积微元()d d 212A r θθ=， 所以d 21()2βαA r θθ=⎰. (5-2-5)图5-5例4 计算阿基米德(Archimedes)螺线（＞）0r a θa =上相应于θ从0到2π的一段弧与极轴所围成图形如图5-6所示的面积.解 由式(5-2-5)得d 22232302114()2630A a θθa θa ππ⎛⎫===π ⎪⎝⎭⎰.图5-6 图5-7例5 求由双纽线()()2222222x y a x y +=-所围成，且在半径为a 的圆内部的图形如图5-7所示的面积.解 由对称性，所求面积应等于第一象限部分面积的4倍，极坐标下双纽线在第一象限部分的方程为222co 2r a s θ=， 04θ≤≤π.圆的方程为r a =. 由 222cos 2r a θr a ⎧=⎪⎨=⎪⎩解得两曲线在第一象限交点为6,a ⎛⎫⎪⎝⎭π，由式(5-2-5)得所求面积d cos d 2264061142222A a θa θθπππ⎡⎤=+⎢⎥⎣⎦⎰⎰42262sin 23a a θπππ=+2(23aπ=+-.第三节 几何体的体积一、 平行截面面积为已知的立体体积考虑介于垂直于x 轴的两平行平面x a =与x b =之间的立体如图5-8所示，若对任意的［,］x a b ∈，立体在此处垂直于x 轴的截面面积可以用x 的连续函数（）A x 来表示，则此立体的体积可用定积分表示.图5-8在［,］a b 内取典型小区间［,d ］x x x +，对应于此小区间的体积近似地等于以底面积为（）Ax ，高为d x 的柱体的体积，故体积元素为()d d V A x x =， 从而d ()b aA x V x =⎰. (5-3-1)例1 一平面经过半径为R 的圆柱体的底圆中心，并与底面交成角α，如图5-9所示，计算此平面截圆柱体所得楔形体的体积V .解法1 建立坐标系如图5-9，则底面圆方程为222x y R +=.对任意的［,］x R R ∈-，过点x 且垂直于x 轴的截面是一个直角三角形，两直角边的长度分别为y =和tan y αα=，故截面面积为()（）tan 2212x R x A α-=.于是立体体积为tan d 221()2R RV R x αx -=-⎰tan d tan 22302()3RαR x x R α=-=⎰.图5-9 图5-10解法2 在楔形体中过点y 且垂直于y 轴的截面是一个矩形如图5-10所示，其长为2x =tan y α，故其面积为()2A yy α=.从而，楔形体的体积为()d tan 322222an 3R R V αy αR y==--⎰tan 323R α=. 二、旋转体的体积由一平面图形绕这平面内一条定直线旋转一周而成的立体称为旋转体. 设一旋转体是由连续曲线（）y f x =，直线x a =和x b =及x 轴所围成的曲边梯形绕x 轴旋转一周而形成的(图5-11)，则对任意的［,］x a b ∈，相应于x 处垂直于x 轴的截面是一个圆盘，其面积为2（）πf x ，于是旋转体的体积为 ()d 2ba V f x x =π⎰. (5-3-2)图5-11例2 计算由椭圆22221y x ab+=(,a b 为正的常数)所围图形绕x 轴旋转而成的旋转体(称之为旋转椭球体，见图5-12)的体积.图5-12解 这个旋转体实际上就是半个椭圆y =及x 轴所围曲边梯形绕x 轴旋转一周而成的立体，于是由式(5-3-2)得()2222a ab V axa-=π-⎰()d 22222a b axxa=π-⎰2322230ab x a x a ⎛⎫=π⋅- ⎪⎝⎭243a b =π.特别地，当a b =时便得到球的体积343πa .例3 求圆域222()()x b a y b a +-≤>绕x 轴旋转而成的圆环体的体积如图5-13所示.图5-13解 如图5-13，上半圆周的方程为2y b +=1y b -=对应于典型区间［,d ］x x x +上的体积微元为d d 2221()V y y x =π-πd 22((b b x ⎡⎤=π+--⎢⎥⎣⎦4x =π.所以4a aV x -=π⎰8b x =π⎰284ab π=π⋅22a b =2π.第四节 曲线的弧长和旋转体的侧面积一、 平面曲线的弧长首先，我们建立平面曲线弧长的概念.设有平面曲线 A B ，在其上任取分点：11,,,,0n n A M M M M B -== ，连接相邻的两个分点得到n 条线段1i i MM-，1,2,,i n = .以()1,i i iρρM M-=表示线段1i i M M -的长度(见图5-14)，记1m ax{}i i nρλ≤≤=,若极限01lim niλi ρ→=∑存在，则定义此极限值为曲线 A B 的长度(即弧长)，并称曲线 AB 是可求长的.图5-14下面用微分元素法来推导弧长的计算公式.设 A B 的方程为()y f x =，［,］x a b ∈，且()f x 在［,］a b 上有一阶连续导数.考虑［,］a b 内的典型小区间［,］x x Δx +，相应于此区间的弧长记为Δs ，Δs 近似地等于弦长，即22222()()()()[()()]Δs Δx Δy Δx f x Δx f x ≈+=++-.由微分中值定理，得,222()()[()]),(Δs ξx x Δx Δx f ξΔx ∈'+≈++，此处＞0Δx ，故得弧长的微分元素(简称弧微分)为d s ==x =. (5-4-1)从而， AB 的长为as x =⎰. (5-4-2)若曲线弧 AB 的方程由参数方程 (),(),x φt y ψt =⎧⎨=⎩ αt β≤≤，给出，设()(),φt ψt 在［,］αβ上具有连续导数，由于()()d d d d ,x φt t y ψt t ='='，因此对于任意的［,］t αβ∈，典型小区间d ［］t t t +,上相应弧长元素为d s t =. (5-4-3)所以，曲线弧 AB 的弧长为αs t =⎰. (5-4-4)式(5-4-1)和(5-4-3)即为弧微分公式，这和第二章第五节所推导的弧微分公式是一致的.例1 两端固定于空中的线缆，由于其自身的重量而下垂成曲线形，称之为悬链线.设一悬链线的方程为e +e ()2sh xxa a y a x a a -== (a为正的常数)，求其在［,］0a 上一段的长.解 d ds x x == =e +e d 1()2xxa a x -,故 e +e d e+e ee 101()()()2x xxx a a a aaas x a a ---===⎰-. 例2 如图5-15所示，计算摆线(sin ),(1cos ),x a t t y a t =-⎧⎨=-⎩()0a > 的一拱(20t π≤≤)的长度.图5-15解 由于d s t =t=d 2sin2ta t =， 所以d d 2202sin2sin22tts a t a t ππ==⎰⎰22(2cos )820t a a π=-=.如果曲线方程由极坐标方程()()r r θαθβ=≤≤给出，且（）r θ存在一阶连续导数，则由 ()cos ,()sin ,x r θθy r θθ=⎧⎨=⎩()αθβ≤≤ 可得()[()cos ]()cos ()sin ,φθr θθr θθr θθ'''==- ()[()sin ]()sin ()cos ,ψθr θθr θθr θθ'''==+从而 ()()()()2222φθψθrθr θ'+'=+'. 所以αs θ=⎰. (5-4-5)例3 求心形线1 (cos )(0)r a θa =+>的全长(见图5-16).图5-16解 由(5-4-5)式有d s θ=θ=θ=.由对称性知02s θπ=⎰d 022cos2θa θπ=⎰ 8sin820θa a π==. *二、 旋转体的侧面积设一旋转体的侧面由一段曲线()()y f x a x b =≤≤绕x 轴旋转一周而得(图5-17).为求其面积A ，我们在［,］a b 上取典型小区间［,d ］x x x +，相应于此区间上的窄带形侧面(图5-17中的阴影部分)可近似地看成弧微分d s 绕x 轴旋转一周而成.于是这一窄带形侧面可以用一个半径为()f x ，高为d s 的圆柱面来近似代替，从而得侧面积的微分元素()(d πd π22A f xs f x x ==.所以2(b aA f x x =π⎰.此处假设()f x 在［,］a b 上可导.图5-17例4 求半径为R 的球的表面积.解 以球心为原点建立一平面直角坐标系，则该球是平面上半圆盘0y ≤≤绕x 轴旋转一周而成的旋转体，其表面积为π2R RA x-=⎰πd π244R Rx -==⎰R R .第五节 定积分在物理学中的应用一、 变力沿直线所做的功由物理学知，若一个大小和方向都不变的恒力F 作用于一物体，使其沿力的方向作直线运动，移动了一段距离s ，则F 所做的功为·W F s =.下面用微分元素法来讨论变力做功问题.设有大小随物体位置改变而连续变化的力()F F x =作用于一物体上，使其沿x 轴作直线运动，力F 的方向与物体运动的方向一致，从x a =移至至＞x b a = (见图5-18).在［,］a b 上任一点x 处取一微小位移d x ，当物体从x 移到d x x +时，()F x 所做的功近似等于d ()F x x ，即功元素d d ()W F x x =，于是d ()b aW F x x =⎰. (5-5-1)图5-18例1 一汽缸如图5-19所示，直径为0.20m ，长为1.00m ，其中充满了气体，压强为5981.0⨯Pa.若温度保持不变，求推动活塞前进0.5m 使气体压缩所作的功.图5-19解 根据波义耳(Boyle )定律，在恒温条件下，气体压强p 与体积V 的乘积是常数，即p V k =.由于压缩前气体压强为5981.0⨯Pa ，所以ππ52981198.00000k =⨯⋅⋅=.建立坐标系如图5-19所示，活塞位置用x 表示，当活塞处于x 处时汽缸中气体体积π211()(0.)V x =-，于是压强为2()(1)(0.1)k p x x =-π，从而活塞上的压力为()1k F x p S x==-.故推动活塞所作功为d 05ln 10.50.9800980010W x x π==-π(-)-⎰x 980000ln2 2.13104(J )=π≈⨯.例2 从地面垂直向上发射一质量为m 的火箭，求将火箭发射至离地面高H 处所作的功.解 发射火箭需要克服地球引力做功，设地球半径为R ，质量为M ，则由万有引力定律知地球对火箭的引力为2GM m F =r，其中r 为地心到火箭的距离，G 为引力常数.当火箭在地面时，r R =，引力为2G M m R.另一方面，火箭在地面时，所受引力应为m g ，其中g 为重力加速度，因此2m g =GM m R， 故有 2=gR G M，于是22=m gR F r.从而，将火箭从r R =发射至r R H =+处所做功为d 111222R H RW r RR H +⎛⎫==- ⎪+⎝⎭⎰m gRm gR r .例3 地面上有一截面面积为20A =m 2，深为4 m 的长方体水池盛满水，用抽水泵把这池水全部抽到离池顶3m 高的地方去，问需做多少功？图5-20解 建立坐标系如图5-20所示.设想把池中的水分成很多薄层，则把池中全部水抽出所做的功W 等于把每一薄层水抽出所做的功的总和.在［0，4］上取小区间［x ，x +d x ］，相应于此小区间的那一薄层水的体积为2d 0x m 3，设水的密度1310ρ=⨯kg ·m -3，故这层水重为d 4210g x ⨯ kg ，将它抽到距池顶3m 高处克服重力所做功为d d 4210(3)x g x W ⨯⋅⋅=+.从而，将全部水抽到离池顶3m 高处所做的功为4023 1.9632424510()d 10x W x g x x ⎛⎫=⨯⋅+⋅=⨯⋅⨯+ ⎪⎝⎭⎰639210J .()=⨯ (其中-29.8m s g =⋅)二、液体静压力由帕斯卡(Pascal )定律，在液面下深度为h 的地方，液体重量产生的压强为p ρg h =，其中ρ为液体密度，g 为重力加速度.即液面下的物体受液体的压强与深度成正比，同一深度处各方向上的压强相等.面积为A 的平板水平置于水深为h 处，平板一侧的压力为p ρg h A =. 下面考虑一块与液面垂直没入液体内的平面薄板，我们来求它的一面所受的压力.设薄板为一曲边梯形，其曲边的方程为，()()y f x a x b =≤≤，建立坐标系如图5-21所示，x 轴铅直向下，y轴与液面相齐.当薄板被设想分成许多水平的窄条时，相应于典型小区间d ［,］x x x +的小窄条上深度变化不大，从而压强变化也不大，可近似地取为ρg x ，同时小窄条的面积用矩形面积来近似，即为d ()f x x ，故小窄条一面所受压力近似地为d d ()p ρg x f x x=⋅.图5-21从而d ()b ap ρgx f x x =⎰. (5-5-2)例4 一横放的圆柱形水桶，桶内盛有半桶水，桶端面半径为0.6m ，计算桶的一个端面上所受的压力.图5-22解 建立坐标系如图5-22所示，桶的端面圆的方程为22360.x y +=.相应于［,d ］x x x +的小窄条上的压力微元d 2p ρg xx =，所以桶的一个端面上所受的压力为060.p x xx =⎰20633(.)ρg =314110N .≈⨯（）其中3110ρ=⨯kg·m -3，98-2m s .g ⋅=. 三、引力由物理学知，质量分别为12,m m ，相距为r 的两质点间的引力的大小为122m m F Gr=，其中G 为引力系数，引力的方向沿着两质点的连线方向.对于不能视为质点的两物体之间的引力，我们不能直接利用质点间的引力公式，而是采用微元法，下面举例说明.例5 一根长为l 的均匀直棒，其线密度为ρ，在它的一端垂线上距直棒a 处有质量为m 的质点，求棒对质点的引力.图5-23解 建立坐标系如图5-23所示，对任意的［，0)x l ∈，考虑直棒上相应于d ［,］x x x +的一段对质点的引力，由于d x 很小，故此一小段对质点的引力可视为两质点的引力，其大小为d d G 22m ρx F a x=+，其方向是沿着两点,(0)a 与(),0x 的连线的，当x 在(),0l 之间变化时，d F 的方向是不断变化的.故将引力微元d F 在水平方向和铅直方向进行分解，分别记为d ，d x y F F ，则d 32G d 22()x m ρxF F x x a ==+，d 32G d 22()y m ρa F F x xa =-=-+.于是，直棒对质点的水平方向引力为32d 022()l x x F G m ρx xa =+⎰32d 2222()()2l G m ρa x a x -=++⎰1222()0l G m ρa x -=-+1(G m ρa=-.铅直方向引力为d 30222()l y x F G m ρa a x =-+⎰12l G m ρa -=-G m ρl =.注意 此例如果将直棒的线密度改为()ρρx =，即直棒是非均匀的，当()ρx 为已知时，直棒对质点的引力仍可按上述方法求得. 四、平均值我们知道，n 个数值12,,,n y y y 的算术平均值为121()n y y y y n=+++ . 在许多实际问题中，需考连续函数在一个区间上所取值的平均值，如一昼夜间的平均温度等.下面将讨论如何规定和计算连续函数()f x 在［,］a b 上的平均值. 先将区间［,］a b n 等分，分点为1＜＜＜0n a x x x b == ，每个小区间的长度为Δx b an=-，()f x 在各分点处的函数值记为1,2,,()()i i y f x i n == .当Δx 很小(即n 充分大)时，在每个小区间上函数值视为相等，故可以用12,,,n y y y 的平均值121()n y y y n+++ 来近似表达()f x 在［,］a b 上的所有取值的平均值.因此，称极限值121lim()n n y y y y n→∞=+++为函数()f x 在［,］a b 上的平均值.由于12lim n n y y y b ay b a n →∞+++-=-120limnx y y y x b a∆→+++=∆-011lim ()ni x i f x x b a ∆→==∆-∑，故1()d bay f x x b a =-⎰.(5-5-3)式(5-5-3)就是连续函数()f x 在［,］a b 上的平均值的计算公式.例6 计算纯电阻电路中正弦交流电sin m i I ωt =在一个周期π2T =ω上的功率的平均值(简称平均功率).解 设电阻为R ，则电路中的电压为m U iR I R tω==sin ，功率为2sin 2m N Ui t I R ω==.一个周期上的平均功率为d d 2221sin sin 2T ωI R ωN R ωt t ωt I t Tπ==π⎰⎰22m md()0220sin 2(1cos 2)442ωωR R ωt ωt ωt ωt I I ππ⎡⎤=-=-⎢⎥ππ⎣⎦⎰22m m22mU I R I ==2m m ，其中m m U I R =表示最大电压，也称为电压峰值，即纯电阻电路中正弦交流电的平均功率等于电流与电压的峰值的乘积的一半.通常交流电器上标明的功率就是平均功率，而交流电器上标明的电流值都是另一种特定的平均值，常称为有效值.一般地，周期性非恒定电流i 的有效值是这样规定的：当电流()i t 在一个周期T 内在负载电阻R 上消耗的平均功率等于取固定值I 的恒定电流在R 上消耗的功率时，称这个固定值为()i t 的有效值.电流()i t 在电阻R 上消耗的功率为()()()()N t U t i t i t R =⋅=2.它在［0，T )上的平均值为d d 221()()T T R N i t R t i t tTT==⎰⎰.而固定值为I 的电流在R 上消耗的功率为2N I R =，因此d 22()T R I R i t t T =⎰， 即I =.例7 求正弦电流s (n )i m i I t t ω=的有效值.解12221s i n 2ωI ωt ωπ⎛⎫ ⎪=⎪π ⎪⎝⎭⎰2m I122sin 242ωωt ωt π⎡⎤⎡⎤⎢⎥=-⎢⎥π⎣⎦⎢⎥⎣⎦2mI=.叫做函数()f x 在［,］a b 上的均方根.第六节 定积分在经济学中的应用一、 最大利润问题设利润函数()()()πx =R x C x -，其中x 为产量，()R x 是收益函数，()C x 是成本函数，若()π,(),()x R x C x 均可导，则使()πx取得最大值的产量x 应满足()()()π0x R x C x '='-'=，即()().R x C x '='因此总利润的最大值在边际收入等于边际成本时取得.例1 设某公司产品生产的边际成本2181()00C x x x '=-+，边际收益为23()00R x x '=-，试求公司的最大利润.解 由于d ππd ()()()()x x R x C x x'''==-223181(00)(00)x x x =---+215100x x=-+，故利润微分元素为d πd 2151()(00)x x xx =-+.产量为0x 时，利润为πd 0200()(15100)x x x xx =-+⎰.另一方面，令π()0x '=，得21525x ±==(负值舍去). 又当20x =时，()π152＜0x x "=-,故20x =时，利润取得最大值，最大利润为πd 202(20)(15100)x xx =-+⎰322015(100)230x xx =-+ 23333.≈.二、资金流的现值与终值1. 连续复利概念设有一笔数量为0A 元的资金存入银行，若年利率为r ，按复利方式每年计息一次，则该笔资金t 年后的本利和为0(1)(1,2,)tt A A r t =+= .如果每年分n 次计息，每期利率为r n，则t 年后的本利和为*01(1,2,)n tt r A A t n ⎛⎫=+= ⎪⎝⎭ .当n 无限增大时，由于e lim (1)n r n r n→∞+=，故e *00lim lim (1)n t r t t n n r A A A n→∞→∞=+=.称公式e 0r tt A A = (5-6-1)为0A 元的现值(即现在价值)在连续复利方式下折算为t 年后的终值(将来价值)的计算公式.公式(5-6-1)可变形为e0r tt A A -= (5-6-2)称(5-6-2)式为t 年末的t A 元的资金在连续复利方式下折算为现值的计算公式.建立资金的现值和终值概念，是为了对不同时点的资金进行比较，以便进行投资决策. 2. 资金流的现值与终值.将流出企业的资金(如成本、投资等)视为随时间连续变化，称之为支出流.类似地，将流入企业的资金(如收益等)视为随时间连续变化，称之为收入流.资金的净流量为收入流与支出流之差.企业单位时间内，资金的净流量称为收益率.设某企业在时段［］0T ,内的t 时刻的收益率为连续函数()f t ，下面我们按连续复利（年利率为r ）方式来求该时段内的收益总现值和总终值. 在［］0T ,上取典型小区间［,d ］t t t +，该时段内收益近似为d ()f t t ，其t 时刻现值为 ed ()r tf t t -.这就是收益总现值的微分元素，故收益总现值为ed 0()T r tP f t t -=⎰. (5-6-3)又由于［,d ］t t t +时段内收益d ()f t t 折算为t T =时刻的终值为 ed ()()T t rf t t -,故收益总终值为ed ()0()T T t rF f t t -=⎰. (5-6-4)当收益率()f t k =（k 为常数）时，该资金流称为稳定资金流或均匀流.例2 某公司投资100万元建成1条生产线，并于1年后取得经济效益，年收入为30万元，设银行年利率为10%，问公司多少年后收回投资.解 设T 年后可收回投资，投资回收期应是总收入的现值等于总投资的现值的时间长度，因此有ed 0.1030100T tt -=⎰，即 0.1300(1e )100t --=. 解得455.0T =，即在投资后的4.055年内可收回投资.习 题 五1.求下列各曲线所围图形的面积：(1)212y x =与228x y += (两部分都要计算)； (2)1y x=与直线y x =及2x =；(3)e e ,x x y y -==与直线1x =；(4)ln y x =，y 轴与直线()ln ,ln 0y a y b b a ==>>； (5)抛物线2y x =和22y x =-+；(6)sin ,cos y x y x ==及直线,44x x ππ=9=；(7)抛物线243y x x =-+-及其在3(0,)-和3,(0)处的切线；(8)摆线sin 1cos (),()x a t t y a t =-=-的一拱2(0)t π≤≤与x 轴； (9)极坐标曲线3ρa si n φ=； (10)极坐标曲线2cos ρa φ=.2.求下列各曲线所围成图形的公共部分的面积： (1)()1cos r a θ=+及2cos r a θ=；(2)r θ=及22in r θ=.3.已知曲线2()f x x x =-与()g x ax =围成的图形面积等于29，求常数a .4.设有一截锥体，其高为h ，上、下底均为椭圆，椭圆的轴长分别为2a ，2b 和2A ，2B 求这截锥体的体积.5.计算底面是半径为R 的圆，而垂直于底面一固定直径的所有截面都是等边三角形的立体体积.6.求下列旋转体的体积：(1)由2y x =与23y x =围成的平面图形绕x 轴旋转；(2)由3，2，0y x x y ===所围图形分别绕x 轴及y 轴旋转； (3)星形线222333x y a +=绕x 轴旋转. 7.求下列曲线段的弧长： (1)22，20y x x =≤≤；(2)ln ,y x x =≤≤(3)2,22x y t x π-π-≤=≤π⎰， . 8.设星形线的参数方程为33，，cos sin 0x a t y a t a ==>，求(1)星形线所围面积；(2)绕x 轴旋转所得旋转体的体积； (3)星形线的全长.9.求对数螺线e a θr =相应于0θ=到θφ=的一段弧长.10.求半径为R ，高为h 的球冠的表面积.11.求曲线段31(0)y x x =≤≤绕x 轴旋转一周所得旋转曲面的面积：12.把长为10m ，宽为6m ，高为5m 的储水池内盛满的水全部抽出，需做多少功？ 13.有一等腰梯形闸门，它的两条底边各长10m 和6m ，高为20m ，较长的底边与水面相齐，计算闸门的一侧所受的水压力.14.半径为R 的球沉入水中，球的顶部与水面相切，球的密度与水相同，现将球从水中取离水面，问做功多少.15.设有一半径为R ，中心角为φ的圆弧形细棒，其线密度为常数ρ，在圆心处有一质量为m 的质点，试求细棒对该质点的引力.16.求下列函数在［,］a a -上的平均值.(1)()f x =(2)()2f x x =. 17.求正弦交流电sin 0i I ωt =经过半波整流后得到电流00sin 0.I ωt t ωi t ωωπ⎧≤≤⎪=⎨π2π⎪≤≤⎩，，， 的平均值和有效值.18.已知电压3sin2()u t t =，求(1)()u t 在02π⎡⎤⎢⎥⎣⎦，上的平均值； (2)电压的均方根值.19.设某企业固定成本为50，边际成本和边际收入分别为2()14111,()1002C x x x R x x ''=-+=-.试求最大利润.20.设某工厂生产某种产品的固定成本为零，生产x (百台)的边际成本为2()C x '=（万元/百台），边际收入为72()R x x '=-（万元/百台)）：(1)求生产量为多少时总利润最大？(2)在总利润最大的基础上再生产100台，总利润减少多少？21.某企业投资800万元，年利率为5%，按连续复利计算，求投资后20年中企业均匀收入率为200万元/年的收入总现值及该投资的投资回收期.22.某父母打算连续存钱为孩子攒学费，设银行连续复利为5%（每年），若打算10年后攒够5万元，问每年应以均匀流方式存入多少钱.。
大一上 高数A 定积分的几何应用
x = b 所围成。 所围成。
bdx
面积表示为定积分的步骤如下
） 的小区间， （1）把区间[a , b]分成n 个长度为 ∆x i 的小区间， 个小窄曲边梯形， 相应的曲边梯形被分为n 个小窄曲边梯形， i 第 小窄曲边梯形的面积为∆Ai ，则 A = ∑ ∆Ai .
三、某些立体的体积
1. 平行截面面积为已知的立体的体积 已知平行截面面积为 A(x)的立体 dV=A(x)dx 的立体
.
V =
∫
b
a
A ( x )d x
A(x)
a
x
V
V =
b
x
已知平行截面面积为 A(y)的立体 的立体
∫
d
c
A ( y )d x
半径为R的正圆柱体被通过其底的直径并与底面成 例7. 半径为 的正圆柱体被通过其底的直径并与底面成α角的 平面所截，得一圆柱楔。求其体积。 平面所截，得一圆柱楔。求其体积。
1
3
1
2
例 2
计算由曲线 y = x 3 − 6 x 和 y = x 2 所围成
y = x3 − 6x
的图形的面积. 的图形的面积
解 两曲线的交点
y = x3 − 6x y = x2
⇒ (0,0), ( −2,4), ( 3,9).
y = x2
− 选 x 为积分变量 x ∈ [−2, 3] (1) x ∈ [−2, 0], dA1 = ( x 3 − 6 x − x 2 )dx ( 2) x ∈ [0,3], dA2 = ( x 2 − x 3 + 6 x )dx
o a x x + dx x b
） （1）U 是与一个变量 x 的变化区间[a, b ]有关 的量； 的量；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019/3/10
第六章 定积分的应用
y x2 y2 b a2 ? b2 ? 1
o
ax
图6-2-5
9
2.极坐标情形
? ? d?
设由曲线? ? ? (? )及射线 ? ? ? 、? ? ? 围成一曲边扇 ? ? ?
? ? ? (? )
d?
形，求其面积．这里，? (? )
在[? , ? ]上连续，且? (? ) ? 0．
成的图形的面积.
解 解方程组
? y2 ? 2x ? ?y? x? 4
得两曲线的交点为
(2,? 2), (8,4).
选 y 为积分变量 y ? [ ? 2, 4]
?
y2 ?
dA ? ? y ? 4 ? ?dy
?
2?
2019/3/10
第六章 定积分的应用
6
所求面积为
? A ?
4 ?2
????
y
?
4
?
y2 2
第二节
定积分在几何上的应用
(Application of the Definite Integral to Geometry)
一、平面图形的面积 二、体积 三、平面曲线的弧长 四、小结
2019/3/10
第六章 定积分的应用
1
一、平面图形的面积
1.直角坐标情形
y ? f (x)
y
y ? f2(x)
y ? f1(x)
2019/3/10
第六章 定积分的应用
8
例4
求椭圆 x 2 a2
?
y2 b2
?
1的面积.
解
椭圆的参数方程
?x
? ?
y
? ?
a cos t bsin t
由对称性知总面积等于 4倍第一象限部分面积．
? A
?
a
4?0
ydx ?
4
0
bsin td(a cos t)
?
2
?
? ? 4ab 2 sin 2 tdt ? ? ab. 0
? 面积元素 dA ? 1[? (?
2
曲边扇形的面积 A ?
)]2
?
d? 1[?
(?
o
)]2
?
d?
?
.
??
图6-2-6
?2
x
2019/3/10
第六章 定积分的应用
10
例 5 求双纽线 ? 2 ? a 2 cos 2? 所围平面图形
的面积.
解 由对称性知总面积 =4倍第 一象限部分面积
A ? 4A1
第六章 定积分的应用
12
二、体积
1.旋转体的体积
旋转体就是由一个平面图形绕这平面内 一条直线旋转一周而成的立体．这直线叫做 旋转轴．
圆柱
2019/3/10
圆锥
图6-2-9
第六章 定积分的应用
圆台
13
一般地，如果旋转体是由连续曲线 y ? f ( x ) 、
直线 x ? a 、 x ? b及x 轴所围成的曲边梯形绕
x 轴旋转一周而成的立体，体积为多少？
取积分变量为 x ， y
y ? f (x)
x ? [ a,b]
在[ a, b]上任取小区 o
x x ? dx
x
间[ x , x ? dx ]，
图6-2-10
取以dx 为底的窄边梯形绕x 轴旋转而成的薄
片的体积为体积元素， dV ? ?[ f ( x )]2 dx
A?
?
?4 4 0
1 a2 cos 2?d?
2
?
a2.
y? x
A1
? 2 ? a2 cos 2?
图6-2-7
2019/3/10
第六章 定积分的应用
11
例 6 求心形线 ? ? a(1 ? cos? )所围平面图形的
面积(a > 0).
解 dA ? 1 a2(1 ? cos? )2 d?
2
利用对称性知
的图形的面积.
解 解方程组
? y ? x3 ? 6x
? ?y
?
x2
得到 两曲 线的 交点为
(0 ,0 ), ( ? 2,4 ), ( 3 ,9 ).
选 x 为积分变量 x ? [ ? 2, 3]
(1) x ? [ ? 2, 0], dA1 ? ( x 3 ? 6 x ? x 2 )dx
(2) x ? [ 0,3], dA2 ? ( x 2 ? x 3 ? 6 x )dx
a x x ? ? xb
图6-2-1（1）
o a x? x b x
图6-2-1（2）
曲边梯形的面积
b
A ? ?a f ( x )dx
曲边梯形的面积
A ? ?ab[ f 2 ( x ) ? f1( x )]dx
2019/3/10
第六章 定积分的应用
2
例 1 计算由两条抛物线 y 2 ? x 和 y ? x 2 所围成的
2019/3/10
第六章 定积分的应用
4
于是所求面积 A ? A1 ? A2
A
?
?0 ( x 3
?2
?
6x
?
x 2 )dx
?
?3(x 2
0
?
x3
?
6x )dx
? 253 . 12
说明：注意各积分区间上被积函数的形式．
问题：积分变量只能选 x吗？
2019/3/10
第六章 定积分的应用
5
例 3 计算由曲线 y 2 ? 2 x 和直线 y ? x ? 4 所围
图形的面积.
解 两曲线的交点
(0,0) (1,1) 选 x 为积分变量 x ? [0,1]
面积元素 dA ? ( x ? x 2 )dx
? A ?
1
(
0
x
?
x 2 )dx
?
?2 3 ??3 x 2
?
x
3
1
?
3 ??0 ?
1. 3
2019/3/10
第六章 定积分的应用
3
例 2 计算由曲线 y ? x 3 ? 6 x 和y ? x 2 所围成
????dy
?y
y
6
4
?
?
? ?
2
?
4y?
6
? ?? 2
?
18
2019/3/10
第六章 定积分的应用
7
如果曲边梯形的曲边为参数方程
? ? ?
x yቤተ መጻሕፍቲ ባይዱ
? ?
? ?
(t) (t)
? 曲边梯形的面积 A ? ?t2 (t )? ?(t )dt . t1
（其中t1 和t2 对应曲线起点与终点的参数值）
在[t1,t2 ]（或[t2 ,t1 ]）上x ? ? (t ) 具有连续导数， y ? ? (t )连续.
y? rx
o
h
r
h
x
取积分变量为 x ，x ? [ 0, h]
图6-2-11
在[ 0, h]上任取小区间[ x , x ? dx ] ，
? ? a ?1 ? cos ? ?
d?
?
o
x
? A ? 2 ?1 a2 ? (1 ? cos? )2 d? 20
图6-2-8
? ? a2 ? (1 ? 2cos? ? cos2 ? )d? 0
?
a2
?3 ??2
?
?
2 sin ?
?
1 sin 2?
4
?? ?? 0
?
3 ?a2. 2
2019/3/10
? 旋转体的体积为
V?
b
?[
f ( x )]2 dx
a
2019/3/10
第六章 定积分的应用
14
例 7 连接坐标原点 O 及点 P(h, r)的直线、直线
x ? h及 x 轴围成一个直角三角形．将它绕 x 轴旋
转构成一个底半径为 r 、高为 h 的圆锥体，计算
圆锥体的体积．
y
P
解 直线 OP方程为