第6章频率响应设计法1
第六章授课内容

内 容备 注6.2.1 无源校正装置 1. 无源超前网络复阻抗:所以超前网络的传递函数为:(6-1) 式中: 由于式(6-1)中1/a 小于1,采用无源超前网络进行串联校正时,整个系统的开环增益要下降a 倍,为了补偿超前网络造成的衰减,需要提高放大器增益,或另外串接一个放大器。
在补偿了1/a 的衰减作用后,超前网络的传递函数是 : (6-2)根据式(6-2)画出的对数频率特性如下图所示。
显然超前网络对频率在1/aT 至1/T 之间的输入信号有明显的微分作用 。
1111R Z R Cs=+22Z R =22112121212()1()()1o c i U s Z R R Cs G s R R U s Z Z R R Cs R R +===⋅++++111aTs a Ts+=⋅+1212R R T C R R =+1221R R a R +=>'1()()1c c aTsG s aG s Ts +==+内 容备 注为了得到最大超前角,根据超前网络式(6-2)的相角计算式:将上式对w 求导,并令其为零,得最大超前角频率 : 由于:故最大超前角频率wm 是两个转折频率1/aT 和1/T 的几何中点。
得最大超前角 :或:由此得: 2. 无源滞后网络()arctan arctan c aT T ϕωωω=-()c ϕω=22(1)arctan1a T aT ωω-+1m T aω=111lg (lg lg )2m T aTω=+m ϕ=1arctan 2a a-1arcsin1m a a ϕ-=+()()20lg 10lg c m c L aG j a ωω==11221Z R Z R Cs==+;内 容备 注无源滞后网络的传递函数为 :式中: 滞后网络的零、极点分布图:采用滞后网络进行校正时,主要是利用其高频幅值衰减的特性,力求避 免最大滞后角发生在校正后系统开环剪切频率wc 附近,以免恶化系统动 态性能。
第6章 谐振与频率响应
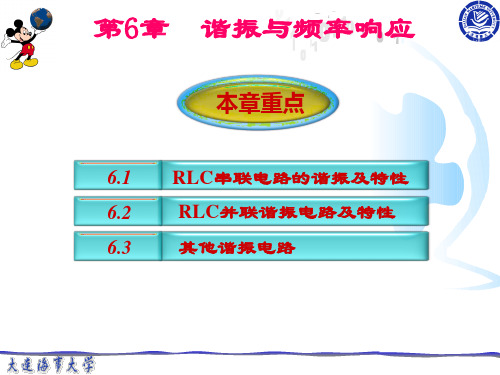
中央台 北京台 北京经济台 f (kHz) 820 640 1026 L 1290 1000 1611 1 -1290 –1660 -1034 ωC 0 X – 660 577 6 6 6 I 0.0173 10 I=U/|Z| I 0 0.5 10 I1 0.0152 10 2 UR0=10 UR1=0.304 UR2=0.346 UR=UR/|Z|
1 L Q R R R C 与 I 同相 (3) 谐振时, U 输入阻抗为纯电阻性,即阻抗Z=R,阻抗|Z|最小 X 0 U U U I I I 最大值 0 Z R R2 X 2
0 L
U R I0 R
电流I 和电阻电压UR达到最大值 I0=U/R (U一定时)
0
1 LC
f0
谐振频率
1 2π LC
仅与电路 参数有关
谐振角频 率
RLC串联电路谐振时的特征
(1) 特性阻抗ρ 谐振时
ω0
1 LC
L 1 L ω0 L 则此时XL ω0 L C LC
特性阻抗 单位:Ω
(2) 品质因数 Q 谐振时特性阻抗 与电阻 R的比值,称之为 串联谐振电路的品质因数,即
U
1 R 2 2
2
=
I0 1 1 Q 2
2
考虑到谐振电流最大,将电流归一化处理 归一化 I 1 H ( ) = 电流 2 I0 1 2 1 Q
归一化电流的幅频特性
归一化 电流
H
谐振
串联谐振:L 与 C 串联时
并联谐振:L 与 C 并联时
u、 i
u、 i
同相
同相
控制工程基础课件第六章 频率特性分析

G
j
arctan
1
n 2
n2
当=0时,G j 1,G j 0;
当=n时,G j 2,G j 90; 当=时,G j ,G j 180。
二阶微分环节的极坐标图也于阻尼比有关,对应不同的 ξ值,形成一簇坐标曲线,不论ξ值如何,当ω=0时,极 坐标曲线从(1,0)点开始,在ω=∞时指向无穷远处。
第6章 频率特性分析
本章介绍线性系统的频域分析方法。该方法是通 过控制系统对正弦函数的稳态响应来分析系统性能的。
频率特性不仅能反映系统的稳态性能,也可用来 研究系统的稳定性和动态性能。
6.2 频率响应与频率特性
一、频率特性的概念
1、频率响应:是系统对正弦输入的稳态响应。
2、频率特性:给线性系统输入某一频率的正弦波,
1 1 jT
G j 1 U jV
1 jT
1
1 T 22
j T 1 T 22
A e j
实频特性为U 虚频特性为V
1; 1+T 2 2
T。 1+T 2 2
幅频特性为A 1 ;
1 T 22
相频特性为 G j arctanT
特殊点:
当=0时,G j 1,G j 0; 当=1/T时,G j 1 ,G j 45;
取拉氏变换为: Xi s
A
s2
2
电路的输出为: X0 s G s Xi s 上式取拉氏反变换并整理得
1A Ts 1 s2 2
x0 t
AT 1 T2
e t/T
2
A sin t arctan T
1 T2 2
x0 t
AT 1 T2
e t/T
2
A sin t arctan T
第6章 放大电路的频率响应

讨论一
为什么波特图开阔了视野?同样长度的横轴, 为什么波特图开阔了视野?同样长度的横轴,在 单位长度不变的情况下,采用对数坐标后, 单位长度不变的情况下,采用对数坐标后,最高频 率是原来的多少倍? 率是原来的多少倍? O 10 10 20 30 102 103 40 50 104 105 60 106 f lg f
' ' C π = C π + Cµ
β0
rb'e
≈
I EQ UT
=?
二、电流放大倍数的频率响应
1. 适于频率从0至无穷大的表达式
& Ic & β= & Ib
U CE
' ' 因为k = − g m RL = 0, 所以 C π = C π + Cµ
& β=
& g mU b'e 1 & U b'e [ + jω (Cπ + Cµ )] rb'e
Vi -
ω0
图06.01RC低通电路
1 Av = 1+ ( f
f0 = fH =
fH
)2
1 2πRC
ϕ = −arctg( f f ) H
由以上公式可做出如图06.02所示的RC低 通电路的近似频率特性曲线:
Av = 1 1+ ( f
fH
)2
ϕ = −arctg( f f ) H
图06.02 RC低通电路的频率特性曲线
讨论二
电路如图。 电路如图。已知各电阻阻 静态工作点合适, 值;静态工作点合适,集电 极电流I 极电流 CQ=2mA;晶体管的 ; rbb’=200Ω,Cob=5pF, , , fβ=1MHz,β0=80。 。 试求解该电路中晶体管高 频等效模型中的各个参数。 频等效模型中的各个参数。
山东大学 自动控制原理 6-1串联校正

5
加入校正装置后使未校正系统的缺陷得到补偿,这 就是校正的作用。 6.1.2 校正方式 常用的校正方式有串联校正、反馈校正、前馈校 正和复合校正四种。 串联校正装置一般接在系统误差测量点之后和放大 器之前,串接于系统前向通道之中;反馈校正装置接 在系统局部反馈通道之中。
串联 校正 控制 器 对 象
1 aTs Gc ( s ) 1 Ts
(1)零极点分布图:
∵a 1
1/T
1/aT
0
∴零点总是位于极点之右,二者的距离由常
14
数a决定。零点的作用大于极点,故为超前网络。
(2)对数频率特性曲线: L()/dB 20dB/dec
1 aTs Gc ( s ) 1 Ts
20lga
特性曲线G(s )/k1所示,但稳态误差也要随之增加,所 以开环放大系数是不能减小的。而改变未校正系统的 其它参数都是比较困难的。这样就得在原系统的基础 上采取另外一些措施,即对系统加以“校正”。 所谓的“校正”,就是在原系统中加入一些参数 可以根据需要而改变的机构或装置,使系统整个特性 发生变化,从而满足给定的各项性能指标。这一附加 的装置称为校正装置。
可见,m出现在1 =1/aT 和2 =1/T 的几何中点。
1 sin m a 1 sin m
上式表明,m仅与a有关。a值选得越大,则超前网络的 微分作用越强。但为了保持较高的系统信噪比,实际选用 的a值一般不大于20。此外,m处的对数幅频值为
Lc ( m ) 10 lg a
17
L()/dB 20dB/dec 10lga 0 20lga
1 aT
1 T
()
0
m m
m
第6章-频率法校正

三、校正方法 方法多种,常采用试探法 试探法。 方法多种,常采用试探法 总体来说,试探法步骤可归纳为: 总体来说,试探法步骤可归纳为: 1.根据稳态误差的要求 确定开环增益K 根据稳态误差的要求, 1.根据稳态误差的要求,确定开环增益K。 2.根据所确定的开环增益 根据所确定的开环增益K 画出未校正系统的博特图,量出(或计算) 2.根据所确定的开环增益K,画出未校正系统的博特图,量出(或计算)未 校正系统的相位裕度。若不满足要求,转第3 校正系统的相位裕度。若不满足要求,转第3步。 3.由给定的相位裕度值 计算超前校正装置应提供的相位超前量( 由给定的相位裕度值, 3.由给定的相位裕度值,计算超前校正装置应提供的相位超前量(适当增 加一余量值) 加一余量值)。 4.选择校正装置的最大超前角频率等于要求的系统截止频率 选择校正装置的最大超前角频率等于要求的系统截止频率, 4.选择校正装置的最大超前角频率等于要求的系统截止频率,计算超前网 络参数a 若有截止频率的要求,则依该频率计算超前网络参数a 络参数a和T ;若有截止频率的要求,则依该频率计算超前网络参数a和 T。 5.验证已校正系统的相位裕度 若不满足要求,再回转第3 验证已校正系统的相位裕度; 5.验证已校正系统的相位裕度;若不满足要求,再回转第3步。
Gc ( s )Go ( s ) = 4.2 × 40( s + 4.4) 20(1 + 0.227 s ) = ( s + 18.2) s ( s + 2) s(1 + 0.5s )(1 + 0.0542s )
未校正系统、校正装置、校正后系统的开环频率特性: 未校正系统、校正装置、校正后系统的开环频率特性:
↑ 指标要求值 ↑ 可取 − 6°
根据上式的计算结果,在曲线上可查出相应的值。 根据上式的计算结果,在曲线上可查出相应的值。 根据下述关系确定滞后网络参数b和 如下 如下: 5根据下述关系确定滞后网络参数 和T如下: ′ 20 lg b + L ′(ω c′ ) = 0
第6章 电路频率响应图文
对于(b)图情况,若以 相量,则N的网络函数
U 2 为响应
西 若以 I2为响应相量,则N的网络函数
安
H2 H3 j H4 j
j I2 S单位
IUI2s2Us无Ω单单位位
Is
(6.1-3) (6.1-4) (6.1-5)
电 观察式(6.1-2)~(6.1-5),显而易见:
子
科 技 大
(1)若网络N的结构、元件值一定,当选定激励端与响应端时,H1(jω)~H4(jω) 只是频率的函数。
西 安
大它只输是出最电大压输U2=出U1功,率所的以一最半大,输因出此功3率分正贝比频于率U点12又,称当为ω半=功ω率c时频,U率2 点U。1
2,
电
子 科
说明:(1)3分贝频率点或半功率频率点即是前述的截止频率点,它只是人为
技 定义出来的一个相对标准。
大 学
(2)按 1
2 关系来定义通频带边界频率即截止频率的实际背景与“历史”原
>ωc时,输出信号是减小了,但不是零,并没有明显截止的“界限”。
第 6-9 页
前一页
下一页
回本章目录
6.2 常用一阶电路的频率响应
网络的截止角频率是个重要概念,在滤波网络中经常用到。那么,截止 角频率的电路含义是什么,如何确定它的数值呢?
实际低通网络的截止角频率是指网络函数的幅值 H( j)下降到 H ( j0) 值 0.707即 1 2 倍时所对应的角频率,记为ωc。
H
j
响应相量 激励相量
(6.1-1)
(4)可以是同一对端钮上 的相量,也可以是非同一
对端钮上的相量。
第 6-2 页
前一页
下一页 回本章目录
6.1 网络函数与频率响应
模拟电子技术基础 第六章 频率响应讲解
1
jCb1
gm ( Rd
||
RL )
Rg Rg Rsi
1
1 1
j(Rd RL )Cb2
1
1 gm
jCs
1
1 1
j( Rsi Rg )Cb1
AVSL
gm (Rd
||
RL )
Rg Rg Rsi
1
1 1
j( Rd RL )Cb2
1
1 gm
jCs
1
1 1
j( Rsi Rg )Cb1
令
AVSM
gm (Rd
||
RL )
Rg Rg Rsi
通带内(中频)增益,与频率无关
f L1
2π( Rsi
1 Rg )Cb1
Cb1引起的下限截止频率
f L2
gm 2πCs
fL3
2π( Rd
1 RL )Cb2
Cs引起的下限截止频率 Cb2引起的下限截止频率
且 2πf
则
AVSL
AVSM
(Rc ||
rbe
RL )
rbe Rsi rbe
1
1 1
j(Rc RL )Cb2
1
1 1
j( Rsi rbe )C1
AVSL
Vo Vs
(Rc || RL )
rbe
rbe Rsi rbe
1
1 1
j(Rc RL )Cb2
1
1 1
j(Rsi
rbe )C1
令
AVSM
20lg|AV|/dB 低频区
(a)
幅频响应曲线,图b是相
频响应曲线。一般有 fH >> fL
0 fL
自动控制原理第六章
G(s)
K0 K p (Ti s 1) Ti s2 (Ts 1)
表明:PI控制器提高系统的型号,可消除控制系统对斜 坡输入信号的稳态误差,改善准确性。
校正前系统闭环特征方程:Ts2+s+K0=0 系统总是稳定的
校正后系统闭环特征方程:TiTs3 Ti s2 K p K0Ti s K p K0 0
调节时间 谐振峰值
ts
3.5
n
Mr
2
1 ,
1 2
0.707
谐振频率 r n 1 2 2 , 0.707
带宽频率 b n 1 2 2 2 4 2 4 4 截止频率 c n 1 4 4 2 2
相角裕度
arctan
低频段:
开环增益充分大, 满足闭环系统的 稳态性能的要求。
中频段:
中频段幅频特性斜 率为 -20dB/dec, 而且有足够的频带 宽度,保证适当的 相角裕度。
高频段:
高频段增益尽 快减小,尽可 能地削弱噪声 的影响。
常用的校正装置设计方法 -均仅适用最小相位系统
1.分析法(试探法)
特点:直观,物理上易于实 现,但要求设计者有一定的 设计经验,设计过程带有试 探性,目前工程上多采用的 方法。
列劳思表:
s3 TiT
K p K0Ti
s2 Ti
K pK0
s1 K p K0 (Ti T )
s0 K p K0
若想使系统稳定,需要Ti>T。如果 Ti 太小,可能造成系 统的不稳定。
5.比例-积分-微分(PID)控制规律
R( s )
E(s)
C(s)
K
p (1
信号与系统第6章 系统的频域分析(6学时)
解决方法:采用拉普拉斯变换
6.3 无失真传输系统与理想滤波器
无失真传输系统 理想滤波器
一、 无失真传输系统
1、定义 若输入信号为x(t),则无失真传输系统的输出 信号y(t)应为 K为正常数
y(t ) K x(t td )
td是延迟时间
h(t ) K (t t d ) 系统的冲激响应为:
系统的频域响应为:H ( j) K e j td
幅度响应 | H (j)| K
相位响应j() td
一、 无失真传输系统
无失真传输系统的幅度和相位响应
| H ( j ) | K
( ) t d
( ) t d
|H(j)|
无失真传输系统应满足两个条件:
例2 已知某LTI系统的输入信号为f(t) = e-t u(t) , 输出信号为y(t) = (e-te-2t) u(t) ,求该系统的频率 响应H(j)和冲激响应h(t)。 解: 利用H(j)与F(j) 、Y(j)的关系 1 F(j ) j 1
1 1 2j 3 Y (j) + = j 1 j 2 j 1 j 2
ZR
VR(j ) R I R(j )
VL(j ) ZL j L I L(j )
ZC VC (j ) 1 IC (j ) j C
例3 图示RC电路系统,激励电压源为x(t),输出电压
y(t)为电容两端的电压vc(t),电路的初始状态为零。 求系统的频率响应H(j)和冲激响应h(t)。
例3 已知描述某LTI系统的微分方程为 y"(t) + 3y'(t) + 2y(t) = x(t), 求系统的频率响应H(j)。 解:利用Fourier变换的微分特性,微分方程的 频域表示式为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L() 20 lg 11 3.01dB
由两条渐近线构成惯性环节 的近似幅频特性,在转折频率1/T 处误差最大,为-3dB。而在0.1/T 处的误差为-0.04dB,因此在低频 和高频各修正10倍频程就可以了。
y(t) 1e p1t 2e p2t ...... ne pnt 0e jt a0*e jt
其中稳态分量:
yss (t) 0e j t a0*e j t
0
G(s)
A s2 2
(s
j)
s- j
-
AG(- j)
2j
0*
G(s)
6.1.1 Bode图法: 典型环节的频率特性
2. 积分环节的Bond图
G(s) 1; G( j) j 1
s
20lg 1 20lg,
是一条在 1处穿越横轴的直线,
其斜率为:
20lg 1 20lg 1
10
20lg10 20lg 2(0 dB)
G( j)
1
2
1
2
j
n
j2 1 n
1
n
j2 n
20 lg
1
1
n
2
2
4
2
n
2
(
)
arctan
1
2
s
n
; s
1
1;
s2
n2
2
s
n
1
依次为比例、积分、惯性、振荡、一阶微分和二阶 微分环节。
6.1.1 Bode图法: 典型环节的频率特性
1. 比例(放大)环节的 Bond图
L(ω)=20 lgK, φ(ω)=0°
比例环节的对数幅 频特性L(ω)和对数相频 特性φ(ω)也都是与ω无 关的水平直线。L(ω)是 一条纵坐标为20 lgK的、 平行于横轴的直线, φ(ω) 是一条与0°线重合的直 线。
0.05s 1
6.1 频率响应
u(t) sin(5t);G(s) 1
0.05s 1
1 0.5
0 -0.5
-1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
6.1 频率响应
u(t) sin(20t); 20 62.8
幅值下降到约0.3,相位滞后约:
6.1.1 频率特性的图示方法:Nyquist图
频率特性函数可以表示成
G(jω)=R(ω)+jI(ω)
代数式
=|G(jω)|∠G(jω) 极坐标式
=|G(jω)| ej ∠G(jω)
指数式
如果将极坐标系与直角坐标系重合, 那么极坐标系下的 向量在直角坐标系下的实轴和虚轴上的投影分别为实频特性 R(ω)和虚频特性I(ω)。
j2 sin + jcos
j( j sin + cos )
jA
dA jd;lnA = j + c; = 0 A = 1,C = 0
A
A = ej cos + jsin
e- j cos jsin
sin
e j
e- j 2j
cos
率变化10倍的一段对数刻度称为“十倍频程,用
“dec”表示,即 Δμ=lg10ω-lgω=1
❖ 纵轴: L=20 lgM(ω), 单位为分贝, 记作dB。
|G()| L()/dB
100 40
10 20
-1 0
10
0.1
1
0.1 - 20
0.01 - 40
1
= lg
10
/ s- 1
对数幅频特性的坐标系,纵坐标单位为dB或绝对值
❖在正弦信号作用下,线性稳定系统的稳态输出是同 频率的正弦信号,输出信号的幅值和相角随输入信号 的频率的变化而变化。
附:欧拉公式的证明
利用cos(t)
e jt
e 2j
j t
; 可得:L(cos t )
s2
s
2
A = cos + jsin
dA
d
sin + jcos
e j
e- j 2
6.1 频率响应
yss (t) j);
❖幅频特性:稳态输出信号与正弦输入信号的幅值之
比是输入信号频率ω的非线性函数,称为幅频特性。
M | G( j) |
❖相频特性:稳态输出信号与正弦输入信号的相位差
K
1 sv
h
i1
1 Tis 1
1 2
(
n
vh
)
i1
Ti 2 s 2
1
2iTi s
1
l
(
j1
js
1)
( S 1
2
(
ml
)
j1
22 i
2i i S
1)
对线性定常系统,不论如何复杂,都是由有限个典 型环节构成的。
11
K; ;
;
s Tis 1
s2
n2
2) 高频段 当ω/ωn>>1, 即ω>>ωn时,
L( )
20
lg
n
2
40 lg
T
40(lg
lg
1 T
)
说明在高频段, 振荡环节的幅频特性曲线近似于
斜率为-40 dB/dec的一条通过(1/T,0)的直线。
3) 转折频率: 低频渐近线与高频渐近线的交点在
频率特性的图形表示是描述系统的输入频率ω从
0到∞变化时频率响应的幅值、 相位与频率之间 关系的一组曲线。 虽然系统的频率特性函数有严 格的数学定义, 但它最大的优点是可以用图示方 法简明、 清晰地表示出来, 这正是该方法获得
广泛应用的原因之一。
1. 极坐标频率特性图(奈奎斯特图)
极坐标频率特性图又称奈奎斯特图(Nyquist)图或幅相频率 特性图。 极坐标频率特性图是当ω从0到∞变化时, 以ω为参变量, 在极坐标图上绘出G(jω)的模|G(jω)|和幅角∠G(jω) 随ω变化的曲 线, 即当ω从0到∞变化时, 向量G(jω)的矢端轨迹。 G(jω)曲线 上每一点所对应的向量都表示与某一输入频率ω相对应的系统 (或环节)的频率响应, 其中向量的模反映系统(或环节)的幅 频特性, 向量的相角反映系统(或环节)的相频特性。
j) |
2j
e-
j
A
e
jt
|
G(
j) |
2j
e
j
A
e
jt
| G( j) | A e j(t) e j(t) ;
2j
yss(t) A | G( j) | sin(t );欧拉公式 AM sin(t ); M | G( j) |; G( j);
第6章 频率响应设计法
6.1 频率响应
线性系统对正弦信号输入的响应,称为频率响应。
Y (s) G(s) U (s)
设G(s)的极点
u(t) Asin(t) U (s) A s2 2
Y (s) G(s)U (s) G(s) A s2 2
互不相同,无 重根,系统稳 定
A s2 2
(s -
j)
s j
AG( j)
2j
G( j) | G( j) | e j ;
G( j)
G(- j) | G(- j) | e- j
- G(- j)
| G( j) || G(- j) |;
6.1 频率响应
yss
(t)
-
|
G(
6
7
8
9
10
相频特 性
-80.54 -81.87 -82.88 -83.66
T 100,() 89.4271
-84.29
4 振荡环节
G(s)
s2
n2 2ns n2
T 2s2
1
2Ts 1
•其中, T为振荡环节的时间常数, ωn=1/T为无阻尼自然振荡 频率, ζ为振荡环节的阻尼比。 其频率特性函数为
t 20t 20 180 0.02 72
6.1 频率响应
幅值特性和相频特性
G(s) 1 0.05s 1
ω=62.8,幅值比0.305,相位滞后72.3⁰
6.1 频率响应
微分方程
将s=jω代入传
s p
递函数,就获 得了频率特性
传递函数
系统
j p
G(jω)。
相频特性斜对称于ω=1/T及φ=450 的点。
惯性环节的对数坐标频率特性
G(s)
1 0.2s 1
s
1
1
5
5
惯性环节渐近线修正值 [20 lg M ()] 20lg (T)2 1 20lg (T)2
10lg[(T)2 1] 20lg(T)
Tω 渐近线 修正值
1) 低频渐近线:当Tω<<1, 即ω<<1/T时, 可忽略Tω, 则
