§2.5等比数列的前n项和(2)学案
2.5等比数列的前n项和(二)

沈丘三高高二数学学案
编制 王立
2.5等比数列的前n 项和(二)
【学习目标】
进一步熟练掌握等比数列的通项公式和前n 项和公式.
【典型例题】
例1 .已知等差数列{n a }的第二项为8,前十项的和为185,从数列{n a }中,依次取出第2
项、第4项、第8项、……、第n 2项,按原来的顺序排成一个新数列{n b }.求数列{n b }的通项公式和前项和公式n S .
例2 .已知{}n a 是等比数列,n S 是其前n 项和.求证:7S ,14S -7S ,21S -14S 成等比数列.
思考:数列k k k k k S S S S S 232,,-- (+∈N k )是否成等比数列?
例3.在等比数列}{n a 中,a 1+a 2+a 3+a 4+a 5=3,a 6+a 7+a 8+a 9+a 10=9, 试求 a 11+a 12+a 13+a 14+a 15的值.
【课堂检测】
1.已知等差数列{a n }的公差d ≠0,且a 1,a 3,a 9成等比数列,则a 1+a 3+a 9 a 2+a 4+a 10
= .
2.在正实数组成的等比数列}{n a 中,若a 4a 5a 6=3,则log 3a 1+log 3a 2+log 3a 8+log 3a 9= .
3.等比数列{a n }中,若S 6=91,S 2=7,求S 4。
4.已知一个项数是偶数的等比数列的首项为1,其奇数项的和为85,偶数项的和为170,求这个数列的公比和项数.
【总结提升】
通过练习进一步熟练掌握等比数列的通项公式和前n 项和公式.。
《 等比数列的前n项和公式 》教案

五个量中“知三求二”(方程思想)。
3.等比数列前n项和公式推导方法:错位相减法。
例1
.
巩固练习:
例2已知{an}是等比数列,已知:
(1) 求
(2) ,求
巩固练习:(1) 求
(2) ,求
例3、求等比数列1、2、4……1024的和:
巩固练习:练习:求等比数列 ……的前6项和。
1、对比等差数列,探究等比数列的前n项和的推导方法。
2、培养学生观察、分析、解决问题的能力。
3、引导学生发现等比数列的前n项和公式的推导方法
培养学生观察、分析、解决问题的能力和不怕困难、勇于探索的求知精神。
1、理解错位相减法。
2、识记等比公式。
辨析公式的特点
及时回顾、复习所学内容,培养学生表达能力和概括能力
一、复习
二、情境引入
三、典型例题
教学实践
教学环节与主要内容
教学目标
教学活动
【复习导入】(时间分配:约2分钟)
回顾等比数列定义,通项公式。等差数列前n项和公式的推导方法:倒序相加法。
【新授】
教学活动Ⅰ(时间分配:约10分钟)
阅读:课本“国王赏麦的故事”。
问题:如何计算
引出课题:等比数列的前n项和。
问题:如何求等比数列 的前n项和公式
1、巩固课堂所学内容。
2、根据学生个体差异和基础及课堂接受情况,区别对待,提出不同训练要求。
学生:回忆并回答,
老师:提问、板书
学生:思考回答
师:展示多媒体投影并语言引导
生:观察、思考、回答
师:引导学生观察公式并分析公式特点
多媒体演示公式推导过程
板书公式
2.5 等比数列的前n项和(共2课时)

变式训练 1 在等比数列{an}中, Sn=a1+a2+„+an, 若 S10=5, S20=15, 则 S30=__________.
[解析]
S10=5,S20-S10=10,又∵S10,S20-S10,S30
-S20 成等比数列,∴(S20-S10)2=S10· (S30-S20),即 100= 5(S30-15).解得 S30=35 1 2 3 [解] 设 Sn= + 2+ 3+„+ n, 2 2 2 2 n-1 n 1 1 2 则有 Sn= 2+ 3+„+ n + n+1, 2 2 2 2 2 n 1 1 1 1 1 两式相减,得 Sn- Sn= + 2+ 3+„+ n- n+1, 2 2 2 2 2 2 1 1 1- n 2 2 n n 1 1 即 Sn= - n+1=1- n- n+1. 2 1 2 2 2 1- 2 n+2 n ∴Sn=2- n-1- n=2- n . 2 2 2 1
= a 1+ q ( S n - a n )
a1 anq Sn 1 q
经过计算,我们得到麦粒总数是
1 2 4 8 2 2 1(粒).
63 64
=18446744073709551615(粒) 已知麦子每千粒约为40克,则折合约为 737869762948382064克≈7378.7亿吨
国王有能 力满足发 明者的要 求吗?
分析:由于每个格子里的麦粒数都是前一 个格子里的麦粒数的2倍,且共有64个格子, 各个格子里的麦粒数依次是
1, 2, 2 , 2 , , 2 ,
于是发明者要求的麦粒总数就是
2
3
63
如何求出该 数列的和?
63
1 2 2 2 2 2 .
第二章 2.5 第1课时 等比数列前n项和公式

§2.5等比数列的前n项和第1课时等比数列前n项和公式学习目标1.掌握等比数列的前n项和公式及公式证明思路.2.会用等比数列的前n项和公式解决有关等比数列的一些简单问题.知识点一等比数列的前n项和公式知识点二 错位相减法1.推导等比数列前n 项和的方法叫错位相减法.2.该方法一般适用于求一个等差数列与一个等比数列对应项积的前n 项和,即若{b n }是公差d ≠0的等差数列,{c n }是公比q ≠1的等比数列,求数列{b n ·c n }的前n 项和S n 时,也可以用这种方法.思考 如果S n =a 1+a 2q +a 3q 2+…+a n q n -1,其中{a n }是公差为d 的等差数列,q ≠1.两边同乘以q ,再两式相减会怎样?知识点三 使用等比数列求和公式时注意事项(1)一定不要忽略q =1的情况;(2)知道首项a 1、公比q 和项数n ,可以用S n =a 1(1-q n )1-q ;知道首尾两项a 1,a n 和q ,可以用S n =a 1-a n q 1-q; (3)在通项公式和前n 项和公式中共出现了五个量:a 1,n ,q ,a n ,S n .知道其中任意三个,可求其余两个.1.在等比数列{a n }中,a 1=b ,公比为q ,则前3项和为b (1-q 3)1-q.( ) 2.求数列{n ·2n }的前n 项和可用错位相减法.( )3.a 1(1-q n )1-q =a 1(q n -1)q -1.( ) 4.等比数列前n 项和S n 不可能为0.( )题型一 等比数列前n 项和公式的直接应用例1 求下列等比数列前8项的和:(1)12,14,18,…; (2)a 1=27,a 9=1243,q <0.反思感悟 求等比数列前n 项和,要确定首项、公比或首项、末项、公比,应特别注意q =1是否成立. 跟踪训练1 (1)求数列{(-1)n +2}的前100项的和;(2)在14与78之间插入n 个数,组成所有项的和为778的等比数列,求此数列的项数.题型二 前n 项和公式的综合利用例2在等比数列{a n}中,a1=2,S3=6,求a3和q.反思与感悟 (1)a n =a 1qn -1,S n =a 1(1-q n )1-q ⎝⎛⎭⎪⎫或S n =a 1-a n q 1-q 两公式共有5个量.解题时,有几个未知量,就应列几个方程求解. (2)当q =1时,等比数列是常数列,所以S n =na 1;当q ≠1时,等比数列的前n 项和S n 有两个公式.当已知a 1,q 与n 时,用S n =a 1(1-q n )1-q 比较方便;当已知a 1,q 与a n 时,用S n =a 1-a n q 1-q比较方便. 跟踪训练2 已知等比数列{a n }是递增数列,S n 是{a n }的前n 项和.若a 1,a 3是方程x 2-5x +4=0的两个根,则S 6= .题型三 利用错位相减法求数列的前n 项和例3 求数列⎩⎨⎧⎭⎬⎫n 2n 的前n 项和.反思感悟 一般地,如果数列{a n }是等差数列,{b n }是公比不为1的等比数列,求数列{a n b n }的前n 项和时,可采用错位相减法.跟踪训练3 求和:S n =x +2x 2+3x 3+…+nx n (x ≠0).分期付款模型典例小华准备购买一部售价为5 000元的手机,采用分期付款方式,并在一年内将款全部付清.商家提出的付款方式为:购买2个月后第1次付款,再过2个月后第2次付款,…,购买12个月后第6次付款,每次付款金额相同,约定月利率为0.8%,每月利息按复利计算,求小华每期付款金额是多少.(参考数据:1.00812≈1.10)[素养评析]本题考查数学建模素养,现在购房、购车越来越多采用分期付款方式,但有关方不一定都会计算,所以建立一个老少皆宜的模型来套用是必要的,在建立模型过程中,要把制约因素抽象为符号表示,并通过前若干项探索规律,抓住这些量之间的关系建立关系式.1.等比数列1,x,x2,x3,…的前n项和S n等于()A.1-x n1-xB.1-x n -11-xC.⎩⎪⎨⎪⎧ 1-x n 1-x ,x ≠1且x ≠0n ,x =1D.⎩⎪⎨⎪⎧1-x n -11-x ,x ≠1且x ≠0n ,x =1 2.设等比数列{a n }的公比q =2,前n 项和为S n ,则S 4a 2等于( ) A .2 B .4 C.152 D.1723.等比数列{a n }的各项都是正数,若a 1=81,a 5=16,则它的前5项的和是( )A .179B .211C .243D .2754.某厂去年产值为a ,计划在5年内每年比上一年产值增长10%,从今年起5年内,该厂的总产值为 .5.已知数列{a n }的前n 项和为S n ,且a n =n ·2n ,则S n = .1.在等比数列的通项公式和前n 项和公式中,共涉及五个量:a 1,a n ,n ,q ,S n ,其中首项a 1和公比q 为基本量,且“知三求二”.2.前n 项和公式的应用中,注意前n 项和公式要分类讨论,即当q ≠1和q =1时是不同的公式形式,不可忽略q =1的情况.3.一般地,如果数列{a n }是等差数列,{b n }是等比数列且公比为q ,求数列{a n ·b n }的前n 项和时,可采用错位相减法求和.一、选择题1.等比数列{a n }中,a 1=2,a 2=1,则S 100等于( )A .4-2100B .4+2100C .4-2-98D .4-2-1002.在等比数列{a n }中,已知a 1=3,a n =48,S n =93,则n 的值为( )A .4B .5C .6D .73.设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则S 5S 2等于( )A .11B .5C .-8D .-114.已知数列{a n }是等差数列,若a 2+2,a 4+4,a 6+6构成等比数列,则数列{a n }的公差d 等于() A .1 B .-1C .2D .-25.设公比为q (q >0)的等比数列{a n }的前n 项和为S n .若S 2=3a 2+2,S 4=3a 4+2,则a 1等于( )A .-2B .-1 C.12 D.236.已知数列{a n }满足3a n +1+a n =0,a 2=-43,则{a n }的前10项和等于 ( ) A .-6(1-3-10) B.19(1-3-10) C .3(1-3-10) D .3(1+3-10)7.一弹球从100米高处自由落下,每次着地后又跳回到原来高度的一半再落下,则第10次着地时所经过的路程和是(结果保留到个位)( )A .300米B .299米C .199米D .166米二、填空题8.设等比数列{a n }的前n 项和为S n ,若a 1=1,S 6=4S 3,则a 4= .9.数列a 1,a 2-a 1,a 3-a 2,…,a n -a n -1,…是首项为1,公比为2的等比数列,那么a n = .10.已知正项数列{a n }满足a 2n +1-6a 2n =a n +1a n .若a 1=2,则数列{a n }的前n 项和S n = . 11.设等比数列{a n }的前n 项和为S n ,若S 3+S 6=2S 9,则数列的公比q = .三、解答题12.(2018·绵阳检测)在等比数列{a n }中,a 2-a 1=2,且2a 2为3a 1和a 3的等差中项,求数列{a n }的首项、公比及前n 项和.13.设数列{a n }满足a 1+3a 2+32a 3+…+3n -1a n =n 3,n ∈N *. (1)求数列{a n }的通项公式;(2)设b n =n a n,求数列{b n }的前n 项和S n .14.在等比数列{a n }中,对任意n ∈N *,a 1+a 2+…+a n =2n -1,则a 21+a 22+…+a 2n 等于() A .(2n -1)2 B.(2n -1)23 C .4n -1 D.4n -1315.已知等差数列{a n }满足a 2=0,a 6+a 8=-10.(1)求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和.。
2.5等比数列的前n项和2

复习引入问题 1:等比来自列定义及通项公式;复习引入
问题 1:等比数列定义及通项公式;
一般地,若一个数列从第二项起,每 一项与它的前一项的比等于同一个常数, 这个数列就叫做等比数列.
复习引入
问题 1:等比数列定义及通项公式;
一般地,若一个数列从第二项起,每 一项与它的前一项的比等于同一个常数, 这个数列就叫做等比数列.
新课讲授
某厂去年的产值记为 1,计划在今后的五 年内每年的产值比上一年增长 10%, 则从今年 起到第五年,这个厂的总产值为多少?
新课讲授
某厂去年的产值记为 1,计划在今后的五 年内每年的产值比上一年增长 10%, 则从今年 起到第五年,这个厂的总产值为多少?
问题 3:从今年起的五年内这个厂的逐年产值 有什么特征?利用什么公式求总产值?
通项公式一:
an a1 q
通项公式二:
n 1
(a1 , q 0)
an am q
n m
(a1 , q 0)
复习引入
问题 2:等比数列的求和公式;
复习引入
问题 2:等比数列的求和公式;
na1 (q 1) S n a1 (1 q n ) (q 1) 1q
例题讲解
2.在等比数列{an}中,已知 S10=5, S20=15,求 S30.
例题讲解
2.在等比数列{an}中,已知 S10=5, S20=15,求 S30.
3.Sn 为等比数列的前 n 项和, Sn≠0,则 * Sk , S 2 k Sk , S 3 k S2 k ( k N ),是等比数列.
例题讲解
1. 某商场今年销售计算机 5000 台.如果平均 每年的销售量比上一年的销售量增加 10%, 那么从今年起,大约几年可使销售量达到 30000 台(结果保留到个位)?
等比数列前n项和(二)

2.5 等比数列的前n 项和(二)[学习目标]1.熟练应用等比数列前n 项和公式的有关性质解题. 2.应用方程的思想方法解决与等比数列前n 项和有关问题. [知识链接]上一节我们学习了等比数列的前n 项和的公式,那么该公式与相应的函数有怎样的关系?等比数列的前n 项和又有怎样的性质?如何利用这些性质解题? [预习导引]1.等比数列的前n 项和的变式(1)当q ≠1时,S n =a 1-a n q 1-q =a n q -a 1 q -1=a 1(1-q n)1-q =a 1(q n-1)q -1;当q =1时,S n =na 1.(2)当公比q ≠1时, S n =a 1(1-q n)1-q 可以变形为S n =-a 11-q ·q n +a 11-q ,设A =a 11-q ,上式可写成S n =-Aq n +A . 由此可见,非常数列的等比数列的前n 项和S n 是由关于n 的一个指数式与一个常数的和构成的,而指数式的系数与常数项互为相反数.当公比q =1时,因为a 1≠0,所以S n =na 1是n 的正比例函数(常数项为0的一次函数). 2.等比数列前n 项和的性质(1)连续m 项的和(如S m 、S 2m -S m 、S 3m -S 2m ),仍构成等比数列.(注意:q ≠-1或m 为奇数) (2)S m +n =S m +q m S n ,特别地S 2n =S n +q n S n ,S 3n =S 2n +q 2n S n . 证明(3)若{a n }是项数为偶数、公比为q 的等比数列,则S 偶S 奇=q .题型一 等比数列前n 项和S n 的函数特征 例1 设f (n )=2+24+27+ (23)+1(n ∈N *),则f (n )等于( )A.27(8n -1)B.27(8n +1-1)C.27(8n +2-1)D.27(8n +3-1)跟踪演练1 若{a n }是等比数列,且前n 项和为S n =3n -1+t ,则t =________.题型二 等比数列前n 项和性质的应用例2在等比数列{a n }中,已知S n =48,S 2n =60,求S 3n .跟踪演练2在等比数列{a n }中,S 30=13S 10,S 10+S 30=140,则S 20等于( )A .90B .70C .40D .30题型三 等差、等比数列前n 项和的综合问题例3 已知数列{a n }的前n 项和为S n ,且S n =2a n -2(n ∈N *),在数列{b n }中,b 1=1, 点P (b n ,b n +1)在直线x -y +2=0上.(1)求数列{a n },{b n }的通项公式; (2)记T n =a 1b 1+a 2b 2+…+a n b n ,求T n .跟踪演练3 在等比数列{a n }中,a n >0(n ∈N *),公比q ∈(0,1),且a 1a 5+2a 3a 5+a 2a 8=25, 又a 3与a 5的等比中项为2. (1)求数列{a n }的通项公式;(2)设b n =log 2a n ,数列{b n }的前n 项和为S n ,当S 11+S 22+…+S nn 最大时,求n 的值.当堂达标1.设{a n }是公比为q 的等比数列,S n 是它的前n 项和,若{S n }是等差数列,则q 等于( ) A .1 B .0 C .1或0 D .-12.等比数列{a n }中,a 1a 2a 3=1,a 4=4,则a 2+a 4+a 6+…+a 2n =( ) A .2n-1 B.4n -13 C.1-(-4)n 5 D.1-(-2)n33.已知等比数列{a n }的前n 项和为S n =k·3n -1-16,则k 的值为( )A.13 B .-13 C.12 D .-12 4.设等比数列{a n }的前n 项和为S n ,若S 6S 3=3,则S 9S 6=________.5.等比数列{a n }共2n 项,其和为-240,且奇数项的和比偶数项的和大80,则公比q =________. 6.在等比数列{a n }中,已知S n =189,q =2,a n =96,求a 1和n .B 组7.设{a n }是由正数组成的等比数列,S n 为其前n 项和,已知a 2a 4=1,S 3=7,则S 5等于( ) A.152 B.314 C.334 D.1728.数列{a n }的前n 项和为S n ,若a 1=1,a n +1=3S n (n ≥1),则a 6等于( ) A .3×44 B .3×44+1 C .45 D .45+19.等比数列{a n }中,前n 项和为S n ,S 3=2,S 6=6,则a 10+a 11+a 12=________.10.已知等比数列{a n }的前n 项和为S n ,若S m ,S n ,S l 成等差数列,求证:对任意自然数k , a m +k ,a n +k ,a l +k 也成等差数列.。
等比数列的前n项和公式 学案(含答案)

第四章 数列4.3.2 等比数列的前n 项和公式学案一、学习目标1. 理解等比数列的前n 项和公式的推导方法;2. 掌握等比数列的前n 项和公式并能运用公式解决一些简单问题. 二、基础梳理1.等比数列的前n 项和公式:当1q ≠时, ()11(1)1n n a q S q q-=≠-或1(1)1n n a a qS q q-=≠-. 2.等比数列的前n 项和的性质(1)当q =1时,n m s m s n =,当1q ≠±时,11nn mm s q s q-=-. (2)m n n m m n n m s s q s s q s +=+=+.(3)设s 偶与s 奇分别是偶数项的和与奇数项的和,若项数为2n ,则s q s =偶奇,若项数为2n +1,则1s a q s -=奇偶.(4)当1q ≠-时,连续m 项的和(232m m m m m s s s s s --⋅⋅⋅,,,)仍成等比数列,公比为2m q m ≥,,注意:连续m 项的和必须非零才能成立. 三、巩固练习1.已知数列{}n a 的前n 项和21n S n =+,正项等比数列{}n b 满足1134,1b a b a ==+,则使61n b S +≥成立的n 的最大值为( ) A.5B.6C.7D.82.已知数列{}n a 为等比数列,11a =,2q =,且第m 项至第()n m n <项的和为112,则m n +的值为( ) A.11B.12C.13D.143.记n S 为数列{}n a 的前n 项和,已知{}n a 和{}n S k - (k 为常数)均为等比数列,则k 的值可能为( )A.1aB.2aC.3aD.13a a +4.5个数依次组成等比数列,且公比为2-,则其中奇数项和与偶数项和的比值为( ) A.2120-B.2-C.2110-D.215-5.已知n S 是等比数列{}n a 的前 n 项和,若存在*m ∈N ,满足22519,1m m mm S a m S a m +==-,则数列{}n a 的公比为( ) A.2-B.2C.3-D.36.已知等比数列{}n a 的公比2q =,前100项的和10090S =,则246100a a a a ++++=( )A.15B.30C.45D.607.(多选)已知等比数列{}n a 的公比为q ,其前n 项的积为n T ,且满足11a >,9910010a a ->,99100101a a -<-,则以下结论正确的是( ) A.01q << B.9910110a a -<C.100T 的值是n T 中最大的D.使1n T >成立的最大正整数数n 的值为1988. (多选)设等比数列{}n a 的公比为q ,其前n 项和为n S ,前n 项积为n T ,并满足条件11a >,201920201a a ⋅>,20192020101a a -<-,则下列结论中正确的是( ) A.20192020S S <B.2019202110S S ⋅-<C.2019T 是数列{}n T 中的最大值D.数列{}n T 无最大值答案以及解析1.答案:D解析:设等比数列{}n b 的公比为q , 由题意可知当2n ≥时,121n n n a S S n -=-=-; 当1n =时,112a S ==,2,1,21,2,n n a n n =⎧∴=⎨-≥⎩213412,18b b a b q ∴==+==. 0n b >,2,2n n q b ∴=∴=,66264b ∴==,2651n ∴≥+,8n ∴≤,∴n 的最大值为8,故选D.2.答案:B解析:由已知,得()()11121121121212n m -⨯-⨯--=--,即()11422127m n m --+⋅-=⨯,则14122217m n m --+⎧=⎨-=⎩,解得57m n =⎧⎨=⎩,所以12m n +=,故选B. 3.答案:C解析:若公比1q =,则{}1,n n S k na k S k -=--不可能为等比数列,因此1q ≠,此时1111111n nn a q a q S k a k k q q q ⎛⎫---=-=+- ⎪---⎝⎭,只需101a k q -=-即可.A 选项,{}1n S a -的首项为0,不满足题意;B 选项, 1211011a a a q q q ⎛⎫-=-=⎪--⎝⎭,即211300124q q q ⎛⎫-=⇒-+= ⎪-⎝⎭不成立;C 选项,21311011a a a q q q ⎛⎫-=-= ⎪--⎝⎭,即23210101q q q q -=⇒-+=-,该方程必然有解,成立;D 选项,()2113111011a a a a q q q ⎛⎫-+=--= ⎪--⎝⎭,即()221101001q q q q q q--=⇒-+=⇒=-,不成立. 4.答案:C解析:由题意可设这5个数分别为,2,4,8,16a a a a a --,其中0a ≠,故奇数项和与偶数项和的比值为416212810a a a a a ++=---,故选C.5.答案:B解析:设数列{}n a 的公比为 q ,若1q =,则22mmS S =,与题中条件矛盾,故1q ≠.()()21211119,811m m mm m m a q S q q q S a q q--==+=∴=--.2132111518,3,8,21m m m m m a a q m q m q q a a q m --+====∴=∴=∴=-. 6.答案:D 解析:1001210090S a a a =+++=,设1399S a a a =+++,则241002S a a a =+++,100290,30S S S S ∴+==∴=,故24100260a a a S +++==.故选D.7.答案:ABD解析:9910010a a ->,991001a a ∴>,0q ∴>.99100101a a -<-,()()99100110a a ∴--<,又11a >,01q ∴<<.故A 正确.由A 选项的分析可知991a >,10001a <<,2991011001a a a ∴=<,9910110a a ∴-<,1009910099T T a T =<,故B 正确,C 不正确.()()()()99198121981198219799100991001T a a a a a a a a a a a ===>,()()()1991991219819911992198991011001001T a a a a a a a a a a a a ===<,∴使1n T >成立的最大正整数数n 的值为198,故D 正确. 8.答案:AC解析:由题意,得20191a >,202001a <<,所以01q <<,等比数列{}n a 是各项都为正数的递减数列,即122019202010a a a a >>>>>>>.因为2020201920200S S a -=>,所以20192020S S <,故A 正确;因为20191220191S a a a =+++>,所以()()22201920212019201920202021201920192020202120191S S S S a a S S a a S ⋅=⋅++=+⋅+>>,即2019202110S S ⋅->,故B 错误;根据122019202010a a a a >>>>>>>,可知2019T 是数列{}n T 中的最大项,故C 正确,D 错误.故选AC.。
高中二年级下学期数学《等比数列的前n项和公式(2)》教学设计
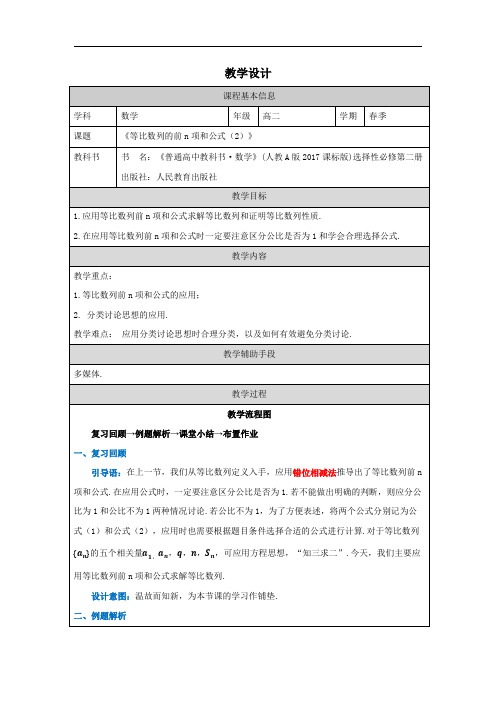
例9已知等比数列 的公比 ,前 项和为 . 成等比数列,并求这个数列的公比.
【问题1】:请同学们回忆一下,我们应该怎样证明一个数列是等比数列?
答:我们主要应用定义法来证明一个数列是等比数列,即证明数列满足递推式:
分析:用数列前 项和的定义来表示
设计意图:通过逐步分析引导学生学会分析问题和解决问题,提高学生的分析问题和解决问题的能力.
师生活动:用数列前n项和的定义来表示 ,再应用等比数列通项公式的变式进行变形化简,证明了该结论.显然不用分类讨论的过程更简洁一些.
提醒同学们注意题目中的条件 .
追问5:请同学们想一想,为何要强调“ ”呢?
追问1:我们应如何表示等比数列的前 项和 ?
分析:我们可以用等比数列的前 项和公式来表示 但条件中并没有公比 是否为 的信息,因此,需要对 是否等于1分类讨论.且当 ,我们应选择用 表示等比数列求和公式.
设计意图:引导学生从证明等比数列和表示等比数列前n项和的角度去解决本题问题,训练学生学会目标分析和问题分析,也为不用分类讨论的方式证明该结论埋下伏笔.
师生活动: 时, 的等比数列.
时,选择公式(1)表示 应用立方差和平方差公式进行化简 的等比数列.显然,分类讨论的书写过程较为繁琐,很多同学都不太喜欢分类讨论,因此引导同学们思考:
追问2:请同学们想一想,不用分类讨论的方式能否证明该结论?
我们尝试从问题的根源入手解决问题.那就是追溯分类讨论的根源.
追问3:为什么要分类讨论?
分析: 时,数列是“ , , , , , ,…”当 为偶数时, 均为零,不能够成等比数列. 是 成等比数列的必要条件.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【学习目标】1.熟练应用等比数列前n 项和公式的有关性质解题.
2.能用等比数列的前n 项和公式解决实际问题.
【学法指导】1.解决与等比数列前n 项和有关问题的关键在于“基本量”以及方程思想方法的灵活
运用.
2.运用等比数列前n 项和解题时要注意“整体思想”方法的灵活运用.
3.利用等比数列的知识解决实际问题,需要从实际问题中抽象出等比数列模型,明确
首项a 1,公比q ,以及项数n 的实际含义,切忌含糊不清.
一.知识导学 1.等比数列{a n }的前n 项和为S n ,当公比q ≠1时,S n = = ;当q =1时,S n = .
2.等比数列前n 项和的性质:
(1)连续m 项的和(如S m 、S 2m -S m 、S 3m -S 2m ),仍构成 数列.(注意:q ≠-1或m 为奇数)
(2)S m +n =S m +q m S n (q 为数列{a n }的公比).
3.设等比数列{a n }的前n 项和为S n ,若S 6S 3=3,则S 9S 6
等于( ) A .2 B .73 C .83
D .3 4.已知数列{a n }的前n 项和S n =a n -1(a 是不为零且a ≠1的常数),则数列{a n }( )
A .一定是等差数列
B .一定是等比数列
C .或者是等差数列,或者是等比数列
D .既非等差数列,也非等比数列
二.探究与发现
【问题情境】一件家用电器,现价20 000元,实行分期付款,每期付款数相同,每月为一期,一个
月付款一次,共付12次,购买后一年还清,月利率为0.8%,按复利计算,那么每期
付款多少元?要解决上述问题,需要了了解复利的计算方法,这正是这一节的主要内
容之一.
【探究点一】等比数列前n 项和S n 与函数的关系
探究 当公比q =1时,因为a 1≠0,所以S n =na 1,是n 的正比例函数(常数项为0的一次函数).
当q =1时,数列S 1,S 2,S 3,…,S n ,…的图象是正比例函数y =a 1x 图象上一些孤立的点.
当公比q ≠1时,等比数列的前n 项和公式是S n =a 11-q (1-q n )=a 1q -1(q n -1).设A =a 1q -1
,则上式可以写为S n =A (q n -1).由此可见,q ≠1时,由等比数列前n 项和S n 构成的点列(1,S 1),(2,S 2),(3,S 3),…,(n ,S n )位于函数y =A (q x -1)的图象上.
问题1 若{a n }是等比数列,它的前n 项和为S n =3n +t ,则t =_____.
2015-2016学年高一年级
数学导学案
11
班级 姓名 学号 编写: §2.5等比数列的前n 项和(2)
问题2 若{a n }是等比数列,且前n 项和为S n =3n -
1+t ,则t =______.
【探究点二】等比数列前n 项和的性质
问题1 等比数列{a n }的前n 项和为S n ,公比为q ,求证:S m +n =S m +q m S n .
问题2 在等比数列{a n }中,若连续m 项的和不等于0,则它们仍组成等比数列.即S m ,S 2m -S m ,
S 3m -S 2m ,…仍组成等比数列.请你证明上述结论.
【探究点三】分期付款问题
问题 在分期付款问题中,贷款a 元,分m 个月付清,月利率为r ,每月还x 元,想一想,每月付款
金额x 元应如何计算?
下面给出了两种推导方法,请你补充完整:
方法一:每个月还款x 元后的剩余欠款按月份构成一个数列,记作{a n },则有:
经过1个月,还款x 元后,剩余欠款为a 1= ;
经过2个月,还款x 元后,剩余欠款为a 2=a 1(1+r )-x =____________________;
经过3个月,还款x 元后,剩余欠款为a 3=a 2(1+r )-x =___________________________; ……
经过m 个月,还款x 元后,剩余欠款为a m =a m -1(1+r )-x = .
由于经过m 个月后,欠款还清,故a m =0,从而有a (1+r )m = 即x = . 方法二:我们可以把该问题分开来看:
一方面,每月付款x 元,共付m 次,m 个月后各期付款到期后的本息和为:
期数 1 2 3 …
m -1 m 本息和
… x 从而到期后(m 个月后),银行共收到付款及利息为:______________________=[(1+r )m -1]r
x ; 另一方面贷款a 元,m 个月后应偿还本息和为 ;
由于m 个月后,贷款全部付清,所以有[(1+r )m -1]r
x = ,故x = . 【典型例题】
例1 已知等比数列前n 项,前2n 项,前3n 项的和分别为S n ,S 2n ,S 3n ,
求证:S 2n +S 22n =S n (S 2n +S 3n ).
小结 运用等比数列的前n 项和公式要注意公比q =1和q ≠1两种情形,在解有关的方程(组)时,通
常用约分或两式相除的方法进行消元.
跟踪训练1 已知S n 是等比数列{a n }的前n 项和,S 3,S 9,S 6成等差数列,求证:a 2,a 8,a 5成等差
数列.
例2 在等比数列{a n }中,a n >0 (n ∈N *),公比q ∈(0,1),且a 1a 5+2a 3a 5+a 2a 8=25,又a 3与a 5的等比中
项为2.
(1)求数列{a n }的通项公式;
(2)设b n =log 2a n ,数列{b n }的前n 项和为S n ,当S 11+S 22
+…+S n n 最大时,求n 的值.
例3 某家用电器一件现价20 000元,实行分期付款,每期付款数相同,每期为一月,购买后一个月开始付款,每月付款一次,共付12次,购买后一年还清,月利率为0.8%,按复利计算,那么每期应付款多少?(1.00812≈1.1)
三.小结
1.深刻理解等差(比)数列的性质,熟悉它们的推导过程是解题的关键.两类数列的性质既有类似的部分,又有区别,要在应用中加强记忆.同样,用好其性质也会降低解题的运算量,从而减少错误.
2.在等差数列与等比数列中,经常要根据条件列方程(组)求解,在解方程时,仔细体会两种情形中解方程组的方法的不同之处.
3.利用等比数列解决实际问题,关键是构建等比数列模型.要确定a1与项数n的实际含义,同时要搞清是求a n还是求S n的问题.。
