高等数学解题方法上1PPT课件
合集下载
全版高等数学上册课件.ppt

f ( x nl) . nl (n N ) 也是 f ( x) 的周 期.
若 在周期函数 f (x)的所有周期中存在 最小的正 周期T ,则称这个最小正周期T 为 f ( x)的 基本周期 .
通常我们所说的函数的周期都是指基本周期.
.精品课件.
27
f ( x) sin x,cos x 的周期为T 2 , 常 f ( x) tan x,cot x 的周期为T , 用 F ( x) Asin(x B) C 的 周 期 为T 2 ,
业成绩以10% 记入期末总评成绩。
4. 辅导答疑:
时间:待定;地点:南堂 112 答疑室。
电话:15020063032
.精品课件.
6
《高等数学练习册》 发放时间、地点及相关要求:
时 间:星期二、三、五(9月20、21、23日)
下午 3:00 — 5:00 地 点:文理楼 237 室 《高等数学练习册》每本售价:17元
定理 函数 f ( x) 在 D 上有界 函数 f ( x) 在 D 上既有上界又有下界.
(3) 若 M 0,xM D f ( xM ) M , 则称 f ( x) 在 D 上无界 .
.精品课件.
21
例6 证明:f ( x) 1 在 ( ,0) 与 (0, ) ( 0) 无界,
x
在任何不包含原点的闭区间 [a, b] 上有界 .
16
有些特殊的函数只能用语言来描述对应法则 f ,
并用约定的符号予以表示:
例1 “x R, 对应的 y 是不超过x 的最大整数”.
记作:y [x] , x R . 称为取整函数
例如:[5.3]= 5, [ - 4.9]= 5 .
当n x n 1 (n Z) 时,
若 在周期函数 f (x)的所有周期中存在 最小的正 周期T ,则称这个最小正周期T 为 f ( x)的 基本周期 .
通常我们所说的函数的周期都是指基本周期.
.精品课件.
27
f ( x) sin x,cos x 的周期为T 2 , 常 f ( x) tan x,cot x 的周期为T , 用 F ( x) Asin(x B) C 的 周 期 为T 2 ,
业成绩以10% 记入期末总评成绩。
4. 辅导答疑:
时间:待定;地点:南堂 112 答疑室。
电话:15020063032
.精品课件.
6
《高等数学练习册》 发放时间、地点及相关要求:
时 间:星期二、三、五(9月20、21、23日)
下午 3:00 — 5:00 地 点:文理楼 237 室 《高等数学练习册》每本售价:17元
定理 函数 f ( x) 在 D 上有界 函数 f ( x) 在 D 上既有上界又有下界.
(3) 若 M 0,xM D f ( xM ) M , 则称 f ( x) 在 D 上无界 .
.精品课件.
21
例6 证明:f ( x) 1 在 ( ,0) 与 (0, ) ( 0) 无界,
x
在任何不包含原点的闭区间 [a, b] 上有界 .
16
有些特殊的函数只能用语言来描述对应法则 f ,
并用约定的符号予以表示:
例1 “x R, 对应的 y 是不超过x 的最大整数”.
记作:y [x] , x R . 称为取整函数
例如:[5.3]= 5, [ - 4.9]= 5 .
当n x n 1 (n Z) 时,
高等数学 (上册) -01-PPT课件

3. xlim 左右极限存在并相等 x ƒ(x) 的存在性 当x<xo时,x→ x 0 ,极限 xlim ƒ(x)= -ƒ(xo-0) 左极限 x
0
0
当x>xo时,x→ x 0 ,极限 xlim ƒ(x)= -ƒ(xo+0) 左极限 x
0
应用-----主要用于分段函数 分段点处求极限
x x0 2
证明: 对 >0要使|sinx-sinxo |=2|sin 2|sin
x x0 2
cos
x x0 |<ε 2
x x0 cos 2
|≤2|sin
x x0 2
|
当 x 很 小 时,|sinx| < |x| 2|sin
x x0 2
|<|2
x x0 2
| = |x-x0|<ε
(1)、ε-x定义:
if 对 >0, x>0,st 当 |x|>x 时 , 有 |ƒ(x)-a|<ε so 称 a 为 ƒ(x) 当 x→∞时的极限 先有ε,再找x
(2)、ε-定义 if对 >0, st当0<|x-xo|< 时,有|ƒ(x)-a|<ε成立,则 limƒ(x)=a 称a是ƒ(x)当x→xo 的极限,记为 x x
iii) 极限过程可以变,但必须是型,且x一模一样 1/(x-1) =1 如:1) lim x 1 [1+(x-1)] 1 .2 x 1 1 2 x lim(1 ) = e1/2 2) lim (1+ ) = x 2 x x 2x 3) lim (1+ x 4) lim ) x = e2 x (1+
大一高数上-1精ppt课件
学习数学,必须做一定数量的习题,做习 题不仅是为了掌握数学的基本运算方法,而且 也可以帮助我们更好地理解概念、理论和思想 方法。但我们不应该仅仅满足于做题,更不能 认为,只要做了题,就算学好了数学。
精选课件PPT
3
高等数学中几乎所有的概念都离不开极限, 因此极限概念是高等数学的重要概念,极限理 论是高等数学的基础理论,极限是高等数学的 精华所在,是高等数学的灵魂。因此很好地理 解极限概念是学习好微积分的关键,同时也是 从初等数学迈入高等数学的一个重要阶梯。
精选课件PPT
19
例2. 函数 y=2。 函数的定义域为D = (-, +)。 函数的值域为Rf ={2}。 函数的图形为一条平行于x 轴的直线。
y
2
y=2
O
精选课件PPT
x
20
例3. 函数 y=|x|= x, x0 称为绝对值函数。 -x, x<0
函数的定义域为D=(-, +)。 函数的值域为Rf =[0, + )。
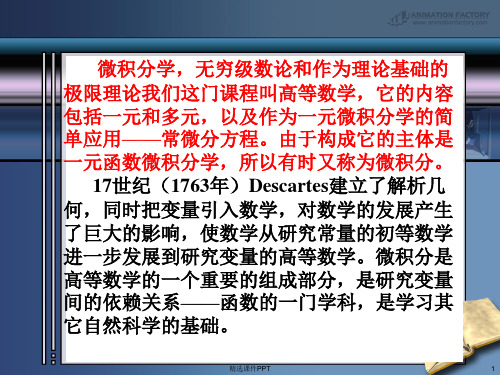
17世纪(1763年)Descartes建立了解析几 何,同时把变量引入数学,对数学的发展产生 了巨大的影响,使数学从研究常量的初等数学 进一步发展到研究变量的高等数学。微积分是 高等数学的一个重要的组成部分,是研究变量 间的依赖关系——函数的一门学科,是学习其 它自然科学的基础。
精选课件PPT
1
高等数学研究的主要对象是函数,主要研 究函数的分析性质(连续、可导、可积等)和 分析运算(极限运算、微分法、积分法等)。 那么高等数学用什么方法研究函数呢?这个方 法就是极限方法,也称为无穷小分析法。从方 法论的观点来看,这是高等数学区别于初等数 学的一个显著标志。
由于高等数学的研究对象和研究方法与初
精选课件PPT
3
高等数学中几乎所有的概念都离不开极限, 因此极限概念是高等数学的重要概念,极限理 论是高等数学的基础理论,极限是高等数学的 精华所在,是高等数学的灵魂。因此很好地理 解极限概念是学习好微积分的关键,同时也是 从初等数学迈入高等数学的一个重要阶梯。
精选课件PPT
19
例2. 函数 y=2。 函数的定义域为D = (-, +)。 函数的值域为Rf ={2}。 函数的图形为一条平行于x 轴的直线。
y
2
y=2
O
精选课件PPT
x
20
例3. 函数 y=|x|= x, x0 称为绝对值函数。 -x, x<0
函数的定义域为D=(-, +)。 函数的值域为Rf =[0, + )。
17世纪(1763年)Descartes建立了解析几 何,同时把变量引入数学,对数学的发展产生 了巨大的影响,使数学从研究常量的初等数学 进一步发展到研究变量的高等数学。微积分是 高等数学的一个重要的组成部分,是研究变量 间的依赖关系——函数的一门学科,是学习其 它自然科学的基础。
精选课件PPT
1
高等数学研究的主要对象是函数,主要研 究函数的分析性质(连续、可导、可积等)和 分析运算(极限运算、微分法、积分法等)。 那么高等数学用什么方法研究函数呢?这个方 法就是极限方法,也称为无穷小分析法。从方 法论的观点来看,这是高等数学区别于初等数 学的一个显著标志。
由于高等数学的研究对象和研究方法与初
高等数学完整版详细 ppt课件

h
lim f(0h)f(0)lim h 1,
h 0
h
h h 0
y y x
o
x
f(0h )f(0 ) h
lim
lim1.
h 0
h
h h 0
即 f (0 )f (0 ), 函y数 f(x)在 x0点不 . 可
四、导数的几何意义
y
f (x0 )表示曲线y f (x) 在点M(x0, f (x0 ))处的 切线的斜率,即
4
4
2. 2
例3 求函 yx数 n(n为正 )的 整导 .数数
解 (xn)lim (xh)nxn
h 0
h
li[n m n 1 x n (n 1 )x n 2 h h n 1 ]nxn1
h 0
2 !
即(xn)nn x 1.
更一般地 (x ) x 1 . ( R )
例如,
y x
f(x0)
0( x 0 ) y f(x 0 ) x x
l x 0 i y m l x 0 i [ f m ( x 0 ) x x ] 0
函f(数 x )在x 0连 点 . 续
注意: 该定理的逆定理不成立.
★ 连续函数不存在导数举例
1. 函 数 f(x)连 续 ,若f(x0)f(x0)则 称x0点 为函f(数 x)的角,函 点数在角点 . 不
xx0
切线 MT的斜率为 ktan lim f(x)f(x0). x x0 xx0
二、导数的定义
定义 设函数 y f ( x)在点 x0的某个邻域内 有定义, 当自变量 x在 x0处取得增量 x (点 x0 x 仍在该邻域内)时, 相应地函数 y取 得增量y f ( x0 x) f ( x0 ); 如果y与 x之比当x 0时的极限存在, 则称函数 y f ( x)在点 x0处可导, 并称这个极限为函 数 y f ( x)在点 x0处的导数, 记为y x x0 ,
全高考数学解题技巧讲解课件PPT

������������|cos θ=������������·������������ =
|������������ |
������ 2-1 ������ 2+1
=
������2 + 1 − ������22+1,
令 ������2 + 1=t(t>1),则|������������|= ������������22-+11=t-2������ .令 f(t)=t-2������ ,则有 f'(t)=1+������22.在
A.
5 5
,
2 3
B.
2 3
,
25 5
C.
5 5
,
7 3
D.
7 3
,
25 5
-7-
答案 (1)C (2)D
解析 (1)设等差数列{an}的公差为 d,∵a4=4,S5=15,
∴
������1 + 3������ = 4,
5������1
+
5×4 2
������
=
15,解得
������1 = 1, ������ = 1.
(1)解题策略:小题巧解,不需“小题大做”,在准确、迅速、合理、 简洁的原则下,充分利用题设和选择支这两方面提供的信息作出判 断.先定性后定量,先特殊后一般,先间接后直接,多种思路选最简.对 于选择题可先排除后求解,既熟悉通法又结合选项支中的暗示及知 识能力,运用特例法、筛选法、图解法等技巧求解.
(2)解决方法:主要分直接法和间接法两大类,具体方法为:直接法, 特值、特例法,筛选法,数形结合法,等价转化法,构造法,代入法等.
A.2 019 B.0 C.1 D.-1 (2)平行四边形 ABCD 中,������������, ������������在������������上投影的数量分别为 3,-1, 则������������在������������上的投影的取值范围是( )
|������������ |
������ 2-1 ������ 2+1
=
������2 + 1 − ������22+1,
令 ������2 + 1=t(t>1),则|������������|= ������������22-+11=t-2������ .令 f(t)=t-2������ ,则有 f'(t)=1+������22.在
A.
5 5
,
2 3
B.
2 3
,
25 5
C.
5 5
,
7 3
D.
7 3
,
25 5
-7-
答案 (1)C (2)D
解析 (1)设等差数列{an}的公差为 d,∵a4=4,S5=15,
∴
������1 + 3������ = 4,
5������1
+
5×4 2
������
=
15,解得
������1 = 1, ������ = 1.
(1)解题策略:小题巧解,不需“小题大做”,在准确、迅速、合理、 简洁的原则下,充分利用题设和选择支这两方面提供的信息作出判 断.先定性后定量,先特殊后一般,先间接后直接,多种思路选最简.对 于选择题可先排除后求解,既熟悉通法又结合选项支中的暗示及知 识能力,运用特例法、筛选法、图解法等技巧求解.
(2)解决方法:主要分直接法和间接法两大类,具体方法为:直接法, 特值、特例法,筛选法,数形结合法,等价转化法,构造法,代入法等.
A.2 019 B.0 C.1 D.-1 (2)平行四边形 ABCD 中,������������, ������������在������������上投影的数量分别为 3,-1, 则������������在������������上的投影的取值范围是( )
高等数学第一章复习课ppt课件.ppt

3.极限的性质
定理 设 lim f ( x) A,lim g( x) B,则 (1) lim[ f ( x) g( x)] A B; (2) lim[ f ( x) g( x)] A B; (3) lim f ( x) A , 其中B 0. g(x) B
推论1 如果lim f ( x)存在,而c为常数,则 lim[cf ( x)] c lim f ( x).
1 o 1
x
(5) 函数的周期性:
设函数 f(x) 的定义域为D,如果存在一个不为零的
数l,使得对于任一 x D,有 x l D .且 f(x+l)=f(x)
恒成立,则称f(x)为周期函数,l 称为 f(x) 的周期.(通
常说周期函数的周期是指其最小正周期).
T 1
y
y x [x]
1
o
1
x
3.反函数
由y f ( x)确定的y f 1( x)称为反函数.
y sinh x
4.隐函数
y f 1( x) ar sinh x
由方程F ( x, y) 0所确定的函数 y f ( x)称为隐函数.
5.反函数与直接函数之间的关系
设函数f ( x)是一一对应
函数, 则
y y f 1( x)
3.连续的充要条件
定理 函数f ( x)在 x0 处连续 是函数f ( x)在 x0 处 既左连续又右连续.
4.间断点的定义
函数f ( x)在点x0处连续必须满足的三个条件: (1) f ( x)在点x0处有定义;
(2) lim f ( x)存在; x x0
(3) lim x x0
f (x)
f ( x0 ).
2.函数的性质
高等数学(第三版)课件:不定积分的积分方法

还应注意到,在换元—积分—还原的解题过程中,关 键是换元,若在被积函数中作变量代换 j(x) = u,还需要在
被积表达式中再凑出 j '(x)dx 即 dj(x),也就是 du ,这样才能
以u为积分变量作积分,也就是所求积分化为
f j(x)dj(x) f (u) du Fj(x) C
在上述解题过程中u可不必写出,从这个意义上讲,第 一换元积分法也称为“凑微分”法.
式而可能使其容易积分.当然在求出原函数后, 还要
将 t j1(x) 代回.还原成x的函数,这就是第二换元
积分法计算不定积分的基本思想.
定理2 设 x j(t) 是单调可导的函数,且
j(t) 0. 如果 f j(t)j(t) dt F(t) C,
则有
f (x) d x f j(t)j(t) d t F(t) C
3
1
2x
dx
1 u
1 2
du
=
1 2
1 du u
12 u C 2
3 2x C.
例4 求 x x2 4 dx.
解 令u x2 4,则du 2xdx,则
x
x2
4dx
1 2
udu
12 3
= 2 3u2 C
1 3
(
x2
3
4)2
C.
例5
求
(lnx)2
dx x
解 1 dx d(ln x), x
= sect dt
= ln | sect tant | C.
x
x2 a2
t
a
根据sec t x ,利用图所示三角形,易得 a
对边 tan t 邻边
x2 a2 , a
第一讲高等数学ppt

第一讲
1 极限与单侧极限
定理:lim
x x0
极限及其运算法则
f ( x ) A lim f ( x ) lim f ( x ) A .
x x0 x x0
例1、 求下列函数极限。
(1 ) f ( x ) x lim f ( x ); ( 2 ) f ( x ) [ x ]
1
记住 lim 结论:
n
n
n 1 , 并可推广到
x
lim x
x
1.
定理2:单调有界数列必有极限。 第一个重要极限
sin x x 1
lim
x 0
( 1 )当 x ( 0 ,
( 2 ) lim sin x x
2
) 时 , 有 sin x x tan x ;
0 0 型极限才有 lim sin x x 1 , 而 lim
x x0
lim g ( x ) lim h ( x ) A , 则 lim f ( x ) A .
x x0 x x0
例10、求下列极限。
( 1 ) lim (
n
1 n 1
2
1 n 2
2
1 n n
2
);
( 2 ) lim
n
n
n.
解题关键:适当放缩,使较小和较大 数列的极限存在且相等。
例12、求下列极限。
( 1 ) lim ( 1
x
3 x
2
) ;
3x
x
( 2 ) lim x 1 x ;
x1
( 3 ) lim (
x
2x 1 2x 1
1 极限与单侧极限
定理:lim
x x0
极限及其运算法则
f ( x ) A lim f ( x ) lim f ( x ) A .
x x0 x x0
例1、 求下列函数极限。
(1 ) f ( x ) x lim f ( x ); ( 2 ) f ( x ) [ x ]
1
记住 lim 结论:
n
n
n 1 , 并可推广到
x
lim x
x
1.
定理2:单调有界数列必有极限。 第一个重要极限
sin x x 1
lim
x 0
( 1 )当 x ( 0 ,
( 2 ) lim sin x x
2
) 时 , 有 sin x x tan x ;
0 0 型极限才有 lim sin x x 1 , 而 lim
x x0
lim g ( x ) lim h ( x ) A , 则 lim f ( x ) A .
x x0 x x0
例10、求下列极限。
( 1 ) lim (
n
1 n 1
2
1 n 2
2
1 n n
2
);
( 2 ) lim
n
n
n.
解题关键:适当放缩,使较小和较大 数列的极限存在且相等。
例12、求下列极限。
( 1 ) lim ( 1
x
3 x
2
) ;
3x
x
( 2 ) lim x 1 x ;
x1
( 3 ) lim (
x
2x 1 2x 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习要纵横结合
,
着眼于提高数学素养。 14
第一讲
高等数学中的
分析问题
和
解决问题
方法
15
一. 数学模型及数学建模方法 ( P511 , 第一节 )
数学模型
客观实际问题内在规律性的数学
结构. 具有形式化、符号化、简洁化的特点.
是一种高度抽象的模型. 有狭义和广义两种解释 . 数学建模方法
• 实验归纳法 • 理论分析法 ( P514 ) 物理模型 数学模型
注意问题:认真听课,扼要记录, 多做题目,总结规律。
6
一提到数学,很多人首先想到的是复杂的公式、 大量的计算、漫天的数字数据、还有百思不得其解数 学题。这与中国的高中教育偏重于对于知识的灌输, 而非对于知识的掌握密切相关。基于应试的压力,数学 教育尤其容易演变为固定类型的题海战术,甚至成为 某种意义上的死记硬背,而非激发学生的创造性思维, 这在根本上就是与数学教育相背道而驰的。这样使学生 对数学产生畏惧、反弹心理。.
才能尝到成功的滋味;
3
哈佛图书馆的训诫
谁也不能随随便便成功, 它来自彻底的自我管理和毅力; 狗一样地学习, 绅士一样地玩; 今天不走,明天要跑; 教育程度代表收入; 即使现在,对手也不停地翻动书页;
没有艰辛,便无所获。
4
科学家语录
培根说:历史使人聪明,诗歌使人机智, 数学使人精细。
马克思:一门科学只有当它达到了能够成功地运用 数学,才算真正发展了。
利于得到某种确定感和安全感。不是为了考高分念书, 而是为了不逃避痛苦与讨厌的事。生活本质上活脱脱 就是一个战场,身处战场绝对不是一安全的事, 8
高等数学方法
(上)
科学方法是打开科学殿堂大门的钥匙 , 是由必然王国通向自由王国的桥梁。
数学方法是数学的灵魂
9
参考书
张晓宁、李安昌:
高等数学方法
中国矿业大学出版社,2002.
高等数学方法
第一讲
主讲教师: 王升瑞
1
惜时如金
唯有奋斗 最风流!
2
哈佛图书馆的训诫
此刻打盹,你将做梦,此刻学习,你将圆梦; 学习时的痛苦是暂时的,未学到的痛苦是终身的; 学习这件事,不是缺乏时间,而是缺乏努力; 学习不是人生的全部,但是人生的一部分; 学习也无法征服,还能做什么呢? 请享受无法回避的痛苦; 只有比别人更早,更勤奋的努力,
7
其实数学背后的思想,数学的证明方法才是数学的 精髓。数学学习关注的是逻辑推演能力。数学是一种 表述简洁、清晰、歧义较少的逻辑体系。在数学中, 不仅各种数字、函数, 就连加、减、乘、除,大于、 小于、等于,以及指数、导数、积分等符号本身,也 都是约定俗成、极少歧义的概念。而几何方法,更是能 用清晰、直观的坐标或图形表达比较复杂的逻辑关系。 学习的目的是得到某种确定感和安全感,并且上学有
伽利略认为:宇宙像一本用数学语言写成的大书, 如果不掌握数学的语言,就像在黑暗的迷宫里游荡, 什么也看不清。
华罗庚:数学是最宝贵的研究精神之一。 勤能补拙是良训,一分辛苦一分才。
5
华罗庚 (1910 - 1985)
“聪明在于勤奋, 天才在于积累” “由薄到厚 ,由厚到薄” “学而优则用, 学而优则创”
B B A
且对任意 有 f()g()0,
C
A
证明存在
0(0,
2
), 使
f(0)g(0)0.
C
D
D
19
不妨设 g(0)0, f(0)0,且对任意 有 f()g()0,
证明存在
0(0,
2
),使
f(0)g(0)0.
证明: 设
h()f()g()C[0,
2
],
又
h(0)0,
h(
2
)0,(转
2
后,对角线互换)。
1. 科学方法的重要性
科学
是什么 , 为什么:
反映自然、社会、思维的客观规律的分科的
知识体系。
技术
做什么 , 怎么做:
进行物资资料生产所凭借的方法和能力。
科学方法
桥梁与钥匙。
12
2. 数学方法的含义
数学
思维的体操
(思路)
数学方法
思维方法
科学的语言
(表达)
对数学规律的认识
解题方法
生活的需要
(应用)
(是数学的灵魂)
由连续函数零点定理可知
,
存在
0(0,
2
),
使 h(0) 0 即 f(0)g(0)
又知 f(0)g(0)0,所以 f(0)g(0)0
思考: 对长方形板凳的稳定问题如何考虑?
提示:相邻两脚之和,并旋转1800。
20
二 .几种常用的分析问题的方法 (P444-455)
1. 简化方法 2. 直观分析法
3. 逆向分析法 4. 类比法
求解和分析
许多物理中的概念都要借助于高等数学中的
数学结构才能说的清楚。
16
例如 , 为什么用 " N"及 " "语言定义极限 ?
• 用圆内接正多边形面积逼近圆面积A .
圆内接正n边形的面积为
An
nr2sincos
nn
o r
找出
(n3,4,5, ) n
0,
精度要求
N (正整数)
,
当 nN时,
边数足够多
13
二. “高等数学方法”的结构与学习方法
(参考前言第二、三段) 第一部分 (第一至第七章)
每节包含: 方法指导, 实例分析, 相关问题
第二部分 (第八至第十一章) 包括综述和提高
(从古典数学向近代数学靠拢 ) 学习方法:
1. 掌握数学内容和数学方法相结合;
2. 重视分析问题和解决问题的方法;
3.
10
目录
第一讲 高等数学中的分析问题和解决问题 方法
第二讲 研究函数与四讲 导数应用的方法 第五讲 积分学的概念、性质和不定积分的
计算法 第六讲 定积分的计算、证明和解应用问题
的方法 第七讲 试题类型及解题方法分析
11
前言
一. 为什么要学“高等数学方法 (参考前言第一段)
要使
f(r)A0
记作
lim f(r)lim r2
r r0
r r0
r02
18
再如 , 椅子稳定问题 (P515~P516)
假设: 四条腿一样长 ; 地面为连续曲面 .
建模:
设 A , C 两脚与地面的距离之和为 g()C[0,2]
B , D 两脚与地面的距离之和为 f()C[0,2]
不妨设 g(0)0, f(0)0,
有
AnA ,
可无限逼近
记作 limAn A. 利用极限知识可求出 :
n
A limr n
2
sin
n
n
cos
r2
n
17
• 测量圆面积
A r2
直接观测量为r 间接观测量为A.
寻找精度 0,
半径真值为 r0 测量圆半径得 r 让 r r0
面积真值为 A 0 计算圆面积为 f (r) r2
任给精度 0,
