高等数学上册习题讲解PPT课件
合集下载
《高等数学》第四版课件-学习指导与习题解析

了解常见无穷级数的性质与求和方法,
如几何级数与幂级数。
3
级数应用
探索级数在实际问题中的应用,如泰勒 级数展开与函数逼近。
常微分方程
一阶常微分方程
研究一阶常微分方程的解法与存在唯一性,探索微 分方程在实际问题中的应用。
二阶常系数齐次线性微分方程
学习二阶常系数齐次线性微分方程的解法,包括特 征方程与特解构造。
微积分学基本定理
不定积分 定积分 牛顿-莱布尼茨公式
计算函数的不定积分,包括常用的积分表达式。
介绍定积分的概念与性质,以及计算定积分的方 法。
理解牛顿-莱布尼茨公式的意义与应用,掌握计算 不定积分与定积分的关系。
无穷级数
1
级数收敛性
学习级数的概念与收敛性判定方法,如
常见级数
2
比较判别法与根值判别法。
《高等数学》第四版课件 -学习指导与习题解析
这份课件旨在通过学习指导与习题解析帮助读者理解和掌握《高等数学》第 四版的重要内容。从数学分析基础到线性变换,让我们一起探索数学的奥妙!
数学分析基础
1
实数与函数
介绍实数与函数的概念,探索数轴与集合等基础知识。
2
极限
学习Epsilon-Delta定义与极限的计算方法与性质。
2 基与维数
了解线性空间的基与维数, 及其在矩阵和向量空间中的 应用。
3 线性变换
研究线性变换的定义与性质,包括线性变换的判断与矩阵表示。
矩阵与行列式
矩阵运算
掌握矩阵的加法、乘法及其性质,了解矩阵的转置 与对角化。
行列式
学习行列式的计算方法,如拉普拉斯展开和性质运 算。
向量分析与曲面积分
1
向量的概念与运算
高等数学上册第六章课件.ppt

(2 , 2)
4
AdA ( y 4 12 y 2 ) d y
2
18
(8 , 4)
x
第二节 定积分在几何中的应用
例
求由摆线
的一拱与 x 轴所围平面图形的面积 .
解
2π
dAA
ydx 0 a (1 cos t ) a (1 cos t ) d t
a
2
4a
X -型绕x轴旋转所围成的立体的体积:
y 2 ( x)
b
b
Vx π ( x)dx π ( x)dx
a
b
2
2
a
2
1
2
2
y 1 ( x)
π [2 ( x) 1 ( x)]dx
a
a
bx
Y-型绕y轴旋转所围成的立体的体积:
d
Vy π [ g g ]dy
2
5 3 1 π
32π a sin u du 32π a 5π 2 a3
0
6 4 2 2
3
2
6
3
第二节 定积分在几何中的应用
y
x x2 ( y )
2a
绕 y 轴旋转而成的体积为
π
π a 2 (t sin t ) 2 a sin t d t
2π
o
πa
πa
4 2 2
2
所围图形的
(利用对称性)
d
o
2a x
第二节 定积分在几何中的应用
心形线(外摆线的一种)
2
2
2
x y ax a x y
2
即 r a(1 cos )
4
AdA ( y 4 12 y 2 ) d y
2
18
(8 , 4)
x
第二节 定积分在几何中的应用
例
求由摆线
的一拱与 x 轴所围平面图形的面积 .
解
2π
dAA
ydx 0 a (1 cos t ) a (1 cos t ) d t
a
2
4a
X -型绕x轴旋转所围成的立体的体积:
y 2 ( x)
b
b
Vx π ( x)dx π ( x)dx
a
b
2
2
a
2
1
2
2
y 1 ( x)
π [2 ( x) 1 ( x)]dx
a
a
bx
Y-型绕y轴旋转所围成的立体的体积:
d
Vy π [ g g ]dy
2
5 3 1 π
32π a sin u du 32π a 5π 2 a3
0
6 4 2 2
3
2
6
3
第二节 定积分在几何中的应用
y
x x2 ( y )
2a
绕 y 轴旋转而成的体积为
π
π a 2 (t sin t ) 2 a sin t d t
2π
o
πa
πa
4 2 2
2
所围图形的
(利用对称性)
d
o
2a x
第二节 定积分在几何中的应用
心形线(外摆线的一种)
2
2
2
x y ax a x y
2
即 r a(1 cos )
高等数学 (上册) -01-PPT课件

3. xlim 左右极限存在并相等 x ƒ(x) 的存在性 当x<xo时,x→ x 0 ,极限 xlim ƒ(x)= -ƒ(xo-0) 左极限 x
0
0
当x>xo时,x→ x 0 ,极限 xlim ƒ(x)= -ƒ(xo+0) 左极限 x
0
应用-----主要用于分段函数 分段点处求极限
x x0 2
证明: 对 >0要使|sinx-sinxo |=2|sin 2|sin
x x0 2
cos
x x0 |<ε 2
x x0 cos 2
|≤2|sin
x x0 2
|
当 x 很 小 时,|sinx| < |x| 2|sin
x x0 2
|<|2
x x0 2
| = |x-x0|<ε
(1)、ε-x定义:
if 对 >0, x>0,st 当 |x|>x 时 , 有 |ƒ(x)-a|<ε so 称 a 为 ƒ(x) 当 x→∞时的极限 先有ε,再找x
(2)、ε-定义 if对 >0, st当0<|x-xo|< 时,有|ƒ(x)-a|<ε成立,则 limƒ(x)=a 称a是ƒ(x)当x→xo 的极限,记为 x x
iii) 极限过程可以变,但必须是型,且x一模一样 1/(x-1) =1 如:1) lim x 1 [1+(x-1)] 1 .2 x 1 1 2 x lim(1 ) = e1/2 2) lim (1+ ) = x 2 x x 2x 3) lim (1+ x 4) lim ) x = e2 x (1+
高等数学上册第七章课件.ppt
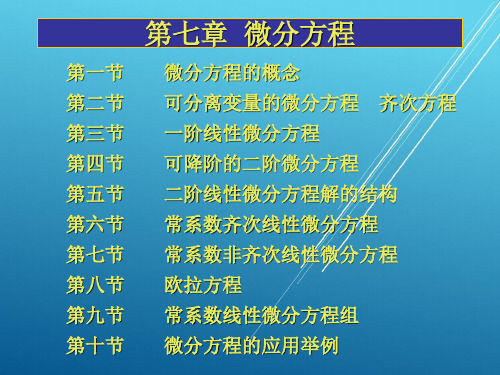
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
高等数学上2_课件1.ppt

FFn1
1, F2 Fn1
1 Fn2
,
n2
写出来为
1,1,2,3,5,8,13,….
例 2.3
bn
Fn Fn1
1, 1 , 2 , 3 , 5 , 8 , 13 , . 2 3 5 8 13 21
bn 是按“大—小—大—小…”依次交错排列的,这
样的数列称振荡数列.显然 bn 是有界的,非单调的.
2
等来代替.
2.1.2 数列极限的概念
●关于数列极限的 N 定义,通过以上几个例子,读 者已有初步认识,再作以下几点注释以便加强.
(2) N 的相应性 一般地, N 随 的变小而变大,
因此有时为强调 N 是依赖 的,也把 N 写作 N ( ) .但这并
不意味 N 是由 唯一确定的.比如对给定的 ,当 N 100 时, n N 便有 xn a 成立,则取 N 101或更大时, n N 时必有 xn a .求 N 的目的在于证实 N 的存在
的项的值随 n 增大而增大,且无限增大. ●若当 n 无限增大时, xn 无限趋向于常数 a ,则说,
当 n 趋于无穷大时,xn 以 a 为极限.
记作
lim
n
xn
a
或
x
a
, (n
)
2.1.2 数列极限的概念
●做定量分析
1n
对例 2.4 中 xn f (n) 1 n
n N 随 n 无限增
大而无限接近 1 的过程做定量分析:
n
它是一个有界的
xn
≤
3
2 振荡数列,图像如图
2.2.
我们会发现,随着 n 的无限增大, xn 以 1 为平衡位置振
荡,而振幅越来越小,并且可以任意的小,即 xn 无限接
高等数学_及其教学软件.上册(上海交通大学,集美大学编)PPT模板

第二章函数极 限与连续
2.1极限
2.1.1数列 的极限
01
2.1.2函数
习题2.1
06
的极限
02
2 . 1 . 5 极 05 限的运算
法则
04
2.1.4极限 的性质
2.1.3函
03
数的左极 限与右极
限
第二章函数极限与连续
2.2两个重要极限
习题2.2
第二章函数 极限与连续
2.3无穷小量与无穷大 量
习题3.5
第
和 导 数 的 应 用
四 章 微 分 中 值 定
理
理第 和四 导章 数微 的分 应中 用值
定
0 1
4.1微分中值 定理
0 4
4.4极值与优 化
0 2
4.2洛必达法 则
0 5
4.5不等式的 证明
0 3
4.3函数的单 调性与凸性
0 6
4.6变化率问 题
第四章微分中值定理和导数的应用
必达法则
第四章微分中值定理和导数的应用
4.3函数的单调性与凸性
4.3.1函数单调性及 其判别法
4.3.2函数的凸性与 曲线的拐点
习题4.3
第四章微分中值定理和导数的应用
4.4极值与优化
4.4.1函数的极 值
4.4.3最优化问 题
4.4.2函数的最 大、最小值
习题4.4
第四章微分中值定理和导数的应用
4.7导数在经济学中的应用 4.8演示与实验
第四章微分中值定理和导数的应用
4.1微分中值定理
4.1.1罗尔中值定理
4.1.3柯西中值定理
4.1.2拉格朗日中值 定理
习题4.1
高等数学上2_课件2.ppt

达标后的函数值:
f (x) A
2.2.2 x趋于有限值x0时函数的极限
●至此,我们用 N ”、“ X ”、“ ” 的语言定 义了七种极限, 下面将列表类比对照.
极限形式: 接近程度指标:
lim f (x) A
x
实现时刻:
X
实现时刻后的自变量: x X
达标后的函数值:
f (x) A
定义 2.2
*在定义 2.2 中, 将“ f (x) 在 b, 上有定义”换作 “ f (x) 在 , a上有定义;将“ x X ”换作“ x X ”
lim
x
f
(x)
A或
f
(x)
A(x
)
.
2.2.1 x趋于无穷大时函数的极限
定义 2.3 设 f (x) 在 , a b, (a ≤b) 上有定义,A
推 论 若 在 x0 的 某 去 心 邻 域 内 f (x) ≥ 0 ( 或
f
(
x)
≤
0
)且
lim
xx0
f
(x)
A ,则 A≥0 ( A≤0 ).
2.2.3 函数极限的性质
● 在 2.2.1,2.2.2 中我们共列举了六种类型的极限:
(1)
lim
x
f
(x) ;
(2)
lim
x
f
(x) ;
(3)
lim
2.2.1 x趋于无穷大时函数的极限
自变量 x 趋向于无穷大有下面三种方式: x ,表示 x 沿 x 轴无限向右推进,趋于正无穷大; x ,表示 x 沿 x 轴无限向左推进,趋于负无穷大; x ,表示 x 沿 x 轴无限向任何一方推进,即 x 趋于 .
《高等数学第一章》PPT课件

思考题解答
f ( x)在x0 连续,
lim x x0
f (x)
f ( x0 )
且 0 f ( x) f ( x0 ) f ( x) f ( x0 )
lim x x0
f (x)
f ( x0 )
lim
x x0
f
2(
x)
lim
x x0
f
(
x
)
断点;在 x 2 是第_____类间断点 .
2、指出 y x 2 x 在 x 0 是第________类间 x ( x 2 1)
断点;在 x 1 是第______类间断点;在 x 1
是第_____类间断点 .
x, x 1
二、研究函数 f ( x)
的连续性,并画出函数
函数 f ( x)在点 x0处不连续(或间断), 并称点x0为 f ( x)的不连续点(或间断点).
1.跳跃间断点 如果 f ( x)在点 x0处左, 右极限都
存在,但f ( x0 0) f ( x0 0), 则称点 x0为函数 f ( x)的跳跃间断点.
例4
讨论函数
f
(x)
x, 1 x,
1.函数在一点连续必须满足的三个条件; 2.区间上的连续函数; 3.间断点的分类与判别;
间断点
第一类间断点:可去型,跳跃型. 第二类间断点:无穷型,振荡型.
(见下图)
第y 一
可去型
类
间
断
点
o x0
x
y
第 二 类 间 断o 点
x0
x
无穷型
y 跳跃型
o
x0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f(0)lim ln(bx2)lnb
x 0
a
1cosx~ 1x2 2
1 ln b
2
高等数学期末辅导
x1 x -1
例2 函数f (x) a
x-1
2xb x-1
在x1处连,则 续a=( 0 ), b=2
解:计算函数值 f(1)? a,计极限值
lim f (x) ?,此时,要考察左右极限,
x1
右极限 f( 1 0 )lim f(x) ? 0 x 1
limcosx x2 sinx
例3. 求 lim xx.
x0
00 型
解:
lim x x limexlnx
x0
x0
e0
1
高等数学期末辅导
例4. 求 xl im0txa2nsxinxx.
0型 0
解: 注意到 ~
原式 xl im0tanxx3x xl im0se3c2xx21
lim
x0
tan2 x 3x2
高等数学上 复习
高等数学期末辅导
考试形式:闭卷 考试时间:2小时
题目类型:选择,填空,计算, 证明,综合
考试注意事项:
签名,时间控制,先易后难, 答题规范。
高等数学期末辅导
一、极限计算
• 主要方法:两个重要极限,无穷小替换, 罗必塔法则,其他方法(有理化、定积分定义 等),特别注意各种方法的结合。如无穷小+罗 必塔,罗必塔+积分上限函数等。
cotx
lim
x0
(1 2x )cotx 1x
1
ln(112xx)
~
2 1
x x
高等数学xl期i m末0(cs辅oinsxx导 12xx) e 2
机动 目录 上页 下页 返回 结束
常用等价无穷小:
sin x~x ;
~
~ arcsinx~x ;
e x 1~ x ;
~
例1. 求 xl im 0tanxx3sinx.
例1 设f xln1x3x x0
A x 0
在x=0处连续,则A=( ) 解:计算函数值f(0)=A, 计极限值 limf (x)3
x0
所以A=3
高等数学期末辅导
例1. 设函数
在 x = 0 连续 , 则 a = 2 , b = e .
提示:
f(0)xl i0m a(1xc2 ox)s
a 2
1coxs~
1 2
x
2
;
~
(1x) 1~x;
解: 原式
原式 xl im 0xx3x
lim
x0
x
1 2
x2
x3
高等数学期末辅导
1
例2. 求 lim(1x2)3 1. x0 cosx1
解:
高等数学期末辅导
分子或分母有理化
例 计算
lim x-3 x3 5 2x2 7
解: lim
x3 5
x-3 2x2 7
f(x0)x l ixm 0 fxx l ix0m fxf(x0)0lixm0y 0
(2) 函数f (x)在点x0处极限存在的充要是条件
函数 f(x)在点 x0处的左右极限存 等在 且
x l x 0 i f x m A f x 0 0 A 且 f x 0 0 A
高等数学期末辅导
x -3 5 2 x 2 7 lim
x 35 2 x 2 75 2 x 2 7
10lxi m 318x-23x2
5lx i3 m 9x-x32
5 6
高等数学期末辅导
罗必塔法则
2) f(x)与 F(x)在 (a)内可 , 导
3)
lim f (x) xa F(x)
存在 (或为
)
limf(x)limf(x) xaF(x) xaF(x)
左极限 f( 1 0 ) lifm (x ) ? 2 b x 1
由连续的定义,可得 a=( 0 ), b=2
高等数学期末辅导
三、导数与微分
26x1
x l im 13x253x25 3x5 e4
高等数学期末辅导
例5: 求下列极限:
(1 )li( m sx i n 1 six n )
x
(2) xl im1s1inx2x
(3)xl im 011 xxcoxt
提示: (1 )six n 1 six n
2 six n 1xcox s1x
2
2
2sin 1 coxs 1x
2 ( x 1x)
2
无穷小
有界
高等数学期末辅导
(2) lim 1 x 2
x1 sin x
令 t x1
lim
t 0
t(t2) sin (t 1)
lim
t 0
t (t 2 ) sin t
lim
t 0
t (t 2 ) t
2
(3)
lim 1 x
x 0 1 x
高等数学期末辅导
例1. 求
0型 0
解: 原式 lim 3x2 3 x1 3x22x1
lim 6x 3 x16x 2 2
注意: 不是未定式不能用洛必达法则 !
lim 6x
lim 6 1
x1 6x 2
x1 6
高等数学期末辅导
例2.
求
lim (sexctaxn).
x 2
型
解: 原式 lim( 1 sinx) lim1sinx x2 coxs coxs x2 cosx
0
0
解: 原式 lim eco2sx(sinx) 1
x0
2x
2e
例7. 确定常数 a , b , c 的值, 使
解:
b0.
原式 =
c ≠0 , 故 a1. 又由
~
,
得
c
1 2
.
高等数学期末辅导
说明 目录 上页 下页 返回 结束
二、连续性(分段函数情形)
(1) 函f数 (x)在x点 0处连 续
函数 f(x)在点 x0处的函数值等 处于 的在 极 该 限
se2xc1ta2n x
1 3
高等数学期末辅导
1
例5.
6
分析: 原式 xl i0m coxxs(sxi2nsxixn) sin x ~ x
xl im0xxs3 ixn
limcosx1
x0
xl im013cxo2 sx
lim
x0
1 2
x
2
3x2
1 6
1cox~s12 x 2
高等数学期末辅导
例6. 求
或 高等数学期末辅导
例1
limxsin1
sin1 lim 5x
1
x
5x n 5 1 5
5x
注意与
limxsin1 0 区别
x0
x
例2. 求
解: 令 tarcsxi,n则 xsitn,因此
原式 lim t t0 sint
sin t 1
t
高等数学期末辅导
例3
lim 13nlim 13n3n3n n n n n
ln im1
n
33
n
3
e3
注意“凑”的技巧,想法凑成公式需 要的形式。
高等数学期末辅导
例4
计算
lim
3x
7
6x1
x 3x 5
解:li m 3 x 7 6 x 1li m 1
2
6 x 1
x 3 x 5
x 3 x 5
lim 1
2
3x5 2 6x1
2 3x5
e4
x 3x5
