2017-2018学年北京市第八中学初三上学期期中数学试卷(无答案)

合集下载

初中数学微专题讲义专题1.6 例谈因式分解的方法与技巧

【专题综述】因式分解是初中代数中一种重要的恒等变形，是处理数学问题重要的手段和工具，也是中考和数学竞赛试题中比较常见的题型。

对于特殊的因式分解，除了掌握提公因式法、公式法、分组分解法、十字相乘法等基本方法外，还应根据多项式的具体结构特征，灵活选用一些特殊的方法和技巧。

这样不仅可使问题化难为易，化繁为简，复杂问题迎刃而解，而且有助于培养探索求新的学习习惯，提高数学思维能力。

【方法解读】一、巧拆项：在某些多项式的因式分解过程中，若将多项式的某一项（或几项）适当拆成几项的代数和，再用基本方法分解，会使问题化难为易，迎刃而解。

例1：因式分解32422+++-b a b a 解：原式＝22423a b a b -+++224241a b a b =-+++-22(44)(21)a ab b =++--+22(2)(1)a b =+--(1)(3)a b a b =++-+【解读】根据多项式的特点，把3拆成4+（-1），即可利用完全平方公式、平方差公式进行因式分解。

【举一反三】因式分解：611623+++x x x 【答案】(1)(2)(3)x x x +++二、巧添项：在某些多项式的因式分解过程中，若在所给多项式中加、减相同的项，再用基本方法分解，也可谓方法独特，新颖别致。

例2：因式分解444yx +解：444x y +422422(44)4x x y y x y =++-2222(2)(2)x y xy =+-=2222(22)(22)x xy y x xy y ++-+学&科网【解读】根据多项式的特点,在444x y +中添上22224,4x y x y -两项，，即可利用完全平方公式、平方差公式进行因式分解。

【举一反三】因式分解4323+-x x 【答案】2(1)(2)x x +-三、巧换元：在某些多项式的因式分解过程中，通过换元，可把形式复杂的多项式变形为形式简单易于分解的多项式，会使问题化繁为简，迅捷获解。

北京市中国人民大学附属中学2024-2025学年上学期八年级期中数学试卷(无答案)

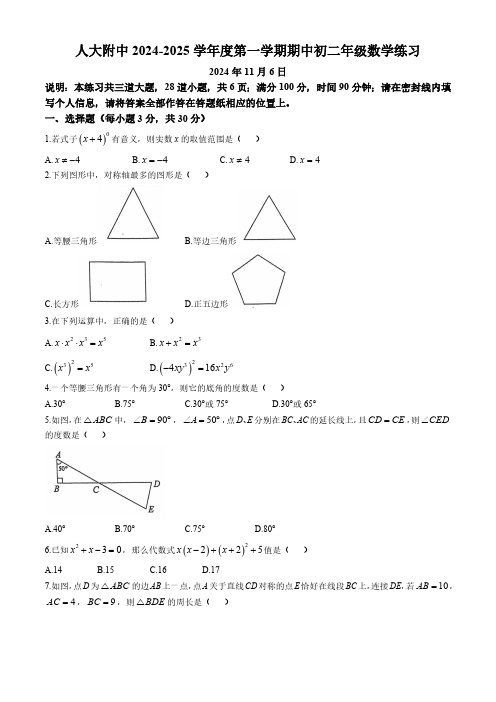
人大附中2024-2025学年度第一学期期中初二年级数学练习2024年11月6日说明：本练习共三道大题，28道小题，共6页；满分100分，时间90分钟；请在密封线内填写个人信息，请将答案全部作答在答题纸相应的位置上。

一、选择题（每小题3分，共30分）1.若式子有意义，则实数x 的取值范围是（）A. B. C. D.2.下列图形中，对称轴最多的图形是（）A.等腰三角形B.等边三角形C.长方形D.正五边形3.在下列运算中，正确的是（）A. B.C. D.4.一个等腰三角形有一个角为30°，则它的底角的度数是（）A.30°B.75°C.30°或75°D.30°或65°5.如图，在中，，，点D 、E 分别在BC 、AC 的延长线上，且，则的度数是（）A.40°B.70°C.75°D.80°6.已知，那么代数式值是（）A.14B.15C.16D.177.如图，点D 为的边AB 上一点，点A 关于直线CD 对称的点E 恰好在线段BC 上，连接DE ，若，，，则的周长是（）()04x +4x ≠-4x =-4x ≠4x =235x x x x⋅⋅=23x x x +=()235x x =()2326416xy x y -=ABC △90B ∠=︒50A ∠=︒CD CE =CED∠230x x +-=()()2225x x x -+++ABC △10AB =4AC =9BC =BDE △A.13B.15C.17D.不能确定8.如右图，在边长为a 的正方形中，剪去一个边长为b 的小正方形，将余下部分剪开后拼成一个梯形，根据两个图形阴影面积的关系，可以得到一个关于a ，b 的恒等式为（）A. B.C. D.9.如图，AD 是的角平分线，且，，那么的度数是（）A.26°B.27°C.28°D.30°10.已知实数a ，b满足，则的值是（）A.65 B.105 C.115 D.2025二、填空题（每空2分，共18分）11.在平面直角坐标系中，点关于x 轴对称的点的坐标为________.12.已知等腰三角形有两条边的长度分别为5，8，则该三角形的周长为________.13.计算：________.14.如图，BD 是的角平分线，点D 是边AC 一点，且满足，若，，则________.()a b >()2222a b a ab b -=-+()2222a b a ab b +=++()()22a b a b a b -=+-()2a ab a a b +=+ABC △AB BD AC +=40BAC B ∠=∠+︒C ∠()()21222a b a b -+=-2234101220241a b a b ++-+()2,1A 20232024122⎛⎫⨯-= ⎪⎝⎭ABC △BE ED =40A ∠=︒110C ∠=︒EDB ∠=15.定义新运算：，则方程的解为_________.16.如图，，点P 在的平分线上，于点C ，点D 在边OB 上，且.则线段OC 的长度为_________.17.如图，在平面直角坐标系中，，，为等腰直角三角形，且，则点C 的坐标为________.18.若，，则的值为________.19.如图，在平面直角坐标系中，直线经过原点和一三象限，点A 为x 轴正半轴上一点，点B 位于第一象限内且在直线上，，，过点B 作直线a 垂直于x 轴，点C ，D 在直线a 上（点D 在点C 上方），且，若线段CD 关于直线对称的线段EF 与坐标轴有交点，则点C 的纵坐标m 的取值范围是________.*a b ab b =-()21*8x x +=60AOB ∠=︒AOB ∠PC OA ⊥8OD DP ==()1,1A -()2,2B ABC △90B ∠=︒7x y -=2y z +=-()2x yz x z y -+-l l 2OB =30AOB ∠=︒1CD =l三、解答题（20-21题每小题4分，22-23题每题4分，24题5分，25题4分，26题5分，27-28题每题7分，共52分）20.计算：（1）；（2）.21.分解因式：（1）；（2）.22.先化简，再求值：，其中，.23.如图，在中，D 为BC 的中点，，，垂足分别为E ，F ，且，连接AD ，求证：AD 是的角平分线.24.小兵遇到一个作图问题：如图，在中，，如何用尺规作图把分成三个等腰三角形.下面是小兵设计的尺规作图过程.作法：①以点A 为圆心，AB 长为半径作弧，交线段BC 于另一点D ；②作线段CD 的垂直平分线，直线交线段AC 于点E ；③连接AD ，DE ，则，，即为所求的等腰三角形.根据小兵设计的尺规作图过程，（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明.证明：由作图可知，①()()53212a a a a -+-÷()()()2332x y x y x y +-++22363ax axy ay -+()()2244a x b x -+-()()()()22223x x x x x y x y y ⎡⎤+--+-+÷⎣⎦3x =-2y =ABC △DE AB ⊥DF AC ⊥BE CF =ABC △ABC △3B C ∠=∠ABC △l l ABD △ADE △CDE △AB AD =∴________.∵，∴.∵直线为线段CD 的垂直平分线，∴（__________）（填推理的依据）.②∴.∴∵，∴.∴.∴（__________）（填推理的依据）.③由①②③得：，，均为等腰三角形.25.已知实数a 、b 满足，，（1）求代数式值；（2）求代数式的值.26.如图，在中，直线MN 是边AB 的垂直平分线，点D 是直线MN 上一点，连接AD ，CD ，满足，求证：CD 为的外角的角平分线.27.对于一个正整数n ，若存在正整数k ，使得n 能表示为k 和的平方差，那么称这个正整数n 为k 系平方差数.例如：，则20为6系平方差数.（1）直接写出10系平方差数.（2）已知为k 系平方差数，求M 的值.（3）已知a ，b 为正整数，，且为k 系平方差数.①直接写出a 与b 之间的数量关系；②若是m 系平方差数，请判断是否为平方差数.若是请直接写出是_______系平方差数（用含m 的代数式来表示）；若不是请写出理由；28.在中，，，D 点是边AB 上一点，E 为边AC 上一点，连接CD ，DE .（1）如图1，，点D 为AB 中点，，，直接写出EC 的长，（2）如图2，，，，连接BE 交CD 于点F ，延长FE 至P ，使得B ∠=∠3B C ∠=∠3ADB C ∠=∠l CE DE =C CDE ∠=∠2AED C CDE C∠=∠+∠=∠3ADB C CAD C ∠=∠+∠=∠2CAD ADB C C ∠=∠-∠=∠AED CAD ∠=∠AD DE =ABD △ADE △CDE △6a b +=4ab =22a b +()23a b a b ab -+ABC △2ACB ADM ∠=∠ABC △ACP ∠2k -222064=-()()()23234126M k k k k =+---+a b >()()222336a b b ab +-+-11a b ++20242022a b -ABC △AB AC =BAC α∠=60α=︒8AB =DE AC ⊥60α=︒3AB BD =DE AC ⊥，连接AP ，①依题意补全图形；②用等式表示线段AP ，BP ，CF 之间的数量关系，并证明，（3）如图3，点E 为定点，，连接BE ，点M 为线段BE 上的一个动点，且满足，当取得最小值时，直接写出的值（用和表示）.PF CF =CBE β∠=BM AD =AM CD +BDC ∠αβ。

20172018北京八中初二上数学期初中中考试卷试题.docx

2017-2018 学年度第一学期期中练习题年级：初二科目：数学班级： __________姓名：________考 1．本试卷共 6 页，共四道大题， 28 个小题，满分 120 分。

考试时间 100 分钟。

生 2．在试卷和答题纸上准确填写班级、姓名、学号须3．答案一律填写在答题纸上，在试卷上作答无效。

知4．考试结束，将试卷和答题纸一并交回。

一、选择题 ( 每小题 3 分，共 30 分 )1．计算 3 2 正确的是 ()1 1 1 B1 A ．D9B ．C ．D ．6962．下列四个图案是轴对称图形的有(OCA)B'D'O' C' A'A ．1 个B ． 2 个C ． 3 个第 3 题图D ． 4 个3．请仔细观察用直尺和圆规作一个角∠ A'O'B'等于已知角∠ AOB 的示意图，根据图形全等的知识，说明画出∠ A'O'B'＝∠ AOB 的依据是 ()A ．边角边，全等三角形对应角相等B ．角边角，全等三角形对应角相等C ．边边边，全等三角形对应角相等D ．斜边直角边，全等三角形对应角相等 4．下列各式中，从左到右的变形是因式分解的是()AA ． (x 2 y)(x 2y) x 2 4y 2B ． x 2 y xy 2 1 xy( x y) 1C ． a 2 - 4ab+ 4b 2= (a - 2b)2D ． ax+ay+a=a (x+y )5 ．根据下列已知条件，能画出唯一的△ABC 的是 ()B DC第 6 题图A ．∠ A ＝ 60°，∠B ＝ 45°， AB ＝4 B ． AB ＝ 4， BC ＝3，∠ A ＝ 30°C ．AB ＝3， BC ＝ 4，CA ＝8D ．∠ C ＝ 90°， AB ＝ 66．如图，在 △ ABC 中， D 是 BC 边上一点，且 AB ＝ AD ＝ DC ， ∠ C ＝ 35°，则∠ BAD 为 ( )A. 25 °B. 35 °C ． 40° D. 50 °7．如果把分式x 2 y中的 x 和 y 都扩大 10 倍，那么分式的值 ()x yA.扩大 10倍B.缩小 10 倍C.是原来的2D. 3不变8．如图，吴伯伯家有一块等边三角形的空地ABC，已知点 E、 F 分别是边 AB、 AC 的中点，量得 EF ＝ 5 米，他想把四边形 BCFE 用篱笆围成一圈放养小鸡，则需用篱笆的长是 () A． 15 米B． 20 米C． 25 米D ． 30 米9．已知 : 如图，△ ABC 中，给出下列四个命题中，真命题的个数是()①若 AB＝AC ，AD⊥ BC，则∠ 1＝∠ 2；②若 AB＝ AC，∠ 1＝∠ 2，则 BD＝ DC；③若 AB＝ AC，BD ＝ DC，则 AD ⊥BC；④若 AB＝ AC， AD ⊥ BC， BE⊥ AC，则∠ 1＝∠ 3；A． 1 个B． 2 个C． 3 个D． 4 个10．如图，点 A，C， D， E 在 Rt △ MON 的边上，∠ MON =90 °， AE⊥ AB 且 AE=AB，BC⊥ CD 且 BC=CD ，BH ⊥ ON 于点 H ， DF ⊥ON 于点 F， OM =12， OE=6 ， BH=3， DF =4，FN =8，图中阴影部分的面积为 ()A． 30B． 50C． 66D ． 80MEDBO AN HC F第 8 题图第9题图第10题图二、填空题 (每空 2 分，共 20 分 )11．实验表明，人体内某种细胞的形状可近似地看作球体，它的直径约为数字 0. 000156 用科学记数法表示为____________cm．12．（ 1）分式x 1有意义的条件是__________ . 3x 22（2）分式x 1的值为 0 的条件是 ________. x 113．如图， D 在 AB 上， E 在 AC 上，且∠ B=∠ C，补充一个条件____________后，可用“ AAS”判断△ ABE≌△ ACD . 14．如图，在△ ABC 中，按以下步骤作图：0.000156cm，第13 题图①分别以 B， C 为圆心，以大于1BC 的同样长为半径画弧，2两弧相交于两点M，N；②作直线MN 交 AB 于点 D，连结 CD .请回答：若 CD =AC，∠ A=50°，则∠ ACB 的度数为 ______.MC B DA N第14 题图15．如图，在△ ABC中，∠C=90°，AD平分CAB ，BC=9cm，BD=6cm，那么点 D 到直线 AB 的距离是cm．16．如图，在Rt△ABC 中，∠ ACB = 90 ，°∠ A = 15 ，°AB 的垂直平分线与AC 交于点 D ，与AB 交于点 E，连结 BD . 若 AD ＝10cm，则 BC 的长为 _______cm.17．如图，在平面直角坐标系xOy 中，已知点A（ 6，2），yB（ 0，1） .在 x 轴上找一点P，使得 PA+PB 最小，则点 P 的坐标是 _______ ，此时△ PAB 的面积是 _______．AC D B第15 题图BEC D A第16 题图ABO x第17 题图18．如图 1，△ ABC 中，AD 是∠ BAC 的平分线，若AB=AC+CD ，那么∠ ACB 与∠ ABC 有怎样的数量关系？小明通过观察分析，形成了如下解题思路：AAB D CB D C图 1E 图2如图 2，延长 AC 到 E，使 CE=CD ，连接 DE ．由 AB=AC+CD ，可得 AE=AB ．又因为 AD 是∠ BAC 的平分线，可得△ ABD≌△ AED ，进一步分析就可以得到∠ ACB 与∠ ABC 的数量关系．（1）判定△ ABD 与△ AED 全等的依据是 ______________________________________ ；（2）∠ ACB 与∠ ABC 的数量关系为： __________________________________.三、解答题（ 19、 20 题每小题 5 分， 21 至 25 题每题 6 分，共 50 分）19．因式分解：（ 1） x 2 y 9 y．（ 2） 2mx 2 4mx2m _______________.20．化简：（ 1） (a 21( a 2)( a 1)315x2 a 2)a 2（ 2）222a2 x y 4x4 yx y21．已知 x 24 x 30 ，求代数式2 x3 2x y xy y 2 的值．22．如图，在 △ ABC 中， AD 是 △ABC 的中线，分别过点 B 、 CA作 AD 及其延长线的垂线 BE 、 CF ，垂足分别为点 E 、 F.求证： BE =CF .FBD CE23．已知： B — O — A 是一条公路，河流 OP 恰好经过桥 O 平分 ∠ AOB.（ 1）如果要从 P 处以最短路径到达公路上一点N ，且点 N 与点 M 不重合，求作路径PN 。

北京市2024~2025学年上学期九年级期中考试数学试卷(无答案)

2024-2025学年度第一学期初三年级数学期中练习学校______ 姓名______ 准考证号______注意事项1．本调研卷共8页，满分100分，时间120分钟.2．在调研卷和答题纸上准确填写学校名称、姓名和准考证号.3．调研卷答案一律填涂或书写在答题纸上，在调研卷上作答无效.4．在答题纸上，选择题用2B 铅笔作答，其他题用黑色字迹签字笔作答.第一部分选择题一、选择题（共16分，每题2分）第1~8题均有四个选项，符合题意的选项只有一个．1．一元二次方程的二次项系数、一次项系数和常数项分别是（）A ．1，3，1B ．，，C ．，，D ．，，2．下面四幅球类的平面图案中，是中心对称图形的是（）A ．B ．C ．D ．3．已知，，三点都在二次函数的图象上，则，，的大小关系为（）A ．B ．C ．D ．4．用配方法解一元二次方程时，变形后的结果正确的是（）A ．B ．C ．D ．5．将抛物线先向右平移2个单位，再向上平移3个单位后，得到的抛物线是（）A ．B ．C ．D ．6．如图，一块含角的三角尺绕点顺时针旋转到的位置，当点，，在一条直线上时，三角尺旋转的角度为（）A ．B ．C ．D ．7．如图，二次函数的图象经过，，三点，下面四2310x x +-=031-131-13-1-()12,A y -()21,B y ()34,C y 25y x =-+1y 2y 3y 123y y y <<312y y y <<231y y y <<321y y y <<241x x -=2(2)1x +=2(2)5x +=2(2)5x -=2(2)3x -=-25y x =25(2)3y x =-+25(2)3y x =++25(2)3y x =--25(2)3y x =+-30︒ABC C A B C ''△B C A 'ABC 30︒120︒60︒150︒2(0)y ax bx c a =++≠(0,54)A (20,57.9)B (40,46.2)C个结论中正确的是（）A ．抛物线开口向上B ．当时，取最大值57.9C ．该抛物线的对称轴的取值范围是D ．当时，一元二次方程总有两个不相等的实数根8．如图，已知正方形的中心为．将正方形绕点逆时针旋转得到正方形，两个正方形的公共点为，，，，，，，．对八边形给出下面四个结论：①该八边形各边长都相等；②该八边形各内角都相等；③点到该八边形各顶点的距离都相等；④点到该八边形各边的距离都相等．上述结论中，所有正确结论的序号是（）A ．①④B ．①③C ．②④D ．①②③④第二部分非选择题二、填空题（共16分，每题2分）9．请写出有一个根为的一元二次方程______．10．请写出一个开口向上，顶点坐标是的抛物线表达式______．11．已知一元二次方程的两个根为，，则______．12．已知关于的一元二次方程有两个相等的实数根，那么______．13．如图，在中，，在同一平面内，将绕点旋转到的位置，使得，则的度数为______．20x =y x h =1020h <<54m >2ax bx c m ++=ABCD O ABCD O 60︒A B C D ''''G H I J K L M N GHIJKLMN O O 2-(1,2)2620x x +-=1x 2x ()()1211x x ++=x 2610x x m ++-=m =ABC △65CAB ∠=︒ABC △A AB C ''△CC AB '∥BAB ∠'13题14．如图，是二次函数的部分图象，由图象可知关于的不等式的解集为______．14题15．如图，在正方形网格中，将绕某一点旋转某一角度得到了，则旋转中心可能是点______（填，，，之—）15题16．下表记录了二次函数中两个变量与的三组对应值：281点，在该函数图象上．若当时，，下列四个结论：①；②；③；④若记二次函数的图象为图形，存在直线与图形有两个交点，则．上述结论中，所有正确结论的序号是______．三、解答题（本题共68分，第17题8分，18-25题每题5分，第26题6分，第27、28题每题7分）17．解方程：2y ax bx c =++x 22ax bx c ++>ABC △A B C '''△1P 2P 3P 4P 2(0)y ax bx c a =++≠x y x2- ynn()11,P x y ()22,Q x y 122x x <<121y y <<0a <126x x +>25510a b c ++->()218,0y ax bx c x x a =++<<≠G y k =G 123x <<（1）；（2）．18．已知是方程的一个根，求代数式的值．19．如图，在中，点，分别在，上，，连接与对角线相交于点．（1）求证：；（2）连接，为的中点，连接．若，求的长．20．已知关于的方程（为实数，）．（1）求证：此方程总有两个实数根；（2）如果此方程的两个实数根都为负整数，求整数的值．21．如图，在平面直角坐标系中，点，，，点与点关于原点对称．（1）点的坐标是______；（2）在图中画出绕着点顺时针旋转后的；（3）在轴上是否存在点，使得的面积等于的面积．若存在，直接写出点的坐标，若不存在，说明理由.22．已知二次函数．（1）将二次函数化成的形式；（2）在平面直角坐标系中画出的图象．25x x =2680x x -+=m 2240x x +-=2(2)(3)(3)m m m +++-ABCD E F AB CD BE DF =EF AC O OE OF =CE G CE OG 2OG =AE x 2(2)20mx m x +--=m 0m ≠m xOy (2,0)A (1,3)B -(1,3)D B C C ABD △A 90︒11AB D △x E ADE △ABC △E 223y x x =+-2()y a x h k =-+223y x x =+-步骤一：列表步骤二：根据表中数值描点，画图.（3）当时，结合函数图象，直接写出的取值范围______．23．如图，用一条长60m 的绳子围成矩形，设边的长为x m.（1）边的长为______m ，矩形的面积为______（均用含的代数式表示）；（2）矩形的面积是否可以是？请给出你的结论，并用所学的方程或者函数知识说明理由．24．二次函数的图象经过点，当时，函数的最小值为.（1）求该二次函数的解析式；（2）直线与抛物线和直线的交点分别为点，点．①当时，______；②结合函数的图象，直接写出时的取值范围______．25．跳水运动是一项以高度、技术和美感为特点的水上运动项目．某跳水运动员进行10米跳台跳水训练，身体（看成一点）在空中的运动轨迹可以看作是抛物线的一部分．建立如图所示的平面直角坐标系，从起跳到落水的过程中，运动员离水面的竖直高度（单位：m ）与离起跳点的水平距离（单位：m ）近似满足函数关系．xy22x -<<y ABCD AB BC ABCD 2m x ABCD 2230m 2(0)y ax bx c a =++≠(3,0)1x =4-x m =2(0)y ax bx c a =++≠3y x =-C D 1m =-CD =4CD ≥m OB y A x 2()y a x h k =-+（1）运动员第一次跳水时水平距离与竖直高度的几组数据如下：水平距离00.250.50.75 1.5竖直高度10.0010.7511.0010.757.00①根据上述数据，运动员第一次跳水的竖直高度的最大值为______m ：②正常情况下，运动员在距水面高度5米之前必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误．若运动员在第一次跳水时在空中调整好入水姿势时，恰好距离起跳点的水平距离为1.7米，那么判断他是否会失误?请说明理由.（2）进水角度是指运动员跳入水中时身体与水平面的夹角，如图中所示．通常情况下，跳水运动员努力控制身体与水面的角度接近垂直，是减小水花的关键因素之一．在第二次跳水时，该运动员的竖直高度与水平距离近似满足函数关系式：，则此时的水花相比第一次跳水的水花______（填“变大”“不变”或“变小”）．26．在平面直角坐标系中，点，在抛物线上，抛物线的对称轴为直线（1）若，则______；（2）若，比较，的大小，并说明理由；（3）已知点也在该抛物线上，若，都有，求的取值范围．27．已知：在中，，，是内的一点，．（1）如图1，请写出与的大小关系，并证明.（2）如图2，点为的中点，连接，.用等式表示，之间的数量关系并证明．28．在平面直角坐标系中，对于图形给出如下定义：图形绕点顺时针旋转得到的图形记为图形，对于图形上任意一点，存在实数满足，则称满足条x y /x m /y mA ∠αy x 28(0.5)12y x =--+xOy (1,)M m (3,)N n 2(0)y ax bx c a =++>x t=m n =t =2t >m n ()0,P x p 010x -<<m p n <<t ABC △AC BC =90ACB ∠=︒E ABC △135AEB ∠=︒ABE ∠CAB ∠F AB EF EC EF EC xOy P P (,)()M a b x a ≠90︒Q Q (,)x y k ||||0k x a y b ---=件的的最大值为图形关于点“旋转最大值”（1）若为原点，，，线段绕点顺时针旋转的图形记为线段．①画出线段；②直接写出线段关于点的“旋转最大值”______；（2）若为原点，，，，直接写出线段关于点的“旋转最大值”______．（3）若点，图形是顺次连接，，，所组成的四边形，图形关于点，则的取值范围是______．k P M M (0,4)B (1,5)C BC M 90︒B C ''B C ''BC M M (,4)B m (1,5)C m +02m ≤≤BC M (,)M t t P (2,1)E t -(2,1)F t --(2,1)G t +-(2,1)H t +P M t。

北京市昌平区回龙观东西学区2024-2025学年上学期九年级期中数学试卷(无答案)

2024—2025学年第一学期回龙观东西学区期中考试试卷初三数学2024.10本试卷共8页，共三部分，28个小题，满分100分．考试时间120分钟．考生务必将答案填涂或书写在答题卡上，在试卷上作答无效．考试结束后，请交回答题卡．一、选择题（共8道小题，每小题2分，共16分）第1-8题均有四个选项，符合题意的选项只有一个1．如果，那么下列比例式成立的是（）A．B ．C ．D ．2．抛物线的图象开口向下，则m 的取值范围是（）A ．B ．C ．D ．m 可取一切实数3．如图，在中，，DE 分别与AB 、AC 相交于点D 、E ，若，，则的值为（）A ．0.5B ．2C ．D ．4．，若，，则与的周长比是（）A ．1：2B ．1：3C ．2：3D ．3：25．将函数化为顶点式，结果是（）A ．B ．C ．D ．6．如图，线段AD ，BC 交于点O ，由下列条件，不能得出的是（）A ．B ．C ．D ．7．关于二次函数的图象，下列说法正确的是（）()230m n n =≠23m n =32m n =23m n =32m n=()213y m x =--1m ≠1m >1m <ABC △DE BC ∥4AD =2DB =:AE EC 2332ABC DEF △△∽1AB =2DE =ABC △DEF △241y x x =-+()()20y a x h k a =-+≠()22y x =--()225y x =--+()223y x =--()221y x =-+AOB DOC △△∽OB OAOC OD=OA ODOB OC=OA ABOD CD=AB CD∥()22y x =--A ．开口向上B ．最高点是（2，0）C ．对称轴是直线D ．当时，y 随x 的增大而减小8．抛物线的部分图象如图所示，对称轴为直线，直线与抛物线都经过点．下列说法：①；②；③若与是抛物线上的两个点，则；④程的两根为，；⑤当时，函数有最大值．其中正确的个数是（）A ．2B ．3C ．4D ．5二、填空题（共8道小题，每小题2分，共16分）9．函数的最大值是______．10．如图，为了估计河的宽度，我们可以在河对岸选定一个目标点A ，在近岸取点B ，使AB 与河岸垂直，在近岸取点C 、E ，使，，AE 与BC 交于点D ．已测得，，，则河宽AB 为______．11．二次函数的图象向右平移2个单位，再向上平移3个单位，得到的二次函数图象表达式是______．12．写出一个当时，y 随x 增大而增大的二次函数表达式______．13．如图，在菱形ABCD 中，点E 在边AD 上，BE 与AC 交于点F ．若，，，则的值为______．14．如图，在边长为1的正方形网格中，的顶点均在格点上，点M ，N 分别是AB ，AC 与网格线的交点，则______．2x =-0x >()20y ax bx c a =++≠1x =-()0y kx c k =+≠()3,0-0ab >40a c +<()12,y -21,2y ⎛⎫⎪⎝⎭12y y <()200ax bx c a ++=≠13x =-21x =1x =-()2y ax b k x =+-21y x =-+BC AB ⊥CE BC ⊥40m BD =20m DC =24m EC =2y x =0x >4AB =60ABC ∠=︒1AF =AEABABC △MN =15．已知二次函数的图象与x 轴有交点，则a 的取值范围是______．16．如图，在平面直角坐标系中，二次函数的图象与x 轴交于A 、C 两点，与y 轴交于点，若P 是x 轴上一动点，点在y 轴上，连接PD ，则C 点的坐标是______，的最小值是______．三、解答题（本题共12道小题，第17题4分，第18-21题，每小题5分，第22-26题，每小题6分，第27、28题，每小题7分，共68分）17．如图，D ，E 分别是的边AB ，AC 上的点，，求证：．18．抛物线与x 轴交于A 、B 两点，A 在B 左侧，与y 轴交于C 点．（1）C 点坐标为______，的面积为______；（2）请在平面直角坐标系中画出函数图象，并回答：不等式的解集是______．19．已知抛物线与x 轴相交于点，，且过点．（1）求此函数的表达式；（2）求顶点坐标．20．如图，在矩形ABCD 中点E 、F 分别在边AD ，DC 上，，，，221y ax x =++22y x x c =-+()0,3B -()0,1D PC +ABC △ADE C ∠=∠AED ABC △△∽243y x x =-+ABC △2430x x -+>()3,0A -()1,0B ()0,1M ABE DEF △△∽6AB =9AE =．（1）求EF 的长；（2）求证；．21．已知二次函数的图象经过，两点．（1）求这个二次函数的解析式：（2）若C 点坐标为，抛物线上是否存在点D ，使的面积为4？若存在，求出D 点坐标；若不存在，请说明理由．22．已知：在在直角坐标系中，点、点的位置如图所示，为OB 的中点，点C 为折线OAB 上的动点，线段PC 把分割成两部分．问：点C 在什么位置时，分割得到的三角形与相似？请在图上画出所有符合要求的线段PC ，并求出相应的点C 的坐标．23．如图，．（1）与是否相似？请说明理由；（2）若，，求BD 的值．24．某公园在垂直于湖面的立柱上安装了一个多孔喷头，从喷头每个孔喷出的水柱形状都相同，可以看作是抛物线的一部分，当喷头向四周同时喷水时，形成一个环状喷泉．安装后，通过测量其中一条水柱，获得如下数据，在距立柱水平距离为d 米的地点，水柱距离湖面的高度为h 米．d （米）0 1.0 3.05.07.0h （米） 3.24.25.04.21.8请解决以下问题：（1）在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；2DE =90BEF ∠=︒212y x bx c =-++()2,0A ()0,6B -()6,0ACD △Rt OAB △()6,0A ()6,8B ()3,4P Rt OAB △Rt OAB △90ABC CDB ∠=∠=︒AC BD ∥ABC △CBD △10AC =6BC =（2）结合表中所给数据或所画图象，直接写出这条水柱最高点距离湖面的高度；（3）求所画图象对应的函数表达式；（4）从安全的角度考虑，需要在这组喷泉外围设立一圈正方形护栏，这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于1米，请通过计算说明公园至少需要准备多少米的护栏（不考虑接头等其他因素）．25．小新想探究一元三次方程的解的情况．根据以往的学习经验，他想到了方程与函数的关系：一次函数的图像与x 轴交点的横坐标即为一次方程的解；二次函数的图象与x 轴交点的横坐标即为一元二次方程的解．如：二次函数的图象与x 轴的交点为和，交点的横坐标和3即为方程的解．根据以上方程与函数的关系，如果我们知道函数的图象与x 轴交点的横坐标，即可知道方程的解．小新为了解函数的图象，通过描点法画出函数的图象：x 012ym12（1）直接写出m 的值______，并画出函数图象；（2）根据表格和图象可知，方程的解有______个，分别为______；（3）借助函数的图象，直接写出不等式的解集______．26．在平面直角坐标系中，已知抛物线．（1）求抛物线的顶点坐标（用含t 的代数式表示）：32220x x x +--=()0y kx b k =+≠()00kx b k +=≠()20y ax bx c a =++≠()200ax bx c a ++=≠223y x x =--()1,0-()3,01-2230x x --=3222y x x x =+--32220x x x +--=3222y x x x =+--⋅⋅⋅3-52-2-32-1-12-1232⋅⋅⋅⋅⋅⋅8-218-5898-2-158-358⋅⋅⋅3222x x x +>+xOy 222y x tx t t =-+-（2）点，在抛物线上，其中，．①若的最小值是，求的最大值；②若对于，，都有，直接写出t 的取值范围．27．在正方形ABCD 中，E 为BC 上一点，点M 在AB 上，点N 在DC 上，且，垂足为点F ．（1）如图1，当点N 与点C 重合时，求证：；（2）将图1中的MN 向上平移，使得F 为DE 的中点，此时MN 与AC 相交于点H ，①依题意补全图2；②用等式表示线段MH ，HF ，FN 之间的数量关系，并证明．28．对于平面直角坐标系中的直线l ：与矩形OABC 给出如下定义：设直线l 与坐标轴交于点M ，N （M ，N 不重合），直线与矩形OABC 的两边交于点P ，Q （P ，Q 不重合），称线段MN ，PQ 的较小值为直线l 的关联距离，记作．特别地，当时，．已知，，．（1）若，则______，______；（2）若，，求b 的值；（3）若，直接写出的最大值及此时以M ，N ，P ，Q为顶点的四边形的对角线交点坐标．()11,P x y ()22,Q x y 112t x t -≤≤+21x t =-1y 2-1y 1x 2x 12y y <MN DE ⊥MN DE =xOy 34y x b =+34y x b =-1d MN PQ =1d MN PQ ==()6,0A ()6,3B ()0,3C 3b =MN =PQ =153d =0b >0b <1d。

北京市第八中学2017-2018学年高一上学期期中考试语文试题含解析

学必求其心得，业必贵于专精2017—2018学年度第一学期期中练习题年级：高一科目:语文A 卷一、基础知识。

1. 下列加粗字的注音,全都正确的一项是A 。

侦缉．（jī）慰藉．(jí）内讧．（hòng）同仞敌忔．（kài) 朝谇．夕替（suì)B 。

巨孹（bò）揣度．（duó）侪．辈（chái）循规蹈矩．（jù）郁邑侘傺．（chì)C. 联袂．（mèi）消弭．（mí）责难．（nàn) 垂涎．三尺（xián）可白公姥．(mǔ）D 。

泥淖．（nào) 木讷．（nè) 忸怩．（ní）方凿圆枘．（ruì）葳蕤．生光（ruí）【答案】D【解析】试题分析：本题主要考查字音辨析.A 项，慰藉（jí)—-(jiè）;B 项,循规蹈矩(jù)-——jǔ；C 项消弭(mí）-—mǐ。

2。

下列加粗字的注音，全都正确的一项是A. 揽茞．（chǎi）横亘．（gèn）秕．糠（bì) 插科打诨．(hún）博闻强识．（zhì）B 。

伶俜．(pīng）匀称．（chèng）羞赧．（nǎn ) 封妻荫．学必求其心得，业必贵于专精子(yìn）刍荛．之见(ráo）C 。

遗．施（wèi）船舷．（xián) 横．祸（hèng）高屋建瓴．（líng）酩酊．大醉（dǐng）D. 否．泰(pǐ）县掾．（yuàn）剔．除（tì) 身陷囹圄．（yǔ）度德量．力（liàng）【答案】C【解析】试题分析：本题主要考查字音辨析。

A 项,插科打诨（hún)—-hùn；B 项，匀称（chèng）—-chèn；D 项剔除（tì）-—tī.3。

2017-2018学年北京市第四中学八年级上学期期中数学试卷含答案.docx

北京四中 2017-2018 学年上学期初中八年级期中考试数学试卷时间： 100 分钟满分：120分一、选择题（每小题 3 分，共 30 分）1. 下列四个汽车标志图中，不是轴对称图形的是（）.2.下列各式从左到右的变形中，是因式分解的是（） .A. x （ a-b） =ax-bxB. x 2 -1+y2=（ x-1）（ x+1 ）+y 2C. y2-1= （ y+1 ）（ y-1）D. ax+bx+c=x （ a+b） +c3.在平面直角坐标系中，点 A ，点 B 关于 y 轴对称，点 A 的坐标是（2，-8），则点 B 的坐标是（） .A. （ -2， -8）B. （ 2， 8）C. （-2， 8）D. （ 8， 2）4.已知 x=3 是分式方程k） .=3 的解，那么实数 k 的值为（x1A. 13C. 6D. 9 B.25.如图，已知△ ABC ≌△ DCB ， AB=10 ，∠ A=60°，∠ ABC=80°，那么下列结论中错误的是（） .A. ∠ D=60°B. ∠DBC=40°C. AC=DBD. BE=106. 下列算式中，你认为正确的是（） .b aB. 1b a=lA.1÷ .ba b b a aC. 3a11D.1b) 2a 2b213a(a a b a b7. 在三角形内，到三角形三条边的距离都相等的点是这个三角形的（）.A. 三条高的交点B. 三条角平分线的交点C. 三条边的垂直平分线的交点D. 三条中线的交点8. 某工程队准备修建一条长 1200 米的道路，由于采用新的施工方式，实际每天修建道路的速度比原计划快 20％，结果提前两天完成任务，若设原计划每天修建道路x 米，则根据题意可列方程为（） .1200120012001200A.(1 2B.2x20%) x(1 20%)xx1200120012001200C.2D.(1 2(120%) xxx20%) x9. 对于非零实数a 、b ，规定 a b= 1 - 1，若 2（ 2x-1 ） =1，则 x 的值为（） .b a5531A.B.C.D. -642610. 如图， D 为∠ BAC 的外角平分线上一点并且满足BD=CD ，∠ DBC= ∠DCB ，过 D 作 DE ⊥ AC 于 E ， DF ⊥ AB 交 BA 的延长线于F ，则下列结论：①△ CDE ≌△ BDF ；② CE=AB+AE ；③∠ BDC= ∠ BAC ；④∠ DAF= ∠ CBD.其中正确的结论有（） .A. 1 个B. 2 个C. 3 个D. 4 个11.若分式x 2的值为 0，则 x 的值为 ___________. x 112. 3 2 =___________ ；用科学记数法表示0.000314=___________.13.x24x化简：=___________.x28x 1614.若 a2+b2-2a-6b+10=0 ，则 a+b=___________.15.如图， AC=DC ， BC=EC ，请你添加一个适当的条件：___________，使得△ ABC ≌△ DEC.16. 如图，△ ABC 中，∠ ACB=90°，AC=BC ， AE 是 BC 边上的中线，过点 C 作 CF⊥ AE ，垂足为点 F，过点B 作 BD ⊥ BC 交 CF 的延长线于点 D， BD=2 ，则△ ABE 的面积为 ________.x m2m17. 若关于 x 的分式方程=3 的解为正实数，则实数m 的取值范围是____________ 。

专题21 尺规作图-2019年中考数学考点总动员系列(原卷版)

2019年中考数学备考之黄金考点聚焦考点二十一：尺规作图聚焦考点☆温习理解1．尺规作图的作图工具限定只用圆规和没有刻度的直尺2．基本作图(1)作一条线段等于已知线段，以及线段的和﹑差；(2)作一个角等于已知角，以及角的和﹑差；(3)作角的平分线；(4)作线段的垂直平分线；(5)过一点作已知直线的垂线．3．利用基本作图作三角形(1)已知三边作三角形；(2)已知两边及其夹角作三角形；(3)已知两角及其夹边作三角形；(4)已知底边及底边上的高作等腰三角形；(5)已知一直角边和斜边作直角三角形．4．与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆)；(2)作三角形的内切圆；(3)作圆的内接正方形和正六边形．5．有关中心对称或轴对称的作图以及设计图案是中考的常见类型6．作图的一般步骤尺规作图的基本步骤：(1)已知：写出已知的线段和角，画出图形；(2)求作：求作什么图形，它符合什么条件，一一具体化；(3)作法：应用“五种基本作图”，叙述时不需重述基本作图的过程，但图中必须保留基本作图的痕迹；(4)证明：为了验证所作图形的正确性，把图作出后，必须再根据已知的定义、公理、定理等，结合作法来证明所作出的图形完全符合题设条件；(5)讨论：研究是不是在任何已知的条件下都能作出图形；在哪些情况下，问题有一个解、多个解或者没有解；(6)结论：对所作图形下结论．考点典例一、应用角平分线、线段的垂直平分线性质画图【例1】（2017四川自贡第22题）两个城镇A，B与一条公路CD，一条河流CE的位置如图所示，某人要修建一避暑山庄，要求该山庄到A，B的距离必须相等，到CD和CE的距离也必须相等，且在∠DCE的内部，请画出该山庄的位置P．（不要求写作法，保留作图痕迹．）【举一反三】A B C为某公园的三个景点，景点A和景点B之间有一条笔直的小路，（2017黑龙江绥化第22题）如图，,,现要在小路上建一个凉亭P，使景点B、景点C到凉亭P的距离之和等于景点B到景点A的距离．请用直尺和圆规在所给的图中作出点P．(不写作法和证明，只保留作图痕迹)考点典例二、画已知直线的平行线，垂线【例2】（北京市燕山区2017届九年级一模）下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.请回答：该作图依据是__________________________________________________．【例3】（北京市海淀区2017-2018学年九年级上学期期中）下面是“作已知三角形的高”的尺规作图过程. 已知：ABC.求作：BC边上的高AD作法：如图，(1)分别以点A和点C为圆心，大于12AC的长为半径作弧，两弧相交于P，Q两点；(2)作直线PQ，交AC于点O；(3)以O为圆心，OA为半径⊙O,与CB的延长线交于点D，连接AD，线段AD即为所作的高.请回答；该尺规作图的依据是___________________________________________________【举一反三】（2017浙江衢州第7题）下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线，则对应选项中作法错误的是（）A ．①B ．②C ．③D ．④考点典例三、画三角形【例4】（2017江苏无锡第24题）如图，已知等边△ABC ，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：（1）作△ABC 的外心O ；（2）设D 是AB 边上一点，在图中作出一个正六边形DEFGHI ，使点F ，点H 分别在边BC 和AC 上．【举一反三】已知：线段a 、c 和∠β（如图），利用直尺和圆规作△ABC ，使BC=a ，AB=c ，∠ABC=∠β．（不写作法，保留作图痕迹）．考点典例四、通过画图确定圆心【例5】（2017浙江嘉兴同学19题）如图，已知ABC ∆，40B ∠=︒．（1）在图中，用尺规作出ABC ∆的内切圆O ，并标出O 与边AB ，BC ，AC 的切点D ，E ，F （保留痕迹，不必写作法）；的度数．（2）连接EF，DF，求EFD【举一反三】(浙江省杭州市余杭区2017届九年级上学期期中)如图，（1）作△ABC的外接⊙O（用尺规作图，保留作图痕迹，不写作法）；（2）若AB=6cm，AC=BC=5cm，求⊙O的半径．课时作业☆能力提升1．（2017广西四市）如图，△ABC中，AB＞AC，∠CAD为△ABC的外角，观察图中尺规作图的痕迹，则下列结论错误的是（）A．∠DAE=∠B B．∠EAC=∠C C．AE∥BC D．∠DAE=∠EAC2．（2016-2017学年江苏盐城东台市第二教育联盟初二上10月考）用尺规作图，不能作出唯一直角三角形的是（）.A．已知两条直角边 B．已知两个锐角C．已知一直角边和直角边所对的一锐角 D．已知斜边和一直角边3．（河南省驻马店市确山县2017-2018学年八年级上学期期中）如图，已知钝角∆ABC，依下列步骤尺规作图，并保留作图痕迹.步骤1：以C为圆心，CA为半径画弧①；步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；步骤3：连接AD，交BC延长线于点H.下列叙述正确的是（）A. AC平分∠BADB. BH垂直平分线段ADC.D. AB=AD4．（福建省晋江市2017年初中学业质量检查）已知点A，点B都在直线l的上方，试用尺规作图在直线l上的值最小，则下列作法正确的是( ).求作一点P，使得PA PBA. B. C. D.5．（2017湖北随州）如图，用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是（）A. 以点F为圆心，OE长为半径画弧B. 以点F为圆心，EF长为半径画弧C. 以点E 为圆心，OE 长为半径画弧D. 以点E 为圆心，EF 长为半径画弧6．（浙江省温州市鹿城区第二十三中学2017学年H 上八年级期中）如图，用尺规作图作“一个角等于已知角”的原理是：因为D O C DOC ∆≅∆''',所以D O C DOC ∠=∠'''.由这种作图方法得到的D O C ∆'''和DOC ∆全等的依据是（）A. SSSB. SASC. ASAD. AAS7．（2017届浙江省杭州市淳安县中考模拟）尺规作图特有的魅力曾使无数人沉湎期中，连当年叱咤风云的拿破仑也不例外，我们可以只用圆规将圆等分。

2017-2018学年北京市第八中学九年级上学期期中数学试题(含答案)

A BCD E2017-2018学年度第一学期期中考试年级：九年级科目：数学班级：________ 姓名：________一、选择题 (每题4分, 共40分) 1. 如果252=+b b a ，那么b a 的值是( )A.21 B.2 C.51D.52. 关于x 的一元二次方程042=++mx x 有两个正整数根，则m 可能取的值为( ) A.0>m B.4>m C. −4，−5 D. 4，53. 将抛物线()312+-=x y 向左平移1个单位，向下平移3个单位后所得抛物线的解析式为( )A.()22-=x y B.()622+-x C.62+=x y D.2x y =4. 如图，在△ABC 中，DE ∥BC ，分别交AB ，AC 于点D ，E ．若AD =1，DB =2，则△ADE 的面积与△ABC 的面积的比等于( ) A .21B .C .D .91 5. 某商店购进一种商品，单价为30元．试销中发现这种商品每天的销售量P （件）与每件的销售价x （元）满足关系：1002P x =-.若商店在试销期间每天销售这种商品获得200元的利润，根据题意，列方程为( )A.()200210030-=-x xB.()200302100=--x x xC.()200210030=-xD. ()()200210030=--x x 6. 如图，点A 、B 、C 、D 、E 、F 、G 、H 、K 都是7×8方格纸中的格点，为使△DEM ∽△ABC ，则点M 所在位置应是F 、G 、H 、K 四点中的( ) A ．K B ．H C ．G D ．F第6题图 ABCDEF G H K. . . . . .第4题图7. 如图，在边长为1的小正方形组成的网格中，△ABC 的三个顶点均在格点上，E 为BC 中点，则sin ∠AEB 的值是( )A.55 B. 54 C. 53 D. 43 8. 若二次函数bx x y +=2的图象的对称轴是经过点(2，0)且平行于y 轴的直线，则关于x 的方程52=+bx x 的解为( ) A. 01=x ，42=xB. 11=x ，52=xC. 11=x ，52-=xD. 11-=x ，52=x9. 如图，在矩形ABCD 中，AB =3，BC =4，点P 在BC 边上运动，连接DP ，过点A 作AE ⊥DP ，垂足为E ，设DP =x ，AE =y ，则能反映y 与x 之间函数关系的大致图象是( )10．如图是二次函数y =ax 2+bx +c( a ≠ 0 )在平面直角坐标系中的图象，根据图形判断 ①b > 0；② a −b +c < 0；③ 2a +b > 0； ④ b 2+8a > 4ac 中正确的是( )A. ①②B. ①③C. ③④D.二、填空题 (每题4分, 共24分)11．已知二次函数()1322+-=x y ．当时，y 随x 的增大而减小．12. 在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，使它与图中阴影部分组成的新图形构成中心对称图形，该小正方形的序号是． 13．如果关于x 的一元二次方程x 2 + 4x – m = 0没有实数根，那么m 的取值范围是________．第12题图第9题图第7题图14．如图，Rt △ABC 中，∠ACB =90°，AC =6cm ，BC =8cm ，动点P 从点B 出发，在BA 边上以每秒5cm 的速度向点A 匀速运动，同时动点Q 从点C 出发，在CB 边上以每秒4cm 的速度向点B 匀速运动，运动时间为t 秒（0＜t ＜2），连接PQ ．若△BPQ 与△ABC 相似，则t 的值为______． 15. 如图，∠AOB ＝90º，将Rt △OAB 绕点O 按逆时针方向旋转至Rt △O A′B′，使点B 恰好落在边A′B′上．已知B tan = 2，OB = 5，则BB′ = ．16．在平面直角坐标系xoy 中，直线x = 2和抛物线2ax y =在第一象限交于点A ，过A 作AB x ⊥轴于点B .如果a 取1，2，3，…，n 时对应的△AOB 的面积为1S ，2S ，3S ，…，n S ，那么=1S _____；=++++n S S S S ...321_____________．三、解答题（共56分）17.(5分)计算：()011345sin 2230cos 3--︒-+︒-18. (5分)解方程:19.(6分) 如图，在△ABC 中，AB=AC=8，BC =6，点D 为BC 上一点，BD =2．过点D 作射线DE 交AC 于点E ，使∠ADE=∠B ．求线段EC 的长度．20.(6分) 已知关于x 的一元二次方程有两个不相等的实数根第19题图第14题图A第15题图APBQ C（1）求k 的取值范围；（2）若k 为正整数，且该方程的根都是整数，求k 的值．21. (5分)如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为格点三角形，图中的△ABC 就是格点三角形．在建立平面直角坐标系后，点B 的坐标为(-1，-1)．(1) 把△ABC 绕点A 按逆时针方向旋转90°后得到△AB 1C 1，画出△AB 1C 1的图形并直接写出点B 1的坐标为；(2) 在现有坐标系下．．．．．．．把△ABC 以点A 为位似中心放大，使放大前后对应边长的比为1 : 2，画出△AB 2C 2．22.(6分)如图，小明住在一栋住宅楼AC 上，他在家里的窗口点B 处，看楼下一条公路的两侧点F 和点E 处（公路的宽为EF ），测得俯角α、β分别为30°和60°，点F 、E 、C 在同一直线上.（1）请你在图中画出俯角α和β．（2）若小明家窗口到地面的距离BC =6米，求公路宽EF 是多少米？（结果精确到0.1米；可能用到的数据73.13≈）23. (5分)已知在△ABC 中，BAC ∠=90°，AD BC ⊥于点D ，点E 为AC 中点，延长ED 、AB 交于点F ．求证：FADFAC AB =24. (7分)已知:二次函数y =ax 2+bx +c ， y 与x 的一些对应值如下表：（1）根据表格中的数据，确定二次函数解析式为；（2）填齐表格中空白处的对应值并利用上表，用五点作图法，画出二次函数y =ax 2+bx +c 的图象. （3）当 1 < x ≤ 4时，y 的取值范围是 ;（4）设y =ax 2 + bx + c 的图象与x 轴的交点为A 、B 两点（A 点在B 点左侧），与y 轴交于点C ，P 点为线段AB 上一动点，过P 点作PE ∥AC 交BC 于E ，连结PC ，当△PEC 的面积最大时，求P 点的坐标．25.(5分)阅读下面材料:F E DCBA小明遇到下面一个问题：如图1所示，AD 是△ABC 的角平分线，m AB =，n AC =，求DCBD的值.小明发现，分别过B ，C 作直线AD 的垂线，垂足分别为E ，F .通过推理计算，可以解决问题（如图2）．（1）请回答，=DCBD参考小明思考问题的方法，解决问题：如图3，四边形ABCD 中，2=AB ，6=BC ，︒=∠60ABC ， BD 平分ABC ∠，BD CD ⊥.AC 与BD 相交于点O .（2）=OC AO （3）=∠DCO tan26. (6分)已知：在等边△ABC 中，点D 为BC 边的中点，点F 在AB 上，连结DF 并延长到点E ，使BDF BAE ∠=∠，点M 在线段DF 上，且DBM ABE ∠=∠. （1）如图，线段AE 、MD 之间的数量关系为；请证明你的结论．（2）在（1）的条件下，延长BM 到P ，使BM MP =，连接CP ，若AB ＝7，AE ＝72，求tan ∠BCP 的值．2017-2018学年度第一学期九年级数学期中练习答案一．选择题（每题4分，共40分，每题只有一个正确答案）：图2图1图3第26题图二．填空题（每题4分，共24分）：三．解答题 ( 共56分)：解：αβ。

北京市第十三中学分校2024-2025学年九年级上学期10月月考数学试卷(无答案)

2024-2025学年度北京市第十三中学分校10月月考九年级数学试卷考生须知1．本试卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷共2页，第Ⅱ卷共4页。

2．本试卷满分100分，考试时间100分钟。

3．在试卷（包括第Ⅰ卷和第Ⅱ卷）密封线内准确填写学校、班级、姓名、学号。

4．考试结束，将试卷及答题纸一并交回监考老师。

一、选择题（共12小题，每小题2分）1．将校徽按顺时针方向旋转90°后得到的图形是图中的（）A ．B ．C ．D ．2．已知m 是关于x 的方程的一个根，则（）A ．5B ．8C ．－8D ．63．在平面直角坐标系中，将抛物线向右平移2个单位长度，向上平移1个单位长度，得到抛物线（）A ．B ．C ．D ．4．下列关于抛物线的说法正确的是（）A ．抛物线的开口方向向下B ．抛物线与y 轴交点的坐标为C ．当时，抛物线的对称轴在y 轴右侧D ．对于任意的实数b ，抛物线与x 轴总有两个公共点5．如图，在中，，，将绕点C 顺时针旋转90°得到，点B 的对应点在边AC上（不与点A ，C 重合），则的度数为（）A ．B ．C ．D ．2230x x --=2242m m -+=2y x =()221y x =-+()221y x =--()221y x =++()221y x =+-22y x bx =+-()0,20b >ABC △90ACB ∠=︒BAC α∠=ABC △A B C ''△B 'AA B ''∠α45α-︒45α︒-90α︒-6．，，三点都在二次函数的图象上，则，，的大小关系为（）A ．B ．C ．D ．7．如图，以40m/s 的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h （单位：m ）与飞行时间t （单位：s ）之间具有函数关系．下列叙述正确的是（）A ．小球的飞行高度不能达到15mB ．小球的飞行高度可以达到25mC ．小球从飞出到落地要用时4sD ．小球飞出1s 时的飞行高度为10m8．抛物线经过点，且对称轴为直线，其部分图象如图所示．对于此抛物线有如下四个结论：①；②；③若，则时的函数值大于时的函数值；④点一定在此抛物线上．其中正确的结论是（）．A ．①②B ．②③C ．②④D ．③④二、填空题（共8小题，每小题2分）9．二次函数的最______值是______．10．在同一个平面直角坐标系xOy 中，二次函数，，的图象如图所示，则，，的大小关系为______．（用“＜”）11,2y ⎛⎫-⎪⎝⎭()21,B y ()34,C y ()22y x k =--+1y 2y 3y 123y y y <<132y y y <<312y y y <<321y y y <<2205h t t =-2y ax bx c =++()2,0-1x =0ac >1640a b c ++=0m n >>1x m =+1x n =-,02c a ⎛⎫-⎪⎝⎭()213y x =--211y a x =222y a x =233y a x =1a 2a 3a11．如图所示，在由边长相同的小正方形组成的网格中，的顶点都在格点（小正方形的顶点）上．将绕点O 按顺时针方向旋转得到，且各顶点仍在格点上，则旋转角的度数是______°．12．抛物线与y 轴的交点坐标是______，与x 轴的交点坐标是______．13．抛物线的顶点第______象限．14．响应国家号召打赢脱贫攻坚战，小明利用信息技术开了一家网络商店，将家乡的土特产销往全国，今年6月份盈利24000元，8月份盈利34560元，求6月份到8月份盈利的月平均增长率．设6月份到8月份盈利的月平均增长率为x ，根据题意，可列方程为______．15．如图，直线和抛物线都经过点和，不等式的解集为______．16．现有函数，如果对于任意的实数n ，都存在实数m ，使得当时，，那么实数a 的取值范围是______．三、解答题（本题共68分）17．用适当的方法求解下列方程：（1）；（2）；ABC △ABC △A B C '''△256y x x =-+26y x x =--y x m =+2y x bx c =++()1,0A ()3,2B 2x bx c x m++≤+()()242x x a y x x x a +<⎧⎪=⎨-≥⎪⎩x m =y n =22150x x --=2420x x --=18．如图，正方形是由正方形ABCD 旋转而成的，点D 在上．（1）直接写出旋转中心、旋转方向与旋转角；（2）若正方形的边长是1，直接写出的长．19．已知关于x 的一元二次方程：．（1）求证：方程总有两个实数根；（2）若方程有一个根为负数，求m 的取值范围．20．已知二次函数图象上部分点的横坐标x 与纵坐标y 的对应值如下表所示：x …－3－2－101…y…－3－4－3…（1）求这个二次函数的表达式；（2）在给定的平面直角坐标系中画出这个二次函数的图象；（3）当时，直接写出y 的取值范围；（4）当时，直接写出x 的取值范围；（5）当时，关于x 的一元二次方程有实根，直接写出t 的取值范围；21．如图，在四边形ABCD 中，，，对角线AC ，BD 交于点O ，AC平分角∠BAD ，过点C 作交AB 的延长线于点E ，连接OE ．（1）求证：四边形ABCD 是菱形；（2）若，求OE 的长．22．如图，排球运动场的场地长18m ，球网高度2.24m ，球网在场地中央，距离球场左、右边界均为9m ．一名球员在场地左侧边界练习发球，排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分．AB C D '''AC 'C D '210x mx m -+-=2y ax bx c =++40x -<<3y >-32x -≤<20ax bx c t ++-=AB DC ∥AB AD =CE AB ⊥AB =4BD =在球运行时，将球与场地左边界的水平距离记为x （米），与地面的高度记为y （米），经多次测试后，得到如下数据：x （米）0124678y （米）22.152.282.442.52.492.44（1）在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；（2）击球点的高度为______米，排球飞行过程中可达到的最大高度为______米；（3）求出y 与x 的函数解析式；（4）判断排球能否过球网，并说明理由．23．法国数学家韦达讨论了方程根的各种有理变换，发现了一元二次方程的根与系数之间的关系：如果一元二次方程的两个根是，，那么，．后来人们将这个一元二次方程根与系数的关系称为“韦达定理”．这一结论同学们由求根公式也很容易得到．请你根据“韦达定理”解决以下三个问题：（1）已知，是方程的两根，则______，______；（2）设，是方程的两个根，则的值是______；（3）若，是两个不相等的实数，且满足，，那么______．24．在平面直角坐标系xOy 中，已知抛物线G ：．（1）直接写出抛物线G 的顶点坐标；（2）若在抛物线G 上有两点，，且，直接写出n 的取值范围；（3）抛物线G 的对称轴与x 轴交于点M ，点M 与点A 关于y 轴对称，将点M 向右平移3个单位得到点B ，若抛物线G 与线段AB 恰有一个公共点，结合图象，求m 的取值范围．25．在平面直角坐标系xOy 中，已知抛物线．（1）直接写出抛物线的对称轴；（2）当时，设抛物线与x 轴交于A ，B 两点（点A 在点B 的左侧），顶点为C ，若为等边三角形，求a 的值；（3）过点（其中）且垂直y 轴的直线l 与抛物线交于M ，N 两点，若对于满足条件的任意t 值，线段MN 的长都不小于1，结合函数图象，直接写出a 的取值范围．26．在等边中，D ，E ，F 分别是边AB ，BC ，CA 上的动点，满足，且．作点E 关于AC 的对称点G ，连接CG ，DG ．()200ax bx c a ++=≠1x 2x 12b x x a +=-12cx x a⋅=1x 2x 22740x x -+=12x x +=12x x ⋅=1x 2x 22630x x -+=2212x x +1x 2x 21125x x -=22225x x -=12x x ⋅=22y x x m =-+()12,y ()2,n y 21y y >243y ax ax a =-+0a >ABC △()0,T t 12t -≤≤ABC △DE EF =60DEF ∠=︒（1）当点D ，E ，F 在如图1所示的位置时，请在图1中补全图形，并证明四边形DBCG 是平行四边形；（2）如图2，当，时，写出线段AB 和DE 的数量关系，并说明理由．AD BD <15BDE ∠=︒。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017-2018学年度第一学期期中练习题年级：初三科目：数学班级：姓名：_________1．下列函数中，y 是x 的反比例函数的是（）A ．x y 3=B ．x y 3= C ．32x y = D ．3+1y x =2．若3x =2y (xy ≠0)，则下列比例式成立的是（）A ．32x y= B ．23x y = C ．32x y = D ．23x y =3．在Rt △ABC 中，∠C =90°，BC =6，AC =8，则sinA 的值是（）A ．43 B ．34 C ．53 D ．544．如图，在△ABC 中，点D ，E 分别在AB ，AC 上，且DE ∥BC ，AD =1，BD =2，那么AEAC的值为（）A ．1:2B ．2:3C ．1:4D ．1:35．如图，小正方形的边长均为1，则下列图中的三角形与ABC ∆相似的是（）6．△ABC 中，若AB ＝6，BC ＝8，∠B ＝120°，则△ABC 的面积为( ) A ．12 B．312C ．324D．348D7．下列说法中错误的是（）A ．在函数2x =y -中，当x =0时y 有最大值0B ．在函数22x =y 中，当x>0时y 随x 的增大而增大C ．抛物线22x =y ，2x =y -，221x =y -中，抛物线22x =y 的开口最小，抛物线2x =y -的开口最大D ．不论a 是正数还是负数，抛物线2x a =y 的顶点都是坐标原点 8．如图，四边形ABCO 是平行四边形，OA =2,AB =6,点C 在x 轴的负半轴上，将平行四边形 ABCO 绕点A 逆时针旋转得到平行四边形ADEF ，AD 经过点O ，点F 恰好落在x 轴的正半轴上.若点D 在反比例函数)0(<=x xky 的图像上，则k 的值为( ) A ．34 B ．12 C ．38 D ．6二、填空题（每题2分，共16分） 9．已知点A （2，n ）在反比例函数xy 6-=的图象上，则n=______. 10．已知点A （1，a ）、点B （3，b ）、点C （-2，c ）都在反比例函数xm y 12+=的图象上，则a 、b 、c 之间的大小关系是__________.11．二次函数23x y -=图象的开口向 ____，顶点坐标为 .12．如图，长4m 的楼梯AB 的倾斜角∠ABD 为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD 为45°，则调整后的楼梯AC 的长为______________m . 13．位于第一象限的点E 在反比例函数xky =的图象上，点F 在x 轴的正半轴上，O 是坐标原点．若EO =EF ，△EOF 的面积等于2，则k =______.第12题图第13题图14．如图，在平行四边形ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则BCDE=______若1=∆DEF S ，则=∆BCF S ________.15．如图，在Rt △ABC 中，∠C =90°，点D 是BC 边的中点，CD =2，tanB =34.则AD 长为________, sin ∠CAD=________.16．如图，已知直线 b x k y +=1与x 轴、y 轴相交于P 、Q 两点，与xk y 2=的图像相交于A （－2，m ）、B （1，n ）两点，连接OA 、OB . 给出下列结论： ①21k k <0；②m +21n =0； ③BO Q AO P S S ∆∆=；④不等式xk b x k 21>+的解集是x <－2或0<x <1，其中正确的结论的序号是 .第14题图第15题图第16题图草稿纸2017-2018学年度第一学期初三数学期中练习答题纸班级：______ 姓名：________ 学号：______ 成绩：_______二、填空题（共16分） 9． n=______ 10．a 、b 、c 之间的大小关系是__________11．开口向 ____，顶点坐标为 12．楼梯AC 的长为______________m 13．k =_____ 14．BCDE =______，则=∆BCF S ________15．AD 长为________，sin ∠CAD =________ 16．正确的结论的序号是三、计算题（共10分） 17．解方程：2610x x --=18．计算：︒-︒+︒60sin 45cos 30tan 32四、解答题（本题共58分，第19-23题，每小题5分，第24题6分，第25题5分，第26、27题，每小题7分，第28题8分）19．如图，平行四边形ABCD 中，点E 在BA 的延长线上，连接CE ，与AD 相交于点F . （1）求证：△EBC ∽△CDF ；（2）若BC ＝8，CD ＝3，AE ＝1，求FD 的长．20．如图，小东在教学楼距地面8米高的窗口C 处，测得正前方旗杆顶部A 点的仰角为37°，旗杆底部B 的俯角为45°，求旗杆AB 的高度.（结果取整数）（参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75，2≈1.414，732.13 ）21．如图，在平面直角坐标系xOy 中，△ABC 的三个顶点分别为A (2，6)，B (4，2), C (6，2).（1）以原点O 为位似中心，将△ABC 缩小为原来的12，得到△DEF . 请在第一象限内，画出△DEF .（2）在（1）的条件下，点A 的对应点D 的坐标为______，点B 的对应点E 的坐标为_______.22．已知，如图，一次函数y=kx+b 的图象与x 轴、yx图2C BA图3C B A D图1C B A 比例函数xny =（n 为常数且n ≠0）的图象在第二象限交于点C ．CD ⊥x 轴，垂直为D ，若OB =2OA =3OD =6．（1）求点A 和点B 的坐标；（2）求反比例函数的解析式；（3）若两函数图象的另一个交点为E ，在x 轴上有一点P ，使得PCE S ∆=21，求点P 的坐标．23．将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“等积线”，其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”（例如圆的直径就是圆的“等积线段”）．解决问题：已知在Rt △ABC 中，∠BAC =90°，AB =AC=（1）如图1，若AD ⊥BC ，垂足为D ，则AD 是△ABC 的一条等积线段，AD 的长为______；（2）在图2和图3中，分别画出一条等积线段，并直接写出它们的长度．（要求：使得图1、图2和图3中的等积线段的长度各不相等）答：图2中的等积线是线段_____，它的长度是_____；图3中的等积线是线段_____，它的长度是_____；24．小聪是一名爱学习的孩子，他在学习完反比例函数后，对函数)3(2-=x x y 的图象和性质进行了探究，探究过程如下，请补充完整．（1）自变量x 的取值范围是全体实数，x 与y 的几组对应数值如下表：其中m =______；（2）如图，在平面直角坐标系xOy 中，描出了以表中各对对应值为坐标的点，请你根据描出的点，画出该函数的图象；（3）观察函数图象，写出一条该函数的性质： _____________________________________________________；（4）进一步探究函数图象发现：①函数图象与x 轴有____个交点，所以对应的方程0)3(2=-x x 有_____个互不相等的实数根；②若关于x 的方程a x x =-)3(2有3个互不相等的实数根，则a 的取值范围是___________.25．阅读材料：在锐角三角函数》的学习中，我们了解了借助太阳光线、平面镜等测量工具可以测量建筑物的高度．综合实践活动课上，数学王老师让同学制作了一种简单测角仪：把一根细线固定在量角器的圆心处，细线的另一端系一个重物（如图一）；将量角器拿在眼前，使视线沿着量角器的直径刚好看到需测量物体的顶端（如图二），这样可以得出需测量物体的仰角α的度数（如图三）．利用这种简单的测角仪，可以帮助我们测量角度．图一图二图三在我校九年级数学《测量》实践活动中，有一位同学参考阅读材料自制了测角仪，他想利用所学的知识测量北海公园白塔的塔顶到山下地面的高度。

请你从下面问题（．．．．．．．．．．．．．．1．）（．．2．）中选取一个问题作答．．．．：（1）这位同学第一次站在琼华岛山下的平地上进行测量活动，他设计了一种测量方案，求出了北海白塔的塔顶到山下地面的高度，下面的图片反映了他的测量方法。

①根据上述思路，在图中标出字母，写出需要并且能测量的角或线段（用图中的字母表示）_____________________________________；测量时使用的工具是____________________；②结合示意图，简要说明计算的思路（不必写出结果）.（2）这位同学第二次站在琼华岛的对岸，巧妙地利用白塔在水中的倒影计算出了塔顶到山下地面的高度，下面的图片反映了他的测量方法。

①根据上述思路，在图中标出字母，写出需要并且能测量的角或线段（用图中的字母表示）____________________________________；测量时使用的工具是____________________； ②结合示意图，简要说明计算的思路（不必写出结果）.26．如图，在平面直角坐标系xOy 中，直线y =-x +3与x 轴交于点C ，与直线AD 交于点)35,34(A ，点D 的坐标为（0,1）（1）求直线AD 的解析式；（2）直线AD 与x 轴交于点B ，若点E 是直线AD 上一动点（不与点B 重合），当以B 、C 、E 为顶点的三角形与BOD 相似时，求点E 的坐标.27．在平面直角坐标系xOy 中，对于点(,)P a b 和点(,)Q a b '，给出如下定义：若⎩⎨⎧-<-≥-=1,1,a b a b b'，则称点Q 为点P 的理想点．例如：点（1,2）的理想点的坐标是（1,-2），点（-2,3）的理想点的坐标是（-2,3）．（1）点（23,-1）理想点的坐标是___________；若点C 在函数22x y =的图象上，则它的理想点是)2,1(-A ，)2,1(-B 中的哪一个？_______________；（2）若点P 在函数)2,242->≤≤-+-=k k x x y （的图象上，其理想点为Q ：① 若其理想点Q 的纵坐标b'的取值范围是106≤≤-b'，求k 的值；② 在①的条件下，若点P 的理想点Q 都不在反比例函数)00(><=x m xm y ，上，求m 的取值范围.28．如图，在△ABC 中，∠BAC =90°，AB=AC ，点D 是△ABC 内一动点（不包括△ABC 的边界），连接AD ．将线段AD 绕点A 顺时针旋转90°，得到线段AE ．连接CD ，BE ．（1）依据题意，补全图形；（2）求证：BE=CD ．（3）延长CD 交AB 于F ，交BE 于G ． ①求证：△ACF ∽△GBF ；②连接BD ，DE ，当△BDE 为等腰直角三角形时，请你直接．．写出AB ：BD 的值.CBAB备用图。