机械臂雅可比矩阵求解推导
机器人第五章

v
的传递比;
v J l 1 J a1
Jl2 J a2
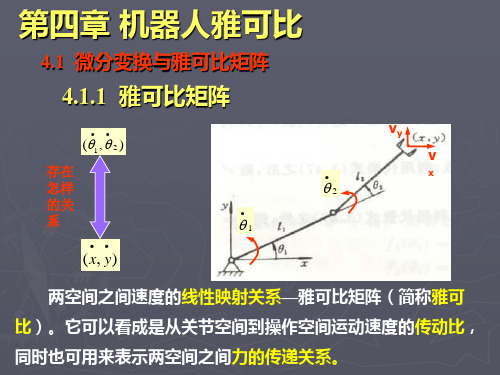
于是,手爪的线速度v 和角速度ω 可表示为各关节 速度 q i 的线性函数,
v J l1q1 J l 2 q2 J ln qn ; ω J a1q1 J a 2 q2 J an qn .
的轴 z i 作微分转动 d i ,相当于微分运动矢量
d
0 0 0 , δ 0 d i 0 1
( p ( p ( p
利用式(5.13)得出手爪相应的微分运动矢量为
xi (q ) 第i行第j列元素为 J ij (q ) q , i 1,2,,6; j 1,2,, n. j
表达了关节空间第j个关节速度对于操作空间第i方向的速度变换;
q R n ,雅可比矩阵 J (q )是从关节空间速度 q 向 对于关节变量
操作空间速度
x
映射的线性变换。
J 式中, li 和 J ai 分别表示关节i的单位关节速度引
起手爪的线速度和角速度。
第三节
2、矢量积的方法
Whitney基于运动坐标系的概念提出求机器人雅 可比的矢量积方法。如下图所示,末端手爪的线速 度v 和角速度 ω 与关节速度 q i 有关。
(1)对于移动关节i,则
z i v z i 0 qi , J i 0 ω
T
之间的关系
第三节
5.3 微分运动和广义速度
刚体或坐标系的微分运动包含微分移动矢量 d 和微分转动矢量δ 。 前者由沿三个坐标轴的微分移动组成;后者 由绕三坐标轴的微分转动组成,即
lio-sam雅克比矩阵公式

一、概述lio-sam雅克比矩阵公式是机器人学和计算机视觉领域中常用的数学工具之一。
它在求解机器人运动学和视觉SLAM(同时定位与地图构建)中起着重要作用。
在本文中,我们将介绍lio-sam雅克比矩阵公式的基本概念和推导过程,以及其在机器人领域中的应用。
二、lio-sam雅克比矩阵公式的概念lio-sam雅克比矩阵公式是指在SLAM问题中,通过对视觉和激光雷达观测模型进行线性化,得到雅克比矩阵的表达式。
雅克比矩阵是对观测模型的各个参数进行求导后得到的矩阵,它能够描述观测数据对于机器人状态变量的影响。
在SLAM问题中,通过lio-sam雅克比矩阵公式,可以将非线性观测模型线性化,从而应用于常见的最优化问题中,如扩展卡尔曼滤波(EKF)和非线性最小二乘(NLS)等。
三、lio-sam雅克比矩阵公式的推导在SLAM问题中,观测模型通常为非线性的,而最优化算法往往要求观测模型是线性的。
需要通过lio-sam雅克比矩阵公式来对观测模型进行线性化。
考虑一个一般的观测模型:\[z = h(x, u) + \varepsilon\]其中,\(z\)为观测数据,\(x\)为机器人的状态变量,\(u\)为控制变量,\(h(·)\)为观测模型函数,\(\varepsilon\)为观测噪声。
对观测模型进行泰勒展开,可以得到:\[h(x, u) \approx h(\hat{x}, \hat{u}) + H\Delta x\]其中,\(\hat{x}\)为机器人状态的估计值,\(\hat{u}\)为控制变量的估计值,\(H\)为雅克比矩阵,\(\Delta x = x - \hat{x}\)为状态变量的增量。
将泰勒展开后的观测模型代入测量方程中,可以得到线性化后的观测模型:\[z \approx z' + H\Delta x + \varepsilon\]其中,\(z' = h(\hat{x}, \hat{u})\)为线性化后的观测数据。
机器人雅可比矩阵知识讲解

x6 f6(q1,q2, ,q6)
注意,如果函数 f1(q) 到 f6(q) 是非线性的,则 f q 是q的 函数,写成 xJ(q)q ,式子两边同除以时间的微分,
上式中,66的偏导数x矩阵J(Jq(q)q)叫做雅可比矩阵。其中
Jijq xiqq j
雅可比矩阵
机器人关节数
*雅可比矩阵的行数取决于机器人的类型
雅可比矩阵在机器人中的应用
可以把雅可比矩阵看作是关节的速度 q 变换到 操作速度V的变换矩阵
在任何特定时刻,q具有某一特定值,J(q)就是一个 线性变换。在每一新的时刻,q已改变,线性变换 也因之改变,所以雅可比矩阵是一个时变的线性变 换矩阵。
在机器人学领域内,通常谈到的雅可比矩阵是 把关节角速度和操作臂末端的直角坐标速度联 系在一起的。
假设矢量yRm为uRn的函数
y= y(u)
y1(u) y2(u)
yy12((uu11,,uu22,, ,,uunn))
ym(u) ym(u1,u2,,un)
对于m=1, (标量对矢量的导数)
u y u y1 1
y1 u2
u y1 n
y相对于u的偏导数定义为
u y u u uyyym 1 2(((u u u))) yu yu u ym 1 1 2 1 1
约束函数C(x),
单位圆上的质点位置约束为 C (x ) xx 1
一般情况下,采用位姿矢量q聚合表达n个粒子的位置。在3D 空间,矢量长度为3n。考虑位置约束C是一个关于位姿矢量q 的未知函数,则速度约束
C C q q
矩阵 C/q 被称作C的雅可比矩阵,记作J。为了进行物理
仿真,求微分 C JqJq,根据力学关系,建立微分约束方
机器人雅可比矩阵

两自由度机器人
对于一个两自由度的机器人,其 雅可比矩阵是一个2x2矩阵,其 中包含了机器人的两个关节角度 和两个关节速度之间的线性关系
。
矩阵形式
雅可比矩阵的矩阵形式为:J = [[a, b], [c, d]],其中a、b、c、d 是机器人关节角度和关节速度之
间的线性关系系数。
计算方法
对于两自由度机器人,可以通过 已知的关节角度和关节速度,以 及机器人运动学方程,计算得到
解析机器人模型
计算偏导数
雅可比矩阵描述了机器人末端与控制输入 之间的关系,通过直接计算机器人关节变 量对末端位置和姿态的偏导数得到。
根据机器人的几何模型和关节类型,解析 机器人的运动学模型,得到末端位置和姿 态与关节变量的关系。
利用解析得到的运动学模型,计算机器人 末端位置和姿态对关节变量的偏导数,得 到雅可比矩阵的元素。
参数优化
调整雅可比矩阵的参数
通过对雅可比矩阵的参数进行调整,如增加或减少矩阵的行 或列,能够优化矩阵的计算过程,提高计算效率。
优化迭代算法的参数
对于使用迭代算法计算雅可比矩阵的情形,通过调整迭代算 法的参数,如增加迭代次数、改变收敛准则等,能够提高计 算精度和速度。
控制策略改进
引入新的控制策略
针对具体应用场景,引入新的控制策略,如采用模糊控制、神经网络等,能够更好地解决机器人控制问题,进而 改进雅可比矩阵的计算效果。
计算方法
对于四自由度机器人,可以通过 已知的关节角度和关节速度,以 及机器人运动学方程,计算得到 雅可比矩阵。
05
雅可比矩阵的优化与改进
优化算法选择
选用高效算法
对于雅可比矩阵的计算,选用高效的算法能够显著提升计算速度和精度,例如采 用数值差分法、有限元法等。
机器人学_机器人雅可比矩阵
0 0 0 1
若Rot(δx,δy,δz) 和Rot(δx‘,δy’,δz‘) 表示两
个不同的微分旋转,则两次连续转动的结果为:
1 (z z ' ) y y ' z z ' 1 (x x' ) Rot(x, y, z ) Rot(x' , y ' , z ' ) (y y ' ) x x' 1 0 0 0 0 0 0 1
Trans(d x , d y , d z )Rot(k , d ) I 44
于是得微分算子Δ
0 k d z k y d 0
k z d 0 k x d 0
k y d k x d 0 0
dx dy dz 0
四. 微分旋转的无序性 当θ→0 时,有sinθ→dθ,cosθ→1.若令δx=dθx,δy=dθy, δz=dθz,则绕三个坐标轴(p16)的微分旋转矩阵分别为
0 0 1 0
0 0 0 1
略去高 阶无穷 小量
0 y 1 xy 1 x Rot( x, x) Rot( y, y ) y x 1 0 0 0 1 xy y 0 1 x Rot( y, y ) Rot( x, x) y x 1 0 0 0
令 Trans(d x , d y , d z )Rot(k , d ) I 44 为微分算子
则相对基系有dT=Δ0T,相对i系有dT=TΔi 。这里Δ的下标不同是由 于微运动相对不同坐标系进行的。
三.微分平移和微分旋转 微分平移变换与一般平移 变换一样,其变换矩阵为:
1 0 Trans(dx, dy, dz) 0 0 0 1 0 0 0 dx 0 dy 1 dz 0 1
机器人雅可比矩阵的微分

机器人雅可比矩阵的微分机器人雅可比矩阵是机器人学中非常重要的一个概念。
它是一个描述机器人末端执行器运动学的矩阵。
通过雅可比矩阵,我们可以推导出机器人各个关节运动对末端执行器运动的影响关系。
首先,我们来看一下什么是机器人末端执行器的运动学。
机器人末端执行器是指机器人手臂的末端部分,它可以进行各种运动和操作。
机器人的运动学则是研究机器人末端执行器在关节运动下的位置、速度和加速度等性质。
通过机器人运动学的建模,我们可以控制和规划机器人的运动,使其完成各种任务。
而雅可比矩阵则是描述了机器人末端执行器的运动学和关节之间的关系。
它可以从关节空间到末端执行器空间的转换。
雅可比矩阵是一个m×n的矩阵,其中m表示机器人末端执行器的自由度,n表示机器人关节的自由度。
雅可比矩阵的元素可以用数学符号表示为J,J(i,j)表示机器人末端执行器的第i个自由度对第j个关节的影响。
利用雅可比矩阵,我们可以得到机器人末端执行器的位置、速度和加速度等信息。
例如,给定机器人关节的坐标、速度和加速度,我们可以通过雅可比矩阵求得末端执行器的位置、速度和加速度。
这些信息对于机器人的运动控制、路径规划和避障等任务非常重要。
此外,雅可比矩阵还可以用于机器人的逆运动学问题。
逆运动学是指已知末端执行器的位置和姿态,求解机器人关节的坐标。
通过雅可比矩阵,我们可以将末端执行器的位置和姿态转化为关节的坐标,从而实现逆运动学的求解。
逆运动学在机器人的精确控制和运动规划中起到了重要的作用。
总结来说,机器人雅可比矩阵是描述机器人关节运动与末端执行器运动之间关系的重要工具。
它能帮助我们理解机器人末端执行器的位置、速度和加速度等运动学性质。
通过雅可比矩阵,我们可以进行机器人的运动控制、路径规划和逆运动学求解等任务。
掌握雅可比矩阵相关的知识,对于机器人学学习和应用具有重要的指导意义。
3.4机器人运动学雅可比矩阵
r f ( )
一般情况:
r f ( )
T m1 n1
r r1 , r2 , , rm R
1 , 2 , , n R
rj f j (1,2 ,,n )
j 1,2,, m
若n>m,手爪位置的关节变量有无限 个解,通常工业用机器人有3个位置变量 和3个姿态变量,共6个自由度(变量)。
f1 n m n R f m n
2、与平移速度有关的雅可比矩阵
相对于指尖坐标系的平移速度,是通过把坐标 原点固定在指尖上,指尖坐标系相对于基准坐 标系的平移速度来描述
O0 x0 y0 z0 Oe xe ye ze
:基准坐标系
:指尖坐标系
机器人雅可比矩阵机器人运动学机器人逆运动学雅可比矩阵matlab雅可比矩阵机器人正逆运动学雅克比矩阵机器人雅可比迭代矩阵家可比矩阵安堂机器人
3.4
机器人的雅可比矩阵
微分运动与速度
1、
微分运动指机构的微小运动,可用来推导不 同部件之间的速度关系。 机器人每个关节坐标系的微分运动,导致机 器人手部坐标系的微分运动,包括微分平移与微 分旋转运动。将讨论指尖运动速度与各关节运动 速度的关系。 前面介绍过机器人运动学正问题
J J1 J2
nm6
r f ( )
对位置方程进行求微分得:
dr J d r J dt dt
两边乘以dt,可得到微小位移之间的关系式
dr Jd
J 表示了手爪的速度与关节速度之间关系, 称之为雅克比矩阵。
f1 1 f J T f m 1
ze
z0
P e
Oe
xe
机器人雅可比矩阵分析
例4.2 如图所示.为了实现平面2R机械手末端沿x0轴以l m/s的速 T 度运动,求相应的关节速度 q 1 2
解:由 可以看出,只要 机械手的雅可比J(q)是满秩的方阵, 相应的关节速度即可解出
J 1 (q) x q
对于平面2R机械手,运动学方程为
平面2R机械手的速 度反解
O
x
optical center
摄像机成像模型
0 f 0
Xw
Yw
x f 0 Zc y 1 0
[1,0] 相应的关节速度 于是得到与末端速度 x 反解为 c12 c1 c12 1 ; 2 l1s2 l2 s2 l1s2
讨论:机械手接近奇异形位时, 关节速度将趋于无穷大。
当2=0; 2=180时,机械手 在水平位置, c12 c1 c12 1 ; 2 l1s2 l2 s2 l1s2
例4.2 如图所示.为了实现平面2R机械手末端沿x0轴以l m/s的速 T 度运动,求相应的关节速度 q 1 2 解:雅可比J(q)为
逆雅可比可为
1 J (q) l1l2 s2
1
l2c12 l c l c 1 1 2 12
T
l1s1 l2 s12 l2 s12
与所有合法位移垂直; 不做功、没有能量增加或 损失; 一个自由度:
=0 合法加速度 C
图5.9 粒子运动满足约束函数C, 并 绕圆周运动。
图 5.10 虚功原理要求约束力只能位于 圆周的法线方向
把作用在所有粒子上的力用一个力矢量表示, 记为Q。 则控制粒子系统的牛顿方程为
WQ q
求微分,
C C q q
四自由度机械手臂运动学分析及雅可比矩阵求解
第 6期
吴
磊等 : 四自 由度机械手臂运动学分析及雅可比矩阵求解
765
设计提供理论依据。 1 机械手臂运动学分析 1 1 正向运动学分析 该机械手臂由 4 个转动关节和 3 个连杆组成 , 终端有一个夹持器。用 D-H 方法建立杆件坐标系。 因为无论转动关节 0 如何旋转, 关节 0 的长度对机 械手臂的运动均无影响 , 所以令基准坐标系 0 与坐 标系 1 原点重 合, 取在关 节 0 与关节 1 的交点处。 原点 O 2 位于关节 2的中心位置 , Z 2 轴沿着关节 2的 方向向右, X 2 轴垂直于关节 1 和关节 2 构成的平面 指向上方。 坐标系 3 与坐标系 4原点重合。 X 3 轴垂直 于关节 2 和关节 3 构成的平面指向上方, X 4 轴垂直 于夹持器所在平面, 如图 1 所示。
[ 2, 3] [ 1]
中, 因为引入了多余的参数 , 使方程复杂度增加, 甚 至会引起无解或者无穷多解的情况 , 需要通过 观察和经验判断才能得出正确的解 , 既给运动学分 析带来了不 便, 又 增加了 机器 人控 制程 序编写 难 度
[ 8~ 11] [ 4~ 7]
。传统建立机械
手臂坐标系的方法是将固定在大地上的笛卡尔坐标 系作为参考坐标系 。这种方法容易引入不必要 的参数 , 增加计算量 , 引起计算误差增大, 使机器人 不能够精确控制。特别是在解机器人逆运动学方程
Abstract : In order to reduce the com p le x ity of k in e m atics and inverse k in e m atics equat io n so lv ing process, i m prove th e accuracy of contro , l and ca lculate the in verse kinem at ic s equation s analyt ica l so lutio n fast and prec isely , an opt i m al m ethod o f setting th e coord in ate system has been put for w ard according to the theo ry o f a robot s 4-DOF m e chanical ar m. The k in e m atics and in verse k in em atics equat io ns of the 4 -DOF m echanical ar m w ere established based on this coord in ate system. The positions of itsm ov ing elem ents and end -effectors w ith the ir re latio nship w ere presented ; th ese m ade the robo t m ove in accordance w ith a scheduled program. F in a lly , the Jacob ia n m atrix w as solved, prov idin g theoret ical basis for realizin g the m echan ica l ar m s program desig n o f velocity control in the C arte sian space . K ey w ord s : m echanical ar m; D-H param eters ; kinem at ics; in verse k in em atics ; Jacob ian m atr ix 机器人运动学着重研究了机器人各个坐标系之 间的运动关系。为了控制机器人的运动, 首先需要 在机器人中建立相应 的坐标系
六自由度机械臂雅可比矩阵计算
六自由度机械臂雅可比矩阵计算机械臂雅可比矩阵是一个非常重要的概念,用于描述机械臂末端位移与关节位移之间的关系。
它可以用于控制机械臂的运动,实现准确的位置控制和轨迹跟踪等任务。
在本文中,我们将详细介绍六自由度机械臂雅可比矩阵的计算方法。
六自由度机械臂是指具有6个可独立运动的关节的机械臂。
常见的六自由度机械臂包括SCARA机械臂、工业机器人等。
对于一个六自由度机械臂,其雅可比矩阵是一个6行6列的矩阵,其元素表示机械臂末端位移在每个关节角度变化下的变化率。
雅可比矩阵的计算方法有两种常见的方法:几何方法和微分方法。
几何方法是一种基于末端位姿和关节角度的几何关系计算雅可比矩阵的方法。
具体步骤如下:1.假设机械臂由n个关节组成,每个关节的旋转轴为z轴,关节坐标系为{X0Y0Z0},末端坐标系为{XnYnZn}。
2.根据DH参数建立机械臂的坐标系链,得到各个坐标系的变换矩阵。
3.将末端坐标系的位姿表示为关节坐标系的位姿,通过一系列的正向变换矩阵计算得到。
4.根据位姿的变换关系,通过求导的方法计算出末端位置向各个关节变量的偏导数。
5.通过逆向传播的方法计算各个偏导数,得到雅可比矩阵。
微分方法是一种基于速度和力学关系计算雅可比矩阵的方法。
具体步骤如下:1.假设机械臂由n个关节组成,每个关节的旋转轴为z轴,关节坐标系为{X0Y0Z0},末端坐标系为{XnYnZn}。
2.根据DH参数建立机械臂的坐标系链,得到各个坐标系的变换矩阵。
3.基于运动学关系,计算出末端速度和各个关节速度之间的关系,得到雅可比矩阵的第一部分。
4. 根据Newton-Euler动力学方程,计算出末端力和各个关节力之间的关系,得到雅可比矩阵的第二部分。
5.将第一部分和第二部分相加,得到雅可比矩阵。
无论使用几何方法还是微分方法,都需要根据具体的机械臂的结构和运动学参数进行计算。
在实际应用中,可以使用数值方法或符号计算方法来求解雅可比矩阵。
数值方法可以通过数值逼近法来计算雅可比矩阵,但计算结果可能不够精确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械臂雅可比矩阵求解推导
摘要:
I.引言
- 介绍机械臂和雅可比矩阵
- 简述机械臂运动学方程
II.雅可比矩阵的定义和性质
- 定义雅可比矩阵
- 说明雅可比矩阵的性质
- 介绍雅可比矩阵在机械臂运动学中的作用
III.雅可比矩阵的求解方法
- 详细推导求解雅可比矩阵的方法
- 说明方法的优缺点及适用范围
IV.机械臂雅可比矩阵的应用实例
- 介绍机械臂雅可比矩阵在实际应用中的例子
- 说明雅可比矩阵对于机械臂运动控制的重要性
V.总结
- 回顾文章的主要内容
- 强调雅可比矩阵在机械臂运动控制中的作用
正文:
I.引言
机械臂是一种广泛应用于工业、医疗、科研等领域的自动化设备。
在机械
臂的运动控制中,雅可比矩阵起到了关键作用。
本文将详细介绍机械臂雅可比矩阵的求解方法及其在机械臂运动学中的应用。
II.雅可比矩阵的定义和性质
雅可比矩阵是一个重要的数学概念,它广泛应用于机器人学中。
对于一个n 维空间的机器人运动,其雅可比矩阵是一个3n×n 的矩阵,表示机器人运动在某一点的速度方向和该点处的运动方向之间的关系。
雅可比矩阵具有以下性质:
1.雅可比矩阵是正交矩阵,即雅可比矩阵的转置等于其逆矩阵。
2.雅可比矩阵的行列式为1,即雅可比矩阵的行列式在所有运动轴上均为1。
在机械臂运动学中,雅可比矩阵用于描述关节空间和笛卡尔空间的运动关系。
具体来说,雅可比矩阵表示了在笛卡尔空间中的速度向量与关节空间中的速度向量之间的关系。
III.雅可比矩阵的求解方法
求解雅可比矩阵的方法有很多,常见的有递推法、数值法、行列式求解法等。
下面以递推法为例,详细推导求解雅可比矩阵的过程。
假设一个机械臂有n 个关节,其关节空间坐标为q,笛卡尔空间坐标为x。
根据正运动学方程,可以得到:
x = T(q)x0
其中,T(q) 是关节空间到笛卡尔空间的变换矩阵,x0 是笛卡尔空间的基点。
雅可比矩阵J 可以表示为:
J = dT(q)/dq
根据链式法则,可以得到:
dT(q)/dq = [dT1(q)/dq, dT2(q)/dq, ..., dTn(q)/dq]
其中,Ti(q) 是第i 个关节的变换矩阵。
因此,可以得到雅可比矩阵的递推公式:
J = [dT1(q)/dq, dT2(q)/dq, ..., dTn(q)/dq]
通过求解上述递推公式,可以得到机械臂的雅可比矩阵。
IV.机械臂雅可比矩阵的应用实例
在实际应用中,机械臂雅可比矩阵被广泛应用于运动控制、路径规划和运动规划等领域。
例如,在运动控制中,可以根据雅可比矩阵计算出末端执行器的速度,进而实现对机械臂的控制。
在路径规划中,可以根据雅可比矩阵计算出机械臂在运动过程中的速度和加速度,从而优化运动路径。
在运动规划中,可以根据雅可比矩阵对机械臂的运动轨迹进行规划,从而实现高效、精确的运动控制。
V.总结
本文详细介绍了机械臂雅可比矩阵的定义、性质、求解方法和应用实例。
作为机械臂运动学中的关键概念,雅可比矩阵在机械臂的运动控制、路径规划和运动规划等领域具有重要的应用价值。
