复数几何意义PPT教学课件
合集下载
复数课件ppt免费

02
复数的应用
Chapter
电路分析中的应用
电路分析中,复数是一种常用的数学工具,用于描述交 流电路中的电压、电流和阻抗等参数。
通过使用复数表示,可以简化计算过程,方便分析和设 计电路。
复数在交流电路分析中的应用包括计算交流阻抗、交流 功率和交流电流等。
信号处理中的应用
在信号处理中,复数常用于表示和处 理信号,如频谱分析和滤波器设计等 。
复数在信号处理中的应用还包括数字 滤波器设计和数字信号处理算法的实 现等。
通过将信号表示为复数形式,可以方 便地进行信号的频域分析和处理,如 傅里叶变换和离散余弦变换等。
控制系统中的应用
在控制系统中,复数常用于描 述系统的传递函数和稳定性等 特性。
通过使用复数表示,可以方便 地分析系统的频率响应和稳定 性,以及设计控制系统的参数 。
实例
$2(cos frac{pi}{3} + i sin frac{pi}{3}) + 1(cos frac{pi}{4} + i sin frac{pi}{4}) = sqrt{3}(cos frac{7pi}{12} + i sin frac{7pi}{12})$。
指数形式的计算
定义
复数指数形式是 $re^{itheta}$,其中 $r$ 是模长,$theta$ 是辐角 。
复数课件ppt免费
目录
• 复数的基本概念 • 复数的应用 • 复数的计算方法 • 复数的历史发展 • 复数的扩展知识
01
复数的基本概念
Chapter
复数的定义
总结词
复数是由实部和虚部构成的数,通常表示为a+bi,其中a是实部,b是虚部,i 是虚数单位。
3.1.2复数的几何意义PPT课件
-2
Z2:2-2i
2021
x
20
例题2
已知某个平行四边形的三个顶 点所对应的复数分别为2,4+2i, -2+4i,求第四个顶点对应的复数.
自己动动手
2021
21
解: y
4
-2
O2 4
x
答案:6i或-4+2i或8-2i
2021
22
扩展题
求下列复数的模:
(1)z1=-5i (2)z2=-3+4i (3)z3=5-5i
(简称复平面)
oa
x
x轴------实轴 y轴------虚轴
复数z=a+bi用点Z(a,b)表示.
2021
8
观察
实轴上的点都表示实数;虚
轴上的点都表示纯虚数,除原点 外,因为原点表示实数0.
复数z=a+bi用点Z(a,b)表示. 复平面内的点Z的坐标是(a,b),而 不是(a, bi),即复平面内的纵坐标 轴上的单位长度是1,而不是i.
(1)i; (2)2-2i; (3)(2+i) ×i; (4)i-1;
2021
18
解: y
(2+i) ×i
4
i-1
2
1
-2 -1 O 2
-2
(2+i) ×i 转化为 -1+2i
i i2 = -1
4
x
2-2i
注意
2021
19
解: y
4
Z3:(2+i) ×i 2 Z4:i-1 1 Z1:i
-2 -1 O 2 4
2021
13
可用下图表示出他们彼此的关系.
复数z=a+bi
复数的几何意义 课件

所以B→A=(5,-5),所以向量B→A对应的复数是 5-5i.
答案:D
归纳升华 解答此类题目的一般思路是先写出向量或点的坐标, 再根据向量的运算求出所求向量的坐标,从而求出向量所 表示的复数.
类型 3 复数的模(互动探究) [典例❸] (1)已知复数 z 满足 z+|z|=2+8i,求复数
z. (2)已知复数 z=3+ai(a 为实数),且|z|<4,求 a 的取
类型 1 复数与复平面上的点(自主研析)
[典例 1] (1)复数 z=cos 23π+isin π3在复平面内对应
的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
(2)已知复数 z=x+1+(y-1)i 在复平面内的对应点
位于第二象限,则点(x,y)所表示的平面区域是( )
A
B
C
D
(3)在复平面内,复数 6+5i,-2+3i 对应的点分别
值范围.
解:(1)法一 设 z=a+bi(a,b∈R),则|z|= a2+b2,
代入方程得 a+bi+ a2+b2=2+8i,
所
以a+ a2+b2=2,解 b=8,
得ab==-8,15,
所以
z=-
15+8i.
法二 原式可化为 z=2-|z|+8i. 所以|z|= (2-|z|)2+82,即|z|2=68-4|z|+|z|2, 所以|z|=17. 代入 z=2-|z|+8i,得 z=-15+8i. (2)因为 z=3+ai(a∈R), 所以|z|= 32+a2, 由已知得 32+a2<42, 所以 a2<7,所以 a∈(- 7, 7).
归纳升华 (1)复数的模表示复数在复平面内对应的点到原点的 距离. (2)计算复数的模时,应先找出复数的实部与虚部, 然后利用模的计算公式进行计算.复数的模是一个非负实 数,可以比较大小. (3)利用复数模的几何意义解题,体现了数形结合的 思想方法.
复数的几何意义及其应用PPT优秀课件

则 ∣ z 1- z 2∣ 的 最 大 值 是 (
)
( A) 6
( B) 5
( C) 4 ( D) 3
解法1:z1 z2z1 (2 i z1 ) 2 z1 i
z1
i
2
max
z1 z2 的最大值是4
解法 2: z1 z2 2i , z1 2i z2
94.对一个适度工作的人而言,快乐来自于工作,有如花朵结果前拥有彩色的花瓣。――[约翰·拉斯金] 95.没有比时间更容易浪费的,同时没有比时间更珍贵的了,因为没有时间我们几乎无法做任何事。――[威廉·班] 96.人生真正的欢欣,就是在于你自认正在为一个伟大目标运用自己;而不是源于独自发光.自私渺小的忧烦躯壳,只知抱怨世界无法带给你快乐。――[萧伯纳]
例1
复 数 z 满 足 条 件 ∣ z+2∣ -∣ z-2∣ =4 则复数 z 所对应的点 Z 的轨迹是
(
)
( 1) 双 曲 线 ( B ) 双 曲 线 的 右 支
( C) 线 段
( D) 射 线
例 2. 若 复 数 z 满 足 条 件 ∣ z∣ = 1 , 求 ∣ z-2i∣ 的 最 值 。
例 3 . 已 知 z 1、 z 2∈ C , 且 ∣ z 1∣ = 1 , 若 z 1+ z 2= 2 i ,
最小值是__________.
2 复数 z 满足条件∣z-2∣+∣z+i∣= 5 ,
则∣z∣的取值范围是(
)
(A)
2
5 5
,
5
(C)1, 5
(B)
2
5 5
,2
(D) 1,2
例2.已知复平面内一个椭圆的两 个焦点对应的复数分别是-1+3 i、 -1- i,且复数 1+i 对应的点正好在这 个椭圆上,则这个椭圆方程的复数 形式是———————————
复数的几何表示ppt课件

指数表示式为
z
3 i
e10 .
内容小结
1.复数的模、辐角、幅角主值; 2.复数的各种表示法.
各种表示法可相互转化,
思考题
1.是否任意复数都有辐角?
它的模为零而辐角不确定.
作业
习题一: 1(2)(4)、2、4(1)(6) 7,8(3)(4)(5)
例4 将通过两点z1 x1 iy1 与 z2 x2 iy2 的直 线用复数形式的方程来表示.
2.用复平面上的向量表示复数
向量 OP与复数 z 一x 一iy对应,故用它表示复数.
y
P
z x iy
z
o
x
注意: 复数 z,点 z,向量 z 可视为同一个概念。
y
z 与 z 在复平面上关于实轴对称. y r
z x yi
O
x
x
z x yi
二、复数的模和幅角
复数z 的模:向量 OP的长度, 记作
由于z 位于第三象限,
arg z arctan ( 1 ) π 3
arctan
1 3
π .
y
3
x
1
arctan y
x
arctan y
x
arctan y x
arctan y x
例2 证明复平面上的三角不等式
(1) z1 z2 z1 z2 ; (2) z1 z2 z1 z2 .
证 两复数的加减运算满足向量的平行四边形法则,
6
6
5π i
z 4e 6 . 习惯上取主辐角
例5 将下列复数化为三角表示式与指数表示式:
z sin i cos ;
5
5
解 r z 1,
sin
复数的几何意义ppt课件(公开课)

阻抗
在交流电路中,电阻、电 感和电容的阻抗可用复数 表示,实部表示电阻,虚 部表示电感和电容。
频域分析
通过傅里叶变换将时域信 号转换为频域信号,频域 信号可用复数表示。
振动与波动的复数描述
简谐振动
简谐振动的位移、速度和加速度可用复数表示,方便进行振幅、 频率和相位的计算。
波的叠加
多个波叠加时,可用复数表示各波的振幅和相位,便于计算合成 波的振幅和相位。
复数的运算与几何意
04
义
复数的加法与减法
01
02
03
加法运算规则
设$z_1 = a + bi$,$z_2 = c + di$,则$z_1 + z_2 = (a + c) + (b + d)i$。
减法运算规则
设$z_1 = a + bi$,$z_2 = c + di$,则$z_1 - z_2 = (a - c) + (b - d)i$。
复数的几何意义ppt课 件(公开课)
目录
• 引言 • 复数的表示方法 • 复数的几何解释 • 复数的运算与几何意义 • 复数在几何中的应用 • 复数在其他领域的应用
引言
01
复数的基本概念
01
02
03
04
定义
复数是形如 $a + bi$ 的数, 其中 $a$ 和 $b$ 是实数,$i$ 是虚数单位,满足 $i^2 = -1$。
实部和虚部
在复数 $a + bi$ 中,$a$ 称 为实部,$b$ 称为虚部。
共轭复数
若 $z = a + bi$,则其共轭复 数为 $a - bi$。
模
7.1.2 复数的几何意义(课件)高一数学(人教A版2019必修第二册)

平面向量
一 一对应
复平面内的点Z(a,b)
2.复数的模
|| = | + i| =
2 + 2
3.共轭复数 如果 = + i,那么ҧ = − i.
一 一对应
作业
习题7.1 第8,10题
(1)
(4)
2 + 5i, (2)
−3 − i, (5)
−3 + 2i,
5,
(3)
(6)
y
2 − 4i,
−3i.
2 5i
3 2i
5
O
x
3 i
3i
2 4i
复数的几何意义
问题2:在平面直角坐标系中,每一个平面向量都可以用一个有序实数
对来表示,而有序实数对与复数是一一对应的.你能用平面向量来表示复
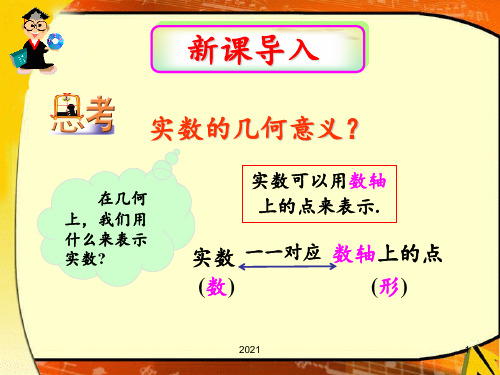
我们知道,实数与数轴上的点一一对应,因此实数可以用
数轴上的点来表示.复数有什么几何意义呢?
一 一对应
(数) 实数
(形) 数轴上的点
o
1
x
复数的几何意义
问题1:根据复数相等的定义,任何一个复数 = + i都可以由一
个有序实数对 (, )唯一确定;反之也对.由此你能想到复数的几何
表示方法吗?
不等式|| > 1的解集是圆 = 1外部所有的点组成的集合,
这两个集合的交集,就是上述不等式组的解集,
也就是满足条件1 < || < 2的点的集合.
容易看出,所求的集合是以原点O为圆心,以1及2为半径的两个圆所夹的圆环,但
不包括圆环的边界.
课堂小结
复数 = +
一 一对应
1.复数几何意义
数学课件ppt复数的几何意义

02
复数在平面坐标系中表示
复平面与坐标系建立
复平面的定义
复平面是一个二维平面,其中横 轴表示实部,纵轴表示虚部。
坐标系的建立
在复平面上,以原点为起点,水平 向右为实轴正方向,垂直向上为虚 轴正方向,建立平面直角坐标系。
坐标表示
复数 $z = a + bi$ 在复平面上对应 的点的坐标为 $(a, b)$。
乘除运算对应几何变换
乘法运算
两复数相乘,其几何意义是对应的两个向量先旋转后伸缩。具体地,设 $z_1 = r_1(cos theta_1 + i sin theta_1)$,$z_2 = r_2(cos theta_2 + i sin theta_2)$,则 $z_1 times z_2 = r_1r_2(cos(theta_1 + theta_2) + i sin(theta_1 + theta_2))$,即模长相乘,辐角相加。
常见函数图像绘制技巧分享
坐标轴选择
在绘制复数函数图像时,可以选择实部-虚部坐标系或模辐角坐标系。不同的坐标系选择会对图像呈现产生不同的 影响。
色彩运用
通过合理运用色彩,可以更加清晰地展示函数的特征和性 质。例如,可以使用不同颜色表示函数的实部和虚部,或 者使用渐变色表示函数的模长变化。
关键点标注
在图像上标注关键点,如零点、极值点、对称中心等,有 助于更好地理解函数的性质和行为。
应用举例:电路分析中相位差计算
交流电路中的电压和电流通常表示为复数形式,其中实部表示幅度,虚部表示相位。通过复数的乘除运算可以方便地计算电 压和电流之间的相位差。
例如,在RLC串联电路中,已知电源电压 $U = 220angle 0^circ V$,电阻 $R = 10Omega$,电感 $L = 0.4H$,电容 $C = 5mu F$。求电流 $I$ 和电阻两端电压 $U_R$ 的相位差。通过复数运算可得 $I = frac{U}{Z}$,其中阻抗 $Z = R + jomega L - jfrac{1}{omega C}$。进一步计算可得相位差 $Delta phi = phi_I - phi_{U_R}$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知复数z对应点A,说明下列各 式所表示的几何意义.
(1)|z-(1+2i)| 点A到点(1,2)的距离
(2)|z+(1+2i)|
点A到点(-1, -2)的距离
(3)|z-1|
点A到点(1,0)的距离 (4)|z+2i|
点A到点(0, -2)的距离
练习:已知复数m=2-3i,若复数 z满足不等式|z-m|=1,则z所对 应的点的集合是什么图形?
4
新课讲解 1.复数加法运算的几何意义?
符合向量加法 的平行四边形
法则.
Z1+ Z2=OZ1 +OZ2 = OZ
y
Z(a+c,b+d)
Z2(c,d)
Z1(a,b)
o
x
2.复数减法运算的几何意义?
符合向量减 法的三角形
法则.
复数z1-z2
y
Z2(c,d)
向量Z2Z1
Z1(a,b)
o
x
|z1-z2|表示什么? 表示复平面上两点Z1 ,Z2的距离
复数的几何意义(一)
一一对应
复数z=a+bi
直角坐标系中的点Z(a,b)
(数)
(形)
z=a+bi Z(a,b)
y
建立了平面直角
坐标系来表示复数的 b 平面 ------复数平面
(复平面)
a
o
x
x轴------实轴
y轴------虚轴
复数的几何意义(二)
复数z=a+bi 一一对应 直角坐标系中的点Z(a,b)
以点(2, -3)为圆心, 1为半径的圆上
3、复数加减法的几何意义
(1) |z1|= |z2| 平行四边形OABC是 菱形
(2) | z1+ z2|= | z1- z2|
平行四边形OABC是 矩形 o
C
z2 z2-z1
z1 A
(3) |z1|= |z2|,| z1+ z2|= | z1- z2| 平行四边形OABC是 正方形
一一对应
一一对应
平面向量 O Z
y
z=a+bi
Z(a,b)
b
a
o
x
复数的模的几何意义
对应平面向量 O Z 的模|O Z |,即复数
z=a+bi在复平面上对应的点Z(a,b)到原点的
距离。
y
| z | = a2 b2
z=a+bi Z (a,b)
O
x
3.2.1复数的Байду номын сангаас数形式的 加减运算及其几何意义
2020/12/11
z1+z2
B
PPT教学课件
谢谢观看
Thank You For Watching
11
