(完整)九年级数学上册旋转单元测试题(含答案),推荐文档
(人教版)九年级上册数学《旋转》单元测试题(含答案)

一.选择1. ( 20XX?广东)在以下交通标记中,既是轴对称图形,又是中心对称图形的是())度,才能与自己重合.2. 一个等边三角形绕其旋转中心起码旋转(A. 30°B . 60°C . 120XXD . 180°【评论】本题考察旋转对称图形的观点:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这类图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.3.在平面直角坐标系中,点(3 ,- 2) 对于原点对称点的坐标是()A.(3,2)B.(-3,-2)C.(-3,2)D.(-3,-2)4.如图,正方形ABCD经过旋转获得正方形AB′C′D′,则旋转的角度为()A. 30 ° B.45 °C. 60°D. 90°5.在等边三角形、平行四边形、矩形和圆这四个图形中,既是轴对称图形,又是中心对称图形的有()A.1个B.2 个C.3 个D.4 个【答案】B6. ( 20XX?苏州)如图,△AOB为等腰三角形,极点 A 的坐标( 2,),底边OB在x轴上.将△AOB绕点 B 按顺时针方向旋转必定角度后得△A′ O′ B′,点A 的对应点A′在x 轴上,则点 O′的坐标为()A.(,)B.(,)C.(,)D.(,4)∴O′D=4×=,7. ( 20XX·浙江金华)如图,将Rt △ ABC绕直角极点顺时针旋90°,获得△ A′B′C,连转结 AA′,若∠1=20XX则∠ B 的度数是【】A.70°B.65°C.60°D.55°在 Rt △ ABC中,∠ B=90° - ∠BAC=90°-25 ° =65°【评论】本题考察了旋转的性质和等腰三角形的性质,娴熟掌握旋转的性质是重点8.( 20XX?天津)如图,在△ ABC 中, AC=BC,点 D、 E 分别是边 AB、AC的中点,将△ ADE 绕点 E 旋转 180°得△ CFE,则四边形ADCF必定是()A.矩形B.菱形C.正方形D.梯形9.(南通中考)如 Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且 AC在直 l 上,将△ ABC点 A 旋到①,可获得点P1,此 AP1=2;将地点①的三角形点P1旋到地点②,可获得点P2,此 AP2=2+ 3 ;将地点②的三角形点P2旋到地点③,可获得点P3,此 AP3=3+ 3 ;⋯按此律旋,直到点P20XX止,AP20XX等于()A. 20XX+6713B. 20XX+6713C. 20XX+6713D. 20XX+671310.( 20XX?孝感)如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D( 5, 3)在边 AB上,以 C为中心,把△ CDB旋转90°,则旋转后点D的对应点 D′的坐标是()A.( 2, 10) B .(﹣ 2, 0) C .( 2,10)或(﹣ 2, 0) D .( 10, 2)或(﹣ 2, 0)二.填空题11.(20XX?益阳)如图,将等边△绕极点A 顺时针方向旋转, 使边 AB 与 重合得△ ,ABCACACD的中点E 的对应点为,则∠的度数是.BC F EAF【答案】 60°【考点】旋转的性质【分析】由旋转的性质找到旋转角即可.12(. 20XX 年广东汕尾)如图,把△ ABC 绕点C 按顺时针方向旋转35°,获得△ A ′ B ′ C ,A ′ B ′交 AC 于点D .若∠ A ′ DC =90°,则∠A =.13. ( 20XX?铁岭)如图,在△ ABC 中, AB=2, BC=3.6,∠ B=60°,将△ ABC 绕点 A 按顺时针旋转必定角度获得△ ADE,当点 B 的对应点 D 恰巧落在BC边上时,则CD的长为.【答案】 1.614.( 20XX?邵阳)如图,在平面直角坐标系xOy中,已知点 A(3,4),将 OA绕坐标原点 O 逆时针旋转90°至OA′,则点A′的坐标是.15.( 20XX?广东)如图,△ABC绕点A顺时针旋转 45°获得△A′B′C′,若∠BAC=90°,AB=AC=,则图中暗影部分的面积等于.∵A B=AC三.解答题16. ( 20XX?毕节)在以下网格图中,每个小正方形的边长均为 1 个单位.在Rt △ ABC中,∠C=90°, AC=3, BC=4.(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;(2)若点 B 的坐标为(﹣3,5),试在图中画出直角坐标系,并标出A、 C两点的坐标;(3)依据( 2)的坐标系作出与△ABC对于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.17.( 20XX?扬州)如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△ DBE后,再把△ ABC沿射线平移至△ FEG, DF、 FG订交于点 H.(1)判断线段DE、FG的地点关系,并说明原因;(2)连结CG,求证:四边形CBEG是正方形.(2)依据旋转和平移的性质可得找出对应线段和角,而后再证明是矩形,后依据邻边相等可得四边形 CBEG是正方形.【解答】(1)解:FG⊥E D原因:【评论】本题主要考察了图形的旋转和平移,娴熟掌握旋转和平移的性质是解决本题的重点。
图形的旋转测试题(含答案)
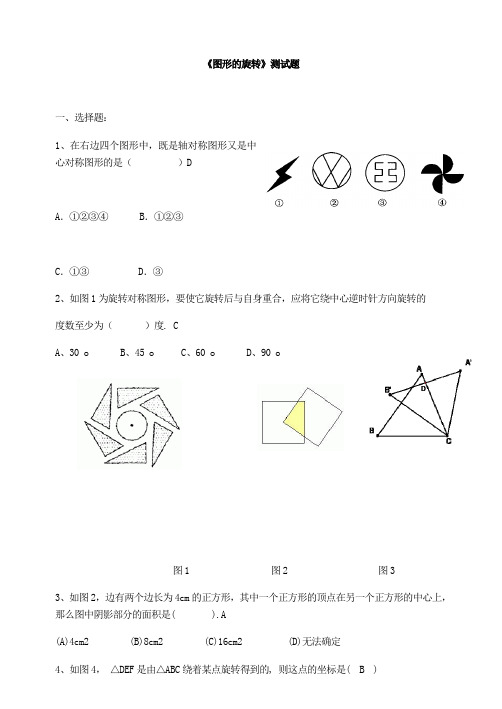
《图形的旋转》测试题一、选择题:1、在右边四个图形中,既是轴对称图形又是中心对称图形的是()DA.①②③④ B.①②③C.①③ D.③2、如图1为旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的度数至少为()度. CA、30 oB、45 oC、60 oD、90 o图1 图2 图33、如图2,边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4,△DEF是由△ABC绕着某点旋转得到的, 则这点的坐标是( B )图5 图4 A. (1,1) B. (0,1) C. (−1,1) D. (2,0)二、填空题5、点a 4(,)与3b (,)关于原点对称,则a b += .-76、如图3,把三角形△ABC 绕着点C 顺时针旋转350,得到△A 'B 'C ,A 'B '交AC 于点D ,若∠A 'DC=900,则∠A 的度数是__________。
5507、如图5, △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6,△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m (0(<m<180()度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______.80(或120(.三、解答题9、作图题(1)如图7,画出△ABC 绕点O 顺时针旋转60°所得到的图形.图6 BA CO图7 图8(2)如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图,在△ABC 中,∠B=900,∠C=300,AB=1,将△ABC 绕顶点A 旋转1800,点C 落在C1处,则C C1的长为( )A .24B .4C .32D .522、如图,△ABC 中,∠ACB=1200,将它绕着点C 旋转300 后得到△DCE ,则∠ACE=∠A+∠E=3、如图,在Rt △ABC 中,∠ACB=90°,∠A=35°,以直角顶点C•为旋转中心,将△ABC 旋转到△A ′B ′C 的位置,其中A ′、B ′分别是A 、B 的对应点,且点B 在斜边A ′B ′上,直角边CA ′交AB 于D ,求∠BDC 的度数.4,如图,正方形ABCD 中,E 在BC 上,F 在AB 上且∠FDE=45°,•△DEC 按顺时针方向转动一个角度后成为△DGA .(1)图中哪一个点是旋转中心?(2)旋转了多少度?(3)指出图中的对应点,对应线段和对应角;(4)求∠GDF 的度数.5、已知如图,正方形ABCD 中,E 为CD 边上一点,F 为BC 边上一点,CE=CF:(1)EBC FDC ∠∠与相等吗?(2)△DCF 能与△BCE 重合吗?(3)试判断BE 与DF 的位置关系并说明理由,6.如图所示,四边形ABCD 中,∠BAD=∠C=90°,AB=AD ,AE ⊥BC 于E ,△BEA 旋转后能与△DFA 重合.(1)旋转中心是哪一点?(2)旋转了多少度?(3)若AE=5cm ,求四边形ABCD 的面积.7,如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连结BK和DM,试用旋转的思想说明线段BK与DM的关系.,8,.如图所示,等边△ABC中,D是AB边上的动点(不与A、B重合),以CD为一边,向上作等边△EDC。
人教版九年级上册数学《旋转》单元测试题含答案

故选C.
考点:1.关于原点对称的点的坐标;2.坐标与图形变化-平移.
6.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A'BC'的位置,则AA'的长为( )
D、因为点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,所以△ODE绕点C顺时针旋转60°得到△OBC,所以D选项错误.
故选C
【点睛】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正六边形和等边三角形的性质.
5. 在直角坐标系中,将点(﹣2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知a<0,则点P(﹣a2,﹣a+1)关于原点的对称点P′在第_____象限.
12.如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合连接CD,则∠BDC的度数为_____度.
13.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,Rt△AB'C'可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段B'C的长为______.
数.
七、(本题满分12分)
22.如图, 口ABCD中,AB⊥AC,AB=1,BC= ,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
(1)试说明 旋转过程中,AF与CE总保持相等;
人教版九年级数学上册 第21~23章阶段 测试题(含答案)

人教版九年级数学上册 第二十一章一元二次方程-第二十三章旋转 同步测试题(满分:150分 时间:120分钟)一、选择题(本大题共10个小题,每小题4分,共40分)每小题都有代号为A 、B 、C 、D 四个答案选项,其中只有一个是正确的,请将正确选项的代号填写在答题框中,填写正确记4分,不填、填错或多填记0分.1.下列图形中,属于中心对称图形的是( )A B C D2.将一元二次方程x 2-2x -2=0配方后所得的方程是( ) A .(x -2)2=2 B .(x -1)2=2 C .(x -1)2=3 D .(x -2)2=3 3.将抛物线y =x 2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数解析式是 ( )A .y =(x +2)2+1 B .y =(x -2)2+1 C .y =(x +2)2-1 D .y =(x -2)2-1 4.在平面直角坐标系中,将点(-2,3)关于原点对称的点向左平移2个单位长度得到的点的坐标是( )A .(4,-3)B .(-4,3)C .(0,-3)D .(0,3) 5.用公式法解方程4y 2=12y +3,解为( ) A .y =-3±62 B .y =3±62 C .y =3±232D .y =-3±2326.已知抛物线y =x 2-8x +c 的顶点在x 轴上,则c 的值是( ) A .16 B .-4 C .4 D .87.已知关于x 的一元二次方程(k -1)x 2-2x +2=0有两个不相等的实数根,则k 的取值范围值是( )A .k<32B .k ≤32C .k <32且k≠1D .k ≤32且k≠18.在同一平面直角坐标系中,函数y =mx +m 和函数y =-mx 2+2x +2(m 是常数,且m≠0)的图象可能是( )9.如图,在△ABC 中,∠CAB =65°,将△ABC 在平面内绕点A 旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )A .35°B .40°C .50°D .65°10.抛物线y =ax 2+bx +c 的顶点为D(-1,2),与x 轴的一个交点A 在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b 2-4ac <0;②a+b +c <0;③c-a =2;④方程ax 2+bx +c -2=0有两个相等的实数根.其中正确结论的个数为( )A .1个B .2个C .3个D .4个 二、填空题(本大题共6个小题,每小题4分,共24分)11.已知x 1,x 2是方程x 2-3x -1=0的两根,则1x 1+1x 2=_______.12.关于x 的方程(m -3)xm 2-7-x =5是一元二次方程,则m =_______.13.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h =-52t 2+20t +1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为_______.14.如图,若将图中的抛物线y =x 2-2x +c 向上平移,使它经过点(2,0),则此时抛物线位于x 轴下方的图象对应的x 的取值范围是_______.15.如图,在边长为1的正方形网格中,A(1,7),B(5,5),C(7,5),D(5,1).若线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标为_______.16.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x 轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为_______.三、解答题(本大题共9小题,共86分)解答题应写出必要的文字说明或推演步骤.17.(8分)解方程:(1)2x2+3=7x; (2)(2x+1)2+4(2x+1)+3=0.18.(8分)关于x的一元二次方程x2+kx-6=0的一个根是3,求方程的另一个根和k 的值.19.(8分)已知在平面直角坐标系内,抛物线y=x2-bx+6经过x轴上两点A,B,点B 的坐标为(3,0),与y轴相交于点C.(1)求抛物线的解析式;(2)求△ABC的面积.20.(10分)如图,在平面直角坐标系中,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0).(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;(2)画出将△ABC绕原点O顺时针方向旋转90°得到的△A2B2O.21.(10分)如图,从一块长80厘米,宽60厘米的铁片中间截去一个小长方形,使截去小长方形的面积是原来铁片面积的一半,并且剩下的长方框四周的宽度一样,求这个宽度.22.(10分)已知关于x的一元二次方程x2-(m-3)x-m=0.(1)试判断原方程根的情况;(2)若抛物线y=x2-(m-3)x-m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(提示:AB =|x2-x1|)23.(10分)如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,22,10,△ADP绕点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;(2)求∠BPQ 的大小.24.(10分)服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x 为正整数)之间所满足的函数关系如图所示.(1)求y 与x 之间所满足的函数关系式,并写出x 的取值范围;(2)设服装厂所获利润为w(元),若10≤x≤50(x 为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?25.(12分)如图,二次函数y =12x 2+bx +c 的图象交x 轴于A ,D 两点并经过点B ,已知点A 的坐标是(2,0),点B 的坐标是(8,6).(1)求二次函数的解析式;(2)若抛物线的对称轴上是否存在一个动点P ,使点P 到点B ,点D 的距离之和最短,若存在,求出点P 的坐标;若不存在,请说明理由;(3)该二次函数的对称轴交x 轴于点C ,连接BC ,并延长BC 交抛物线于点E ,连接BD ,DE ,求△BDE 的面积.参考答案一、选择题二、填空题、11、-3 12、-3 13、4s 14、0<x<2 15、(3,3)或(6,6) 16、1三、解答题17、(1)解:x 1=12,x 2=3. (2)解:x 1=-1,x 2=-2.18、解:设它的另一个根是a ,由根与系数的关系,得⎩⎪⎨⎪⎧3a =-6,3+a =-k ,解得⎩⎪⎨⎪⎧a =-2,k =-1. ∴方程的另一个根是-2,k 的值为-1.19、解:(1)把点B 的坐标(3,0)代入抛物线y =x 2-bx +6得0=9-3b +6,解得b =5, ∴抛物线的解析式y =x 2-5x +6.(2)令x 2-5x +6=0,解得x 1=3,x 2=2;令x =0,得y =6. ∴A(2,0),B(3,0),C(0,6). ∴S △ABC =12×(3-2)×6=3.20、解:(1)如图所示,△A 1B 1C 1为所求作的三角形.(2)如图所示,△A 2B 2O 为所求作的三角形.21、解:设长方框的宽度为x 厘米,则减去小长方形的长为(80-2x)厘米,宽为(60-2x)厘米,由题意,得(80-2x)(60-2x)=12×80×60.解得x 1=10,x 2=60(不合题意,舍去). 答:长方框的宽度为10厘米.22、解:(1)Δ=(m -3)2-4(-m)=m 2-2m +9=(m -1)2+8,∵(m-1)2≥0,∴Δ=(m-1)2+8>0.∴原方程有两个不相等的实数根.(2)存在最小值.理由如下:由题意知,x1,x2是原方程的两根,∴x1+x2=m-3,x1·x2=-m.∵AB=|x1-x2|,∴AB2=(x1-x2)2=(x1+x2)2-4x1x2=(m-3)2-4(-m)=(m-1)2+8.∴当m=1时,AB2有最小值8,∴AB有最小值,最小值为2 2.23、解:(1)证明:∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°.∵△ADP沿点A旋转至△ABP′,∴AP=AP′,∠PAP′=∠DAB=90°.∴△APP′是等腰直角三角形.(2)∵△APP′是等腰直角三角形,∴PP′=2PA=2,∠APP′=45°.∵△ADP沿点A旋转至△ABP′,∴PD=P′B=10.在△PP′B中,PP′=2,PB=22,P′B=10,∵(2)2+(22)2=(10)2,∴PP′2+PB2=P′B2.∴△P′P2B为直角三角形,∠P′PB=90°.∴∠BPQ=180°-∠APP′-∠P′PB=180°-45°-90°=45°.24、解:(1)当10≤x≤50时,设y 与x 之间的函数关系式为y =kx +b ,则⎩⎪⎨⎪⎧10k +b =100,50k +b =80.得⎩⎪⎨⎪⎧k =-0.5,b =105.∴当10≤x≤50时,y 与x 之间的函数关系式为y =-0.5x +105. 当x >50时,y =80,∴y 与x 之间的函数关系式为y =⎩⎪⎨⎪⎧-0.5x +105(10≤x≤50),80(x>50).(2)由题意,得w =(-0.5x +105-65)x =-0.5x 2+40x =-0.5(x -40)2+800,∴当x =40时,w 取得最大值,此时w =800.答:批发该种服装40件时,服装厂获得利润最大,最大利润是800元. 25、解:(1)将A(2,0),B(8,6)代入y =12x 2+bx +c ,得⎩⎪⎨⎪⎧2+2b +c =0,32+8b +c =6.解得⎩⎪⎨⎪⎧b =-4,c =6. ∴二次函数的解析式为y =12x 2-4x +6.(2)∵y=12x 2-4x +6=12(x -4)2-2,∴对称轴为直线x =4.连接AB 交抛物线对称轴于点P ,连接PD.∵点A ,点D 是抛物线y =12x 2-4x +6与x 轴的交点,∴点A 和点D 关于直线x =4对称,∴PA =PD.∴PB+PD =PA +PB =AB ,此时PB +PD 的值最小. 设AB 所在直线的解析式为y =kx +d(k≠0), 将A(2,0),B(8,6)代入y =kx +d ,得⎩⎪⎨⎪⎧2k +d =0,8k +d =6,解得⎩⎪⎨⎪⎧k =1,d =-2. ∴AB 所在直线的解析式为y =x -2.当x =4时,y =4-2=2,∴点P 的坐标为(4,2).∴在抛物线的对称轴上存在一个动点P(4,2),使点P 到点B ,点D 的距离之和最短. (3)由(2)知,二次函数图象的顶点坐标为(4,-2),∴点C 的坐标为(4,0). ∵点A ,点D 关于直线x =4对称且A(2,0), ∴点D 的坐标为(6,0).∴CD=6-4=2.设直线BC 的解析式为y =mx +n(m≠0),将点B(8,6),C(4,0)代入y =mx +n ,得⎩⎪⎨⎪⎧8m +n =6,4m +n =0,解得⎩⎪⎨⎪⎧m =32,n =-6.∴直线BC 的解析式为y =32x -6.联立⎩⎪⎨⎪⎧y =32x -6,y =12x 2-4x +6,解得⎩⎪⎨⎪⎧x 1=3,y 1=-32,⎩⎪⎨⎪⎧x 2=8,y 2=6. ∴点E 的坐标为(3,-32).∴S △BDE =S △CDB +S △CDE =12CD·y B +12CD·(-y E )=12×2×6+12×2×32=152.。
人教版数学九年级上册《旋转》单元测试题(附答案)
16.如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠B′AB等于_____.
17.在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB,连接线段AB,若直线y=kx-2与△OAB有交点,则k的取值范围是____.
三、解答题
19.不同的“基本图形”的旋转可能具有相同的旋转效果.如图,点O是六个正三角形的公共顶点,这个图案可以看作是哪个“基本图形”以点O为旋转中心经过怎样旋转组合得到的?
20.如果把钟表的时针在任一时刻所在的位置作为起始位置,那么时针旋转出一个平角及一个周角,至少需要多长时间?
21.如图,△ABC绕点O旋转后,顶点A 对应点为A′,试确定旋转后的三角形.
( )
A.105°B.115°C.120°D.135°
【答案】C
【解析】
试题分析:∵DE=DF,∠EDF=30°,∴∠DEF= (180°﹣∠EDF)=75°,∴∠DEC=105°,∵∠C=45°,∴∠CDE=180°﹣45°﹣105°=30°,∴∠BDN=120°,故选C.
考点:旋转的性质.
10.如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为()
2.点A的坐标为(2,3),则点A关于原点的对称点A′的坐标为()
人教版九年级数学上册第23章旋转、24章圆 综合测试题(含答案)

九年级上册23章、24章综合测试题〔答案〕学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题〔共 14 小题,每题 3 分,共 42 分〕1.左边图形通过〔〕变换可以得到右边图形.A.顺时针旋转90∘B.平移C.逆时针旋转90∘D.旋转100∘2.以下语句中不正确的有〔〕①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;④长度相等的两条弧是等弧.A.3个B.2个C.1个D.以上都不对3.如图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,将格点△ABC〔顶点在小正方形的顶点上〕分别作以下三种变换:①先以点A为中心顺时针旋转90∘,再向右平移4格,最后向上平移4格;②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针旋转90∘;③先以直线MN为轴作轴对称图形,再向上平移4格,最后以点A的对应点为中心顺时针旋转90∘.其中,能将△ABC变换成△PQR的种数是〔〕A.0种B.1种C.2种D.3种4.一个长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚〔顺时针方向〕,木板点A位置的变化为A→A l→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30∘的角,那么点A滚到A2位置时共走过的途径长为〔〕A.7 2πcmB.236πcm C.43πcm D.52πcm5.如图,在扇形铁皮AOB中,OA=20,∠AOB=36∘,OB在直线l上.将此扇形沿l按顺时针方向旋转〔旋转过程中无滑动〕,当OA第一次落在l上时,停顿旋转.那么点O所经过的道路长为〔〕A.20πB.22πC.24πD.20π+10√5−106.如图,⊙O是△ABC的外接圆,∠A=40∘,那么∠OCB等于〔〕A.60∘B.50∘C.40∘D.30∘7.以下有关圆的一些结论:①与半径长相等的弦所对的圆周角是30∘;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的选项是〔〕A.①②③B.①③④C.②③D.②④8.如图,两个半径为1,圆心角为90∘的扇形OAB和扇形O′A′B′叠放在一起,点O′在弧AB上,四边形OPO′Q是正方形,那么阴影局部的面积等于〔〕A.π2−1 B.π4−12C.π2−2 D.π4−19.⊙O的半径为4cm,A是线段OP的中点,OP=8cm,点A与⊙O的位置关系是〔〕A.在圆内B.在圆上C.在圆外D.不能确定10.如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上挪动时,〔不与点A、B重合〕,以下关于点P描绘正确的选项是〔〕第 1 页A.到CD的间隔保持不变B.到D点间隔保持不变C.等分BD^D.位置不变11.如图,小红要制作一个高为8cm,底面圆直径是12cm的圆锥形小漏斗,假设不计接缝,不计损耗,那么她所需纸板的面积是〔〕A.60πcm2B.48πcm2C.120πcm2D.96πcm212.如图,等腰三角形ABC中,AC=AB=√41,BC=10,以A为圆心,8为直径的圆与直线BC的位置关系为〔〕A.相离B.相切C.相交D.相切或相离13.如图,在平面直角坐标系中,菱形ABCD的顶点C的坐标为(−1, 0 ),点B的坐标为(0, 2),x+5与x轴、y轴分别交于点N、M.将菱形ABCD沿x轴向右点A在第二象限,直线y=−12平移m个单位,当点A落在MN上时,那么m为〔〕A.1B.2C.3D.414.如图,△ABC内接于⊙O,∠BAC=120∘,AB=AC,BD为⊙O的直径,AB=3,那么AD的值为〔〕A.6B.3√5C.5D.3√3二、填空题〔共 6 小题,每题 3 分,共 18 分〕15.一条弧长等于10π,它的半径等于30,那么它的圆心角等于________.16.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA,OB,OC,OD的中点,假设⊙O的半径为2,那么阴影局部的面积为________.17.底面半径为1,母线长为4的圆锥的侧面积等于________.18.工艺美术中,常需设计对称图案.在如图的正方形网格中,点A,D的坐标分别为(1, 0),(9, −4).请在图中再找一个格点P,使它与的4个格点组成轴对称图形,那么点P的坐标为________〔假如满足条件的点P不止一个,请将它们的坐标都写出来〕.19.如图,假设将△ABC的绕点C顺时针旋转90∘后得到△DEC,那么A点的对应点D的坐标是________,B点的对应点E的坐标是________,请画出旋转后的△DEC.〔不要求写画法〕20.将一个自然数旋转180∘后,可以发现一个有趣的现象,有的自然数旋转后还是自然数.例如,808,旋转180∘后仍是808.又如169旋转180∘后是691.而有的旋转180∘后就不是自然数了,如37.试写一个五位数,使旋转180∘后仍等于本身的五位数________.〔数字不得完全一样〕三、解答题〔共 5 小题,每题 10 分,共 50 分〕21.如图,在Rt△ABC中,∠ACB=90∘,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.求:(1)旋转角的大小;(2)假设AB=5,AC=4,求BE的长.22.根据图所示,图形2、3、4、5与6分别可以看成是由图形1经过图形的什么变换而得到的?假设是轴对称,请指出图形的对称轴;假设是平移,请指出平移的方向与平移的间隔;假设是旋转,请指出旋转的中心和旋转的角度;假设是几个变换的结合,请分别加以说明.23.残缺的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.测得AB=24cm,CD=8cm.求这个圆的半径.24.△ABC各顶点坐标分别为A(5, 1),B(2, 3),C(0, 0),将它绕原点顺时针方向旋转90∘,得到△A1B1C1(1)求A1,B1,C1的坐标;(2)求△A1B1C1的面积.25.,如图,在梯形ABCD中,AD // BC,DA=DC,以点D为圆心,DA长为半径的⊙D与AB相切于A,与BC交于点F,过点D作DE⊥BC,垂足为E.(1)求证:四边形ABED为矩形;(2)假设AB=4,ADBC =34,求CF的长.答案1.A2.C3.D4.B5.C6.B7.C8.A9.B10.D11.A12.B13.C14.D15.60度16.817.4π18.(9, −6)(2, −3)19.3,02,220.1181121.解:(1)∵△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上,∴∠ACE=90∘,即旋转角为90∘;(2)在Rt△ABC中,∵AB=5,AC=4,∴BC=√52−42=3,∵△ABC绕着点C旋转得到△DCE,∴CE=CA=4,∴BE=BC+CE=3+4=7.22.解:图1绕图1和图2的对应点连线的中点旋转180∘得到图2;图1沿直线l1平移AE长度得到图3;图1与图4关于直线l2成轴对称,将图1沿直线l2翻折得到图4,对称轴是直线l2;图1绕点O旋转180∘后,再沿直线l2翻折得到图5;图1沿直线l1平移AE长度,再沿直线l2翻折得到图6.23.圆的半径为13cm.24.解:(1)如图,△ABC绕原点顺时针方向旋转90∘得到△A1B1C1,点A1,B1,C1的坐标分别为(5, −1),(3, −2),(0, 0);(2)△A1B1C1的面积=5×2−12×2×3−12×2×1−12×1×5=3.5.第 3 页25.(1)证明:∵⊙D与AB相切于点A,∴AB⊥AD,∵AD // BC,DE⊥BC,∴DE⊥AD,∴∠DAB=∠ADE=∠DEB=90∘,∴四边形ABED为矩形.(2)解:∵四边形ABED为矩形,∴DE=AB=4,∵DC=DA,∴点C在⊙D上,∵D为圆心,DE⊥BC,∴CF=2EC,∵AD BC =34,设AD=3k(k>0)那么BC=4k,∴BE=3k,EC=BC−BE=4k−3k=k,DC=AD=3k,由勾股定理得DE2+EC2=DC2,即42+k2=(3k)2,∴k2=2,∵k>0,∴k=√2,∴CF=2EC=2√2.。
【初三数学】抚顺市九年级数学上(人教版)第二十三章旋转单元测试题(含答案)

人教版九年级上册第二十三章旋转单元测试(含答案)一、选择题1、在图所示的4个图案中既有图形的旋转,还有图形轴对称的是()2、右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是( D )A ①⑤B ②④C ③⑤D ②⑤3、在我国古代数学家赵爽所著《勾股圆方图注》中所画的图形(如图),下列说法正确是()A 它是轴对称图形,但不是中心对称图形B 它是轴对称图形,又是中心对称图形C 它是中心对称图形,但不是轴对称图形D 它既不是轴对称图形,也不是中心对称图形4、下列图形中,是中心对称的图形有()①正方形;②长方形;③等边三角形;④线段;⑤角;⑥平行四边形。
A.5个B.2个C.3个D.4个5、在平面直角坐标系中,点P(2,—3)关于原点对称的点的坐标是()A.(2,3)B.(—2,3)C.(—2,—3)D.(—3,2)6、将图形按顺时针方向旋转900后的图形是( )A D7、如图所示,图中的一个矩形是另一个矩形顺时针AB CD P P 1 方向旋转90°后形成的个数是( )A l 个B 2个C 3个D 4个8、如图,把图①中的△ABC 经过一定的变换得到图②中的,如果图①中△ABC 上点P 的坐标为,那么这个点在图②中的对应点的坐标为( )A .B .C .D .9、下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度为( )A ︒30B ︒45C ︒60D ︒9010、如图,点P 是正方形ABCD 内一点,将△ABP 绕点B 沿顺时针方向旋转后与△CBP 1重合,若PB=5,那么PP 1=( )A 5B 53C 6 D2二、填空题(每小题3分,共30分) 11、一条线段绕其上一点旋转90°与原来的线段位置 关系.12、用示意图写出具有“中心对称图形”特征的汉字和英文字母各3个: .13、钟表的分针匀速旋转一周需要60分钟,它的旋转中心是____________,经过20分钟,分针旋转了____________。
深圳华升学校初中部九年级数学上册第三单元《旋转》测试题(含答案解析)

一、选择题1.如图,在ABC 中,,90AB AC BAC =∠=︒,直角EPF ∠的顶点P 是BC 的中点,两边PE 、PF 分别交AB 、AC 于点E 、F ,当EPF ∠在ABC 内绕点P 旋转时,下列结论错误的是( )A .AE CF =B .EPF 为等腰直角三角形C .EP AP =D .2ABC AEPF S S =四边形2.如图,在等边△ABC 中,AC=8,点O 在AC 上,且AO=3,点P 是边AB 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD ,要使点D 恰好落在BC 上,则AP 的长是( ).A .4B .5C .6D .83.如图,将等边ABC 绕点C 逆时针旋转得到A B C '',旋转角为()060αα︒<<︒.若160BDA '∠=︒,则α的大小是( )A .20°B .40°C .60°D .80° 4.如图,将ABC 绕点C 顺时针旋转80°,得到DEC ,若3120B A ∠=∠=︒,则α∠的度数是( )A .60︒B .50︒C .40︒D .305.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D . 6.如图,在平面直角坐标系中,将正方形OABC 绕点O 逆时针旋转45°后得到正方形111OA B C ,依此方式,绕点O 连续旋转2020次得到正方形202020202020OA B C ,如果点A 的坐标为(1,0),那么点2020B 的坐标为( )A .(﹣1,1)B .(20)-,C .(﹣1,﹣1)D .(02)-, 7.下列命题的逆命题是真命题的是( )A .等边三角形是等腰三角形B .若22ac bc >,则a b >C .成中心对称的两个图形全等D .有两边相等的三角形是等腰三角形8.已知等边△ABC 的边长为8,点P 是边BC 上的动点,将△ABP 绕点A 逆时针旋转60°得到△ACQ ,点D 是AC 边的中点,连接DQ ,则DQ 的最小值是( )A .2B .4C .23D .不能确定 9.下列图形中,既是轴对称图形又是中心对称图形的是( )A .等边三角形B .平行四边形C .正五边形D .菱形 10.如图,将△ABC 绕点A 逆时针旋转一定角度,得到△ADE ,若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为().A.60 °B.75°C.85°D.90°11.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有()A.3种B.4种C.5种D.6种12.如图,在△ABC中,AB=2.2,BC=3.6,∠B=60°,将△ABC绕点A按逆时针方向旋转得到△ADE,若点B的对应点D恰好落在BC边上时,则CD的长为()A.1.5 B.1.4 C.1.3 D.1.2二、填空题13.如图,把△ABC绕点C顺时针旋转得到△A'B'C',此时A′B′⊥AC于D,已知∠A=50°,则∠B′CB的度数是_____°.14.如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,则点E与点C之间的距离是_________cm.15.如图,将一个含30°角的直角三角板ABC 绕点A 顺时针旋转α(0°<α<360°),使得点B 、A 、C ′在同一直线上,则α=______.16.一副直角三角板如图放置,其中90ACB PRQ ∠=∠=,45A ∠=,60Q ∠=,点P 在斜边AB 上,现将三角板PRQ 绕着点P 顺时针旋转,当QR 第一次与AC 平行时,APR ∠的度数是__________.17.如图,在平面直角坐标系中,点1P 的坐标22,⎛⎫ ⎪ ⎪⎝⎭,将线段1OP 绕点O 按顺时针方向旋转45°,再将其长度伸长为1OP 的2倍,得到线段2OP ;又将线段2OP 绕点O 按顺时针方向旋转45°,长度伸长为2OP 的2倍,得到线段3OP ;如此下去,得到线段4OP 、5OP ,……,n OP (n 为正整数),则点2020P 的坐标是_________.18.如图,把Rt △ABC 绕顶点C 顺时针旋转90°得到Rt △DFC ,若直线DF 垂直平分AB ,垂足为点E ,连接BF ,CE ,且BC =2.下面四个结论:①BF =22; ②∠CBF =45°;③∠CED =30°;④△ECD 的面积为223+,其中正确的结论有_____.(填番号)参考答案19.如图,O 是正△ABC 内一点,3OA =,4OB =,5OC =,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ',下列结论正确有______.(请填序号)①点O 与O '的距离为4;②150AOB ∠=︒;③633AOBO S '=+四边形;④9634AOC AOB S S +=+△△.20.在平面直角坐标系中,将点P (﹣3,2)绕点Q (﹣1,0)顺时针旋转90°,所得到的对应点P '的坐标为____.三、解答题21.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,ABC 的顶点均在格点上,点C 的坐标为(2,4)-.(1)以原点O 为旋转中心,画出把ABC 逆时针旋转90°的图形111A B C △; (2)在(1)的条件下,求出经过111A B C 、、三点的抛物线的解析式.22.已知ABC 是边长为4的等边三角形,边AB 在射线OM 上,且6OA =,点D 是射线OM 上的动点,当点D 不与点A 重合时,将ACD △绕点C 逆时针方向旋转60°得到BCE ,连接DE .(1)如图1,求证:CDE △是等边三角形.(2)设OD t =,①如图2,当610t <<时,CDE △的周长存在最小值,请求出此最小值;②如图1,若06t <<,直接写出以D 、E 、B 为顶点的三角形是直角三角形时t 的值.23.已知:点D 是等腰直角三角形ABC 斜边BC 所在直线上一点(不与点B 重合),连接AD .(1)如图1,当点D 在线段BC 上时,将线段AD 绕点A 逆时针方向旋转90︒得到线段AE ,连接CE .求证:,BD CE BD CE =⊥;(2)如图2,当点D 在线段BC 延长线上时,将线段AD 绕点A 逆时针方向旋转90︒得到线段AE ,连接CE ,请画出图形.上述结论是否仍然成立,并说明理由;(3)根据图2,请直接写出,,AD BD CD 三条线段之间的数量关系.24.已知在平面直角坐标系中,A(﹣2,0)、B(3,﹣1)、C(2,2),格中每一格表示一个单位长度,请解答以下问题:(1)求作出△ABC;(2)将△ABC平移,使得平移后点C的对应点为原点,A、B的对应点分别为A1,B1,请作出平移后的△A1B1O,并直接写出平移的距离为;(3)将△ABC绕点A逆时针旋转90°,得到△AB2C2,B、C的对应点分别为B2、C2,请作出△AB2C2,并求出B2、C2点的坐标.25.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,求BD的长?26.解下列方程:(1)x2-2x-24=0 (2)用配方法解方程:x2+6x﹣1=0.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】利用旋转的思想观察全等三角形,寻找条件证明三角形全等.根据全等三角形的性质对题中的结论逐一判断.【详解】∵AB=AC ,∠BAC=90°,P 是BC 中点,∴AP=CP ,AP ⊥BC ,∠C=∠B=∠BAP=∠CAP=45°,∵∠APE 、∠CPF 都是∠APF 的余角,∴∠APE=∠CPF ,在△APE 和△CPF 中,45APE CPF AP CP EAP FCP ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴△APE ≌△CPF (ASA ),∴AE=CF ,EP=PF ,S △AEP =S △CPF ,∴△EPF 是等腰直角三角形,S 四边形AEPF =12S △ABC ,即2S 四边形AEPF =S △ABC , A 、B 、D 均正确, ∵旋转过程中,EP 的长度的变化的,故EP≠A P ,C 错误;故选:C .【点睛】本题考查了旋转的性质,全等三角形的判定和性质,等腰直角三角形的判定及性质的运用,解答时证明三角形全等是关键.2.B解析:B【分析】连接DP ,根据题意,得OP OD =,=60DOP ∠,从而得到120AOP COD ∠+∠=;再根据等边三角形和三角形内角和性质,得120AOP OPA ∠+∠=,从而得COD OPA ∠=∠,通过全等三角形判定,即可得到答案.【详解】如图,点D 落在BC 上,连接DP∵线段OP 绕点O 逆时针旋转60°得到线段OD∴OP OD =,=60DOP ∠∴180120AOP COD DOP ∠+∠=-∠=∵等边△ABC∴180120AOP OPA A ∠+∠=-∠=∴COD OPA ∠=∠即:OP OD COD OPA A C =⎧⎪∠=∠⎨⎪∠=∠⎩∴AOP CDO △≌△∴AP OC =∵AC=8,AO=3∴5OC AC AO =-=∴5AP OC ==故选:B .【点睛】本题考查了等边三角形、全等三角形、旋转、三角形内角和的知识;解题的关键是熟练掌握等边三角形、全等三角形、旋转、三角形内角和的性质,从而完成求解.3.A解析:A【分析】利用旋转的性质结合等边三角形的性质和三角形外角的性质,可得出答案;【详解】解:如图,∵ABC 和A B C ''均为等边三角形,∴60A A '∠=∠=︒由旋转得,旋转角为ACA α'∠=,∵160BDA '∠=︒∴160DOA A ''∠+∠=︒∴100DOA '∠=︒∵DOA COA '∠=∠,180ACA CAA COA ''∠+∠+∠=︒ ∴20ACA '∠=︒∴α的大小是20°故选:A【点睛】本题主要考查旋转的性质以及等边三角形的性质和三角形外角的性质等知识,正确掌握旋转的性质是解题关键.4.A解析:A【分析】根据旋转的性质找到对应点、对应角、对应线段作答.【详解】解:∵3120B A ∠=∠=︒∴120B ∠=︒,40A ∠=︒∵△ABC 绕点C 逆时针旋转80°得到△DEC ,∴∠D=∠A=40°,∠DEC=∠B=120°,∴∠DCE=180°-40°-120°=20°,∵∠DCA=80°∴∠α=∠DCA-∠DCE=80°-20°=60°.故选:A .【点睛】本题考查旋转的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度. 5.C解析:C【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A 、不是轴对称图形,是中心对称图形,故此选项不合题意;B 、是轴对称图形,不是中心对称图形,故此选项不符合题意;C 、是轴对称图形,也是中心对称图形,故此选项符合题意;D 、不是轴对称图形,是中心对称图形,故此选项不合题意;故选:C .【点睛】此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图形重合. 6.C解析:C【分析】根据图形可知:点B 在以O 为圆心,以OB 为半径的圆上运动,由旋转可知:将正方形OABC 绕点O 逆时针旋转45°后得到正方形OA 1B 1C 1,相当于将线段OB 绕点O 逆时针旋转45°,可得对应点B 的坐标,根据规律发现是8次一循环,可得结论.【详解】解:如图,∵四边形OABC是正方形,且OA=1,∴B(1,1),连接OB,由勾股定理得:2,由旋转得:OB=OB1=OB2=OB32,∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,∴B1(02),B2(-1,1),B3(20),B4(-1,-1),…,发现是8次一循环,所以2020÷8=252…4,∴点B2020的坐标为(-1,-1)故选:C.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.也考查了坐标与图形的变化、规律型:点的坐标等知识,解题的关键是学会从特殊到一般的探究规律的方法,属于中考常考题型.7.D解析:D【分析】先根据逆命题的定义分别写出各命题的逆命题,然后根据等腰三角形的性质、不等式的性质、中心对称的性质等进行判断.【详解】A、逆命题为:等腰三角形是等边三角形,是假命题,故本选项错误;B、逆命题是:如果a>b,则ac2>bc2,是假命题,故本选项错误;C、逆命题为:全等的两个图形成中心对称,是假命题,故本选项错误;D、逆命题为:等腰三角形是有两边相等的三角形,故本选项正确;故选:D【点睛】本题考查了命题与定理的知识,解题的关键是能够正确的写出一个命题的逆命题,并熟悉课本中的性质定理.8.C解析:C【分析】依据旋转的性质,即可得到∠BCQ=120°,当DQ⊥CQ时,DQ的长最小,再根据勾股定理,即可得到DQ的最小值.【详解】如图,由旋转可得∠ACQ=∠B=60°,又∵∠ACB=60°,∴∠BCQ=120°,∵点D是AC边的中点,∴CD=4,当DQ⊥CQ时,DQ的长最小,此时,∠CDQ=30°,∴CQ=1CD=2,2∴224223-=,∴DQ的最小值是3故选:C.【点睛】此题考查旋转的性质,解题关键在于掌握对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角.9.D解析:D【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A、是轴对称图形,不是中心对称图形.故不符合题意;B、不是轴对称图形,是中心对称图形.故不符合题意;C、是轴对称图形,不是中心对称图形.故不符合题意;D、是轴对称图形,也是中心对称图形.故符合题意.故选:D.【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.10.C解析:C【解析】试题分析:根据旋转的性质知,∠EAC=∠BAD=65°,∠C=∠E=70°.如图,设AD⊥BC于点F.则∠AFB=90°,∴在Rt△ABF中,∠B=90°-∠BAD=25°,∴在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,即∠BAC的度数为85°.故选C.考点: 旋转的性质.11.C解析:C【分析】根据轴对称图形的定义:沿某条直线折叠,直线两旁的部分能完全重合的图形是轴对称图形进行解答.【详解】如图所示:,共5种,故选C.【点睛】此题主要考查了利用轴对称设计图案,关键是掌握轴对称图形的定义.12.B解析:B【分析】运用旋转变换的性质得到AD=AB,进而得到△ABD为等边三角形,求出BD即可解决问题.【详解】解:如图,由题意得:AD=AB,且∠B=60°,∴△ABD为等边三角形,∴BD=AB=2,∴CD=3.6﹣2.2=1.4.故选:B.【点睛】该题主要考查了旋转变换的性质、等边三角形的判定等几何知识点及其应用问题;牢固掌握旋转变换的性质是解题的关键.二、填空题13.40【分析】由旋转的性质可得∠A=∠A=50°∠BCB=∠ACA由直角三角形的性质可求∠ACA=40°=∠B′CB【详解】解:∵把△ABC绕点C顺时针旋转得到△ABC∴∠A=∠A=50°∠BCB=∠解析:40【分析】由旋转的性质可得∠A=∠A'=50°,∠BCB'=∠ACA',由直角三角形的性质可求∠ACA'=40°=∠B′CB.【详解】解:∵把△ABC绕点C顺时针旋转得到△A'B'C',∴∠A=∠A'=50°,∠BCB'=∠ACA'∵A'B'⊥AC∴∠A'+∠ACA'=90°∴∠ACA'=40°∴∠BCB'=40°故答案为40.【点睛】本题考查了旋转的性质,熟练运用旋转的性质是本题的关键.14.【解析】试题解析:5【解析】试题连接EC,即线段EC的长是点E与点C之间的距离,在Rt△ACB中,由勾股定理得:BC=2222AB AC-=-=(cm),325∵将△ABC绕点B顺时针旋转60°得到△FBE,∴BC=BE,∠CBE=60°,∴△BEC是等边三角形,∴EC=BE=BC=5cm.15.150°【分析】根据旋转的性质得出∠BAC=∠B′AC′=30°求出∠BAB′即可【详解】解:∵将一个含30°角的直角三角板ABC绕点A顺时针旋转α(0°<α<360°)使得点BAC′在同一直线上∴解析:150°【分析】根据旋转的性质得出∠BAC=∠B′AC′=30°,求出∠BAB′即可.【详解】解:∵将一个含30°角的直角三角板ABC绕点A顺时针旋转α(0°<α<360°),使得点B、A、C′在同一直线上,∴∠BAC=∠B′AC′=30°,∴∠BAB′=180°-∠B′AC′=180°-30°=150°,即α=150°,故答案为150°.【点睛】本题考查了旋转的性质和邻补角的定义,能根据旋转的性质求出∠B′AC′的度数是解此题的关键.16.135°【分析】利用平行线的性质即可解决问题【详解】解:根据题意如图:∵QR∥AC∴DF∥BC∴∠FDB=∠ABC=45°∴故答案为:135°【点睛】本题考查平行线的判定和性质解题的关键是灵活运用所解析:135°【分析】利用平行线的性质即可解决问题.【详解】解:根据题意,如图:∵QR ∥AC ,90ACB PRQ ∠=∠=,∴DF ∥BC ,∴∠FDB=∠ABC=45°,∴18045135APR ∠=︒-︒=︒,故答案为:135°.【点睛】本题考查平行线的判定和性质,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.17.(0-22019)【分析】根据题意得出OP1=1OP2=2OP3=4如此下去得到线段OP3=4=22OP4=8=23…OPn=2n -1再利用旋转角度得出点P2020的坐标与点P4的坐标在同一直线上进解析:(0,-22019)【分析】根据题意得出OP 1=1,OP 2=2,OP 3=4,如此下去,得到线段OP 3=4=22,OP 4=8=23…,OP n =2n-1,再利用旋转角度得出点P 2020的坐标与点P 4的坐标在同一直线上,进而得出答案.【详解】解:∵点P 1的坐标为22⎛ ⎝⎭,将线段OP 1绕点O 按顺时针方向旋转45°,再将其长度伸长为OP 1的2倍,得到线段OP 1;∴OP 1=1,OP 2=2,∴OP 3=4,如此下去,得到线段OP 4=23,OP 5=24…,∴OP n =2n-1,由题意可得出线段每旋转8次旋转一周,∵2020÷8=252…4,∴点P 2020的坐标与点P 4的坐标在同一直线上,正好在y 轴负半轴上,∴点P 2020的坐标是(0,-22019).故答案为:(0,-22019).【点睛】此题主要考查了点的变化规律,根据题意得出点P 2014的坐标与点P 6的坐标在同一直线上是解题关键.18.①②④【分析】利用旋转的性质得CF =CB =2∠BCF =90°则可得△CBF 为等腰直角三角形于是可对①②进行判断;由于直线DF 垂直平分AB 则FA =FBBE =AE 于是根据等腰三角形的性质和三角形外角性质解析:①②④【分析】利用旋转的性质得CF =CB =2,∠BCF =90°,则可得△CBF 为等腰直角三角形,于是可对①②进行判断;由于直线DF 垂直平分AB ,则FA =FB ,BE =AE ,于是根据等腰三角形的性质和三角形外角性质可计算出∠ECA=∠A=22.5°,然后根据三角形内角和可计算出∠CEF,从而可对③进行判断;作EH⊥BD于H,如图,根据三角形中位线性质得EH=1AC=2+1,利用旋转性质得CD=CA=2+22,则利用三角形面积公式可计算出2△ECD的面积,从而可对④进行判断.【详解】∵把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,∴CF=CB=2,∠BCF=90°,∴△CBF为等腰直角三角形,∴BF=2BC=22,∠CBF=45°,所以①②正确;∵直线DF垂直平分AB,∴FA=FB,BE=AE,∴∠A=∠ABF,而∠BFC=∠A+∠ABF=45°,∴∠A=22.5°,∵CE为斜边AB上的中线,∴EC=EA,∴∠ECA=∠A=22.5°,∴∠CEF=180°﹣90°﹣2×22.5°=45°,所以③错误;作EH⊥BD于H,如图,∵把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,∴CD=CA=2+22,∵点E为AB的中点,∴EH=1AC=2+1,2∴△ECD的面积=1•(2+1)•(2+22)=22+3,所以④正确.2故答案为:①②④.【点睛】考查了旋转的性质,旋转的性质有:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.19.①②④【分析】连接根据旋转的性质即可得到为等边三角形进而可求证①②③的正确性然后将△AOB绕点A逆时针旋转60°至连接OD易得△ACD也为等边三角形由此可求解【详解】解:连接如图所示:∵线段BO以点解析:①②④【分析】连接OO ',根据旋转的性质即可得到OBO '△为等边三角形,进而可求证①②③的正确性,然后将△AOB 绕点A 逆时针旋转60°至ACD △,连接OD ,易得△ACD 也为等边三角形,由此可求解.【详解】解:连接OO ',如图所示:∵线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ',∴,60BO OB O BO ''=∠=︒,O A OC '=,∴OBO '△为等边三角形,∵3OA =,4OB =,5OC =,∴4BO OB '==,5O A OC '==,故①正确;∴22225O O AO O A ''+==,∴90AOO '∠=︒,∴150AOB AOO O OB ''∠=∠+∠=︒,故②正确;过点B 作BE ⊥OO '于点E ,如图所示,∴2OE EO '==, ∴2223BE OB EO =-=, ∴2134324BOO S OO BE O O '''=⋅==, ∴134436432O OB AOO AOBO S SS '''=+=⨯⨯+=+四边形,故③错误; 将△AOB 绕点A 逆时针旋转60°至ACD △,连接OD ,如图所示:同理易得△AOD 为等边三角形,OD=OA=3,OB=DC=4,∠ODC=90°,∴2139=3436324AOC AOB AOD ODC AOCD S S S SS +=+=⨯⨯=四边形△△④正确; ∴正确的有①②④;故答案为①②④.【点睛】本题主要考查勾股定理逆定理、等边三角形的性质与判定及旋转的性质,熟练掌握勾股定理逆定理、等边三角形的性质与判定及旋转的性质是解题的关键.20.(12)【分析】根据题意画出图形即可解决问题【详解】如图观察图象可知P (12)故答案为:(12)【点睛】本题考查坐标与图形变化-旋转解题的关键是理解题意学会利用图象法解决问题属于中考常考题型解析:(1,2).【分析】根据题意,画出图形即可解决问题.【详解】如图,观察图象可知,P '(1,2).故答案为:(1,2).【点睛】本题考查坐标与图形变化-旋转,解题的关键是理解题意,学会利用图象法解决问题,属于中考常考题型.三、解答题21.(1)△A 1B 1C 1为所求见详解图;(2)2210433y x x =-+-. 【分析】(1)先连结OA 、OB 、OC ,以O 点为旋转中心,分别以OA 、OB 、OC 逆时针旋转90º到OA 1、OB 1、OC 1,再顺次连结A 1B 1,B 1C 1,C 1A 1即可(2)先求出A 、B 、C 三点坐标,结合旋转后的位置求出A 1(1,0),B 1(5,0),C 1(4,2),由A 1(1,0),B 1(5,0),两点在x 轴上,利用交点式抛物线解析式设出函数解析式,把C 1坐标代入求出a 值,再化为一般式即可【详解】(1)如图所示,连结OA 、OB 、OC ,以O 点为旋转中心,分别以OA 、OB 、OC 逆时针旋转90º到OA 1、OB 1、OC 1,再顺次连结A 1B 1,B 1C 1,C 1A 1,则△A 1B 1C 1为所求; (2)由A (0,-1),B (0,-5),C (2,-4)则A 1(1,0),B 1(5,0),C 1(4,2), 由A 1(1,0),B 1(5,0),两点在x 轴上,设出经过111A B C 、、三点的抛物线的解析式为()()15y a x x =--,把C 1(4,2)代入抛物线的解析式,()()24145a =--, 解得23a =-, ()()2153y x x =---, 2210433y x x =-+-.【点睛】本题考查旋转变换问题,掌握旋转作图的方法与步骤,会通过旋转后的位置,确定点的坐标,会用待定系数法求抛物线解析式是解题关键.22.(1)见解析;(2)①63②2【分析】(1)由旋转的性质得到∠DCE=60°,DC=EC ,即可得到结论;(2)①存在,由等边三角形的性质可得△CDE 的周长=3CD ,当CD ⊥AB 时,CD 有最小值,即可求解;②由题意可得∠BED=90°,由直角三角形的性质可求解.【详解】解:(1)∵证明:将ACD △绕点C 逆时针方向旋转60°得到BCE ,∴60DCE ∠=︒,DC EC =,∴CDE △是等边三角形:(2)①∵CDE △是等边三角形,∴CDE △的周长3CD =,当610t <<时,由垂线段最短可知,当CD AB ⊥时,CDE △的周长最小,此时,CD =∴CDE △的最小周长3CD ==②存在,当0<t <6时,由旋转可知,∠ABE=60°,∠BDE <60°,∴∠BED=90°,由(1)可知,△CDE 是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA ,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA-DA=6-4=2,∴t=2.【点睛】本题是几何变换综合题,考查了旋转的性质,等边三角形的性质,直角三角形的性质,垂线段最短等知识,灵活运用这些性质解决问题是本题的关键.23.(1)证明见解析;(2)图见解析,结论仍然成立,理由见解析;(3)2222AD BD CD =+.【分析】(1)先根据等腰直角三角形的定义可得,90,45AB AC BAC ABC ACB =∠=︒∠=∠=︒,再根据旋转的性质可得,90AD AE DAE =∠=︒,然后根据角的和差可得BAD CAE ∠=∠,最后根据三角形全等的判定定理与性质、垂直的定义即可得证;(2)先根据旋转的定义画出图形,再根据旋转的性质可得,90AD AE DAE =∠=︒,然后根据角的和差可得BAD CAE ∠=∠,最后根据三角形全等的判定定理与性质、垂直的定义即可得证;(3)如图(见解析),先在Rt ADE △中,根据勾股定理可得222DE AD =,再在Rt CDE △中,根据勾股定理可得22222DE CE CD BD CD =+=+,由此即可得出答案.【详解】(1)ABC 是等腰直角三角形,,90,45AB AC BAC ABC ACB ∴=∠=︒∠=∠=︒,由旋转的性质得:,90AD AE DAE =∠=︒,BAC CAD DAE CAD ∴∠-∠=∠-∠,即BAD CAE ∠=∠,在ABD △和ACE △中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,()ABD ACE SAS ∴≅,,45BD CE ACE ABD ∴=∠=∠=︒,90BCE ACB ACE ∴∠=∠+∠=︒,BD CE ∴⊥;(2)成立,理由如下:由题意,画出图形如下:由旋转的性质得:,90AD AE DAE =∠=︒,BAC CAD DAE CAD ∴∠+∠=∠+∠,即BAD CAE ∠=∠,在ABD △和ACE △中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,()ABD ACE SAS ∴≅,,45BD CE ACE ABD ∴=∠=∠=︒,90BCE ACB ACE ∴∠=∠+∠=︒,BD CE ∴⊥;(3)如图,连接DE ,,90AD AE DAE =∠=︒,∴在Rt ADE △中,22222=+=DE AD AE AD ,由(2)可知,,BD CE BD CE =⊥,∴在Rt CDE △中,22222DE CE CD BD CD =+=+,2222AD BD CD ∴=+,即,,AD BD CD 三条线段之间的数量关系为2222AD BD CD =+.【点睛】本题考查了等腰直角三角形的性质、旋转的性质、勾股定理、三角形全等的判定定理与性质等知识点,熟练掌握旋转的性质是解题关键.24.(1)作图见解析;(2)22;(3)作图见解析;B2(﹣4,4),C2(﹣1,5)【分析】(1)根据点的坐标作出三角形即可;(2)分别作出A,B的对应点A1,B1即可;(3)分别作出B,C的对应点B2、C2即可.【详解】解:(1)如图,△ABC即为所求;(2)如图△A1B1O即为所求,平移的距离为22;故答案为22.(3)如图△A B2C2即为所求B2、C2点的坐标分别为(﹣4,4),(﹣1,5)【点睛】本题考查了作图-旋转变换,平移变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题.25.5【分析】连接BE,如图,根据旋转的性质得∠BCE=60°,CB=CE,BD=AE,再判断△BCE为等边三角形得到BE=BC=4,∠CBE=60°,从而有∠ABE=90°,然后利用勾股定理计算出AE即可.【详解】解:连接BE,如图,∵△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,∴∠BCE=60°,CB=CE,BD=AE,∴△BCE为等边三角形,∴BE=BC=4,∠CBE=60°,∵∠ABC=30°,∴∠ABE=90°,在Rt△ABE中,223+4=5,∴BD=5.故答案为:5.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.26.(1)x=-4,x=6;(2)x=﹣10.【解析】试题分析:(1)把左边进行因式分解即可;(2)用配方法解方程即可.试题解:(1)(x+4)(x-6)=0,x=-4,x=6.(2)x2+6x+9=10,即(x+3)2=10,x=﹣10.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
旋转单元测试题一、选择题:1、大自然中存在很多对称现象,下列植物叶子的图案中既是轴对称,又是中心对称图形的是()A.B.C.D.2、下列图形中,是中心对称图形又是轴对称图形的有()①平行四边形;②菱形;③矩形;④正方形;⑤等腰梯形;⑥线段;⑦角.A.2 个B.3 个C.4 个 D.5 个3、如图,在平面直角坐标系xOy 中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是()A.(0,0)B.(1,0)C.(1,﹣1)D.(2.5,0.5)4、在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是()A.点A B.点B C.点C D.点D5、如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A 旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.35°B.40°C.50°D.65°6、如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A 顺时针旋转90°后得到△AB′C′(点B 的对应点是点B′,点C 的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )A.32°B.64° C.77°D.87°A. B. C.D.7、平面直角坐标系中,将点 A (1,2)绕点 P (﹣1,1)顺时针旋转 90°到点 A′处,则点的坐标为( )A .(﹣2,3)B .(0,﹣1)C .(1,0)D .(﹣3,0)8、如图,在平面直角坐标系中将△ABC 绕点 C (0,﹣1)旋转 180°得到△A 1B 1C 1,设点 A 1 的坐标为(m ,n ), 则点 A 的坐标为()A .(﹣m ,﹣n )B .(﹣m ,﹣n ﹣2)C .(﹣m ,﹣n ﹣1)D .(﹣m ,﹣n+1)9、如图,在△ABO 中,AB⊥OB,OB= ,AB=1,把△ABO 绕点 O 旋转 150°后得到△A 1B 1O,则点 A 1 的坐标为()A .(-1,- )B .(-1,- )或(-2,0)C .(- ,-1)或(0,-2)D .(- ,-1)10、把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边 AB=6,DC=7,把三角板DCE 绕点 C 顺时针旋转 15°得到△D 1CE 1(如图乙),此时 AB 与 CD 1 交于点 O ,则线段 AD 1 的长为( )11、如图,OA⊥OB,等腰直角△CDE 的腰 CD 在 OB 上,∠ECD=45°, 将△CDE 绕点 C 逆时针旋转 75°,点 E 的对应点 N 恰好落在 OA 上,则的值为( )A .B .5C .4D .12、如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点 P 是BC 中点,两边 PE、PF 分别交 AB、AC 于点E、F,当∠EPF在△ABC内绕顶点 P 旋转时(点E 不与A、B 重合),给出以下四个结论:①AE=CF;②△EPF 是等腰直角三角形;③2S 四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )A.4 个B.3 个C.2 个D.1 个二、填空题:13、下列图形中:①圆;②等腰三角形;③正方形;④正五边形,既是轴对称图形又是中心对称图形的有个.14、如图,是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是.15、在平面直角坐标系中,点 P(1,1),N(2,0),△MNP 和△M1N1P1的顶点都在格点上,△MNP 与△M1N1P1 是关于某一点中心对称,则对称中心的坐标为.16、如图,△ABC中,∠BAC=40°,把△ABC绕点A 逆时针旋转60°,得△ADE,则∠EAC的度数为.17、如图,在平面直角坐标系中,点 A、B 的坐标分别为(3,2)、(-1,0),若将线段 BA 绕点 B 顺时针旋转90°得到线段 BA',则点 A'的坐标为.18、如图,P 是等边三角形 ABC 内一点,将线段 AP 绕点A 顺时针旋转60°得到线段 AQ,连接 BQ.若PA=6,PB=8,PC=10,则四边形 APBQ 的面积为.三、作图题:19、每个小方格都是边长为 1 个单位长度,正方形 ABCD 在坐标系中的位置如图所示.(1)画出正方形 ABCD 关于原点中心对称的图形;(2)画出正方形 ABCD 绕点D 点顺时针方向旋转90°后的图形;(3)求出正方形 ABCD 的点B 绕点D 点顺时针方向旋转90°后经过的路线.四、解答题:20、如图,已知∠B=∠D,∠1=∠2,AB=AD.求证:AC=AE.21、在平面直角坐标系中,点 A 的坐标是(0,3),点 B 的坐标是(﹣4,0),将△AOB 绕点 A 逆时针旋转90°得到△AEF,点 O、B 的对应点分别是点 E、F.(1)请在图中画出△AEF.(2)请在 x 轴上找一个点 P,使PA+PE 的值最小,并直接写出 P 点的坐标为.22、如图,将矩形边交边于点绕点.顺时针旋转,得到矩形,点的对应点恰好落在的延长线上,(1)求证:.(2)若,,求的长.23、一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点 M 放在△ABC的斜边AB 的中点处,设 AC=BC=a.(1)如图 1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为,周长为;(2)将图 1 中的△MNK绕顶点 M 逆时针旋转45°,得到图 2,此时重叠部分的面积为,周长为;(3)如果将△MNK绕M 旋转到不同于图 1,图2 的位置,如图 3 所示,猜想此时重叠部分的面积为多少?并试着加以验证.24、如图,△ABC 中,AB=AC=2,∠BAC=45°,将△ABC 绕点 A 按顺时针方向旋转角得到△AEF,且00<≤1800,连接 BE、CF 相交于点 D.(1)求证:BE=CF;(2)当 =900时,求四边形 AEDC 的面积.参考答案1、D2、C3、C4、B5、C6、C7、B8、B9、B10、B11、C12、B13、2 个.14、3 .15、(2,1)16、答案为60°.17、(1,-4);18、 24+9.19、解:(1)如图,正方形A′B′C′D′为所作;(2)如图,正方形 CFED 为所作;(3)BD== ,所以正方形ABCD 的点B 绕点D 点顺时针方向旋转90°后经过的路线长==π.20、由∠1=∠2,同时加∠DAC,得∠BAC=∠DAE,又∠B=∠D,AB=AD所以,ΔBAC 与ΔDAF 全等所以,AC=AE21、解:(1)如图,△AEF 为所作;(2)作点 A 关于x 轴的对称点A′,连结EA′交x 轴于P 点,如图,因为PA=PA′,所以PA+PE=PA′+PE=EA′,所以此时 PA+PB 的值最小,因为OP=AE=,所以P 点坐标为(,0).故答案为(,0).22、解:(1)连结AC、,如图.∵四边形ABCD 为矩形,∴∠ABC90°,即.由旋转,得,∴.(2)∵四边形为矩形,∴.∵,∴.由旋转,得,∴.∵,∴设,则.在≌.∴ .中,,由勾股定理,得.解得.∴.23、解:(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为a2,周长为(1+ )a.(2)∵重叠部分是正方形∴边长为a,面积为a2,周长为2a.(3)猜想:重叠部分的面积为.理由如下:过点 M 分别作 AC、BC 的垂线 MH、MG,垂足为 H、G设MN 与AC 的交点为 E,MK 与BC 的交点为 F∵M 是△ABC 斜边 AB 的中点,AC=BC=a∴MH=MG=又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形 CGMH 的面积∵正方形CGMH 的面积是MG•MH=×=∴阴影部分的面积是.24、(1)①证明:由旋转可知,∠EAF=∠BAC,AE=AB,AF=AC.∴∠EAF+∠BAF=∠BAC+∠BAF,即∠BAE=∠CAF,又∵AB=AC. ∴AE=AF. ∴△ABE≌△ACF,∴BE=CF ②当 =900时,即∠BAE=∠CAF=900.∵AB=AE,AC=AF,∴∠ABE=∠AEB=450,∠ACF=∠AFC=450.又∠EAF=∠BAC=450,∴∠AFC=∠EAF,∠ABE=∠BAC,∴ED∥CD,AC∥ED.又 AE=AC,∴四边形 AEDC 是菱形,∴EE=ED=D C=CA过点A 作AH⊥DC于点H,则AH= ,∴.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
