结构动力学newmark法程序
newmark-integral method -回复

newmark-integral method -回复什么是新马克积分法(Newmark Integration Method)?新马克积分法,又称为Newmark Integration Method,是一种用于结构动力学分析的数值计算方法。
它是由美国工程师Nathan Newmark 于20世纪50年代初开发的。
新马克积分法可以用于分析结构在地震或其他动力荷载作用下的响应。
新马克积分法基于结构的运动方程,通过离散化时间步长,将连续时间的问题转化为离散时间的问题。
这种方法是基于中点积分的一阶差分离散化方法,它可以精确地模拟结构的振动响应。
新马克积分法的步骤如下:1. 定义系统的初始条件:首先需要定义结构的初始位移、初始速度和初始加速度。
这些初值可以通过实际测量或基于结构几何和质量特性的估计得出。
2. 确定时间步长:选择适当的时间步长用于离散化求解。
时间步长的选择取决于结构的特性以及所需的计算精度。
通常情况下,时间步长越小,计算结果越精确,但计算量也越大。
3. 计算加速度:基于初始条件和结构的动力学方程,可以通过求解牛顿第二定律得到当前时间步长下的加速度。
在新马克积分法中,采用中点积分的方法计算加速度。
4. 更新速度和位移:根据当前时间步长下的加速度,可以通过积分计算更新速度和位移。
由于采用中点积分的方法,需要先根据当前时间步长的加速度估计下一个时间步长的速度和位移。
然后,根据速度和位移的更新公式进行迭代计算,直至满足收敛要求。
5. 更新初始条件:将当前时间步长的速度和位移作为下一个时间步长的初始条件,并进一步迭代计算。
6. 重复步骤3至5,直至达到所需的计算时间或满足其他收敛准则。
新马克积分法的优点是可以精确地模拟结构的动力响应,并且可以考虑结构的非线性特性。
相比于其他数值计算方法,新马克积分法的数值稳定性较好,计算精度较高。
然而,由于需要迭代计算,计算量较大,且每个时间步长的计算结果都依赖于前一个时间步长的结果,所以计算效率较低。
newmark算法

function [X,t] = newmark(M,C,K,f,dt,gam,beta,Xi,Xdi)% % 输入参数说明:% [M] = 质量(nxn)% [C] = 阻尼矩阵(nxn)% [K] = 刚度矩阵(nxn)% {f} = 激励力矩阵(nxm), f的第k列是t(k)时刻的激励力,m-1为总的计算步数% dt = 步长% beta= Newmark 常数(1/6 or 1/4 usually)% gam = Newmark 常数(1/2)% Xi = 初始位移向量(nx1)% Xdi = 初始速度向量(nx1)% % 输出参数说明:% {t} = 时间(mx1)% [X] = 响应(nxm),X的第k列为t(k)时刻的位移响应%================================================================ n = size(M,1);m = size(f,2);t = zeros(m,1);X = zeros(n,m);Xd = zeros(n,m);Xdd = zeros(n,m);% 系数c0 = 1/(beta*dt*dt) ;c1 = gam/(beta*dt) ;c2 = 1/(beta*dt) ;c3 = 1/(beta*2) - 1 ;c4 = gam/beta - 1 ;c5 = 0.5*dt*(gam/beta - 2 ) ;c6 = dt*(1 - gam ) ;c7 = dt* gam;% 初始刚度Keff = c0*M + c1*C + K ;Kinv = inv(Keff) ;% 初始加速度R0 = f(:,1);Xddi= inv(M)*(R0 - K*Xi - C*Xdi);% 第一步f(:,1) = f(:,1) + M*(c0*Xi+c2*Xdi+c3*Xddi) ...+C*(c1*Xi+c4*Xdi+c5*Xddi);X(:,1) = Kinv*f(:,1);Xdd(:,1)= c0*(X(:,1)-Xi) - c2*Xdi - c3*Xddi ;Xd(:,1) = Xdi + c6*Xddi + c7*Xdd(:,1);t(1) = 0;% 后续步% ========================for i=1:m-1t(i+1) = t(i) + dt;f(:,i+1) = f(:,i+1) + M * ...(c0*X(:,i)+c2*Xd(:,i)+c3*Xdd(:,i)) ...+ C*(c1*X(:,i)+c4*Xd(:,i)+c5*Xdd(:,i)) ;X(:,i+1) = Kinv*f(:,i+1) ;Xdd(:,i+1)= c0*(X(:,i+1)-X(:,i))-c2*Xd(:,i)-c3*Xdd(:,i) ;Xd(:,i+1) = Xd(:,i)+c6*Xdd(:,i)+c7*Xdd(:,i+1) ;end;程序转自xyz999newmark方法方法介绍/wiki/Newmark-beta_methodfunction [X,t] = newmark(M,C,K,f,dt,gam,beta,Xi,Xdi)% % 输入参数说明:% [M] = 质量(nxn)% [C] = 阻尼矩阵(nxn)% [K] = 刚度矩阵(nxn)% {f} = 激励力矩阵(nxm), f的第k列是t(k)时刻的激励力,m-1为总的计算步数% dt = 步长% beta= Newmark 常数(1/6 or 1/4 usually)% gam = Newmark 常数(1/2)% Xi = 初始位移向量(nx1)% Xdi = 初始速度向量(nx1)% % 输出参数说明:% {t} = 时间(mx1)% [X] = 响应(nxm),X的第k列为t(k)时刻的位移响应%================================================================ n = size(M,1);m = size(f,2);t = zeros(m,1);X = zeros(n,m);Xd = zeros(n,m);Xdd = zeros(n,m);% 系数c0 = 1/(beta*dt*dt) ;c1 = gam/(beta*dt) ;c2 = 1/(beta*dt) ;c3 = 1/(beta*2) - 1 ;c4 = gam/beta - 1 ;c5 = 0.5*dt*(gam/beta - 2 ) ;c6 = dt*(1 - gam ) ;c7 = dt* gam;% 初始刚度Keff = c0*M + c1*C + K ;Kinv = inv(Keff) ;% 初始加速度R0 = f(:,1);Xddi= inv(M)*(R0 - K*Xi - C*Xdi);% 第一步f(:,1) = f(:,1) + M*(c0*Xi+c2*Xdi+c3*Xddi) ...+C*(c1*Xi+c4*Xdi+c5*Xddi);X(:,1) = Kinv*f(:,1);Xdd(:,1)= c0*(X(:,1)-Xi) - c2*Xdi - c3*Xddi ;Xd(:,1) = Xdi + c6*Xddi + c7*Xdd(:,1);t(1) = 0;% 后续步% ========================for i=1:m-1t(i+1) = t(i) + dt;f(:,i+1) = f(:,i+1) + M * ...(c0*X(:,i)+c2*Xd(:,i)+c3*Xdd(:,i)) ...+ C*(c1*X(:,i)+c4*Xd(:,i)+c5*Xdd(:,i)) ;X(:,i+1) = Kinv*f(:,i+1) ;Xdd(:,i+1)= c0*(X(:,i+1)-X(:,i))-c2*Xd(:,i)-c3*Xdd(:,i) ;Xd(:,i+1) = Xd(:,i)+c6*Xdd(:,i)+c7*Xdd(:,i+1) ;end;。
固体力学中的数值方法_Newmark算法

Newmark 算法程序计算报告1.Newmark 算法理论基础在~t t t +∆的时间区域内,Newmark 积分方法采用下列的假设,即()2112t t t t t t t tt t t t t t t tδδαα+∆+∆+∆+∆=+-+∆⎡⎤⎣⎦⎡⎤⎛⎫=+∆+-+∆ ⎪⎢⎥⎝⎭⎣⎦a a a a a a a a a (1.1) 其中α和δ是按积分精度和稳定性要求决定的参数。
另一方面,α和δ取不同的值则代表了不同的数值积分方案。
当1/6,1/2αδ==时,(1.1)式相应于线性加速度法,因为这时他们可以由下式得到()/ (0)t t t t t t t t ττ+∆+∆=+-∆≤≤∆a a a a (1.2)当1/4,1/2αδ==时,Newmark 算法相应于常平均加速度法这样一种无条件稳定的积分方案。
此时,t ∆内的加速度为()12t t t t t +∆+∆=+a a a (1.3) 因此,将(1.1)式可以得到()211112t t t t t t t t t ααα+∆+∆⎛⎫=---- ⎪∆∆⎝⎭a a a a a (1.4) 代入到动力学平衡方程中可以得到22111112 112t t t t t t t t t t t t t t t t δαααααδδδααα+∆+∆⎡⎤⎛⎫⎛⎫++=+++-+ ⎪ ⎪⎢⎥∆∆∆∆⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫⎛⎫+-+-∆ ⎪ ⎪⎢⎥∆⎝⎭⎝⎭⎣⎦K M C a Q M a a a C a a a (1.5)2.Newmark 算法计算步骤(1)形成刚度矩阵 K 、质量矩阵M 、阻尼矩阵 C 。
(2)给定0 a ,0a ,和0a(3)选择时间步长t ∆及参数α和δ,并计算积分常数。
这里要求:()20.5,0.250.5δαδ≥≥+()012324567111,,,121,2,1,2c c c c t t t t c c c t c t δααααδδδδαα====-∆∆∆∆⎛⎫=-=-=∆-=∆ ⎪⎝⎭(4)形成有效刚度矩阵01ˆˆc c + K :K =K +M C (5)三角分解ˆˆTK:K =LDL 对于每一个时间步长(1)计算时间t t +∆的有效载荷()()023145ˆt t t t t t t t t t c c c C c c c +∆+∆=++++++Q Q M a a a a a a(2)求解时间t t +∆的位移ˆT t t t t+∆+∆=LDL a Q (3)计算时间t t +∆的加速度和速度()02367t t t t t t t t t t t t tc c c c c +∆+∆+∆+∆=---=++a a a a a a a a a3.程序设计思路(1) 读入质量矩阵、刚度矩阵、阻尼矩阵、载荷列向量;读入初始状态值,如初始位移、初始速度、初始加速度;读入控制变量,如时间步长、时间步; (2) 计算8个积分常数;(3) 计算有效刚度矩阵ˆK并对有效刚度矩阵ˆK 进行LU 分解; (4) 求解时间t t +∆的有效载荷向量ˆt t+∆Q ; (5) 求解时间t t +∆的位移t t +∆a ;(6) 求解时间t t +∆的的加速度t t +∆a 和速度t t +∆a (7)计算下一时刻的有效载荷向量并循环。
wilson法和newmark法的理论过程

第三章离散化结构动力方程的解法(2013.4.24)§3.1 绪言对于一个实际结构,由有限元法离散化处理后,应用瞬时最小势能原理可导出动力方程[]{}[]{}[]{}{}++=(3.1)M u C u K u F(t)这里,{}u、{}u、{}u及{}F t分别表示加速度、速度、位移及所()作用的外力矢量,他们都是与时间有关的。
从数学的角度来看,式(3.1)是一个常系数的二阶线性常微分方程组,对于它的求解原则上并无困难。
但是,由于[]M、[]C 和[]K的阶数非常高,使得式(3.1)的求解必须花费很大的代价,便促使人们去寻求一些效率高的近似计算方法。
目前,用于求解式(3.1)的方法,大致可分为两大类。
一是坐标变换法,它是对结构动力方程式(3.1),在求解之前,进行模态坐标变换,实际上就是一种Ritz变换,即把原物理空间的动力方程变换到模态空间中去求解。
现在,普遍使用的方法是模态(振型)迭加法,即用结构的前q阶实际主模态集(主振型阵)构成坐标变换阵进行变换。
通过这一变换,实现降阶,求较好的近似解,而且,还用解除耦合的办法,简化方程的计算。
还有一种所谓假设模态法,即是用一组假设模态,构成模态坐标变换阵进行变换,获得一组降阶的而不解耦的模态基坐标方程。
显然,这种方法的计算精度,取决于所假设的模态。
用Ritz矢量法求解的近似模态作为假设模态,可得到满足要求的精度。
二是直接积分法,它是对式(3.1)在求解之前,不进行坐标变换,直接进行数值积分计算。
这种方法的特点是对时域进行离散,将式(3.1)分为各离散时刻的方程,然后,将该时刻的加速度和速度用相邻时刻的各位移线性组合而成,于是,式(3.1)就化为一个由位移组成的该离散时刻上的响应值,通常又称为逐步积分法。
线性代数方程组的解法与静力时刻的位移来线性组合,就导致了各种不同的方法。
主要有中央差分法,Houbolt 方法,Wilson -θ法和Newmark 方法等。
关于Newmark_法机理的一种解释

( 5), 则有
u&( S) =
u&i +
1 2
$u&i
( 6)
积分后可得速度和位移分别为
uÛ( S) = uÛi + u&i S+
1 2
$u&i S
( 7)
u( S) = ui + Ûui S+
1 2
u&i S2
+
1 4
$u&i S2
( 8)
取 S= $ti 即可获得步距末端的反应值, 考虑到 $u&i = u&i+ 1 - u&i, 有
是不 连续的, 且同真实荷载值不重合。因此, N ewm ark- B 法亦可看作 是一种基 于荷载 分段插 值类型 的数 值分析方法, 可以从荷载分布模式假定的角度解释 N ewm ark- B 法 的数值机理 。最后, 通过一个 单自 由度体系实例阐释了本文结论的正确性。
关键 词: N ewm ark- B方 法; 分段精确法; 算法机理
在已知 ti 及其以前时刻的全部反应的前提下, 为了求得 ti+ 1时刻的动力反应, N ewm ark法假定 [ 1]
uÛi+ 1 = Ûui + ( 1 - C) $ti u&i + C$ti u&i+ 1
( 3)
ui+ 1
=
ui +
$ti Ûui +
(
1 2
-
B) ( $ti ) 2u&i +
u&( S) = u&i + G( S) # $u&i
结构动力学数值算法

K xn1 Qn1
参数不同选取包含着三个经典算法
1)
1 2
,
1 4
Newmark 平均加速度法, 梯形公式
2)
1 2
,
1 6
Newmark 线加速度法
3)
1 2
,
0
中心差分法
纽马克法的解题步骤
初始值计算
(1)形成系统矩阵 K,M 和 C
(2)定初始值
x0
,
.
x0
,
..
x0
。
(3)选择时间步长 t ,参数 、 (按上页选)。
其中 A1,A2,A3 为该矩阵的三个特征向量,分 别为矩阵的迹的一半、各阶主子式的和以及矩阵的 行列式,分别表达如下:
A1
18
6
32 2
3 2
(2 2
32
6)
2
32
A2
42
32 3 62 2 18 (2 2 6)
12
A3
6
6
2 32 (2 2
2 2
6)
3
32
此外,在几个不同时刻应用数值算法,然后将
(2)求解 t t 时刻的位移
(LDLT )xtt Qtt
(3)计算 t t 时刻的加速度和速度
..
.
..
xtt a0 (xtt xt ) a2 xt a3 xt
.
.
..
..
xtt xt a6 xt a7 xtt
5.1.2 威尔逊- 法的解题步骤 1. 初始值计算 (1)形成系统矩阵 K,M 和 C
如果算法的稳定性要求对步长的选取有限制,称 算法是有条件稳定的,反之为无条件稳定的。
判断方法:放大矩阵的谱半径小于等于 1 成立的 充分条件是
newmark法计算多自由度结构响应

Newmark方法是一种用于计算自由结构多度响应的数值技术。
在地震工程中通常用于预测地震加载下的建筑物和其他结构的行为。
Newmark方法考虑了结构的质量,硬度和坝积,以计算迁移,速度,以及每个自由度的加速。
这使得工程师能够评价结构反应,并评估损坏或故障的可能性。
要使用Newmark方法,结构首先分为离散自由度,一般在关节或连接点。
然后根据结构几何和物质特性来确定每一自由度的质量、坚硬度和筑坝特性。
这些属性用于构成结构的支配性运动方程,这些方程可以使用Newmark方法进行数字解析。
Newmark方法是一个迭代过程,它计算每个时段的结构响应。
每个自由度的迁移、速度和加速都根据应用负荷、结构特性和坝积效应加以更新。
通过穿越每个时间步,Newmark方法可以准确预测结构随时间推移的动态响应。
Newmark方法的关键优势之一是它能够同时对结构中的线性和非线性行为进行衡算。
这在地震工程中尤其重要,在强地运动下,建筑物和其他结构的反应可以高度非线性。
Newmark方法使工程师能够准确捕捉地震加载下的结构的复杂行为,对它的性能和脆弱性提供了宝贵的见解。
除地震工程外,Newmark方法也被用于风力工程和振动分析等其他领域。
在这些应用中,该方法可用于评估结构对不同类型的环境装载的动态反应,使工程师能够优化设计并确保结构安全。
总体而言,Newmark方法是预测多度自由结构的动态响应的有力工具。
它对非线性行为和复杂装载条件的衡算能力,使它成为在不同领域工作的工程师的一种宝贵的技术。
通过使用Newmark方法,工程师可以更深入地了解结构行为,做出知情的决定,以确保建筑环境的安全和复原力。
三种Newmark法计算
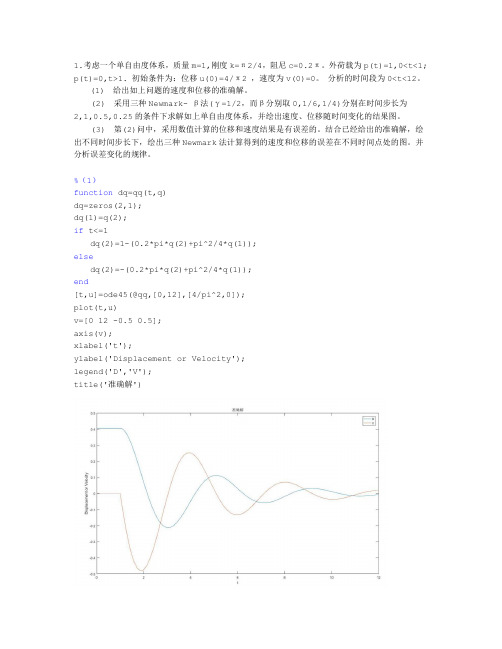
1.考虑一个单自由度体系,质量m=1,刚度k=π2/4,阻尼c=0.2π。
外荷载为p(t)=1,0<t<1; p(t)=0,t>1. 初始条件为:位移u(0)=4/π2 ,速度为v(0)=0。
分析的时间段为0<t<12。
(1) 给出如上问题的速度和位移的准确解。
(2) 采用三种Newmark- β法(γ=1/2,而β分别取0,1/6,1/4)分别在时间步长为2,1,0.5,0.25的条件下求解如上单自由度体系,并绘出速度、位移随时间变化的结果图。
(3) 第(2)问中,采用数值计算的位移和速度结果是有误差的。
结合已经给出的准确解,绘出不同时间步长下,绘出三种Newmark法计算得到的速度和位移的误差在不同时间点处的图。
并分析误差变化的规律。
%(1)function dq=qq(t,q)dq=zeros(2,1);dq(1)=q(2);if t<=1dq(2)=1-(0.2*pi*q(2)+pi^2/4*q(1));elsedq(2)=-(0.2*pi*q(2)+pi^2/4*q(1));end[t,u]=ode45(@qq,[0,12],[4/pi^2,0]);plot(t,u)v=[0 12 -0.5 0.5];axis(v);xlabel('t');ylabel('Displacement or Velocity');legend('D','V');title('准确解')%(2)function [D,V,A]=NM_beta(n,dt,beta,gama,d,v,K,M,C,P)a0=1/(beta*dt^2);a1=gama/beta/dt;a2=1/beta/dt;a3=1/2/beta-1;a4=gama/beta-1;a5=dt/2*(gama/beta-2);a6=dt*(1-gama);a7=dt*gama;Kd=K+a0*M+a1*C;a=(P-C*v-K*d)/M;D(1)=d;V(1)=v;A(1)=a;if beta==0for i=1:n-1D(i+1)=D(i);A(i+1)=A(i);V(i+1)=V(i);endelsefor i=1:n-1Pdi=P+M*(a0*D(i)+a2*V(i)+a3*A(i))+C*(a1*D(i)+a4*V(i)+a5*A(i));D(i+1)=inv(Kd)*Pdi;A(i+1)=a0*(D(i+1)-D(i))-a2*V(i)-a3*A(i);V(i+1)=V(i)++a6*A(i)+a7*A(i+1);endendD=D';V=V';A=A';endclearbeta=1/4; %还取了1/6、0gama=0.5;dt=0.25; %还取了0.5、1(当时间步长取2时,P(t)的分段情况不知如何处理,故不予展示)tm=12;tn=1;N=tm/dt+1;D=zeros(N,1);n=tn/dt+1;d=4/pi^2;v=0;K=pi^2/4;M=1;C=0.2*pi;P=1;[D_1,V_1,A_1]=NM_beta(n,dt,beta,gama,d,v,K,M,C,P); d=D_1(n);v=V_1(n);D(1:n,1)=D_1;V(1:n,1)=V_1;A(1:n,1)=A_1;m=(tm-tn)/dt+1;P=0;[D_2,V_2,A_2]=NM_beta(m,dt,beta,gama,d,v,K,M,C,P); D((n+1):(m+n-1),1)=D_2(2:m,1);V((n+1):(m+n-1),1)=V_2(2:m,1);A((n+1):(m+n-1),1)=A_2(2:m,1);t=0:dt:12;plot(t,D,t,V);xlabel('t');ylabel('Displacement or Velocity');legend('D','V');title('\beta=1/4 \Deltat=0.25');grid on(3)当beta一定时,时间步长越短,误差越小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用matlab编程实现Newmark-β法计算多自由度体系的动力响应
姓名:***
学号:**************
专业:结构工程
用matlab 编程实现Newmark -β法 计算多自由度体系的动力响应
一、Newmark -β法的基本原理
Newmark-β法是一种逐步积分的方法,避免了任何叠加的应用,能很好的适应非线性的反应分析。
Newmark-β法假定:
t u u u u
t t t t t t ∆ββ∆∆]}{}){1[(}{}{+++-+= (1-1)
2]}{}){2
1
[(}{}{}{t u u t u
u u t t t t t t ∆γγ∆∆∆+++-++= (1-2) 式中,β和γ是按积分的精度和稳定性要求进行调整的参数。
当β=0.5,γ=0.25时,为常平均加速度法,即假定从t 到t +∆t 时刻的速度不变,取为常数)}{}({2
1
t t t u u ∆++ 。
研究表明,当β≥0.5, γ≥0.25(0.5+β)2时,Newmark-β法是一种无条件稳定的格式。
由式(2-141)和式(2-142)可得到用t t u ∆+}{及t u }{,t u
}{ ,t u }{ 表示的t t u ∆+}{ ,t t u ∆+}{ 表达式,即有
t t
t t t t t u u t u u t u
}){121
(}{1)}{}({1}{2
----=++γ∆γ∆γ∆∆ (1-3) t t t t t t t u t u
u u t u
}{)21(}){1()}{}({}{ ∆γ
β
γβ∆γβ∆∆-+-+-=++ (1-4) 考虑t +∆t 时刻的振动微分方程为:
t t t t t t t t R u K u C u
M ∆∆∆∆++++=++}{}]{[}]{[}]{[ (1-5) 将式(2-143)、式(2-144) 代入(2-145),得到关于u t +∆t 的方程
t t t t R u K ∆∆++=}{}]{[ (1-6)
式中
][][1
][][2
C t M t
K K ∆γβ∆γ++
= )}{)12(}){1(}{]([)}){121
(}{1}{1](
[}{}{2
t t t t t t t t u t u
u t C u u t u t
M R R ∆γ
β
γβ∆γβγ∆γ∆γ∆-+-++-+++=+
求解式(2-146)可得t t u ∆+}{,然后由式(2-143)和式(2-144)可解出t t u
∆+}{ 和t t u ∆+}{ 。
由此,Newmark-β法的计算步骤如下:
1.初始计算:
(1)形成刚度矩阵[K ]、质量矩阵[M ]和阻尼矩阵[C ];
(2)给定初始值0}{u , 0}{u
和0}{u ; (3)选择积分步长∆t 、参数β、γ,并计算积分常数
2
01t ∆γα=
,t ∆γβα=1,t ∆γα12
=,1213-=γα, 14-=
γβα,)2(25-=γ
β
∆αt ,)1(6β∆α-=t ,t ∆βα=7; (4)形成有效刚度矩阵][][][][10C M K K αα++=; 2.对每个时间步的计算:
(1)计算t +∆t 时刻的有效荷载:
)}{}{}{]([)}{}{}{]([}{}{541320t t t t t t t t t t u u
u C u u
u M F F αααααα∆∆++++++=++
(2)求解t +∆t 时刻的位移:
[]t t t
t F u K ∆+∆+=}{}
{
(3)计算t +∆t 时刻的速度和加速度:
t t t t t t t u u u u u
}{}{)}{}({}{320 ααα∆∆---=++ t t t t t t u u u u
∆∆αα++++=}{}{}{}{76 Newmark-β方法是一种无条件稳定的隐式积分格式,时间步长∆t 的大小不影响解
的稳定性,∆t 的选择主要根据解的精度确定。
二、 本文用Newmark -β法计算的基本问题
四层框架结构在顶部受一个简谐荷载01
4=sin(
)t
F F t π的作用,力的作用时间1t =5s ,计算响应的时间为100s ,分2000步完成。
阻尼矩阵由Rayleigh 阻尼构造。
具体数据如下图:
图一:结构基本计算简图三、计算Newmark-β法的源程序
m=[1,2,3,4];
m=diag(m);
k= [800 -800 0 0;
-800 2400 -1600 0;
0 -1600 4800 -3200;
0 0 -3200 8000];
c=0.05*m+0.02*k;
f0=100;
t1=5;
nt=2000;
dt=0.01;
alfa=0.25;
beta=0.5;
a0=1/alfa/dt/dt;
a1=beta/alfa/dt;
a2=1/alfa/dt;
a3=1/2/alfa-1;
a4=beta/alfa-1;
a5=dt/2*(beta/alfa-2);
a6=dt*(1-beta);
a7=dt*beta;
d=zeros(4,nt);
v=zeros(4,nt);
a=zeros(4,nt);
for i=2:nt
t=(i-1)*dt;
if (t<t1), f=[f0*sin(4*pi*t/t1);0;0;0]; else f=[0;0;0;0]; end
ke=k+a0*m+a1*c;
fe=f+m*(a0*d(:,i-1)+a2*v(:,i-1)+a3*a(:,i-1))+c*(a1*d(:,i-1)+a4*v(:,i-1)+a5*a(:,i-1 ));
d(:,i)=inv(ke)*fe;
a(:,i)=a0*(d(:,i)-d(:,i-1))-a2*v(:,i-1)-a3*a(:,i-1);
v(:,i)=v(:,i-1)+a6*a(:,i-1)+a7*a(:,i);
end
四、计算结果截图
最后程序分别计算出四个质点的位移、速度、加速度响应。
现将部分截图如下:
图二:1质点的位移响应图三:4质点的位移响应
图四:1质点的速度响应图五:4质点的速度响应
图六:1质点的加速度响应图七:4质点的加速度响应。
