单自由度受动力荷载的newmark程序
中心差分法计算单自由度体系动力反应

中心差分法计算单自由度体系动力反应首先,考虑一个单自由度体系,由质点和一个弹簧组成。
系统的运动可以由以下常微分方程描述:m*x''(t)+c*x'(t)+k*x(t)=F(t)其中,m是质点的质量,x(t)是质点的位移,c是阻尼系数,k是弹簧刚度,F(t)是施加在质点上的外力。
为了使用中心差分法计算系统的动力反应,我们需要将上述方程转化为离散形式。
首先,将时间t划分为等间隔的离散时刻t0, t1, t2, ...,其中t0是初始时刻,tn是第n个离散时刻。
令Δt = tn+1 - tn为时间步长。
将位移x(t)和外力F(t)在时刻tn处展开为泰勒级数:x(tn) = x(nΔt)F(tn) = F(nΔt)x(tn+1) = x((n+1)Δt)F(tn+1) = F((n+1)Δt)然后,在动力方程中将位移和外力替换为对应的离散形式:m*(x(tn+1) - 2*x(tn) + x(tn-1))/Δt^2 + c*(x(tn+1) - x(tn-1))/(2*Δt) + k*x(tn) = F(tn)根据上述离散形式的动力方程,我们可以得到关于位移x((n+1)Δt)的递推关系式:(m + c*Δt/(2) + k*Δt^2)*x(tn+1) - (m - c*Δt/(2))*x(tn) = Δt^2*F(tn) + (2*m - k*Δt^2)*x(tn-1)由于x(tn-1)是已知量,而x(tn)和x(tn+1)是未知量,我们可以根据上述递推关系式进行迭代计算,从而得到系统在每个离散时刻的位移。
具体的计算步骤如下:1.初始化系统的初始条件,包括初始位移x(0)和初始速度x'(0)。
2. 根据初始条件,计算第一个离散时刻tn = t0下的位移x(t0)。
3. 根据递推关系式,计算系统在下一个离散时刻tn+1 = tn + Δt 下的位移x(tn+1):(m + c*Δt/(2) + k*Δt^2)*x(tn+1) = Δt^2*F(tn) + (2*m -k*Δt^2)*x(tn-1) + (m - c*Δt/(2))*x(tn)解上述方程,得到x(tn+1)的值。
结构动力学5任意荷载反应时域频域

u( ) 0
5.1 时域分析方法—Duhamel积分
1、单位脉冲反应函数 u( ) 0
u( ) 1
m
无阻尼体系的单位脉冲反应函数为:
[n (t
)]
t
0
t
有阻尼体系的单位脉冲反应函数为:
h(t
)
u(t)
1
mD
e n (t )
sin[D (t
)]
t
0
t
5.1 时域分析方法—Duhamel积分 1、单位脉冲反应函数
3、应用Fourier逆变换,由频域解U(ω)得到时域解u(t):
U () 逆Fu(t)
5.2 频域分析方法—Fourier变换法 离散Fourier(DFT)变换
在用频域法分析中涉及到两次Fourier变换,均为无穷域 积分,特别是Fourier逆变换,被积函数是复数,有时 涉及复杂的围道积分。当外荷载是复杂的时间函数 (如地震动)时,用解析型的Fourier变换几乎是不可 能的,实际计算中大量采用的是离散Fourier变换。
i2nU ()
n2U ()
1 m
P()
单自由度体系运动的频域解为:
U () H (i)P()
H (i)
1 k
[1
(
1
/ n )2]
i[2
(
/ n )]
H(iω)—复频反应函数,i是用来表示函数是一复数。
再利用Fourier逆变换,即得到体系的位移解:
u(t) 1 H (i)P()eitd 2
例如,对于无阻尼体系,当存在非零初始条件时,问题 的完整解为:
u(t)
u(0)
cosnt
u(0)
n
华工杜哈梅积分的单自由度matlab程序

华工杜哈梅积分的单自由度matlab程序华工杜哈梅积分求单自由度-matlabclcclear%输入数据,开始可以改参数了。
aa=10;%输入时间长度bb=0.01;%输入精度%%%%%t=bb:bb:aa;t1=t;%不用改%%%%%theta=1;%输入荷载频率w=2;%输入自振频率m=1;%输入质量p0=4;%输入荷载幅值%%%%p0=p0*ones(1,aa/bb);%不用改%%%%%p=p0.*sin(theta*t).*(theta*t<=pi)+0.*(theta.*t>pi);%荷载函数%%%%%%%%修改参数完毕,接下来的就不用管了。
%y2=3/16*(1/(1-0.25))*(sin(theta*t1)-0.5*sin(w*t1));for i=1:(aa/bb)for j=1:icanshu1(j)=p(j)/(m*w)*bb*sin(w*(t(i)-t1(j)));%杜哈梅积分中的被积函数%canshu2(j)=p(j)*b*cos(w*t1(j));%速度的A%canshu3(j)=p(j)*b*sin(w*t1(j));%速度的Bend%v(i)=cos(w*t(i))/m*sum(canshu2)+sin(w*t(i))/m*sum(cansh u3);%%速度值y(i)=sum(canshu1);%%位移值endfor i=1:aa/bb-1v1(i)=(y(i+1)-y(i))/bb;%计算速度endfor i=1:(aa/bb-2)a(i)=(v1(i+1)-v1(i))/bb;%计算加速度endhold on%%plot(t1,y2)plot(t,y,'linewidth',3)%画位移图plot(t(1:aa/bb-1),v1,'-r','linewidth',1.8)%画速度图%plot(t,v,'k')plot(t(1:aa/bb-2),a,'m')%画加速度图hold offlegend('\fontsize{9}\fontname{黑体}位移','\fontsize{9}\fontname{黑体}速度','\fontsize{9}\fontname{黑体}加速度')%i=find(y==(max(y)));%disp('时间')%t(i-3:i+3)'%disp('荷载')%p(i-3:i+3)'%disp('位移')%y(i-3:i+3)'%disp('速度')%v1(i-3:i+3)'%disp('加速度')%a(i-3:i+3)'上传-有心人献给苦于作业的人。
基于Newmark-β法的建筑结构地震响应简化计算

基于Newmark-β法的建筑结构地震响应简化计算摘要:地震是人类最严重的自然灾害之一,分析地震荷载下建筑结构体系的振动响应十分重要。
而对于建筑结构体系,一般将其离散为多自由度体系。
地震荷载下多自由度体系的响应可以采用中心差分法、分段解析法、Newmark-β法、Wilson-法等方法进行分析,其中Newmark-β法可以用来求解任意荷载下多自由度体系响应分析,包括地震荷载下的多自由度体系响应分析,精度较高。
本文主要结合振型叠加法和Newmark-β法思想,将建筑结构简化为多自由度体系,采用Python语言进行编程以获得基于Newmark-β法的建筑结构地震响应简化计算程序,最后通过简化算例验证了该算法程序的可行性,且由于Newmark-β法是一种显式求解法,故求解速度较快。
关键词:建筑结构;Newmark-β法;多自由度;地震响应;简化计算中图分类号:文章编号: 1000-565X1 引言地震是人类最严重的自然灾害之一。
有关记录表明,二十世纪因地震灾害造成的死亡人数至少在120万人以上。
发生在1976年我国的唐山大地震,死亡人数超过24.2万,因地震造成的直接间接损失超过百亿元。
减少因地震造成的生命财产损失对于国民经济的发展和人民生命财产的安全意义重大,其主要途径是工程结构抗震设计。
随着人类抗震经验的不断积累以及电子计算机的飞速进步,地震工程的理论和应用得到很大发展。
从早期的线性单自由度分析到如今的高度复杂的结构体系非线性弹塑性分析,并结合大型的模拟地震台作为检验,人们已经积累了一套相对完善的反映工程实际的抗震设计方法。
而地震反应的理论分析中,对响应的准确计算和分析是抗震设计的前提和基础。
结构地震响应计算方法经历了从静力法到反应谱法[1],最后落脚在时程分析法[2]的三大发展历程。
静力法只有在自振周期远小于地面运动周期时才足够精确,它忽略了结构自身的动力特性,因而存在很大局限性。
上世纪40年代提出了反应谱理论,但设计过程仍是静态方法,且无法反映许多实际复杂因素。
结构动力学newmark法程序

用matlab编程实现Newmark-β法计算多自由度体系的动力响应姓名:***学号:**************专业:结构工程用matlab 编程实现Newmark -β法 计算多自由度体系的动力响应一、Newmark -β法的基本原理Newmark-β法是一种逐步积分的方法,避免了任何叠加的应用,能很好的适应非线性的反应分析。
Newmark-β法假定:t u u u ut t t t t t ∆ββ∆∆]}{}){1[(}{}{+++-+= (1-1)2]}{}){21[(}{}{}{t u u t uu u t t t t t t ∆γγ∆∆∆+++-++= (1-2) 式中,β和γ是按积分的精度和稳定性要求进行调整的参数。
当β=0.5,γ=0.25时,为常平均加速度法,即假定从t 到t +∆t 时刻的速度不变,取为常数)}{}({21t t t u u ∆++ 。
研究表明,当β≥0.5, γ≥0.25(0.5+β)2时,Newmark-β法是一种无条件稳定的格式。
由式(2-141)和式(2-142)可得到用t t u ∆+}{及t u }{,t u}{ ,t u }{ 表示的t t u ∆+}{ ,t t u ∆+}{ 表达式,即有t tt t t t t u u t u u t u}){121(}{1)}{}({1}{2----=++γ∆γ∆γ∆∆ (1-3) t t t t t t t u t uu u t u}{)21(}){1()}{}({}{ ∆γβγβ∆γβ∆∆-+-+-=++ (1-4) 考虑t +∆t 时刻的振动微分方程为:t t t t t t t t R u K u C uM ∆∆∆∆++++=++}{}]{[}]{[}]{[ (1-5) 将式(2-143)、式(2-144) 代入(2-145),得到关于u t +∆t 的方程t t t t R u K ∆∆++=}{}]{[ (1-6)式中][][1][][2C t M tK K ∆γβ∆γ++= )}{)12(}){1(}{]([)}){121(}{1}{1]([}{}{2t t t t t t t t u t uu t C u u t u tM R R ∆γβγβ∆γβγ∆γ∆γ∆-+-++-+++=+求解式(2-146)可得t t u ∆+}{,然后由式(2-143)和式(2-144)可解出t t u∆+}{ 和t t u ∆+}{ 。
newmark法程序法计算多自由度体系地动力响应

用matlab 编程实现Newmark -β法计算多自由度体系的动力响应用matlab 编程实现Newmark -β法 计算多自由度体系的动力响应一、Newmark -β法的基本原理Newmark-β法是一种逐步积分的方法,避免了任何叠加的应用,能很好的适应非线性的反应分析。
Newmark-β法假定:t u u u ut t t t t t ∆ββ∆∆]}{}){1[(}{}{+++-+= (1-1)2]}{}){21[(}{}{}{t u u t uu u t t t t t t ∆γγ∆∆∆+++-++= (1-2) 式中,β和γ是按积分的精度和稳定性要求进行调整的参数。
当β=0.5,γ=0.25时,为常平均加速度法,即假定从t 到t +∆t 时刻的速度不变,取为常数)}{}({21t t t u u ∆++ 。
研究表明,当β≥0.5, γ≥0.25(0.5+β)2时,Newmark-β法是一种无条件稳定的格式。
由式(2-141)和式(2-142)可得到用t t u ∆+}{及t u }{,t u}{ ,t u }{ 表示的t t u ∆+}{ ,t t u ∆+}{ 表达式,即有t tt t t t t u u t u u t u}){121(}{1)}{}({1}{2----=++γ∆γ∆γ∆∆ (1-3) t t t t t t t u t uu u t u}{)21(}){1()}{}({}{ ∆γβγβ∆γβ∆∆-+-+-=++ (1-4) 考虑t +∆t 时刻的振动微分方程为:t t t t t t t t R u K u C uM ∆∆∆∆++++=++}{}]{[}]{[}]{[ (1-5) 将式(2-143)、式(2-144) 代入(2-145),得到关于u t +∆t 的方程t t t t R u K ∆∆++=}{}]{[ (1-6)式中][][1][][2C t M tK K ∆γβ∆γ++= )}{)12(}){1(}{]([)}){121(}{1}{1]([}{}{2t t t t t t t t u t uu t C u u t u tM R R ∆γβγβ∆γβγ∆γ∆γ∆-+-++-+++=+求解式(2-146)可得t t u ∆+}{,然后由式(2-143)和式(2-144)可解出t t u∆+}{ 和t t u ∆+}{ 。
Newmark

多自由度系统的振动——Newmark-β数值积分方法要求:(1)计算程序可以求出多自由度系统在任意荷载作用下的响应;(2)编写程序流程图;(3)做示例验算;(4)总结分析算法的稳定性及精度。
算例:计算图示结构的响应。
阻尼采用Rayleigh阻尼,α、β值自拟。
答:(1)程序流程图:是否(2)程序代码:%Newmark-β法求多自由度结构的响应dt=0.001; %计算时间间隔a=0.0452; b=0.0463; %计算阻力矩阵的α,β(Rayleigh阻尼) A=0.5;B=0.25; %Newmark-β法中的α,βa0=1/(A*dt^2); a1=B/(A*dt); a2=1/(A*dt); a3=1/(2*A)-1;a4=B/A-1; a5=dt/2*(B/A-2); a6=dt*(1-B); a7=B*dt;%计算所需数据T=30; %计算终点时刻n=T/dt+1;t=0:dt:T; %时间向量m=3; %质点个数M=[1,0,0;0,1,0;0,0,1]; %质量矩阵y=ones(m,n); %位移矩阵v=ones(m,n); %速度矩阵ac=ones(m,n); %加速度矩阵%确定初始位移、初速,计算初始加速度y(:,1)=[0;0;0];v(:,1)=[0;0;0];%K=[t(1)+1,0,0;0,t(1)+1,0;0,0,t(1)+2];%以时间为自变量的刚度矩阵K=[1,-1,0;-1,3,-2;0,-2,5];%常量刚度矩阵C=a.*K+b.*M;F=[sin(t(1));0;0]; %t0时刻荷载向量ac(:,1)=M\(F-C*v(:,1)-K*y(:,1)); %t0时刻加速度%计算等效刚度矩阵、位移向量、加速度向量、速度向量fori=2:n%K=[t(i)+1,0,0;0,t(i)+1,0;0,0,t(i)+2];%以时间为自变量的刚度矩阵C=a.*K+b.*M;F=[sin(t(i));0;0];F1=F+M*(a0*y(:,i-1)+a2*v(:,i-1)+a3*ac(:,i-1))...+C*(a1*y(:,i-1)+a4*v(:,i-1)+a5*ac(:,i-1)); %等效力K1=K+a0*M+a1*C; %等效刚度矩阵y(:,i)=K1\F1; %计算位移向量ac(:,i)=a0*(y(:,i)-y(:,i-1))-a2*v(:,i-1)-a3*ac(:,i-1);%计算加速度向量v(:,i)=v(:,i-1)+a6*ac(:,i-1)+a7*ac(:,i);%计算速度向量end%提取某些指点的位移、速度、加速度向量,绘制响应图plot(t,y(1,:),':b',t,y(2,:),'-r',t,y(3,:),'--g');grid onlegend('质点1','质点2','质点3');xlabel('时间t');ylabel('位移y');figure(2)plot(t,v(1,:),':b',t,v(2,:),'-r',t,v(3,:),'--g');grid onlegend('质点1','质点2','质点3');xlabel('时间t');ylabel('速度v');figure(3)plot(t,ac(1,:),':b',t,ac(2,:),'-r',t,ac(3,:),'--g');grid onlegend('质点1','质点2','质点3');xlabel('时间t');ylabel('加速度ac');程序运行结果:(3)算法稳定性及精度Newmark-β法基于泰勒公式将t(k+1)时刻的速度、位移在t(k)时刻展开,并将未知项做近似替换。
三种Newmark法计算
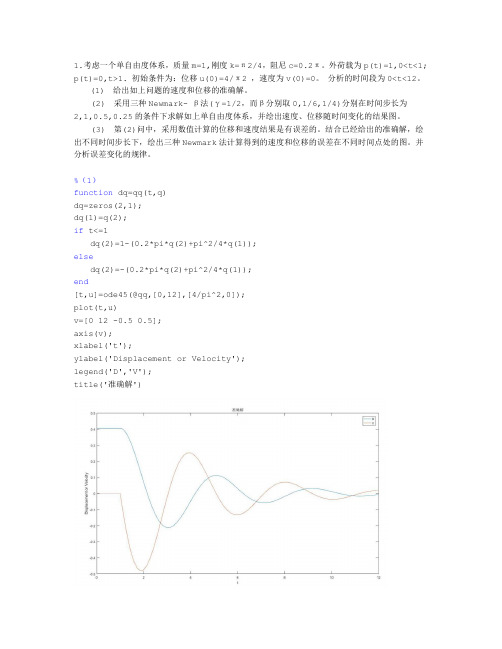
1.考虑一个单自由度体系,质量m=1,刚度k=π2/4,阻尼c=0.2π。
外荷载为p(t)=1,0<t<1; p(t)=0,t>1. 初始条件为:位移u(0)=4/π2 ,速度为v(0)=0。
分析的时间段为0<t<12。
(1) 给出如上问题的速度和位移的准确解。
(2) 采用三种Newmark- β法(γ=1/2,而β分别取0,1/6,1/4)分别在时间步长为2,1,0.5,0.25的条件下求解如上单自由度体系,并绘出速度、位移随时间变化的结果图。
(3) 第(2)问中,采用数值计算的位移和速度结果是有误差的。
结合已经给出的准确解,绘出不同时间步长下,绘出三种Newmark法计算得到的速度和位移的误差在不同时间点处的图。
并分析误差变化的规律。
%(1)function dq=qq(t,q)dq=zeros(2,1);dq(1)=q(2);if t<=1dq(2)=1-(0.2*pi*q(2)+pi^2/4*q(1));elsedq(2)=-(0.2*pi*q(2)+pi^2/4*q(1));end[t,u]=ode45(@qq,[0,12],[4/pi^2,0]);plot(t,u)v=[0 12 -0.5 0.5];axis(v);xlabel('t');ylabel('Displacement or Velocity');legend('D','V');title('准确解')%(2)function [D,V,A]=NM_beta(n,dt,beta,gama,d,v,K,M,C,P)a0=1/(beta*dt^2);a1=gama/beta/dt;a2=1/beta/dt;a3=1/2/beta-1;a4=gama/beta-1;a5=dt/2*(gama/beta-2);a6=dt*(1-gama);a7=dt*gama;Kd=K+a0*M+a1*C;a=(P-C*v-K*d)/M;D(1)=d;V(1)=v;A(1)=a;if beta==0for i=1:n-1D(i+1)=D(i);A(i+1)=A(i);V(i+1)=V(i);endelsefor i=1:n-1Pdi=P+M*(a0*D(i)+a2*V(i)+a3*A(i))+C*(a1*D(i)+a4*V(i)+a5*A(i));D(i+1)=inv(Kd)*Pdi;A(i+1)=a0*(D(i+1)-D(i))-a2*V(i)-a3*A(i);V(i+1)=V(i)++a6*A(i)+a7*A(i+1);endendD=D';V=V';A=A';endclearbeta=1/4; %还取了1/6、0gama=0.5;dt=0.25; %还取了0.5、1(当时间步长取2时,P(t)的分段情况不知如何处理,故不予展示)tm=12;tn=1;N=tm/dt+1;D=zeros(N,1);n=tn/dt+1;d=4/pi^2;v=0;K=pi^2/4;M=1;C=0.2*pi;P=1;[D_1,V_1,A_1]=NM_beta(n,dt,beta,gama,d,v,K,M,C,P); d=D_1(n);v=V_1(n);D(1:n,1)=D_1;V(1:n,1)=V_1;A(1:n,1)=A_1;m=(tm-tn)/dt+1;P=0;[D_2,V_2,A_2]=NM_beta(m,dt,beta,gama,d,v,K,M,C,P); D((n+1):(m+n-1),1)=D_2(2:m,1);V((n+1):(m+n-1),1)=V_2(2:m,1);A((n+1):(m+n-1),1)=A_2(2:m,1);t=0:dt:12;plot(t,D,t,V);xlabel('t');ylabel('Displacement or Velocity');legend('D','V');title('\beta=1/4 \Deltat=0.25');grid on(3)当beta一定时,时间步长越短,误差越小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单自由度体系受动力荷载Newmark法小程序
W = 200 kip; k = 12.2 k/in;po = 36.6 kip; t1 = 0.4 sec
.△t=0.05s
Repeat the analysis assuming zero damping.
Include both cases (zero and 2% damping) on same plot
Solution
The computer program is as followed:
p0 = 0; p1 = 36.6; p2 = 0;
t0 = 0; t1 = 0.4;
u0 = 0; v0 = 0;
dt = 0.05; % Solution time step
n = t1/dt/2;
nn = 10; % Dynamic load cycle Number
p = [p0:p1/n:p1, p1-p1/n:-p1/n:p2]; % One cycle input load
for ii = 1:72
a(1,ii) = 0;
end
p=[p,a];
t = [t0:dt:t1*nn]'; % Total time
m = 200/386; k = 12.2; zeta = 0.05; % System mass, stiffness and damping ratio gamma = 0.5; beta = 0.25; % Define the method
omega = sqrt(k/m);
c = 2*m*omega*zeta; % Damping
[u1,v1,a1] = dynresp(m,k,c,p,dt,0,0,gamma,beta);
[u2,v2,a2] = dynresp(m,k,0,p,dt,0,0,gamma,beta);
figure
plot(t,u1,t,u2)
figure
plot(t,v1,t,v2)
figure
plot(t,a1,t,a2)
function [u,v,a] = dynresp(m,k,c,p,dt,u0,v0,gamma,beta)
% solve the dynamic response of SDOF
% u = displacement of the structural response
% v = velocity
% a = acceleration
% m = mass of the system
% k = stiffness of the system
% c = damping
% p = input dynamic load for the system
% gamma, beta = Newmark's Method selection
% t = input load duration
% u0, v0 = initial displacement and velocity
n = length(p);
% dt = t/(n-1);
u(1) = u0;
v(1) = v0;
a(1) = (p(1)-c*v0-k*u0)/m;
k1 = k+gamma*c/(beta*dt)+m/(beta*dt^2);
pm1 = m/(beta*dt)+gamma*c/beta;
pm2 = m/2/beta+dt*(gamma/2/beta-1)*c;
dp = p(2:n)-p(1:n-1);
for ii = 1:n-1
dp1(ii) = dp(ii)+pm1*v(ii)+pm2*a(ii);
du(ii) = dp1(ii)/k1;
dv(ii) = gamma*du(ii)/beta/dt-gamma*v(ii)/beta+dt*(1-gamma/2/beta)*a(ii);
da(ii) = du(ii)/beta/dt^2-v(ii)/beta/dt-a(ii)/2/beta;
u(ii+1) = u(ii)+du(ii);
v(ii+1) = v(ii)+dv(ii);
a(ii+1) = a(ii)+da(ii);
end
u = u';
v = v';
a = a';
The result:。
