第二章补充习题
第二章补充习题及答案普通化学

第二章补充习题及答案普通化学概念、习题与解答化学反应基本原理——判断题1、指定单质的fGm、fHm、Sm皆为零。
(错:指定单质S不为零,)θmθθθ(错:升高温度正逆反应速率都增大,不会减小)10、反应活化能越大,反应速率也越大。
(错:相同温度下,活化能越大,速率常数越小,一般讲速率也越小)11、若反应速率方程式中浓度的指数等于反应方程式中反应物的系数,则该反应使基元反2、ΔrSm>0的反应都能自发进行。
(错:该条件只能判断对应温度孤立系统、标准状态下自发)3、rGm<0的反应必能自发进行。
(错:该条件只能判断对应温度标准状态4、若生成物的分子数比反应物的分子数多,则该反应的ΔrSm>0(错:主要看气体分子数)5、CaCO3在高温下可以发生分解反应,故该反应为吸热熵增。
(对:)6、根据能量最低原理,放热反应是自发进行的。
(错:影响自发性因素还有混乱度)7、冰在室温下自动融化成水,是熵增起了重要作用的结果。
(对:)8、化学反应的熵变与温度有关,但随温度变化不明显。
(对:温度变化没有引起状态变化的前提下)9、对于可逆反应C()+H2O(g)=CO(g)+H2(g),rHm0,升高温度使正增大,逆减小,故平衡向右移动。
应。
(错:例如H2(g)+I2(g)=2HI的反应就不是基元反应)12、反应级数取决于反应方程式中反应物的计量系数。
(错:非基元反应必须以试验为依据)13、根据分子碰撞理论,具有一定能量的分子在一定方位上发生有效碰撞,才可能生成产物。
(对)14、根据质量作用定律,反应物浓度增大,则反应速率加快,所以反应速率常数增大。
(错:速率常数与浓度无关)15、反应速率常数与温度有关,而与反应物浓度无关。
(对)二、选择题1热力学函数的定义与性质1-1下列各热力学函数中,哪一个为零:(B)(A)fGm(I2,g.298K)(B)fHm(Br2,l.298K)概念、习题与解答(C)Sm(H2,g.298K)(D)fGm(O3,g.298K)(E)fHm(CO2,g.298K)(C)对孤立体系而言,rSm>0的反应总是自发进行的。
第二章 蛋白质补充习题及答案

第二章蛋白质一、填空题1. 组成蛋白质分子的碱性氨基酸有________________、________________和________________。
酸性氨基酸有________________和________________。
2. 在下列空格中填入合适的氨基酸名称。
(1)________________是带芳香族侧链的极性氨基酸。
(2)________________和________________是带芳香族侧链的非极性氨基酸。
(3)________________是含硫的极性氨基酸。
(4)________________或________________是相对分子质量小且不含硫的氨基酸,在一个肽链折叠的蛋白质中它能形成内部氢键。
(5)在一些酶的活性中心中起作用并含羟基的极性较小的氨基酸是________________。
3. 氨基酸的等电点(pI)是指________________。
4. 脯氨酸与茚三酮反应产生________________色的物质,而其它氨基酸与茚三酮反应产生________________色的物质。
5. 实验室常用的甲醛滴定是利用氨基酸的氨基与中性甲醛反应,然后用碱(NaOH)来滴定________________上放出的________________。
6.通常可用紫外分光光度法测定蛋白质的含量,这是因为蛋白质分子中的________________、________________和________________三种氨基酸的共轭双键有紫外吸收能力。
7. 在α-螺旋中C=O和N-H基之间形成的氢键最稳定,因为这三个原子以________________排列。
8. 维持蛋白质构象的化学键有________________、________________、________________、________________、________________和________________。
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
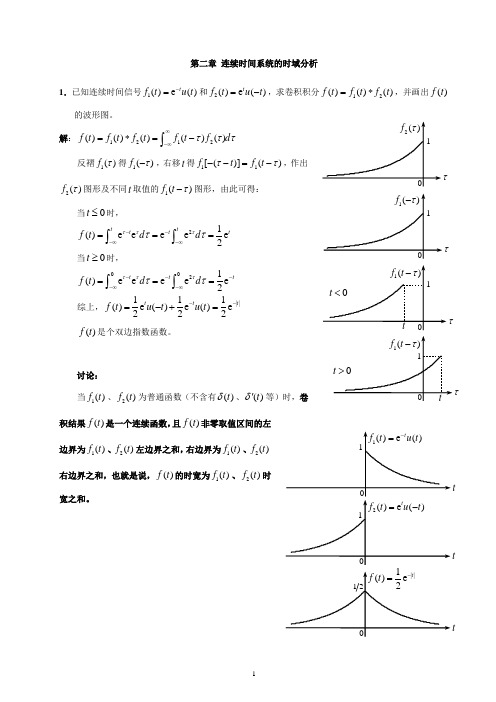
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
生物统计第二章 补充习题及答案

第二章习题及答案(来源:《生物统计学学习指导》李春喜等,科学出版社,2008:p14-15)一、填空1.变量的分布有两个明显的基本特征,即和。
二、判断1.计数资料也称为连续性变异资料。
计量资料也称为不连续性变异资料或间断性变异资料。
()三、选择题(《生物统计学题解及练习》杜荣赛高等教育出版社。
2003.p164)1.下面的变量属于非连续性变量的是( )。
A. 身高B. 体重C. 血型D. 血压2.身高、体重、年龄这一类数据属于()。
A. 离散性数据B. 计数数据C. 连续性数据D. 质量性状资料3.身高、体重、年龄这一类数据属于()。
A. 离散性数据B. 计数数据C. 计量资料D. 质量性状资料4.每十人中男性人数,每一万人中得H1N1流感人数,每亩麦田中杂草株数等,这一类数据属于()。
A. 离散性数据B. 连续性数据C. 计量资料D. 质量性状资料5.每十人中男性人数,每一万人中得H1N1流感人数,每亩麦田中杂草株数等,这一类数据属于()。
A. 计数数据B. 连续性数据C. 计量资料D. 质量性状资料6.频数按其组值的次序排列起来,称为()。
A. 频数排列B. 频数分布C. 组值排列D. 二项分布四、计算题1. 现以50枚受精种蛋孵化出雏鸡的天数为例,说明计数资料的整理。
21 20 20 21 23 22 22 22 21 22 20 23 22 23 22 19 22 2324 22 19 22 21 21 21 22 22 24 22 21 21 22 22 23 22 22小鸡出壳天数在19─24天范围内变动,有6个不同的观察值。
用各个不同观察值进行分组,共分为6组,可得表2-3形式的次数分布表。
表2-3 50枚受精种蛋出雏天数的次数分布表孵化天数划线计数次数(f)19 ║ 220 ║│ 321 ╫╫╫╫1022 ╫╫╫╫╫╫╫╫║║2423 ╫╫║║924 ║ 2合计50从表2-3可以看出:种蛋孵化出雏天数大多集中在21−23天,以22 天的最多,孵化天数较短(19−20天)和较长(24天)的都较少。
数学补充习题七年级上册答案

数学补充习题七年级上册答案第一章:整数1. 填空题(1) -3 (2) 7 (3) -5 (4) -14 (5) 22. 选择题(1) D (2) B (3) C (4) A (5) D3. 解答题(1) 同号相加,异号相消;(2) 同号为正,异号为负;(3) (-6) + (+7) = (+1);(4) 借助数轴即可得出答案为8。
第二章:分数1. 填空题(1) 5/6 (2) 1/4 (3) 2/5 (4) 5/12 (5) 3/102. 选择题(1) B (2) C (3) D (4) B (5) A3. 解答题(1) 1 1/4;(2) 3/5;(3) 12/75;(4) 除以一个数等于乘以其倒数。
第三章:代数式与简单方程1. 填空题(1) 4 (2) 24 (3) 4a (4) 9 (5) p2. 选择题(1) D (2) B (3) A (4) C (5) D3. 解答题(1) a = 3;(2) n = 5;(3) x = 10;(4) 3a + 8 = 23;(5) p/4 = 6;(6) y - 6 = 13。
第四章:图形的初步认识1. 填空题(1) 圆 (2) 正方形 (3) 矩形 (4) 梯形 (5) 三角形2. 选择题(1) A (2) C (3) B (4) D (5) B3. 解答题(1) 正方形的周长为4a;(2) 长方形的周长为2(a+b);(3) 三角形的周长为a+b+c;(4) 周长为10,设一边长为x,则另一边长为4-x,解方程2x + 2(4-x) = 10可以求得x=3,所以矩形的长为4,宽为3。
第五章:数据与统计1. 填空题(1) 中位数 (2) 众数 (3) 平均数 (4) 0 (5) [2, 7, 9, 9, 10]2. 选择题(1) D (2) A (3) C (4) B (5) C3. 解答题(1) 平均数为8;(2) 众数为7;(3) 分别为奇数和偶数。
数学补充习题答案三年级上册

数学补充习题答案三年级上册数学是一门需要动脑筋的学科,而习题则是帮助我们巩固知识、提高思维能力的重要工具。
在三年级上册的数学课本中,有许多有趣的习题,下面我将为大家提供一些数学补充习题的答案。
第一章:数字与数的概念1. 用阿拉伯数字写出下面各个数:a) 三十五:35b) 四十八:48c) 六十七:67d) 九十九:992. 用汉字写出下面各个数:a) 22:二十二b) 37:三十七c) 59:五十九d) 84:八十四第二章:加法与减法1. 计算下面的算式:a) 25 + 18 = 43b) 47 - 19 = 28c) 63 + 25 = 88d) 82 - 36 = 462. 填写空格,使等式成立:a) 27 + ___ = 40,答案:13b) 52 - ___ = 34,答案:18c) 15 + ___ = 30,答案:15d) 44 - ___ = 25,答案:19 第三章:整十数的加法与减法1. 计算下面的算式:a) 30 + 20 = 50b) 80 - 40 = 40c) 50 + 30 = 80d) 70 - 20 = 502. 填写空格,使等式成立:a) 40 + ___ = 50,答案:10b) 60 - ___ = 30,答案:30c) 50 + ___ = 80,答案:30d) 90 - ___ = 60,答案:30 第四章:数的顺序1. 用<、>或=填空:a) 25 ___ 35,答案:<b) 45 ___ 45,答案:=c) 60 ___ 50,答案:>d) 75 ___ 85,答案:<2. 用适当的数字填空:a) 30 ___ 40,答案:31b) 50 ___ 50,答案:50c) 70 ___ 60,答案:61d) 80 ___ 90,答案:81第五章:乘法与除法1. 计算下面的算式:a) 5 × 4 = 20b) 8 ÷ 2 = 4c) 6 × 7 = 42d) 12 ÷ 3 = 42. 填写空格,使等式成立:a) 7 × ___ = 35,答案:5b) 16 ÷ ___ = 4,答案:4c) 9 × ___ = 54,答案:6d) 24 ÷ ___ = 8,答案:3第六章:长度与质量1. 用适当的单位填空:a) 1 条短尺等于 ___ 厘米,答案:10b) 1 公斤等于 ___ 克,答案:1000c) 1 米等于 ___ 厘米,答案:100d) 1 公斤等于 ___ 千克,答案:12. 判断下面的说法是否正确:a) 1 公尺等于 100 厘米,正确。
财务管理第二章课后补充习题及课堂例题及答案(学生版)

第二章财务管理的价值观念课后补充计算题:1、某人希望以8%的年利率,按每半年付款一次的方式,在3年内等额偿还现有的6 000元债务,问每次应偿还多少?2、一农户购置了一台新收割机,他估计新机器头两年不需要维修,从第3年末开始的10年中,每年需支付200元维修费,若折现率为3%,问10年维修费的现值为多少?3、某人在2000年1月1日存入银行1000元,年利率为10%。
要求计算:(1)每年复利一次,2003年1月1日存款账户余额是多少?(2)每季度复利一次,2003年1月1日存款账户余额是多少?(3)若1000元,分别在2000年、2001年、2002年和2003年1月1日存入250元,仍按10%利率,每年复利一次,求2003年1月1日余额?(4)假定分4年存入相等金额,为了达到第一问所得到的账户余额,每期应存入多少金额?(5)假定第三问为每季度复利一次,2003年1月1日余额是多少?(6)假定第四问改为每季度复利一次,每年应存入多少金额?4、某人拟明年年初借款42000元,从明年年末开始,每年年末还本付息6000元,连续10年还清,设预定最低借款利率为8%,问此人是否能按计划借到款项?5、有人在今后五年中每年末借给你2 500元,要求你在随后的10年中,每年末归还2 500元于他,若年利率为5%,问你是否接受这笔借款?6、某工商管理研究生计划从银行借款10 000元,利率12%,半年计息一次。
这笔借款在四年内分期等额摊还,每半年还款一次。
第一次还款是从今天起的6个月后,问:(1)贷款的实际年利率是多少?(2)计算每半年应付的偿还额。
(3)计算第二个半年所付的本金和利息。
7、某公司准备投资开发新产品,现有三个方案可供选择。
根据市场预测,三种不同市场状况的预计年报酬率如下表:试计算投资开发各种新产品的风险大小。
8、某公司去年支付的股利为每股1元,一位投资者预计公司股利按固定比率5%增长,该公司股票的β系数为 1.5,无风险利率为8% ,所有股票的平均报酬率为15%。
矩阵补充习题含答案

第二章 矩阵补充习题1.已知对于n 阶方阵A ,存在自由数k ,使得kA 0=,试证明矩阵E –A 可逆,并写出其逆矩阵的表达式(E 为n 阶单位阵).【详解】 由代数公式kk-11-a (1a)(1+a++a )=-以及A 与E 可交换,有k k 1E-A (E A)(E+A+A )-=-+,而k A 0=故有k 1(E A)(E+A+A )E --+=可知E –A 可逆,且有-1k 1E-A E+A+A -=+().2.设A 为n 阶非奇异矩阵,α为n 维列向量,b 为常数.记分块矩阵*0T E P AA α⎛⎫= ⎪-⎝⎭,T A Q b αα⎛⎫= ⎪⎝⎭,其中*A 是矩阵A 的伴随矩阵,E 为n 阶单位矩阵. (1) 计算并化简PQ ;(2) 证明:矩阵Q 可逆的充分必要条件是1TA b αα-≠.【分析】 本题的关键是对于含*A 的计算或证明题,首先应联想到关系式**AA A A A E ==.另外,在进行矩阵乘法运算中要注意哪些是矩阵,哪些是向量,哪些是数,左乘还是右乘.【详解】 (1)因**AA A A A E ==,故***0T T T T T E AA PQ AA A A A A b A b αααααααα⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪--+-+⎝⎭⎝⎭⎝⎭=()10T A A b A ααα-⎛⎫⎪ ⎪-⎝⎭.(2)由(1)可得 ()21TP Q A b A αα-=-,而,0,PQ P Q P A ==≠且,故 ()1T Q A b A αα-=-.由此可知,0Q ≠的充分必要条件为1T A b αα-≠,即矩阵Q 可逆的充分必要条件是1T A b αα-≠.【评注】 本题综合考查了矩阵乘法运算、矩阵乘积行列式的性质以及伴随矩阵的性质.要特别注意重要公式:**AA A A A E ==,且A 可逆时,有()()*11*1**1,,,A A A A A AA A A A A A----====.3.设A 和B 均为n n ⨯矩阵,则必有(A) .B A B A +=+ (B) AB=BA. (C) BA AB =. (D) 111)(---+=+B A B A . 【 】【详解】 矩阵的乘法运算不满足交换律,因此一般BA AB ≠,但B A AB =,而行列式是数,可交换,于是有B A AB =BA A B ==,可见应选(C).对于(A), (D),主要考查行列式和矩阵的运算性质,均可通过反例说明不成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 试用结构图等效化简求图2-32所示各系统的传递函数
)
()
(s R s C .
解 (a )
所以: 4
321324321
43211)()
(G G G G G G G G G G G G G G s R s C ++++= (b )
所以: H
G G G s R s C 22
11)()(--=
(c )
2. 试用梅逊增益公式求上题中各结构图对应的闭环传递函数。
解 (a )图中有1条前向通路,3个回路,有1对互不接触回路
,,,2111432111G G L G G G G P -==∆=
,,,21321323432)(1L L L L L G G L G G L +++-=∆-=-=
4
32132432143211
11)()(G G G G G G G G G G G G G G P s R s C ++++=∆∆=
(b )图中有2条前向通路,1个回路
,,,,,H G L G P G P 2122211111
==∆-==∆= 11L -=∆
H
G G G P P s R s C 22
122111)()(--=
∆∆+∆=
(c )图中有1条前向通路,3个回路
,,,211132111G G L G G G P -==∆=
,,,)(132********L L L G G G L G G L ++-=∆-=-=
3
2132213211
11)()(G G G G G G G G G G P s R s C +++=∆∆=
3. 求图中系统从v 到y的传递函数。
解:
4. 已知系统方程组如下:
⎪⎪⎩⎪⎪⎨
⎧=-=-=--=)
()()()()]()()([)()]()()()[()()()]()()[()()()(3435233
612287111s X s G s C s G s G s C s X s X s X s G s X s G s X s C s G s G s G s R s G s X 试绘制系统结构图,并求闭环传递函数
)
()
(s R s C 。
解 系统结构图如下图解所示。
利用结构图等效化简或梅逊增益公式可求出系统的闭环传递函数为
8
43217432154363243211)()
(G G G G G G G G G G G G G G G G G G G G s R s C -+++=
5. 试用梅逊增益公式求图中系统的闭环传递函数。
解:
图中有2条前向通路,3个回路,有1对互不接触回路
112311
P G G G =∆=,, 234211111,P G G L G H =∆=-=+,
,,,3213213332111H H H G G G L H G L H G L -==-=
,21321)(1L L L L L +++-=∆
则有
1122
123341111331231231133
()()(1)
1P
P C s R s G G G G G G H G H G H G G G H H H G H G H ∆+∆=∆
++=
+-+-
6.建立图示系统的微分方程。
其中外力)(t F ,位移)(t x 为输入量;位移)(t y 为输出量;k (弹性系数),f (阻尼系数)和m (质量)均为常数。
解:如图解所示,取A,B 两点分别进行受力分析。
对A 点有
)()(111dt
dy
dt dx f x x k -=- (1)
对B 点有
y k dt
dy
dt dx f 21)(=- (2)
联立式(1)、(2)可得:
dt
dx k k k y k k f k k dt dy
2112121)(+=
++
7.系统结构图如下:分别用等效变换和梅逊公式法求系统的闭环传递
函数)(s Φ.
解(1):等效变换法:
1423121
12423423
14123
1442232121123
()()()
()
1[]()
1s C s R s G G G G G G H G H G G G G G G G G G G G G G G H G G H G G H G G G ∴Φ=
+=
++++++=
+++++
解(2):梅逊公式法:系统有2条前向通道,5个回路,没有不相交的回路。
41243212321211G G H G G G G H G G H G G +++++=∆
1G 1241213211= == ∆∆=G P G G G P
14123
1442232121123
1(s)C(s)R(s)
G G G G G G G G H G G H G G H G G G Φ=
++++++
8.求传递函数
解:回路4个:
3
3
3
2
1
2
2
1
1
i
H
G H G G H G H G L --+-=∑
两两不接触回路两个:Ⅰ-Ⅱ, Ⅱ-Ⅳ
L L L )
H G )(H (G )H )(G H G (L L k
j
i
33222
2
1
1
j i =-+-=∑∑
3
2322121333212211H H G G H H G G H G H G G H G H G 1 --++-+=∆∴
前向通道两条:
112123222p G G ;1p G ;1-G H =∆==∆=
1122
1232211221233312122323
p p (s)G G G (1-G H )
1G H G H G G H G H G G H H G G H H ∆+∆∴Φ=
∆
+=
+-++--
9.已知系统结构图,求?)
s (R )
s (C =
解:本结构图有2条前向通道,6个回路(其中I ,V 两回路不相交)
H
G G G G G H 1H)(1 G G G (s) H
1; G p 1
; G G p H G G G G G H 1 )H )].(G ([)]}G ([)G (G G G G H {1321123212321211321123332112-+++++-=Φ∴+=∆-==∆=-++++=---+----------=∆
● 求()[]t L δ
()()t 1t '=δ 解: ()[]()[]()1010s 1s t 1L t L =-=-⋅='=∴-δδ ● 求[]t cos L ω
解:[][]222211s L cos t L sin t s s s ωωωωωωω'=
=⋅⋅=++。
