2.4 线段、角的轴对称性(3) 2
2.4 线段、角的轴对称性(4)

【练习】
如图,在△ABC中,AB=AC,点D在BC上, DE⊥AB,DF⊥AC,垂足分别为E、F,且 DE=DF.求证:D是BC的中点.
2.4 线段的轴对称性
【例3】
在三角形ABC中∠BAC的角平分线与BC的垂直平 分线相交于D点,DN⊥AC,DM⊥AB.求证: BM=CN.
2.3 设计Байду номын сангаас对称图案
2.4 线段的轴对称性
【练习】
已知:如图,在△ABC中,点O是∠ABC、∠ACB外 角的平分线的交点,那么点O在∠A的平分线上吗?证 明你的结论.
2.4 线段的轴对称性
【例2】
已知:如图,AD是△ABC的角平分线,DE ⊥ AB, DF ⊥ AC,垂足分别为E、F. 求证:AD垂直平分EF.
2.4 线段的轴对称性
初中数学 八年级(上册)
2.4 线段、角的轴对称 性(4)
2.4 线段的轴对称性
【活动】
在△ABC中,用直尺和圆规分别作角平分线AD、 BE,AD、BE相交于点P,再作∠C的角平分线, 你有什么发现?
2.4 线段的轴对称性
【例1】
已知:如图,△ABC的角平分线AD、BE相交于点P. 求证:点P在∠C的平分线上.
2.4线段-角的对称性

lQABP§线段,角的轴对称性(1)教学案主备人:赵廷尧自主学习问题1:如图,线段AB ,通过折叠,能否是使点A 与点B 重合问题2:线段是轴对称图形吗上面操作中的折痕是什么 <问题3:在折痕上任意取一点C ,连接AC 、BC ,AC 与BC 的数量关系怎样你能证明吗通过以上三个问题的解决你知道了什么 几何语言:∵MN ⊥AB ,AC =BC ,∴_______(线段垂直平分线上的点到线段两 端的距离相等). "探究活动例1、线段的垂直平分线外的点,到这条线段两端的距离相等吗为什么变形:在例1的条件下:1、若AP=6,BP=4,求△QPB 的周长;2、若△QPB 的周长为12,△APB 的周长为17,求AB ; %3、若△QPB 的周长为12,AB =7,求△APB 的周长。
4、若△QCB 的周长为24,△APB 的周长与四边形BPQC 的周长之差为12,求CQA BC例2、如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若BC=25cm ,求△AEG的周长D FC ·例3、如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂线分别与AD、BC相交于点E、F,连接AF.求证:AE=AF.(【课堂练习】:已知:如图,AB=AC=12 cm,AB的垂直平分线分别交AC、AB于D、E,△ABD的周长等于29 cm,求DC的长.\§线段,角的轴对称性(1)达 标 自 测班级 学号 姓名自测内容1.线段垂直平分线上的点到 距离相等。
2、如图,直线MN 是线段AB 的垂直平分线,垂足为D ,点P 是MN 上一点.若AB =10 cm ,则BD =_______cm ;若PA =10 cm ,则PB =_______cm .3.如图,在ΔABC 中,AB 的中垂线交AC 与点E ,若AC=9,AE:CE=2:1,则B 、E 两点间的距离是 。
苏教版八年级上册数学线段、 角的轴对称性补充习题答案【三篇】

苏教版八年级上册数学线段、角的轴对称性补充习题答案【三篇】2.4线段、角的轴对称性(1)答案1、由点D在线段AB的垂直平分线上,可知DA=DB.于是△BDC的周长=BD+DC+BC=DA+DC+BC=AC+BC=9.2、 (1)图略;(2)OA=OB=OC.∵点O在线段AB的垂直平分线m上,∴OA=OB(线段垂直平分线上的点到线段两端的距离相等).同理,OB=OC.∴OA=OB=OC.2.4线段、角的轴对称性(2)答案1、点D在线段AC的垂直平分线上,∵BC=BD+DC,BC=BD+AD,∴BD+DC=BD+AD.∴DC=DA.∴点D在线段AC的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上).2、∵∠1=∠2,AC=AC,∠3=∠4,∴△ABC≌△ADC,∴AB=AD,CB=CD.∴点A在线段BD的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上).同理,点C在线段BD的垂直平分线上,∴AC是线段BD的垂直平分线(两点确定一条直线).2.4线段、角的轴对称性(3)答案1、过点D作DE⊥AB,垂足为E.∵AD平分∠BAC,DC⊥AC,DE⊥AB,∴DE=DC(角平分线上的点到角两边的距离相等).根据题意,得DC=6.∴点D到AB的距离为6.2、 DE=DC.∵AD平分∠BAC,DB⊥AB,DF⊥AC,∴DB=DF(角平分线上的点到角两边的距离相等).又BE=CF,∴Rt△DBE≌Rt△DFC.∴DE=DC.3、∵∠FEB=∠FDC=90°,∠BFE=∠CFD,BE=CD,∴△BEF∽△CDF.∴FE=FD.∴点F在∠MAN的平分线上(角的内部到角两边距离相等的点在角的平分线上).。
第7讲线段与角的轴对称性

142
∴∠C=∠A=20°,∠BDC=90°, ∴∠CBD=90°﹣∠A=70°. 故选:D.
学习,为了追寻更好的自己!
例 3、如图,在△ABC 中,DE 和 DF 分别是边 AB 和 AC 的垂直平分线,且 D 点在 BC 边上,
连接 AD,则∠BAC=
°.
【分析】根据线段垂直平分线的性质得出 BD=AD,AD=CD,求出∠B=∠BAD,∠C
学习,为了追寻更好的自己!
第七讲 线段与角的轴对称性
一、知识梳理
要点一、线段的轴对称性 (1)线段是轴对称图形,线段的垂直平分线是它的对称轴. (2)线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等; (3)线段垂直平分线的性质定理的逆定理(判定定理):到线段两个端距离相等的点
在 线段的垂直平分线上. 要点诠释: 线段的垂直平分线的性质是证明两线段相等的常用方法之一.同时也给出了引辅助线的
பைடு நூலகம்
【点评】本题考查了线段垂直平分线的性质,等腰三角形的性质,三角形的内角和定理
等知识点,注意:线段垂直平分线上的点到线段两个端点的距离相等.
【变式 1】如图在△ABC 中 MP,NQ 分别垂直平分 AB、AC,若 BC 的长度为 9,则△APQ
的周长是
.
【分析】根据线段的垂直平分线的性质得出 AP=BP,AQ=CQ,求出△APQ 的周长=BC, 再代入求出即可.
145
学习,为了追寻更好的自己!
【详解】
解:作 OD⊥AB 于 D,OE⊥AC 于 E,OF⊥BC 于 F,连接 OC,
∵点 O 为∠ABC 与∠CAB 的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,
∴OE=OD=OF,
2.4线段、角的轴对称性(3)作业纸
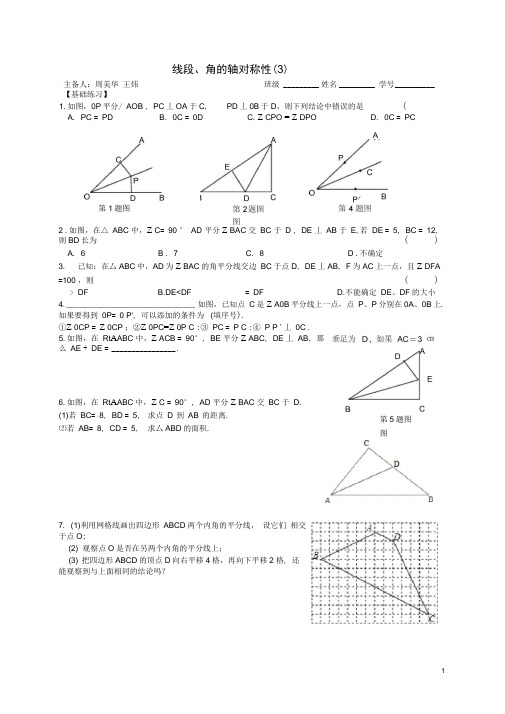
1线段、角的轴对称性(3)【基础练习】2 .如图,在△ ABC 中,Z C = 90 ° AD 平分Z BAC 交 BC 于 D , DE 丄 AB 于 E ,若 DE = 5, BC = 12, 则BD 长为 ( ) A . 6 B . 7C . 8D .不确定3. 已知:在厶ABC 中,AD 为Z BAC 的角平分线交边 BC 于点D , DE 丄AB , F 为AC 上一点,且Z DFA=100°,则 ()4. _____________________________ 如图,已知点 C 是Z A0B 平分线上一点,点 P 、P 分别在0A 、0B 上.如果要得到 0P = 0 P', 可以添加的条件为 (填序号).①Z 0CP = Z 0CP ;②Z 0PC =Z 0P C :③ PC = P C :④ P P '丄 0C .7. (1)利用网格线画出四边形 ABCD 两个内角的平分线, 设它们 相交于点O ;(2) 观察点O 是否在另两个内角的平分线上;(3) 把四边形ABCD 的顶点D 向右平移4格,再向下平移2 格, 还能观察到与上面相同的结论吗?主备人:周美华 王炜班级 _________ 姓名 _________ 学号 __________5.如图,在 Rt A ABC 中,Z ACB = 90°, BE 平分Z ABC , DE 丄 AB , 那么 AE + DE = ________________ .6.如图,在 Rt A ABC 中,Z C = 90°, AD 平分Z BAC 交 BC 于 D . (1)若 BC = 8, BD = 5, ⑵若 AB = 8, CD = 5, 求点D 到AB 的距离. 求厶ABD 的面积. 第5题图 图1.如图,0P 平分/ AOB , PC 丄OA 于C , PD 丄0B 于D ,则下列结论中错误的是 ( A . PC = PD B . 0C = 0DC . Z CPO = Z DPOD . 0C = PC> DFB.DE<DF= DFD.不能确定 DE 、DF 的大小第1题图A&已知:如图,点B、C分别在/ MAN的两边上,BD丄AM , CE丄AN,垂点分别为D、E, BD、CE相交于点F,且BF = CF .证明:点F在/ A的角平分线上.NOA, DN OB,9•如图,射线0C在/ AOB的内部,点D、E在射线OC上,DMEP OA, EQ OB,垂足分别为M、N、P、Q,且EP = EQ . 求证:DM =DN .【拓展提升】1 . △ ABC的周长为60,/ A和/B的角平分线相交于点P,若点P到边AB的距离为10,则厶ABC 的面积为.2 .如图,/ AOB= 90 °将三角尺的直角顶点落在/ AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与/ AOB的两边分别相交于点E、F.⑴求证:PE= PF.(2)若将三角板绕点P旋转,使得点E落在AO的延长线上,(1)中的结论还成立吗?请你画出相应的图形,并证明你的结论•完成时间: ____________家长签字: ____________2。
2.4-2 线段和角的轴对称性

用直尺、圆规作已知线段垂直平分线的一般步骤: 活动3 画一画 回顾作法:
1.分别以A 、B为圆心, 1 大于 AB长为半径画弧;
2
M
A
2. 两弧相交于点M、N;
B
3.过点M、N作直线.
∴直线MN即为线段AB 的 垂直平分线.
N
活动4
再画画 如图,任意三角形ABC,边AB、BC的 垂直平分线 l1 、 l2交于点O
.
画板 Z J G 反 共
P
A
B
在线段垂直平分线外, 不存在到线段两端距 离相等的点.
定理: 到线段两端距离相等的点 在线段的垂直 平分线上.
数量关系 位置关系
P
A B
推理格式:
∵ PA=PB
∴点P在线段AB的垂直平分线上
如图,点MN为直线l上两点,且满足 l MA=MB,NA=NB
GO
M B
完成以下填空:
A
∵MA=MB, N AB ∴点M在线段 的垂直平分线上. (理由是 到线段两端距离相等的点在线段 的垂直平分线上 又∵ NA=NB , ∴点N在线段AB的垂直平分线上. ∴直线MN是线段AB的 垂直平分线 . (理由是 两点确定一条直线 )
)
活动2
l
回顾、发现
如图,已知直线l 是线段AB的垂直平分线
作PO平分∠APB
1 2
共线
∵PO平分∠APB ∴ ∠1=∠2 在△POA和△POB中 PO=PO ∠1=∠2 PA=PB ∴△POA≌△POB(SAS) ∴∠AOP=∠BOP, OA=OB 又∵A、O、B三点共线 ∴∠AOP + ∠BOP=180° ∴∠AOP =90° ∴ PO⊥AB 又∵OA=OB ∴ PO垂直平分AB 即P在线段AB垂直平分线上
2.4线段、角的轴对称性(第1课时)(同步课件)八年级数学上册同步精品课堂(苏科版)

∵∠BAC=∠BAD+∠CAE+∠DAE
∴∠DAE=∠BAC-(∠BAD+∠CAE)=2α-180°
思维拓展
在△ABC中,∠BAC=α,边AB的垂直平分线交BC于点D,边AC的垂直平
分线交BC于点E,连接AD,AE,则∠DAE的度数为______________.
P
● 2
●
●
A●
●
P3
O
●
B(A)
新知归纳
线段的垂直平分线的性质定理:
线段的垂直平分线上的点到线段两端的距离相等.
符号语言:
l
∵点P在线段AB的垂直平分线上,
●
A●
∴ PA=PB
(线段的垂直平分线上的点到线段两端的距离相等).
用途:
相等的线段
P
●
O
B
操作与思考
思考4 线段的垂直平分线外的点,到这条线段两端的距离相等吗?
B
理由: 在l上另取一点P,连接PA、PB、PA'.
由作图可知,l是AA'的垂直平分线,
A
∴ AP=A'P,AM=A'M,
l
M
A'
∴ AM+BM=A'M+BM=A'B,
P
AP+BP=A'P+BP,
由“两点之间线段最短”可得:
A'B<A'P+BP.
即AM+BM最短.
课堂小结
线
段
垂
直
平
分
线
的
性
质
内容
2.4 线段、角的轴对称性(3) 2

在操作中感知角的轴 养口头表达能力.
3, 直线 OC 是∠AOB 的角平分线,
明确结论.
OC 翻折, 你有什么发现?角平分线
称轴吗?
第 1 页
共 3 页
2014-1-6
凤凰初中数学配套教学软件_教学设计
学生独立思考、积极探究.方法 不一,具体如下: 1.利用“AAS”证明△ODP≌ △OEP 后,说明 PD 与 PE 相等.
“角”的轴对称性又如何呢?与线段有什么异同和联
,我们就进入今天愉快的数学探究之旅.
:
积极思考, 动手操作, 提出猜想.
让学生动手操作,感
薄纸上画∠AOB,它是轴对称图形吗?如果是,对称
称性,猜想对称轴的位置
为什么?
究作铺垫,同时激发学 趣. 动手操作, 验证猜想, 描述发现,
A O 2-23 C B
相等,再结合证明两个
得到的结论.
实 “过一点有且只有一条直线与已知 路,让学生寻找到演绎推 直线垂直” ,说明 PD 与 PE 相等.
B
培养学生的动手能力和探 下面的证明积累经验.
讨论后共同小结:
师生互动,锻炼学生
线上的点有什么特点?
角平分线上的点到角两边的距 能力,培养学生勇于发表 离相等. 1. 猜想角平分线性质定理的逆 能力.
D O E 2-24 P A C
问题虽然比较简单,
线是否也有像线段垂直平分线一样的特殊性质呢?
受到 PD 与 PE 相等,但
在∠AOB 的角平分线 OC 任意取一点 P,PD⊥OA,
进行推理说明还是有困难
D 与 PE 相等吗?为什么?
学生从角平分线的定义入
明,你发现了什么?用
2.利用角的轴对称性和基本事
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O E Q
B
通过上述研究,你得到了什么结论?
2.4 线段、角的对称性(3)
说说你本节课你有什么收获?
2.4 线段、角的对称性(3)
作业:
P58习题2.4,分析第7、8题的思路,任 选1题写出过程.
初中数学
八年级(上册)
2.4
作
线段、角的对称性(3)
者:王正东(盐城市射阳县长荡初级中学)
AOB
2.4 线段、角的对称性(3)
做一做
在一张薄纸上画 ∠AOB,操作并思考: 它是轴对称图形吗? 为什么?
A O B
2.4 线段、角的对称性(3)
想一想
角是轴对称图形,它的对称轴在哪里?为什么?
A O
C
B
角是轴对称图形,角平分线所在的直线是它的对称轴.
2.4 线段、角的对称性(3)
想一想
如图,在∠AOB的角平分线OC任意取一点P, PD⊥OA,PE⊥OB,PD与PE相等吗?为什么?
D A P C E B
O
定理
角平分线上的点到角两边的距离相等.
2.4 线段、角的对称性(3)
想一想
角内部一点到角两边的距离相等,那么这个点 在这个角的角平分线上吗?
