Shape of the Yield Curve Under CIR Single Factor Model A Note working paper
投资学第7版Test Bank答案完整可编辑

Multiple Choice Questions1. The term structure of interest rates is:A) The relationship between the rates of interest on all securities.B) The relationship between the interest rate on a security and its time to maturity.C) The relationship between the yield on a bond and its default rate.D) All of the above.E) None of the above.Answer: B Difficulty: EasyRationale: The term structure of interest rates is the relationship between two variables, years and yield to maturity (holding all else constant).2. The yield curve shows at any point in time:A) The relationship between the yield on a bond and the duration of the bond.B) The relationship between the coupon rate on a bond and time to maturity of thebond.C) The relationship between yield on a bond and the time to maturity on the bond.D) All of the above.E) None of the above.Answer: C Difficulty: Easy3. An inverted yield curve implies that:A) Long-term interest rates are lower than short-term interest rates.B) Long-term interest rates are higher than short-term interest rates.C) Long-term interest rates are the same as short-term interest rates.D) Intermediate term interest rates are higher than either short- or long-term interestrates.E) none of the above.Answer: A Difficulty: EasyRationale: The inverted, or downward sloping, yield curve is one in which short-term rates are higher than long-term rates. The inverted yield curve has been observedfrequently, although not as frequently as the upward sloping, or normal, yield curve.4. An upward sloping yield curve is a(n) _______ yield curve.A) normal.B) humped.C) inverted.D) flat.E) none of the above.Answer: A Difficulty: EasyRationale: The upward sloping yield curve is referred to as the normal yield curve, probably because, historically, the upward sloping yield curve is the shape that has been observed most frequently.5. According to the expectations hypothesis, a normal yield curve implies thatA) interest rates are expected to remain stable in the future.B) interest rates are expected to decline in the future.C) interest rates are expected to increase in the future.D) interest rates are expected to decline first, then increase.E) interest rates are expected to increase first, then decrease.Answer: C Difficulty: EasyRationale: An upward sloping yield curve is based on the expectation that short-term interest rates will increase.6. Which of the following is not proposed as an explanation for the term structure ofinterest rates?A) The expectations theory.B) The liquidity preference theory.C) The market segmentation theory.D) Modern portfolio theory.E) A, B, and C.Answer: D Difficulty: EasyRationale: A, B, and C are all theories that have been proposed to explain the term structure.7. The expectations theory of the term structure of interest rates states thatA) forward rates are determined by investors' expectations of future interest rates.B) forward rates exceed the expected future interest rates.C) yields on long- and short-maturity bonds are determined by the supply and demandfor the securities.D) all of the above.E) none of the above.Answer: A Difficulty: EasyRationale: The forward rate equals the market consensus expectation of future short interest rates.8. Which of the following theories state that the shape of the yield curve is essentiallydetermined by the supply and demands for long-and short-maturity bonds?A) Liquidity preference theory.B) Expectations theory.C) Market segmentation theory.D) All of the above.E) None of the above.Answer: C Difficulty: EasyRationale: Market segmentation theory states that the markets for different maturities are separate markets, and that interest rates at the different maturities are determined by the intersection of the respective supply and demand curves.9. According to the "liquidity preference" theory of the term structure of interest rates, theyield curve usually should be:A) inverted.B) normal.C) upward slopingD) A and B.E) B and C.Answer: E Difficulty: EasyRationale: According to the liquidity preference theory, investors would prefer to be liquid rather than illiquid. In order to accept a more illiquid investment, investors require a liquidity premium and the normal, or upward sloping, yield curve results.Use the following to answer questions 10-13:Suppose that all investors expect that interest rates for the 4 years will be as follows:10. What is the price of 3-year zero coupon bond with a par value of $1,000?A) $863.83B) $816.58C) $772.18D) $765.55E) none of the aboveAnswer: B Difficulty: ModerateRationale: $1,000 / (1.05)(1.07)(1.09) = $816.5811. If you have just purchased a 4-year zero coupon bond, what would be the expected rateof return on your investment in the first year if the implied forward rates stay the same?(Par value of the bond = $1,000)A) 5%B) 7%C) 9%D) 10%E) none of the aboveAnswer: A Difficulty: ModerateRationale: The forward interest rate given for the first year of the investment is given as 5% (see table above).12. What is the price of a 2-year maturity bond with a 10% coupon rate paid annually? (Parvalue = $1,000)A) $1,092B) $1,054C) $1,000D) $1,073E) none of the aboveAnswer: D Difficulty: ModerateRationale: [(1.05)(1.07)]1/2 - 1 = 6%; FV = 1000, n = 2, PMT = 100, i = 6, PV =$1,073.3413. What is the yield to maturity of a 3-year zero coupon bond?A) 7.00%B) 9.00%C) 6.99%D) 7.49%E) none of the aboveAnswer: C Difficulty: ModerateRationale: [(1.05)(1.07)(1.09)]1/3 - 1 = 6.99.Use the following to answer questions 14-16:The following is a list of prices for zero coupon bonds with different maturities and par value of $1,000.14. What is, according to the expectations theory, the expected forward rate in the thirdyear?A) 7.00%B) 7.33%C) 9.00%D) 11.19%E) none of the aboveAnswer: C Difficulty: ModerateRationale: 881.68 / 808.88 - 1 = 9%15. What is the yield to maturity on a 3-year zero coupon bond?A) 6.37%B) 9.00%C) 7.33%D) 10.00%E) none of the aboveAnswer: C Difficulty: ModerateRationale: (1000 / 808.81)1/3 -1 = 7.33%16. What is the price of a 4-year maturity bond with a 12% coupon rate paid annually? (Parvalue = $1,000)A) $742.09B) $1,222.09C) $1,000.00D) $1,141.92E) none of the aboveAnswer: D Difficulty: DifficultRationale: (1000 / 742.09)1/4 -1 = 7.74%; FV = 1000, PMT = 120, n = 4, i = 7.74, PV = $1,141.9217. The market segmentation theory of the term structure of interest ratesA) theoretically can explain all shapes of yield curves.B) definitely holds in the "real world".C) assumes that markets for different maturities are separate markets.D) A and B.E) A and C.Answer: E Difficulty: EasyRationale: Although this theory is quite tidy theoretically, both investors and borrows will depart from their "preferred maturity habitats" if yields on alternative maturities are attractive enough.18. An upward sloping yield curveA) may be an indication that interest rates are expected to increase.B) may incorporate a liquidity premium.C) may reflect the confounding of the liquidity premium with interest rateexpectations.D) all of the above.E) none of the above.Answer: D Difficulty: EasyRationale: One of the problems of the most commonly used explanation of termstructure, the expectations hypothesis, is that it is difficult to separate out the liquidity premium from interest rate expectations.19. The "break-even" interest rate for year n that equates the return on an n-periodzero-coupon bond to that of an n-1-period zero-coupon bond rolled over into a one-year bond in year n is defined asA) the forward rate.B) the short rate.C) the yield to maturity.D) the discount rate.E) None of the above.Answer: A Difficulty: EasyRationale: The forward rate for year n, fn, is the "break-even" interest rate for year n that equates the return on an n-period zero- coupon bond to that of an n-1-periodzero-coupon bond rolled over into a one-year bond in year n.20. When computing yield to maturity, the implicit reinvestment assumption is that theinterest payments are reinvested at the:A) Coupon rate.B) Current yield.C) Yield to maturity at the time of the investment.D) Prevailing yield to maturity at the time interest payments are received.E) The average yield to maturity throughout the investment period.Answer: C Difficulty: ModerateRationale: In order to earn the yield to maturity quoted at the time of the investment, coupons must be reinvested at that rate.21. Which one of the following statements is true?A) The expectations hypothesis indicates a flat yield curve if anticipated futureshort-term rates exceed the current short-term rate.B) The basic conclusion of the expectations hypothesis is that the long-term rate isequal to the anticipated long-term rate.C) The liquidity preference hypothesis indicates that, all other things being equal,longer maturities will have lower yields.D) The segmentation hypothesis contends that borrows and lenders are constrained toparticular segments of the yield curve.E) None of the above.Answer: D Difficulty: ModerateRationale: A flat yield curve indicates expectations of existing rates. Expectations hypothesis states that the forward rate equals the market consensus of expectations of future short interest rates. The reverse of C is true.22. The concepts of spot and forward rates are most closely associated with which one ofthe following explanations of the term structure of interest rates.A) Segmented Market theoryB) Expectations HypothesisC) Preferred Habitat HypothesisD) Liquidity Premium theoryE) None of the aboveAnswer: B Difficulty: ModerateRationale: Only the expectations hypothesis is based on spot and forward rates. A andC assume separate markets for different maturities; liquidity premium assumes higheryields for longer maturities.Use the following to answer question 23:23. Given the bond described above, if interest were paid semi-annually (rather thanannually), and the bond continued to be priced at $850, the resulting effective annual yield to maturity would be:A) Less than 12%B) More than 12%C) 12%D) Cannot be determinedE) None of the aboveAnswer: B Difficulty: ModerateRationale: FV = 1000, PV = -850, PMT = 50, n = 40, i = 5.9964 (semi-annual);(1.059964)2 - 1 = 12.35%.24. Interest rates might declineA) because real interest rates are expected to decline.B) because the inflation rate is expected to decline.C) because nominal interest rates are expected to increase.D) A and B.E) B and C.Answer: D Difficulty: EasyRationale: The nominal rate is comprised of the real interest rate plus the expectedinflation rate.25. Forward rates ____________ future short rates because ____________.A) are equal to; they are both extracted from yields to maturity.B) are equal to; they are perfect forecasts.C) differ from; they are imperfect forecasts.D) differ from; forward rates are estimated from dealer quotes while future short ratesare extracted from yields to maturity.E) are equal to; although they are estimated from different sources they both are usedby traders to make purchase decisions.Answer: C Difficulty: EasyRationale: Forward rates are the estimates of future short rates extracted from yields to maturity but they are not perfect forecasts because the future cannot be predicted with certainty; therefore they will usually differ.26. The pure yield curve can be estimatedA) by using zero-coupon bonds.B) by using coupon bonds if each coupon is treated as a separate "zero."C) by using corporate bonds with different risk ratings.D) by estimating liquidity premiums for different maturities.E) A and B.Answer: E Difficulty: ModerateRationale: The pure yield curve is calculated using zero coupon bonds, but coupon bonds may be used if each coupon is treated as a separate "zero."27. The on the run yield curve isA) a plot of yield as a function of maturity for zero-coupon bonds.B) a plot of yield as a function of maturity for recently issued coupon bonds trading ator near par.C) a plot of yield as a function of maturity for corporate bonds with different riskratings.D) a plot of liquidity premiums for different maturities.E) A and B.Answer: B Difficulty: Moderate28. The market segmentation and preferred habitat theories of term structureA) are identical.B) vary in that market segmentation is rarely accepted today.C) vary in that market segmentation maintains that borrowers and lenders will notdepart from their preferred maturities and preferred habitat maintains that marketparticipants will depart from preferred maturities if yields on other maturities areattractive enough.D) A and B.E) B and C.Answer: E Difficulty: ModerateRationale: Borrowers and lenders will depart from their preferred maturity habitats if yields are attractive enough; thus, the market segmentation hypothesis is no longerreadily accepted.29. The yield curveA) is a graphical depiction of term structure of interest rates.B) is usually depicted for U. S. Treasuries in order to hold risk constant acrossmaturities and yields.C) is usually depicted for corporate bonds of different ratings.D) A and B.E) A and C.Answer: D Difficulty: EasyRationale: The yield curve (yields vs. maturities, all else equal) is depicted for U. S.Treasuries more frequently than for corporate bonds, as the risk is constant acrossmaturities for Treasuries.Use the following to answer questions 30-32:30. What should the purchase price of a 2-year zero coupon bond be if it is purchased at thebeginning of year 2 and has face value of $1,000?A) $877.54B) $888.33C) $883.32D) $893.36E) $871.80Answer: A Difficulty: DifficultRationale: $1,000 / [(1.064)(1.071)] = $877.5431. What would the yield to maturity be on a four-year zero coupon bond purchased today?A) 5.80%B) 7.30%C) 6.65%D) 7.25%E) none of the above.Answer: C Difficulty: ModerateRationale: [(1.058) (1.064) (1.071) (1.073)]1/4 - 1 = 6.65%32. Calculate the price at the beginning of year 1 of a 10% annual coupon bond with facevalue $1,000 and 5 years to maturity.A) $1,105B) $1,132C) $1,179D) $1,150E) $1,119Answer: B Difficulty: DifficultRationale: i = [(1.058) (1.064) (1.071) (1.073) (1.074)]1/5 - 1 = 6.8%; FV = 1000, PMT = 100, n = 5, i = 6.8, PV = $1,131.9133. Given the yield on a 3 year zero-coupon bond is 7.2% and forward rates of 6.1% in year1 and 6.9% in year 2, what must be the forward rate in year 3?A) 8.4%B) 8.6%C) 8.1%D) 8.9%E) none of the above.Answer: B Difficulty: ModerateRationale: f3 = (1.072)3 / [(1.061) (1.069)] - 1 = 8.6%34. An inverted yield curve is oneA) with a hump in the middle.B) constructed by using convertible bonds.C) that is relatively flat.D) that plots the inverse relationship between bond prices and bond yields.E) that slopes downward.Answer: E Difficulty: EasyRationale: An inverted yield curve occurs when short-term rates are higher thanlong-term rates.35. Investors can use publicly available financial date to determine which of the following?I)the shape of the yield curveII)future short-term ratesIII)the direction the Dow indexes are headingIV)the actions to be taken by the Federal ReserveA) I and IIB) I and IIIC) I, II, and IIID) I, III, and IVE) I, II, III, and IVAnswer: A Difficulty: ModerateRationale: Only the shape of the yield curve and future inferred rates can be determined.The movement of the Dow Indexes and Federal Reserve policy are influenced by term structure but are determined by many other variables also.36. Which of the following combinations will result in a sharply increasing yield curve?A) increasing expected short rates and increasing liquidity premiumsB) decreasing expected short rates and increasing liquidity premiumsC) increasing expected short rates and decreasing liquidity premiumsD) increasing expected short rates and constant liquidity premiumsE) constant expected short rates and increasing liquidity premiumsAnswer: A Difficulty: ModerateRationale: Both of the forces will act to increase the slope of the yield curve.37. The yield curve is a component ofA) the Dow Jones Industrial Average.B) the consumer price index.C) the index of leading economic indicators.D) the producer price index.E) the inflation index.Answer: C Difficulty: EasyRationale: Since the yield curve is often used to forecast the business cycle, it is used as one of the leading economic indicators.38. The most recently issued Treasury securities are calledA) on the run.B) off the run.C) on the market.D) off the market.E) none of the above.Answer: A Difficulty: EasyUse the following to answer questions 39-42:Suppose that all investors expect that interest rates for the 4 years will be as follows:39. What is the price of 3-year zero coupon bond with a par value of $1,000?A) $889.08B) $816.58C) $772.18D) $765.55E) none of the aboveAnswer: A Difficulty: ModerateRationale: $1,000 / (1.03)(1.04)(1.05) = $889.0840. If you have just purchased a 4-year zero coupon bond, what would be the expected rateof return on your investment in the first year if the implied forward rates stay the same?(Par value of the bond = $1,000)A) 5%B) 3%C) 9%D) 10%E) none of the aboveAnswer: B Difficulty: ModerateRationale: The forward interest rate given for the first year of the investment is given as 3% (see table above).41. What is the price of a 2-year maturity bond with a 5% coupon rate paid annually? (Parvalue = $1,000)A) $1,092.97B) $1,054.24C) $1,028.51D) $1,073.34E) none of the aboveAnswer: C Difficulty: ModerateRationale: [(1.03)(1.04)]1/2 - 1 = 3.5%; FV = 1000, n = 2, PMT = 50, i = 3.5, PV =$1,028.5142. What is the yield to maturity of a 3-year zero coupon bond?A) 7.00%B) 9.00%C) 6.99%D) 4%E) none of the aboveAnswer: D Difficulty: ModerateRationale: [(1.03)(1.04)(1.05)]1/3 - 1 = 4%.Use the following to answer questions 43-46:The following is a list of prices for zero coupon bonds with different maturities and par value of $1,000.43. What is, according to the expectations theory, the expected forward rate in the thirdyear?A) 7.23B) 9.37%C) 9.00%D) 10.9%E) none of the aboveAnswer: B Difficulty: ModerateRationale: 862.57 / 788.66 - 1 = 9.37%44. What is the yield to maturity on a 3-year zero coupon bond?A) 6.37%B) 9.00%C) 7.33%D) 8.24%E) none of the aboveAnswer: D Difficulty: ModerateRationale: (1000 / 788.66)1/3 -1 = 8.24%45. What is the price of a 4-year maturity bond with a 10% coupon rate paid annually? (Parvalue = $1,000)A) $742.09B) $1,222.09C) $1,035.66D) $1,141.84E) none of the aboveAnswer: C Difficulty: DifficultRationale: (1000 / 711.00)1/4 -1 = 8.9%; FV = 1000, PMT = 100, n = 4, i = 8.9, PV =$1,035.6646. You have purchased a 4-year maturity bond with a 9% coupon rate paid annually. Thebond has a par value of $1,000. What would the price of the bond be one year from now if the implied forward rates stay the same?A) $995.63B) $1,108.88C) $1,000.00D) $1,042.78E) none of the aboveAnswer: A Difficulty: DifficultRationale: (925.16 / 711.00)]1/3 - 1.0 = 9.17%; FV = 1000, PMT = 90, n = 3, i = 9.17, PV = $995.63Use the following to answer question 47:47. Given the bond described above, if interest were paid semi-annually (rather thanannually), and the bond continued to be priced at $917.99, the resulting effective annual yield to maturity would be:A) Less than 10%B) More than 10%C) 10%D) Cannot be determinedE) None of the aboveAnswer: B Difficulty: ModerateRationale: FV = 1000, PV = -917.99, PMT = 45, n = 36, i = 4.995325 (semi-annual);(1.4995325)2 - 1 = 10.24%.Use the following to answer questions 48-50:48. What should the purchase price of a 2-year zero coupon bond be if it is purchased at thebeginning of year 2 and has face value of $1,000?A) $877.54B) $888.33C) $883.32D) $894.21E) $871.80Answer: D Difficulty: DifficultRationale: $1,000 / [(1.055)(1.06)] = $894.2149. What would the yield to maturity be on a four-year zero coupon bond purchased today?A) 5.75%B) 6.30%C) 5.65%D) 5.25%E) none of the above.Answer: A Difficulty: ModerateRationale: [(1.05) (1.055) (1.06) (1.065)]1/4 - 1 = 5.75%50. Calculate the price at the beginning of year 1 of an 8% annual coupon bond with facevalue $1,000 and 5 years to maturity.A) $1,105.47B) $1,131.91C) $1,084.25D) $1,150.01E) $719.75Answer: C Difficulty: DifficultRationale: i = [(1.05) (1.055) (1.06) (1.065) (1.07)]1/5 - 1 = 6%; FV = 1000, PMT = 80, n = 5, i = 6, PV = $1084.2551. Given the yield on a 3 year zero-coupon bond is 7% and forward rates of 6% in year 1and 6.5% in year 2, what must be the forward rate in year 3?A) 7.2%B) 8.6%C) 8.5%D) 6.9%E) none of the above.Answer: C Difficulty: ModerateRationale: f3 = (1.07)3 / [(1.06) (1.065)] - 1 = 8.5%Use the following to answer questions 52-61:52. What should the purchase price of a 1-year zero coupon bond be if it is purchased todayand has face value of $1,000?A) $966.37B) $912.87C) $950.21D) $956.02E) $945.51Answer: D Difficulty: DifficultRationale: $1,000 / (1.046) = $956.0253. What should the purchase price of a 2-year zero coupon bond be if it is purchased todayand has face value of $1,000?A) $966.87B) $911.37C) $950.21D) $956.02E) $945.51Answer: B Difficulty: DifficultRationale: $1,000 / [(1.046)(1.049)] = $911.3754. What should the purchase price of a 3-year zero coupon bond be if it is purchased todayand has face value of $1,000?A) $887.42B) $871.12C) $879.54D) $856.02E) $866.32Answer: E Difficulty: DifficultRationale: $1,000 / [(1.046)(1.049)(1.052)] = $866.3255. What should the purchase price of a 4-year zero coupon bond be if it is purchased todayand has face value of $1,000?A) $887.42B) $821.15C) $879.54D) $856.02E) $866.32Answer: B Difficulty: DifficultRationale: $1,000 / [(1.046)(1.049)(1.052)(1.055)] = $821.1556. What should the purchase price of a 5-year zero coupon bond be if it is purchased todayand has face value of $1,000?A) $776.14B) $721.15C) $779.54D) $756.02E) $766.32Answer: A Difficulty: DifficultRationale: $1,000 / [(1.046)(1.049)(1.052)(1.055)(1.058)] = $776.1457. What is the yield to maturity of a 1-year bond?A) 4.6%B) 4.9%C) 5.2%D) 5.5%E) 5.8%Answer: A Difficulty: ModerateRationale: 4.6% (given in table)58. What is the yield to maturity of a 5-year bond?A) 4.6%B) 4.9%C) 5.2%D) 5.5%E) 5.8%Answer: C Difficulty: ModerateRationale: [(1.046)(1.049)(1.052)(1.055)(1.058)]1/5 -1 = 5.2%59. What is the yield to maturity of a 4-year bond?A) 4.69%B) 4.95%C) 5.02%D) 5.05%E) 5.08%Answer: C Difficulty: ModerateRationale: [(1.046)(1.049)(1.052)(1.055)]1/4 -1 = 5.05%60. What is the yield to maturity of a 3-year bond?A) 4.6%B) 4.9%C) 5.2%D) 5.5%E) 5.8%Answer: B Difficulty: ModerateRationale: [(1.046)(1.049)(1.052)]1/3 -1 = 4.9%61. What is the yield to maturity of a 2-year bond?A) 4.6%B) 4.9%C) 5.2%D) 4.7%E) 5.8%Answer: D Difficulty: ModerateRationale: [(1.046)(1.049)]1/2 -1 = 4.7%Essay Questions62. Discuss the three theories of the term structure of interest rates. Include in yourdiscussion the differences in the theories, and the advantages/disadvantages of each.Difficulty: ModerateAnswer:The expectations hypothesis is the most commonly accepted theory of term structure.The theory states that the forward rate equals the market consensus expectation of future short-term rates. Thus, yield to maturity is determined solely by current and expected future one-period interest rates. An upward sloping, or normal, yield curve wouldindicate that investors anticipate an increase in interest rates. An inverted, or downward sloping, yield curve would indicate an expectation of decreased interest rates. Ahorizontal yield curve would indicate an expectation of no interest rate changes.The liquidity preference theory of term structure maintains that short-term investorsdominate the market; thus, in general, the forward rate exceeds the expected short-term rate. In other words, investors prefer to be liquid to illiquid, all else equal, and willdemand a liquidity premium in order to go long term. Thus, liquidity preference readily explains the upward sloping, or normal, yield curve. However, liquidity preferencedoes not readily explain other yield curve shapes.Market segmentation and preferred habitat theories indicate that the markets fordifferent maturity debt instruments are segmented. Market segmentation maintains that the rates for the different maturities are determined by the intersection of the supply and demand curves for the different maturity instruments. Market segmentation readilyexplains all shapes of yield curves. However, market segmentation is not observed in the real world. Investors and issuers will leave their preferred maturity habitats if yields are attractive enough on other maturities.The purpose of this question is to ascertain that students understand the variousexplanations (and deficiencies of these explanations) of term structure.63. Term structure of interest rates is the relationship between what variables? What isassumed about other variables? How is term structure of interest rates depictedgraphically?Difficulty: ModerateAnswer:Term structure of interest rates is the relationship between yield to maturity and term to maturity, all else equal. The "all else equal" refers to risk class. Term structure ofinterest rates is depicted graphically by the yield curve, which is usually a graph of U.S.governments of different yields and different terms to maturity. The use of U.S.governments allows one to examine the relationship between yield and maturity,holding risk constant. The yield curve depicts this relationship at one point in time only.This question is designed to ascertain that students understand the relationshipsinvolved in term structure, the restrictions on the relationships, and how therelationships are depicted graphically.64. Although the expectations of increases in future interest rates can result in an upwardsloping yield curve; an upward sloping yield curve does not in and of itself imply the expectations of higher future interest rates. Explain.Difficulty: ModerateAnswer:The effects of possible liquidity premiums confound any simple attempt to extractexpectation from the term structure. That is, the upward sloping yield curve may be due to expectations of interest rate increases, or due to the requirement of a liquiditypremium, or both. The liquidity premium could more than offset expectations ofdecreased interest rates, and an upward sloping yield would result.The purpose of this question is to assure that the student understands the confounding of the liquidity premium with the expectations hypothesis, and that the interpretations of term structure are not clear-cut.。
Yield Curve
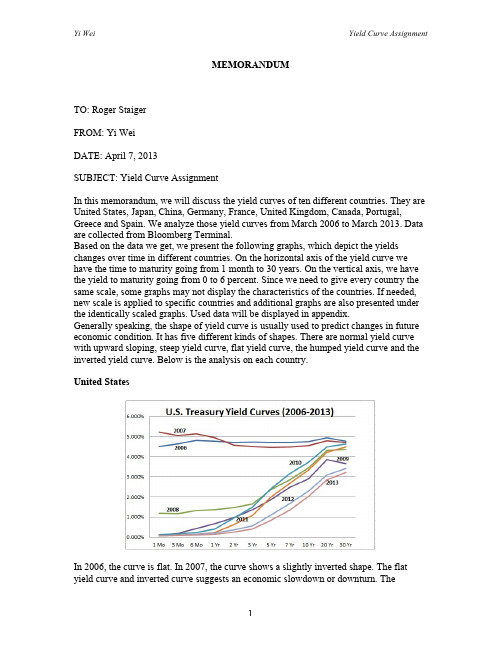
MEMORANDUMTO: Roger StaigerFROM: Yi WeiDATE: April 7, 2013SUBJECT: Yield Curve AssignmentIn this memorandum, we will discuss the yield curves of ten different countries. They are United States, Japan, China, Germany, France, United Kingdom, Canada, Portugal, Greece and Spain. We analyze those yield curves from March 2006 to March 2013. Data are collected from Bloomberg Terminal.Based on the data we get, we present the following graphs, which depict the yields changes over time in different countries. On the horizontal axis of the yield curve we have the time to maturity going from 1 month to 30 years. On the vertical axis, we have the yield to maturity going from 0 to 6 percent. Since we need to give every country the same scale, some graphs may not display the characteristics of the countries. If needed, new scale is applied to specific countries and additional graphs are also presented under the identically scaled graphs. Used data will be displayed in appendix.Generally speaking, the shape of yield curve is usually used to predict changes in future economic condition. It has five different kinds of shapes. There are normal yield curve with upward sloping, steep yield curve, flat yield curve, the humped yield curve and the inverted yield curve. Below is the analysis on each country.United StatesIn 2006, the curve is flat. In 2007, the curve shows a slightly inverted shape. The flat yield curve and inverted curve suggests an economic slowdown or downturn. Theinverted curve implies long-term rates are lower than short-term rates. This abnormal situation could happen under the circumstance that the expected inflation in long-term will decrease or the supply of bond will decrease significantly. Banks earn money by short-term borrowing and long-term lending spread. Thus, banks have fewer incentives to lend money to finance economic activities.The time is right before the financial crisis.From year 2008 to year 2013, we have steep yield curve. The normal curve is upward sloping which shows the risk compensation increases with maturity. If the increase of long-term yield is higher than that of the short-term, the curve will become a steep curve. The steep curve usually happens when economy starts to expand after an economic recession. Economic stagnation has already suppressed the short-term rate. Rates will begin to go up if increasing economic activities needs capital. United States is slowing recovering from the recession.JapanWe can see that from 2006 till now, the Japanes sovereign yield curves are upward sloping curves, which remain below 2.5%. The low level rates suggest that the economy remains in the doldrums. During the past ten years, Japan has been in a quite depressed condition--deflation. After financial crisis, like other countries, investors tend to choose treasury bond to avoid risks. Bond demand surged, which drove down the prices.In 2013, the main economic goal of Japanese government is to push the inflation to 2% by depressing Japanese sovereign yield and depreciating yen.ChinaBasically, all the eight years’ yield curves are normal curves, which indicate that the economic condition in China is much better than that in other countries. There is an obvious yield drop from 2008 to 2009 due to the financial crisis. People transferred their assets to a more secured place like treasury bond, bringing down the prices. At the mean time, the government adopted stimulus plans which include loose monetary policy after the crisis. From 2010 to 2013, the yield curve shift upwards, implying a steady recovery of economy.GermanyThe yield curve in 2006 is high. In 2007, the curve is flat. And in 2008 the curve is inverted. The yield curves of the three years show the consequeneces of global economic downturn caused by financial crisis. During post-crisis time, the yield curve shifts downward year after year. The short-term rates in 2012 and 2013 is almost zero, suggesting a sluggish economy mainly caused by the bad influence of European Debt Crisis.FranceUnited KingdomThe curves in 2006, 2007 and 2008 are basically inverted curves because of the global financial crisis. Like Germany, the yield curves from 2009 to 2013 shift downward. Although UK is not a member of Eurozone, it is a member of European Union. Its products mainly exported to European countries. The downturn in Eurozone certainly affected its performance. UK lowered interest rates to stimulate investments. CanadaGreecePortugalSpainAppendixU.S. 2006 2007 2008 2009 2010 2011 2012 2013 1 M o 4.500% 5.210% 1.200% 0.090% 0.120% 0.070% 0.080% 0.070% 3 M o 4.630% 5.050% 1.180% 0.200% 0.170% 0.100% 0.080% 0.090% 6 M o 4.810% 5.120% 1.320% 0.420% 0.240% 0.140% 0.150% 0.110%1 Y r 4.770% 4.930% 1.370% 0.670% 0.400% 0.230% 0.210% 0.140%2 Y r 4.690% 4.570% 1.470% 0.980% 0.960% 0.630% 0.370% 0.250%3 Y r 4.720% 4.500% 1.650% 1.360% 1.490% 1.080% 0.560% 0.400% 5 Y r 4.690% 4.460% 2.370% 1.870% 2.420% 2.000% 1.110% 0.840% 7 Y r 4.700% 4.470% 2.840% 2.480% 3.150% 2.680% 1.670% 1.350% 10 Y r 4.730% 4.540% 3.440% 2.890% 3.710% 3.330% 2.290% 2.010% 20 Y r 4.930% 4.780% 4.300% 3.840% 4.480% 4.210% 3.080% 2.850% 30 Y r 4.750% 4.690% 4.350% 3.660% 4.630% 4.470% 3.410% 3.220%Japan 2006 2007 2008 2009 2010 2011 2012 2013 1 M o 0.074% 0.590% 0.576% 0.247% 0.122% N/A N/A N/A 3 M o 0.124% 0.597% 0.555% 0.247% 0.121% 0.118% N/A 0.048% 6 M o 0.131% 0.580% 0.526% 0.299% 0.114% 0.132% 0.105% 0.045%1 Y r 0.564% 0.774% 0.560% 0.410% 0.140% 0.168% 0.110% 0.058%2 Y r 0.738% 0.850% 0.589% 0.509% 0.189% 0.215% 0.114% 0.042%3 Y r 0.955% 0.969% 0.654% 0.650% 0.332% 0.265% 0.169% 0.040% 5 Y r 1.335% 1.219% 0.768% 0.815% 0.613% 0.495% 0.364% 0.119% 7 Y r 1.538% 1.390% 0.887% 0.969% 0.944% 0.693% 0.654% 0.280% 10 Y r 1.720% 1.839% 1.744% 1.700% 1.804% 1.211% 1.047% 0.620% 20 Y r 2.089% N/A N/A N/A N/A 2.079% 1.800% 1.613% 30 Y r 2.330% N/A 2.594% 1.994% 2.340% 2.215% 1.964% 1.766%China 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A N/A N/A N/A N/A 2.850% 2.600% 3 M o 1.440% 1.840% 3.600% 1.100% 1.420% 2.500% 2.850% 2.700% 6 M o 1.600% 1.950% 3.650% 1.200% 1.450% 2.700% 2.800% 2.700%1 Y r 1.580% 2.111% 3.519% 1.062% 1.508% 2.852% 2.855% 2.745%2 Y r 1.951% 2.294% 3.639% 1.369% 1.948% 3.236% 2.980% 3.055%3 Y r 2.051% 2.543% 3.703% 1.576% 2.386% 3.246% 2.977% 3.095% 5 Y r 2.354% 2.823% 3.904% 2.352% 2.702% 3.494% 3.168% 3.275% 7 Y r 2.601% 2.968% 3.993% 2.757% 3.022% 3.722% 3.436% 3.465% 10 Y r N/A 3.190% 4.116% 3.100% 3.436% 3.921% 3.540% 3.575% 20 Y r N/A N/A N/A N/A N/A N/A N/A N/A 30 Y r N/A N/A N/A N/A N/A N/A N/A N/AGermany 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A N/A N/A N/A N/A N/A N/A 3 M o 2.503% 3.754% 3.829% 0.609% 0.254% N/A N/A N/A6 M o 2.665% 3.847% 3.792% 0.751% 0.380% 0.619% 0.021%-‐0.017%1 Y r 2.975% 3.982% 3.641% 0.947% 0.557% 0.867% 0.071% 0.012%2 Y r 3.192% 3.890% 3.243% 1.328% 1.031% 1.130% 0.160% 0.023%3 Y r 3.232% 3.877% 3.201% 1.688% 1.432% 1.524% 0.278% 0.044% 5 Y r 3.453% 3.866% 3.319% 2.240% 2.183% 2.112% 0.666% 0.244% 7 Y r 3.580% 3.889% 3.502% 2.723% 2.659% 2.584% 1.167% 0.580% 10 Y r 3.684% 3.903% 3.730% 3.057% 3.153% 3.051% 1.786% 1.247% 20 Y r 3.928% 4.092% 4.400% 4.120% 3.804% 3.362% 2.534% 1.964% 30 Y r 3.926% 4.060% 4.437% 3.919% 3.928% 3.656% 2.685% 2.292% France 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A 3.908% 0.804% 0.294% 0.573% 0.045% N/A 3 M o 2.508% 3.752% 3.860% 0.673% 0.288% 0.732% 0.076% 0.023% 6 M o 2.687% 3.842% 3.833% 0.758% 0.377% 0.904% 0.129% 0.032%1 Y r 2.905% 3.959% 3.680% 0.902% 0.597% 1.188% 0.253% 0.089%2 Y r 3.301% 3.890% 3.247% 1.936% 1.665% 1.561% 0.513% 0.181%3 Y r 3.403% 3.881% 3.368% 2.380% 1.908% 1.913% 0.804% 0.375% 5 Y r 3.536% 3.892% 3.524% 2.858% 2.659% 2.649% 1.797% 0.916% 7 Y r 3.643% 3.910% 3.695% 3.241% 3.098% 2.960% 2.264% 1.240% 10 Y r 3.855% 4.042% 4.333% 4.058% 3.827% 3.470% 2.957% 2.064% 20 Y r 3.960% 4.117% 4.585% 4.234% 4.114% 3.883% 3.574% 2.908% 30 Y r N/A N/A N/A N/A N/A 3.952% 3.716% 3.186% UK 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A N/A 0.549% 0.510% 0.488% N/A 0.348% 3 M o 4.473% 5.350% N/A 0.608% 0.420% 0.559% N/A 0.320% 6 M o 4.462% 5.363% N/A N/A 0.525% 0.623% N/A 0.344%1 Y r 4.372% 5.284% 3.992% 0.934% 0.655% 0.763% 0.415% 0.178%2 Y r 4.416% 5.156% 3.790% 1.996% 1.866% 1.197% 0.456% 0.222%3 Y r 4.395% 5.089% 3.871% 2.215% 2.379% 1.615% 0.605% 0.343% 5 Y r 4.366% N/A N/A N/A 3.297% 2.256% 1.178% 0.816% 7 Y r 4.348% 4.896% 4.214% 2.495% 3.719% 2.995% 1.680% 1.313% 10 Y r 4.271% 4.666% 4.471% 3.568% 4.532% 3.525% 2.369% 1.935% 20 Y r 4.024% 4.264% 4.358% 3.935% 4.630% 4.237% 3.236% 2.900% 30 Y r N/A N/A N/A N/A N/A 4.293% 3.430% 3.290%Canada 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A N/A 0.256% 0.165% 0.879% 0.865% N/A 3 M o 3.714% 4.142% 2.185% 0.427% 0.202% 0.931% 0.930% 0.935% 6 M o 3.820% 4.101% 2.442% 0.511% 0.330% 1.030% N/A 0.990% 1 Y r 3.930% 4.104% 2.522% 0.599% 0.718% 1.269% N/A 1.019% 2 Y r 3.913% 3.925% 2.427% 0.963% 1.561% N/A N/A N/A 3 Y r 3.968% 3.902% 2.543% 1.413% 1.870% 1.625% 1.269% 0.988% 5 Y r 4.082% 3.915% 2.854% 1.872% 2.796% 2.206% 1.514% 1.291% 7 Y r 4.141% 3.951% 3.116% 2.232% 2.996% N/A 1.698% 1.399% 10 Y r 4.194% 4.017% 3.481% 2.869% 3.492% 3.062% 2.092% 1.780% 20 Y r 4.288% 4.147% 3.988% 3.734% 4.073% N/A N/A N/A 30 Y r 4.222%4.107%4.016%3.596%4.066%3.742%2.713%2.543%Greece 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A N/A N/A N/A N/A N/A N/A 3 M o 2.703% 3.896% 4.062% 1.701% 2.905% 6.591% N/A 3.454% 6 M o 2.846% 4.003% 3.869% 2.005% 3.044% 4.816% N/A 4.160% 1 Y r 3.102% 4.016% 3.798% 1.856% 3.720% N/A N/A N/A 2 Y r 3.305%3.978%3.588%3.273%4.649%N/A N/A N/A 3 Y r 3.429% 3.966% 3.747% 4.407% 5.285% 15.986% N/A N/A 5 Y r 3.528% 3.999% 3.896% 5.042% 5.718% 15.689% N/A N/A 7 Y r 3.772% 4.045% 4.074% 5.302% 5.883% 13.538% N/A N/A 10 Y r 3.983% 4.163% 4.409% 6.028% 6.209% 13.311% N/A N/A 20 Y r 4.136% N/A N/A N/A N/A N/A N/A N/A 30 Y r 4.332% 4.451% 5.184% 6.462% 6.371%N/A15.770%10.416%Yi Wei Yield Curve Assignment11Portuga l 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A N/A N/A N/A N/A N/A N/A 3 M o 2.580% 3.769% 4.064% 1.043% N/A N/A 2.259% 0.611% 6 M o 2.744% 3.810% 3.943% 0.876% 0.693% 2.863% 2.689% 0.732% 1 Y r 2.986% 3.968% 3.792% 1.076% 0.992% 4.307% 3.735% 1.092% 2 Y r 3.277% 3.992% 3.678% 2.311% 1.816% N/AN/A N/A 3 Y r 3.378% 3.926% 3.511% 2.905% 2.495% 6.090% 12.153% 2.911% 5 Y r 3.560% 3.948% 3.647% 3.536% 3.363% 7.206% 15.687% 4.136% 7 Y r 3.651% 3.951% 3.821% 4.008% 3.821% 7.242% 15.955% 4.988% 10 Y r N/A 4.066% 4.310% 4.692% 4.244% 7.414%14.944% 5.737% 20 Y r N/A N/A N/A N/A N/A N/A N/A N/A 30 Y r N/A 4.264% 4.858% 4.796% 4.827% N/A N/A N/A Spain 2006 2007 2008 2009 2010 2011 2012 2013 1 M o N/A N/A N/A N/A N/A N/A N/A N/A 3 M o 2.570% 3.750% 3.940% 0.900% 0.360% 1.225% 0.390% 0.281% 6 M o 2.725% 3.845% 3.875% 1.000% 0.440% 1.625% 0.657% 0.733% 1 Y r 2.960% 3.940% 3.680% 1.200% 0.725% 1.950% 1.258% 1.354% 2 Y r 3.176% 3.943% 3.353% 1.912% 1.486% N/A 1.666% 1.498% 3 Y r 3.315% 3.884% 3.449% 2.515% 1.997% 2.802% 2.353% 2.321% 5 Y r 3.510% 3.887% 3.501% 3.205% 2.867% 3.773% 3.261% 3.208% 7 Y r 3.607% 3.907% 3.605% 3.681% 3.317% 4.367% 4.254% 3.675% 10 Y r 3.702% 3.962% 4.136% 4.056% 3.871% 4.932% 5.001% 4.529% 20 Y r N/A N/A 4.658% 4.760% 4.570% N/A N/A N/A 30 Y r 3.974%4.135%4.722%4.636%4.780%5.771%5.851%5.332%。
Yield Stress Understanding Materials

Yield Stress Understanding MaterialsYield stress is an important concept in materials science and engineering, as it helps us understand how materials behave under stress and at what point they start to deform permanently. It is a critical parameter for designing and testing materials for various applications, from building structures to manufacturing processes. In this response, I will explore the significance of yield stress, its measurement, and its implications for different materials.First and foremost, it is essential to understand what yield stress actually means. In simple terms, yield stress is the point at which a material undergoes a permanent deformation or change in shape when subjected to stress. Before this point, the material can deform elastically, meaning it can return to its original shape once the stress is removed. However, beyond the yield stress, the material will experience plastic deformation, and it will not return to its original shape. This is a crucial factor to consider when designing structures or products that will be subjected to various forces and loads.The measurement of yield stress is typically done through a tensile test, where a sample of the material is subjected to increasing amounts of tensile stress until it starts to deform. The point at which this deformation becomes permanent is the yield stress. This test provides valuable data for engineers and scientists to understand the mechanical properties of different materials and to determine their suitability for specific applications. For example, in the aerospace industry, where materials need to withstand extreme conditions, knowing the yield stress of a material is crucial for ensuring the safety and reliability of aircraft components.Different materials exhibit different behaviors when it comes to yield stress. For example, brittle materials such as ceramics have a distinct yield point, beyond which they fail catastrophically. On the other hand, ductile materials like most metals exhibit a more gradual transition from elastic to plastic deformation, making them more suitable for applications where some degree of deformation is acceptable. Understanding these differences is essential for selecting the right materials for a given application and for predicting their behavior under different loading conditions.Moreover, the concept of yield stress is not only relevant for engineers and scientists but also for the general public. For instance, when we drive over a bridge or use a piece of furniture, we are relying on the fact that the materials used in these structures have been carefully chosen and tested to ensure that they can withstand the forces they will experience. The yield stress of these materials plays a crucial role in determining their longevity and safety, and it is important for the public to have confidence in the materials used in the products and infrastructure they rely on every day.In conclusion, yield stress is a fundamental concept in materials science and engineering, with far-reaching implications for various industries and everyday life. Its measurement and understanding are essential for designing safe and reliable structures and products, as well as for advancing the field of materials science. By considering the yield stress of different materials, we can make informed decisions about their use and ensure that they meet the requirements of specific applications. As technology advances and new materials are developed, the importance of yield stress will continue to be a central focus in the quest for stronger, more durable, and more efficient materials.。
indifference curve定义英文

indifference curve定义英文Indifference Curve: A Fundamental Concept in Microeconomic TheoryIn the realm of microeconomic theory, the concept of the indifference curve stands as a fundamental tool for understanding consumer behavior and preferences. An indifference curve is a graphical representation of the various combinations of two goodsor services that provide the same level of utility or satisfaction to a consumer. This means that the consumer is indifferent between any two points on the same indifference curve, as they offer the same overall level of well-being.The indifference curve is a crucial component of the consumer theory, which aims to explain how individuals make decisions about the allocation of their limited resources to maximize their satisfaction. The underlying assumption is that consumers have a set of preferences that can be ranked and compared, and they seek to choose the combination of goods that provides the highest level of utility.The shape of the indifference curve is typically characterized by adownward slope, reflecting the principle of diminishing marginal rate of substitution. This principle states that as the consumer acquires more of one good, the amount of the other good they are willing to give up in order to maintain the same level of utility decreases. In other words, the consumer becomes less willing to substitute one good for the other as they consume more of the first good.The slope of the indifference curve at any given point is known as the marginal rate of substitution (MRS). The MRS represents the rate at which the consumer is willing to trade one good for another while maintaining the same level of utility. As the consumer moves along the indifference curve, the MRS changes, reflecting the changing preferences of the consumer.The indifference curve has several important properties that are essential to understanding consumer behavior:1. Downward-sloping: Indifference curves slope downward from left to right, reflecting the principle of diminishing marginal rate of substitution.2. Convex to the origin: Indifference curves are typically convex to the origin, meaning that they become flatter as the consumer moves away from the origin. This reflects the diminishing marginal rate of substitution.3. Non-intersecting: Indifference curves do not intersect with each other, as this would imply that the consumer is indifferent between two different levels of utility, which contradicts the fundamental assumption of rational preferences.4. Higher indifference curves represent higher levels of utility: As the consumer moves to higher indifference curves, they are able to achieve higher levels of utility or satisfaction.The indifference curve analysis is a powerful tool in microeconomic theory, as it allows economists to understand and predict consumer behavior. By analyzing the shape and position of a consumer's indifference curves, economists can determine the consumer's optimal consumption bundle, given their budget constraints. This, in turn, can be used to derive the consumer's demand curve for various goods and services, which is a fundamental building block of market analysis.In conclusion, the indifference curve is a central concept in microeconomic theory, providing a framework for understanding and analyzing consumer preferences and decision-making. Its properties and applications are essential for understanding the behavior of individuals in the marketplace and the broader dynamics of economic systems.。
cir超脑词汇很有趣的记忆单词方法哦第十二课

第十二课1. match [记忆方法] 音:卖吃2. outline [记忆方法] out外面; line线外面(de)线就是“轮廓”.3. prevail [记忆方法] vail小费; pre提前提前给小费是很“流行“(de)事.4. pronounce [记忆方法] pro提前; nounce说话5. quarrel [记忆方法] 音:扣肉6. reinforce [记忆方法] re一再; in投入; force力量一再(de)投入力量就是“强化、加强”.7. report [记忆方法] port港口be report to8. resort [记忆方法] stort储备; re反复反复储备是为了“恢复”实力.9. rough [记忆方法] tough坚硬(de)10. scope [记忆方法] cope警察11. serve [记忆方法] servant仆人service服务serf农奴12. shrug [记忆方法] shur音:舒; g胳让胳膊舒服一下就要“耸肩”.13. spirit [记忆方法] s誓; p必; ir为; it他势必为了他是“精神可贵”(de).14. stiff [记忆方法] cliff悬崖从悬崖掉下来(de)人就会变得“僵硬”(de).15. swarm [记忆方法] 音:死暖和“拥挤”(de)“人群”是死缓和(de).16. tend [记忆方法] tender温柔(de)温柔(de)“照顾”.17. tiresome [记忆方法] tir讨厌; some adj标志18. wire [记忆方法] cable粗绳子wire细绳子19. yield [记忆方法] field田地田地中会有“产量”.20. accurate [记忆方法] accur occur ;rate速率出现非常(de)数字要“精确(de)”.21.accuse [记忆方法] ac增加; cuse说话“指责”(de)时候一般会增加说话.accuse sb. of sth职责某人某事,如果无of则不选accuse.22. afford [记忆方法] a一个; for为了; d(de)一个你为了得到(de)东西一定要“负担”得起.can affordcan’t afford23. ambulance [记忆方法] am像; bul bull; lance烂撞、烂闯“救护车”像共牛一样烂撞、烂闯.24. anticipate [记忆方法] pate馅饼; anti反对; ci塞表面反对塞给馅饼其实内心满是“期待”.25. anxiety [记忆方法] anxious焦急(de)、渴望(de)26. apply [记忆方法] application申请表appliance家用电器applicant申请人27. atmosphere [记忆方法] at在; mos most; p僻静; here 这在这最僻静“大气层、大气”.28. bargain [记忆方法] bar酒吧; gain获得在酒吧获得(de)东西一般都是在外面很便宜(de)“便宜物”.29. beam [记忆方法] be是;am(de)30. blame [记忆方法] 音:不累吗你该被责备:You are to blame. blame 没有被动形式31. bond [记忆方法] 连接、关系32. breathe [记忆方法] take breath作个呼吸hold one’s breath摒住呼吸33. calculate [记忆方法] cal call; cu(刻)苦; late晚叫你做“计算”题到很晚.34.cautious [记忆方法] 音:阔衫死35.有很多拧归(de)衬衫要“谨慎小心”别被抢了caution谨慎小心35. ceremony [记忆方法] mony money; ce 塞;re反复反复塞钱(de)地方就是“典礼”.36. circle [记忆方法] The circle of life.生生不息37. circular [记忆方法] circu圆; ar adj标志38. claw [记忆方法] law法律在动物之间(de)法律是用“爪子”解决(de).39. cliff [记忆方法] stiff僵硬(de)40. comment [记忆方法] recommend赞扬comment on41. comprehension [记忆方法] prehen理解; con过来; sin n 标志42. conceal [记忆方法] con过来; cea保密章走过来朝学生盖了一个保密章就是“隐蔽”起来.43. confidence [记忆方法] con走过来音:非得我得confident自信(de)、秘密基地confidential亲启44. conquest [记忆方法] conquer征服(con过来;quer音:克服)45. conscious [记忆方法] sci感觉; ous adj 标志;con过来过来之后(de)感觉才“意识到”.be conscious of 对……有意识46. convince [记忆方法] con过来; vin win; ce死过来把它赢死就是“使(他)信服”.47. coolie [记忆方法] cooky小甜饼; PL:cookies48. criticism [记忆方法] critcize批评、挑剔49. cruise [记忆方法] cru绕圈; se see在海上绕圈(de)看就是“巡航”.题干中有船即选cruise50. custom [记忆方法] accustom习惯。
工程英语测试题及答案

工程英语测试题及答案一、选择题(每题2分,共20分)1. What is the term used to describe the process of turning raw materials into finished products?A. FabricationB. AssemblyC. MachiningD. Casting答案:A2. The primary function of a ________ is to convert electrical energy into mechanical energy.A. MotorB. GeneratorC. TransformerD. Inverter答案:A3. In engineering, the term "stress" refers to:A. The internal resistance of a material to deformationB. The force applied to a materialC. The change in shape of a materialD. The rate of change of force答案:A4. Which of the following is not a type of welding process?A. Arc weldingB. Gas weldingC. Ultrasonic weldingD. Friction welding答案:C5. The process of designing and building a structure is known as:A. EngineeringB. ArchitectureC. ConstructionD. All of the above答案:D6. What does the abbreviation "CAD" stand for in the field of engineering?A. Computer-Aided DesignB. Computer-Aided DraftingC. Computer-Aided DevelopmentD. Computer-Aided Documentation答案:A7. The SI unit for pressure is:A. PascalB. NewtonC. JouleD. Watt答案:A8. A ________ is a type of joint that allows for relative movement between connected parts.A. Rigid jointB. Revolute jointC. Fixed jointD. Pin joint答案:B9. The process of removing material from an object to achieve the desired shape is known as:A. MachiningB. CastingC. ForgingD. Extrusion答案:A10. In engineering, the term "specification" refers to:A. A detailed description of the requirements of aprojectB. A list of materials to be used in a projectC. The estimated cost of a projectD. The timeline for a project答案:A二、填空题(每题1分,共10分)11. The ________ is the process of cutting a flat surface ona material.答案:sawing12. A ________ is a type of bearing that allows for rotation.答案:ball bearing13. The term "gearing" refers to the use of gears to transmit ________.答案:motion14. The ________ is the study of the properties of materials.答案:material science15. In a hydraulic system, a ________ is used to control the flow of fluid.答案:valve16. The ________ is the process of heating and cooling a material to alter its physical properties.答案:heat treatment17. The ________ is a tool used to measure the hardness of a material.答案:hardness tester18. A ________ is a type of joint that connects two parts ata fixed angle.答案: hinge joint19. The ________ is the process of joining two pieces ofmetal by heating them to a molten state.答案:fusion welding20. The ________ is the study of the behavior of structures under load.答案:structural analysis三、简答题(每题5分,共30分)21. Define the term "mechanical advantage" in engineering.答案:Mechanical advantage is the ratio of output force to input force in a simple machine, indicating how much the machine amplifies the force applied to it.22. Explain the concept of "factor of safety" in engineering design.答案:The factor of safety is a ratio used in engineering to ensure that a structure or component can withstand loads beyond the maximum expected in service, providing a margin of safety against failure.23. What is the purpose of a "stress-strain curve" in material testing?答案:A stress-strain curve is a graphical representation of the relationship between the stress applied to a material and the resulting strain, used to determine the material's mechanical properties such as elasticity, yield strength, and ultimate strength.24. Describe the difference between "static" and "dynamic" loads in engineering.答案:Static loads are constant forces that do not changeover time, while dynamic loads are forces that vary in magnitude or direction over time, often due to movement or vibrations.25. What is "creep" in the context of material behavior under load?答案:Creep。
电源英语——精选推荐
电源行业英语英文外语专业词汇术语翻译(A)1 backplane 背板2 Band gap voltage reference 带隙电压参考3 benchtop supply 工作台电源4 Block Diagram 方块图5 Bode Plot 波特图6 Bootstrap 自举7 Bottom FET Bottom FET8 bucket capcitor 桶形电容9 chassis 机架10 Combi-sense Combi-sense11 constant current source 恒流源12 Core Sataration 铁芯饱和13 crossover frequency 交叉频率14 current ripple 纹波电流15 Cycle by Cycle 逐周期16 cycle skipping 周期跳步17 Dead Time 死区时间18 DIE T emperature 核心温度19 Disable 非使能,无效,禁用,关断20 dominant pole 主极点21 Enable 使能,有效,启用22 ESD Rating ESD额定值23 Evaluation Board 评估板24 Exceeding the specifications below may result in permanent damage to the device, ordevice malfunction. Operation outside of the parameters specified in the Electrical Characteristics section is not implied. 超过下面的规格使用可能引起永久的设备损害或设备故障。
建议不要工作在电特性表规定的参数范围以外。
25 Failling edge 下降沿26 figure of merit 品质因数27 float charge voltage 浮充电压28 flyback power stage 反驰式功率级29 forward voltage drop 前向压降30 free-running 自由运行31 Freewheel diode 续流二极管32 Full load 满负载33 gate drive 栅极驱动34 gate drive stage 栅极驱动级35 gerber plot Gerber 图36 ground plane 接地层37 Henry 电感单位:亨利38 Human Body Model 人体模式39 Hysteresis 滞回40 inrush current 涌入电流41 Inverting 反相42 jittery 抖动43 Junction 结点44 Kelvin connection 开尔文连接45 Lead Frame 引脚框架46 Lead Free 无铅47 level-shift 电平移动48 Line regulation 电源调整率49 load regulation 负载调整率50 Lot Number 批号51 Low Dropout 低压差52 Miller 密勒53 node 节点54 Non-Inverting 非反相55 novel 新颖的56 off state 关断状态57 Operating supply voltage 电源工作电压58 out drive stage 输出驱动级59 Out of Phase 异相60 Part Number 产品型号61 pass transistor pass transistor62 P-channel MOSFET P沟道MOSFET63 Phase margin 相位裕度64 Phase Node 开关节点65 portable electronics 便携式电子设备66 power down 掉电67 Power Good 电源正常68 Power Groud 功率地69 Power Save Mode 节电模式70 Power up 上电71 pull down 下拉72 pull up 上拉73 Pulse by Pulse 逐脉冲(Pulse by Pulse)74 push pull converter 推挽转换器75 ramp down 斜降76 ramp up 斜升77 redundant diode 冗余二极管78 resistive divider 电阻分压器79 ringing 振铃80 ripple current 纹波电流81 rising edge 上升沿82 sense resistor 检测电阻83 Sequenced Power Supplys 序列电源84 shoot-through 直通,同时导通85 stray inductances. 杂散电感86 sub-circuit 子电路87 substrate 基板88 T elecom 电信89 Thermal Information 热性能信息90 thermal slug 散热片91 Threshold 阈值92 timing resistor 振荡电阻93 T op FET T op FET94 Trace 线路,走线,引线95 Transfer function 传递函数96 Trip Point 跳变点97 turns ratio 匝数比,=Np / Ns。
term structure models
13.3Term structure models13.3.1Expectations hypothesis model-Simplest "model"a)short rate b)expectations to get other pricesy (1)t +1−δ=φ(y (1)t −δ)+εt +1f (2)t =E t (y (1)t +1)=δ+φ(y (1)t −δ)f (3)t =E t (y (1)t +2)=δ+φ2(y (1)t −δ)f (N )t=E t (y (1)t +N −1)=δ+φN −1(y (1)t −δ)y (2)t=12h E t (y (1)t +1)+y (1)t i =12h δ+φ(y (1)t −δ)+y (1)t i y (2)t −δ=1+φ2³y (1)t −δ´...y (N )t−δ=1+φ+φ2+..N ³y (1)t −δ´=1−φN N (1−φ)³y (1)t−δ´Result:1Di fferent shapes,upward and downward sloping.Up when short rates expected to rise.More complex shapes?Move past AR(1)!2.No average slope —E (y (i ))all the same.Well,we imposed expectations!3.Yields move in lockstep —a "1factor model”13.3.2“Term structure model”in generalIngredients:1)Write a time series model for the discount factor in discrete or continuous time.2a)Solve M forward,M t,t +n =M t +1M t +2...M t +n .ThenP (n )t=E t [M t,t +n ]2b)Solve di fferential /di fference equation,i.e.solve P (n )t“backward”from P (0)t=1,P (n )t =E t h M t,t +1P (n −1)t +1iResult:P (n )t=function of state variables that drive M .This is easiest for logs.Translation from levels to logs:either continuous time or lognormal distributions.13.3.3Discrete-time single-factor V asicekHere:A standard “single factor model”—“discrete-time Vasicek.”The end result:³y (1)t +1−δ´=φ³y (1)t −δ´+v t +1.f (2)t =δ+φ³y (1)t −δ´−∙12+λ¸σ2εf (3)t=δ+φ2³y (1)t −δ´−∙12(1+φ)2+λ(1+φ)¸σ2ε....y (2)t =δ+(1+φ)³y (1)t −δ´−1µ1+λ¶σ2εy (3)t=δ+(1+φ+φ2)3³y (1)t −δ´−13½12£1+(1+φ)2¤+λ[1+(1+φ)]¾σ2ε....Intuition for now:the first equation tells you where interest rates are going over time .The second and third sets of equations tell you where each forward rate is at any date,depending only on where the short rate is on that date;a single factor model.Derivation:•Suppose m follows the time series model.x t +1−δ=φ(x t −δ)+εt +1m t +1=ln M t +1=−1λ2σ2ε−x t −λεt +1This is just a model for m ,with a convenient “state variable”x t .Intuition:x t shifts the mean of ln m t +1around.If you remember that R f =1/E (m ),you can see that specifying a model for the mean of m is the key to thinking about interest rates.The 1/2σ2term just shifts the mean of ln m t down,and o ffsets a 1/2σ2term which willpop up later.To be speci fic,εand v are iid Normal with σ2ε,σ2v ,σεv .δ,ρ,λare free parameters;we’ll pick these to make the model fit as well as possible.•Bond prices.P (n )t=E t (M t +1M t +2....M t +n )This is easier to do recursively,P (0)t=1P (n )t=E t ³m t +1P (n −1)t +1´.•Here we go.P (1)t =E t (M t +1)=E t e m t +1P (1)t=e −12λ2σ2ε−x t +12λ2σ2ε=e −x tp (1)t =ln E t (m t +1)=−x t y (1)t=x tNow you see why I set up the problem with the 1/2λ2σ2εto begin with!The one year interest rate “reveals the latent state variable x t ”•I could have written the model asy (1)t +1−δ=φ³y (1)t −δ´+εt +1m t +1=−1λ2σ2ε−y (1)t −λεt +1“a short rate process plus a market price of risk.”Then,by taking −ln E t (M t +1)Iwould have checked that the y (1)t the model produces is the same y (1)t I started with.Take your pick.Which is more confusing:a)starting with an x t you “can’t see”andthen showing that it turns out to be y (1)t ?b)starting with an assumed y (1)t process and then showing that it’s in fact the one period rate,that the model is “self-consistent”(in the language of CP appendix.)•On to the next price.P (2)t=E t ³m t +1P (1)t +1´=E t ³em t +1+p (1)t +1´=E t ³e −1λ2σ2ε−x t −λεt +1−x t +1´P (2)t=E t ³e−12λ2σ2ε−x t −λεt +1−δ−φ(x t −δ)−εt +1´P (2)t=E t ³e−2δ−(1+φ)(x t −δ)−12λ2σ2ε−(1+λ)εt +1´p (2)t =−2δ−(1+φ)(x t −δ)−1λ2σ2ε+1(1+λ)2σ2εp (2)t=−2δ−(1+φ)(x t −δ)+(1+λ)σ2ε•From prices,we find yields and forwards,y (2)t=δ+(1+φ)(x t −δ)−1µ1+λ¶σ2εf (2)t=p (1)t −p (2)t=−δ−(x t −δ)+2δ+(1+φ)(x t −δ)−(12+λ)σ2ε=δ+φ(x t −δ)−(12+λ)σ2ε•Now the rest of the maturities.You can “solve the discount rate forward and integrate”p (3)t=log E t (M t +1M t +2M t +3)=log E t e −12λ2σ2ε−x t −λεt +1−12λ2σ2ε−x t +1−λεt +2−12λ2σ2ε−x t +2−λεt +3=log E t e −3δ−3λ2σ2ε−(1+φ+φ2)(x t −δ)−λεt +1−λεt +2−λεt +3−(1+φ)εt +1−εt +2This will work after much algebra•Instead,let’s do it recursively“derive a differential equation for price as a function ofstate variables.”GuessP(n)t=A n−B n(x t−δ)thenP(n)t=E t³M t+1P(n−1)t+1´A n−B n(x t−δ)=log E tµexpµ−12λ2σ2ε−x t−λεt+1¶exp(A n−1−B n−1(x t+1−δ))¶=log E tµexpµ−12λ2σ2ε−x t−λεt+1+A n−1−B n−1φ(x t−δ)−B n−1εt+1¶¶=log E tµexpµ−δ+A n−1−(1+B n−1φ)(x t−δ)−12λ2σ2ε−λεt+1−B n−1εt+1¶A n−B n(x t−δ)=−δ+A n−1−(1+B n−1φ)(x t−δ)+µB n−1λ+12B2n−1¶σ2εThe constant and the term multiplying x t must separately be equal.Thus,B n=1+B n−1φA n=−δ+A n−1+µB n−1λ+12B2n−1¶σ2εWe have“transformed the solution of a stochastic differential equation plus integral tothe solution of an ordinary differential equqation.•That’s easy to solveB0=0B1=1B2=1+φB3=1+φ+φ2B n=n−1X j=0φj=1−φn1−φA0=0A1=−δA2=−2δ+µλ+12¶σ2εA3=−3δ+∙(1+φ)λ+12(1+φ)2¸σ2εA4=−4δ+∙¡1+φ+φ2¢λ+12¡1+φ+φ2¢2¸σ2εYou see the pattern from here•Yields,forwards,returns,etc.follow.y(n)t=−1/n×p(n)t.Forwards are even simpler,f(n) t =p(n−1)t−p(n)t=(A n−1−A n)−(B n−1−B n)(x t−δ) =−δ+µB n−1λ+12B2n−1¶σ2ε+φn−1(x t−δ)•Result:³y (1)t +1−δ´=φ³y (1)t −δ´+εt +1.f (2)t=δ+φ³y (1)t −δ´−(12+λ)σ2εf (3)t =δ+φ2³y (1)t −δ´−∙12(1+φ)2+λ(1+φ)¸σ2εf (4)t=δ+φ3³y (1)t −δ´−∙12¡1+φ+φ2¢2+λ(1+φ+φ2)¸σ2ε...y (2)t =δ+(1+φ)³y (1)t −δ´−1µ1+λ¶σ2εy (3)t=δ+(1+φ+φ2)3³y (1)t −δ´−13½12£1+(1+φ)2¤+λ[1+(1+φ)]¾σ2ε...1.Just like EH but now a risk premium!2.Shapes:A steady decline from σ2terms,(risk premim)+exponential decay from y (1)−E (y (1)).(expectations hypothesis)3.“Short rate process”plus “one factor model.”All yields move in lockstep indexedby y (1)t (or any other yield).The shape is tied to the level.It looks like “you can price other bonds by arbitrage”but that is only because we restrict our model to have one factor.4.y (1)is also su fficient to forecast all yields.5.Risk premium comes from cov (m,y (1))=λσ2ε“market price of interest rate risk”.If there were a security whose payo ffwere εt +1its price would be driven by cov (m,εt +1).6.The premium can go either way depending on the sign of λ.My guess:lowery (1)t +1means higher m (bad state)means +(m =..−ε)sign and negative premium.This is a typical result.The real term structure ought to slope down,as long term bonds are safer for long-term investors.However,as long as we separate market prices of risk from consumption and interest data (as we did with the CAPM!)we can incorporate an upward sloping yield curve with λ<07.The risk premium is constant over time though —as we’ll see not in data.8.“Risk neutrality”λ=0does not mean “expectations”since there is another term.This is Another force for typical downward slope.However,it’s quantitatively very small,since σε≈0.019.Another way to see risk premia is to look at returns,r (n )t +1=p (n −1)t +1−p (n )t =(A n −1−A n )−B n −1(x t +1−δ)+B n (x t −δ)=δ−µB n −1λ+1B 2n −1¶σ2ε−B n −1(x t +1−δ)+B n (x t −δ)Expected returnsE t r(n)t+1=δ−µB n−1λ+1B2n−1¶σ2ε+(B n−B n−1φ)(x t−δ)E t r(n)t+1=δ−µB n−1λ+1B2n−1¶σ2ε+(x t−δ)E t rx(n)t+1=−µB n−1λ+1B2n−1¶σ2εYou see the expected returns differ by maturity,but the risk premium is constant over time—not what Fama-Blissfind.10.The limiting yield and forward rate are constants.There is no true“level”shift.We’ll see this is quite general—“level shifts”imply an arbitrage opportunity at the long end of the yield curve.11.Yields can be negative—they are normally distributed here.M>0means P>0not P<1.The CIR modelfixes this up.•Let’s see an example.1.I chose some parameters tofit the FB zero coupon bond data.I ran a regressionof y(1)t+1on y(1)t to getρ;I took the variance of errors from that regression to get σε;I took the meanδ=E³y(1)t´.Finally,I picked the market price of riskλto fit the average5year forward spread:f(5)t=δ+ρ4³y(1)t−δ´−∙1¡1+ρ+ρ2+ρ3¢2+λ(1+ρ+ρ2+ρ3)¸σ2εE³f(5)t´−δ232ε−1¡1+ρ+ρ2+ρ3¢λ=−2.I plot y(n)t for a bunch of y(1)t.The dashed lines in the right hand graph give theexpectations hypothesis terms from above,so you can see the distortion from risk aversionλand the Jensen’s inequatlityσ2εterm.Cool!This captures some basic patterns;yields are upward sloping when lower, downward sloping when higher.The substantial risk premium I estimated to match the average upward slope does introduce a substantial deviation of the model from expectations at the long end.3.Note already:the parametersφ,λcan be chosen to match the cross section ofyields—the shapes of these curves—or the time series—the AR(1)coefficient of the short rate and the expected bond returns.These do not necessarily give the same answer,a sign of model misspecification.4.Take the history of y(1)t.Find the model-implied y(n)t:compare with data.5.You can see a decentfit—upwward sloping yields when the interest rate is low.But you can see yields are going up to a constant long-term value,rather than someAnswer:we need a two-factor model....。
gre考试数学真题试卷
gre考试数学真题试卷GRE考试数学真题试卷一、选择题(每题1分,共20分)1. If the function f(x) = 3x^2 - 2x + 1, what is the value of f(1)?A. 0B. 2C. 3D. 4E. 52. What is the derivative of the function g(x) = 4x^3 - x^2 + 7?A. 12x^2 - 2xB. 12x^2 + 2xC. 12x^3 - 2xD. 12x^3 + 2xE. 12x^3 - 2x^23. The area under the curve of y = x^2 from x = 0 to x = 2 is:A. 2B. 4C. 8D. 10E. 124. If a and b are the roots of the quadratic equation x^2 +5x + 6 = 0, what is the value of a + b?A. -3B. -2C. -1D. 0E. 15. The slope of the line passing through the points (2, 3) and (4, 7) is:A. 1B. 2C. 3D. 4E. 56. What is the value of sin(30°)?A. 1/2B. √2/2C. √3/2D. 2/√3E. 1/√27. The integral of the function h(x) = 3x + 2 is:A. x^3 + 2x + CB. x^3 + 2x^2 + CC. x^2 + 2x + CD. 3x^2 + 2x + CE. 3x^2 + 2x^3 + C8. The equation of a circle with center (3, 4) and radius 5 is:A. (x - 3)^2 + (y - 4)^2 = 25B. (x - 3)^2 + (y - 4)^2 = 1C. (x - 3)^2 + (y - 4)^2 = 100D. (x - 3)^2 + (y - 4)^2 = 625E. (x - 3)^2 + (y - 4)^2 = 09. The volume of a sphere with radius 4 is:A. 256πB. 512πC. 1024πD. 2048πE. 4096π10. If the sequence 2, 6, 18, 54, ... is a geometric sequence, what is the common ratio?A. 2B. 3C. 4D. 5E. 6二、填空题(每题2分,共20分)11. If the sum of the first n terms of an arithmetic sequence is given by S_n = n^2, then the 5th term of the sequence is__________.12. The equation of the line perpendicular to y = 2x - 1 and passing through the point (1, 3) is __________.13. The value of the definite integral ∫(0 to 1) x^2 dx is__________.14. If the function f(x) = sin(x) + cos(x), then f''(x) is__________.15. The area of a triangle with vertices at (0,0), (3,0), and (0,4) is __________.16. The limit of the function (1 + 1/n)^n as n approaches infinity is __________.17. The value of e^(iπ) is __________.18. The standard deviation of the data set {2, 4, 6, 8, 10} is __________.19. If a fair coin is tossed 5 times, the probability of getting exactly 3 heads is __________.20. The value of the binomial coefficient C(n, k) when。
高二英语圆锥曲线单选题50题(答案解析)
高二英语圆锥曲线单选题50题(答案解析)1.The equation of an ellipse is x²/25 + y²/16 = 1. The length of the major axis is:A.5B.8C.10D.16答案:C。
本题考查椭圆的基本性质。
对于椭圆方程x²/a² + y²/b² = 1,a 表示长半轴,b 表示短半轴。
在本题中a = 5,长轴长为2a = 10。
选项A 是长半轴的长度;选项B 和D 与长轴长无关。
2.The foci of the ellipse x²/36 + y²/20 = 1 are located at:A.(±4,0)B.(±2,0)C.(0,±4)D.(0,±2)答案:A。
根据椭圆方程x²/a² + y²/b² = 1,c² = a² - b²,可得c = 4。
焦点在x 轴上时,焦点坐标为(±c,0)。
选项B 中c 的值错误;选项C 和D 焦点位置错误。
3.If the eccentricity of an ellipse is 1/3 and the length of the major axis is 12, then the distance between the foci is:A.4B.6C.8D.10答案:C。
离心率e = c/a,已知离心率为1/3,长轴长2a = 12,可得a = 6。
由e = c/a 可得c = 2。
焦点间距离为2c = 8。
选项A、B、D 计算错误。
4.The equation of an ellipse with center at the origin, major axis along the x-axis, and length of major axis 8 and eccentricity 1/2 is:A.x²/16 + y²/12 = 1B.x²/12 + y²/16 = 1C.x²/32 + y²/28 = 1D.x²/28 + y²/32 = 1答案:A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Shape of the Yield Curve Under CIR Single Factor Model:A NoteRaymond KanUniversity of TorontoJune,1992AbstractThis note derives the shapes of the yield curve as a function of the current spot rate under Cox,Ingersoll,and Ross(CIR)(1985b)single factor model.Corresponding results reported inCIR are shown to be incorrect.1IntroductionIn Cox,Ingersoll,and Ross(CIR)(1985a,b),they develop a general equilibrium model of the term structure of interest rates.The term structure of interest rates are linked directly to the specifica-tions of preferences,technologies,and the distributions of the underlying sources of uncertainty.As a special case,they derive a single factor model of the term structure.Under this single factor model,the interest rate dynamics can be expressed as:dr=κ(θ−r)dt+σ√rdz(1)where dz is a standard Weiner process,andκ,θ,andσ2are constants,withκθ≥0,andσ2>0.When the current spot rate is r,the yield-to-maturity of aτ-period pure discount bond is then given by:R(r,τ)=rB(τ)−log A(τ)τ(2)whereA(τ)≡2γe(κ+λ+γ)τ/2(κ+λ+γ)(eγτ−1)+2γ2κθ/σ2,(3)B(τ)≡2(eγτ−1)(κ+λ+γ)(eγτ−1)+2γ,(4) 1γ=(κ+λ)2+2σ21/2.(5)From(2),it is easy to seeR(r,0)=r,(6)R(r,∞)=2κθγ+κ+λ.(7)In other words,when the current spot rate is r,the yield curve starts at r and approaches a limit of2κθγ+κ+λas maturity increases to infinity.CIR provide a characterization of the shape of the yield curve as a function of the current spotrate.They claim that when r≤2κθγ+κ+λ,the yield curve is uniformly rising.With r≥κθκ+λ,theyield curve is falling.For2κθγ+κ+λ<r<κθκ+λ,the yield curve is humped.It is easy to see this characterization of the yield curve is incorrect because if the yield curve ishumped when r=2κθγ+κ+λ,then the yield curve cannot be uniformly increasing for all r<2κθγ+κ+λ.Otherwise,R(r,τ)will be a discontinuous function of r for someτ>0,which is contrary to(2)that R(r,τ)is a linear function of r for afixedτ.In fact,for r that is less than but close to2κθγ+κ+λ,the yield curve must also be humped and it has to go above the long-term yield2κθγ+κ+λbefore approaching this limit.Another problem of this characterization is we needκ+λ>0in order for2κθγ+κ+λ<κθκ+λ.However,the model does not always imply this condition.In particular,when theterm premium is positive,λis negative and forκsmall enough,κ+λcould be negative as well.1 In the next section,we will provide the correct characterization of the yield curve as a function of the spot rate under CIR single factor model.2Characterization of the Shape of the Yield CurveBefore we derive the shape of the yield curve as a function of the current spot rate,wefirst note that the yield curve is in fact determined by only three parameters:κ+λ,κθ,andσ2.Therefore, 1In Gibbons and Ramaswamy(1988),they estimate the CIR single factor model andfind thatˆκ+ˆλis−0.7.In the next section,we will show that the yield curve can only be humped or increasing whenκ+λ≤0and r≥0.2by lettingα=κθandβ=κ+λ,we can express the yield curve as follows:R(r,τ)=f(τ)+g(τ)r(8) wheref(τ)≡−2αlog2γe(γ+β)τ/2(γ+β)(eγτ−1)+2γσ2τ=2ασ2τlog(γ+β)(eγτ−1)+2γ2γ−α(γ+β)σ2,(9)g(τ)≡2(eγτ−1)[(γ+β)(eγτ−1)+2γ]τ,(10)γ=β2+2σ21/2.(11)Wefirst prove the following lemmata:Lemma1f(τ)is an increasing function ofτ.It starts out at0with a slope ofα/2whenτ=0 and approaches a limit of2αγ+βasτ→∞.Proof:f (τ)=2ασ2τ2(γ+β)γτeγτ(γ+β)(eγτ−1)+2γ+log2γ(γ+β)(eγτ−1)+2γ=2ασ2τ2F(γτ)(12)where F(x)is defined as:F(x)=xe xe x−1+a+logae x−1+a,a=2γγ+β>1.(13)With L’Hˆo pital’s Rule,one can easily show f(0)=0,f(∞)=2αγ+β,and f (0)=α/2.Note thatF(0)=0and F (x)=xe x(a−1)(e x−1+a)2>0for x>0.Therefore we have F(x)>0for x>0and f (τ)>0 forτ>0.Lemma2g(τ)starts out at1with a slope of−β/2whenτ=0and approaches a limit of0as τ→∞.Ifβ≥0,g(τ)is a uniformly decreasing function ofτ.Ifβ<0,g(τ)first increases to a maximum value and then decreases to0.3g (τ)=−2 β(e γτ−1)2+γ e 2γτ−2γτe γτ−1 [(γ+β)(e γτ−1)+2γ]2τ2=−(γ−β)2σ2τ2G (γτ)(14)where G (x )is defined as:G (x )=(2−a )(e x −1)2+a (e 2x −2xe x −1)(e x −1+a )2,a =2γγ+β>1.(15)With L’Hˆo pital’s Rule,one can easily show g (0)=1,g (∞)=0,and g (0)=−β/2.Consider the numerator of G (x ).By Taylor series expansion,we have(2−a )(e x −1)2+a (e 2x −2xe x −1)=∞ i =2a i x i i !(16)wherea i =(2i −2)(2−a )+(2i −2i )a,i ≥2.(17)If β≥0,we have a ≤2and a i ≥0.Therefore G (x )≥0for x ≥0and g (τ)is a decreasing function of τfor τ≥0.When β<0,we have a 2<0and note that whenever a i >0,it implies a i +1>0.Therefore,a i changes sign only once and by a simple extension of Descartes’Rule of Signs,G (x )has only one positive root.2Hence,when β<0,g (τ)is an increasing function when τ=0and it reaches a maximum value before decreasing to 0as τ→∞.We now describe the yield curve by the following proposition:Proposition 1If κ+λ>0,the yield curve is uniformly falling when r ≥κθκ+λand it is uniformly rising when 0≤r ≤κθγ.For κθγ<r <κθκ+λ,the yield curve first increases to a maximum value andthen decreases to the long-term yield2κθγ+κ+λ.If κ+λ≤0,the yield curve is uniformly rising when 0≤r ≤κθγ.For r >κθγ,the yield curve first increases to a maximum value and then decreases to the long-term yield2κθγ+κ+λ.2Let Z be the number of positive zeros of a power series with radius of convergence ρ=∞and let the number of changes of signs in the sequence of coefficients be C .Then Z ≤C and C −Z is a non-negative even number.In our case,C =1and we must have Z =1.See,for example,P´o lya and Szeg¨o (1976,Part V)for a proof of this result.4R2(r,τ)=∂R(r,τ)∂τ=f (τ)+g (τ)r=2ασ2τ2F(γτ)−r(γ−β)4αG(γτ)=2ασ2τ2H(r,γτ)(18)where H(r,x)is defined as:H(r,x)=F(x)−r(γ−β)4αG(x).(19)Wefirst show that for afixed r,H(r,x)can have at most one positive root.H2(r,x)=∂H(r,x)∂x=F (x)−r(γ−β)4αG (x)=xe x(a−1)(e x−1+a)2−r(γ−β)4α2axe x(e x+1−a)(e x−1+a)3=xe x(e x−1+a)3∞i=0b i x ii!,(20)where b i are obtained by Taylor series expansion and they are:b0=a(a−1)1−rβα,(21)b i=(a−1)1−rγα,i≥1.(22)Therefore,b i can change sign at most once and H2(r,x)can have at most one positive root.Since H(r,0)=0,H(r,x)can also have at most one positive root by Rolle’s theorem.Hence,the yield curve can change direction at most once.Ifβ>0,b i will change sign if and only ifαγ<r<αβ.If β≤0,b i will change sign if and only if r>αγ.In other words,forβ>0,the yield curve is humped if and only ifαγ<r<αβand forβ≤0,the yield curve is humped if and only if r>αγ.By lemmata1and2,we have R2(r,0)=f (0)+g (0)r=α−βr2.Ifβ>0,R2(r,0)>0when r<αβand R2(r,0)≤0when r≥αβ.Therefore,the yield curve will be uniformly falling if r≥αβand it will be uniformly increasing if r≤αγ.Forαγ<r<αβ,the yield curve is humped.Ifβ≤0,5R2(r,0)is always positive and the yield curve can only be upward sloping or humped.For r≤αγ, the yield curve is uniformly increasing,and for r>αγ,the yield curve is humped.3SummaryWe derive the correct characterization of the yield curve under CIR single factor model.For 0≤r≤κθγ,the yield curve is uniformly increasing.Forκ+λ>0,the yield curve is uniformly .For all the other cases,the yield curve is humped.decreasing if r≥κθκ+λReferences[1]Cox,John C.,Ingersoll,Jonathan E.,Jr.,and Ross,Stephen A.(1985a),“An IntertemporalGeneral Equilibrium Model of Asset Prices,”Econometrica,53,363–384.[2]Cox,John C.,Ingersoll,Jonathan E.,Jr.,and Ross,Stephen A.(1985a),“A Theory of theTerm Structure of Interest Rates,”Econometrica,53,385–407.[3]Gibbons,Michael R.,and Ramaswamy,Krishna(1988),“The Term Structure of Interest Rates:Empirical Evidence,”Working Paper,Stanford University and University of Pennsylvania. [4]P´o lya,George,and Szeg¨o,Gabor(1976),“Problems and Theorems in Analysis,”Volume II,Translated by Claude Elias Billigheimer,Springer-Verlag,Berlin,Heidelberg,New York.6。
