初中二次函数知识点总结

二次函数知识点

一、二次函数概念：

1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征：

⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项． 二、二次函数的基本形式

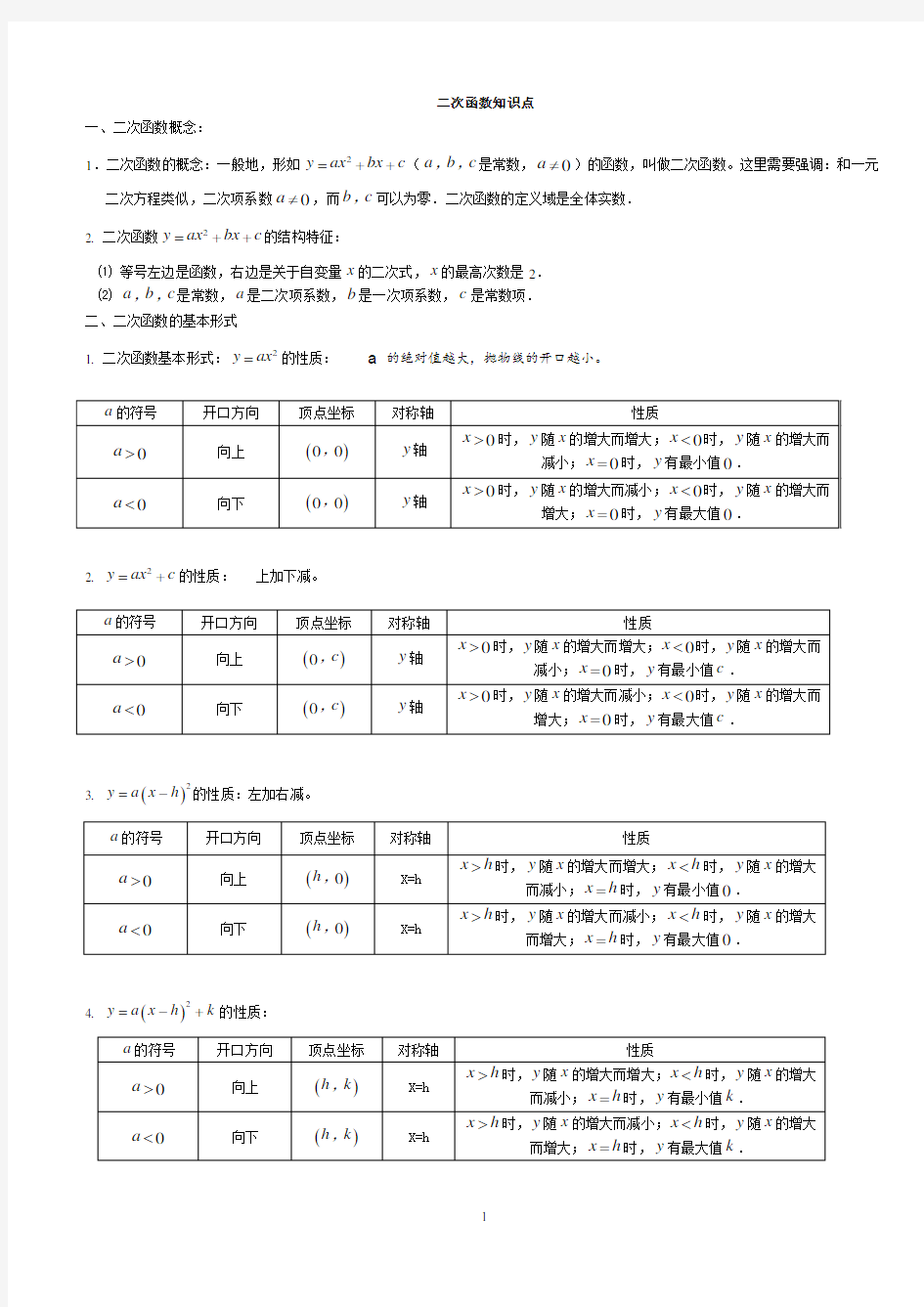
1. 二次函数基本形式：2y ax =的性质：

a 的绝对值越大，抛物线的开口越小。

2. 2

y ax c =+的性质： 上加下减。

3. ()2

y a x h =-的性质：左加右减。

4. ()2

y a x h k =-+的性质：

a 的符号

开口方向 顶点坐标

对称轴

性质

0a > 向上

()00， y 轴 0x >时，y 随x 的增大而增大；0x <时，y 随x 的增大而

减小；0x =时，y 有最小值0．

0a <

向下

()00，

y 轴

0x >时，y 随x 的增大而减小；0x <时，y 随x 的增大而

增大；0x =时，y 有最大值0．

a 的符号

开口方向 顶点坐标 对称轴 性质

0a > 向上 ()0c ， y 轴 0x >时，y 随x 的增大而增大；0x <时，y 随x 的增大而

减小；0x =时，y 有最小值c ．

0a <

向下

()0c ，

y 轴

0x >时，y 随x 的增大而减小；0x <时，y 随x 的增大而

增大；0x =时，y 有最大值c ．

a 的符号

开口方向 顶点坐标 对称轴 性质

0a > 向上

()0h ， X=h

x h >时，y 随x 的增大而增大；x h <时，y 随x 的增大

而减小；x h =时，y 有最小值0．

0a <

向下 ()0h ，

X=h

x h >时，y 随x 的增大而减小；x h <时，y 随x 的增大

而增大；x h =时，y 有最大值0．

a 的符号

开口方向 顶点坐标 对称轴 性质 0a > 向上 ()h k ， X=h x h >时，y 随x 的增大而增大；x h <时，y 随x 的增大

而减小；x h =时，y 有最小值k ．

0a <

向下

()h k ，

X=h

x h >时，y 随x 的增大而减小；x h <时，y 随x 的增大

而增大；x h =时，y 有最大值k ．

三、二次函数图象的平移 1. 平移步骤：

方法一：⑴ 将抛物线解析式转化成顶点式()2

y a x h k =-+，确定其顶点坐标()h k ，；

⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：

向右(h >0)【或左(h <0)】平移 |k|个单位

向上(k >0)【或下(k <0)】平移|k |个单位

向右(h >0)【或左(h <0)】平移|k|个单位

向右(h >0)【或左(h <0)】

平移|k|个单位

向上(k >0)【或下(k <0)】平移|k |个单位

向上(k >0)【或向下(k <0)】平移|k |个单位

y=a (x-h )2+k

y=a (x-h )2

y=ax 2+k

y=ax 2

2. 平移规律

在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”． 方法二： ⑴

c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成

m c bx ax y +++=2（或m c bx ax y -++=2）

⑵

c bx ax y ++=2沿x 轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或

c m x b m x a y +-+-=)()(2）

四、二次函数()2

y a x h k =-+与2

y ax bx c =++的比较

从解析式上看，()2

y a x h k =-+与2

y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即

2

2424b ac b y a x a a -?

?=++ ???

，其中2424b ac b h k a a -=-=

，． 五、二次函数2

y ax bx c =++图象的画法

五点绘图法：利用配方法将二次函数2

y ax bx c =++化为顶点式2

()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，

、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.

画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.

六、二次函数2

y ax bx c =++的性质

1. 当0a >时，抛物线开口向上，对称轴为2b

x a =-，顶点坐标为2424b ac b a a ??-- ???

，．

当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2b

x a =-时，y 有最小值244ac b a

-．

2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ??-- ?

??

，．当2b

x a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2b

x a =-时，y 有最大值244ac b a

-．

七、二次函数解析式的表示方法

1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；

2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；

3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）.

注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点 即2

40b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.

八、二次函数的图象与各项系数之间的关系 1. 二次项系数a

二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．

⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．

总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b

在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下， 当0b >时，02b

a

-<，即抛物线的对称轴在y 轴左侧； 当0b =时，02b a -

=，即抛物线的对称轴就是y 轴； 当0b <时，02b

a ->，即抛物线对称轴在y 轴的右侧． ⑵ 在0a <的前提下，结论刚好与上述相反，即 当0

b >时，02b

a

->，即抛物线的对称轴在y 轴右侧； 当0b =时，02b a -

=，即抛物线的对称轴就是y 轴； 当0b <时，02b

a

-<，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．

ab 的符号的判定：对称轴a

b

x 2-

=在y 轴左边则0>ab ，在y 轴的右侧则0

3. 常数项c

⑴ 当0c >时，抛物线与

y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正；

⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置．

总之，只要a b c ，

，都确定，那么这条抛物线就是唯一确定的． 二次函数解析式的确定：

根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：

1. 已知抛物线上三点的坐标，一般选用一般式；

2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；

3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；

4. 已知抛物线上纵坐标相同的两点，常选用顶点式． 九、二次函数图象的对称

二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称

2

y a x b x c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；

()2y a x h k =-+关于x 轴对称后，得到的解析式是()2

y a x h k =---；

2. 关于

y 轴对称

2y a x b x c

=++关于y 轴对称后，得到的解析式是2y ax bx c =-+；

()2

y a x h k =-+关于y 轴对称后，得到的解析式是()2

y a x h k =++；

3. 关于原点对称

2y a x b x c =++关于原点对称后，得到的解析式是2

y ax bx c =-+-； ()2

y a x h k =-+关于原点对称后，得到的解析式是()2

y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）

2

y a x b x c =++关于顶点对称后，得到的解析式是22

2b y ax bx c a

=--+-；

()2y a x h k =-+关于顶点对称后，得到的解析式是()2

y a x h k =--+．

5. 关于点()m n ，

对称 ()2

y a x h k =-+关于点()m n ，

对称后，得到的解析式是()2

22y a x h m n k =-+-+- 根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式． 十、二次函数与一元二次方程：

1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：

一元二次方程2

0ax bx c ++=是二次函数2

y ax bx c =++当函数值0y =时的特殊情况.

图象与x 轴的交点个数：

① 当2

40b ac ?=->时，图象与x 轴交于两点()()1200A x B x ，

，，12()x x ≠，其中的12x x ，是一元二次方程()2

00ax bx c a ++=≠的两根．这两点间的距离2214b ac

AB x x a

-=-=.

② 当0?=时，图象与x 轴只有一个交点；

③ 当0?<时，图象与x 轴没有交点.

1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >；

2' 当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <．

2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；

3. 二次函数常用解题方法总结：

⑴ 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程；

⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式；

⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ，b ，c 的符号，或由二次函数中a ，b ，c 的符号判断图象的位置，要数形结合；

⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴的一个交点坐标，可由对称性求出另一个交点坐标.

⑸ 与二次函数有关的还有二次三项式，二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数；下面以0a >时为例，揭示二次函数、二次三项式和一元二次方程之间的内在联系：

图像参考：

y=

x 22

y=2x 2

y=x 2

y=-2x 2

y= -x 2

y= -x 22

0?> 抛物线与x 轴有两

个交点

二次三项式的值可正、可零、可负

一元二次方程有两个不相等实根

?=

抛物线与x 轴只有一个交点

二次三项式的值为非负

一元二次方程有两个相等的实数根

?<

抛物线与x 轴无交点

二次三项式的值恒为正 一元二次方程无实数根.

y=2x 2-4

y=2x 2+2

y=2x 2

y=3(x+4)2

y=3(x-2)2

y=3x 2

y=-2(x+3)2

y=-2(x-3)2

y=-2x 2

十一、函数的应用

二次函数应用??

???

刹车距离何时获得最大利润最大面积是多少

二次函数考查重点与常见题型

1． 考查二次函数的定义、性质，有关试题常出现在选择题中，如： 已知以

x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点，

则m 的值是

2． 综合考查正比例、反比例、一次函数、二次函数的图像，习题的特点是在

同一直角坐标系内考查两个函数的图像，试题类型为选择题，如：

如图，如果函数

b kx y +=的图像在第一、二、三象限内，那么函数12-+=bx kx y 的图像大致是（ ）

y y y y

1 1

0 x o-1 x 0 x 0 -1 x A B C D

3． 考查用待定系数法求二次函数的解析式，有关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题，如： 已知一条抛物线经过(0,3)，(4,6)两点，对称轴为3

5

=

x

，求这条抛物线的解析式。 4． 考查用配方法求抛物线的顶点坐标、对称轴、二次函数的极值，有关试题为解答题，如： 已知抛物线2

y ax bx c =++（a ≠0）与x 轴的两个交点的横坐标是－1、3，与y 轴交点的纵坐标是－32

（1）确定抛物线的解析式；（2）用配方法确定抛物线的开口方向、对称轴和顶点坐标.

y=2(x-4)2-3

y=2(x-4)2

y=2x 2

5．考查代数与几何的综合能力，常见的作为专项压轴题。 【例题经典】

由抛物线的位置确定系数的符号

例1 （1）二次函数2y ax bx c =++的图像如图1，则点),

(a

c

b M 在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限

（2）已知二次函数y=ax 2+bx+c （a ≠0）的图象如图2所示，?则下列结论：①a 、b 同号；②当x=1和x=3时，函数值相等；③4a+b=0；④当y=-2时，x 的值只能取0.其中正确的个数是（ ） A ．1个 B ．2个 C ．3个 D ．4个

(1) (2)

【点评】弄清抛物线的位置与系数a ，b ，c 之间的关系，是解决问题的关键． 例2.已知二次函数y=ax 2+bx+c 的图象与x 轴交于点(-2，O)、(x 1，0)，且1

结论：①aO；③4a+cO ，其中正确结论的个数为( ) A 1个 B. 2个 C. 3个 D ．4个 答案：D

会用待定系数法求二次函数解析式

例3.已知：关于x 的一元二次方程ax 2+bx+c=3的一个根为x=-2，且二次函数y=ax 2+bx+c 的对称轴是直线x=2，则抛物线的顶点坐标为( )

A(2，-3) B.(2，1) C(2，3) D ．(3，2) 答案：C

例4、（2006年烟台市）如图（单位：m ），等腰三角形ABC 以2米/秒的速度沿直线L 向正方形移动，直到AB 与CD 重合．设x 秒时，三角形与正方形重叠部分的面积为y m 2． （1）写出y 与x 的关系式；

（2）当x=2，3.5时，y 分别是多少？

（3）当重叠部分的面积是正方形面积的一半时， 三角形移动了多长时间？求抛物线顶点坐标、 对称轴.

例5、已知抛物线y=

12

x 2+x-

52

．

（1）用配方法求它的顶点坐标和对称轴．

（2）若该抛物线与x 轴的两个交点为A 、B ，求线段AB 的长．

【点评】本题（1）是对二次函数的“基本方法”的考查，第（2）问主要考查二次函数与一元二次方程的关系．

例6.已知：二次函数y=ax 2-(b+1)x-3a 的图象经过点P(4，10)，交x 轴于)0,(1x A ，)0,(2x B 两点)(21x x <，交y 轴负半轴于

C 点，且满足3AO=OB ．

(1)求二次函数的解析式；(2)在二次函数的图象上是否存在点M ，使锐角∠MCO>∠A CO?若存在，请你求出M 点的横坐标的取值范围；若不存在，请你说明理由．

(1)解：如图∵抛物线交x 轴于点A(x 1，0)，B(x2，O)， 则x 1·x 2=3<0，又∵x 1

∴x 2>O ，x 1

∴点A(-1，O)，P(4，10)代入解析式得解得a=2 b=3 ∴．二次函数的解析式为y-2x 2-4x-6．

(2)存在点M 使∠MC0<∠ACO ．

(2)解：点A 关于y 轴的对称点A ’(1，O)，

∴直线A ，C 解析式为y=6x-6直线A'C 与抛物线交点为(0，-6)，(5，24)． ∴符合题意的x 的范围为-1

当点M 的横坐标满足-1∠ACO ． 例7、 “已知函数

c bx x y ++=

2

2

1的图象经过点A （c ，－2）

，

求证：这个二次函数图象的对称轴是x=3。”题目中的矩形框部分是一段被墨水污染了无法辨认的文字。

（1）根据已知和结论中现有的信息，你能否求出题中的二次函数解析式？若能，请写出求解过程，并画出二次函数图象；若不能，请说明理由。

（2）请你根据已有的信息，在原题中的矩形框中，填加一个适当的条件，把原题补充完整。

点评： 对于第（1）小题，要根据已知和结论中现有信息求出题中的二次函数解析式，就要把原来的结论“函数图象的对称轴是x=3”当作已知来用，再结合条件“图象经过点A （c ，－2）”，就可以列出两个方程了，而解析式中只有两个未知数，所以能够求出题中的二次函数解析式。对于第（2）小题，只要给出的条件能够使求出的二次函数解析式是第（1）小题中的解析式就可以了。而从不同的角度考虑可以添加出不同的条件，可以考虑再给图象上的一个任意点的坐标，可以给出顶点的坐标或与坐标轴的一个交点的坐标等。 [解答] （1）根据

c bx x y ++=

2

2

1的图象经过点A （c ，－2），图象的对称轴是x=3，得

???

?

???=?

--=++,3212,

2212

b

c bc c 解得???=-=.2,3c b 所以所求二次函数解析式为.232

12

+-=

x x y 图象如图所示。 （2）在解析式中令y=0，得

0232

12

=+-x x ，解得.53,5321-=+=x x 所以可以填“抛物线与x 轴的一个交点的坐标是（3+)0,5”或“抛物线与x 轴的一个交点的坐标是).0,53(-令x=3代入解析

式，得

,25-=y 所以抛物线23212+-=x x y 的顶点坐标为),2

5

,3(-所以也可以填抛物线的顶点坐标为)25,3(-等等。

函数主要关注：通过不同的途径（图象、解析式等）了解函数的具体特征；借助多种现实背景理解函数；将函数视为“变化过程中

变量之间关系”的数学模型；渗透函数的思想；关注函数与相关知识的联系。 用二次函数解决最值问题

例1已知边长为4的正方形截去一个角后成为五边形ABCDE （如图），其中AF=2，BF=1．试在AB 上求一点P ，使矩形PNDM 有最大面积．

例2 某产品每件成本10元，试销阶段每件产品的销售价x （元）?与产品的日销售量y （件）之间的关系如下表：

x （元） 15 20 30 … y （件） 25 20 10 …

若日销售量y 是销售价x 的一次函数．

（1）求出日销售量y （件）与销售价x （元）的函数关系式；

（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？?此时每日销售利润是多少元？ 【解析】

（

1）设此一次函数表达式为y=kx+b ．则1525,

220

k b k b +=??

+=? 解得k=-1，b=40，?即一次函数表达式为y=-x+40．

（2）设每件产品的销售价应定为x 元，所获销售利润为w 元 w=（x-10）（40-x ）=-x 2+50x-400=-（x-25）2+225．

产品的销售价应定为25元，此时每日获得最大销售利润为225元．

二次函数

一、选择题：

1. 抛物线3)2(2+-=x y 的对称轴是（ ）

A. 直线3-=x

B. 直线3=x

C. 直线2-=x

D. 直线2=x

2. 二次函数c bx ax y ++=2的图象如右图，则点),

(a

c b M 在（ ）

A. 第一象限

B. 第二象限

C. 第三象限

D. 第四象限

3. 已知二次函数c bx ax y ++=2，且0+-c b a ，

则一定有

（ ） A. 042>-ac b

B. 042=-ac b

C. 042<-ac b

D. ac b 42-≤0

4. 把抛物线c bx x y ++=2向右平移3个单位，再向下平移2个单位，所得图象的解析式是532+-=x x y ，则

有（ ）

A. 3=b ，7=c

B. 9-=b ，15-=c

C. 3=b ，3=c

D. 9-=b ，21=c

5. 已知反比例函数x

k

y =

的图象如右图所示，则二次函数222k x kx y +-=的图象大致为（ ）

O

x

y

A

O x

y

B

O x

y

C

O

x

y

D

6. 下面所示各图是在同一直角坐标系内，二次函数c x c a ax y +++=)(2与一次函数c ax y +=的大致图象，有

且只有一个是正确的，正确的是（ ）

O

x

y

A

O x

y

B

O x

y

C

O

x

y

D

7. 抛物线322+-=x x y 的对称轴是直线（ ）

A. 2-=x

B. 2=x

C. 1-=x

D. 1=x

8. 二次函数2)1(2+-=x y 的最小值是（ ）

O x

y

O

x

y

A. 2-

B. 2

C. 1-

D. 1

9. 二次函数c bx ax y ++=2的图象如图所示，若

c b a M ++=24c b a N +-=，b a P -=4，则

（ ）

A. 0>M ，0>N ，0>P

B. 0N ，0>P

C. 0>M ，0P

D. 0N ，0

10. 将二次函数322+-=x x y 配方成

k h x y +-=2)(的形式，则y =______________________.

11. 已知抛物线c bx ax y ++=2与x 轴有两个交点，那么一元二次方程02=++c bx ax 的根的情况是

______________________.

12. 已知抛物线c x ax y ++=2与x 轴交点的横坐标为1-，则c a +=_________. 13. 请你写出函数2)1(+=x y 与12+=x y 具有的一个共同性质：_______________. 14. 有一个二次函数的图象，三位同学分别说出它的一些特点：

甲：对称轴是直线4=x ；

乙：与x 轴两个交点的横坐标都是整数；

丙：与y 轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3.

请你写出满足上述全部特点的一个二次函数解析式：

15. 已知二次函数的图象开口向上，且与y 轴的正半轴相交，请你写出一个满足条件的二次函数的解析式：

_____________________.

16. 如图，抛物线的对称轴是1=x ，与x 轴交于A 、B 两点，若B 点坐标是)0,3(，则A 点的坐标是________________.

O

x

y

A B

1 1

16题图

三、解答题：

1. 已知函数12-+=bx x y 的图象经过点（3，2）.

（1）求这个函数的解析式；

（2）当0>x 时，求使y ≥2的x 的取值范围.

2 1 -1 O x

y

2. 如右图，抛物线n x x y ++-=52经过点)0,1(A ，与y 轴交于点B .

（1）求抛物线的解析式；

（2）P 是y 轴正半轴上一点，且△PAB 是以AB 为腰的等腰三角形，试求点P 的坐标.

1. 如图，有一座抛物线形拱桥，在正常水位时水

面AB 的宽为

20m ，如果水位上升3m 时，水面CD 的宽是10m. （1）求此抛物线的解析式；

（2）现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥280km （桥长忽略不计）.

货车正以每小时40km 的速度开往乙地，当行驶1小时时，忽然接到紧急通知：前方连降暴雨，造成水位以每小时0.25m 的速度持续上涨（货车接到通知时水位在CD 处，当水位达到桥拱最高点O 时，禁止车辆通行）. 试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要

使货车安全通过此桥，速度应超过每小时多少千米？

2.

3.

4. 某机械租赁公司有同一型号的机械设备40套. 经过一段时间的经营发现：当每套机械设备的月租金为270元

时，恰好全部租出. 在此基础上，当每套设备的月租金提高10元时，这种设备就少租出一套，且未租出的一

套设备每月需要支出费用（维护费、管理费等）20元，设每套设备的月租金为x （元），租赁公司出租该型号设备的月收益（收益=租金收入－支出费用）为y （元）.

（1）用含x 的代数式表示未租出的设备数（套）以及所有未租出设备（套）的支出费用； （2）求y 与x 之间的二次函数关系式；

（3）当月租金分别为4300元和350元时，租赁公司的月收益分别是多少元？此时应该租出多少套机械设备？

请你简要说明理由； （4）请把（2）中所求的二次函数配方成a

b a

c a b x y 44)2(22-++=的形式，并据此说明：当x 为何值时，租赁公司出租该型号设备的月收益最大？最大月收益是多少？

O x

y

1

-1 B

A