薄膜光学与薄膜技术_第01篇-01-薄膜光学的理论基础
合集下载
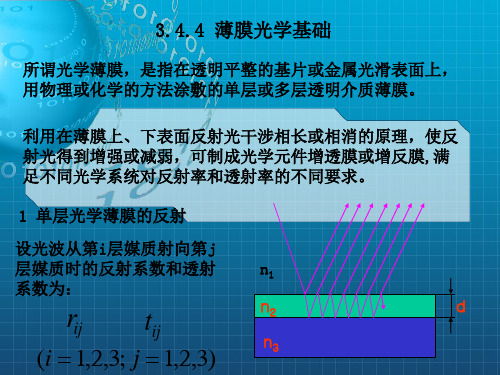
《薄膜光学基础》PPT课件
1 2
3
先考虑由基底g和膜层3
g
组成的单层膜系统。
由式(3-225)可得，此单层膜系统的反射系数：
r r23 r3g exp( j) 1 r23r3g exp( j)
由于是λ。/4膜系，所以：
r r23 r3g 1 r23r3g
1
再考虑由膜层2和反射系
2
数为 r 的等效膜层(3,g)
2
R1
nA nA
nI nI
式中
nI
nH2 nG
是镀第一层膜后的等效折射率。若在高折射率膜层上再镀一层
低折射率膜层，其反射率为
2
R2
nA nA
nII nII
式中
nII
nL2 nI
nL nH
2
nG
是镀双层膜后的等效折射率。依此类推，当膜层为偶数(2p)层 时， (HL)p膜系的等效折射率为
3
组成的“单层膜”系统。
g
这样，此“单层膜”系统的反射系数：
r r12 r 1 r12 r
最后得到双层膜系统的反射系数：
r r12 r23 r3g r12r23r3g 1 r12r23 r12r3g r23r3g
考虑到正入射的菲涅耳系数：
rij
ni ni
nj nj
令r＝0，可得双层减反膜的材料折射率条件：
此时反射率最小，透过率最大：
Rm
r12 1
r23 r12r23
2
n22 n22
n1n3 n1n3
2
Rm
r12 1
r23 r12r23
2
n22 n22
n1n3 n1n3
2
当满足下面条件时，R＝0，消反射：
薄膜光学5
薄 膜 光 学——基础理论
前一次课旳主要内容
光学薄膜在倾斜入射时旳体现 考虑到基片背面反射时旳情况 对称膜系旳等效折射率 矢量法 麦克劳德纳图解法简介 用麦克劳德纳图解法解释单、双层增透膜
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
经典膜系简介
❖增透膜 ❖分光膜 ❖反射膜 ❖滤光片 ❖特殊膜系
i n3 n1
in1
Y C / B n12 / n3
显然，在中心波优点旳反射率与单层膜相同。
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
单 层 膜 、 λ/4-λ/4和 λ/2-λ/2型 双 层 增 透 膜 理 论 曲 线
5
4 3 2
% Reflectance
薄 膜 光 学——经典膜系
1.2 双层增透膜
上面讨论旳λ0／4- λ0／4 构造旳V形膜只能 在较窄旳光谱范围内有效地减反射，所以仅合适 于工作波段窄旳系统中应用．厚度为λ0／4- λ0／ 2型旳双层增透膜，在中心波长λ0两侧， 可望有 两个反射率极小值，反射率曲线呈W型，所以也 有把这种双层增膜称作为W型膜旳．对于中心波 长膜层和基片组合旳特征矩阵为
n1
Y n0
n2
n3
n0
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
当折射率完全满足以上关系旳材料不能找到时，能够经 过厚度旳调整来到达，如图所示，n0、n3分别为入射介 质和基片旳折射率，n1和n2为折射率己拟定旳低折射率 和高折射率材料旳膜层，δ1、δ2便是待定旳膜层位相厚 度，用矢量法进行分析:
值为离开原点． 2． 矢量之间旳夹角仅决定于膜层旳光学厚度和所考察
前一次课旳主要内容
光学薄膜在倾斜入射时旳体现 考虑到基片背面反射时旳情况 对称膜系旳等效折射率 矢量法 麦克劳德纳图解法简介 用麦克劳德纳图解法解释单、双层增透膜
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
经典膜系简介
❖增透膜 ❖分光膜 ❖反射膜 ❖滤光片 ❖特殊膜系
i n3 n1
in1
Y C / B n12 / n3
显然，在中心波优点旳反射率与单层膜相同。
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
单 层 膜 、 λ/4-λ/4和 λ/2-λ/2型 双 层 增 透 膜 理 论 曲 线
5
4 3 2
% Reflectance
薄 膜 光 学——经典膜系
1.2 双层增透膜
上面讨论旳λ0／4- λ0／4 构造旳V形膜只能 在较窄旳光谱范围内有效地减反射，所以仅合适 于工作波段窄旳系统中应用．厚度为λ0／4- λ0／ 2型旳双层增透膜，在中心波长λ0两侧， 可望有 两个反射率极小值，反射率曲线呈W型，所以也 有把这种双层增膜称作为W型膜旳．对于中心波 长膜层和基片组合旳特征矩阵为
n1
Y n0
n2
n3
n0
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
当折射率完全满足以上关系旳材料不能找到时，能够经 过厚度旳调整来到达，如图所示，n0、n3分别为入射介 质和基片旳折射率，n1和n2为折射率己拟定旳低折射率 和高折射率材料旳膜层，δ1、δ2便是待定旳膜层位相厚 度，用矢量法进行分析:
值为离开原点． 2． 矢量之间旳夹角仅决定于膜层旳光学厚度和所考察
薄膜光学2
薄 膜 光 学——基础理论
平面电磁波理论——E和H的关系
比 较 可 得( 1)：
N E r H； 同 理 E可 得 ：
H N r E ； 这 说 明r、E、H三 个 量 相 互 垂 直
电 磁 波 是 横 波E，、H不 但 垂 直 ， 而 且 数 值 间还 有
一 定 的 比 例: N H ， 这 是N的 另 一 种 表 达 式 rE
薄 膜 光 学——基础理论
麦克斯韦方程组
E——电场强度 D——电位移矢量 H——磁场强度 B——磁感应强度 μ——磁导率
j——电流密度矢量 jD——位移电流矢量 ρ ——电荷密度 ε ——介电常数 σ ——电导率
个向同性、均匀介质物质方程：
D =ε E B =μ H j = σE
薄 膜 光 学——基础理论
薄 膜 光 学——基础理论
平面电磁波理论——反射和折射定律
对于倾斜入射：引进一个修正光纳η
仿 照 光 纳 定 义 ，的 定 义 为 ：
H
ta
n
k
Etan
;
H
ta n
k
Etan
a对 于TM (横 磁 波 ） P光,与 于 界 面 平 行
Etan
E
c os
可 得 到 p
N
c os
同 理b当E垂 直 于 入 射 平 面 时s N cos
薄 膜 光 学——基础理论
电磁波谱
电磁波谱
光是电磁波
薄 膜 光 学——基础理论
薄膜的干涉
两束光产生干涉的条件： •频率相同 •振动方向一致 •位相相同或位相差恒定
薄 膜 光 学——基础理论
薄膜的双光束干涉
薄 膜 光 学——基础理论
光学薄膜基础理论
n0 cos1 N1 cos0 n0 cos1 N1 cos0
可见rs、rp都是复数，rs rs eis 和rp rp ei p的
辐角是反射的位相变化，反射率由模的平方确定
波长为 546nm的 光入射到金 属Ag和Cu 上的情形
第二种介质为吸收时的情况
不管入射角如何，反射光的位相变化不 再是00或1800而是它们中间的某一角度, 同时s—分量和P—分量之间有一个不为0的 相对位相差, 因而当入射光为线偏振光在吸 收介质上反射后通常成为椭圆偏振光， 正 是基于这种认识，利用反射光的椭圆偏振 测量就可确定吸收介质的光学常数。
η2/Y。由于λ/2和λ/4的光学厚度的膜层组成的膜系比较简
单，所以膜系设计常常用指定波长1/4的倍数来表示，一般
只用两种或三种不同的膜料构造膜系， λ/4光学厚度的常用
缩写符号是H、M、L分别表示高、中、低折射率。
λ/2和λ/4的光学厚度
当膜层的光学厚度为λ/2时
cos
i sin
i
sin cos
sin0
ik1
可 见1为 复 数， 除0 1 0时 ，1不 再 为折 射 角 ；
当0
1
0时 ，rp
rs
n0 n1 ik1 n0 n1 ik
第二种介质为吸收时的情况
当0 0时情况要复杂的多
rs
rs
eis
n0 cos0 n0 cos0
N1 cos1 N1 cos1
rp
rp
ei p
负向行进的波位相因子应乘以ei
单层膜的反射
在膜层内E和H在边界a上的值为：
E1a
E1bei ,即k
E1a
1 2
Hb
1
第三章 薄膜光学基础理论1
可表示为
2 结合(9)式N = -i 0 0
可推出
2 N i t ( S0 r )
(14)
S0：平面波单位传播矢量 r：坐标矢径 类似的， H H 0e
2 N i t ( S0 r )
又 =2 ， =c /N， c = ，代入下式，得
E E0 e (8) i t x i t x i t 2 Nx EEe =E e =E e
i t x 0 0 0
(11)
(11)式含义：波长为的单色平面波沿正x方向传播 若一平面波沿给定的余弦方向( , , )传播， (11)式变成 E E0 e
1
0 0
0和 0是 真 空 中 的 介 电 常 数 和 磁 导 率
电磁波在真空中的速度与在介质中的速度之比称为
绝对折射率n （简称折射率）即
1 c 1 n ( ) 2 ( r r ) 2 00
之外，大多数物质的 r 1
因此： n
r ( r ) 相对介电常数（磁导率）除了磁性物质
薄膜光学
主要授课内容
薄膜理论——光学薄膜的基础理论，分析光学 薄膜的有效方法 薄膜设计——几种典型膜系介绍 制造设备 制备工艺 薄膜材料及性质
薄 膜 光 学——基础理论
麦克斯韦方程组
微分形式 积分形式
D B 0 B E t H ( j jD )
i t 2 nx
说明在导电介质（ 0，因而k 0）是一个衰减波， 消光系数k 是介质吸收电磁波能量的度量。 时，振幅衰减到原来的1 e 2 k 【介质内产生的电流将波的能量转换为热能】 当x =
光学薄膜-基础知识
稳定性和光学性能。
热导率
表示薄膜材料导热的能 力，影响光学薄膜的散
热性能。
光学常数
描述薄膜材料对光传播 的影响，如折射率、消
光系数等。
机械性能参数
硬度
表示薄膜材料的抗划痕能力， 影响光学薄膜的耐用性。
弹性模量
表示薄膜材料的刚度，影响光 学薄膜的稳定性和抗冲击能力 。
抗张强度
表示薄膜材料抵抗拉伸的能力 ，影响光学薄膜的耐用性和稳 定性。
反射率
表示光在薄膜表面反射的比例，影响光的利 用率。
吸收率
表示光被薄膜吸收的比例，影响光的损耗。
透射率
表示光透过薄膜的比例，影响光的透过效果。
干涉效应
由于多层薄膜对光的干涉作用，影响光的相 位和振幅。
物理性能参数
密度
薄膜材料的密度，影响 光学薄膜的质量和稳定
性。
热膨胀系数
薄膜材料受热后的膨胀 程度，影响光学薄膜的
更稳定的性能等。
多功能化
光学薄膜正朝着多功能化的方向发 展，如抗反射、抗眩光、增透、偏 振等功能，以满足不同应用场景的 需求。
环保化
随着环保意识的提高，光学薄膜的 环保性能也受到了越来越多的关注， 如使用环保材料、降低生产过程中 的环境污染等。
技术挑战
制造工艺
光学薄膜的制造工艺非常复杂， 需要高精度的设备和技术，如何 提高制造工艺的稳定性和重复性
02
它是一种重要的光学元件，广泛 应用于各种领域，如显示、照明 、通信、摄影等。
光学薄膜的特性
01
02
03
高反射性
通过选择合适的膜层材料 和厚度，可以获得高反射 率，用于增强光的反射效 果。
高透射性
通过调整膜层的折射率和 厚度，可以获得高透射率， 用于提高ቤተ መጻሕፍቲ ባይዱ的透射效果。
热导率
表示薄膜材料导热的能 力，影响光学薄膜的散
热性能。
光学常数
描述薄膜材料对光传播 的影响，如折射率、消
光系数等。
机械性能参数
硬度
表示薄膜材料的抗划痕能力， 影响光学薄膜的耐用性。
弹性模量
表示薄膜材料的刚度，影响光 学薄膜的稳定性和抗冲击能力 。
抗张强度
表示薄膜材料抵抗拉伸的能力 ，影响光学薄膜的耐用性和稳 定性。
反射率
表示光在薄膜表面反射的比例，影响光的利 用率。
吸收率
表示光被薄膜吸收的比例，影响光的损耗。
透射率
表示光透过薄膜的比例，影响光的透过效果。
干涉效应
由于多层薄膜对光的干涉作用，影响光的相 位和振幅。
物理性能参数
密度
薄膜材料的密度，影响 光学薄膜的质量和稳定
性。
热膨胀系数
薄膜材料受热后的膨胀 程度，影响光学薄膜的
更稳定的性能等。
多功能化
光学薄膜正朝着多功能化的方向发 展，如抗反射、抗眩光、增透、偏 振等功能，以满足不同应用场景的 需求。
环保化
随着环保意识的提高，光学薄膜的 环保性能也受到了越来越多的关注， 如使用环保材料、降低生产过程中 的环境污染等。
技术挑战
制造工艺
光学薄膜的制造工艺非常复杂， 需要高精度的设备和技术，如何 提高制造工艺的稳定性和重复性
02
它是一种重要的光学元件，广泛 应用于各种领域，如显示、照明 、通信、摄影等。
光学薄膜的特性
01
02
03
高反射性
通过选择合适的膜层材料 和厚度，可以获得高反射 率，用于增强光的反射效 果。
高透射性
通过调整膜层的折射率和 厚度，可以获得高透射率， 用于提高ቤተ መጻሕፍቲ ባይዱ的透射效果。
第一篇-第一章 薄膜光学的理论基础解读
对于可见光波段是透明的，而半导体锗对于 波长大于2μm的红外波段是透明的，等等。 图1-1给出的是一些常用光学介质的透光范围。
氟化镁(MgF2) 氟化钙(CaF2) 氟化钡(BaF2) 石英(SiO2) 紫外石英(SiO2) 熔石英(SiO2) 玻璃(BK-7) 硅(Si) 锗(Ge) 硫化锌(ZnS) 砷化镓(GaAs) 硒化锌(ZnSe) 碲化镉(CdTe) 0.1 0.2 0.3 0.4 0.5 0.6 1.0 2.0 3.0 4.0 5.0 6.0 10.0
薄膜光学与薄膜技术基础
合导电体。麦克斯韦方程是描述一切宏观电 磁现象的普遍规律，因而，薄膜光学中描述 光传播特性的光波动方程可以由麦克斯韦方 程导出。 考虑时谐电磁场，空间任一点的电场强 度和磁场强度随时间作正弦或余弦变化，场 量随时间变化的因子取ejωt，则有
E(r; t ) Re E r e jt D(r; t ) Re D r e jt jt H r e H(r; t ) Re jt B ( r ; t ) Re B r e
式中
(1-3)
薄膜光学与薄膜技术基础
在求解具体的薄膜光学问题时，麦克斯 韦方程还涉及反映介质特性的关系，即电磁 场量之间关系的物质方程
D 0 r E B 0 H J E
(1-4)
- 12 e 淮 8 . 85 10 式中 0 （F/m）为真空介电常数, r - 7 m = 4 p? 10 为复相对介电常数； 0 （H/m）为
真空磁导率；σ为电导率。 式（1-2）和式（1-4）构成麦克斯韦方程 的限定形式，当 r 和 σ 给定之后，就可以针
薄膜光学与薄膜技术基础
薄膜光学技术-1第一章 薄膜光学特性计算基础
tp
2N 0co0s N0co1sN1co0s
1
s
Kcos0 cos1
p
其中，计算
r
和
s
t
时，公式中的
s
应代入 s ；
计算 rp和 t p时，公式中的应代入 p 。
显然,引入修正导纳的好处是菲涅耳公式的形式简化易记了。
第20页
2 单一界面的反射率和透射率
RIr Ii
EE00ri22
2
r201 01
求解依据：
E、H、k0 之间的右旋法则
电磁场的边界条件 在两种介质的分界面上没有面电荷和面电流的情 况下，电磁场量H和E的切向分量是连续的。
第15页
垂直入射
由切向分量连续：
H
i 0
N0
N1
E
i 0
k0
H1t
E
r 0
kE0 1t
k0
H
r 0
E0i E0r E1t
(1)
H0i H0r H1t
p N / cos 第22页
3 等效界面思想
将一个多界面的薄膜系统等效地看作一个单一界 面。等效界面两侧的介质分别是入射介质和等效介质。 入射介质的折射率仍旧是N0，等效介质具有等效光 学导纳。 因此，薄膜系统的反射率就是等效界面的反射率， 而等效界面的反射率计算公式是：
2
R 0 Y 0 Y
s Ncos
H
i 0
N0 N1
p 偏振
Ei0 0 Ei0 cos 0
1 H1t
H
r 0
0
E1t E1t cos1
E0r cos 0
H与界面平行
Htan H
E0r
EtanEcos
光学薄膜-基础知识
光学薄膜
----基础知识介绍
光学薄膜-基础知识
光是什么？
光是一种电磁波，（在真空中的）可见光波长范围是700~400nm ；红外光为约700 到107nm量级;紫外光1-400nm；比紫外光短的还有X射线、γ射线（<0.001nm）等； 而比红外长的就是我们熟悉的无线电波
光学薄膜-基础知识
什么叫光的干涉？
%
五、反射膜
在光学薄膜中，反射膜和增透膜几乎同样重 要。 对于光学仪器中的反射系统来说，一般单 纯金属膜的特性大都已经满足常用要求。在某 些应用中，要求更高的反射率则可用金属增强 镜。 而全介质多层反射膜，由于这种反射膜具 有最大的反射率和最小的吸收率因而在激光应 用和一些高要求的系统中得到了广泛的使用。
介质带通滤光片的结构为：介质反射膜/间隔层/ 介质反射膜/间隔层/介质反射膜．但是滤光片也可以
是混合结构，例如用一层金属膜如银膜代替两间隔之 间的介质反射膜形式如下：
介质反射膜/间隔层/金属膜/间隔层/介质反射膜
这是金属诱导透射滤光片的基本形式
这种滤光片的最大好处：长波无次峰、透射率较高
光学薄膜-基础知识
光学薄膜的类型与符号
光学薄膜-基础知识
光学薄膜的依附体 ——基板
光学薄膜-基础知识
光学上常用的基板
一、玻璃----在光学应用上最重要 二、陶瓷 三、光学晶体 四、光学塑料（如PC、PMMA等） 五、金属
光学薄膜-基础知识
一、玻璃
玻璃可以分为：
1、普通玻璃 2、无色光学玻璃 3、有色光学玻璃 4、特殊玻璃等
金属滤光片 全介质滤光片 双半波、三半波全介质滤光片 金属诱导透射滤光片
光学薄膜-基础知识
% T r a n s m it t a n c
----基础知识介绍
光学薄膜-基础知识
光是什么？
光是一种电磁波，（在真空中的）可见光波长范围是700~400nm ；红外光为约700 到107nm量级;紫外光1-400nm；比紫外光短的还有X射线、γ射线（<0.001nm）等； 而比红外长的就是我们熟悉的无线电波
光学薄膜-基础知识
什么叫光的干涉？
%
五、反射膜
在光学薄膜中，反射膜和增透膜几乎同样重 要。 对于光学仪器中的反射系统来说，一般单 纯金属膜的特性大都已经满足常用要求。在某 些应用中，要求更高的反射率则可用金属增强 镜。 而全介质多层反射膜，由于这种反射膜具 有最大的反射率和最小的吸收率因而在激光应 用和一些高要求的系统中得到了广泛的使用。
介质带通滤光片的结构为：介质反射膜/间隔层/ 介质反射膜/间隔层/介质反射膜．但是滤光片也可以
是混合结构，例如用一层金属膜如银膜代替两间隔之 间的介质反射膜形式如下：
介质反射膜/间隔层/金属膜/间隔层/介质反射膜
这是金属诱导透射滤光片的基本形式
这种滤光片的最大好处：长波无次峰、透射率较高
光学薄膜-基础知识
光学薄膜的类型与符号
光学薄膜-基础知识
光学薄膜的依附体 ——基板
光学薄膜-基础知识
光学上常用的基板
一、玻璃----在光学应用上最重要 二、陶瓷 三、光学晶体 四、光学塑料（如PC、PMMA等） 五、金属
光学薄膜-基础知识
一、玻璃
玻璃可以分为：
1、普通玻璃 2、无色光学玻璃 3、有色光学玻璃 4、特殊玻璃等
金属滤光片 全介质滤光片 双半波、三半波全介质滤光片 金属诱导透射滤光片
光学薄膜-基础知识
% T r a n s m it t a n c
光学薄膜-基础知识
四、带通滤光片
从光学薄膜的角度来讲，最有意义的进 展是1899年出现的法布里-珀珞干涉仪。 它是干涉带通滤光片的一种基本结构。而 自从1940年出现金属-介质滤光片以来， 它已经在光学、光谱学、激光、天文物理 学等各个领域得到了广泛的应用。
四、带通滤光片
法布里—珀珞的结构
四、带通滤光片
带通的主要参数
4、特殊玻璃
特殊玻璃可以包括 A、耐辐射玻璃
B、石英玻璃
C、隔热玻璃 D、微晶玻璃 E、耐热玻璃 F、硬质玻璃等。
二、光学塑料
塑料是什么？
塑料是一种以合成树脂或天然树脂(一般为高分 子聚合物)为基本成分，在加工过程中，可塑制成型， 产品最终能保持形状不变的材料。光学塑料乃是一 种可以与玻璃竞争的透明塑料。它具有一定的光学 特性、机械特性和化学特性，能满足光学零件的要 求，从而逐渐构成光学三大基本材料之—(玻璃、光 学晶体和光学塑料)。
数大，可分为冕火石（KF）、轻火石（QF）、钡火石 （BaF）、重火石（ZF）、镧H火石（LaF）等。
共有160多种之多。
无色光学玻璃一些技术指标
1、nd----指587.7nm(氦黄线)处的折射率； 2、nD----指589.3nm(钠黄线)处的折射率；
3、相对色散（阿贝数） υd 、 υD
----由nf(486.1nm)和nc(656.3nm)确定： υd= (nd -1)/(nf - nc)
类别 折射率nd允许差 值 ±2×10-4 类别 折射率nd允许差值
00
2
±7×10-4
0
±3×10-4
3
±10×10-4
1
±5×10-4
4
±20×10-4
玻璃的光学均匀性以一块玻璃中各部位间的折射率微差最大值 △nmax表示时，按下表分为4类。 类别 H1 折射率最大微差，△nmax ±2×10-6
光学薄膜基础知识
光学薄膜基础知识光学薄膜讲解内容：①光学薄膜的理论基础及应用范围和发展前景②光学薄膜基础理论知识③镀膜制备技术④镀膜材料⑤镀膜检测光学薄膜是一门综合性非常强的工程技术科学。
它的理论基础是电磁场理论和麦克斯韦方程，涉及光在传播过程中，通过多层介质时的反射、反射各偏振性能等。
随着科学的进步和人们生活水平的不断提高，促使镀膜技术得到了非速的发展。
在许多情况下，人们关心的是材料的表面，在普通的基底材料上若镀以适当的膜，就可以获得奇迹般的效果。
膜是物质存在的一种形式。
多年来，在膜的理论、制备工艺、测试方法和应用等方面，进行了大量的研究和开发工作，已发展成为一门新兴的边缘科学——膜学。
它涉及物理学、化学、数学等基础学科和材料、等离子体、真空、测量与控制等技术领域。
它是多种学科综合的产物，同时也促进了相关学科和技术的发展。
膜学是材料中最活跃、最富成效、最有前途的一项技术。
镀膜的方法很多，分类方法也各不相同。
按膜层的形成方法分类，可以分为干式镀膜和湿式镀膜。
干式镀膜是指要真空的条件下，应用物理或化学的方法，将材料汽化成原子、分子或使成电离成离子，并通过气相过程，在基体表面沉积一层具有特殊性能的薄膜技术。
因此也有人称为气相过程或真空镀膜。
在干式镀膜中有以真空镀、溅射镀膜、离子镀为代表的物理气相沉积（PVD）和化学气相沉积（CVD）。
湿式镀膜是指将工件置于电解质溶液中，通过化学、电化学的方法，使其表面形成镀层，所以也有人称溶液法为液相沉积法，它可以分为电镀、化学镀、化学转化膜处理几种。
镀膜技术应用广泛，如太阳能电池、太阳能集热管、集成电路、半导体器件、平板显示器、光控及节能玻璃、信息储存作用器件、敏感元件、工模具超硬涂层及手表、眼镜、卫生洁具等日用品精钸层、塑料制品金属化、包装用塑料薄膜等各个领域，在工业现代化和国民经济发展中的越来越大，在国内外生产、科研、教学领域受到普遍重视，得到了迅猛发展。
光学薄膜基础理论知识光波：紫外光、可见光、红外光。
薄膜光学4
Ra
Rb(TaTa RaRa) 1RaRb
如 果 没 有 吸 R收 Ra Rb 2RaRb 1RaRb
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——基础理论
考虑到基片背面反射的情况
同理：对于透射率
TTaTbTaTbRbRa1RaRb RaRb 2
T TaTb 1RaRb
对于红外高折射率材料Si、Ge等尤其要考虑基片 中多次反射的非相干叠加
的 概 念 不 再 存 在 ，对这应时的 波 长 范 围 截止区。
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——基础理论
对称膜系的等效折射率
对于M11的绝对值小于1的情况：
令一个周期性对称膜系 的基本周期的特征矩阵 为：
M
cos
iE sin
i sin
E
cos
膜系的特征矩阵为：
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——基础理论
对称膜系的等效折射率
由于对称膜系的待征矩阵和单层膜的特征矩阵具有相同 的性质，可以假定以相似的形式来表示：
M pq p M M 1 21 1 M M 1 22 2 icE soin s E icsoin s
因此它可以用一层特殊的等效单层膜来描写， 这层等效膜
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——基础理论
本此课的主要内容
•对称膜系的等效折射率 •矢量法 •麦克劳德纳图解法简介 •用麦克劳德纳图解法解释单、双层增透膜
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——基础理论
对称膜系的等效折射率
对于单层膜我们可以用一个矩阵M单来表示，对于 一个多层膜可以用一组矩阵的乘积来表示：M多 =M1M2M3…Mn，一般来讲M多中的每一层都是无 吸收介质时，矩阵M多中m11和m22为纯实数，m12 和m21为纯虚数，并且，行列式值为1，但是一般 情况下m11和m22并不相等，这一点与单层膜的性 质是不同的，所以在数学上就不能等同于一个单 层膜。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
c r 0r 0n2
（1-5）
式中n表示介质的折射率，均匀介质取常数值。 （2）对于各向同性线性非均匀介质，介质
非导电 s = 0, r 为实函数，则有
r r 0r r 0n2 r (1-6)
非均匀介质折射率n随空间变量变化。
k = w me
（1-25）
则方程（1-22）和方程（1-23）就化为理想介 质中的复矢量波动方程。
薄膜光学与薄膜技术基础
波数 k 也称之为空间角频率。波数 k 与
波速 u 及角频率 w之间的关系为
k = w me = w = wn uc
（1-26）
式中
u= 1 = c me n
（1-27）
为光波在介质中的传播速度，c为真空中的光
界面上的自由电流面密度复振幅矢量。如果
把边界条件写成标量形式，有
ìïïíïïî
E%1t H%1t
= -
E%2t H%2t
=
J%s
(1-18)
式中 E%1t 、E%2t 和 、 H%1t H%2t 分别表示介质1和介质2分 界面上电场和磁场复振幅矢量的切向分量。J%s 为分界面上 p2 2 4 2 2
n
1 2
p2 1 4 2 2
（1-11）
式中 n 称之为导电介质的折射率，a 称之为消
光系数。由式（1-11）可以看出，导电介质
的折射率和消光系数是光波频率的函数，所
以光波在导电介质中传播或在导电介质表面
CsI
KI CsBr
BaF2
KBr
CaF2
KCI
SiO2
NaCI
NaF
0.8 100 200
紫外
400 600 800 可见光
2000
LiF
4000 10,000 红外
60,000
波长 λ (nm)
图 1-4 常用光学晶体的折射率随波长和频率的变化曲线
AgCI（氯化银）、BaF2（氟化钡）、CsI（碘化铯）、CsBr（溴化铯）、 CaF2（氟化钙）、KI（碘化钾）、KBr（溴化钾）、KCI（氯化钾）、 LiF（氟化锂）、NaCI（氯化纳）、NaF（氟化钠）、SiO2（二氧化硅）
薄膜光学与薄膜技术基础
介质对光的吸收分为两类：一般吸收和 选择吸收。一般吸收与波长无关，吸收系数 很小；选择吸收与波长紧密相关，吸收系数 很大。选择吸收与构成介质的电偶极子有关， 反映了介质中原子结构的本质。
光学介质的折射率随波长而改变的现象 称之为介质的色散。色散与吸收密切相关， 根据经典振子模型，可以说明色散和吸收现 象。假设单原子中有Z个电子， fi 个电子对应 的振子固有圆频率和衰减系数分别为 w0i和 gi ， 则由振子的运动方程求解可得介质的相对介
薄膜光学与薄膜技术基础
e为常数，介质电导率为 ，由麦克斯韦方程 式（1-2）第一式两边取旋度，并将式（1-2） 中的第二式代入，得到
H 2c0H
利用矢量恒等式
H H 2H
且 炎 H%= 0 ，有
（1-20） （1-21）
2H kc2H 0
石英(SiO2) 紫外石英(SiO2)
熔石英(SiO2)
玻璃(BK-7)
硅(Si)
硫化锌(ZnS)
锗(Ge)
砷化镓(GaAs)
硒化锌(ZnSe)
碲化镉(CdTe)
0.1 0.2 0.3 0.4 0.5 0.6
1.0 2.0 3.0 4.0 5.0 6.0 10.0 / m
图 1-1 常用光学材料的透光范围
速，n 为介质的折射率。
描述波动特性的基本物理量波数 k 、波
长 l 、角频率 w、周期 T和频率 f 之间的关
薄膜光学与薄膜技术基础
系为
k = 2p = 2pn l
（1-28）
w= 2p = 2pf T
u= lf
（1-29） （1-30）
式中 n 为空间频率。
1.2.2 理想介质中的平面波解 理想介质中的波数 k为实数，采用分离变
jk?r
（1-32）
式中k 称为波传播矢量，简称波矢量。假设
E%0 = E0e jj e
（1-33）
则有
H%0 =
薄膜光学与薄膜技术基础
第一篇 薄膜光学理论基础
第一章 薄膜光学的电磁理论基础 曹建章
薄膜光学与薄膜技术基础
薄膜光学的理论基础是光的电磁理论，其 内容包括：光的干涉、偏振和吸收，平面电 磁波以及平面电磁波在介质表面的反射和透 射等。鉴于后续章节的需要，本章简要介绍 麦克斯韦方程、描述介质特性的物质方程、 平面电磁波的解形式以及光强和电磁波谱。 1.1 麦克斯韦方程
示在时间 t 内电流密度衰减到初始值的 1 / e 。
met - 1代表电子运动的阻尼系数。
在介质均匀的情况下，利用麦克斯韦方程
薄膜光学与薄膜技术基础
（1-2）可导出金属材料的介电常数为
c
0 r
0N
2
0
1
2
2 p
j
1
（1-8）
式中no和ne 分别称之为寻常光和非寻常光的折 射率。
实际的薄膜光学问题求解，场中存在多
种介质，光波传播在介质分界面上必须满足
电磁场边界条件，其矢量形式为
薄膜光学与薄膜技术基础
ìïïíïïïî
n? n?
(E%1 (H%1
E%2 )= 0 ) H%2 = J%s
（1-17）
式中 E%1 、H%1 和E%2 、H%2 分别表示介质1和介质2 分界面两侧的电场和磁场复振幅矢量。J%s 为分
考虑时谐电磁场，空间任一点的电场强
度和磁场强度随时间作正弦或余弦变化，场
量随时间变化的因子取ejωt，则有
E(r;
t
)
Re
E
r
e
jt
D(r;t) Re D r e jt
H(r;t) Re H r e jt
B(r;t) Re B r e jt
薄膜光学与薄膜技术基础
小。如果介质为非导电介质，J%s = 0，则磁场 的边界条件简化为
H%1t - H%2t = 0
（1-19）
1.2 平面电磁波
光波在薄膜介质中传播都假定是以平面
波形式传播，因此，下面从麦克斯韦方程出 发推导平面光波的解形式。
1.2.1 复矢量波动方程—齐次矢量亥姆霍兹 方程
假设均匀线性各向同性介质，介电常数
介质对光不透明。在此波段内，折射率随波 长的增加而增加，称之为反常色散，如图1-3 所示。
n
吸
收
带
吸
吸
收
收
带
带
1 红外
01
可见光
02
紫外
图 1-3 折射率随频率的变化曲线
03
X-射线
薄膜光学与薄膜技术基础
图1-4给出的是其他一些常用光学晶体的折射 率随波长和频率的变化曲线。（属一般吸收）
折射率 n
反射和透射都存在色散。
（4）对于通常的光学介质，其特征表现为
在某一光频范围的辐射是透明的，比如玻璃
薄膜光学与薄膜技术基础
对于可见光波段是透明的，而半导体锗对于 波长大于2μm的红外波段是透明的，等等。 图1-1给出的是一些常用光学介质的透光范围。
氟化镁(MgF2) 氟化钙(CaF2)
氟化钡(BaF2)
式中 N%为复折射率，w为光波圆频率。 wp为
金属的等离子体频率，大小为
wp =
Ne2 =
mee0
m0s c2 t
式中 c 表示真空中的光速。
令
（1-9）
r r ji , N n j
（1-10）
薄膜光学与薄膜技术基础
式（1-8）和式（1-10）联立求解，得到
n2
2
薄膜光学与薄膜技术基础
（3）金属材料对光的吸收体现在电导率s ? 0 在金属材料中，由于电子运动是自由的，所
以在光波交变电场的作用下，通过电子运动 方程的求解，可得金属材料的电导率为率
s = Ne2 t me
（1-7）
式中 N 为单位体积的导电电子数，me 为电子
质量，- e 为电子电荷。t 称为弛豫时间，表
真空磁导率；σ为电导率。
式（1-2）和式（1-4）构成麦克斯韦方程 的限定形式，当 r 和 σ 给定之后，就可以针
薄膜光学与薄膜技术基础
对具体问题进行求解。下面就薄膜光学中涉
及的介质参数作简单讨论。
（1）对于各向同性线性均匀介质，介质非 导电 s = 0， r 取实常数，则式（1-3）简化为
量法求解亥姆霍兹方程（1-23），仅考虑沿正 方向传播的波，得到电场强度矢量的平面波解
薄膜光学与薄膜技术基础
E%(x, y,z)= E%0e- jk?r
（1-31）
代入麦克斯韦方程（1-2）第二式，得磁场 强度矢量的平面波解为
H%(x, y, z) = H%0e- jk?r =
k´ E%0 e wm
宏观上讲，光的电磁理论全面揭示了光 的主要性质，不仅适合各向同性介质，也适 合各向异性介质；不仅适用于均匀介质，也 适合非均匀介质；不仅适合吸收介质，也适
薄膜光学与薄膜技术基础
合导电体。麦克斯韦方程是描述一切宏观电 磁现象的普遍规律，因而，薄膜光学中描述 光传播特性的光波动方程可以由麦克斯韦方 程导出。
3 1015
2.8
3 1014
频率 f (Hz)
3 1013
3 1012