土力学第三章吐得渗透性
合集下载
土力学课件第三章土的渗透性
(3) 所损失的水头 ③E点测压管水柱高度
hE ( z1 h1 ) h f h f (i 1)h
H E hE Z E ( z1 h1 ) Z E (i 1)h
举例2
某板桩支挡结构，由于基坑内外土层存在水位差而发生 渗流，渗流流网如图所示，已知土层渗透系数k1＝ 3.2×10-3cm/s，A点、B点分别位于基坑底面以下1.2m和 2.6m处，试求： （1）整个渗流去的单宽流量q； （2）AB短的平均流速vAB； （3）图中A点和B点的孔隙水压力uA与uB。
3. 流速：
q (1)渗流模型的平均流速 v A q (2)真实流速 vr Ar
(3)相比
q vA vr Ar vr nA
v vr n
vr v
(二) 达西定律
1. 定义： 是指水在土中的渗流速度与水头梯度成正比
v ki
q kAi
2. 适用范围： 层流的情况，一般只适 用于中砂、细砂和粉砂 3. 粘土中
Hkiy ii
q q1 q2
h ii H i
i 1 n
3.3 土中二维渗流及流网
一、二维渗流方程 1. 连续条件微分方程
v x v z 0 x z
2. 基本微分方程 2h 2h k x 2 k z 2 0 各向异性土 x z
2h 2h 2 0 2 x z
aL h1 aL h1 k ln 2.3 lg At h2 At h 2
2. 现场测定渗透系数
dh q Aki 2rhk dr dr q 2rkhdh r
q ln(r 2 / r 1) k (h2 2 h12 )
q ln(r2 / r1 ) k 2.3 (h2 2 h12 )
土力学课件(3土的渗透性与渗流)详解
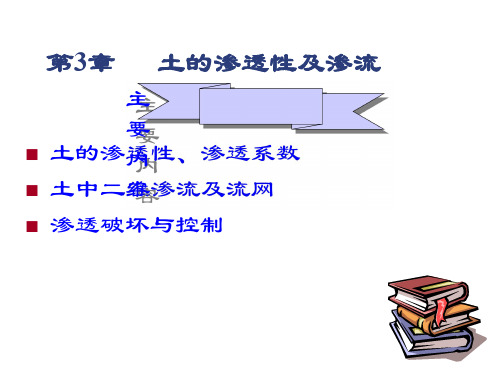
管内减少水量＝流经试样水量
－adh=kAh/Ldt 分离变量
积分
k＝2.3
aL
At2
t1 lg
h1 h2
k＝
aL
A t2
t1 ln
h1 h2
3、影响渗透系数的主要因素 (1)土的粒度成分
v 土粒愈粗、大小愈均匀、形状愈圆滑，渗透系数愈大
v 细粒含量愈多，土的渗透性愈小，
(2)土的密实度 土的密实度增大，孔隙比降低，土的渗透性也减小 土愈密实渗透系数愈小
(3)土的饱和度 土的饱和度愈低，渗透系数愈小
(4)土的结构 扰动土样与击实土样，土的渗透性比同一密度 原状土样的小
(5)水的温度(水的动力粘滞系数) 水温愈高，水的动力粘滞系数愈小 土的渗透系数则愈大
k20 kT T 20
(6)土的构造
T、20分别为T℃和20℃时水的动 力粘滞系数，可查表
水平方向的h>垂直方向v
n
qx q1x q2x qnx qix i1
达西定律
qx kxiH
平均渗透系数
q1x k1 qx q2x k2
q3x k3
H1 H2 H H3
n
qix k1iH 1 k 2iH 2 k n iH n
i 1
整个土层与层面平行的渗透系数
k x
1 H
n
kiH i
i1
(2)垂直渗透系数
H
隧道开挖时，地下 水向隧道内流动
在水位差作用下，水透过土体孔隙的现象称为渗透
渗透
在水位（头）差作用下，水透过土体孔隙的现象
渗透性
土体具有被液体透过的性质
土的渗流 土的变形 土的强度
相互关联 相互影响
土力学 第3章 土的渗透性
第1章作业讲解1-13 某土样的含水量为6％，天然重度为16kN/m3，土粒比重为 某 样的含水 为 ％， 然重度为 / ， 粒 重为 2.70，若土的孔隙比不变，为使土样能够完全饱和，问1000cm3 土样中需加多少水？ 解答： w0 = 6% γ 0 = 16kN / m 3Gs = 2.70γ s = ρs g =e0 =e0 =V = 1000cm 3ms g = Gs ρ w1 g Vsw0 =2.7 × 1 × 10 × (1 + 6%) − 1 = 0.7887 16γ s (1 + w0 ) −1 γ0Gs ρ w1 g (1 + w0 ) −1 =mw 0 msw0 mw 0 m = = w0 1 + w0 ms + mw0 m0γ0 wGs e = e0 = Srw=mw0 = m0ms =S r = 100%γ w0 w0 = 0V 1 + w0 g 1 + w0mw 0 γ 0 1 16 6 1 = V = × 1000 × = 1509.4 g w0 g 1 + w0 10 1.06e0 0.7887 = = 29.21% 2.70 Gsmw0 = ms w0mw = ms wΔmw = mw − mw0 = ms ( w − w0 ) = 1509.4 × (29.21% − 6%) = 350.33g第1章作业讲解z/b=1.15 l/b=1.7z/b=1.151.0 1.2l/b=1.7 l/b=1 7 1.6 0.1914 0.1705 l/b=1.7 / 1.7 0.19345 0.1731 l/b=1.7 / 1.7 0.17811.8 0.1955 0.1757z/b=1.151.0 1.2z/b=1.15第三章土的渗透性第 3 章土的渗透性四川大学水电学院 省岩土工程重点实验室第三章土的渗透性： 内容§3.1 概述§3.2 土的渗透理论 §3.3 §3 3 二维渗流与流网 §3.4 渗透力及渗透破坏类型 §3.5 有效应力原理第三章3.1 概述碎散 碎散性多孔介质 能量差渗流三相体系 系孔隙流体流动 水、气等流体在土孔隙或其它透水 性介质（如土工建筑物）中的流动 现象 土体等多孔介质具有被水、气等流 体等多 介质 有 等 体透过的性质非饱和土的渗透性 饱和土的渗透性土颗粒土中水 渗流渗透性 渗透特性 应力、变形、强度 和稳定第三章3.1 概述板桩围护下的基坑渗流板桩墙 基坑 透水层 不透水层渗水压力 渗流量 渗透变形 扬压力第三章3.1 概述土石坝坝基坝身渗流防渗斜墙及铺盖土石坝浸润线渗流量 渗透变形透水层 不透水层第三章3.1 概述水井渗流Q天然水面 透水层渗流量不透水层第三章3.1 概述降雨入渗引起的滑坡渗流问题： 渗透力？ 入渗过程？第三章3.2 土的渗透理论§3.1 概述§3.2 土的渗透理论§3.3 §3 3 二维渗流与流网 §3.4 渗透力及渗透破坏类型 §3.5 有效应力原理1.水力梯度或水力坡降水力梯度或水力降水头（总能量）：gv uz h w 22++=γA u Δhz ：位置水头（基准面高程）Ah 1h 2wγwB u γu/γw ：压力水头BL z Az B基准面v 2/(2g)：流速水头≈0uz h +=：wγ测管水头1.水力梯度或水力坡降水力梯度或水力降A点总水头A u ΔhwAA 1u z h γ+=Ah 1h 2wγwB u γBLz Az B基准面u B点总水头wBB 2z h γ+=Δ水力坡降水头差12h h h Δ=−Lh i =层流：相邻两个水分子运动的轨迹互相平行而不混流状态紊流：相邻两个水分子运动的轨迹互相混交，呈不规则运动2.达西定律西定律1856年，Darcy 对均匀的砂土进行了一维渗透试验，得出了层流条件下，土中渗透速度与能量（水头）损失之间关系的渗透规律即层流;恒定流渗透规律，即达西定律。
土力学第三章 土的渗透性
l
s
§3 土的渗透性
l 实际应用 H
测管水头 h
△h
s
s
0
水力坡降
确定孔压
i H / l
l
（h h z）
确定流速
确定流量
vi k i i
H qi k s i kH; li q Mqi MkH
M ——流道数
§3.5 渗透力与渗透稳定性
粒径大小及级配 孔隙比 矿物成分 结构
水的动力粘滞系数 饱和度（含气量） —对k影响很大，封闭气泡
§3 土的渗透性
三.层状地基的渗透系数
天然土层多呈层状
§3.3
确立各层的ki 根据渗流方向确定等效渗流系数 等效渗透系数
§3 土的渗透性
三.层状土的渗透系数 水平渗流
条件:
h ii i L
一. 渗透力
§3.5 渗透力与渗透变形
w h1 h2
U1
§3 土的渗透性
一. 渗透力
§3.5 渗透力与渗透变形
a b
j
贮水器 hw L
土粒
Δh h1
土样
h2
0
0
滤网
渗
流
§3 土的渗透性
一. 渗透力
§3.5 渗透力与渗透变形
一、渗流力的概念
以网格中的孔隙水 为研究对象
h1 h0 b
△h
w h1
A
Ww wVw wVs wV w ab
dh h1
dr h h2
地下水位≈测压管水面
不透水层
Q ln
r2 2 k (h 2 h1 ) 2 r1
k
Q ln(r2 / r1 ) 2 h 2 h1 2
土力学课件 第三章 土的渗透性
一、渗透力的计算（１）
一般情况下，渗透力的大小与计算点的位置有关。
根据对渗流流网中网格单元的孔隙水压力和土粒间作 用力的分析，可以得出渗流时单位体积内土粒受到的 渗透力为
h j J /V w w i l
这里 i 为水力梯度。
当饱和土休的存在有水头差时，水体就会通过土 体间的孔隙流动，渗流时：渗透水要受到土骨架的阻 力T 。
为了使渗流模型在渗流特性上与真实的渗流相一致， 三. 渗透模型（３） 它还应该符合以下要求：
1. 在同一过水断面，渗流模型的流量等于真实渗 流的流量； 2. 在任意截面上，渗流模型的压力与真实渗流的
压力相等；
3. 在相同体积内，渗流模型所受到的阻力与真实 渗流所受到的阻力相等。
有了渗流模型，就可以采用液体运动的有关概念和
三、渗透系数的确定
渗透系数 k 是综合反映土体渗透能力的一个指标，
其数值的正确确定对渗透计算有着非常重要的意义。
影响渗透系数大小的因素: • 土体颗粒的形状、大小 • 不均匀系数 • 水的粘滞性
要建立计算渗透系数 k 的精确理论公式比较困难， 通常可通过试验方法或经验估算法来确定 k 值。
1.实验室测定法（１）
两边同除F，又
T W
z1 z2 cos , h1 H1 z1 , h2 H 2 z2 L
H1 H 2 W i L
w h1 F
TLF
w h2 F
动水力为：
J T W i
动水力方向：与渗流方向相同
W LF
一渗透力的计算（４） 当饱和土体的存在有水头差时，水体就会通过土体间
水在土中流动的过程中将受到土阻力的作用，使水 头逐渐损失。同时，水的渗透将对土骨架产生拖曳力， 导致土体中的应力与变形发生变化。这种渗透水流作 用对土骨架产生的拖曳力称为渗透力。
土力学_第3章(土的渗透性及土的有效应力)
Байду номын сангаас室内试验
渗透系数测定 现场试验
常 水 头 变 水 头 抽水试验 注水试验
<10-3cm/s 的粉土和 粘土
①常水头渗透试验 截面积为A，流径L；
压力水头维持不变； 试验开始时，水自上而下流经土样； 待渗流稳走后，测得水量Q； 同时读得a、b两点水头差h。
则得：
a
k>10-3cm/s 的砂土
（2）渗透力
定义：单位土体内土颗粒所受的渗流作用力为渗透力 j。 体积力，单位：kn/m3
渗流流过土体，土颗粒对水流产生阻力，造成水头损失h。
j i w
1 公式推导请见清华—土力学，p56-57
2 a
H
h
（3）渗流作用下土的有效应力 （A）渗流向下流动时的a点有效应力
1
H
h
' h 'h w
由此求得渗透系数：
h0 aL k ln( ) A(t1 t 0 ) h1
变水头渗透试验装置
③现场抽水（注水）试验
Q r2 k ln 2 2 (h2 h1 ) r1
（摘自：清华—土力学，p44）
nv ' L k h
（？）
④利用渗透系数判断土层的透水性
（a）强透水层：K > 10-3cm/s （b）中等透水层： K ＝ 10-3 ～ 10-5 cm/s
二、达西定律及其适用范围
（1）土中水的渗流
水流
①渗流：水在土体孔隙中流动的现象。（清华—土力学） ②渗流：水在压力坡降作用下穿过土中连通孔隙发生流动的现象。
（冯国栋—土力学）
水头：单位重量的水所具有的能量。总水头＝势水头＋压力水头＋动水头
土力学第三章：土的渗透性和渗流
vA v q vA vs Av vs nA n
孔隙率n ,则Av nA
【例3.2】 某土样采用南 55型渗透仪在实验室进 行渗透系数试验，试验高度为2.0cm ，面积30cm 2 ， 3 40 cm 160 cm 试样水头 ，渗透水量为 24h 共 ，求该土样 的渗透系数？ h 40cm 0 i 【解】水力梯度 L 2cm 20
静水 A zB
0 基准面
测管水头：测管水面到基准面的垂 zA 直距离，等于位置水头和压力水头 0 之和，表示单位重量液体的总势能 在静止液体中各点的测管水头相等
2）水力坡降 水在任意一点的总水头：单位重量水体所具有的能量
v2 h z w 2g uw
uA w
渗流的速度很小，忽略 hA 不计，则总水头：
u w
zA
0
L
B
h2 0
zB
基准面
测管水头
A点总水头： B点总水头： 水头差：
uA h1 z A w
水力坡降：
i h L
u h2 zB B w
h h1 h 2
【例3.1】渗流试验装置如图 a a b b c c 3.2，试求： （1）土样中 、 和 3个截面的压力水头和总水头； （2）截面a a 至 ， 至 及 至 c c的水头损失； c c a a b b b b （3）水在土样中渗流的水力梯度。
1856 年达西(Darcy)在研究城 市供水问题时进行的渗流试验 达西定律：在层流状态的渗 流中，渗透速度 v 与水力坡降 i 的一次方成正比，并与土的 性质有关 渗透系数 k: 反映土的透水性 能的比例系数，其物理意义 为水力坡降 i ＝ 1 时的渗流速 度 ， 单 位 ： cm/s, m/s, m/day 渗透速度 v ：土体试样全断面 的平均渗流速度，也称假想
【土力学系列】第3章 土的渗透性和渗流
变水头渗透试验装置
3.现场抽水试验
粗颗粒土或成层的土，室内试验时不易取得原状土样； 小土样不能反映天然土层的结构性。
现场方法：野外注水试验和野外抽水试验等
图3-9 抽水试验
抽水量为Q 观测孔距离分别为rl和r2 ，水位高度h1和h2 r处水面高度h，过水断面A＝2rh
图3-9 抽水试验
h1=hh2=4010=30cm
图3-4 Darcy渗透定律
例题3-2 两种土,土样1位于土样2的上部， 长度都是20cm,总水头损失40cm，土样l渗 透系数为0.03cm/s，土样2水力坡降为0.5。 求土样2的渗透系数和土样1的水力坡降。
[解] 土样1的水力坡降 i1=h1/L1=1.5 水在土样1和土样2中渗流时的速度相同:
(h22 h12 )
分析表3-1渗透系数值: 表3-1 渗透系数参考值
可见：不同土类的渗透系数值差异很大 渗透系数的测定十分重要
4. 影响土的渗透性的因素
（1）土的粒度成分及矿物成分。 （2）结合水膜厚度。 （3）土的结构构造。 （4）水的粘滞度。
3.3 渗流破坏和控制
3.3.1 渗透力的计算 概念：水流作用在单位体积土体中土颗粒上的力。
3.4 流网及其应用
3.4.1 平面渗流基本微分方程 3.4.2 流网的性质及应用
（自学）
作业：
3-1 3-2 3-3 3-4
水体的平衡
结论：
渗透力是水流对单位体积土体颗粒的作用力； 是一种体积力 渗透力的大小与水力坡降成正比，方向与渗流方向一致。
临界水力坡降： 考察图3-11(b)中一土单元：
（a）向下渗流
（b）向上渗流
图3-11 渗流方向对土颗粒作用力的影响
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
H 1
sat H 2
σ’=σ- u=γwH
u
2
H1saH t2
u=γwH
2
σ’=σ-u =γH1+γsatH2ห้องสมุดไป่ตู้γwH2 =γH1+(γsat-γw)H2 =γH1+γ’H2
地下水位下降引起 σ’ 增大的部分
地下水位下降会引起 σ’增大，土会产生 压缩，这是城市抽水 引起地面沉降的主要 原因之一。
律v i
k: 反映土的透水性能的比例系数，称为渗透系数 物理意义：水力坡降i＝1时的渗流速度 单位：mm/s, cm/s, m/s, m/day
在层流状态的渗流中，渗透速度v与水力坡降i 的一次方成正比，并与土的性质有关。
v ki
注意： v：假想渗流速度，土体试样全断面的平均渗流速度
A
vs：实际平均渗流速度，孔隙断面的平均渗流速度
m
水压力对变形也没有直接的影响，土体不
会因为受到水压力的作用而变得密实。
σz=u=100MPa 15
二. 饱和土中孔隙水压力和有效应力的计算 1. 自重应力情况
(1) 静水条件 地下水 位 海洋 土 毛细饱和 区
(2) 稳定渗流条件
16
二. 饱和土中孔隙水压力和有效应力的计算
(1) 静水条件 地下水 位
二.渗透变形（渗透破坏）
7
一. 渗透力
渗透力的性质 物理意义：单位土体内土骨架所受到的渗透水流的拖曳力，它是体积力
大小： j = γwi 方向：与 i 方向一致（均质土与渗流方向一致） 作用对象：土骨架
8
二.渗透变形（渗透破坏） 土工建筑物及地基由于渗流作用而出现的变形或破坏
基本类型
流土 管涌
形成条件
第三章
土的渗透性
1
§3-1概述
碎散性 多孔介质
渗流
三相体系 能量差
孔隙流体流动
土颗粒 土中水
水、气等流体在土体等多孔介质 的孔隙中流动的现象
渗流
土体等多孔介质具有被水、气等 流体透过的性质
渗透性
非饱和土的渗透性 饱和土的渗透性
渗透特性 强度特性 变形特性
2
二. 渗透试验与达西定律
2.达西定律
渗透定
经验判断： i i icr
Fs [ i ] : 允许坡降
Fs: 安全系数1.5～2.0
13
§3.4 有效应力原理
孔隙流体
三相体系
土＝ 固体颗粒骨架 + 孔隙水 + 孔隙气体
受外荷载作用
总应力由土骨架和孔隙流体共同承受 对所受总应力，骨架和孔隙流体如何分担？ 它们如何传递和相互转化？ 它们对土的变形和强度有何影响？
总应力
Terzaghi （1923） 有效应力原理 固结理论
土力学成为独立的学科
14
一. 有效应力原理的基本概念
'u （1）
（2） 土的变形与强度都只取决于有效应力
①变形的原因
颗粒间克服摩擦相对滑移、滚动—与 σ’ 有关；
接触点处应力过大而破碎—与 σ’ 有关。
②强度的成因 凝聚力和摩擦—与σ’ 有
Re＜5时层流 Re ＞200时紊流 200＞ Re ＞5时为过渡区
4
二. 渗透试验与达西定律 两种特例：
（1）粗粒土： ①砾石类土中的渗流常不符合达西定律 ②砂土中渗透速度 vcr=0.3-0.5cm/s
（2）粘性土： 致密的粘土 i > i0, v = k(i - i0 )
v vcr o
v
o i0
Hw h
渗流压密
砂层，承压水
A
Hwh
s aH t
u
uw(Hh) saH tw(Hh)
Hwh 渗透压力: wh
19
关③孔隙水压力的作用
对土颗粒间摩擦、土粒的破碎没有贡献，
试想： 海底与土粒间的接触压力 哪一种情况下大？
并且水不能承受剪应力，因而孔隙水压力
对土的强度没有直接的影响；
1m
它在各个方向相等，只能使土颗粒本身
受到等向压力，由于颗粒本身压缩模量很
104
大，故土粒本身压缩变形极小。因而孔隙 σz=u=0.01MPa
防治措施
9
二.渗透变形（渗透破坏） 1. 基本类型
流土 在向上的渗透作用下，表层局部土体颗粒同时发生悬浮移动的现象
渗流
坝体 粘性土k1<<k2
砂性土k2
原因： W J 0 i icr
icr
Gs 1 1 e
和土的密实程度有关
10
二.渗透变形（渗透破坏） 1. 基本类型
管涌
在渗流作用下，一定级配的无粘性土中的细小颗粒，通过较大颗 粒所形成的孔隙发生移动，最终在土中形成与地表贯通的管道。
管涌
原因：
内因—— 有足够多的粗颗粒形 成大于细粒径的孔隙通道
管涌破坏
外因——渗透力足够大
11
二.渗透变形 1. 基本类型
流土与管涌的比较
流土
管涌
现象 土体局部范围的颗粒同时发 生移动
位置 只发生在水流渗出的表层
土类 只要渗透力足够大，可 发生在任何土中
历时 破坏过程短
土体内细颗粒通过粗粒形成的 孔隙通道移动
17
§3 土体中的应力计算 §3.5 有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
(2) 稳定渗流条件
Δh
H
粘土 层
γsat
砂层，承压水 向上渗流
Δh H γsat
砂层，排水 向下渗流
18
二. 饱和土中孔隙水压力和有效应力的计算
土水整体分析
向上渗流: Δh
向下渗流:
H
粘土层 γsat
可发生于土体内部和渗流 溢出处
一般发生在特定级配的无 粘性土或分散性粘土
破坏过程相对较长
后果 导致下游坡面产生局部滑动等 导致结构发生塌陷或溃口
12
二.渗透变形 2.形成条件
流土
无压重时： i < icr : i > icr : i = icr :
土体处于稳定状态 土体发生流土破坏 土体处于临界状态
n Av A
A > Av
v
vs
v n
Av
Q＝vA ＝ vsAv
3
二. 渗透试验与达西定律 适用条件：
层流（线性流）
岩土工程中的绝大多数渗流问 题，包括砂土或一般粘土，均 属层流范围
在粗粒土孔隙中，水流形态可 能会随流速增大呈紊流状态， 渗流不再服从达西定律。
可用雷诺数Re进行判断：
Re
v d10
v kim (m 1)
i
i
5
三. 渗透系数的测定及影响因素 1. 测定方法
室内试验测定方 法 野外试验测定方
常水头试验法 变水头试验法 井孔抽水试验 井孔注水试验
法
6
§3.3 渗透力与渗透破坏类型
渗透力
渗透变形
一. 渗透力 1、试验观察 2、物理本质 土水整体分析 3、计算方法 土水隔离分析
sat H 2
σ’=σ- u=γwH
u
2
H1saH t2
u=γwH
2
σ’=σ-u =γH1+γsatH2ห้องสมุดไป่ตู้γwH2 =γH1+(γsat-γw)H2 =γH1+γ’H2
地下水位下降引起 σ’ 增大的部分
地下水位下降会引起 σ’增大，土会产生 压缩，这是城市抽水 引起地面沉降的主要 原因之一。
律v i
k: 反映土的透水性能的比例系数，称为渗透系数 物理意义：水力坡降i＝1时的渗流速度 单位：mm/s, cm/s, m/s, m/day
在层流状态的渗流中，渗透速度v与水力坡降i 的一次方成正比，并与土的性质有关。
v ki
注意： v：假想渗流速度，土体试样全断面的平均渗流速度
A
vs：实际平均渗流速度，孔隙断面的平均渗流速度
m
水压力对变形也没有直接的影响，土体不
会因为受到水压力的作用而变得密实。
σz=u=100MPa 15
二. 饱和土中孔隙水压力和有效应力的计算 1. 自重应力情况
(1) 静水条件 地下水 位 海洋 土 毛细饱和 区
(2) 稳定渗流条件
16
二. 饱和土中孔隙水压力和有效应力的计算
(1) 静水条件 地下水 位
二.渗透变形（渗透破坏）
7
一. 渗透力
渗透力的性质 物理意义：单位土体内土骨架所受到的渗透水流的拖曳力，它是体积力
大小： j = γwi 方向：与 i 方向一致（均质土与渗流方向一致） 作用对象：土骨架
8
二.渗透变形（渗透破坏） 土工建筑物及地基由于渗流作用而出现的变形或破坏
基本类型
流土 管涌
形成条件
第三章
土的渗透性
1
§3-1概述
碎散性 多孔介质
渗流
三相体系 能量差
孔隙流体流动
土颗粒 土中水
水、气等流体在土体等多孔介质 的孔隙中流动的现象
渗流
土体等多孔介质具有被水、气等 流体透过的性质
渗透性
非饱和土的渗透性 饱和土的渗透性
渗透特性 强度特性 变形特性
2
二. 渗透试验与达西定律
2.达西定律
渗透定
经验判断： i i icr
Fs [ i ] : 允许坡降
Fs: 安全系数1.5～2.0
13
§3.4 有效应力原理
孔隙流体
三相体系
土＝ 固体颗粒骨架 + 孔隙水 + 孔隙气体
受外荷载作用
总应力由土骨架和孔隙流体共同承受 对所受总应力，骨架和孔隙流体如何分担？ 它们如何传递和相互转化？ 它们对土的变形和强度有何影响？
总应力
Terzaghi （1923） 有效应力原理 固结理论
土力学成为独立的学科
14
一. 有效应力原理的基本概念
'u （1）
（2） 土的变形与强度都只取决于有效应力
①变形的原因
颗粒间克服摩擦相对滑移、滚动—与 σ’ 有关；
接触点处应力过大而破碎—与 σ’ 有关。
②强度的成因 凝聚力和摩擦—与σ’ 有
Re＜5时层流 Re ＞200时紊流 200＞ Re ＞5时为过渡区
4
二. 渗透试验与达西定律 两种特例：
（1）粗粒土： ①砾石类土中的渗流常不符合达西定律 ②砂土中渗透速度 vcr=0.3-0.5cm/s
（2）粘性土： 致密的粘土 i > i0, v = k(i - i0 )
v vcr o
v
o i0
Hw h
渗流压密
砂层，承压水
A
Hwh
s aH t
u
uw(Hh) saH tw(Hh)
Hwh 渗透压力: wh
19
关③孔隙水压力的作用
对土颗粒间摩擦、土粒的破碎没有贡献，
试想： 海底与土粒间的接触压力 哪一种情况下大？
并且水不能承受剪应力，因而孔隙水压力
对土的强度没有直接的影响；
1m
它在各个方向相等，只能使土颗粒本身
受到等向压力，由于颗粒本身压缩模量很
104
大，故土粒本身压缩变形极小。因而孔隙 σz=u=0.01MPa
防治措施
9
二.渗透变形（渗透破坏） 1. 基本类型
流土 在向上的渗透作用下，表层局部土体颗粒同时发生悬浮移动的现象
渗流
坝体 粘性土k1<<k2
砂性土k2
原因： W J 0 i icr
icr
Gs 1 1 e
和土的密实程度有关
10
二.渗透变形（渗透破坏） 1. 基本类型
管涌
在渗流作用下，一定级配的无粘性土中的细小颗粒，通过较大颗 粒所形成的孔隙发生移动，最终在土中形成与地表贯通的管道。
管涌
原因：
内因—— 有足够多的粗颗粒形 成大于细粒径的孔隙通道
管涌破坏
外因——渗透力足够大
11
二.渗透变形 1. 基本类型
流土与管涌的比较
流土
管涌
现象 土体局部范围的颗粒同时发 生移动
位置 只发生在水流渗出的表层
土类 只要渗透力足够大，可 发生在任何土中
历时 破坏过程短
土体内细颗粒通过粗粒形成的 孔隙通道移动
17
§3 土体中的应力计算 §3.5 有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
(2) 稳定渗流条件
Δh
H
粘土 层
γsat
砂层，承压水 向上渗流
Δh H γsat
砂层，排水 向下渗流
18
二. 饱和土中孔隙水压力和有效应力的计算
土水整体分析
向上渗流: Δh
向下渗流:
H
粘土层 γsat
可发生于土体内部和渗流 溢出处
一般发生在特定级配的无 粘性土或分散性粘土
破坏过程相对较长
后果 导致下游坡面产生局部滑动等 导致结构发生塌陷或溃口
12
二.渗透变形 2.形成条件
流土
无压重时： i < icr : i > icr : i = icr :
土体处于稳定状态 土体发生流土破坏 土体处于临界状态
n Av A
A > Av
v
vs
v n
Av
Q＝vA ＝ vsAv
3
二. 渗透试验与达西定律 适用条件：
层流（线性流）
岩土工程中的绝大多数渗流问 题，包括砂土或一般粘土，均 属层流范围
在粗粒土孔隙中，水流形态可 能会随流速增大呈紊流状态， 渗流不再服从达西定律。
可用雷诺数Re进行判断：
Re
v d10
v kim (m 1)
i
i
5
三. 渗透系数的测定及影响因素 1. 测定方法
室内试验测定方 法 野外试验测定方
常水头试验法 变水头试验法 井孔抽水试验 井孔注水试验
法
6
§3.3 渗透力与渗透破坏类型
渗透力
渗透变形
一. 渗透力 1、试验观察 2、物理本质 土水整体分析 3、计算方法 土水隔离分析