二次根式的加减乘除混合运算练习题(附答案)
二次根式混合运算125题(有答案)ok(可编辑修改word版)

二次根式混合运算 125 题(有答案)1、2、3、4、5、6、7、.8、9、.10、;11、.12、;13、;14、.15、;16、.17、.18、19、20、;21、22、.23、24、25、26、;.27、28、;;29、;30、31、;(5);32、33、;34、;35、36、3 ﹣9+337、÷(3×)38、39、40、;.41、42、43、44、45、;46、.47、(﹣)2﹣;48、;49、;50、.51、;52、.53、3 ﹣﹣+(﹣2)(+2)54、55、56、57、58、59、2÷﹣(2﹣)260、﹣2 +(﹣1)261、(+2)﹣.62、63、64、65、.66、67、.68、69、70、3﹣(﹣)71、72、﹣273、74、75、﹣ 76、77、÷78、×+÷79、80、81、.82、83、 ﹣84、85、(+1)2﹣286、(+1)(1﹣)﹣(﹣1)2+(+1)287、88、89、90、;91、.92、;﹣ ﹣93、;;94、95、;96、 ;97、98、||+ ;99、;;100、﹣101、(+)2008()2009.102、;103、;104、.105、(3 +)÷ ;106、107、;108、;﹣﹣ 109、.110、﹣1111、( )(+)+2114、+|﹣3|﹣2﹣1(4)(﹣2)×﹣6115、 (2);116、;117、118、.119、.120、121、122、+6a ;×.﹣123、124、(2)(7+4 )(7﹣4 )+(2+ )125、参考答案1、原式=2 ﹣3 =﹣ ;2、原式= × = =30;3、原式=2﹣12=﹣10.4、原式=5、原式==﹣6a . 6、原式= ;7、原式=()2﹣(﹣1)2=2﹣(3﹣2+1)=8、原式=. 9、.原式=(3 ﹣2 +3 )×=( +3 )×=1+10、原式=﹣+=;11、原式=(4 +)÷3 =12、原式=2 +3 ﹣=;13、原式= =; 14、原式=(7+)(7+)=14×2=15、原式= =3+6﹣10=﹣1;16、原式=2﹣=﹣2.17、原式= ﹣2 +=3﹣2+=18、原式=(3﹣2)(3+2)=18﹣12=6;19、原式= (2 ﹣ +)= ( +)= +120、原式=﹣3•5÷=﹣15÷=﹣15;21、原式=3 +﹣2 +﹣3 =;22、原式=3a+﹣2b23、原式=3﹣2+1﹣(2﹣3)=5﹣2.24、原式==25、原式=2+1﹣( ﹣ )=3﹣1=2.26、原式=17﹣(19﹣)=﹣2+ ;=2.=27、原式=2 ﹣3 ﹣2 =﹣3.28、原式=4 +12 = ;29、原式=+2 ﹣10 = ;30、原式=4 ﹣+=;31、原式=6﹣5=1;32、原式=12+18﹣12= ;33、原式=(2 + )×﹣2=3﹣2=1;34、原式=+×6﹣m =2m +3m ﹣m =0;35、原式= ++1= ﹣1++1=36、原式=12 =(12﹣3﹣+6)= ;37、原式=6÷(×)=6÷6=38、原式=+3﹣2 =3 +3﹣2 =3+ .39、原式= ++ ×1=6+1+=7+ .40、原式=×3+6×﹣2x•=2 +3 ﹣2 =3 ;41、原式=2 ﹣+3﹣2=2 ﹣2 +142、原式=(6 ﹣+ ﹣2 )÷2﹣3=3﹣+﹣﹣3=﹣+﹣;43、原式== =444、=(4÷2)=45、原式=2+3﹣7=﹣2;46、原式= = =14.47、原式=10﹣7+=3+;48、原式= ×(2 ﹣+)= + ×= +1;49、原式=﹣1;50、原式=2+3+2﹣(2﹣3)=5+2+1=6+251、原式=4 +﹣4 = ;52、原式=(4 ﹣2 +6 )÷=2 +253、原式=6 ﹣3 ﹣+5﹣4=(6﹣3﹣)+1= +1=.﹣﹣54、原式= =;55、原式=56、原式=[ ﹣( ﹣ )][+( ﹣)]=5﹣(﹣)2=5﹣(5﹣2)=2.57、原式=4×2 ﹣16 +12﹣16﹣8 =﹣4﹣16; 58、原式= + ﹣+3 =59、原式=2﹣(4﹣4 +2)=2﹣6+4 =6 ﹣6.60、原式=×2 ﹣2×3+5﹣2 +1=﹣6﹣2+6=6﹣7.61、原式=a+2 =2. 62、原式= ;63、原式=﹣ +=﹣+=0. 64、=2+﹣2=.65、==66、原式=9﹣14+4=﹣;67、原式= ﹣4 3=﹣12 =﹣11 .68、原式=2 × =12;69、原式= ×3 ×=﹣;70、原式=12﹣2 +6=16;71、原式=(4﹣2 +6)×=2+272、原式=27÷(3×)×﹣8=3×﹣8 =﹣8;73、原式=()2﹣( )2=3﹣(2+2 +5)=﹣4﹣274、原式=3+8=11;75、原式=2﹣12=﹣10;76、原式=5+﹣6=0;77、原式= ÷=÷ =1.78、原式== =4+=4+ .79、原式= = =;80、原式==9+6=15;﹣﹣81、原式=(+)2﹣ =3+2+2=5+82、原式= = ;83、原式=84、原式=5﹣6=﹣1; 85、原式=4+ =86、(1+)(1﹣)﹣(﹣1)2+(+1)2=1﹣()2﹣(2﹣2+1)+2+2+1=1﹣2﹣2+2﹣1+2+2 +1=4 ﹣1.87、原式=+4× +1=++1=1+ .88、原式=(40 ) =30=15; 89、原式=2 +2=2+ . 90、原式= = =;91、原式== =12. 92、原式=2+2 +4 +2 = ; 93、原式=9﹣14 +24=;94、原式=(7+4)(7﹣4)+4﹣3=49﹣48+1=2;95、原式=﹣4× +9﹣12﹣()=﹣8 +9﹣12﹣ +1=﹣11;96、原式=﹣+ =2x + =;97、原式=2a (b98、原式=× + )=2ab+3﹣5=2﹣4;+ab=99、原式=12﹣4+1=13﹣4 ;100、原式=2+=;101、原式= ()=102、原式=3×2﹣2×3 +5×4=6﹣6 +20=20;103、原式=7﹣3+2=6;104、原式=•(﹣)× =﹣=﹣ 105、原式=3 ÷ +÷ =3+=;106、原式=3﹣1﹣=2﹣107、原式= +1﹣ ×2 =2+1﹣2=1;﹣ ﹣ ﹣﹣﹣=3﹣2=1.= +1 =﹣=﹣ =3﹣2=1.108、原式=3﹣2 +1﹣1=3﹣2 ;109、原式=+4 ﹣3=110、﹣1= ﹣1= ﹣1=0;111、()()+2=﹣+2=5﹣7+2=0;112、+|﹣3|﹣2﹣1=1+3﹣ =3 ;113、( ﹣2)×﹣6=﹣4114、原式=4﹣5=﹣1; 115、原式=×=1; 116、原式=5﹣2﹣5+2= ;117、原式=4﹣2+﹣1=3﹣=﹣9=﹣118、原式=119、原式=120、原式= 121、原式=3+6a =2a +3a=5a;122、原式=123、原式= =12;124、原式=49﹣48+2+ =3+.125、原式=== .﹣二次根式混合运算---- 21。
初中数学二次根式的混合运算专项训练题6(附答案详解)

初中数学二次根式的混合运算专项训练题6(附答案详解)1.计算:②÷2.计算(1;(2(3)2+;(4)⨯324.计算:4(1--|3|-5.计算:6.计算:(1()(22-.7.解答下列各题(1-(2)解方程组24 4523 m nm n-=-⎧⎨-=-⎩8.计算:(1)(29.已知x =,y =,求22x xy y -+的值.1011.计算:(12)﹣2(﹣2)0+|212.计算或解方程:(1)(2)23(2)12x +=13.计算(1(24-- 14.计算:(1)⎛- ⎝;(215.计算下列各题:(1)×4÷;(2)﹣2+2×. 16.计算(1))2(2)17. 计算:-2-1+-(-1)218. )211-19.(1(22|.20. 计算:-2))21.计算:(1)2+ (2)(6-. 22.计算:(1)÷(2)2(11)+-23.计算与化简:(1(2(2)(22+24.(1)计算:﹣(2)计算: 020171|2(1)3++--25.计算:14++-(2)(⎛÷⨯ ⎝26.计算(1(2)((3)227.计算:(1)16521082+⨯- (2)127324122÷+-⨯ 28.计算(1)23318(6)--÷-.(2)2(32)(13)(13)-+-+.29.计算(1); (2)(3+)(﹣2); (3)(+﹣)÷ 30.计算题:(1)1(436312)33÷(2)211)(23)(23)3++参考答案1.①0;②2. 【解析】【分析】①直接化简二次根式进而计算得出答案;②直接利用二次根式的乘除运算法则化简得出答案.【详解】﹣=0;②÷=3÷. 【点睛】此题主要考查二次根式的混合运算,熟练掌握,即可解题.2.(1)2;(2)3;(3)34+(4)18-. 【解析】【分析】(1)根据二次根式的乘、除法公式和合并同类二次根式法则计算即可;(2)根据二次根式的乘、除法公式和合并同类二次根式法则计算即可;(3)根据平方差公式、完全平方公式、二次根式的乘法公式和合并同类二次根式法则计算即可;(4)根据乘法分配律、二次根式的乘法公式和合并同类二次根式法则计算即可;【详解】解:(1)原式=2=+2=(2)原式=3=-3=(3)原式()23827=-++135=-++34=+(4)原式(=-⨯+63=-⨯-18=--【点睛】此题考查的是二次根式的混合运算,掌握平方差公式、完全平方公式、二次根式的乘、除法公式和合并同类二次根式法则是解决此题的关键.3.+1.【解析】【分析】先利用平方根的性质,然后化简后合并即可.【详解】解:原式+1+1.【点睛】此题考查二次根式的混合运算,解题关键在于掌握把二次根式化为最简二次根式.4.(1;(2)6-【解析】【分析】(1)先根据二次根式的乘法法则和零指数幂的意义计算,然后化简后合并即可; (2)用分配律计算,然后化简,去绝对值符号,合并同类二次根式即可.【详解】解:(1)原式414=⨯==(2)原式(33=-3=-6-.【点睛】 本题考查二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.5.5.【解析】【分析】利用乘法分配律可简便计算.【详解】⨯+⨯=1+4=5【点睛】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.6.()1 4+;()2 1+【解析】【分析】(1)根据二次根式乘除法和减法可以解答本题;(2)先利用平方差公式和完全平方公式计算,然后合并即可.【详解】()1原式=4=4=+()2原式()181232=---65=-+1=+7.(1)6;(2)125m n ⎧=⎪⎨⎪=⎩【解析】【分析】(1)原式利用立方根和二次根式的运算法则计算即可求出值;(2)方程组利用加减消元法求出解即可.【详解】解:(1)原式=﹣﹣+8=6;(2)244523m n m n -=-⎧⎨-=-⎩①②, ①×5﹣②得:6m =3,解得:m =12, 把m =12代入①得:n =5,则方程组的解为125mn⎧=⎪⎨⎪=⎩.【点睛】此题考查了解二元一次方程组以及二次根式的混合运算,熟练掌握运算法则是解本题的关键.8.(1)(2)4.【解析】【分析】(1)先化简二次根式,再计算二次根式的乘除法即可;(2)先计算二次根式的乘除法,再化简二次根式,然后计算二次根式的加减法即可.【详解】(1)原式2=8 =⨯=(2)原式==4=+【点睛】本题考查了二次根式的化简、二次根式的加减乘除法,熟记运算法则是解题关键.9.11.【解析】【分析】根据题意,先求出x y-和xy的值,然后利用完全平方变形求值,即可得到答案. 【详解】解:∵x=+y=-,∴x﹣y=xy==2﹣3=﹣1,则原式=x2﹣2xy+y2+xy=(x﹣y)2+xy=2﹣1=12﹣1=11.【点睛】本题考查了求代数式的值,二次根式的混合运算,完全平方公式变形求值,解题的关键是熟练掌握运算法则进行计算.10【解析】【分析】根据二次根式的除法法则计算即可.【详解】===11【点睛】本题考查的知识点是二次根式的混合运算,掌握二次根式混合运算的运算顺序以及运算法则是解此题的关键.11.【解析】【分析】直接利用零指数幂的性质以及负指数幂的性质、绝对值的性质、二次根式以及立方根的运算法则分别化简得出答案.【详解】解:原式=4﹣﹣2=.【点睛】本题考查实数的运算,难点也在于对原式中零指数幂、负指数幂、绝对值、二次根式以及立方根的运算化简,关键要掌握这些知识点.12.(1)﹣1.5;(2)x=0或﹣4.【解析】【分析】(1)首先计算开方,然后从左向右依次计算,求出算式的值是多少即可.(2)根据:3(x+2)2=12,可得:(x+2)2=4,所以x+2=±2,据此求出x的值是多少即可.【详解】解:(1)=﹣6+1.5+3=﹣1.5(2)∵3(x+2)2=12,∴(x+2)2=4,∴x+2=±2,解得:x=0或x=﹣4.【点睛】此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.13.(1;(2)4.【解析】【分析】(1)先把二次根式化为最简二次根式,然后合并即可;(2)先进行二次根式的乘除运算,然后去绝对值后合并即可.【详解】(1)原式=-=(2)原式=4﹣+4﹣4.【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍..14.(1-(2)10【解析】【分析】(1)先将各二次根式化为最简二次根式,然后合并同类二次根式;(2)根据二次根式的乘除法则计算即可.【详解】解:(1)原式===.(2)原式===10【点睛】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.15.(1);(2)18﹣10【解析】【分析】(1)先把各二次根式化为最简二次根式,然后进行二次根式的乘除法运算;(2)先进行去括号和二次根式的乘法运算,然后化简后合并即可.【详解】解:(1)×4÷==3÷=10;(2)﹣2+2×=6+12﹣=18﹣.【点睛】 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.16.(1)(2) 【解析】【分析】(1)根据二次根式的运算法则计算即可.(2)根据二次根式的运算法则计算即可.【详解】(1)原式﹣(5﹣3)﹣2(2)原式﹣2﹣4.【点睛】本题考查二次根式的计算,熟练掌握二次根式的运算法则是解题关键.17.-4.【解析】【分析】根据二次根式的运算法则以及负整数指数幂的意义即可求出答案.【详解】解:原式()(.【点睛】本题考查二次根式的混合运算,解题的关键是熟练运用二次根式的运算法则,本题属于基础题型.18..3【解析】【分析】先利用平方差公式计算,然后把二次根式化为最简二次根式后合并即可.【详解】解:原式-(3-1)-23=.3【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.19.(1)4.2;(2【解析】【分析】(1)直接利用二次根式以及立方根的性质分别化简得出答案;(2)直接利用二次根式以及立方根的性质分别化简得出答案.【详解】解:(1)原式0.231 4.2=++=;(2)原式(152224=-+⨯- 15222=-+-=【点睛】本题考查了二次根式、立方根、以及绝对值的化简,严格按照其性质法则进行化简即可. 20.8【解析】【分析】化简得到原式=2)),然后利用平方差公式计算.【详解】解:原式=())=2))=2(5-1)=8.【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.21.(1)11;(2)【解析】【分析】(1)分别化简各项,然后进行加减计算即可;(2)先算乘法,然后进行减法运算即可.【详解】(1)原式23(1)15=---+3115=--+11=;(2)原式63=⨯==.【点睛】此题主要考查二次根式的混合运算,熟练掌握,即可解题.22.(1)10;(2)﹣9 【解析】【分析】(1)把根号外和根号内分别相乘除,然后化简即可;(2)先算乘法和完全平方,再去括号,计算加减即可.【详解】解:(1)原式1(24=⨯÷=110=⨯,10=;(2)原式(81=+-,=+9=-.9【点睛】本题主要考查了二次根式的混合运算,关键是掌握计算顺序和运算法则.23.(13;(2)-3【解析】【分析】(1)先把根式化简,再把同类二次根式合并即可.(2)根据平方差公式和分母有理化,分别计算,再把结果合并即可.【详解】=-++=;解:(1)原式(3)633+=-=--=-(2)(22464613【点睛】本题主要考查了实数的运算法则,解题的关键是熟知实数的性质.24.(1)(2)-2【解析】【分析】(1)第一项根据二次根式的除法计算,第二、三项根据二次根式的性质化简,然后合并同类二次根式即可;(2)先逐项化简,再算加减即可.【详解】(1)﹣==(2) 020171|2(1)3++--=121-=-2.【点睛】本题考查了二次根式的混合运算,熟练掌握二次根式的运算法则是解答本题的关键.25.(1(2【解析】【分析】(1)先把二次根式化为最简二次根式,然后合并即可;(2)先把二次根式化为最简二次根式,再把除法运算化为乘法运算,然后合并后进行二次根式的乘除运算.【详解】解:(1)原式==(2)原式==15-=【点睛】 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.26.(1);(2)1.【解析】【分析】(1)根据二次根式的乘除法则运算;(2)利用完全平方公式和平方差公式计算.【详解】(1=4=;(2)原式=20﹣7﹣(5﹣)=13﹣=1.【点睛】本题考查了无理数的混合运算,掌握无理数混合运算法则、完全平方公式和平方差公式是解题的关键.27.(1)(2)3【解析】【分析】(1)先化简二次根式和进行二次根式的乘法,然后按照合并同类二次根式的法则进行加减运算即可;(2)先化简二次根式和进行二次根式的乘除法,然后按照合并同类二次根式的法则进行加减运算即可.【详解】解:(1)原式-(2)原式=3+=3+【点睛】本题考查了二次根式的混合运算,掌握运算法则和运算顺序是解题关键.28.(1)43-;(2)326-. 【解析】【分析】 (1)直接利用算术平方根以及立方根性质分别化简再计算即可得出答案.(2)直接利用二次根式的混合运算法则,先用完全平方公式和平方差公式计算,再化简得出答案.【详解】解:(1)23318(6)--÷-126=--÷113=-- 43=-; (2)2(32)(13)(13)-+-+322613=+-+-326=-.【点睛】此题主要考查了实数运算,正确化简各数是解题关键.29.(1)2(2) (3) 【解析】【分析】(1)根据二次根式的乘除法法则进行计算即可;(2)利用多项式乘多项式法则进行展开,然后合并同类二次根式即可;(3)先把各二次根式化简为最简二次根式,然后把括号内合并后进行二次根式的除法运算即可.【详解】(1)原式==2; (2)原式=3﹣6+5﹣2=﹣1;(3)原式=()÷=()÷=﹣3.【点睛】本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.30.(1)4;(2723 -【解析】【分析】(1)原式利用二次根式除法法则计算即可求出值;(2)原式利用完全平方公式,以及平方差公式计算即可求出值.【详解】解:(1)原式=33133123=2﹣1+3 =4;(2)原式=1233-﹣3=73 33 -=733-.【点睛】本题考查了二次根式的混合运算,解题的关键是掌握运算法则和运算律,注意乘法公式的运用.。
二次根式混合计算练习(附答案)

【解析】
试题分析:根据运算顺序化各根式为最简二次根式后合并即可.
试题解析:原式 .
考点:二次根式运算.
30.2.
【解析】
试题分析:针对有理数的乘方,二次根式化简,零指数幂,负整数指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.
试题解析:原式 .
考点:1.实数的运算;2.有理数的乘方;3.二次根式化简;4.零指数幂;5.负整数指数幂.
试题解析:解:原式=18-1+3-4 +4=24-4 .
考点:二次根式的计算.
26. .
【解析】
试题分析:根据二次根式的混合运算顺序和运算法则计算即可.
试题解析:
考点:二次根式的混合运算.
27.(1) .(2)4.
【解析】
试题分析:
掌握二次根式的运算性质是解题的关键.一般地,二次根式的乘法: ;二次根式的除法: ;二次根式的加减时,先将二次根式化为最简二次根式,再将被开方数相同的二次根式进行合并.计算时,先算乘除法,能化简的根式要先进行化简再计算,最后计算加减法,即合并同类项即可.
二次根式混合计算
1.计算题
(1) (2) .
2.计算: .
3.计算:(2- )(2+ )+ -
4.计算( - )0- +
6、计算: 0+ 2
7.计算( )( + + +…+ )
8.计算: ×( + )- -|2 -3|+ .
9.计算: .
10.计算:(1) + - ; (2)(5-2 )×( - );
试题解析:
解:(1)原式
(2)原式
考点:1、二次根式的化简;2、实数的运算.
28. .
【解析】
二次根式混合运算125题(含答案)
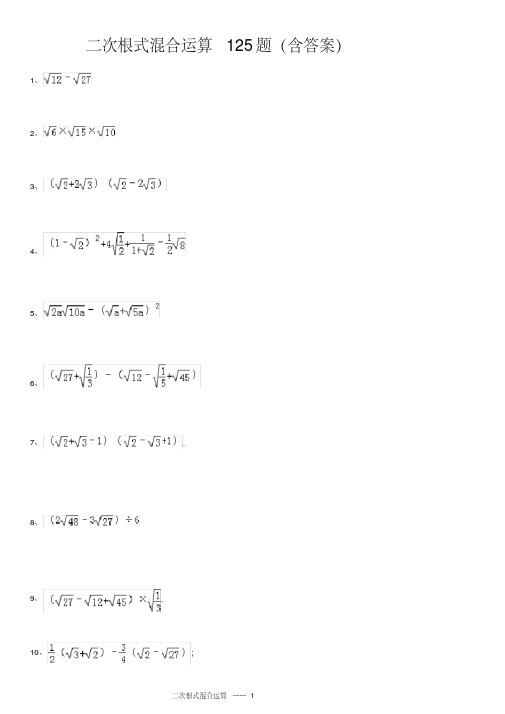
65、
.
66、 67、
.
二次根式混合运算 ---- 8
68、 69、
70、 3 ﹣( ﹣
)
71、
72、
﹣2
73、 74、 75、 76、
二次根式混合运算 ---- 9
77、
÷
78、 × + ÷ ﹣
79、
80、
81、
﹣.
82、 83、 84、
二次根式混合运算 ---- 10
85、( +1) 2﹣ 2 86、( +1)( 1﹣ )﹣( ﹣ 1) 2+( +1) 2 87、 88、
58、原式 = + ﹣
+3 =
59、原式 =2
﹣( 4﹣ 4 +2 )=2 ﹣6+4 =6 ﹣ 6.
60、原式 = ×2 ﹣ 2×3 +5﹣ 2 +1= ﹣ 6 ﹣ 2 +6=6 ﹣ 7 .
61、原式 =a+2 62、原式 =
63、原式 =﹣
=2 . ;
+ =﹣ + =0 .
64、
=2 + ﹣2 = .
89、
90、
;
91、 92、
. ;
93、
;
二次根式混合运算 ---- 11
94、 95、 96、
; ; ;
97、
98、 | ﹣ |+ ﹣
;
99、
;
; 100、
101、( + ) 2008( ﹣ ) 2009.
二次根式混合运算 ---- 12
102、
;
103、
;
104、
.
二次根式混合运算题含答案

二次根式混合运算题含答案二次根式混合运算125题(含答案)1、2、3、4、5、6、7、.8、9、.11、.12、;13、;14、.15、;16、.17、.19、20、;21、22、.23、24、25、26、;.27、28、;;29、;30、31、;(5);32、33、;34、;35、36、3﹣9+337、÷(3×)38、39、40、;.41、43、44、45、;46、.47、(﹣)2﹣;48、;49、;51、;52、.53、3﹣﹣+(﹣2)(+2)54、55、56、57、59、2÷﹣(2﹣)260、﹣2+(﹣1)261、(+2)﹣.62、63、64、65、.66、68、69、70、3﹣(﹣)71、72、﹣273、74、75、76、77、÷78、×+÷﹣79、80、81、﹣.82、83、84、85、(+1)2﹣286、(+1)(1﹣)﹣(﹣1)2+(+1)287、88、89、90、;91、.92、;93、;;94、95、;96、;97、98、|﹣|+﹣;99、;;100、101、(+)2008(﹣)2009.102、;103、;104、.105、(3+)÷;106、107、;108、;109、.111、(﹣)(+)+2+|﹣3|﹣2﹣1(4)(﹣2)×﹣6 114、115、(2﹣);116、;117、118、.119、.120、121、122、+6a;﹣×.123、124、(2)(7+4)(7﹣4)+(2+)125、参考答案1、原式=2﹣3=﹣;2、原式=×==30;3、原式=2﹣12=﹣10.4、原式==2.5、原式===﹣6a.6、原式=;7、原式=()2﹣(﹣1)2=2﹣(3﹣2+1)=8、原式=.9、.原式=(3﹣2+3)×=(+3)×=1+10、原式=﹣+=;11、原式=(4+)÷3=12、原式=2+3﹣=;13、原式==;14、原式=(7+)(7+)=14×2=15、原式==3+6﹣10=﹣1;16、原式=2﹣=﹣2.17、原式=﹣2+=3﹣2+=18、原式=(3﹣2)(3+2)=18﹣12=6;19、原式=(2﹣+)=(+)=+120、原式=﹣35÷=﹣15÷=﹣15;21、原式=3+﹣2+﹣3=;22、原式=3a+﹣2b23、原式=3﹣2+1﹣(2﹣3)=5﹣2.24、原式==25、原式=2+1﹣(﹣)=3﹣1=2.26、原式=17﹣(19﹣)=﹣2+;29、原式=+2﹣10=;30、原式=4﹣+=;31、原式=6﹣5=1;32、原式=12+18﹣12=;33、原式=(2+)×﹣2=3﹣2=1;34、原式=+×6﹣m=2m+3m﹣m=0;35、原式=++1=﹣1++1=36、原式=12=(12﹣3﹣+6)=;37、原式=6÷(×)=6÷6=38、原式=+3﹣2=3+3﹣2=3+.39、原式=++×1=6+1+=7+.40、原式=×3+6×﹣2x=2+3﹣2=3;41、原式=2﹣+3﹣2=2﹣2+142、原式=(6﹣+﹣2)÷2﹣3=3﹣+﹣﹣3=﹣+﹣;43、原式===444、=(4÷2)=45、原式=2+3﹣7=﹣2;46、原式===14.47、原式=10﹣7+=3+;48、原式=×(2﹣+)=+×=+1;49、原式=﹣1;50、原式=2+3+2﹣(2﹣3)=5+2+1=6+251、原式=4+﹣4=;52、原式=(4﹣2+6)÷=2+253、原式=6﹣3﹣+5﹣4=(6﹣3﹣)+1=+155、原式==.56、原式=[﹣(﹣)][+(﹣)]=5﹣(﹣)2=5﹣(5﹣2)=2.57、原式=4×2﹣16+12﹣16﹣8=﹣4﹣16;58、原式=+﹣+3=59、原式=2﹣(4﹣4+2)=2﹣6+4=6﹣6.60、原式=×2﹣2×3+5﹣2+1=﹣6﹣2+6=6﹣7.61、原式=a+2=2.62、原式=;63、原式=﹣+=﹣+=0.64、=2+﹣2=.65、=﹣=66、原式=9﹣14+4=﹣;67、原式=﹣43=﹣12=﹣11.68、原式=2×=12;69、原式=×3×=﹣;70、原式=12﹣2+6=16;71、原式=(4﹣2+6)×=2+272、原式=27÷(3×)×﹣8=3×﹣8=﹣8;73、原式=()2﹣()2=3﹣(2+2+5)=﹣4﹣274、原式=3+8=11;75、原式=2﹣12=﹣10;76、原式=5+﹣6=0;77、原式=÷=÷=1.78、原式=﹣==4+=4+.79、原式===;80、原式==9+6=1581、原式=(+)2﹣=3+2+2﹣=5+82、原式==;83、原式=;84、原式=5﹣6=﹣1;85、原式=4+=87、原式=+4×﹣+1=++1=1+.88、原式=(40)=30=15;89、原式=2+2=2+.90、原式===;91、原式===12.92、原式=2+2+4+2=;93、原式=9﹣14+24=;94、原式=(7+4)(7﹣4)+4﹣3=49﹣48+1=2;95、原式=﹣4×+9﹣12﹣()=﹣8+9﹣12﹣+1=﹣11;96、原式=﹣+=2x+=;97、原式=2a(b﹣×+)=2ab﹣+ab=98、原式=﹣+3﹣5=2﹣4;99、原式=12﹣4+1=13﹣4;100、原式=2+﹣=;101、原式=()=102、原式=3×2﹣2×3+5×4=6﹣6+20=20;103、原式=7﹣3+2=6;104、原式=(﹣)×=﹣=﹣105、原式=3÷+÷=3+=;106、原式=3﹣1﹣=2﹣107、原式=+1﹣×2=2+1﹣2=1;108、原式=3﹣2+1﹣1=3﹣2;109、原式=+4﹣3=110、﹣1=﹣1=﹣1=0;111、()()+2=﹣+2=5﹣7+2=0;112、+|﹣3|﹣2﹣1=1+3﹣=3;113、(﹣2)×﹣6=﹣4﹣=﹣9﹣=﹣114、原式=4﹣5=﹣1;115、原式=×=1;116、原式=5﹣2﹣5+2=;117、原式=4﹣2+﹣1=3﹣118、原式==3﹣2=1.120、原式=+1=121、原式=3+6a=2a+3a=5a;122、原式=﹣=﹣=3﹣2=1.123、原式==12;124、原式=49﹣48+2+=3+.125、原式===.。
二次根式的混合运算(习题及答案)

单 单:系数除以系
数,字母除以字母.
多 单:借用乘法分
配律.
公 ①平方差公式__________________________ 式 ②完全平方公式________________________
2. 我们知道如果一个三角形的三边长固定,那么这个三角形就 固定.若给出任意一个三角形三边长,你能求出它的面积吗? 小明翻阅了各种资料后发现,古希腊的几何学家海伦(Heron, 约公元 50 年),在数学史上以解决几何测量问题而闻名,在 他的著作《度量》一书中,给出了一个公式“如果一个三角
4
2
聪明的小明通过自己的推导发现,这两个公式实质是一致的:
1 [a2b2 ( a2 b2 c2 )2]
4
2
( 1 ab)2 ( a2 b2 c2 )2
2
4
(1 ab a2 b2 c2 )(1 ab a2 b2 c2 )
2
4
2
4
2ab a2 b2 c2 2ab a2 b2 c2
解:原式=
(6) 2
1 8
1 2
18
2 2
1 3
解:原式=
(7) (3 2 8)( 3 3) 解:原式=
(8) ( 6 2)2 解:原式=
(9) ( 5 3 2)( 5 3 2) 解:原式=
3
(10) (7+2 3)(7 2 3) ( 5 1)2 解:原式=
(11)
(5)2
思考小结
1. amn , amn , amn , ambm 相加,不变 系数,系数,字母,字母 乘法分配律
(3) 47 1 3
(6) 2 3 4 2 3
(9) 2 6 (12) 11
二次根式混合运算题含答案

二次根式混合运算125题(含答案)7、.8、9、.10、;11、.12、;13、;14、.15、;16、.17、.18、19、20、;21、22、.25、26、;.27、28、;;29、;30、31、;(5);32、33、;34、;35、36、3﹣9+337、÷(3×)38、39、40、;.41、42、43、44、45、;46、.47、(﹣)2﹣;48、;49、;50、.51、;52、.53、3﹣﹣+(﹣2)(+2)55、56、57、59、2÷﹣(2﹣)260、﹣2+(﹣1)261、(+2)﹣.62、63、64、65、.67、.68、69、70、3﹣(﹣)71、72、﹣273、74、75、76、77、÷78、×+÷﹣79、80、81、﹣.82、83、84、85、(+1)2﹣286、(+1)(1﹣)﹣(﹣1)2+(+1)287、88、89、90、;91、.92、;93、;;94、95、;96、;97、98、|﹣|+﹣;99、;;100、101、(+)2008(﹣)2009.102、;103、;104、.105、(3+)÷;106、107、;108、;109、.110、﹣1111、(﹣)(+)+2+|﹣3|﹣2﹣1(4)(﹣2)×﹣6 114、115、(2﹣);116、;117、118、.119、.120、121、122、+6a;﹣×.123、124、(2)(7+4)(7﹣4)+(2+)125、参考答案1、原式=2﹣3=﹣;2、原式=×==30;3、原式=2﹣12=﹣10.4、原式==2.5、原式===﹣6a.6、原式=;7、原式=()2﹣(﹣1)2=2﹣(3﹣2+1)=8、原式=.9、.原式=(3﹣2+3)×=(+3)×=1+10、原式=﹣+=;11、原式=(4+)÷3=12、原式=2+3﹣=;13、原式==;14、原式=(7+)(7+)=14×2=15、原式==3+6﹣10=﹣1;16、原式=2﹣=﹣2.17、原式=﹣2+=3﹣2+=18、原式=(3﹣2)(3+2)=18﹣12=6;19、原式=(2﹣+)=(+)=+120、原式=﹣3?5÷=﹣15÷=﹣15;21、原式=3+﹣2+﹣3=;22、原式=3a+﹣2b23、原式=3﹣2+1﹣(2﹣3)=5﹣2.24、原式==25、原式=2+1﹣(﹣)=3﹣1=2.26、原式=17﹣(19﹣)=﹣2+;27、原式=2﹣3﹣2=﹣3.28、原式=4+12=;29、原式=+2﹣10=;30、原式=4﹣+=;31、原式=6﹣5=1;32、原式=12+18﹣12=;33、原式=(2+)×﹣2=3﹣2=1;34、原式=+×6﹣m=2m+3m﹣m=0;35、原式=++1=﹣1++1=36、原式=12=(12﹣3﹣+6)=;37、原式=6÷(×)=6÷6=38、原式=+3﹣2=3+3﹣2=3+.39、原式=++×1=6+1+=7+.40、原式=×3+6×﹣2x?=2+3﹣2=3;41、原式=2﹣+3﹣2=2﹣2+142、原式=(6﹣+﹣2)÷2﹣3=3﹣+﹣﹣3=﹣+﹣;43、原式===444、=(4÷2)=45、原式=2+3﹣7=﹣2;46、原式===14.47、原式=10﹣7+=3+;48、原式=×(2﹣+)=+×=+1;49、原式=﹣1;50、原式=2+3+2﹣(2﹣3)=5+2+1=6+251、原式=4+﹣4=;52、原式=(4﹣2+6)÷=2+253、原式=6﹣3﹣+5﹣4=(6﹣3﹣)+1=+154、原式==;56、原式=[﹣(﹣)][+(﹣)]=5﹣(﹣)2=5﹣(5﹣2)=2.57、原式=4×2﹣16+12﹣16﹣8=﹣4﹣16;58、原式=+﹣+3=59、原式=2﹣(4﹣4+2)=2﹣6+4=6﹣6.60、原式=×2﹣2×3+5﹣2+1=﹣6﹣2+6=6﹣7.61、原式=a+2=2.62、原式=;63、原式=﹣+=﹣+=0.64、=2+﹣2=.65、=﹣=66、原式=9﹣14+4=﹣;67、原式=﹣43=﹣12=﹣11.68、原式=2×=12;69、原式=×3×=﹣;70、原式=12﹣2+6=16;71、原式=(4﹣2+6)×=2+272、原式=27÷(3×)×﹣8=3×﹣8=﹣8;73、原式=()2﹣()2=3﹣(2+2+5)=﹣4﹣274、原式=3+8=11;75、原式=2﹣12=﹣10;76、原式=5+﹣6=0;77、原式=÷=÷=1.78、原式=﹣==4+=4+.79、原式===;80、原式==9+6=1581、原式=(+)2﹣=3+2+2﹣=5+82、原式==;83、原式=;84、原式=5﹣6=﹣1;85、原式=4+=86、(1+)(1﹣)﹣(﹣1)2+(+1)2=1﹣()2﹣(2﹣2+1)+2+2+1=1﹣2﹣2+2﹣1+2+2+1=4﹣1.88、原式=(40)=30=15;89、原式=2+2=2+.90、原式===;91、原式===12.92、原式=2+2+4+2=;93、原式=9﹣14+24=;94、原式=(7+4)(7﹣4)+4﹣3=49﹣48+1=2;95、原式=﹣4×+9﹣12﹣()=﹣8+9﹣12﹣+1=﹣11;96、原式=﹣+=2x+=;97、原式=2a(b﹣×+)=2ab﹣+ab=98、原式=﹣+3﹣5=2﹣4;99、原式=12﹣4+1=13﹣4;100、原式=2+﹣=;101、原式=()=102、原式=3×2﹣2×3+5×4=6﹣6+20=20;103、原式=7﹣3+2=6;104、原式=?(﹣)×=﹣=﹣105、原式=3÷+÷=3+=;106、原式=3﹣1﹣=2﹣107、原式=+1﹣×2=2+1﹣2=1;108、原式=3﹣2+1﹣1=3﹣2;109、原式=+4﹣3=110、﹣1=﹣1=﹣1=0;111、()()+2=﹣+2=5﹣7+2=0;112、+|﹣3|﹣2﹣1=1+3﹣=3;113、(﹣2)×﹣6=﹣4﹣=﹣9﹣=﹣114、原式=4﹣5=﹣1;115、原式=×=1;116、原式=5﹣2﹣5+2=;117、原式=4﹣2+﹣1=3﹣118、原式==3﹣2=1.119、原式==120、原式=+1=121、原式=3+6a=2a+3a=5a;122、原式=﹣=﹣=3﹣2=1.123、原式==12;124、原式=49﹣48+2+=3+.125、原式===.。
二次根式乘除加减练习测试题附参考答案

二次根式乘除加减练习测试题附参考答案The pony was revised in January 2021二次根式的乘除,加减练习题双基演练1.23×(-25)=_________,a ×ab =________.2.(2×7)2=_______,22(2)(3)⨯=________.3.15×5=_________, 3.6 5.4⨯=_________,3bc ×13c b-=_______. 4.设长方形的长a=250,宽b=332,则面积S=________.5.已知,x>0,y>0,则2x y ·2xy =__________.6.化简462a a b +结果等于()A .a 2(a 2+b )B .a (a 2+b )C .a 222a ab +D .a 2221a b +7.已知a=2,b=10,用含a 、b 的代数式表示20,这个代数式是()A .a+bB .abC .2aD .2b8.若29x -=3x -·3x +,则x 的取值范围是()A .-3≤x ≤3B .x>-3C .x ≤3D .-3<x<3能力提升93153×(-1210 313223③3m ·3n m ·223m n n ④52xy y ×(-323x y )×35x y10.计算(23-×23+)2002=_______.11.当x<0,y<0时,下列等式成立的是()A .2x y x y =-B .2xy y x =C .393x y x xy =-D .429x y =3x 2y12.若把根号外的因式移到根号内,则a 1a-等于() A .-a -B .a -C .-a D .a13.仿照20.5=22×0.5=220.5⨯=2的做法,化简下列各式:①100.1=②515= 聚焦中考14.下列各数中,与数32-积为有理数的是( )A 32+B 32-C 32+-D 315.已知b a <,化简b a 3-的正确结果是( )A ab a --B ab a -C ab aD ab a -16.观察分析下列数据,寻找规律:0,3,6,3,32,15,……那么第10个数是_____17.(2004。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次根式的加减乘除混合运算练习题
一、单选题
1.计算()0221+-的结果是( ).
A. 5
B. 4
C. 3
D. 2 2.若一个数的平方根与它的立方根完全相同,这个数是( )
A.1
B.1-
C.0
D.1,0±
3.16的平方根是( )
A.4
B.4-
C.4± 4.有下列说法:
①负数没有立方根;
②一个数的立方根不是正数就是负数;
③一个正数或负数的立方根和这个数同号,0的立方根是0;
④如果一个数的立方根是这个数本身,那么这个数必是1或0.
其中错误的是( )
A.①②③
B.①②④
C.②③④
D.①③④
( )
A.2±
B.4±
C.4
D.2 6.下列各组数中互为相反数的是( )
A.2-
B.2-
C.2与2(
D.|
7.2(的平方根是x ,64的立方根是y ,则x y +的值为( )
A.3
B.7
C.3或7
D.1或7
8.下列等式正确的是( )
712± B.32- 3=- 4=
9.如图,用正方形制作的“七巧板”拼成了一只小猫,若小猫头部(图中涂色部分)的面积是2100cm ,则原正方形的边长为( )
A.10cm
B.15cm
C.20cm
D.25cm
10.一个正数的两个平方根分别是21a -与2a -+,则a 的值为( )
A.1-
B.1
C.2-
D.2
二、计算题
11.计算:
(1)
12.求下列各数的立方根.
1.27-
2.0.008
3.12527
13.计算下列各式的值.
1.35(5)()7
-÷-
-
-
14.一个正数x 的平方根是35a -与3a -,求a 和x 的值.
15.已知21a -的算术平方根是3,34a b ++的立方根是2,求4a b +的平方根.
16.化简:
17.化简:
18.计算:
19.计算: 22-
三、填空题
20.已知m ,n 为两个连续的整数,且m n <<,则m n +=__________.
21.827
-的立方根为______. 22.小红做了棱长为5cm 的一个正方体盒子,小明说:“我做的盒子的体积比你的大3218cm . ”则小明的盒子的棱长为__________cm .
23.一个正数x 的平方根是23a -与5a -,则x =________.
1的整数部分是____________
参考答案
1.答案:A
解析:原式415=+=,故选:A
2.答案:C
解析:任何实数的立方根都只有一个,而正数的平方根有两个,它们互为相反数,0的平方根是0,负数没有平方根,所以这个数是0,故选C.
3.答案:C
解析:16的平方根是4±.故选C.
4.答案:B
解析:正数的立方根是正数,负数的立方根是负数,0的立方根是0.立方根等于它本身的数有0,1和−1.所以①②④都是错误的,③正确.故选:B.
5.答案:D
解析:∵64的算术平方根是8,8的立方根是2,
∴这个数的立方根是2.故选D.
6.答案:A
解析:选项A.2-2=,
选项B.2-2-,
选项C.2与2(2=,
选项D.|=
故选A.
7.答案:D
解析:∵2(9=,9的平方根3x =±,4y =,
∴7x y +=或1.故答案为7或1.
8.答案:D
解析:A.原式712
=,错误; B.原式3322
⎛⎫=--= ⎪⎝⎭,错误; C.原式没有意义,错误;
D.原式4=,正确,
故选D.
9.答案:C
解析:()21100400cm 4
÷=20(cm)=. ∴原正方形的边长为20cm .
故选:C.
10.答案:A
解析:∵一个正数的两个平方根分别是21a -与2a -+,
∴(21)(2)0a a -+-+=,解得:1a =-.
故选A.
11.答案:(1)原式==(2)原式63328=+-+=
解析:
12.答案:1.∵3(3)27-=-,
∴27-的立方根是3-.
2.∵3(0.2)0.008=,
∴0.008的立方根是0.2
3.∵35125()327
=, ∴12527的立方根是53
解析:
13.答案:1.原式5125()71687
=-⨯--=. 2.原式=
311722-=-. 3.原式=5712944
-+=- 4.原式=115611056
⨯-⨯=-=. 解析:
14.答案:因为一个正数有两个平方根,它们互为相反数,所以正数x 的平方根互为相反数,即3530a a -+-=,
解得1a =.
当1a =时,352a -=-,
()2
24x =-=. 解析:
15.答案:21a -的算术平方根是3,34a b ++的立方根是2 219,348a a b ∴-=++=5,11,49a b a b ==-∴+=解得43a b ∴+±的平方根是 解析:
16.答案:
解析:
17.= 解析:
18.答案:17
4
解析:
19.答案:解析:
20.答案:7
解析:∵91116<<,即34<<,∴3m =,4n =,因此7m n +=. 21.答案:23
-
解析:a 827-的立方根是23
-. 故答案为23
-. 22.答案:7
解析:小红做的正方体的盒子的体积是335125cm =.
则小明的盒子的体积是3125218343cm +=.
设盒子的棱长为cm x ,则3343x =,
∵37343=,∴7x =,故盒子的棱长为7cm .
23.答案:49
解析:∵一个正数x 的平方根为23a -和5a -,
∴()()2350a a -+-=,解得:2a =-.
∴237a -=-,57a -=,∴()2749x =±=.
故答案为:49.
24.答案:3
解析:162045,3R 4,1<<<∴<的整数部分是3.故答案为:3。
