东南大学《工程矩阵理论》工程矩阵理论期终考试(A)
工程矩阵理论(2009)(工科硕士)

分块矩阵的乘法规则
设 A aij , B bij s n nt
A11 A21 A A p1 A12 A22 Ap 2
将这两个矩阵分块:
B12 B1r B22 B2 r Bq 2 Bqr
A1q B11 A2 q B21 , B B Apq q1
21
例5
1 0 初等行变换 增广矩阵 0 0 1 1 1 1 0 1 1 3 4 0 0 1 11 22 0 0 0 0 0 1
1 0 初等行变换 0 0
1 0 0
5 0 1 0 14 26 0 0 1 11 22 0 0 0 0 0 4
35
例1
1.V F n 2.V 3.V 4.V 5.V 6.V F nn F [ x] Fn [ x] C, F R C, F C
36
例1(续)
7.V R, F C
8.V R , F R, 通常运算
9.V R , F R
22
例6
求齐次线性方程组的基础解系: x1 x2 x3 x4 x5 0 2 x 2 x 3 x 3 x x 0 1 2 3 4 5 3x1 3x2 x3 2 x4 4 x5 0 x1 x2 4 x3 5 x4 5 x5 0
23
例7
设A是s n矩阵,b是s维列向量。证明: 1.r ( A) r ( AH A); 2.线性方程组AH Ax AH b恒有解。
24
3.向量组的极大无关组和秩
若向量组1 , 2 , , s的部分组 i1 , i2 , ir 线性无关, 且1 , 2 , , s中每个向量均可由 i1 , i2 , ir 线性表示, 则称 i1 , i2 , ir 是向量组1 , 2 , , s的一极大无关组, 称r是 向量组1 , 2 , , s的秩。
东南大学考试卷(A卷)

个人资料整理,仅供个人学习使用1 / 5东 南 大 学 考 试 卷(A 卷)课程名称 自动检测技术 考试学期 08-09--2得分 适用专业 自动化考试形式 闭卷 考试时间长度 100分钟个人资料整理,仅供个人学习使用一、填空题(共36分,每题6分)1、根据被测参量与时间的关系,测量误差可分为静态误差和动态误差两大类。
(2*3’)2、常见的被测参量可分为热工量、电工量、机械量、物性和成分量、光学量、状态量。
(6*1’)3、工业检测仪表(系统)常以最大引用误差作为判断其精度等级的尺度。
(6’)4、压力传感器常见的型式有应变式、压阻式、压电式、电容式等。
(4*1.5’)5、1989年7月第77届国际计量委员会批准建立了新的国际温标,简称ITS一90。
ITS一90基本内容为:(1)重申国际实用温标单位仍为K;(2)把水的三相点时温度值定义为0.01℃(摄氏度),同时相应把绝对零度修订为-273.15℃。
(3*2’)6、流量仪表的主要技术参数有流量范围、量程和量程比、允许误差和精度等级和压力损失。
(4*1.5’)二、问答题(共42分,每题14分)1、简述测量不确定度和测量准确度两者的异同点。
答:测量不确定度与测量准确度都是描述测量结果可靠性的参数。
(4’)其区别在于:测量准确度因涉及一般无法获知的“真值”而只能是一个无法真正定量表示的定性概念;测量不确定度的评定和计算只涉及已知量,因此,测量不确定度是一个可以定量表示的确定数值。
在实际工程测量中,测量准确度只能对测量结果和测量设备的可靠性作相对的定性描述,而作定量描述必须用测量不确定度。
(10’)共3 页第 1 页2、我国国家标准规定的工业用标准热电偶有几种?其中测温上限最高的热电偶其分度号是什么?它额定测温上限温度值是多少?热电偶具有哪些特点,使它成为是工业和武备试验中温度测量应用最多的器件?答:2 / 5个人资料整理,仅供个人学习使用3 / 5我国工业用标准热电偶有8种,(2’)其中分度号为S 、R 、B 的三种热电偶均由铂、铂铑合金制成,属贵金属热电偶;分度号为K 、N 、T 、E 、J 五种热电偶,由镍、铬、硅、铜、锰、镁、钴等金属的合金制成,属贱金属热电偶。
东南大学《工程矩阵理论》工程矩阵理论期终考试(A)

12东南大学考试卷(A)Array课程名称工程矩阵理论考试学期08-09-2 得分
适用范围工科硕士研究生考试形式闭卷考试时间长度150分钟
1.地子空间地一组基是;
2.若线性空间地线性变换在基下地矩阵是,则在基下地矩阵是;
3.如果矩阵满足,并且地秩为,则行列式;
4.若矩阵,则矩阵函数地行列式;
5.若是维单位列向量,是正定地,则参数满足条件.
二.(12%)设矩阵.讨论地可能地Jordan标准形.并问:当参数满足什么条件时,矩阵与是相似地.
三.(20%)记,上地变换定义为:对,.
1.证明:是上地线性变换;
2.求在地基下地矩阵;
3.求地特征值及相应地特征子空间地基;
4.问:是否存在地基,使得在这组基下地矩阵是对角阵?如存在,试给出这样地一组基及相应地对角阵;如不存在,请说明理由.
四.(10%)设.试将表示成关于地次数不超过2地多项式.
五.(8%)求地广义逆矩阵.
六.(15%)假设是有限维欧氏空间,是单位向量,上地线性变换定义如下:对任意,.
1.证明:是上地正交变换.
2.在中定义内积:对,.于是,成为欧氏空间.分别求中向量及地长度,并求正实数及单
位向量,使得如上地正交变换将变成.
七.证明题(20%)
1.假设是矩阵,分别是、酉矩阵.证明:.
2.假设是正规矩阵.若地特征值地模都等于1,证明:是酉矩阵.
3.假设是Hermite矩阵,其中,是地子矩阵,并且都是方阵.若是正定地.证明关于行列
式地不等式:.。
线性代数与解析几何__东南大学(5)--08-09-3线性代数期末考试试卷A

2. 假 设 A = (aij )nᄡn 是 n ᄡ n 实 对 称 矩 阵 , li (1 ᆪ i ᆪ n) 是 A 的 特 征 值 。 证 明 :
n
nn
� �� li2 =
ai2j 。
i =1
i=1 j=1
共 4页
第
页
秩相同,并且, b3 可以由a1,a2 线性表示。求参数 m, n 的值。
共 4页
第
页
1. 当参数 a 满足什么条件时,齐次线性方程组 Ax = 0 有非零解? 2. 当 Ax = 0 有非零解时,求其基础解系。
2. (10%)设二次型 f (x1, x2 , x3 ) = x12 - 4x1x2 + 3x22 + 4x2 x3 + kx32 , g(z1, z2 , z3 ) = z1z3 。 1. 求一可逆线性变换 x = Cy 将 f 化成标准型。 2. 问:当参数 k 满足什么条件时,存在可逆线性变换将 f 变成 g ?
弊
;
7. 如果 2 阶矩阵 A 的特征值是 2 和 3,则 A 的伴随矩阵 A* 的特征值是
;
此 答 卷
�1 -1 1 �
8.
若 2 是 A = ����-x3
4 -3
y 5
����的二重特征值,且
A
相似于对角阵,则
(
x,
y)
=
;
无
9. 如果二次型 x12 + tx22 + 4tx1x2 是正定的,则参数 t 满足条件
满足条件
;
场
2.
设
k
>
0
,向量 a
=
(k, 0,
k )T
工程矩阵理论试题A
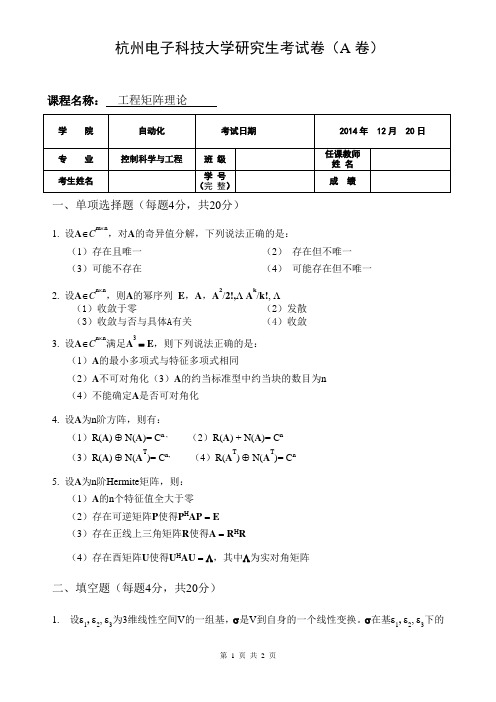
杭州电子科技大学研究生考试卷(A卷)课程名称:工程矩阵理论一、单项选择题(每题4分,共20分)1. 设A∈C m⨯n,对A的奇异值分解,下列说法正确的是:(1)存在且唯一(2)存在但不唯一(3)可能不存在(4)可能存在但不唯一2. 设A∈C n⨯n,则A的幂序列E,A,A2/2!, A k/k!,(1)收敛于零(2)发散(3)收敛与否与具体A有关(4)收敛3. 设A∈C n⨯n满足A3= E,则下列说法正确的是:(1)A的最小多项式与特征多项式相同(2)A不可对角化(3)A的约当标准型中约当块的数目为n(4)不能确定A是否可对角化4. 设A为n阶方阵,则有:(1)R(A) ⊕ N(A)= C n , (2)R(A) + N(A)= C n(3)R(A) ⊕ N(A T)= C n, (4)R(A T) ⊕ N(A T)= C n5. 设A为n阶Hermite矩阵,则:(1)A的n个特征值全大于零(2)存在可逆矩阵P使得P H AP=E(3)存在正线上三角矩阵R使得A=R H R(4)存在酉矩阵U使得U H AU=Λ,其中Λ为实对角矩阵二、填空题(每题4分,共20分)1. 设ε1, ε2, ε3为3维线性空间V的一组基,σ是V到自身的一个线性变换。
σ在基ε1, ε2, ε3下的矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211a a a a a a a a a ,则σ在基ε3, 2ε2, 3ε1下的矩阵为。
2. 设方阵A 满足A 2= 3A, 则sin (3A ) = 。
3.矩阵A = diag 21312,,0203⎛⎫⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,则A 的最小多项式为 。
4. 设X = (x 1, x 2, , x n )T 为变向量,α = (a 1, a 2, , a n )T 为常向量,H = (h ij )n ⨯n 为常矩阵,则:,()=HX X XT D D。
5. 设A ∈C n ⨯n 为Hermite 矩阵,X ∈C n ,A 的n 个特征值为λ1,λ2, ,λn ,满足λ1 ≤ λ2 ≤ ≤ λn ,则: XX AXX H X H 0max ≠ =。
工程矩阵理论

精彩摘录
精彩摘录
《工程矩阵理论》是一本深入浅出,理论与实践相结合的优秀教材。它用清 晰的语言和丰富的例子,为读者揭示了矩阵理论在工程领域中的广泛应用和深远 影响。以下是本书中的一些精彩摘录,它们从不同的角度展示了矩阵理论的魅力 和重要性。
精彩摘录
“矩阵不仅是数学中的一个基本工具,也是工程师解决实际问题的重要武器。 在信号处理、控制系统、电路设计、图像处理等领域,矩阵理论都发挥着不可替 代的作用。”这段话强调了矩阵理论在工程实践中的广泛应用,提醒我们要重视 矩阵理论的学习和应用。
目录分析
目录分析
《工程矩阵理论》是一本专注于工程领域的矩阵理论教材,其目录结构精心 组织,内容深入且全面。本书旨在向工科研究生提供关于矩阵论的深入理解和应 用技能。以下是对这本书目录的详细分析。
目录分析
目录首先引入了“线性空间与线性映射”这一章节。线性空间是矩阵理论的 基础,它定义了向量空间的性质和运算规则。线性映射则描述了线性空间之间的 变换关系,这是理解矩阵在空间中如何操作的关键。
精彩摘录
“矩阵的秩是矩阵理论中的一个核心概念,它反映了矩阵行列之间的线性关 系。在解决实际问题时,通过计算矩阵的秩,我们可以判断系统的可控性、可观 性、稳定性等关键性质。”这段话揭示了矩阵秩在工程问题中的重要应用,体现 了矩阵理论在解决实际问题中的价值。
精彩摘录
“特征值和特征向量是矩阵理论中的两个重要概念,它们与矩阵的对角化、 相似变换等概念紧密相关。在控制系统的稳定性分析、信号处理中的滤波器设计 等领域,特征值和特征向量的应用广泛而深入。”这段话展示了特征值和特征向 量在矩阵理论中的重要地位,以及它们在工程实践中的应用。
精彩摘录
“矩阵分解是矩阵理论中的一个重要方法,它可以将一个复杂的矩阵分解为 几个简单的矩阵的乘积。通过矩阵分解,我们可以简化计算过程,揭示矩阵的内 在结构,为解决实际问题提供便利。”这段话阐述了矩阵分解的重要性和应用, 体现了矩阵理论在解决实际问题中的灵活性和实用性。
矩阵论试卷及答案(2011A)

三(20分)设
(1) 证明: 是 的线性子空间,并求 的基和维数;
(2) 在 中定义变换 ,其中 为 的伴随矩阵, 证明: 为线性变换;
(3) 求 在(1)中所取基下的矩阵表示;
(4) 求(2)中线性变换 的值域 和核 ,并确定它们的维数.
(1)因为 ,则 非空。对任意 都有 则 是 的子空间.
(iii)写出 的Jordan标准形;
(2)设 ,试问A和B是否相似?并说明原因。
(1) , ;………5分
行列式因子
不变因子
初等因子 ……...8分
A的Jordan标准形为 ……..3分
(2)矩阵A,B的行列式因子均为 , A,B相似.
………4分
或A,B 的特征值均为-1和2,有两个互异的特征值,所以A,B均相似于 ,所以,A,B相似。
………3分
共5页第5页
五(20分)(1)设 , .
(i)求A的奇异值分解;
(ii)计算广义逆矩阵 ;
(iii)用广义逆矩阵判定线性方程组 是否相容。若相容,求其通解;若不相容,求其极小最小二乘解;
(2)设 ,判定矩阵级数 是否收敛。若收敛,求其和。
(1)(i) , 的奇异值为 , 对应于特征值3和2的标准正交特征向量为 , 对应于特征值3和2,0的标准正交特征向量分别为 , ,则 的奇异值分解为
Ni南京航空航天大学2010级硕士研究生
共5页第1页
2010~ 2011学年第1学期《矩阵论》课程考试A卷答案
考试日期:2011年1月12日,课程编号:A000003,命题教师:阅卷教师:
学院专业学号姓名成绩
一(20分)(1)设 。
(i)求 的特征多项式和 的全部特征值;
东南大学线性代数期末考试卷

东 南 大 学 考 试 卷 ( A 卷 ) 课程名称 线性代数 考试学期 得分 使用专业 考试形式 闭 卷 考试时间长度 120分钟 题号 一 二 三 四 五 六 七 八 得分 一、(10%)选择题 1. 设3×2矩阵A =(A 1,A 2),B =(B 1,B 2)其中A 1,A 2,B 1,B 2是3维列向量. 若A 1,A 2线性无关, 则B 1,B 2线性无关的充要条件是( ). A.矩阵A 与B 等价 B. A 1,A 2能由B 1,B 2线性表示 C.向量组A 1,A 2与B 1,B 2等价 D. B 1,B 2能由A 1,A 2线性表示 2. 设A 为n 阶矩阵, E 为n 阶单位矩阵, 则下列叙述中, ( )是错误的. A. A 与E 合同的充分必要条件是A 正定 B. A 与E 相似的充分必要条件是A =E C. A 与E 相似的充分必要条件是行列式|A |=1 D. A 与E 等价的充分必要条件是行列式|A |≠0 3. 设A 为2×3矩阵, 交换A 的第一行和第二行得到矩阵B ,则( ). A. A (010100001)=B B. (010100001)A =B C. (0110)A =B D. A (0110)=B 4. 下列关于n 阶方阵A 的叙述中, 除了( )之外, 其余三个是相互等价的. A.齐次线性方程组Ax =0有非零解 B. A 的秩小于n C. A 是可逆矩阵 D.行列式|A |=0 5. 设A,B 都是m ×n 矩阵, 则下列矩阵中, ( )一定是对称矩阵.A. AB T +BA TB. A +BC. AB TD. AB T A二、(30%)判断题[ ] 6. (1234)的伴随矩阵为(4−3−21).[ ] 7. 设A,B 都是m ×n 矩阵, 则A 与B 等价的充分必要条件是它们的秩相等.[ ] 8. 设α1,α2,…,αs 为n 维列向量组, 若其中有一个向量αi 为零向量, 则α1,α2,…,αs 一定线性相关.[ ] 9. 若α,β为向量组α,β,γ的一个极大线性无关组, 而且β,γ也线性无关, 则β,γ也是学号姓名密封线α,β,γ的一个极大线性无关组.[ ] 10. 设A 为n 阶矩阵, 若对于任意的n 维列向量x , 有‖Ax ‖=‖x ‖则A 必为正交矩阵.[ ] 11. 设A 与B 都是n 阶正交矩阵, 则A +B 也是正交矩阵.[ ] 12. 设α与β都是非齐次线性方程组Ax =b 的解, 则α+β也是非齐次线性方程组Ax =b 的解.[ ] 13. 设α是非齐次线性方程组Ax =b 的解, β是齐次线性方程组Ax =0的解, 则α,β线性无关.[ ] 14. 若矩阵A 与B 相似, 则A 2与B 2相似.[ ] 15.矩阵A 与B 相似的充分必要条件是A 2与B 2相似.[ ] 16. 若矩阵A 与B 具有相同的特征多项式, 则A 与B 相似.[ ] 17. 设A 与B 都是n 阶实对称矩阵, 若A 与B 具有相同的特征多项式, 则A 与B 相似.[ ] 18. 二次型f (x 1,x 2)=(x 1,x 2)(1203)(x 1x 2)的矩阵为(1203). [ ] 19. 二次型f (x 1,x 2)=(x 1,x 2)(1203)(x 1x 2)是正定的. [ ] 20. 设多项式f (x )=2x 3−5x +7, A 为三阶方阵, 则f (A )=2A 3−5A +7.三、填空题(10%)21. 设A 为3×2矩阵, B =AA T 则B 的行列式|B |= _______.22. 设向量α=(123)与β=(1−2a)正交, 则 a = _______.23. 设α为非零的3维列向量, A =ααT , 则A 的正惯性指数= ________.24. 设A 为3阶矩阵,E 为3阶单位矩阵. 若A 2=E ,则r (A −E )+r (A +E )= ________.(注: 这里r (A −E )表示A −E 的秩,r (A +E )表示A +E 的秩.)25. 若向量组α,β,γ线性无关, α+β,β−γ,α+kγ线性相关, 则k = ________.四、(10%)设A =(a 11a 11111111a 11a ). 计算行列式|A |, 并针对a 的不同取值, 求A 的秩.五、(10%)设A =(0210),B =(12103410). 求矩阵X , 使得AX =B +X.六、(10%)设A =(20011000a )与B =(100010002) 相似. 求a 以及可逆矩阵P 使得 P −1AP =B .七、(10%)已知4阶方阵A=(α1,α2,α3,α4),其中α1,α2,α3,α4均为 4 维列向量, α2,α3,α4线性无关, 且α1=α2+α3−2α4.如果b=α1−α2+α3−α4, 求线性方程组Ax=b的通解.八、(10%)设二次型f(x1,x2,x3)=(x1+x2+x3)2.请写出该二次形的矩阵A,并写出该二次型在正交变换下的标准形.(不必写出所用的正交变换)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2东南大学考试卷(A)
课程名称工程矩阵理论考试学期0 8- 09- 2 得分
(15%)填空题
1.地子空间地一组基是;
2.若线性空间地线性变换在基下地矩阵是,则在基下地矩阵是;
3.如果矩阵满足,并且地秩为,则行列式;
4.若矩阵,则矩阵函数地行列式;
5.若是维单位列向量,是正定地,则参数满足条件•
(12%)设矩阵.讨论地可能地Jordan标准形.并问:当参数满足什么条件时,矩阵与是相似地.
(20%)记,上地变换定义为:对,.
1.证明:是上地线性变换;
2.求在地基下地矩阵;
3.求地特征值及相应地特征子空间地基;
4.问:是否存在地基,使得在这组基下地矩阵是对角阵?如存在,试给出这样地一组基及相应地对角阵;如不存在,请说明理由
四. (10% )设.试将表示成关于地次数不超过2地多项式.
五. (8%)求地广义逆矩阵.
六.
(15%)假设是有限维欧氏空间,是单位向量,上地线性变换定义如下:对任意,.
1. 证明:是上地正交变换.
2. 在中定义内积:对,.于是,成为欧氏空
间
.分别求中向量及地长度,并求正实数及单位向量,使得如上地正交变换将变成
.
七.
证明题(20%)
1. 假设是矩阵,分别是、酉矩阵.证明:.
2. 假设是正规矩阵.若地特征值地模都等于1证明:是酉矩阵.
3. 假设是Hermite矩阵,其中,是地子矩阵,并且都是方阵.若是正定地.证明关于行列
式地不等式:.
适用范围工科硕士研究生考试形式闭卷考试时间长度150分钟。
