三向应力状态的广义胡克定律
合集下载
材料学 胡克定律
l
b=50mm h=100mm
解: 梁为拉伸与弯曲的组合变形. A点有拉伸引起的正应力和弯曲 引起的切应力.
（拉伸） （负）
（1）A点处的主应变1， 2 ， 3
A
x = 20
x = 30
（2）A点处的线应变 x , y , z
例题14 简支梁由18号工字钢制成. 其上作用有力F= 15kN, 已知
2.三向等值应力单元体的体积应变（The volumetric strain of triaxial-equal stress element body）
三个主应力为
m
单元体的体积应变
m
m
这两个单元体的体积应变相同 单元体的三个主应变为
2
1
dy
3
dz dx
m
m
m
如果变形前单元体的三个棱边成某种比例,由于三个棱边应 变相同,则变形后的三个棱边的长度仍保持这种比例. 所以在三向
因此,该圆筒变形后的厚度并无变化,仍然为 d =10mm .
例题13 已知矩形外伸梁受力F1,F2作用. 弹性模量E=200GPa,泊
松比m= 0.3, F1=100KN,F2=100KN. 求:（1）A点处的主应变 1,2 , 3 （2）A点处的线应变 x , y , z
F1
b
F2 A
F2 z
a
例题10 边长 a = 0.1m 的铜立方块,无间隙地放入体积较大,变形
可略去不计的钢凹槽中,如图所示. 已知铜的弹性模量E=100GPa,
泊松比μ=0.34,当受到F=300kN的均布压力作用时,求该铜块的主
应力,体积应变以及最大切应力.
解:铜块横截面上的压应力
Fa
三向应力状态的广义胡克定律
1、静平衡方程 2、变形协调方程
转 角
Ml max EI Pl 2 max 2 EI ql 3 max 6 EI Ml Ml 、 3EI 6 EI
max
Pl 2 16 EI Z ql 3 24 EI Z
挠 度
ymax Ml 2 2 EI
Pl 3 ymax 3EI4 ql ymax 8EI
2 2
2
2
1 r3 W
M T
2
2
r4
M 2 T 2 ( ) 3( ) W Wt
r4
1 W
M 0.75T
2
2
对于拉、弯、扭同时存在作用在圆形截面时:
N M 2 T 2 N M 2 T 2 r 3 ( ) ( ) r 4 ( ) 0.75( ) A W W A W W
max
轴向拉.压
扭
转
弯
曲
NL ＝ T L M EIf ( x ) L ＝ 变形 G IP EA Tmax 180 L f max f max 刚度条件 GI P L
x
虎克定律
E
G
超静定 问题
在单元体上两个剪应力共同指定的象限 既为主应力1所在象限
1.应力圆的画法
y
y
R
c
B2 B1
x
x
D2 (y ,y)
D1 (x ,x)
o
x y
2 1.在—坐标系中， 该点的横纵坐标代表单元体以 量取横坐标OB1=x， x轴为外法线方向面上的应力 纵坐标B1D1=x得到D1点。 情况。同样方法得到D2点。
应力与应变间的关系
22
例题7-7 边长 a = 0.1m 的铜立方块, 无间隙地放入体积较
大, 变形可略去不计的钢凹槽中, 如图 所示。 已知铜的弹 性模量 E=100GPa, 泊松比 =0.34, 当受到P=300kN 的均布 压力作用时, 求该铜块的主应力. 体积应变以及最大剪应力。
P a
y
z
x
23
y
解：铜块上截面上的压应力为
9
3、 特例
（1）平面应力状态下(假设 Z = 0 )
x
1 E
(
x
y)
y
1 E
(
y
x)
z E ( x y)
xy
xy
G
10
（2） 广义胡克定律用主应力和主应变表示时 三向应力状态下：
1
1
E [ 1
(
2
3)]
2
1 E
[
2
(
3
1)]
3
1 E
[
3
( 1
2)]
(7-7-6)
11
平面应力状态下 设 3 = 0, 则
x y z x y y z z x
y
σy
上面
x y z x y y z z x
1、各向同性材料的广义胡克定律 （1）符号规定
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量：拉应力为正
σz
x
o
压应力为负。 z
前面
3
(b)三个剪应力分量: 若正面(外法线与坐标轴
dxdydz
dxdydz(1 1 2 3) dxdydz
dxdydz
广义胡克定律90391
§10.4 空间应力状态及广义胡克定律一、空间应力状态简介当单元体上三个主应力均不为零时的应力状态称为空间应力状态，也称为三向应力状态。
本节只讨论在已知主应力σ1、σ2、σ3的条件下，单元体的最大正应力和最大剪应力。
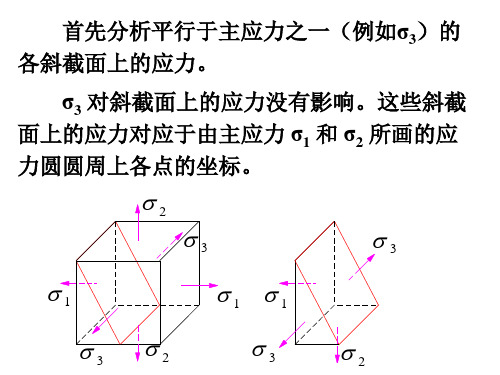
先研究一个与σ1平行的斜截面上的应力情况，如图10-16(a)所示。
该斜面上的应力σ、τ与σ1无关，只由主应力σ2、σ3决定。
于是，可由σ2、σ3确定的应力圆周上的点来表示平行于σ1某个斜面上的正应力和剪应力。
同理，在平行于σ2或σ3的斜面上的应力σ、τ，也可分别由（σ1、σ3）或（σ1、σ2）确定的应力圆来表示。
这样作出的3个应力圆称作三向应力圆，如图10-16（d）所示。
当与三个主应力均不平行的任意斜面上的正应力和剪应力必然处在三个应力圆所围成的阴影范围之内的某一点D。
D点的纵横坐标值即为该斜面上的正应力和剪应力。
由于D点的确定比较复杂且不常用，在此不作进一步介绍。
图10-16 空间应力状态及其应力圆二、最大、最小正应力和最大剪应力从图10-16(d)看出，在三个应力圆中，由σ1、σ3所确定的应力圆是三个应力圆中最大的应力圆，又称极限应力圆。
画阴影线的部分内，横坐标的极大值为Al点，而极小值为B1点，因此，单元体正应力的极值为：σmax=σ1，σmin=σ3单元体中任意斜面上的应力一定在σ1和σ3之间。
而最大剪应力则等于最大应力圆上Gl 点的纵坐标，即等于该应力圆半径： 13max 2σστ-=Gl 点在由σ1和σ3所确定的圆周上，此圆周上各点的纵横坐标就是与σ2轴平行的一组斜截面上的应力，所以单元体的最大剪应力所在的平面与σ2轴平行，且与σ1和σ3主平面交450。
三、广义胡克定律在研究单向拉伸与压缩时，已经知道了在线弹性范围内，应力与应变成线性关系，满足胡克定律 E σε= （a ）此外，轴向变形还将引起横向尺寸的变化，横向线应变根据材料的泊松比可得出：'E σεμεμ=-=- （b ）在纯剪切的情况下，根据实验结果，在剪应力不超过剪切比例极限时，剪应力和剪应变之间的关系服从剪切胡克定律，即G τγ= 或 G τγ=（c ）对于复杂受力情况，描述物体一点的应力状态，通常需要9个应力分量，如图10.1所示。
应力状态分析3广义胡克定律与强度理论土
03
应力状态分析有助于了解结构的承载能力和稳定性， 为工程设计和安全评估提供依据。
应力状态分类
01
02
03
平面应力状态
物体受力作用在两个相互 垂直的平面上，且这两个 平面上的应力分量不相等。
平面应变状态
物体受力作用在两个相互 垂直的平面上，且这两个 平面上的应变分量不相等。
三向应力状态
物体在三个相互垂直的方 向上均受到应力作用，且 三个方向的应力分量都不 相等。
地基承载力特征值的确定需要考虑地质勘查报告、建筑物类型、基础形式等多种因素。
地基变形分析
地基变形分析是指对建筑物地基在不同荷载作用下的变形情况进行评估和分析，以确保建筑物在使用过程中不会发生过大的 沉降、倾斜或裂缝等不良现象。
地基变形分析的方法包括：沉降观测、倾斜测量、裂缝监测等。
感谢您的观看
THANKS
有限元法
有限元法是一种数值分析方法，通过 将土体离散化为有限个单元体，建立 数学模型并求解，可以更准确地模拟 土坡的应力分布和变形情况。
有限元法的优点在于能够考虑土体的 非线性特性和复杂的边界条件，适用 于大型复杂土坡的稳定性分析。
地基承载力特征值
地基承载力特征值是指地基在垂直荷载作用下所能承受的极限压力，是评估建筑物地基稳定性的重要 指标。
在有限元分析中，强度理论用于模拟和分析复杂应力状态 下结构的响应和行为，为工程实践提供更精确和可靠的计 算结果。
04
土的特性与力学行为
土的分类与性质
土的分类
根据土的成因、粒径、物质组成等， 可以将土分为多种类型，如碎石土、 砂土、粘性土等。
土的性质
土的性质包括物理性质和力学性质。 物理性质包括密度、含水量、孔隙比 等；力学性质包括抗剪强度、压缩性、 抗拔能力等。
应力状态分析有助于了解结构的承载能力和稳定性， 为工程设计和安全评估提供依据。
应力状态分类
01
02
03
平面应力状态
物体受力作用在两个相互 垂直的平面上，且这两个 平面上的应力分量不相等。
平面应变状态
物体受力作用在两个相互 垂直的平面上，且这两个 平面上的应变分量不相等。
三向应力状态
物体在三个相互垂直的方 向上均受到应力作用，且 三个方向的应力分量都不 相等。
地基承载力特征值的确定需要考虑地质勘查报告、建筑物类型、基础形式等多种因素。
地基变形分析
地基变形分析是指对建筑物地基在不同荷载作用下的变形情况进行评估和分析，以确保建筑物在使用过程中不会发生过大的 沉降、倾斜或裂缝等不良现象。
地基变形分析的方法包括：沉降观测、倾斜测量、裂缝监测等。
感谢您的观看
THANKS
有限元法
有限元法是一种数值分析方法，通过 将土体离散化为有限个单元体，建立 数学模型并求解，可以更准确地模拟 土坡的应力分布和变形情况。
有限元法的优点在于能够考虑土体的 非线性特性和复杂的边界条件，适用 于大型复杂土坡的稳定性分析。
地基承载力特征值
地基承载力特征值是指地基在垂直荷载作用下所能承受的极限压力，是评估建筑物地基稳定性的重要 指标。
在有限元分析中，强度理论用于模拟和分析复杂应力状态 下结构的响应和行为，为工程实践提供更精确和可靠的计 算结果。
04
土的特性与力学行为
土的分类与性质
土的分类
根据土的成因、粒径、物质组成等， 可以将土分为多种类型，如碎石土、 砂土、粘性土等。
土的性质
土的性质包括物理性质和力学性质。 物理性质包括密度、含水量、孔隙比 等；力学性质包括抗剪强度、压缩性、 抗拔能力等。
三向应力
z
s z s 30 s 120 ) （
我们应该把X，Y，Z理解 成任意三个垂直的方向
特例（主单元体）
s
2
s3
s1
s
2
s1
1 2 3
1 E 1 E 1 E (s 1 s 2 ) (s s 1 )
s1
1 2 3
1 E 1 E 1 E (s 1 0 )
xy
2 xy
x y
例： 已知一点在某一平面内的 1、 2、 3、方向上的应变 1、
2、 3，三个线应变，求该面内的主应变。
解：由
x cos i y sin i
2 2
i
xy
sin i cos i
i =1,2,3这三个方程求出 x， y， x y；然后在求主应变。
2
co s 2
xy
2
sin 2
x y
2
sin 2
y
xy
2
co s 2
2 s x s t
2
s
s x s
s x s
2
y
cos 2 t xy sin 2
y
sin 2 t xy cos 2
二、应变分析图解法——应变圆（ Strain Circle）
1） x1 方 向 的 线 应 变 ； .沿 2）x1 y 1角 的 剪 应 变 。 .
dx
f ( x , y , z , xy , ) g ( x , y , z , xy , )
y1
y
x1
dy
三向应力状态简介
变形比能： 1 u 2
2
1 1 1 u 1 1 2 2 3 3 2 2 2
1 3
变形比能： 1 1 1 u 1 1 2 2 3 3 2 2 2
1 2 2 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E 1
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
解： 1 50MPa
2 50MPa 3 50MPa max 1 3
2 50MPa
CL10TU33
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
CL10TU34
解：
120 40 2 2
3(1 2 ) 2 1 2 2 m ( 1 2 3 ) uv 2E 6E
u f u uv
12 2 2 2 m ( 1 2 ) ( 2 3 ) ( 3 1 ) 6E
m
1 2 3
3
3 ( 1 2 ) 1 2 3 m 变形比能 = 体积改变比能 + 形状改变比能 E 3 K u = u + u
v
f CL10TU41
1 2 2 u 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E
1 式中：
E 1 体积弹性模量 K 3 (12 2 ) 2 （ 3 1 ） E 1 2 3 m 1 3 3 （ 1 2 ） 3 E 当 05 . 时， 0
2
3 1
1 3
§7-4各向同性材料的应力、应变关系一、广义胡克定律
σy
解： （1）求应变εx, εy ,εz 根据广义胡克定律：
σx
O
= ε x
1 E
(σ
x
−
µσ
y
)
=
1 200 ×
109
(160
×
106
+
0.25
×
40
×
106
)
=
8.5 ×10−4
εy
=1 E
(σ
y
−
µσ x )
= 200
1 ×
109
(−40 × 106
−
0.25×160×106 )
=−4 × 10−4
例: 刚性块D=5.001cm凹座，内放d=5cm刚性
圆柱体，F=300kN, E=200GPa, µ = 0.3,无摩擦，
求圆柱体主应力。
解：
σ3
=− F A
=− π30×05×012043
=−153MPa
F
设圆柱体胀满凹座
ε2 = (5.001− 5) 5= 0.0002
由对称性，可设 σ1 = σ2 = −q
(2) 坐标系转动30o，求 ε γ 30, 30/120
解：（ii）由应力转轴公式
σ= 30
σx
+σ y
2
+
σx
−σ
2
y
cos 2 × 30
−τ x
sin 2 × 30
= 160 − 40 + 160 + 40 cos 60 = 110MPa
2
2
（应力单位：MPa）
τ 30
σ
x
−σ
2
y
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 当一个为曲线一个为折线时，则以折线的转 折点为界分段，对每部分使用图乘法，然后 求代数和；
• 图乘法只适用于直杆，不适用于曲杆。
1 11X1 12 X 2 13 X 3 1P 0 2 21X1 22 X 2 X 23X 3 2P 0 3 31X1 32 X 2 33X 3 3P 0
B1
x y
1.在—坐标系中，
2
该点的横纵坐标代表单元体以
量取横坐标OB1=x， x轴为外法线方向面上的应力
纵坐标B1D1=x得到D1点。情况。同样方法得到D2点。
2.连D1D2交轴于c点，即以c点为圆心，cd为半径作圆。
R 1 2
x y 2 4 2
R c
x y
2
应
力
圆
(
x
2
T
IP
My
IZ
QS Z
IZb
强度 条件
max
N max Amin
jy jy
max
Tmax WP
max
M max WZ
max
轴向拉.压 扭 转
弯曲
变形
L＝ NL EA
＝ T L
G IP
EIf (x) M x
刚度条件 L L
Tmax 180
dxi
li
T (x)i GI p
T (x)i P
dxi
li
N ( x)i EAi
N (x)i P
dxi
莫 弯曲: 尔
l
M
x
M
EI
x
dx
积 拉、压:
分 公
扭转：
n N i N i li
i 1
EAi
l
T
x
T x
GI p
dx
式
l
组合变形的圆截面杆
N
(
x) N ( EI
x)dx
l
T
x
T x
三向应力状态的 广义胡克定律
轴向拉.压 剪 切 扭 转
弯曲
受力 P
PP
mm
P
变形特点
P
m
P
m 9549 P(kw)
n(r / min)
内力
轴力 N
剪力 Q
扭矩 T 剪力Q P一侧
(截面法) N P一侧 挤压力 Pjy T m一侧 弯矩m Px一侧
应力
N
A
＝ Q
Ajq
jy
Pjy Ajy
当对称结构上受对称荷载作用时,在对称截面 上,只有对称内力，反对称内力等于零。
当对称结构上受反对称荷载作用时，在对称截 面上只有反对称内力，对称内力等于零。
1、构件作等加速度直线运动和匀速转动时的应力 计算(惯性力问题)
2*、重冲物击从对h一高个处结自构由动落荷下系：数K只d 有一1个，自1 由落2h体st
y
)2
2
=
1 2
2
x
y
2
4
2 x
圆轴发生扭转变形时，最大拉应力发生在（ 斜） 截面上，最大剪应力发生在（ 横 ）截面上。
m
塑性材料： [] ＜[]
m
材料被剪断，断口平齐
脆性材料：[] ＜[]
材料被拉断，断口与轴线 450角
三向应力状态的广义胡克定律
2
1
1 E
1
2
3
1
2
1 E
2
3
1
Pl3 3EI
ymax
ql 4 8EI
ymax
Pl 3 48EI Z
ymax
5ql 4 384 EI Z
b h
y d
y
bh3 I z 12
z
Iy
hb3 12
bh 2 Wz 6
Wy
hb 2 6
Iz
I y
d 4
64
Wz
Wy
d 3
32
z
IP
D 4
32
(1 4 )
Wt=
d
D 3
( 1- 4 )
GIP
fmax
f
max
虎克定律 E G
超静定 问题
1、静平衡方程 2、变形协调方程
转角
max
Ml EI
max
Pl 2 2EI
max
ql 3 6EI
Ml 、Ml 3EI 6EI
max
Pl 2 16 EI Z
max
ql 3
24EI Z
挠度
Ml 2 ymax 2EI
ymax
两端固定
＝0.5
两端铰支
＝1.0
cr
2E 2
p
GI p
dx
l
M
(
x)M EI
(
x)dx
※式中： N ( x)、T ( x)、M ( x) :
_____构件在求位移点处沿所求位移方向只有单位力 作用时，构件中产生的内力.
M (x)M (x)dx M C
l
EI
EI
• M x，M x的图中一定有一个是线性的；
• 当弯矩图较复杂时，采用叠加方法；
( M )2 3( T )2
W
Wt
r4
1 W
M 2 0.75T 2
对于拉、弯、扭同时存在作用在圆形截面时:
r3
( N M )2 ( T )2 AW W
r4
( N M )2 0.75( T )2
AW
W
ay
iz2 yP
az
i
2 y
zP
1、中性轴不能将横截面分为两部分
2、截面核心的形状受截面外边界控制
3
3
1 E
3
1
2
主应力和主应变的方向重合。1 2 3
y
y
z
x
x
x
1 E
x
y
y
1 E
y
x
z
E
x
y
G
y
y
z
x x
1 1 （ 2 3）
1 3
1（[
2
1
）2
2
2
3
2
3
1
2
]
r
r
莫尔强度理论：
1
[ t ] [ c ]
3
[
t
]
r3 2 4 2 r4 2 3 2
垂直冲击动荷系数中的st是结构中受冲击点沿
冲击方向的静位移。
*水平冲击:
Kd
d st
v2 g st
水平冲击中的 st 是假设冲击物重量沿水平 方向作用时，在冲击点沿冲击方向的静位移。
各种支承压杆临界载荷的通用公式：
Pcr
2 EImin （l）2
一端自由，一端固定 ＝2.0
一端铰支，一端固定 ＝0.7
16
D
x y
2
x y cos 2
2
x sin 2
x y sin 2
2
x cos 2
tg2 2 x x y
max( mix)
x
y
2
(
x
2
y
)2
2 x
在单元体上两个剪应力共同指定的象限
既为主应力1所在象限
1.应力圆的画法
y
y
R
x
c
x
o B2
(y ,Dy)2
D1(x ,x)
3、中性轴和力的作用点分别在截面形心两侧
组
合
Q(x)
变
Q(x)
形
的
变 杆内总变形能:
形U
N 2 (x) dx
T 2 (x)dx
M 2 (x) dx
能
l 2EA
l 2GIP
l 2EIPiU i卡氏第二定理：Q(x) Q(x)
Pi
U i
li
M (x)i EI
M (x)i P
危险点处于单相应力状态
双向弯曲（原形横截面）
M
M
2 Z
M
2 Y
M
W
M
2 Z
M
2 Y
W
x
max
( M Z WZ
FN Mzy
AI
MY )
WMYyz I
r3 2 4 2 r4 2 3 2
圆形截面：Wt 2W
r3
( M )2 4( T )2
W
Wt
r3
1 W
M2 T2
r4
• 图乘法只适用于直杆，不适用于曲杆。
1 11X1 12 X 2 13 X 3 1P 0 2 21X1 22 X 2 X 23X 3 2P 0 3 31X1 32 X 2 33X 3 3P 0
B1
x y
1.在—坐标系中，
2
该点的横纵坐标代表单元体以
量取横坐标OB1=x， x轴为外法线方向面上的应力
纵坐标B1D1=x得到D1点。情况。同样方法得到D2点。
2.连D1D2交轴于c点，即以c点为圆心，cd为半径作圆。
R 1 2
x y 2 4 2
R c
x y
2
应
力
圆
(
x
2
T
IP
My
IZ
QS Z
IZb
强度 条件
max
N max Amin
jy jy
max
Tmax WP
max
M max WZ
max
轴向拉.压 扭 转
弯曲
变形
L＝ NL EA
＝ T L
G IP
EIf (x) M x
刚度条件 L L
Tmax 180
dxi
li
T (x)i GI p
T (x)i P
dxi
li
N ( x)i EAi
N (x)i P
dxi
莫 弯曲: 尔
l
M
x
M
EI
x
dx
积 拉、压:
分 公
扭转：
n N i N i li
i 1
EAi
l
T
x
T x
GI p
dx
式
l
组合变形的圆截面杆
N
(
x) N ( EI
x)dx
l
T
x
T x
三向应力状态的 广义胡克定律
轴向拉.压 剪 切 扭 转
弯曲
受力 P
PP
mm
P
变形特点
P
m
P
m 9549 P(kw)
n(r / min)
内力
轴力 N
剪力 Q
扭矩 T 剪力Q P一侧
(截面法) N P一侧 挤压力 Pjy T m一侧 弯矩m Px一侧
应力
N
A
＝ Q
Ajq
jy
Pjy Ajy
当对称结构上受对称荷载作用时,在对称截面 上,只有对称内力，反对称内力等于零。
当对称结构上受反对称荷载作用时，在对称截 面上只有反对称内力，对称内力等于零。
1、构件作等加速度直线运动和匀速转动时的应力 计算(惯性力问题)
2*、重冲物击从对h一高个处结自构由动落荷下系：数K只d 有一1个，自1 由落2h体st
y
)2
2
=
1 2
2
x
y
2
4
2 x
圆轴发生扭转变形时，最大拉应力发生在（ 斜） 截面上，最大剪应力发生在（ 横 ）截面上。
m
塑性材料： [] ＜[]
m
材料被剪断，断口平齐
脆性材料：[] ＜[]
材料被拉断，断口与轴线 450角
三向应力状态的广义胡克定律
2
1
1 E
1
2
3
1
2
1 E
2
3
1
Pl3 3EI
ymax
ql 4 8EI
ymax
Pl 3 48EI Z
ymax
5ql 4 384 EI Z
b h
y d
y
bh3 I z 12
z
Iy
hb3 12
bh 2 Wz 6
Wy
hb 2 6
Iz
I y
d 4
64
Wz
Wy
d 3
32
z
IP
D 4
32
(1 4 )
Wt=
d
D 3
( 1- 4 )
GIP
fmax
f
max
虎克定律 E G
超静定 问题
1、静平衡方程 2、变形协调方程
转角
max
Ml EI
max
Pl 2 2EI
max
ql 3 6EI
Ml 、Ml 3EI 6EI
max
Pl 2 16 EI Z
max
ql 3
24EI Z
挠度
Ml 2 ymax 2EI
ymax
两端固定
＝0.5
两端铰支
＝1.0
cr
2E 2
p
GI p
dx
l
M
(
x)M EI
(
x)dx
※式中： N ( x)、T ( x)、M ( x) :
_____构件在求位移点处沿所求位移方向只有单位力 作用时，构件中产生的内力.
M (x)M (x)dx M C
l
EI
EI
• M x，M x的图中一定有一个是线性的；
• 当弯矩图较复杂时，采用叠加方法；
( M )2 3( T )2
W
Wt
r4
1 W
M 2 0.75T 2
对于拉、弯、扭同时存在作用在圆形截面时:
r3
( N M )2 ( T )2 AW W
r4
( N M )2 0.75( T )2
AW
W
ay
iz2 yP
az
i
2 y
zP
1、中性轴不能将横截面分为两部分
2、截面核心的形状受截面外边界控制
3
3
1 E
3
1
2
主应力和主应变的方向重合。1 2 3
y
y
z
x
x
x
1 E
x
y
y
1 E
y
x
z
E
x
y
G
y
y
z
x x
1 1 （ 2 3）
1 3
1（[
2
1
）2
2
2
3
2
3
1
2
]
r
r
莫尔强度理论：
1
[ t ] [ c ]
3
[
t
]
r3 2 4 2 r4 2 3 2
垂直冲击动荷系数中的st是结构中受冲击点沿
冲击方向的静位移。
*水平冲击:
Kd
d st
v2 g st
水平冲击中的 st 是假设冲击物重量沿水平 方向作用时，在冲击点沿冲击方向的静位移。
各种支承压杆临界载荷的通用公式：
Pcr
2 EImin （l）2
一端自由，一端固定 ＝2.0
一端铰支，一端固定 ＝0.7
16
D
x y
2
x y cos 2
2
x sin 2
x y sin 2
2
x cos 2
tg2 2 x x y
max( mix)
x
y
2
(
x
2
y
)2
2 x
在单元体上两个剪应力共同指定的象限
既为主应力1所在象限
1.应力圆的画法
y
y
R
x
c
x
o B2
(y ,Dy)2
D1(x ,x)
3、中性轴和力的作用点分别在截面形心两侧
组
合
Q(x)
变
Q(x)
形
的
变 杆内总变形能:
形U
N 2 (x) dx
T 2 (x)dx
M 2 (x) dx
能
l 2EA
l 2GIP
l 2EIPiU i卡氏第二定理：Q(x) Q(x)
Pi
U i
li
M (x)i EI
M (x)i P
危险点处于单相应力状态
双向弯曲（原形横截面）
M
M
2 Z
M
2 Y
M
W
M
2 Z
M
2 Y
W
x
max
( M Z WZ
FN Mzy
AI
MY )
WMYyz I
r3 2 4 2 r4 2 3 2
圆形截面：Wt 2W
r3
( M )2 4( T )2
W
Wt
r3
1 W
M2 T2
r4