苏科版七年级上:有理数与无理数教学设计
【推荐】苏科初中数学七年级上册《2.2 有理数与无理数》教案 (5)
六.预习指导
板书设计
教学反思
(3)因为 ,…两个相同分数因数的乘积都为分数,所以a不可能是分数.也可按书P16、问题6选取无限多大于1且小于2的两个相同分数的乘积来考查。体会“无限”的过程,认可找不到一个数的平方等于2,即a也不可能是分数。
在等式a2=2中,a既不是整数,也不是分数,也就是不能写成 的形式,所以a不是有理数,但在现实生活中确实存在像a这样的数,由此看来,数又不够用了.
二.合作、探究、展示
有理数包括整数和分数,那么有理数范围是否就能满足我们实际生活的需要呢?下面我们就来共同研究这个问题.
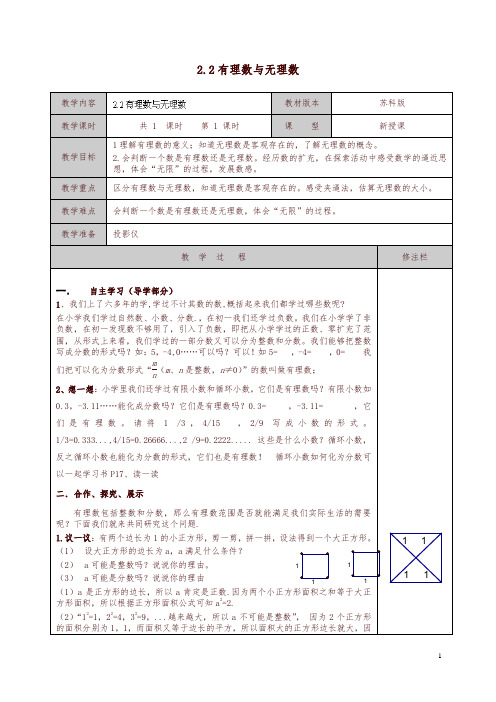
1.议一议:有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大正方形。
(1) 设大正方形的边长为a,a满足什么条件?
(2)a可能是整数吗?说说你的理由。
(3)a可能是分数吗?说说你的理由
2.2有理数与无理数
教学内容
教材版本
苏Байду номын сангаас版
教学课时
共1课时第1课时
课型
新授课
教学目标
1理解有理数的意义;知道无理数是客观存在的,了解无理数的概念。
2.会判断一个数是有理数还是无理数。经历数的扩充,在探索活动中感受数学的逼近思想,体会“无限”的过程,发展数感。
教学重点
区分有理数与无理数,知道无理数是客观存在的。感受夹逼法,估算无理数的大小。
教学难点
会判断一个数是有理数还是无理数,体会“无限”的过程。
教学准备
投影仪
教学过程
修注栏
一.自主学习(导学部分)
1、我们上了六多年的学,学过不计其数的数,概括起来我们都学过哪些数呢?
在小学我们学过自然数、小数、分数.,在初一我们还学过负数。我们在小学学了非负数,在初一发现数不够用了,引入了负数,即把从小学学过的正数、零扩充了范围,从形式上来看,我们学过的一部分数又可以分为整数和分数。我们能够把整数写成分数的形式吗?如:5,-4,0……可以吗?可以!如5=,-4=,0=我们把可以化为分数形式“ (m、n是整数,n≠0)”的数叫做有理数;
有理数与无理数苏教版数学初一上册教案

有理数与无理数苏教版数学初一上册教案
《数学初一上册》是苏教版的一本初中数学教材,以下是《数学初一上册》中有关有
理数与无理数的教案:
教案一:有理数的概念及表示
教学目标:
1. 理解有理数的概念和特点;
2. 掌握有理数的表示方法。
教学过程:
1. 复习:复习整数的概念和表示方法;
2. 引入:通过例题,让学生发现整数之间可以使用分数互相转换,引出有理数的概念;
3. 讲解:介绍有理数的定义,并讲解有理数的表示方法(分数、小数、整数);
4. 运用:设计一些练习题,让学生练习使用各种方法表示有理数。
教案二:无理数的定义和性质
教学目标:
1. 理解无理数的概念和特点;
2. 了解无理数的表示方法;
3. 掌握无理数的一些性质。
教学过程:
1. 复习:复习有理数的表示方法;
2. 引入:通过开平方的例子,让学生发现无理数的存在;
3. 讲解:介绍无理数的概念和定义,并讲解无理数的表示方法(根号、小数);
4. 拓展:讲解无理数的性质,如无理数与有理数的运算、无理数的比较等;
5. 运用:设计一些练习题,让学生练习使用无理数进行计算和比较。
以上是两个教案的简要介绍,具体的教学内容和教学方法可以根据《数学初一上册》教材的教学目标和教学内容进行拓展和调整。
苏科初中数学七年级上册《2.2 有理数与无理数》教案 (7)【精品】

教学内容
2.2有理数与无理数
复习目标
1理解有理数的意 义;知道无理数是客观 存在的,了解无理数的概念。
2.会判断一个数是有理数还是无 理数。经历数的扩充,在探索活动中感受数学 的逼近思想,体会“无 限”的过程,发展数感。
复习重点
区分有理数与无理数,知道无理数是客观存在的。估算无理数的大小。
探索:a的小数部分是多少?
6.定义
有理数总可 以用有限小数或无限循环小数表示。
反之,任何有限小数或无限循环小数也都是有理数。
无限不循环小数是无理数,反之,无理数就是无限不循环小数。
7.更多无理数
(1)圆周率型
(2)构造型
典型例题
例1下列各数中,哪些是有理数?哪些是无理 数?
3.14 , -4/3, 0.57, 0.101000100 0001…(相邻两个1之间0的个数逐次加2)
复习难点
会判断一个数是有理数还是无理数,体会“无限”的过程。
教学过程
二次备课
情景引入:
小数是否可以与分数互化?
探究学习:
1.回顾整数与分数的概念:
整数有正整数、0、负整数,如1,2,3,0,-1,-2,-3等。
分数有正分数、负分数,分数的形式为(m、n是整数,n≠0)
2.整数也可以表示成分数的形式:
边长a
面积S
1 <a<2
1<S<4
1.4<a<1.5
1.96<S<2.25
1.41<a<1.42
1.9881<S<2.0164
1.414<a<1.415
1.999396<S<2.002225
1.4142<a<1.4143
1.99996164<S<2.000244 49
七年级数学上册2.2有理数与无理数教学设计(新版)苏科版

有理数与无理数教学目标1.理解有理数的意义.2.知道无理数是客观存在的,了解无理数的概念.3.会判断一个数是有理数还是无理数.4.经历数的扩充,在探索活动中感受数学的逼近思想,体会“无限”的过程,发展数感.重点难点1.区分有理数与无理数,知道无理数是客观存在的.2.感受估算法,估算无理数的大小.3.会判断一个数是有理数还是无理数,体会“无限”的过程.教学过程一、课堂活动:1.知识回顾下列给出的各数,哪些是正数?哪些是负数?哪些是整数?哪些是分数?-8.4 , 22 , 617-,0.33 , 0 , 53-, -9 答:正数:22 , 0.33 负数:-8.4 , 617- , 53- , -9 整数:22 , 0 , -9 分数:-8.4 , 617- , 0.33 , 53- 昨天我们学习了正数、负数,因此我们可以把数如何分类呢?整数和分数呢?生答:数:正数、0、负数;整数:正整数、0、负整数;分数:正分数、负分数.3. 实际上,所有的整数都可以写成分母是1的分数;如:5,-4, 0[答]可以!如5=51,-4= 4411--或,0=01; 小结:我们把可以化为分数形式“m n (m 、n 是整数,n ≠0)”的数叫做有理数;4.想一想:小学里我们还学过有限小数和无限循环小数,它们是有理数吗?有限小数如0.3,-3.11,... ...能化成分数吗?它们是有理数吗?答: 0.3=310,-3.11=31110-,它们是有理数. (2)请将13,415,29写成小数的形式. 答: 13=0.333...,415=0.26666...,29=0.2222..... 问:这些是什么小数?答:无限循环小数小结:反之循环小数也能化为分数的形式,它们也是有理数!循环小数如何化为分数可以一起学习书P17 读一读二、讲授新课有理数分类(1)有理数:包括整数和分数,(2)有理数还可分为正有理数、0和负有理数;有理数的分类:那么是不是所有的数都是有理数呢?下面我们就来共同研究这个问题.议一议:有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大正方形.(1)设大正方形的边长为a ,a 满足什么条件?答:22=a(2)a 可能是整数吗?说说你的理由.答:不可能,因为112=,422=,(3)a 可能是分数吗?说说你的理由,并与同伴交流.可按书P16 问题6选取无限多大于1且小于2的两个相同分数的乘积来考查.体会“无限”的过程,认可找不到一个数的平方等于2,即a 也不可能是分数.小结:经过讨论可知,在等式a 2=2中,a 既不是整数,也不是分数,也就是不能写成 m n的形式,所以a 不是有理数,a 是一个无限不循环小数,它的值是1.414 213 562 373….概念:无限不循环小数叫做无理数.(此处可处理优学第9题)小学学过的圆周率π是无限不循环小数,它的值是3.141 592 653 589…,因此π是无理数.三、例题讲解:把下列各数填在相应的括号内:正数集合{ }负数集合{ }正有理数集合{ }负有理数集合{ }归纳总结——有理数与无理数的主要区别(1)无理数是无限不循环小数,有理数是整数或有限小数或无限循环小数.(2)任何一个有理数都可以化为分数的形式,而无理数则不能.五、课时小结 1.什么叫无理数?2.数的分类?3.如何判定一个数是无理数还是有理数.六、反馈作业课作《课课练》 家作《优学》七、教学反思 中国书法艺术说课教案今天我要说课的题目是中国书法艺术,下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。
【精编】苏科初中数学七年级上册《2.2 有理数与无理数》教案 (7)

有限小数可以化成 的形式,是有理数。1/3=0.333...,4/15=0.26666...,2 /9=0.2222.....这些是什么小数?循环小数,反之循环小数也能化为分数的形式,它们也是有理数!
循环小数如何化为分数可以一起学习书P17、读一读
探索:a的小数部分是多少?
6.定义
有理数总可以用有限小数或无限循环小数表示。
反之,任何有限小数或无限循环小数也都是有理数。
无限不循环小数是无理数,反之,无理数就是无限不循环小数。
7.更多无理数
(1)圆周率型
(2)构造型
典型例题
例1下列各数中,哪些是有理数?哪些是无理数?
3.14 , -4/3, 0.57, 0.101000100 0001…(相邻两个1之间0的个数逐次加2)
会判断一个数是有理数还是无理数,体会“无限”的过程。
教学过程
二次备课
情景引入:
小数是否可以与分数互化?
探究学习:
1.回顾整数与分数的概念:
整数有正整数、0、负整数,如1,2,3,0,-1,-2,-3等。
分数有正分数、负分数,分数的形式为 (m、n是整数,n≠0)
2.整数也可以表示成分数的形式:
如 , ,
有理数与无理数
教学内容
2.2有理数与无理数
复习目标
1理解有理数的意义;知道无理数是客观存在的,了解无理数的概念。
2.会判断一个数是有理数还是无理数。经历数的扩充,在探索活动中感受数
区分有理数与无理数,知道无理数是客观存在的。估算无理数的大小。
复习难点
整数和分数都是有理数。
4.将有理数进行分类。
5.议一议:有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大正方形。
苏科初中数学七上《有理数与无理数》教案

2.2 有理数与无理数教学目标1.理解有理数的意义和会对有理数进行分类;2.了解无理数的意义. 教学重点1.有理数的意义和分类;2.无理数的意义.教学难点有理数的分类,区分有理数和无理数. 教学过程(教师)学生活动设计思路 有理数我们学过整数(正整数、负整数、零)和分数(正分数、负分数).实际上,所有整数都可以写成分母为1的分数的形式.如 55=,144=,1--0=.1我们把能写成分数形式mn(m 、n 是整数,n ≠0)的数叫做有理数.想一想:小学里学过的有限小数和无限循环小数是有理数吗? 根据有理数的定义,有理数可以进行如下的分类:⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数,或⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数 结合55=,144=,1--0=,1体会整数可化成分母为1的分数形式.30.310=,3113.11100-=-,10.3333=,40.266615=.有限小数和无限循环小数都可以化为分数,它们都是有理数.引入有理数的定义,并按照定义说明整数、分数是有理数.通过将有限小数和无限循环小数转化为分数,说明有限小数和无限循环小数也是有理数,为有理数的分类做好铺垫.无理数议一议:是不是所有的数都是有理数呢?将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.如果大正方形的边长为a ,那么a 2=2.a 是有理数吗?事实上,a 不能写成分数形式mn(m 、n 是整数,n ≠0),a 是无限不循环小数,它的值是1.414 213 562 373….无限不循环小数叫做无理数.小学学过的圆周率π是无限不循环小数,它的值是3.141 592 653 589…,π是无理数.此外,像0.101 001 000 1…、-0.101 001 000 1…这样的无限不循环小数也是无理数.通过拼图,探索,让学生感受a 不能化为分数的形式,引出a 这个无限不循环小数,从而得到无理数的定义.通过π进一步说明无理数的确存在.根据无理数的定义,我们还可以构造像0.101 001 000 1…、-0.101 001 000 1…这样的无理数.有理数的分类根据有理数的定义,有理数包括整数和分数,即⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数,或⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数 结合有理数的两种不同分类,体会分类思想. 渗透分类思想,加深对有理数的认识,初步体会数系扩张的过程.课堂练习:将下列各数填入相应括号内:169.36--,,,42,0,-0.33,0.333,1.414 213 56,-2π,3.303 003 000 3,-3.141 592 6.正数集合:{ …}; 负数集合:{ …}; 正有理数集合:{ …}; 负有理数集合:{ …}.独立完成,课堂交流.正数集合:{9.3,42,0.333,1.414 213 56,3.303 003 000 3,…}; 负数集合:{166--,,-0.33,2π-,-3.141 592 6,…}; 正有理数集合:{9.3,42,0.333,1.414 213 56,…}; 负有理数集合:{166--,,-0.33,-3.141 592 6, …}. 当堂巩固所学知识.课堂小结:谈谈你这一节课有哪些收获. 回顾本节的教学内容,从知识和方法两个层面进行总结. 归纳知识体系,提炼思想和方法.。
最新苏科版七年级数学上册《有理数与无理数2》教学设计

2.2 有理数与无理数教学目标1.理解有理数的意义和会对有理数进行分类;2.了解无理数的意义.教学重点 1.有理数的意义和分类; 2.无理数的意义.教学难点 有理数的分类,区分有理数和无理数.教学过程有理数我们学过整数(正整数、负整数、零)和分数(正分数、负分数).实际上,所有整数都可以写成分母为1的分数的形式.如 55=,144=,1--00=.1我们把能写成分数形式m n(m 、n 是整数,n ≠0)的数叫做有理数. 想一想:小学里学过的有限小数和无限循环小数是有理数吗?根据有理数的定义,有理数可以进行如下的分类:⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数,或⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数 结合55=,144=,1--00=,1体会整数可化成分母为1的分数形式.30.310=,3113.11100-=-,10.3333=,40.266615=. 有限小数和无限循环小数都可以化为分数,它们都是有理数.无理数议一议:是不是所有的数都是有理数呢?将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.如果大正方形的边长为a,那么a2=2.a是有理数吗?事实上,a不能写成分数形式mn(m、n是整数,n≠0),a是无限不循环小数,它的值是1.414 213 562 373….无限不循环小数叫做无理数.小学学过的圆周率π是无限不循环小数,它的值是3.141 592 653 589…,π是无理数.此外,像0.101 001 000 1…、-0.101 001 000 1…这样的无限不循环小数也是无理数.通过拼图,探索,让学生感受a不能化为分数的形式,引出a这个无限不循环小数,从而得到无理数的定义.通过π进一步说明无理数的确存在.根据无理数的定义,我们还可以构造像0.101 001 000 1…、-0.101 001 000 1…这样的无理数.有理数的分类根据有理数的定义,有理数包括整数和分数,即⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数,或⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数 结合有理数的两种不同分类,体会分类思想. 课堂练习: 将下列各数填入相应括号内:169.36--,,,42,0,-0.33,0.333,1.414 213 56,-2π,3.303 003 000 3,-3.141 592 6. 正数集合:{ …};负数集合:{ …};正有理数集合:{ …};负有理数集合:{ …}. 独立完成,课堂交流. 正数集合:{9.3,42,0.333,1.414 213 56,3.303 003 000 3,…}; 负数集合:{166--,,-0.33,2π-,-3.141 592 6, …}; 正有理数集合:{9.3,42,0.333,1.414 213 56,…}; 负有理数集合:{166--,,-0.33,-3.141 592 6, …}. 课堂小结:谈谈你这一节课有哪些收获.。
苏科版数学七年级上册2.2《有理数与无理数》教学设计

苏科版数学七年级上册2.2《有理数与无理数》教学设计一. 教材分析《有理数与无理数》是苏科版数学七年级上册第2章第2节的内容。
这一节主要介绍了有理数和无理数的概念,以及它们的特点。
教材通过实例和问题,引导学生理解和掌握有理数和无理数的概念,以及它们在实际问题中的应用。
二. 学情分析七年级的学生已经学习了实数的概念,对数的运算也有了一定的了解。
但是,对于有理数和无理数的概念,以及它们的特点,可能还比较陌生。
因此,在教学过程中,需要通过实例和问题,引导学生理解和掌握有理数和无理数的概念,以及它们的特点。
三. 教学目标1.理解有理数和无理数的概念,以及它们的特点。
2.掌握有理数和无理数的运算方法。
3.能够应用有理数和无理数的概念和运算方法,解决实际问题。
四. 教学重难点1.有理数和无理数的概念。
2.有理数和无理数的运算方法。
五. 教学方法采用问题驱动的教学方法,通过实例和问题,引导学生理解和掌握有理数和无理数的概念,以及它们的特点。
在教学过程中,注重学生的参与和思考,鼓励学生提出问题和解决问题。
六. 教学准备1.教材和教案。
2.课件和教学辅助材料。
3.练习题和测试题。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生思考实数的分类。
例如,问学生:“你们知道吗,有些数可以表示成两个整数的比,而有些数却不能。
你们能找出这样的数吗?”让学生列举一些例子,从而引出有理数和无理数的概念。
2.呈现(15分钟)通过PPT或者黑板,呈现有理数和无理数的定义和特点。
有理数是可以表示成两个整数比的数,无理数则不能。
有理数包括整数、分数和小数,而无理数则是无限不循环的小数。
3.操练(15分钟)让学生通过实际的例子,理解和掌握有理数和无理数的概念。
可以让学生做一些练习题,例如判断一个数是有理数还是无理数,或者将一个无理数近似为有理数。
4.巩固(10分钟)通过一些练习题,巩固学生对有理数和无理数的理解和掌握。
可以让学生做一些有关有理数和无理数的运算题,例如加减乘除等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理数的分类
根据有理数的定义,有理数包括整数和分数,即 ,或
有理数
我们学过整数(正整数、负整数、零)和分数(正分数、负分数).实际上,所有整数都可以写成分母为1的分数的形式.如
我们把能写成分数形式 (m、n是整数,n≠0)的数叫做有理数.
想一想:
小学里学过的有限小数和无限循环小数是有理数吗?
根据有理数的定义,有理数可以进行如下的分类:
,或
结合 体会整数可化成分母为1的分数形式.
正有理数集合:{ …};
负有理数集合:{ …}.
当堂巩固所学知识.
课堂小结:
谈谈你这一节课有哪些收获.
回顾本节的教学内容,从知识和方法两个层面进行总结.
归纳知识体系,提炼思想和方法.
, , , .
有限小数和无限循环小数都可以化为分数,它们都是有理数.
引入有理数的定义,并按照定义说明整数、分数是有理数.通过将有限小数和无限循环小数转化为分数,说明有限小数和无限循环小数也是有理数,为有理数的分类做好铺垫.
无理数
议一议:是不是所有的数都是有理数呢?
将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.
结合有理数的两种不同分类,体会分类思想.
渗透分类思想,加深对有理数的认识,初步体会数系扩张的过程.
课堂练习:
将下列各数填入相应括号内: , , , ,-2π, , .
正数集合:{…};
负数集合:{…};
正有理数集合:{…};
负有理数集合:{…}.
独立完成,课堂交流.
正数集合:{
…};
负数集合:{ …};
数学教学设计
教 材:义务教育教科书·数学(七年级上册)
作者:钱颖(苏州市振华中学校)
2.2有理数与无理数
教学目标
1.理解有理数的意义和会对有理数进行分类;
2.了解无理数的意义.
教学重点
1.有理数点
有理数的分类,区分有理数和无理数.
教学过程(教师)
学生活动
设计思路
如果大正方形的边长为a,那么a2=2.a是有理数吗?
事实上,a不能写成分数形式 (m、n是整数,n≠0),a是无限不循环小数,它的值是1.414 213 562 373….
无限不循环小数叫做无理数.
小学学过的圆周率π是无限不循环小数,它的值是3.141 592 653 589…,π是无理数.
此外,像0.101 001 000 1…、-0.101 001 000 1…这样的无限不循环小数也是无理数.
