Matlab数字衍射光学实验讲义(一)
Matlab数字衍射光学实验(二).
clear;close all;lamda=0.6328;%入射光波长,单位umz=200.0e3;%传播距离,单位umh=2e3;w=2e3;%模拟光波的大小,单位umdx=10.0;dy=10.0;%抽样间隔,单位umM=h/dx;N=w/dy;%抽样点数a0=1;%初始振幅大小为 1x0=0;y0=0;%模拟光源位于坐标原点k=2*pi/lamda;%波数%---------球面波表示-------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%M个点,两点之间的距离为dxSphFunct=a0/z.*exp(i*k*z).*exp(i*pi/(lamda*z).*((x-x0).^2+(y-y 0).^2));%球面波I=abs(SphFunct).^2;%光强度I1=I./max(max(I));%归一化强度,二维所以求两次max()Ph=angle(SphFunct);%相位,函数angle()表示取相位figure(1);imagesc(I1);%做出球面波的强度分布图，没有强度变化，均匀光斑,这里做了彩图figure(2);P=(Ph+pi)/(2*pi);%归一化相位imshow(P);%画出球面波的相位分布图figure(3);imagesc(P);%画出球面波相位分布的彩图clear;close all;lamda=0.6328;%入射光波长umh=2e3;w=2e3;%模拟光波的大小um dx=10.0;dy=10.0;%抽样间隔umM=h/dx;N=w/dy;%抽样点数A=1;%振幅为 1k=2*pi/lamda;%波数theta=pi/6;%设定theta为30度a=pi/2-theta;%波矢与x轴夹角b=pi/2;%波矢与y轴夹角c=theta;%波矢与z轴夹角z=0;%-----------平面波----------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%抽样网格pingmianbo=A.*exp(i*k.*(x.*cos(a)+y.*cos(b)+z.*cos(c)));%平面波公式I=abs(pingmianbo).^2;%光强度I1=I./max(max(I));%归一化强度Ph=angle(pingmianbo);%相位figure(1);imshow(I1)%做出强度分布图,没有强度变化，均匀光斑figure(2);imagesc(I1);%画出强度分布彩图figure(3);P=(Ph+pi)/(2*pi);%归一化相位imshow(P);%画出相位分布图像figure(4);imagesc(P);%做出相位分布彩图clear;close all;lamda=0.6328;%入射光波长umz=100.0e3;%传播距离umh=2e3;w=2e3;%模拟光波的大小umdx=10.0;dy=10.0;%抽样间隔umM=h/dx;N=w/dy;%抽样点数a0=1;%设定振幅x1=-0.2e3;y1=0;%相当于将上图逆时针旋转90度后的S1,距原点0.2mmx2=0.2e3;y2=0;%相当于将上图逆时针旋转90度后的S2,距原点0.2mmk=2*pi/lamda;%波数%---------球面波---------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%抽样网格wave1=a0/z.*exp(i*k*z).*exp(i*pi/(lamda*z).*((x-x1).^2+(y-y1).^2));%第一束球面波wave2=a0/z.*exp(i*k*z).*exp(i*pi/(lamda*z).*((x-x2).^2+(y-y2).^2));%第二束球面波wave=wave1+wave2;%两束球面波相遇,即为两者复振幅之和I=abs(wave).^2;%光强度I1=I./max(max(I));%归一化强度Ph=angle(wave);%相位函数angle()表示取相位figure(1);imshow(I1);%画出球面波的强度分布图,没有强度变化,均匀光斑figure(2);P=(Ph+pi)/(2*pi);%归一化相位imshow(P);%画出球面波的相位分布图figure(3);imagesc(P);%画出球面波的相位分布彩图clear;close all;lamda=0.6328;%入射光波长umh=2e3;w=2e3;%模拟光波的大小umdx=10.0;dy=10.0;%抽样间隔umM=h/dx;N=w/dy;%抽样点数A=1;%设定振幅为 1k=2*pi/lamda;%波数theta1=-0.25*pi/180;%第一束平面波与z轴夹角theta2=0.25*pi/180;%第二束平面波与z轴夹角a1=pi/2-theta1;%波矢与x轴夹角b1=pi/2;%波矢与y轴夹角c1=theta1;%波矢与z轴夹角a2=pi/2-theta2;%波矢与x轴夹角b2=pi/2;%波矢与y轴夹角c2=theta2;%波矢与z轴夹角z=0e3;%----------平面波表示----------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%二维抽样网格wave1=A.*exp(i*k.*(x.*cos(a1)+y.*cos(b1)+z.*cos(c1)));%第一束平面波wave2=A.*exp(i*k.*(x.*cos(a2)+y.*cos(b2)+z.*cos(c2)));%第二束平面波wave=wave1+wave2;%两束光相遇I=abs(wave).^2;%光强度I1=I./max(max(I));%归一化强度Ph=angle(wave);%相位figure(1);imshow(I1);%画出强度分布图figure(2);imagesc(I1);%画出强度分布彩图figure(3);P=(Ph+pi)/(2*pi);%归一化强度imshow(P);%做出相位分布图figure(4);imagesc(P);%做出相位分布彩图。
光学衍射图样的MATLAB仿真
1、建立几何模型：在Matlab中建立一个单缝衍射模型，包括一个光源、一 个单缝和一个观察点。
2、设置光源和观察条件：设置光源的波长为600纳米，强度为1瓦，方向为 垂直于缝的方向；观察点位于缝的右侧1米处，观察角度为45度。
3、进行仿真计算：利用Matlab中的相关函数进行仿真计算，得到观察点处 光的强度分布。
光学衍射图样的MATLAB仿真
目录
01 摘要
03 二、衍射的基本原理
02 一、引言 04 三、MATLAB在光学仿
真中的应用
目录
05 四、光学衍射图样的 MATLAB仿真
07 六、结论与展望
06 五、具体例子 08 参考内容
摘要
本次演示介绍了使用MATLAB进行光学衍射图样仿真的方法。首先介绍了衍射 的基本原理和MATLAB在光学仿真中的应用，然后详细阐述了如何使用MATLAB进行 衍射图样的仿真。通过具体的例子，展示了如何使用MATLAB模拟不同条件下的衍 射现象，并解释了仿真结果。最后，总结了本次演示的主要内容和贡献，并指出 了未来可能的研究方向。
参考内容
引言
光学衍射在许多领域中都具有重要应用，例如光学仪器设计、光谱分析、光 信息处理等。对光学衍射进行仿真可以帮助人们更好地理解光学系统的性能，预 测光的传播行为，优化光学设计。本次演示将介绍如何使用Matlab进行光学衍射 仿真。
准备工作
在进行光学衍射仿真之前，需要做好以下准备工作： 1、安装Matlab：首先需要安装Matlab软件，版本要求至少为R2018a或更高。
其中E(x,y)是电场强度，λ是光的波长，c是光速。通过求解这个方程，可 以得到衍射图样的电场分布。
三、MATLAB在光学仿真中的应 用
基于Matlab的光学实验仿真
基于Matlab的光学实验仿真一、本文概述随着科技的快速发展，计算机仿真技术已成为科学研究、教学实验以及工程应用等领域中不可或缺的一部分。
在光学实验中，仿真技术能够模拟出真实的光学现象，帮助研究者深入理解光学原理，优化实验设计，提高实验效率。
本文旨在探讨基于Matlab的光学实验仿真方法，分析Matlab在光学实验仿真中的优势和应用，并通过具体案例展示其在光学实验仿真中的实际应用效果。
通过本文的阐述，读者将能够了解Matlab在光学实验仿真中的重要作用，掌握基于Matlab的光学实验仿真方法，从而更好地应用仿真技术服务于光学研究和实验。
二、Matlab基础知识Matlab，全称为Matrix Laboratory，是一款由美国MathWorks公司出品的商业数学软件，主要用于算法开发、数据可视化、数据分析以及数值计算等领域。
Matlab以其强大的矩阵计算能力和丰富的函数库，在光学实验仿真领域具有广泛的应用。
Matlab中的变量无需预先声明，可以直接使用。
变量的命名规则相对简单，以字母开头，后面可以跟字母、数字或下划线。
Matlab支持多种数据类型，包括数值型（整数和浮点数）、字符型、逻辑型、结构体、单元数组和元胞数组等。
Matlab的核心是矩阵运算，它支持多维数组和矩阵的创建和操作。
用户可以使用方括号 [] 来创建数组或矩阵，通过索引访问和修改数组元素。
Matlab还提供了大量用于矩阵运算的函数，如矩阵乘法、矩阵转置、矩阵求逆等。
Matlab具有强大的数据可视化功能，可以绘制各种二维和三维图形。
在光学实验仿真中，常用的图形包括曲线图、散点图、柱状图、表面图和体积图等。
用户可以使用plot、scatter、bar、surf和volume 等函数来创建这些图形。
Matlab支持多种控制流结构，如条件语句（if-else）、循环语句（for、while）和开关语句（switch）。
这些控制流结构可以帮助用户编写复杂的算法和程序。
光学matlab
光学与MATLAB光学与MATLAB 的结合是现代光学研究和工程中的常见应用。
光学是研究光的行为和性质的学科，而MATLAB 是一个强大的数学计算和编程工具。
将两者结合起来，可以实现复杂的光学模拟、分析和设计。
以下是一些关于光学和MATLAB 结合的深入探讨：1.光波的数学描述：光波在空间中传播时，可以视为一个电场和磁场的波动。
在直角坐标系中，这可以用麦克斯韦方程组来描述。
MATLAB 中提供了用于解决这些方程的工具，如`pdepe` 或`fvm`。
使用这些工具，可以模拟光波在各种介质中的传播。
2.干涉和衍射：干涉是当两束或多束相干光波相遇时，它们的光程差会导致光强分布发生变化的现象。
衍射是光波绕过障碍物边缘时的传播行为。
MATLAB 的`optics` 工具箱提供了多种函数，可以模拟和分析干涉和衍射现象。
3.光学系统设计：光学系统设计涉及透镜、反射镜、棱镜等的光学性能的优化。
使用MATLAB 的`optics` 工具箱，可以模拟和分析这些系统的性能，并进行优化设计。
4.光谱分析：光谱分析涉及从光谱数据中提取信息，如物质成分、温度等。
MATLAB 中有专门用于光谱分析的工具箱，如`spectrum`，可以用于分析光谱数据。
5.图像处理：在光学中，图像处理是一个重要的分支，涉及对图像的增强、恢复和识别等操作。
MATLAB 的`image processing` 工具箱提供了各种算法，可以用于图像处理中的各种任务。
6.光子晶体和光子器件：光子晶体是具有周期性折射率变化的介质，可以控制光的传播。
光子器件是利用光子晶体和其他结构实现的特定功能的光学器件。
MATLAB 可以模拟和分析这些复杂系统的性能和行为。
7.光通信：光通信利用光波作为信息载体，通过光纤进行传输。
MATLAB 可以模拟和分析光通信系统中的各种效应，如色散、损耗和噪声等。
8.应用实例：假设我们需要模拟一个简单的干涉现象。
我们可以使用MATLAB 的`control` 工具箱中的`fftinterf` 函数来模拟干涉条纹的形成：首先，我们需要生成两个相干的正弦波：（1）% 定义参数（2）wavelength = 500e-9; % 波长(m)（3）angle = pi/4; % 入射角(rad)（4）k = 2*pi/wavelength; % 波数(1/m)（5）d = 1; % 双缝间距(m)（6）x0 = 0; % 双缝中心x 坐标(m)（7）y0 = 0; % 双缝中心y 坐标(m)（8）sigma = wavelength/(2*pi); % 单缝线宽(m)（9）L = 10; % 屏幕到双缝的距离(m)（10）x = -L:L; % x 坐标范围(m)（11）% 计算双缝的透过率函数（12）t1 = exp(-(x-x0).^2/(2*sigma^2)); % 单缝透过率函数(1/m^2)（13）t2 = exp(-(x-x0-d).^2/(2*sigma^2)); % 双缝透过率函数(1/m^2)（14）% 生成双缝透过率函数的时间序列（15）t = t1.*t2; % 双缝总透过率函数(1/m^2)（16）% 计算相干光的振幅和相位分布（17）E = t.*exp(1i*2*pi*k*(x.^2)/(2*(L^2))); % 双缝产生的电场分布(V/m)接下来，我们可以使用MATLAB 的`fftinterf` 函数来模拟干涉条纹的形成：（1）% 计算干涉条纹的强度分布（2）I = abs(fftshift(fft(E).*conj(fft(E)))); % 干涉条纹的强度分布(V^2/m^2)（3）% 显示干涉条纹的强度分布（4）imagesc(x, y, I);（5）axis square;（6）colorbar;（7）title('干涉条纹的强度分布');这只是一个简单的例子，实际上MATLAB 可以进行更复杂的模拟和分析，包括光的传输、光与物质的相互作用等。
衍射标量设计方法 matlab
一、介绍衍射标量设计方法在光学领域中，衍射标量设计方法是一种用于设计光学系统的重要手段。
这种方法主要基于波动理论，通过计算光波的传播过程来确定光学系统的参数和结构，从而实现特定的光学功能。
衍射标量设计方法在光学成像、激光器设计、光学通信等领域都有着广泛的应用。
二、衍射标量设计方法的基本原理衍射标量设计方法的基本原理是利用衍射理论来描述光波的传播过程。
在衍射理论中，光波的传播可以用衍射积分来表达，根据衍射积分表达式，可以求解出某一特定的光学系统对输入光场的响应。
通过对这一响应进行分析和优化，可以确定光学系统的参数和结构，从而实现特定的光学功能。
三、衍射标量设计方法的建模与分析1.建立光学系统的数学模型在衍射标量设计方法中，首先需要建立光学系统的数学模型。
这一模型通常是一个线性的传递函数，描述了光学系统对输入光场的响应。
通过这一传递函数，可以将输入光场和输出光场之间的关系用数学方程表达出来。
2.分析光学系统的参数和结构在建立了数学模型之后，需要对光学系统的参数和结构进行详细的分析。
这一分析通常包括对光学元件的性能参数、尺寸和位置等进行考虑，以确定最佳的设计方案。
四、matlab在衍射标量设计方法中的应用1.光学系统的仿真与优化matlab是一种强大的数学建模与仿真软件，可以帮助工程师和科研人员对光学系统进行仿真和优化。
通过matlab的光学仿真工具箱，可以方便地建立光学系统的数学模型，并对其进行优化，以实现更好的光学性能。
2.光学系统的快速原型设计除了仿真和优化，matlab还可以用于快速原型设计。
借助matlab的可视化编程环境和丰富的函数库，可以快速地建立光学系统的原型，并进行实时的调试和优化，大大提高了光学系统的设计效率。
五、总结衍射标量设计方法是一种重要的光学系统设计方法，通过对光波的传播过程进行建模和分析，可以实现对光学系统的快速优化和设计。
而matlab作为一种强大的数学建模与仿真工具，为光学系统的设计提供了便利的评台，帮助工程师和科研人员实现光学系统的快速原型设计和优化。
Matlab数字衍射光学实验(一)
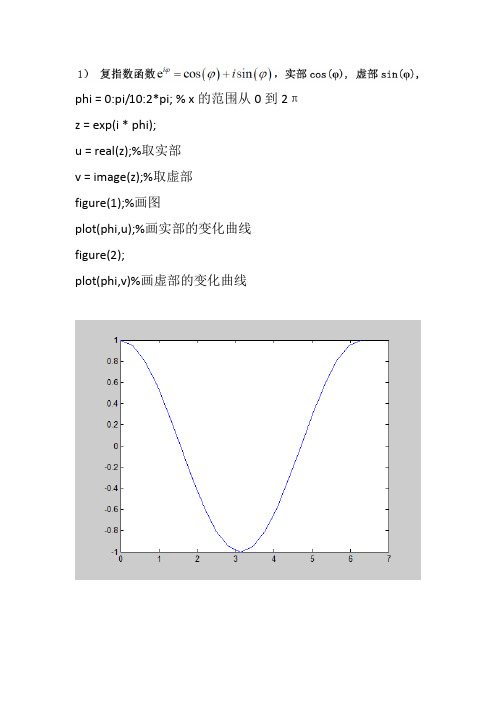
phi = 0:pi/10:2*pi; % x的范围从0到2πz = exp(i * phi);u = real(z);%取实部v = image(z);%取虚部figure(1);%画图plot(phi,u);%画实部的变化曲线figure(2);plot(phi,v)%画虚部的变化曲线clear;%清除内存close all;%关闭所有窗口x=linspace(0,2*pi,100);%设置横坐标范围及网格y1=sqrt(x);%开根号figure(1);plot(x,y1,'r')%做出y1的曲线,'r'代表图线为红色clear;%清除内存close all;%关闭所有窗口x=linspace(-2*pi,2*pi,100);%100个数横坐标从-2pi到2pi y1=besselj(1,x);%第一类贝塞尔函数,一阶y2=besselj(0,x);%第一类贝塞尔函数,0阶figure(1);plot(x,y1,'r');figure(2);plot(x,y2,'b');clear;close all;[x,y]=meshgrid(-2:.05:2,-2:.05:2);%设置二维网格z=sinc(x).*sinc(y);figure(1);imshow(z);%二维灰度图figure(2);imagesc(z);%二维彩图figure(3);mesh(z);%三维图像clear;close all;a=5;x=linspace(-5,5,100);y1=exp(-pi.*(x/a).^2);%第一类贝塞尔函数,一阶b=2;y2=exp(-pi.*(x/b).^2);%第一类贝塞尔函数,一阶figure(1);plot(x,y1,'r');figure(2);plot(x,y2,'b');clear;close all;a=1;b=1;[x,y]=meshgrid(-2:.05:2,-2:.05:2);%设置二维网格z=exp(-pi.*((x/a).^2+(y/b).^2));%高斯函数figure(1);imagesc(z);figure(2);mesh(z);clear;close all;M=100;%x方向抽样点数N=100;%y方向抽样点数w=10;%缝的宽度d=10;%缝偏离中心的位置obj1=zeros(M,N);%赋值为0的一个二维矩阵,大小为M*N obj1(:,(N/2-w/2):N/2+w/2)=1.0;%设置缝在y向中心,且缝的宽度为wfigure(1);imshow(obj1);obj2=zeros(M,N);obj2(:,(N/2-d)-w/2:(N/2-d)+w/2)=1.0;%缝偏离中心位置d个像素figure(2);imshow(obj2);clear;close all;M=100;%x方向抽样点数N=100;%y方向抽样点数w=10;%缝的宽度d=10;%缝偏离中心的位置obj1=zeros(M,N);%赋值为0的一个二维矩阵,大小为M*N obj1(:,(N/2+d)-w/2:(N/2+d)+w/2)=1.0;%设置缝在y向中心,且缝的宽度为wobj2=zeros(M,N);obj2(:,(N/2-d)-w/2:(N/2-d)+w/2)=1.0;%缝偏离中心位置d个像素obj3=obj1+obj2;figure(1);imshow(obj3);clear;close all;M=100;N=100;w=10;%缝宽obj=zeros(M,N);obj((M/2-w/2):(M/2+w/2),(N/2-w/2):(N/2+w/2))=1.0;%缝处于中心位置figure(1);imshow(obj);figure(2);imagesc(obj);figure(3);mesh(obj);。
理想透镜衍射matlab
理想透镜衍射matlab
在MATLAB中，可以使用物理光学工具箱来模拟理想透镜的衍射
效应。
衍射是光通过边缘或孔径时发生的偏折现象，理想透镜的衍
射模拟可以帮助我们理解光的传播规律和光学系统的性能。
首先，我们需要定义理想透镜的参数，包括透镜的曲率半径、
折射率等。
然后，我们可以使用MATLAB中的衍射函数（例如fft2）来模拟透镜的衍射效应。
具体步骤如下：
1. 定义透镜参数，包括透镜的孔径大小、曲率半径、折射率等
参数。
2. 生成输入光场，可以使用MATLAB中的函数生成一个表示入
射光场的二维矩阵，可以是单色光或者白光。
3. 衍射计算，使用MATLAB中的快速傅里叶变换函数fft2对输
入光场进行衍射计算，得到透镜后的光场分布。
4. 显示结果，可以使用MATLAB中的图像显示函数imshow来显
示衍射后的光场分布，观察衍射效应。
在模拟理想透镜的衍射过程中，需要考虑透镜的孔径大小、入射光波长、透镜的焦距等因素，这些参数都会影响衍射效应的模拟结果。
此外，还可以通过调整透镜参数、入射光场的波前形状等来进一步探究理想透镜的衍射特性。
总的来说，通过MATLAB中物理光学工具箱提供的函数和工具，我们可以比较直观地模拟理想透镜的衍射效应，从而更好地理解光学系统的行为。
希望这个回答能够帮到你，如果你有更多关于理想透镜衍射模拟的问题，欢迎继续提问。
实验7 衍射的Matlab模拟
实验7衍射的Matlab模拟一、实验目的：掌握衍射的matlab模拟。
二、实验内容：1）单个圆孔夫朗和费衍射的matlab模拟2）双圆孔夫朗和费衍射的matlab模拟3）同一波长，狭缝数量分别为1、2、3、6、9、10时候的夫朗和费衍射的matlab模拟4）对4个不同波长的光照射时，狭缝数量分别为1、3时候的夫朗和费衍射的matlab 模拟5）单个圆孔菲涅尔衍射的matlab模拟6）模拟圆孔（或者单缝）衍射时，衍射屏到接收屏距离不同的时候衍射的图样1)clearclclam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;hh=(2*BESSELJ(1,x)).^2./x.^2;b(:,i)=(hh)'.*5000;B=b/max(b);endimage(xs,ys,b);colormap(gray(n));figure;plot(xs,B);colormap(green);-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-3-3-2-10123x 10-300.10.20.30.40.50.60.70.80.912)%双圆孔夫琅禾费衍射clear all close all clc %lam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:m r=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;h=(2*BESSELJ(1,x)).^2./x.^2;d=10*a;deltaphi=2*pi*d*xs(i)/lam;hh=4*h*(cos(deltaphi/2))^2;b(:,i)=(hh)'.*5000;end image(xs,ys,b);colormap(gray(n));-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-33)lamda=500e-9;%波长N=[1236910];for j=1:6a=2e-4;D=5;d=5*a;ym=2*lamda*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(j)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure(j);subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);plot(B1,ys,'k');end-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为2-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为3-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为9狭缝数为6-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.0254）lamda=400e-9:100e-9:700e-9;%波长N=[13];a=2e-4;D=5;d=5*a;for j=1:4ym=2*lamda(j)*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for k=1:2for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda(j);beta=pi*d*sinphi/lamda(j);B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(k)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);狭缝数为10plot(B1,ys,'k');end end-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02Lamda=400nm,N=1-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025Lamda=400nm,N=3Lamda=500nm,N=1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03Lamda=500nm,N=3Lamda=600nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04Lamda=600nm,N=3Lamda=700nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.045）clearclcN=300;r=15;a=1;b=1;I=zeros(N,N);[m,n]=meshgrid(linspace(-N/2,N/2-1,N));D=((m-a).^2+(n-b).^2).^(1/2);i=find(D<=r);I(i)=1;subplot(2,2,1);imagesc(I)colormap([000;111])axis imagetitle('衍射前的图样')L=300;M=300;[x,y]=meshgrid(linspace(-L/2,L/2,M));lamda=632.8e-6;k=2*pi/lamda;z=1000000;Lamda=700nm,N=3h=exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z); H=fftshift(fft2(h));%传递函数B=fftshift(fft2(I));%圆孔频谱G=H.*B;U=fftshift(ifft2(G));Br=(U/max(U));subplot(2,2,2);imshow(abs(U));axis image;colormap(hot)%figure,imshow(C);title('衍射后的图样');subplot(2,2,3);mesh(x,y,abs(U));subplot(2,2,4);plot(abs(Br))6)lamda=500e-9;%波长N=1;%缝数，可以随意更改变换a=2e-4;D=3:7;d=5*a;for j=1:5ym=2*lamda*D(j)/a;xs=ym;%屏幕上y的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:nsinphi=ys(i)/D(j);alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);endNC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1)image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2)plot(B1,ys,'k');end-0.4-0.200.20.4-0.015-0.01-0.00500.0050.010.01500.51-0.015-0.01-0.0050.0050.010.015D=3m-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025D=5m D=4m-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04D=7m D=6m。
matlab计算衍射
matlab计算衍射衍射是一种波传播时遇到障碍物或开口时发生的现象，对于光学、声学等领域具有重要意义。
本文将介绍MATLAB在衍射计算中的基本原理、常用方法以及实际应用，旨在为研究者提供一个全面的MATLAB衍射计算指南。
一、引言衍射是波在传播过程中遇到障碍物或开口时发生的波动现象，广泛应用于光学、声学、天文学等领域。
MATLAB作为一种高效的数学建模和计算工具，在衍射计算中有着广泛的应用。
本文将深入探讨MATLAB在衍射计算中的基本原理、方法和实际应用。
二、MATLAB中的衍射基本原理赫姆霍兹方程：衍射计算的基础是赫姆霍兹方程，描述了波场的传播和衍射现象。
MATLAB通过数值方法求解赫姆霍兹方程，实现波场的模拟。
傅里叶光学：利用傅里叶光学原理，将衍射问题转化为频域中的问题。
MATLAB提供了强大的傅里叶变换工具，可以对衍射场景进行频谱分析。
三、MATLAB中的衍射计算方法傅里叶衍射公式：利用傅里叶变换和逆变换，可以在频域中高效计算衍射场景。
MATLAB的fft和ifft函数可用于实现这一计算过程。
衍射积分公式：利用衍射积分公式，通过对波场的积分来计算衍射图样。
MATLAB的数值积分函数可以方便地应用于这一过程。
四、MATLAB中的衍射实际应用光学衍射模拟：MATLAB可用于模拟各种光学衍射现象，如单缝衍射、双缝衍射、光栅衍射等。
通过调整参数，可以实时观察衍射图样的变化。
声学衍射计算：在声学领域，MATLAB可以用于计算声波在不同环境中的衍射效应，对声学设备的设计和优化提供支持。
天文学应用：对于射电天文学等领域，MATLAB可用于计算射电波在宇宙中的传播和衍射，帮助天文学家理解观测数据。
五、MATLAB衍射计算的优势与挑战优势：MATLAB提供了丰富的数学函数和工具箱，使得衍射计算更加简便高效。
其图形用户界面（GUI）也有助于直观地展示计算结果。
挑战：随着衍射计算问题的复杂化，需要更高级的数值方法和算法，这对MATLAB的计算性能提出了一定的挑战。
光的干涉和衍射的matlab模拟
光的干涉和衍射的matlab模拟单缝夫琅和费衍射是光的衍射现象之一，如图2所示。
当单色光波通过一个狭缝时，光波会向周围扩散，形成一系列同心圆环。
这些圆环的亮度分布是由夫琅和费衍射公式描述的，即。
其中为入射光波长，为狭缝宽度，为衍射角。
夫琅和费衍射公式表明，随着衍射角的增大，圆环的半径会减小，而亮度则会逐渐减弱。
在MATLAB中，可以通过输入实验参数，如光波长和狭缝宽度，来观察圆环的亮度分布和半径随衍射角的变化情况。
同时，还可以探讨不同波长和狭缝宽度对圆环亮度和半径的影响。
4双缝衍射双缝衍射是光的干涉和衍射现象的结合，如图3所示。
当一束单色光波通过两个狭缝时，光波会在屏幕上形成一系列干涉条纹和衍射环。
干涉条纹的亮度分布与___双缝干涉相同，而衍射环的亮度分布则由夫琅和费衍射公式描述。
在MATLAB中，可以通过输入实验参数，如光波长、双缝间距和双缝宽度，来观察干涉条纹和衍射环的亮度分布和条纹间距、环半径随实验参数的变化情况。
同时，还可以探讨不同实验参数对干涉条纹和衍射环的影响。
5衍射光栅衍射光栅是一种利用衍射现象制成的光学元件，如图4所示。
当一束单色光波通过光栅时，光波会被分为多个衍射光束，形成一系列亮度不同的衍射条纹。
衍射条纹的亮度分布与夫琅和费衍射公式描述的圆环类似，但是条纹间距和亮度分布会受到光栅常数的影响。
在MATLAB中，可以通过输入实验参数，如光波长和光栅常数，来观察衍射条纹的亮度分布和条纹间距随实验参数的变化情况。
同时，还可以探讨不同实验参数对衍射条纹的影响。
总之，通过MATLAB模拟光的干涉和衍射现象，可以更加直观地理解和掌握这些重要的光学现象，同时也可以为实验设计和数据分析提供有力的工具和支持。
本文介绍了___双缝干涉、单缝夫琅禾费衍射和衍射光栅光谱的计算机模拟。
当一束单色平行光通过宽度可调的狭缝，射到其后的光屏上时，形成一系列亮暗相间的条纹。
单缝夫琅禾费衍射的光强分布可以通过惠更斯-费涅耳原理计算。
Matlab在物理学中的应用--光的衍射
光的干涉和衍射一、实验目的① 学习用用模拟实验方法探究光的干涉和衍射问题.② 进一步熟悉MA TLAB 编程.二、实验内容和要求1. 双缝干涉模拟实验杨氏双缝干涉实验是利用分波前法获得相干光束的典型例子. 如图2.24所示，单色光通过两个窄缝s 1，s 2射向屏幕，相当于位置不同的两个同频率同相位光源向屏幕照射的叠合，由于到达屏幕各点的距离（光程）不同引起相位差，叠合的结果是在有的点加强，在有的点抵消，造成干涉现象.图2.24 双缝干涉示意图 考虑两个相干光源到屏幕上任意点P 的距离差为1221r r r r r ==∆=- （2.19） 引起的相位差为2πrϕλ∆=设两束相干光在屏幕上P 点产生的幅度相同，均为A 0，则夹角为φ的两个矢量A 0的合成矢量的幅度为A =2A 0 cos(φ/2)第二章 数理探究试验 135光强B 正比于振幅的平方，故P 点光强为B =4B 0cos 2(φ/2) （2.20）运行sy211.m 程序得到干涉条纹如图2.27所示.clear all %sy211.mlam=500e-9; %输入波长a=2e-3; D=1;ym=5*lam*D/a; xs=ym; %设定光屏的范围n=101;ys=linspace(-ym,ym,n); % 把光屏的y 方向分成101点for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2);r2=sqrt((ys(i)+a/2).^2+D^2);phi=2*pi*(r2-r1)/lam;B(i,:)=4*cos(phi/2).^2;endN=255; % 确定用的灰度等级为255级Br=(B/4.0)*N; %使最大光强对应于最大灰度级（白色）subplot(1,2,1)image(xs,ys,Br); %画干涉条纹colormap(gray(N));subplot(1,2,2)plot(B,ys) %画出光强变化曲线图2.25中左图是光屏上的干涉条纹，右图是光屏上沿y 轴方向光强的变化曲线. 从图中也不难看出，干涉条纹是以点o 所对应的水平线为对称，沿上下两侧交替，等距离排列，相邻亮条纹中心间距为2.5×10－4m. -0.4-0.200.20.4-1.5-1-0.500.511.5x 10图2.25 单色光的干涉条纹这与理论推导和实验结果基本一致.下面我们从理论上加以推导，由上面的式（2.19）可得22212121()()2d r r r r r r y -=+-=-1.5 -1 -0.5 0 0.5 1 1.5 -0.4 -0.2 0 0.4 0.2基于MA TLAB 的数学实验136 考虑到a ，y 很小，（r 1+r 2）=2D ，所以21D r r y a-= 这样就得到点P 处于亮条纹中心的条件为20122D y k k a λ==±±，，，， （2.21） 因此，亮条纹是等间距的，相邻条纹间距为94150010 2.510m 0.002D a λ--=⨯=⨯. 问题2.39：推导出点P 处于暗条纹中心的条件并与模拟结果相比较，看是否一致？ 考虑到纯粹的单色光不易获得，通常都有一定的光谱宽度，这种光的非单色性对光的干涉会产生何种效应，下面我们用MA TLAB 计算并仿真这一问题.非单色光的波长不是常数，必须对不同波长的光分别处理再叠加起来. 我们假定光源的光谱宽度为中心波长的±10%，并且在该区域均匀分布. 近似取11根谱线，相位差的计算表达式求出的将是不同谱线的11个不同相位. 计算光强时应把这11根谱线产生的光强叠加并取平均值，即211012π4cos ()211k kk k r B B ϕλϕ=∆==∑ 将程序sy211.m 中的9，10两句换成以下4句，由此构成的程序就可仿真非单色光的干涉问题. N1=11;dL=linspace(-0.1,0.1,N1);%设光谱相对宽度±10%， lam1=lam*(1+dL');%分11根谱线，波长为一个数组 Phi1=2*pi*(r2-r1)./ lam1;%从距离差计算各波长的相位差 B(i, :)=sum(4*cos(Phi1/2).^2)/N1; %叠加各波长并影响计算光强运行修改后的程序得到的干涉条纹如图2.26所示. 可以看出，光的非单色性导致干涉现象的减弱，光谱很宽的光将不能形成干涉.第二章 数理探究试验 137-0.4-0.200.20.4-1.5-1-0.500.511.5-3-3图2.26 非单色光的干涉条纹 2. 单缝衍射的模拟实验一束单色平行光通过宽度可调的狭缝，射到其后的光屏上. 当缝宽足够小时，光屏上形成一系列亮暗相间的条纹，这是由于从同一个波前上发出的子波产生干涉的结果. 当光源到衍射屏的距离和光屏到衍射屏的距离都是无穷大时，即满足远场条件时，我们称这种衍射为夫琅禾费衍射. 所以夫琅禾费衍射中入射光和衍射光都是平行光. 为了模拟单缝衍射现象，我们把单缝看成一排等间隔光源，共NP 个光源分布在A ～B 区间内，离A 点间距为yp ，则屏幕上任一点S 处的光强为NP 个光源照射结果的合成.如图2.27所示，子波射线与入射方向的夹角ϕ称为衍射角，0=ϕ时，子波射线通过透镜后，必汇聚到O 点，这个亮条纹对应的光强称为主极大. NP 个光源在其他方向的射线到达S 点的光程差，应等于它们到达平面AC 的光程差，即sin yp ϕ∆=，其中sin ys Dϕ≈ ys 为S 点的纵坐标，则与A 点光源位相差为2π2πyP ys Dαλλ=∆=s O基于MA TLAB 的数学实验 138 -0.4-0.200.20.4-1.5-1-0.500.511.5-3-3图2.28 单缝衍射条纹图2.27 单缝衍射的模拟实验设单缝上NP 个光源的振幅都为1，在x ，y 轴上的分量各为cos sin αα，，合振幅的平方为：()()22COSa COSa ∑+∑. 又光强正比于振幅的平方，所以相对于O 点主极大光强也为22(cos )(sin )0I I αα=+∑∑程序sy212.m 模拟了单缝衍射现象，这里取波长λ=500nm ，缝宽a =1mm ，透镜焦距D =1m ，运行结果如图2.28所示.clear all %sy212.mlam=500e-9;a=1e-3;D=1;ymax=3*lam*D/a; %屏幕范围（沿y 向）Ny=51; %屏幕上的点数（沿y 向）ys=linspace(-ymax,ymax,Ny);NP=51;yP=linspace(0,a,NP); %把单缝分成NP 个光源for i=1:Ny %对屏幕上y 向各点作循环SinPhi=ys(i)/D;alpha=2*pi*yP*SinPhi/lam; SumCos=sum(cos(alpha)); SumSin=sum(sin(alpha));B(i,:)=(SumCos^2+SumSin^2)/NP^2;end N=255; % 确定用的灰度等级为255级%使最大光强对应于最大灰度级（白色）Br=B/max(B)*N; subplot(1,2,1)%画衍射条纹，用灰度级颜色图image(ymax,ys,Br); colormap(gray(N));subplot(1,2,2)%画屏幕上光强曲线 plot(B,ys,'*',B,ys);grid;分析图2.28中的衍射条纹，我们可以看出所有亮暗条纹都平行于单缝，O 点光强为最大，这都和理论推导结果相一致.问题2.40： 从理论上讲，中央亮条纹的半角宽和第一条暗条纹的衍射角都应等于λ/a ，各次极大角宽都等于中央亮条纹的半角宽，图2.28模拟的衍射条纹符合这个结论吗？3. 光栅衍射的模拟实验有大量等宽度、等间距的平行狭缝组成的光学系统称为衍射光栅. 单缝宽度a 和刻第二章 数理探究试验 139痕宽度b 之和称为光栅常数d ，d =a +b . 光栅衍射条纹是单缝衍射和缝间干涉的共同结果.设光栅有N 条狭缝，透镜焦距为D ，理论分析可以得到，光屏上P 点的夫琅禾费衍射光强I P /I 0分布为220sin sin ()()sin P I N I αβαβ= 式中sin sin sin s y a d Dππαϕβϕϕλλ==≈，， 运行程序sy213.m 得到衍射条纹如图2.29所示.clear all %sy213.mlam=632.8e-9; N=2;a=2e-4; D=5;d=5*a;ym=1.89*lam*D/a;xs=ym; %设定光屏的范围n=1001;ys=linspace(-ym,ym,n); % y 方向分成1001点for i=1:nSinphi=ys(i)/D;alpha=pi*a*Sinphi/lam;beta=pi*d*Sinphi/lam;B(i, :)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2 ;B1=B/max(B); %将最大光强设为1endNC=255;Br=B/max(B)*NC;subplot(1,2,1)image(xs,ys,Br); %画衍射条纹colormap(gray(NC))subplot(1,2,2)plot(B1,ys) %画出沿y 向的相对光强变化曲线问题2.41：程序sy213.m 中d =5a ，观察图2.29衍射条纹，看有无缺级现象，为什么？改变sy213.m 中的波长、缝宽、光栅常数值，看衍射条纹有何变化？试加以解释.基于MA TLAB 的数学实验 140-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025图2.29 光栅衍射条纹第二章数理探究试验141 《车辆制冷与空调》第二次作业参考答案《车辆隔热壁》、《制冷方法与制冷剂》、《蒸汽压缩式制冷》一．简答题1.什么是隔热壁的传热系数？它的意义是什么？答：隔热壁的传热系数指车内外空气温度相差1℃时，在一小时内，通过一平方米热壁表面积所传递的热量。
用MATLAB语言模拟光衍射实验
第14卷第4期大 学 物 理 实 验 V ol.14N o.42001年12月出版PHY SIC A L EXPERI ME NT OF C O LLEGE Dec.2001收稿日期:2001-07-30文章编号:1007-2934(2001)04-0047-02用MAT LAB 语言模拟光衍射实验周 忆(安徽省科学技术培训中心,合肥,230031) 梁 齐(合肥工业大学,合肥,230009)摘 要:用M AT LAB 语言模拟编写了光衍射的模拟实验程度,给出了五种元件的夫琅和费衍射图。
关键词:衍射;模拟;M AT LAB 语言中图分类号:O4-39 文献标识码:A光的衍射现象是光具有波动性的重要特征,衍射无论在理论研究还是在大学物理教学中都占有较重要的地位。
笔者利用MAT LAB 较强的绘图和图像功能,针对多种衍射元件(单缝、双缝、光栅、矩孔、圆孔)编写了光衍射的模拟实验程序。
在计算机的模拟光的衍射,条件限制较少,对于衍射的实验教学是一种较好的补充。
程序首先根据衍射强度分布的理论公式及实验参数建立衍射相对强度的数据矩阵B (x ,y )然后利用image (B )和colormap (gray )命令绘出衍射图样。
同时,也绘制了衍射光强分布的二维或三维图。
单缝夫琅和费衍射的模拟结果见图1。
衍射光强公式为I =I 0(sin u/u )2,u =(πa sin θ/λ),a 是缝宽,λ是入射光的波长,θ是衍射角。
设观察屏位于单缝后正透镜的焦平面上,f 为透镜的焦距,x 为屏上横向坐标。
θ=arctan (x/f )。
模拟分成三组:第一组,λ=600nm ,f =600mm ,(a )a =0.20mm ;(b )a =0.10mm ;(c )a =0.05mm 第二组,a =0.10mm ,f =600mm ,(d )λ=500nm ;(e )a =600nm ;(f )λ=700nm第三组,a =0.10mm ,λ=600nm ,(g )f =300mm ;(h )f =600mm ;(i )f =900mm以下内容中,取λ=600nm ,f =600mm ,衍射图样横坐标x 和纵坐标y 的范围均为[-20,20]mm 。
matlab计算衍射
matlab计算衍射【原创实用版】目录1.引言2.MATLAB 计算衍射的原理3.MATLAB 计算衍射的实践应用4.MATLAB 计算衍射的优点与局限性5.结论正文1.引言衍射是光学中的一个重要现象，它揭示了光的波动性。
在光学研究中，衍射的分析与计算具有重要的意义。
MATLAB 作为一种强大的光学仿真软件，可以方便地用于计算衍射。
本文将从 MATLAB 计算衍射的原理、实践应用、优点与局限性等方面进行介绍。
2.MATLAB 计算衍射的原理MATLAB 计算衍射主要基于光学的物理原理和数学方法。
其中，菲涅尔 - 基尔霍夫衍射积分公式是计算光波场和光强度分布的常用方法。
此外，MATLAB 提供了丰富的光学元件库和函数，如透镜、光栅、单缝等，可以方便地构建光学系统并进行仿真计算。
3.MATLAB 计算衍射的实践应用MATLAB 在衍射计算方面的应用非常广泛，包括夫琅禾费衍射、双缝干涉、平面光栅衍射、单缝衍射等。
通过 MATLAB 仿真计算，可以直观地观察到各种衍射现象，有助于深入理解光的波动性。
同时，MATLAB 还可以计算衍射的光强度分布，为光学设计和实验提供参考数据。
4.MATLAB 计算衍射的优点与局限性MATLAB 计算衍射具有以下优点：（1）MATLAB 易于学习和使用，方便进行衍射计算；（2）MATLAB 提供了丰富的光学元件库和函数，可以方便地构建光学系统；（3）MATLAB 计算衍射的结果可视化程度高，便于观察和分析。
然而，MATLAB 计算衍射也存在一定的局限性：（1）需要对光学原理有一定了解才能进行有效计算；（2）计算过程中可能涉及到复杂的数学运算，需要具备一定的数学基础；（3）MATLAB 计算衍射的结果受计算机性能和仿真参数设置等因素影响，可能存在一定误差。
5.结论MATLAB 作为一种强大的光学仿真软件，可以方便地用于计算衍射。
通过 MATLAB 计算衍射，可以深入了解光的波动性，并为光学设计和实验提供参考数据。
光的干涉和衍射的Matlab数值模拟
发 Ｊ． 中国 ［］ 何永华． 电厂及变电站的二次 回路Ｅ］ 北京 ： ３
电 力 出 版 社 ，０ ７ ４— １ ２０ ，４６ ．
Ｄｅ ｉｎ ａ ｄ Ｐｒ ｓ ｎｔ ｔｏ ｆＣｉｃ ｉ ｅ ｋｅ ｎｔｏ ｉ ｎ ｌ ｓｇ ｎ ｅ ｅ ａ ｉｎ ｏ ｒ ｕ ｔＢｒ ａ ｒＣｏ ｒ ｌＳ ｇ ａ
后 的平 均值 ， （ ） 由 ３ 式决 定 ：
中可 以看 出每 级 明纹 的光强 都是 相 同的 。 另外 ， 红 光 的波 长最 长 ， 其相 邻两 条 明 （ ）条 纹 的 间距 最 暗
宽， 而蓝光的波长最小 ， 其相邻两条明 （ 条纹 暗） 的间距 最窄 。 生通 过对 程序 的学 习 ， 可 以 自行 学 还
改变双缝间距和双缝与接收屏间距 的数值 ， 观察 各个 物理 量 的改变 对 干涉条 纹 的影 响 。
（光 的干 涉光强分布 图 ａ 】
１ 杨 氏双缝干涉 的数值模拟
１ １ 干 涉 的 图案和光 强分 布 ．
杨 氏双缝 干 涉 实验 中 ， 一束 平 行 光 垂 直 照 射 到双缝 上 ， 双缝 作 为新 的次 级光 源 ， 发 出 的两束 其 光相 干叠加后 ， 在接收屏 上产生 明暗相 间的条 纹［ 。 ３ ］ 空气的折 射率 一 １令两束光 的光强相 同， 为 Ｌ。 ， 都
［］ 焦彦军 ， １ 张新 国． 电力 系统继 电保 护 通用仿 真 分析
系统的 方 案设 计 Ｉ］ 电力 系 统及 其 自动 化 学 报 ， － ． Ｊ
２ ０ ， ３ ２ ： ４４ ． ０ １ １ （ ） ４ — ６
王彦 黄智伟． 高校 仿真教学 的调 查与研究 Ｅ］ 徐祖华 ， ， ２
基于Matlab的光学衍射仿真
基于Matlab的光学衍射实验仿真摘要光学试验中衍射实验是非常重要的实验. 光的衍射是指光在传播过程中遇到障碍物时能够绕过障碍物的边缘前进的现象, 光的衍射现象为光的波动说提供了有力的证据. 衍射系统一般有光源、衍射屏和接受屏组成，按照它们相互距离的大小可将衍射分为两大类，一类是衍射屏与光源和接受屏的距离都是无穷远时的衍射，称为夫琅禾费衍射，一类是衍射屏与光源或接受屏的距离为有限远时的衍射称为菲涅尔衍射.本文用Matlab软件对典型的衍射现象建立了数学模型，对衍射光强分布进行了编程运算，对衍射实验进行了仿真。
最后创建了交互式GUI界面，用户可以通过改变输入参数模拟不同条件下的衍射条纹.本文对于衍射概念、区别、原理及光强分布编程做了详细全面的介绍关键字：Matlab；衍射；仿真;GUI界面;光学实验Matlab-based Simulation of Optical Diffraction ExperimentAbstractOptical diffraction experiment is a very important experiment. is the diffraction of light propagation of light in the obstacles encountered in the process to bypass the obstacles when the forward edge of the phenomenon of light diffraction phenomenon of the wave theory of light provides a strong Evidence。
diffraction systems generally have light, diffraction screen and accept the screen composition，size according to their distance from each other diffraction can be divided into two categories, one is the diffraction screen and the light source and the receiving screen is infinity when the distance between the diffraction Known as Fraunhofer diffraction, one is diffraction screen and the light source or accept a limited away from the screen when the diffraction is called Fresnel diffraction.In this paper, Matlab software on a typical phenomenon of a mathematical model of diffraction, the diffraction intensity distribution of the programming operation，the diffraction experiment is simulated. Finally, create an interactive GUI interface, users can change the input parameters to simulate different conditions of the diffraction pattern.This concept of the diffraction, difference, intensity distribution of programming principles and a detailed comprehensive descriptionKey word：matlab;diffraction; simulation；gui interface；optical experiment目录1 绪论 (1)1.1光学仿真的研究意义 (1)1.2国内外研究现状 (2)1。
利用MATLAB语言进行光学衍射现象的仿真
利用MATLAB语言进行光学衍射现象的仿真储林华（安庆师范学院物理与电气工程学院安徽安庆246011）指导教师：张杰摘要：光的衍射是光的波动性的一种重要表现，因此对光的衍射现象的研究，不仅具有重要的理论意义，而且在光学仪器研制和成像分析等诸多实际应用方面均有重要价值，但是其衍射光强的计算非常复杂，对实验条件的要求非常高，通常情况下很难得到满意的效果，严重影响了光学的教学。
本文从衍射的相关理论知识出发，首先介绍了惠更斯--菲涅耳原理及其数学表示形式，然后重点讨论了单色光经各种对称光学衍射元件（单缝，双缝，光栅，圆孔）的夫琅和费衍射情况，并分别给出了它们在焦平面上的衍射光强计算公式，最后利用科学计算软件MA TLAB对光的衍射现象进行了仿真，所得到的图样细致逼真，使整个物理过程变得直观形象，且与实验所得到的衍射图样进行了比较，两者吻合得很好，从而为光学的理论分析和实验教学提供了一种新的途径。
关键词：光的衍射，光栅衍射，圆孔衍射，Matlab，计算机仿真0 引言光的衍射现象是光具有波动性的重要特征，因此对衍射现象的研究无论在理论上还是在实践中都有很重要的意义。
对光的衍射现象的研究，始于17世纪，当时著名的荷兰科学家惠更斯提出了光是一种波的假说，并根据波动理论提出了光的传播理论——即惠更斯原理[1]，根据这一原理，他解释了光的反射定律和折射定律，给出了折射率的意义，光在两种介质中的速度比。
到了19世纪，法国年轻的科学家菲涅耳，根据叠加原理把惠更斯原理进一步具体化，给出了光在传播过程中光强学计算公式，这就是著名的惠更斯-菲涅耳原理[2]。
但由于在实际应用过程中，障碍物形状的不规则性，导致光强的计算公式几乎无解析解，只能进行一些数值计算。
针对衍射计算中出现的困难，近代的研究人员想到运用科学的计算软件MA TLAB，利用其较强的绘图和图象功能，编写计算程序，使得多种衍射元件（单缝，双缝，光栅，矩孔，圆孔）下的衍射现象得以在计算机中形象地被模拟仿真。
衍射的Matlab 模拟
r
P
则 K
1 1 cos 2
13
将近似条件代入得到：菲涅耳－基尔霍夫衍射近似公式
exp ikR i ~ E P A 2 R
exp ikr 1 cos d r
( n,l ) ( n,r )
2
2
x1 x y1 y x 2 y 2 取上式前三项 r z1＋ z1 2 z1
x2 y2 exp[ ik ( z1 )] 2 z1 ~ E x, y iz1 ~ k i xx1 yy1 dx1dy1 E x1 , y1 exp z1
y1 x1
进一步的计算需要 将exp( ikr )中的r表 示成(x,y,z)的函数。
Q C z1 K
r
P
x
P0 E
孔径 的衍射
16
2.菲涅耳近似（对位相项的近似）
r z1 ( x x1 ) 2 y y1 z1 1
2 2
x x1 2 y y1 2
非平行光衍射光源面和接收面非物象共扼面源点和场点均满足远场近似源点和场点均在无限远处平行光衍射光源面和接收面物菲涅耳衍射夫琅和费衍射121
衍射的MATLAB模拟
刘雁 三峡大学理学院 2013.4
内容提要
衍射的基本理论
单缝衍射的Matlab模拟
一衍射的基本原理
光的衍射现象：光波在空间传播遇到障碍时，其传播方
2 2 夫琅合费衍射对z的要求 =600nm, x1 y1
x z
2
1
y1
2
max
2cm2
MATLAB 傅立叶变换 和衍射积分 模拟光学
MATLAB编程用两种方法模拟光学实验摘要：利用MA TLAB软件编程实现了用衍射积分的方法对单缝衍射、杨氏双缝干涉、黑白光栅衍射的计算机模拟；以及用傅立叶变换方法对简单孔径衍射、黑白光栅及正弦光栅夫琅和费衍射的模拟。
关键词：MA TLAB；衍射积分；傅立叶变换；计算机模拟引言：美国Mathworks公司推出的MA TLAB，是一种集数值计算、符号预算、可视化建模、仿真和图形处理等多种功能于一体的优秀图形化软件。
本文介绍了通过MA TLAB软件编程实现用衍射积分和傅立叶变换实现夫琅和费衍射计算机模拟的方法。
计算机模拟为衍射实验的验证提供一条简捷、直观的途径。
从而加深了对物理原理、概念和图像的理解。
正文：大学教学课程中引入计算机模拟技术正日益受到重视，与Basic、C和Fortran相比，用MA TLAB软件做光学试验的模拟，只需要用数学方式表达和描述，省去了大量繁琐的编程过程。
下面来介绍利用MA TLAB进行光学模拟的两种方法。
（一）衍射积分方法：该方法首先是由衍射积分算出接收屏上的光强分布，然后根据该分布调制色彩作图，从而得到衍射图案。
1．单缝衍射。
把单缝看作是np个分立的相干光源，屏幕上任意一点复振幅为np个光源照射结果的合成，对每个光源，光程差Δ=ypsinΦ,sinΦ=ys/D,光强I=I0(Σcosα)2+(Σsinα)2，其中α=2Δ/λ=πypys/λ D编写程序如下，得到图1lam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam;图1 单缝衍射的光强分布 sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2;endN=255;Br=(B/max(B))*N;subplot(1,2,1)image(ym,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys); 2． 杨氏双缝干涉两相干光源到接收屏上P 点距离r 1=(D 2+(y-a/2)2)1/2, r 2=(D 2+(y+a/2)2)1/2,相位差Φ=2π（r 2-r 1）/λ,光强I=4I 0cos 2（Φ/2）编写程序如下，得到图2 clear lam=500e-9 a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n); for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2);r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); endN=255;Br=(B/4.0)*N subplot(1,2,1) image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys) 3． 光栅衍射公式：I=I 0（sin α/α）2（sin(λβ)/sin β）2α=(πa/λ)sin Φ β=(πd/λ)sin Φ 编写程序如下：得到图3clearlam=500e-9;N=2; a=2e-4;D=5;d=5*a; ym=2*lam*D/a;xs=ym; n=1001;ys=linspace(-ym,ym,n); for i=1:nsinphi=ys(i)/D; alpha=pi*a*sinphi/lam; beta=pi*d*sinphi/lam;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2; B1=B/max(B);end图2 杨氏双缝干涉的光强分布图3 黑白光栅衍射光强分布NC=255;Br=(B/max(B))*NC; subplot(1,2,1) image(xs,ys,Br); colormap(gray(NC)); subplot(1,2,2) plot(B1,ys);（二）傅立叶变换方法：在傅立叶变换光学中我们知道夫琅和费衍射场的强度分布就等于屏函数的功率谱。
3_衍射的MATLAB计算[1]
![3_衍射的MATLAB计算[1]](https://img.taocdn.com/s3/m/585e2bd5b14e852458fb5788.png)
三(2)衍射的MATLAB 计算•一、狭缝衍射的Fresnel积分计算(直接)•二、远场衍射计算(FT)•三、近场衍射计算(看做卷积，先求FT，再X，再IFFT)•四、直接卷积核(看做卷积，直接计算)•五、园域函数•六、FT平面位移与干涉2006-3-10衍射的MATLAB计算比较1近场衍射2 1.5 1 0.5 0 -2 1.5 irradiance 1 0.5 0 -2 1.5 1 0.5 0 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2Nf =1subplot(3,1,1); slit(1); subplot(3,1,2); slit(8); ylabel('irradiance'); 8 N f =subplot(3,1,3); slit(16); xlabel('x/w');-1.5-1-0.500.511.52N f = 16-1.5 -1 -0.5 0 x/w 0.5 1 1.5 22006-3-10衍射的MATLAB计算比较11极近场衍射1.5 1 0.5 0 -2 1.5 irradiance 1 0.5 0 -2 1.5 1 0.5 0 -2N f = 10-1.5 -1 -0.5 0 0.5 1 2 subplot(3,1,1); slit(10); subplot(3,1,2); slit(100); N f = 100ylabel('irradiance') subplot(3,1,3); slit(1000); xlabel('x/w'); 1.5 2 1.5-1.5-1-0.500.51N f = 1000-1.5 -1 -0.5 0 x/w 0.5 1 1.5 22006-3-10衍射的MATLAB计算比较12衍射区域w2 Nf = Fresnel 数 λz w2 w = 1; ⇒ = 1 N f =1 ⇒ N f = λz bb=wb=λzw=λww Nf衍射扩散(b)几何阴影区(w)2wzNf >1“近” 场2006-3-10Nf <1“远”场衍射的MATLAB计算比较夫琅和费Nf ≈013Fresnel 区域2π 1 (x 2 + y 2 )2 << 1 3 λ 8 z12 2π 1 4 w << 1 3 λ 8 z12展开中忽略的第一项在 “近场” Nf >13w2 Nf = λ z12π4 ≈12π 1 ⎛ λ N f ⎞ 4 ⎜ ⎟ w << 1 λ 8 ⎜ w2 ⎟ ⎝ ⎠⎛w⎞ N f << ⎜ ⎟ ⎝λ⎠2 3令 λ = 0.5 µm 以及 w = 1 mm, 那么 Nf << 160 令 l = 0.5 mm,当w = 10 mm, 那么 Nf << 7402006-3-10 衍射的MATLAB计算比较 14二、远场衍射的计算⎡e ⎤ ⎛x 2π ⎞ ⎛ ⎞ N f ⎥ q⎜ ; N f ⎟ ∫ u1 (α )q(α ; N f )exp⎜ − j α x ⎟dα u2 ( x ) = ⎢ b ⎝ ⎠ ⎠ ⎣ j ⎦ ⎝wjkz12 1 2w2 Nf = λ z12b=⎛α ⎞ u1 (α ) = rect ⎜ ⎟ ⎝2⎠归一化坐标中狭缝宽 度 ＝2wλ z12wU1 (ξ ) = 2 sinc(2ξ )2 ⎛ x⎞ u2 = 4 N f sinc 2 ⎜ 2 ⎟ ⎝ b⎠ξ=x b将峰值归一化: 将irradiance 乘以0.25，2006-3-10 衍射的MATLAB计算比较并且不考虑 Nf.15远场例子N=1024; D=32; k=-N/2:N/2-1; x = (D/N)*k; dx = x(2)-x(1); f = rect(x/2); z = fftshift(fft(fftshift(f)))*dx; fx = (1/D)*k; fy = z.*conj(z)/4; frange=2; idx = find(abs(fx)<frange); plot(fx(idx),fy(idx),'k'); xlabel('x/b'); ylabel('normalized irradiance');1 0.9 0.8 normalized irradiance 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -2 -1.5 -1 -0.5 0 x/b 0.5 1 1.5 22006-3-10衍射的MATLAB计算比较16远场衍射的Matlab 代码function [fy, fx] = fslit(a) N=1024; D=32; k=-N/2:N/2-1; x = (D/N)*k; dx = x(2)-x(1); f = qchirp(x,a).*rect(x/2); xrange = 2; idx=find(abs(x)<xrange); subplot(2,1,1); plot(x(idx),real(f(idx)),'k',x(idx),imag(f(idx)),'b'); axis([-xrange xrange -1.5 1.5]); xlabel('x/w'); ylabel('f(x)'); z = fftshift(fft(fftshift(f)))*dx; fx = (1/D)*k; fy = z.*conj(z); if (a<1) fy = 0.25*fy; else fy = fy*a; fx = fx/a; end frange=2; idx = find(abs(fx)<frange); subplot(2,1,2); plot(fx(idx),fy(idx),'k'); %axis([-frange frange 0 1.0]); if (a<1) xlabel('x/b'); else xlabel('x/w'); end ylabel('|F|^2');2006-3-10衍射的MATLAB计算比较171.5 1 0.5 f(x) 0 -0.5 -1 -1.5 -2 -1.5 -1远场计算Nf = 1黒色为实数部分, 兰色为虚部部分tu1 (α )q(α ; N f )-0.50 x/w0.511.5221.5 |F|210.50 -2-1.5-1-0.5⎡e ⎤ ⎛x 2π ⎞ ⎛ ⎞ α x ⎟ dα N f ⎥ q⎜ ; N f ⎟ ∫ u1 (α )q(α ; N f )exp⎜ − j u2 ( x ) = ⎢ b ⎠ ⎝ ⎠ ⎣ j ⎦ ⎝wjkz121 20 x/w0.511.522006-3-10 fslit(1);衍射的MATLAB计算比较18远场计算 Nf = 81.5 1 0.5 f(x) 0 -0.5 -1 -1.5 -2 -1.5 -1 -0.5 0 x/w 0.5 1 1.5 2黒色为实数部分, 兰色为虚部部分t1.4 1.2 1 |F|2 0.8 0.6 0.4 0.2 0 -2 -1.5 -1 -0.5 0 x/w 0.5 1 1.5 22006-3-10 fslit(8);衍射的MATLAB计算比较19同直接计算的比较1.6 1.4 1.2 irradiance 1 0.8 0.6 0.4 0.2 0 -2 -1.5 -1 -0.5 0 x/w 0.5 1 1.5 2Nf =1function compare(a)Blue：远场计算, Black：直接计算.compare(1); 2006-3-10[fy fx] = fslit(a); [y x] = slit(a); idx = find(abs(fx)<2.0); subplot(1,1,1); plot(fx(idx),fy(idx),'b',x,y,'k'); if (a<1) xlabel('x/b'); ylabel('normalized irradiance'); else xlabel('x/w'); ylabel('irradiance'); 衍射的MATLAB计算比较 20 endb b远场衍射的Matlab代码function [outp, inp] = fourier(fcn),N=1024;D=sqrt(N);k = -N/2:N/2-1;[xs,ys] = meshgrid(k*D/N);dx= D/N;;dy= D/N;f = feval(fcn,xs,ys);A = sum(sum(f))*dx*dy;subplot(1,2,1);range = 4;xr= k/D;idx= find( (-range <= xr) & (xr<range) );inp= f(idx,idx);imshow(inp);x = xs(idx,idx);y = ys(idx,idx);z = fftshift(fft2(fftshift(f)))*(dx*dy/A);fy= z.*conj(z);subplot(1,2,2);frange= 4;idx= find( (-frange<= xr) & (xr<frange) );outp= fy(idx,idx);logim(outp,3);2006-3-10衍射的MATLAB计算比较45。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2015 级光电工程专业综合实验-信息光学专题实验
imagesc(z) figure(2) mesh(z) %%---------------------matlab 代码-------------------------
改变参数 a，b 的取值，观察模拟结果变化。 4）第一类贝塞尔函数 besselj（v,z）
1. 实验目的:
掌握基本的 Matlab 编程语言，了解其编程特点；模拟几种常用函数，了解其编 程过程及图像显示命令函数，掌握 Matlab 画图方法；通过设计制作一系列光学 研究物体掌握其编程方法； 掌握光波的 matlab 编程原理及方法， 初步了解 Matlab
2
2015 级光电工程专业综合实验-信息光学专题实验
4
2015 级光电工程专业综合实验-信息光学专题实验
figure(4) surfl(x,y,z)%三维 %%---------------------matlab 代码-------------------------
改变变量 a，b 观察模拟图像变化。
x 2 x 3）高斯函数：一维高斯函数 Gauss exp a a
二维高斯函数： sinc
x y x y , sinc sinc ，a，b 为正数。 a b a b
2 2 x y x y x y Gauss , Gauss Gauss exp a b a b a b
二维 sinc 函数： sinc
x y x y , sinc sinc ，a，b 为正数。 a b a b
%%---------------------matlab 代码------------------------clear %清除内存 close all %关闭所有窗口 [x,y] = meshgrid(-2:.05:2, -2:.05:2); %设置二维网格 z=sinc(x).*sinc(y); %sinc 函数 figure(1) imshow(z) %二维灰度图 figure(2) imagesc(z) %二维彩色 figure(3) mesh(z)%三维
%%---------------------matlab 代码------------------------clear %清除内存 close all %关闭所有窗口 a=5;%常数 x=linspace(-5,5,100);%设置一维横坐标范围及网格 y1=exp(-pi.*(x/a).^2);%第一类贝塞尔函数，一阶 figure(1)% 图 1 b=2;%常数 y2=exp(-pi.*(x/b).^2);%第一类贝塞尔函数，一阶 figure(1)% 图 1 plot(x,y1,'r')%画函数 1 的曲线，‘r’代表图像颜色,红色 figure(2) % 图 2 plot(x,y2,'b') %画函数 2 的曲线，‘b’代表图像颜色，蓝色 %%--------------------------------------------------------
注意******，matlab 编程中的编码输入必须在英文输入法下，否则程序将不被 识别。 二．常用物体的 Matlab 模拟 1）单缝
%%%%%%%%%%%%------------------------------clear close all %%%%%%%%%%%---------------参数设定---------------L=2;%物体总长度(mm) M=100;%x 方向抽样点数 dx=L/M;%抽样间隔(mm) N=M;%y 方向抽样点数 w=10; % 单缝的宽度,单位像素个数 d=10;% 缝偏离中心位置 %%%%%%%%%%----------单缝-----------obj1=zeros(M,N);%赋值为 0 的一个二维矩阵，大小为 M*N； obj1(:,(N/2-w/2):N/2+w/2)=1.0; %缝宽范围内赋值为 1，缝处于中心位置 figure(1);
当中 a、b 为 1 时，
2 2 Gauss x, y exp ( x y )
%%---------------------matlab 代码------------------------clear %清除内存 close all %关闭所有窗口 a=1;b=1; [x,y] = meshgrid(-2:.05:2, -2:.05:2); %设置二维网格 z=exp(-pi.*((x/a).^2+(y/b).^2)); %高斯函数 figure(1)
3
2015 级光电工程专业综合实验-信息光学专题实验
%%%---------------------------------------------------------------改变变量 phi 观察曲线变化。 2）开根号：sqrt（x） ，
%%-------------------------clear %清除内存 close all %关闭所有窗口 x=linspace(0,2*pi,100);%设置横坐标范围及网格 y1=sqrt(x); %开根号 figure% 图 plot(x,y1,'r')%画函数 1 的曲线，‘r’代表图像颜色,红色 %%------------------------------------------------
2015 级光电工程专业综合实验-信息光学专题实验
实验注意事项（必读）
1． 没有弄清楚实验内容者，禁止接触实验仪器。 2． 注意激光安全。绝对不可用眼直视激光束，或借助有 聚光性的光学组件观察激光束，以免损伤眼睛。 3． 注意用电安全。He-Ne 激光器电源有高压输出，严禁 接触电源输出和激光头的输入端，避免触电。 4． 注意保持卫生。严禁用手或其他物品接触所有光学元 件（透镜、反射镜、分光镜等）的光学表面；特别是 在调整光路中，要避免手指碰到光学表面。 5． 光学支架上的调整螺丝， 只可微量调整。 过度的调整， 不仅损坏器材，且使防震功能大减。 6． 实验完成后，将实验所用仪器摆放整齐，清理一下卫 生。
实验过程中要切记以上注意事项。如 有违犯，将严重影响你的实验成绩！
1
2015 级光电工程专业综合实验-信息光学专题实验
Matlab 数字衍射光学实验一
计算机仿真过程是以仿真程序的运行来实现的。仿真程序运行时，首先要对 描述系统特性的模型设置一定的参数值， 并让模型中的某些变量在指定的范围内 变化，通过计算可以求得这种变量在不断变化的过程中，系统运动的具体情况及 结果。仿真程序在运行过程中具有以下多种功能： 1）计算机可以显示出系统运动时的整个过程和在这个过程中所产生的各种现象 和状态。具有观测方便，过程可控制等优点； 2）可减少系统外界条件对实验本身的限制，方便地设置不同的系统参数，便于 研究和发现系统运动的特性； 3）借助计算机的高速运算能力，可以反复改变输入的实验条件、系统参数，大 大提高实验效率。 因此． 计算机仿真具有良好的可控制性(参数可根据需要调整)、 无破坏性(不会因为设计上的不合理导致器件的损坏或事故的发生)、 可复现性(排 除多种随机因素的影响，如温度、湿度等)、易观察性(能够观察某些在实际实验 当中无法或者难以观察的现象和难以实现的测量，捕捉稍纵即逝的物理现象，可 以记录物理过程的每一个细节)和经济性(不需要贵重的仪器设备)等特点。 Matlab 是 MathWorks 公司于 1982 年推出的一套高性能的数值计算和可视化 软件。 它集数值分析、 矩阵运算、 信号处理和图形显示于一体， 构成了一个方便、 界面友好的用户环境。它还包括了 ToolBox(工具箱)的各类问题的求解工具，可 用来求解特定学科的问题。Matlab 的长处在于数值计算，能处理大量的数据，而 且效率比较高。MathWorths 公司在此基础上开拓了符号计算、文字处理、可视 化建模和实时控制能力，增强了 Matlab 的市场竞争力，使 Matlab 成为市场主流 的数值计算软件。Matlab 产品族支持概念设计、算法开发、建模仿真、实时实现 的理想的集成环境。其主要功能有：数据分析、数值和符号计算、工程与科学绘 图、控制系统设计、数字图像信号处理、财务工程，建模、仿真、原型开发，应 用开发，图形用户界面。 在光学仪器设计和优化过程中，计算机的数值仿真已经成为不可缺少的手 段。通过仿真计算，可以大幅度节省实验所耗费的人力物力，特别是在一些重复 实验工作强度较大且对实验器材、实验环境等要求较苛刻的情况下。如在大型激 光仪器的建造过程中， 结合基准实验的仿真计算结果可为大型激光器的设计和优 化提供依据。仿真光学实验也可应用于基础光学教学。光学内容比较抽象，如不 借助实验，很难理解，如光的干涉、菲涅耳衍射、夫琅禾费衍射等。传统的光学 实验需要专门的实验仪器和实验环境。其操作比较烦琐，误差大现象也不明显， 对改变参数多次观察现象也多有不便。MATLAB 是当今国际上公认的在科技领 域方面最为优秀的应用软件和开发环境。 利用它对光学实验仿真可避免传统实验 中的缺点，强大的功能使光学实验变得简便准确。基于 MATLAB 的科学可视化 功能对光学仿真实验现象进行计算机模拟的效果更加准确明显。
%%---------------------matlab 代码------------------------clear %清除内存 close all %关闭所有已打开的窗口 x=linspace(-2*pi,2*pi,100);%设置一维横坐标范围及网格，pi为常数π y1=besselj(1,x);%第一类贝塞尔函数，一阶 y2=besselj(0,x);%第一类贝塞尔函数，0 阶 figure(1)% 图 1 plot(x,y1,'r')%画函数 1 的曲线，‘r’代表图像颜色,红色 figure(2) % 图 2 plot(x,y2,'b') %画函数 2 的曲线，‘b’代表图像颜色，蓝色 %%%-------------------------------------------------