高等土力学第四讲2012
高等土力学

(7).土体变形完全是由空隙水排出和超静水压力消散引起的
土的本构关系
太沙基方程:
2u u Cv 2 z t
k C v 其中:固结系数 mv
mv
k
为常数
关系。
1 x ( y x ) E 1 y y ( z x ) E 1 z z ( y x ) E 2(1 ) xy xy E 2(1 ) yz yz E 2(1 ) zx zx E
可写为:
3 I1 2 I 2 I3 0
土的本构关系
应力不变量: 第一应力不变量 第二应力不变量
I1 x y z
2 2 2 I 2 x y y z z x xy yz zx
第三应力不变量
f c tan
c:粘聚强度
tan
:摩擦强度
影响土强度的因素: 1.颗粒矿物成分的影响 2.粗粒土颗粒的几何性质 3.土的组成 4.土的状态
5.土的结构
土的强度
有效应力原理: 作用在饱和土体上的总应力由两种介质承担,一种是:孔隙水压力,
另一种是:土颗粒组成的骨架上的有效应力,而土的抗剪强度由:有效
y
1 zy 2
1 xz 2 1 yz 2 z
故有6个分量是独立的:
x y z xy yz zx
土的本构关系
三个应变不变量
I1 x y z 1 2 3 1 2 I 2 x y y z z x ( xy 2 yz 2 zx ) 1 2 2 3 31 4 I 3 1 2 3
高等土力学(李广信)2.3 土的应力变形特性

uniaxial loading
cyclic loading
0 0
5 10 σ =100kPa σ3=100kPa
3
15 ε1 00
ε1(%)
ε1(%)
10 σ3σ =3000kPa =200kPa
3
5
15
ε1
图2-15 减载体缩(1) -
白河堡粘土的三轴试验结果:加载与减载体积都收缩
图2-16 各种应力路径的中密砂三轴试验及减载体缩 -
1
12
2 4 3
(σ1-σ3) (100kPa) σ3)
10
8 Shear Stress Volume Strain 6
残余状态
4 εv (1/100)
2
1 2 4 3
0 0 2 4 6 8 10 12
-2 εa (1/100)
图2-8 用DDA计算的密砂应力应变曲线 -
各 向 等 压 压 缩 试 验 结 果
a2b比较图223不同应力路径的应力应变曲线图224正常固结粘土在不同应力增量方向上的应变增量方向图225?平面上应力路径转折时的应变路径应力历史正常固结与超固结或拟似超固结土图226正常固结与超固结土的应力应变曲线
2.3 土的应力变形特性
特性:非线性、弹塑性、压硬性、剪胀性、 各向异性、结构性、流变性、应变硬(软)化、 减载体缩。
图2-9 各向等压试验 -
图2-10 承德中密砂的三轴试验( σ3=500kPa) -
土的体积收缩趋势 剪应力引起的体胀有恢复的趋势;
但是剪应力引起的体积收缩是不可恢复的;
各种形式的应力的重复总是引起体缩的积累。
σ τ
体缩
体胀
图2-11 剪应力下的颗粒的运动与体变 -
高等土力学(李广信)4.3_土的渗透性

土水特征曲线 的拟合公式 :
残余含水率:含水率低于它,需很大 吸力进一步减少含水率
[1
ln(1 S / ln(1 106
Sr ) / Sr )
]
{ln[e
s
(S
/
a)n ]}m
溶质势 0
纯水中溶质势设为零,即0=0 溶解有离子的溶液中溶质势0<0
c a (1 Sr )n
a
aua
RT
Da*
Da
c ua
Da
[a (1 S)n]
ua
Ja
Da*
ua y
Da*
a
g
ha y
Da*a gia y
Ja
a
Va t
ava
va Dagiay
ka Da*g
hw(A)>hw(B),水由A流向B
图4-22
基质势与吸力: m s (ua uw )
ua pa 0 m wh uw s
土-水特征曲线坐标的另一种表 示:体积含水率
vw v
Sr
n
Sre 1 e
进气值点
r残余含水率
图4-23 土水特征曲线
达西定律的适用范围 粗粒土:层流与紊流
图4-26 层流与紊流
粘性土:起始水力坡降:由于结合水的粘滞性, 需要一定的水力坡降克服其抗剪强度-屈服剪应 力
图4-27
4.3.3 非饱和土的渗透性
图4-28 三种状态的非饱和土
土的饱和度比较高时(>85%~90%),土的孔隙主要被 水所占据。气体呈气泡状被水所包围,可随水一起流动, 称为气封闭状态。这种混和的流体是可压缩的,在较高压 力势下,气泡可能压缩和溶解,使孔隙水饱和度进一步提 高。一般可按饱和土计算渗透与固结问题。
高等土力学04土中水及渗流计算-知识归纳整理

求知若饥,虚心若愚。 第 116 页/共 195 页
千里之行,始于足下。 第 117 页/共 195 页
求知若饥,虚心若愚。 第 118 页/共 195 页
千里之行,始于足下。 第 119 页/共 195 页
求知若饥,虚心若愚。 第 120 页/共 195 页
千里之行,始于足下。 第 121 页/共 195 页
求知若饥,虚心若愚。 第 176 页/共 195 页
千里之行,始于足下。 第 177 页/共 195 页
求知若饥,虚心若愚。 第 178 页/共 195 页
千里之行,始于足下。 第 179 页/共 195 页
求知若饥,虚心若愚。 第 180 页/共 195 页
千里之行,始于足下。 第 181 页/共 195 页
求知若饥,虚心若愚。 第 62 页/共 195 页
千里之行,始于足下。 第 63 页/共 195 页
求知若饥,虚心若愚。 第 64 页/共 195 页
千里之行,始于足下。 第 65 页/共 195 页
求知若饥,虚心若愚。 第 66 页/共 195 页
千里之行,始于足下。 第 67 页/共 195 页
求知若饥,虚心若愚。 第 32 页/共 195 页
千里之行,始于足下。 第 33 页/共 195 页
求知若饥,虚心若愚。 第 34 页/共 195 页
千里之行,始于足下。 第 35 页/共 195 页
求知若饥,虚心若愚。 第 36 页/共 195 页
千里之行,始于足下。 第 37 页/共 195 页
求知若饥,虚心若愚。 第 122 页/共 195 页
千里之行,始于足下。 第 123 页/共 195 页
求知若饥,虚心若愚。 第 124 页/共 195 页
高等土力学(李广信)5.4 土的三维固结

[vx dxdydz vy dydxdz vz dzdxdy]dt v dtdxdydz
x
y
z
t
流出水量=体积压缩
vx
k
w
u x
,vy
k
w
u y
, vz
k
w
u z
达西定律
k 2u v
w
t
连续性方程
k 2u v
w
t
v
p K
1 2v' E'
3u
x y z
v
t
1 2v' E'
t
v' 0.5 Cv1 Cv2 Cv3
v' 0 Cv1 2Cv2 3Cv3
3. 固结系数的比较
Cv1
w
kE'(1 ')
(1 v' )(1 2v' )
太沙基一维固结理论
Cv
k
mv w
k 1 e= Esk
av w
w
Es
1 (1 )(1-2
)E
二者的固结系数是一致的
5.4.3 两种固结论理的比较——原理与条件
2 2 2 2 x 2 y 2 z 2
方程及未知数个数
2us
(
'
G' G'
)
v
x
1 G'
u x
0
未知数4个:
us, vs ws :土骨架
2vs
(
'
G G'
'
)
v
y
1 G
'
u y
0
的位移 u:孔隙水压力 三个方程
土的基本性质高等土力学课件
Bazant ZP, Oh BH. Microplane model for creep of anisotropic clay. J Eng Mech, ASCE, 1983.
59
蠕变微观机理
9次2×21点在二十面上的非正交对称分布
60
蠕变微观机理
9次2×21点在球面上的正交对称分布
61
蠕变微观机理
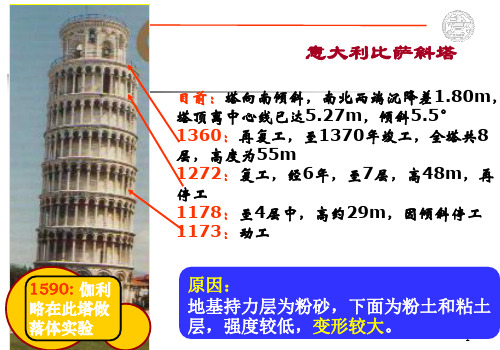
原因: 地基持力层为粉砂,下面为粉土和粘土 层,强度较低,变形较大。
1
2
3
4
1995年阪神地震大阪的街道路面液化
5
1999年台湾大地震中台中县由于液化引 起的楼房倒塌
6
赵洲桥
隋朝石工李春所建,他把石台砌筑于密 实的粗砂 层上,一千三百多年来估计沉 降仅几厘米。
7
提纲
土的构成 土的物理化学性质 土的基本力学性质 土的分类
11次2×33点在多面上的正交对称分布
62
变形
本构模型 固结理论
63
土的分类
64
塑性指数分类指标界限值及土类名称
0 13
7
国家建委TJ7-74规范 砂土
轻亚粘土
水利部土工实验6规范 砂土 砂壤土
10
17
亚粘土 粘土
壤土
粘土
交通部79规范 冶金部冶基规103-77
地质矿产部84规范
砂土 砂土 砂土
ij
f
.
(n)ds
.
ij ij
3
2
bijkm
s
1
.
k2 T
sh1
.
T
k1
f
(n)ds
. km
.
ij
57
蠕变微观机理
高等土力学(李广信)2.5 土的弹塑性模型的一般原理

面重合,即f=g。
不相适应(不相关联)的流动(nonassociated
flow rule):塑性势面不必与屈服面重合fg。
dpij
dij
Drucker 假说:对于稳定材 料:
图2-42 Drucker 假说
认为A与A´在同一屈服面上
图2-41
三轴试验与真三轴试验确定塑性应变增量方向
2.5.3流动规则与硬化定律
1. 流动规则 (flow rule) 2. 硬化定律 (strain-hardening law)
1. 流动规则(flow rule):用以确定塑性应变增量 向量的方向的规则(或者确定塑性应变增量的 各个分量间的比例关系)-塑性应变增量向量 正交于塑性势面。所以也称为正交规则。
d
ijd
P ij
0
屈服面的外凸 与塑性应变增 量向量的正交
锥形屈服面与帽子屈服面 q
dpij dpij
p 图2-43 与两种屈服面的正交的塑性应变
表现土的塑性剪胀与剪缩,锥形屈服面会使剪胀量过 大,一般采用不相适应的流动规则
2. 加工(应变)硬化定律 (strain-hardening law): 是确定在一定的应力增量作用下引起的塑性应变增
2.5.2屈服准则与屈服面
1. 屈服准则 2. 屈服函数 3. 屈服面与屈服轨迹 4. 土的屈服面与屈服轨迹的一般形式 5.土的屈服面与屈服轨迹的确定
1. 屈服准则(yield criterion)
判断是否发生塑性变形的准则 -判断加载与卸载的准则
ABBຫໍສະໝຸດ AABA B
A、B在屈服面上, A B不在屈服面上
(完整word版)高等土力学

1.简述强度折减法的原理及分析过程抗剪强度折减系数法的理论2.1抗剪强度折减系数法的概念抗剪强度折减系数(SSRF:Shear Strength Reduction Factor)定义为:在外荷载保持不变的情况下,边坡内土体所发挥的最大抗剪强度与外荷载在边坡内所产生的实际剪应力之比。
这里定义的抗剪强度折减系数,与极限平衡分析中所定义的土坡稳定安全系数在本质上是一致的。
2.2抗剪强度折减系数法的具体内容折减系数sF的初始值取得足够小,以保证开始时是一个近乎弹性的问题。
然后不断增加sF的值,折减后的抗剪强度指标逐步减小,直到某一个折减抗剪强度下整个土坡发生失稳,那么在发生整体失稳之前的那个折减系数值,即土体的实际抗剪强度指标与发生虚拟破坏时折减强度指标的比值,就是这个土坡的稳定安全系数。
2.3抗剪强度折减系数法的优点结合有限差分法的抗剪强度折减系数法较传统的方法具有如下优点:(1)能够对具有复杂地貌、地质的边坡进行计算;(2)考虑了土体的本构关系,以及变形对应力的影响;(3)能够模拟土坡的边坡过程及其滑移面形状(通常由剪应变增量或者位移增量确定滑移面的形状和位置);(4)能够模拟土体与支护结构(超前支护、土钉、面层等)的共同作用;(5)求解安全系数时,可以不需要假定滑移面的形状,也无需进行条分。
2.简述确定土体临界失稳模式最优化方法的数学模型及其分析过程3.结合塑性力学上限定理,简述斜条分法作为土体稳定上限解的理论依据4.如何理解垂直条分法作为土体稳定分析的下限解5.边坡稳定、土压力和地基承载力的联系和区别?P323-324什么是加工硬化?什么是加工软化?金属材料在再结晶温度以下塑性变形时,由于晶粒发生滑移,出现位错的缠结,使晶粒拉长、破碎和纤维化,使金属的强度和硬度升高,塑性和韧性降低的现象,称加工硬化或冷作硬化。
岩土中什么是压硬性?剪胀性?压硬性随着压缩过程的进行,岩土的压缩模量逐步提高的现象,如应力应变曲线逐步变缓,就是压硬性的表现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
浙江工业大学建筑工程学院
弹塑性理论回顾: 德鲁克(Drucker )公设?依留辛公设? 屈服准则 流动—正交法则 硬化规律
3
浙江工业大学建筑工程学院
弹性-完全塑性
增量弹塑性
刚塑性
几种塑性模型
d ij d d
e ij
p ij 4
浙江工业大学建筑工程学院
不同塑性模型的应用
1)刚塑性理论-极限平衡法:刚体滑动法、各种条分法、
f f df d ij dH 0 ij H f f H p d ij d ij 0 ij H ijp f f H g d ij d 0 p ij H ij ij
T f f d ij d ij d T f H g f H g p H ijp ij H
T
f d d A
T
23
A:塑性硬化模量
浙江工业大学建筑工程学院
2.5.4弹塑性本构模型的模量矩阵的一般表达式
d d
e
d
p
T
f d d A
g [ D]d [ D]d [ D]d
B 为屈服点;
A´非屈服点
7
浙江工业大学建筑工程学院
2. 屈服函数 (yield function, yield equation) 屈服准则的数学表达式
f ( ij , H ) 0
对于刚塑性和弹性-塑性模型:H为常数;
对于弹塑性模型:H一般是塑性应变的函数。
8
浙江工业大学建筑工程学院
e
{d}
24
浙江工业大学建筑工程学院
g f D D d =Dd d T f g A+ D
T g f D D = D T d f g A+ D =D ep d
滑移线法(不计变形,不计过程)。
2)弹-塑性理论:在一定范围为弹性,超过某一屈服条件 为塑性变形。数值计算中出现“塑性区”。 3)(增量)弹塑性理论模型:一开始就是弹塑性变形同时 发生,不能够分开,屈服面不断发展。
5
浙江工业大学建筑工程学院
2.5.2屈服准则与屈服面
1. 屈服准则
2. 屈服函数
3. 屈服面与屈服轨迹
10
浙江工业大学建筑工程学院
4. 土的屈服面与屈服轨迹的形状
1)由于土是一种摩擦材料,人们认为只是在应 力比变化时颗粒间才会相对滑动位移(MohrCoulomb, ;广义Mises;广义Tresca: 锥形屈 服面)
q q
p
锥形屈服面
射线屈服轨迹
p
11
浙江工业大学建筑工程学院
2) 又由于土在各向等压条件下也会发生颗粒相对 运动,土变密实,所以出现各种“帽子”屈服 面(Cam-clay;清华模型)
dp Mpd
'
dp ' p ' d v Mp ' q ' d ' 1 e p
(10)=(1) +(9)
45
浙江工业大学建筑工程学院
1 ' d d v dp ' 1 e p
p V
(11)
p d Mp q d
32
浙江工业大学建筑工程学院
各向等压的加载与卸载
v=N- lnp:初始加载 v=v- lnp:回弹曲线
33
浙江工业大学建筑工程学院
2.6.2 超固结土及完全的物态边界面
1.正常固结粘土 2.轻超固结粘土:OCR比较小,卸载范围不大 3.强超固结粘土:OCR很大, 卸载后的应力比先 期固结应力小很多
2.6.3 弹性墙与屈服轨迹
1. 弹性墙
正常固结粘土与轻超固结粘土(wet clay)
各向等压固结: 加载:NCL 卸载-弹性墙
41
浙江工业大学建筑工程学院
弹性墙
弹性墙
42
浙江工业大学建筑工程学院
2. 能量方程
dE p d v q d
' '
(1)
变性能=弹性变性能+塑性变性能
dE dW dW
C-U:固结不排水试验有效应力路径
29
浙江工业大学建筑工程学院
NCL: normal consolidation line CSL: critical state line q=M p v=N- lnp(NCL)
N
v=- lnp (CSL) p=exp(-v)/
正常固结粘土的排水与不排水应力路径
(6)
dW
e
pd
e v
1 e
dp ' (7)
44
浙江工业大学建筑工程学院
2) 假定塑性变性能可表示为:
dW p Mpd
p p V
p
Mpd
p
(8):这是一个重 要假设
(4) (9)= (8)+ (7)
dW pd qd
dE dW dW
e p
1 e
T
相适应 f=g
26
浙江工业大学建筑工程学院
2.6 土的剑桥模型
2.6.1 正常固结粘土的物态边界面
2.6.2 超固结土和完全的物态边界面
2.6.3 弹性墙与屈服轨迹 2.6.4 修正的剑桥模型
27
浙江工业大学建筑工程学院
2.6.1 正常固结粘土的物态边界面
三轴应力状态:
偏应力: q=
22
浙江工业大学建筑工程学院
d
P ij
g d ij
f d d T f H g p H
T
f A H
H g p
14
浙江工业大学建筑工程学院
试验搜索屈服点 认为A与A´在同一屈服面上
15
浙江工业大学建筑工程学院
三轴试验与真三轴试验确定塑性应变增量方向
16
2.5.3流动规则与硬化定律
1. 流动规则 (flow rule) 2. 硬化定律 (strain-hardening law)
17
浙江工业大学建筑工程学院
e
p
(2)
其中
dW pd qd
e e v
e
dW pd qd
p p v
p
(3)
(4)
43
浙江工业大学建筑工程学院
塑性变性能的基本假设:
1)假设一切剪应变是不可恢复的,亦即:
d 0
e
(5)
dv e dp ' e d V 1 e 1 e p'
4. 土的屈服面与屈服轨迹的形状
5.土的屈服面与屈服轨迹的确定
6
浙江工业大学建筑工程学院
1. 屈服准则(yield criterion) 判断是否发生塑性变形的准则 -判断加载与卸载的准则
A B B
B
A
A
A
B
A、B在屈服面上, A B不在屈服面上 屈服-弹塑性应变的判断准则
加卸载的判断(应变硬化情况)
f d ij 0 ij
为加载,同时发生弹性、 塑性变形
f 0
f d ij 0 ij
为中性变载,只产生弹性变形
f d ij 0 ij
为卸载,只产生弹性变形
f <0 在屈服面之内,弹性变形
9
浙江工业大学建筑工程学院
3. 屈服面与屈服轨迹 屈服面-屈服准则在应力空间中的几何表示: 1)三维应力空间:屈服面 2)二维应力空间:屈服轨迹
18
浙江工业大学建筑工程学院
dpij
dij
ij
Drucker 公设:对于稳定材料:
1)屈服面的外凸性
d ij d
P ij
0
2)与塑性应变增量向量的正交
19
浙江工业大学建筑工程学院
锥形屈服面与帽子屈服面 q
dpij dpij
p 与两种屈服面的正交的塑性应变
表现土的塑性剪胀与剪缩,锥形屈服面会使剪胀量过大, 20 一般采用不相适应的流动规则
完全的物态边界面
37
浙江工业大学建筑工程学院 完全的物态边界面
包括超固结土的 完全的物态边界 面-(状态只能在 面内和面上)
完全的物态边界面
38
浙江工业大学建筑工程学院
HS
超固结
CS
正常固结
排水试验的应力体变曲线
39
浙江工业大学建筑工程学院
正常固结土与超固结土的应力路径
40
浙江工业大学建筑工程学院
H-UH: 不排水试验,负孔压,
pm
强度超过临界状态线 峰值强度(TS)与残余强度 (临界线上)
排水试验的应 力应变曲线
36 重超固结粘土的路径
浙江工业大学建筑工程学院
完全的物态边界面: 0T:零应力线(无拉应力) TS:超固结土的强度线-Hvorslev面 CS:v=常数的Roscoe 面
包括了正常固结土、重超固结土的 可能的(极限)应力状态
25
T
浙江工业大学建筑工程学院
g f D D Dep=D T f g A+ D
T
不相适应fg
f f D D Dep=D T f f A+ D
q q
p
q p
帽子屈服面
p
