统计学例题-统计整理
统计学各章练习——统计整理

第三章统计整理一、名词1、统计整理:根据统计研究的任务与要求,对统计调查所搜集到的原始资料进行分组、汇总,使其条理化、系统化的工作过程。
统计整理包括对原始资料和次级资料的整理。
2、统计分组:根据统计研究的目的和现象总体内在的特点,将总体按某个标志(或几个标志)划分为若干个性质不同的组成部分的一种统计方法。
总体这组成部分称为“组”。
3、分配数列:在统计分组的基础上,将总体中所有单位按组归类整理,并按一定顺序排列,形成总体中各个单位在各组间的分布状况,称为分配数列。
4、变量数列:按数量标志分组形成的分配数列。
二、填空1、统计分组有两方面的含义:对总体而言是(分),对总体单位而言是(合)。
通过统计分组,既要体现(组内的同质性),又要体现(组间的差异性)。
2、统计分组按分组标志的性质不同,分为按(品质标志)分组和按(数量标志)分组。
3、统计分组的作用是划分(现象类型)、研究(现象总体的内部结构)、揭示(现象之间的依存关系)。
4、统计分组的关键在于(分组标志的选择)。
5、分配数列中的(次数)表示标志值在各组中出现的次数,称之为(频数),(各组次数与总次数之比)叫做比重,也称为频率。
6、人口按性别、民族、文化程度分组,属于按(品质标志)分组,而工人按年龄、工资水平分组,则属于按(数量标志)分组。
7、在变量分组中,(离散变量)可以进行单项分组,也可以进行组距分组,而(连续变量)只能进行组距分组。
8、变量数列有(单项数列)和(组距数列)两种,其中(组距数列)又可分为(等距数列)和(异距数列)两种。
9、从外表形式看,统计表是由(总标题)、(横行标题)、(纵栏标题)、(指标数值)等构成;从内容看,统计表包括(主词)和(宾词)两部分。
10、按主词是否分组和分组的程度,统计表可以分为(简单表)、(简单分组表)、(复合分组表)。
11、统计分析报告的结构一般可分为四个部分,即:(基本情况与背景资料)、(成绩和经验)、(问题与原因)、(建议与措施)。
统计学计算题整理

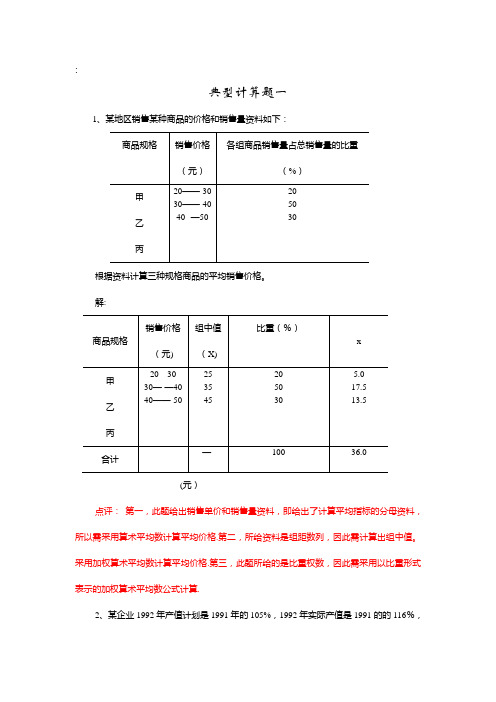
:典型计算题一1、某地区销售某种商品的价格和销售量资料如下:根据资料计算三种规格商品的平均销售价格。
解:36==∑∑ffxx (元)点评: 第一,此题给出销售单价和销售量资料,即给出了计算平均指标的分母资料,所以需采用算术平均数计算平均价格。
第二,所给资料是组距数列,因此需计算出组中值。
采用加权算术平均数计算平均价格。
第三,此题所给的是比重权数,因此需采用以比重形式表示的加权算术平均数公式计算。
2、某企业1992年产值计划是1991年的105%,1992年实际产值是1991的的116%,问1992年产值计划完成程度是多少解:%110%105%116===计划相对数实际相对数计划完成程度。
即1992年计划完成程度为110%,超额完成计划10%。
点评:此题中的计划任务和实际完成都是“含基数”百分数,所以可以直接代入基本公式计算。
3、某企业1992年单位成本计划是1991年的95%,实际单位成本是1991年的90%,问1992年单位成本计划完成程度是多少解: 计划完成程度%74.94%95%90==计划相对数实际相对数。
即92年单位成本计划完成程度是%,超额完成计划%。
点评:本题是“含基数”的相对数,直接套用公式计算计划完成程度。
4、某企业1992年产值计划比91年增长5%,实际增长16%,问1992年产值计划完成程度是多少解:计划完成程度%110%51%161=++=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
5、某企业1992年单位成本计划比1991年降低5%,实际降低10%,问1992年单位成本降低计划完成程度是多少解:计划完成程度%74.94%51%101=--=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
6、某企业产值计划完成103%,比上期增长5%,问产值计划规定比上期增加多少 解:103%=105%÷(1+x )x=%即产值计划规定比上期增加%.点评:计划完成程度=103%,实际完成相对数=105%,设产值计划规定比上期增加x,则计划任务相对数=1+x,根据基本关系推算出x.7、某煤矿某月计划任务为5400吨,各旬计划任务是均衡安排的,根据资料分析本月生产情况.=104%),但在节奏性方面把握不解:从资料看,尽管超额完成了全期计划(5400好。
统计学概念整理 以及试题(附答案)

一基本概念、1、统计总体简称总体是我们要调查或统计某一现象全部数据的集合。
总体单位是构成总体的各个个别单位,它是组成总体的基本单位,也是调查项目的直接承担者。
如:对工业企业进行调查,全国工业企业是总体,每一个工业企业就是单位。
2标志与指标指标是反映统计总体的数量特征,标志反映的是总体单位的特征。
指标分为数量指标和质量指标。
(都可以用数量表示)数量指标,反映总体总规模或总水平,如人口数,产量,耕地面积。
质量指标,反映总体内在质量,如产品合格率,劳动生产率等。
标志分为品质标志和数量标志。
品质标志,如人的性别,籍贯等。
(只能用文字表示)数量标志,人的年龄,身高,职工工资等。
(用数量表示)关系:1)、指标反映的是总体,标志反映的是单位;2)、表示方法不同(文字还是数字);3)、标志是构成指标的基础,指标是标志的汇总,在一定情况下可以互相转化。
如A同学,性别女,女是A的标志,B同学,性别男,男是B的标志……假设一共有5位男同学,3位女同学,男女性别比为5:3,这个5:3就是指标了。
没有前面每个同学的性别标志,就不能通过加总得到后面的5:3.3从统计学而言,理论上,一切认识的对象均可被量化。
而其量化的方法则无外乎四种--定量、定比、定序、定类。
(定距尺度没有绝对零点,比如IQ)1、定类尺度:也称类别尺度或名义尺度,是将调查对象分类,标以各种名称,并确定其类别的方法。
它实质上是一种分类体系。
2、定序尺度:也称等级尺度或顺序尺度,是按照某种逻辑顺序将调查对象排列出高低或大小,确定其等级及次序的一种尺度。
3、定距尺度:也称等距尺度或区间尺度,是一种不仅能将变量(社会现象)区分类别和等级,而且可以确定变量之间的数量差别和间隔距离的方法。
4、定比尺度:也称比例尺度或等比尺度,是一种除有上述三种尺度的全部性质之外,还有测量不同变量(社会现象)之间的比例或比率关系的方法。
4.变异与变量在一个总体中,当某标志在每个总体单位上的具体表现都相同时,称此标志为不变标志。
统计学计算题整理
:典型计算题一1、某地区销售某种商品的价格和销售量资料如下:根据资料计算三种规格商品的平均销售价格。
解:(元)点评:第一,此题给出销售单价和销售量资料,即给出了计算平均指标的分母资料,所以需采用算术平均数计算平均价格.第二,所给资料是组距数列,因此需计算出组中值。
采用加权算术平均数计算平均价格.第三,此题所给的是比重权数,因此需采用以比重形式表示的加权算术平均数公式计算.2、某企业1992年产值计划是1991年的105%,1992年实际产值是1991的的116%,问1992年产值计划完成程度是多少?解:.即1992年计划完成程度为110%,超额完成计划10%。
点评:此题中的计划任务和实际完成都是“含基数"百分数,所以可以直接代入基本公式计算。
3、某企业1992年单位成本计划是1991年的95%,实际单位成本是1991年的90%,问1992年单位成本计划完成程度是多少?解:计划完成程度。
即92年单位成本计划完成程度是94。
74%,超额完成计划5。
26%.点评:本题是“含基数”的相对数,直接套用公式计算计划完成程度。
4、某企业1992年产值计划比91年增长5%,实际增长16%,问1992年产值计划完成程度是多少?解:计划完成程度点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数"的相对数,才能进行计算。
5、某企业1992年单位成本计划比1991年降低5%,实际降低10%,问1992年单位成本降低计划完成程度是多少?解:计划完成程度点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
6、某企业产值计划完成103%,比上期增长5%,问产值计划规定比上期增加多少?解:103%=105%÷(1+x)x=1。
9%即产值计划规定比上期增加1.9%.点评:计划完成程度=103%,实际完成相对数=105%,设产值计划规定比上期增加x,则计划任务相对数=1+x,根据基本关系推算出x。
统计学例题

一、判断题1.社会经济统计的研究对象是社会经济现象总体的各个方面。
( x)2.统计调查过程中采用的大量观察法,是指必须对研究对象的所有单位进行调查。
( x)3.总体的同质性是指总体中的各个单位在所有标志上都相同。
(x)4.某一职工的文化程度在标志的分类上属于品质标志,职工的平均工资在指标的分类上属于质量指标。
(v)5.总体单位是标志的承担者,标志是依附于总体单位的。
(v)6.全面调查和非全面调查是根据调查结果所得到的资料是否全面来划分的。
(x)7.对我国主要粮食作物产区进行调查,以掌握全国主要粮食作物生长的基本情况,这种调查是重点调查。
(v)8.在对现象进行分析的基础上,有意识地选择若干具有代表性的单位进行调查,这种调查属于重点调查。
(x)9.统计分组的关键问题是确定组距和组数。
(x)10.分配数列的实质是把总体单位总量按照总体所分的组进行分配。
(v)11.某企业职工按文化程度分组形成的分配数列是一个单项式分配数列。
(x)12.连续型变量和离散型变量在进行组距式分组时,均可采用相邻组组限重叠的方法确定组限。
(v)13.分组以后,各组的频数越大,则组的标志值对于全体标志水平所起的作用也越大;而各组的频率越大,则组的标志值对全体标志水平所起的作用越小。
(x)14.同一个总体,时期指标值的大小与时期长短成正比,时点指标值的大小与时点间隔成反比。
(v)15.某企业生产某种产品的单位成本,计划在上年的基础上降低2%,实际降低了3%,则该企业差一个百分点,没有完成计划任务。
(x)16.某年甲、乙两地社会商品零售额之比为1:3,这是一个比例相对指标。
(x)17.全国粮食总产量与全国人口数对比计算的人均粮食产量是平均指标。
(x)18.根据分组资料计算算术平均数,当各组单位数出现的次数均相等时,按加权算术平均数计算的结果与按简单算术平均数计算的结果相同。
(v)19.权数对算术平均数的影响作用只表现为各组出现次数的多少,与各组次数占总次数的比重无关。
第三章--统计整理-幻灯片(1)
如某班学生按年龄分组:17岁,18岁,19岁, 20岁, 21岁,22岁。
组距式分组
将作为分组依据的数量标志的整个取 值范围依次划分为若干个满足互斥性
和包容性的区间,用这些数值区间作
为组的名称。
某班学生统计 学原理成绩分 组
60分以下 60—70分 70—80分 80—90分 90分以上
组距式分组中的一些概念 《统计学原理》第三章 统计整理
对教师 的分类
按性别分类
男性 女性
高级 按职称分类 中级 共计7组
初级 2+3+2
青年 按年龄分类
中年
复合分组体系
对教师 的分类
按性别 分类
按职称 分类
按年龄 分类
《统计学原理》第三章 统计整理
共计12组 男 2×3×2
女 高级
中级
初级 青年 中年
《统计学原理》第三章 统计整理
统计资料的再分组
• 统计资料的再分组就是把统计分 组资料按某种要求,重新划定各 组界限,再将资料中的单位数或 比重分布重新做出调整。
对总体单位而言,是“合”,即将性质相同的 个体组合起来,在同一组内则保持着相同的性 质。
分组
《统计学原理》第三章 统计整理
25%
33%
分组前
分组后
42%
作用:1·区分事物的性质
例:按所有制性质划分,我国现有8种经济类型:
国有经济;集体经济;私营经济;个体经济 联营经济;股份制经济;外商投资经济;港 澳台投资经济
将统计调查得到的原始资料进行科
统计整理 学的分类和汇总,使之成为系统化、
条理化的综合资料,以反映研究总 体的特征。
地位 是统计调查的继续,统计分析的前提 和基础,起着承前启后的作用。
统计学计算题

第三章统计整理例 1、某厂工人日产量资料如下:(单位:公斤)162 158 158 163 156 157 160 162 168 160164 152 159 159 168 159 154 157 160 159163 160 158 154 156 156 156 169 163 167试根据上述资料,编制组距式变量数列,并计算出频率。
解:将原始资料按其数值大小重新排列。
152158 159154 154 156 156 156 156 157 157 158 158 159 159 159 159 160 160 160 162 162 163 163 163 164 167168 168 169最大数=169,最小数=152,全距=169-152=17n=30, 分为 6 组例 2、某企业 50 个职工的月工资资料如下:113 125 78 115 84 135 97 105 110 130105 85 88 102 101 103 107 118 103 87116 67 106 63 115 85 121 97 117 10794 115 105 145 103 97 120 130 125 127122 88 98 131 112 94 96 115 145 143试根据上述资料,将50 个职工的工资编制成等距数列,列出累计频数和累计频率。
解:将原始资料按其数值大小重新排列。
63 97 117 118工人按日产量分组(公斤)152-154155-157158-160161-163164-166 工人数(人)361151比率(频率)(%)10.0020.0036.6016.7067 78 84 85 85 87 88 88 94 94 96 97 97 98 101 102 103 103 103 105 105 105 107 110 112 113 115 115 115 115 116 118 120 121 122 125 125 127 130 130 131 135 143 145 145按工资额分组(元)60-70 70-80 80-90频数216工人数频率( %)4212频数239向上累计频率( %)4618频数504847向下累计频率(%)1009694例 3、有 27 个工人看管机器台数如下:5 4 2 4 3 4 3 4 4 2 4 3 4 3 26 4 4 2 2 3 4 5 3 2 4 3试编制分布数列。
统计学整理资料

统计学整理资料选择题(A)1.某地区抽查1000名成年人的血压并制作成频数表,这属于___资料A.计量资料 B.计数资料 C.等级资料D。
半定量资料(B)2.上述调查按血压正常与否整理资料,其中高血压患者200名,血压正常者800名,这属于___资料A.定量资料B。
计数资料C。
等级资料D。
半定量资料(C)3.对变异的事物可采用抽样观察,其主要目的是___A.反映某个体情况B。
反映某样本情况 C.反映某总体情况D。
上述都是(D)4.从4个市级医院外科病史中随机抽样,反映全市外科医护质量,你认为____ A.可以,抽样面广B。
不可以,可能样本大小C。
可以,是随机抽样D.不可以,不能反映研究总体(A)5.概率P=0,则表示______A事件必然不发生B。
某事件必然发生(P=1)C。
某事件发生的可能性很小(P接近0)D。
某事件发生的可能性很大(P接近1)(A)6.要减少抽样误差,最切实可行的方法是___A.增加观察对象(样本含量)B。
控制个体变异C。
遵循随机化原则抽样D.严格挑选研究对象(B)7.表示正态分布计量资料集中趋势的统计指标是____A.M B.x(上划线请标示) C.G D.S(A)8.欲从频数表了解计量资料的分布情况,可通过观察各组的___A.频数B.组中值C.组距D.上,下限(B)9.标准差越大的意义,下列认识中错误的___A.观察个体之间变异越大 B.观察个体之间变异越小C.样本的抽样误差可能越大D.样本对总体的代表性可能越差(B)10.血清学滴度资料最常计算___表示其平均水平A.算术均数 B.几何均数 C.中位数 D.全距(C)11.某厂发生食物中毒,9名患者潜伏期分别为:16,2,6,3,30,5,10,2,24(小时),问该食物中毒的平均潜伏期为___(小时)A.5B.5.5C.6D.10(A)12.来自同一总体的两个样本,___小的那个样本均数估计总体均数更可靠A.Sx (上划线请标示)B.SC.CVD.t.0.05(v)Sx(上划线请标示)(B)13.下列___公式可用于估计总体均数可信区间(95%)(选项请自己填写打不出,谢谢)(C)14.当自由度V→∞时,t0.05值____A.≠1,96B.<1.96C.=1.96D.>1.96(A)15.随着自由度的增加,t值____A.变小B.增大C.不变D.视情况而定(B)16.下列____公式可用于估计95%样本均数分布范围(选项请自己填写打不出,谢谢)(C)17.关于t检验的作用的认识,确切地是检验____A.x(上划线请标示)之间是否存在抽样误差B.u之间是否存在抽样误差C.x(上划线请标示)之间的差别由抽样误差引起的概率大小D.u之间的差别由抽样误差引起的概率大小(B)18.在两样本均数比较的t检验中,无效假设(H0)的正确表达应为__A.u1≠u2B.u1=u2C.x1≠x2D.x1=x2(C)19.在t检验中,当t>t0.05(v)时,则结论为___A.P>0.05B.P>=0.05C.P<0.05D.P<=0.05(A) 20.抽样调查男生和女生各100名,并分别统计出身与体重均数,其中同性别的身高与体重均数不可作假设检验,是因为__A.资料不具备可比性B.身高资料不呈正态分布C.体重资料不呈正态分布D.样本含量较小(C)21.由10对(20个)数据组成的资料作配对t检验,其自由度等于___A.10B.20C.9D.18(C) 22.对两样本均数作t检验,n1=20,n2=20,其自由度等于___A.19B.20C.38D.40(C) 23.将同类高血压病患者若干随机分成两组,一组给予传统医疗方法,另一组给予新医疗方法,以各组治疗前后血压的平均下降值为指标,比较两种医疗方法的效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-
-
29
例:单项式分组
育龄妇女生育子女存活数
按存活数分组(个)
0 1 2 3 4 5 合计
人数 f
7 24 35 20 10 4 100
2019/10/31
30
例:品质数列
按企业类型分组
国有企业 独资企业 合资企业 民营企业
合计
频数 f
24 35 20 10
89
2019/10/31
品质数列
31
例:组限的重叠(连续)排列
—
次数/频数
第三章 统计数据的整理
34
志值 D.总体各单位具有某一共同的品质标志或数量标志。
简单现象总体
车间名称
一车间 二车间 合计
产量(万件)
2011 f0 9 6
2012 f1 14 12
15
26
4
复杂现象总体
产品
A 产品 B 产品 C 产品 合计
产量
单位
f
吨
900
千件
160
立方米
500
-
-
5
简单现象总体(与前比较)
产 品 单位
认识统计总体:
3,调查某市的失业率,则调查对象是全市的:
A.就业人口, B.失业人口, C.总人口, D.经济活动人口(A+B)。
统计总体的同质性指:
A.总体各单位具有全部共同的品质标志或数量标志 B.总体各单位具有全部共同的品质标志属性或数量标
志值 C.总体各单位具有某一共同的品质标志属性或数量标
第三章 统计数据的整理
20
例 某企业电子元件耐用时数抽样资料
单位:小时
830 880 1 170 1 080 1 250 1 360 1 410 1170
810 1 130 1 080 1 010 1 270 1 250
1 230 1 050 1 270 1 230 1 140 1 050
1 100 1 100 1 420 1 260 1 190 1 250
700~800,800~900 900~1000,……
10~49,50~99, 100~199,……
月工资水平 800~1000,1000~1500, (元/人) 1500~1800,1800~2000
第三章 统计数据的整理
16
例:
某小组10名学生某课程的考试成 绩如下(单位:分)
65,69,74,76,78,80,80, 84,88,89
第三章 统计数据的整理
12
随机数表的应用
可以从表中的任意一个位置开始,方 向也可自由选择。
如:350882513998900927…… 对应的(两位数)学号为:35,50,
08,25,51, 13, 39,09, 27,……
10/31/2019
13
例 简单分组的平行排列
按经济成分 分组
公有经济 非公有经济
按企业规模 分组
大型企业 中型企业 小型企业
按企业登记注册类型 分组
内资企业 外商投资企业 港澳台商投资企业
注:不属于复合分组 每一组只能固定一个因素,同时又掩盖了其他因
素对差异的影响。
第三章 统计数据的整理
14
平行排列与重叠排列
平行排列
重叠排列
技术人员
技术职称
企业 总 数 高称职称 中级职称 初级职称
10/31/2019
23
1、将原始资料按其数值大小重新排列
36 82 89 90 93 96 97 99 100 104 106 107 107 108 108 109 112 112 113 114 105 115 117 119 121 121 123 125 125 129
10/31/2019
24
2、确定全距
确定全距前,要检查数据组两端有没 有极端值。
计算全距前应去掉极端值。本例有极 端值36。
全距 = 129‐82 = 47
10/31/2019
25
3、确定组距和组数
组距= 全距/组数 组距应采用整数,最好是5或10的整
倍数 组距 = 47/5 = 9.4,调整为10
10/31/2019
26
4、确定组限
如果变量值相对集中,无特大或特小的极 端值时,则采用闭口式;
反之,如果有特大或特小的极端值时,则 采用开口式。
本例可设置下限开口组,最大组的上限可 取整数130
10/31/2019
27
5、编制变量数列
注:当关注标 志值较大的各 组分布时,用 向下累计
单位:小时
频率 ( fi / ∑ fi )
0.10 0.02 0.16 0.22 0.22 0.14 0.08 0.06
合计
50
1.00
第三章 统计数据的整理
22
例
某公司下属30家连锁店的营业额如下,试编制分 布数列(单位:百万元)。 89 129 125 107 112 121 97 36 100 108 114 106 117 90 108 104 109 112 93 113 105 107 115 121 119 96 123 99 82 125
某班学生统计学考试成绩
按考试成绩分组 学生人数 f
60分以下
7
60~70
8
70~80
16
80~90
6
90分以上
3
合计
40
按上限不在内原则: 将70分归入此组
2019/10/31
32
例:组限的衔接(间断)排列
下限开口组 上限开口组
按学生年龄分组 学生人数 f
9岁以下
7
10~19岁
28
20~29岁
35
10
时间概念总体
某省国有企业科技人员统计表
年份
2001 2002 2003 2004
科技人员总数年 (人) 334 784 351 844 372 711 379 016
平均每万人中 科技人员(人)
108.4 112.1 116.8 117.1
11
随机数表
688 680 800 668 152 562 941 288 434 433 584 475 717 498 314 773 547 312 422 350 882 513 998 900 927 879 566 162 904 524 569 853 789 201 832 781 246 598 361 252 359 323 439 386 300 394 578 135 852 699 980 242 732 689 131 258
名称
男女
合 计
男
女
合 计
男
女
合 计
男
女
合 计
合计
第三章 统计数据的整理
15
例:组距式分组举例
分组形式 等距分组
异距分组
统计总体
某市所有 医院
某市所有 商业职工 某市所有 商业企业
某市所有 居民家庭
分组标志 (变量)
病床数 (张)
月工资水平 (元/人)
职工人数 (人)
各个组别 (各变量值组)
100~199,200~299 300~399,400~499
学生数 (人)
2 3 5 10
次数/频数
比重 (%)
20 30 50 100.00
频率
第三章 统计数据的整理
19
表 学生按考试成绩分组 (变量分布数列)
考试成绩 (分)
65~75 75~85 85~95
合计
学生数 (人)
3 5 2
10
比重 (%)
30 50 20
100.00
思考:表3与表4哪个组距数列较真实地反映总体内各 单位的实际分布特征?
A 产品 B 产品 C 产品
合计
吨 千件 立方米
-
产值(万元)
3 000 1 850 2 800 7 650
6
单层总体:
某小组10名学生某课程的考试成 绩如下(单位:分)
65,69,74,76,78,80,80, 84,88,89
7
多层总体
性别
男生 女生 合计
学生数(人)
40 60 100
合计
单位:小时
频数或次数 频率
( fi ) ( fi / ∑ fi )
5
0.10
1
0.02
8
0.16
11
0.22
11
0.22
7
0.14
4
0.08
3
0.06
累计 频数
5 6 14 25 36 43 47 50
累计 频率
0.10 0.12 0.28 0.50 0.72 0.86 0.94 1.00
50
1.00
1 180 1 580 1 210 1 460 1 070 1 370 1 200 1 630 1 180 1 030 870 1 150 1 380 1 510 1 010 860 1 260 1 350 930 1 420 1 160 1 320 1 380 1 310
注:等距分8组,组距为100,以800为第一组下限。
30~39岁
20
40岁以上
10
合计
100
2019/10/31
33
频率密度(或次数密度)
考试成绩 (分)
40~60 60~80 80~90 90~100
合计
学生数 (人)
4 5 7 4
20
比重 (%)
20 25 35 20
100.00
频数 密度
