3.1.1 椭圆(第一课时)(精讲)(解析版)
3.1 椭圆 课件1 (北师大选修2-1)
小知识 与《几何原本》齐名的《圆锥曲线论》
公元前三世纪产生了具有完整体系的欧 几里得的《几何原本》。半个世纪以后,古 希腊的另一位数学家阿波罗尼斯又著《圆锥 曲线论》(8卷)—以其几乎将圆锥曲线的全 部性质网罗殆尽而名垂史册。 在解析几何之前的所有研究圆锥曲线的著 作中,没有一本达到象《圆锥曲线论》那样 对圆锥曲线研究得如此详尽的程度。 解析几何是由费尔马和笛卡尔分别创立的。 自从有了解析几何,圆锥曲线的研究才开辟 了新的纪元。
自学教材P28-29页例3之前内容,思考解答下列问题 (1)在椭圆标准方程中,x、y的取值范围分别是什么? 你是怎样探得的? (2)请结合椭圆标准方程确定椭圆的对称性。 (3)请结合图形说明什么是椭圆的顶点? y 若该椭圆的标准方程是 B2(0,b)
x2 y2 2 1(a b 0) 2 a b
A2(-a,0)
A1(a,0)
则它的顶点坐标分别是什么? (4)什么叫椭圆离心率?
o
B1(0,-b) (1)
x
思考:[1]离心率的取值范围是什么?
[2]离心率对椭圆形状有什么影响? y 离心率对椭圆形状的影响: 1)e 越接近 1,c 就越接近 o x ( a ),从而 b就接近( 0 ),椭 圆形状就越( 扁 )。 2)e 越接近 0,c 就越接近 ( 0 ),从而 b就越( a ), 椭圆就越圆( 圆 )。 3)当e =0时,a 与b有什么关系?此时椭圆变成什么 3)当e =0时,a =b,此时椭圆变成圆。 形状?
a ,0
(
),(0,
c,0)
b)
(
b ,0
),(0,
(0,
c)
a)
长半轴长为a,短半轴长为b.
a,b,c关系
椭圆第一课时PPT课件

练习、求过点P(2,3)且与圆
(x-1)2+(y+2)2=1 相切的直线方程.
回顾:求过定点的切线方程的基本方法: (待定系数法) (1)点在圆上 —— 一解; (2)点不在圆上 —— 两解
圆的标准方程(1) 例5、图2-9是某圆拱桥的一孔圆拱的示意图, 该拱跨度AB=20米,拱高OP=4米,在建造 是每隔4米需用一个支撑,求支柱A2P2的长 度(精确到0.01米)
圆的标准方程(1)
例2:求以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆的方程。
小结:直线与圆的位置关系。
练习: P77 2
圆的标准方程(1)
例3:求过A(4,-1)且与直线y=2x相切于点P (1,2)的圆的方程。 小结:求圆的方程的方法:
㈠找出圆心、半径; ㈡待定系数法。
例4、已知圆的方程是x2+y2=r2,求经过圆上的 一点M(x0,y0)的切线方程。
2点不在圆上两解例5图29是某圆拱桥的一孔圆拱的示意图该拱跨度ab20米拱高op4米在建造是每隔4米需用一个支撑求支柱a2p2的长度精确到001米pp2圆的标准方程1paba1a2a3a4o总结
圆的标准方程(1) 一、圆的定义
平面内与定点的距离等于定长的点的集合(轨迹) 是圆。定点就是圆心;定长就是半径。
二、 圆的标准方程:
(x-a)2+(y-b)2=r2
其中圆心(a,b)半径为r。
特别地当圆心为原点时,方程为
2 2 2 x +y =r
圆的标准方程(1) 练习: 1、 P77 1; 2、说出下列圆的圆心和半径: (1)(x – 2)2 + y2 =10 (2) x2 +(y – 1)2 =25 (3) x2 +(y – 11)2 =16 (4)(x + 1)2 +(y – 1)2 =36 3、求圆心和半径: (1)x2 + y2 – 2x – 1= 0 (2)x2 + y2 – 10x –12y + 51 = 0
椭圆及其标准方程(一)课件-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册
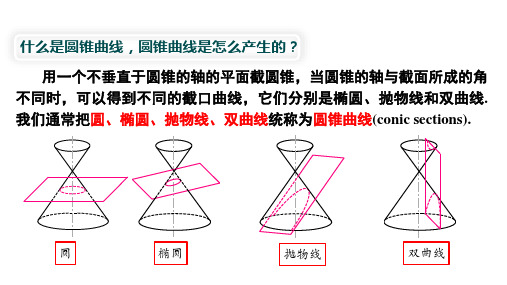
解得a 2 10,b2 6.
x2 y2
∴所求椭圆的标准方程为
1.
10 6
练习(第49页)
1.如果椭圆
+
= 上一点 P 到焦点的距离等于 6,则点 P 到另一
个焦点的距离为
.
【详解】解:根据椭圆的定义
又椭圆
∴
+
+
+
= ,
是
回忆一下我们是如何求圆轨迹方程的?
建系
建立适当的平面直角坐标系
设点
列式
设曲线上任意一点M的坐标为(x, y)
类比这个方法,
我们开始求椭圆
找出限制条件P(M),并列出几何等式
的标准方程
代换
把坐标代入限制条件P(M) 列出方程
化简
化简方程
新知探究
观察椭圆的形状,你认为怎样建立坐标系可使所得的椭圆方程形式简单?
2
a
b
2
2
•F
2
O
x
•F
1
椭圆的标准方程:
标准方程
x2
y2
2 1 (a b 0)
2
a
b
y2 x2
2 1 (a b 0)
2
a
b
y
y
不
同
点
图
形
•
F1
O
M
•
F2
•F2
O
x
x
•F1
焦点坐标
相
同
点
M
F1 (c,0), F2 (c,0)
F1 (0, c), F2 (0, c)
【课件】椭圆及其标准方程(第一课时)+课件高二上学期数学人教A版(2019)选择性必修第一册

由图3.1-3可知, 1 = 2 = , 1 = 2 = ,
令 = = 2 − 2
那么方程⑤就是
2
2
(
>
>0)
⑥
+
=1
2
2
2 = 2 − 2
思考3:为什么2 − 2 要用 2 表示?
简洁,美观,对称,和谐
(3)就一般情况而言,求曲线的方程有哪些步骤?
伸”?由此你能发现椭圆与圆之间的关系吗?
变式.如图,垂直轴,垂足为 ,点在的延长线上,且
3
= .当
2
点在圆 2 + 2 =4上运动时,求点的轨迹方程,并说明轨迹的形状.
相关点法
解:设 , , (0 ,0 ),
因为 (0 ,0 )在圆 2 + 2 =4上,所以02 +02 =4①
将方程④两边同除以2 (2
2
2
+ 2 2=1
−
>c>0,所以2 − 2
− 2 ),得 2
由椭圆的定义可知,2>2c>0,即
④
⑤
> 0.
思考1:为什么要用2,2c而不是 , c表示椭圆的定长与焦距?
为了使焦点和长轴端点的坐标都不出现分数形式
图3.1-3
思考2:观察图3.1-3,你能从中找出表示
因吗?如果本章我们用坐标法来研究圆锥曲线,大家能在回顾用坐
标法研究直线与圆的基础上,猜想本章研究的大致思路与构架吗?
明确:采用坐标法研究圆锥曲线的最大好处是可以程序化地、精确
地计算.
3.1.1椭圆及其标准方程(教学课件(人教版))

k AM
x
y
5
,kBM
y x5
( x 5).
y
M •
A
O
Bx
点M的轨迹为除去(-5,0),(5,0)两点的椭圆。
三、题型与方法
解决与椭圆有关的轨迹问题的三种方法
1.直接法:直接法是求轨迹方程的最基本的方法,根据所满足的几何条件,将几何 条件{M|p(M)}直接翻译成x,y的情势,即F(x,y)=0,然后进行等价变换,化简为 f(x,y)=0. 2.定义法:用定义法求椭圆方程的思路是先视察、分析已知条件,看所求动点轨迹 是否符合椭圆的定义.若符合椭圆的定义,则用待定系数法求解即可. 3.相关点法:有些问题中的动点轨迹是由另一动点按照某种规律运动而形成的,只 要把所求动点的坐标“转移”到另一个动点在运动中所遵循的条件中去,即可解决问 题,这种方法称为相关点法.
3.a, b, c 满足的关系有: ① a2 b2 c2 ; ② a b 0 ; ③ a c 0 .
三、题型与方法
题型一 求椭圆的标准方程
跟踪训练:1.求与椭圆x2+y2=1 有相同焦点,且过点(3, 15)的椭圆的标准方程.
25 9
法一:因为所求椭圆与椭圆x2+y2=1 的焦点相同,设所求椭圆的标准方程为x2+y2=1(a>b>0).
解1:(相关点代入法)设点M的坐标为(x, y),点P的坐标为(x0, y0), 则点D的坐标为(x0, 0).由点M是线段PD的中点,得
y •P
•M
∵点P(x0,y0)在圆x2+y2=4上, ∴x02+y02=4
OD
x
把x0=x,y0=2y代入上式,得x2+(2y)2=4,即
∴点M的轨迹是椭圆。
人教版高中数学选择性必修第一册3.1.1第一课时椭圆及其标准方程
人A数学选择性必修1
返回导航 上页 下页
[例 3] (1)方程k-x24+10y-2 k=1 表示焦点在 x 轴上的椭圆,则实数 k 的
取值范围是( C )
A.(4,+∞) B.(4,7)
C.(7,10)
D.(4,10)
分析:(1)根据椭圆焦点位置求椭圆方程中的参数范围时,考虑两个分 式对应的分母都大于0,然后根据焦点所在坐标轴确定对应分母的大 小.
人A数学选择性必修1
返回导航 上页 下页
[解析] (1)由 a=4,c= 15,得 b2=a2-c2=1, ∵焦点在 y 轴上,∴其标准方程为1y62 +x2=1. (2)法一:由于椭圆的焦点在 x 轴上,所以设它的标准方程为ax22+by22=1(a >b>0). 由椭圆的定义知 c=2,
2a= 52+22+-322+ 52-22+-322=2 10,
C.94
D.14
解析:依题意a=10,且|PF1|+|PF2|=6+|PF2|=2a=20⇒|PF2|=14.
人A数学选择性必修1
返回导航 上页 下页
3.适合条件a=4,b=1,焦点在x轴上的椭圆的标准方程为 ___1x_62_+__y_2_=__1______. 解析:由已知,所求方程为:4x22+1y22=1,即1x62 +y2=1.
人A数学选择性必修1
返回导航 上页 下页
[例1] (1)已知F1(-3,0),F2(3,0),|PF1|+|PF2|=8,则动点P的轨迹是
(B)
A.圆
B.椭圆
C.直线
D.线段
(2)已知F1(0,-3),F2(0,3),|PF1|+|PF2|=6,则动点P的轨迹是( D )
A.圆
B.椭圆
高中数学 3.1第1课时椭圆及其标准方程课件 北师大版选修2-1

① 解得①②得-3<a<-1 或 a>1.
当 a>1 时,③不成立.当-3<a<-1 时,得 a<-2. 综上可得:a 的取值范围是-3<a<-2.
最值问题
F1 是x92+y52=1 的左焦点,P 是椭圆上的动点,A(1,1) 为定点,则|PA|+|PF1|的最小值为________________.
[解析] (1)∵椭圆的焦点在 x 轴上,所以设它的标准方程为ax22 +by22=1(a>b>0).
∵2a= 5+32+0+ 5-32+0=10,2c=6. ∴a=5,c=3, ∴b2=a2-c2=52-32=16. ∴所求椭圆的方程为:2x52 +1y62 =1.
(2)∵椭圆的焦点在 y 轴上,所以设它的标准方程为:ay22+bx22= 1(a>b>0).
3.已知△ABC 的顶点 B、C 在椭圆x32+y2=1 上,顶点 A 是
椭圆的一个焦点,且椭圆的另外一个焦点在 BC 边上,则△ABC
的周长是( )
A.2 3
B.6
C.4 3
D.12
[答案] C
[解析] 设椭圆的另一个焦点为 F(如图),
则 △ ABC 的 周 长 为 (|AB| + |BF|) + (|CA| + |CF|) = 2a + 2a =
∴-2c≤|PF1|-|PF2|≤2c, ∴2a-2c≤2|PF1|≤2a+2c,即 a-c≤|PF1|≤a+c
∴|PF1|的最大值为 a+c,最小值为 a-C.
[总结反思] 椭圆上到某一焦点的最远点与最近点分别是长 轴的两个端点,应掌握这一性质.
[总结反思] 椭圆的焦点在哪个坐标轴上主要看标准方程 中x2和y2项分母的大小,如果x2项的分母大于y2项的分母,则椭 圆的焦点在x轴上;反之,焦点在y轴上.由于本题中x2和y2项 分母的大小不确定,因此需要进行分类讨论.
2024-2025学年高二数学选择性必修第一册(配湘教版)课件3.1.1椭圆的标准方程

又由椭圆的定义知|PF1|+|PF2|=2a=4.
在△F1PF2中,由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos∠F1PF2,
即4=(|PF1|+|PF2|)2-2|PF1|·|PF2|-2|PF1|·|PF2|cos 60°,
即4=16-3|PF1|·|PF2|.
1
= ,
4
1
= 2.
2
故椭圆的标准方程为 4
+
2
=1.
2
+
2
=1.
4
角度2定义法
【例2】一个动圆与圆Q1:(x+3)2+y2=1外切,与圆Q2:(x-3)2+y2=81内切,试求
这个动圆圆心的轨迹方程.
分析 设出动圆的圆心及半径,利用两圆相切的几何条件列式求解.
解 两定圆的圆心和半径分别为Q1(-3,0),r1=1;Q2(3,0),r2=9.
2 2
+
4
3
=1上的一点,F1,F2是椭圆的两个焦点,且
∠F1PF2=60°,则△F1PF2的面积是
√3
.
分析结合∠F1PF2=60°,借助椭圆的定义及余弦定理求出|PF1|·|PF2|后,利用
三角形的面积公式求解.
解析 由椭圆的标准方程知 a=2,b=√3,
∴c= 2 - 2 =1,∴|F1F2|=2.
圆的条件是 m>n>0,其表示焦点在 y 轴上的椭圆的条件是 n>m>0.
(2)若给出椭圆方程 Ax2+By2=C,则应先将该方程转化为椭圆的标准方程的形
式
2
+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.1 椭圆考点一椭圆的定义【例1】(1)(2020·上海徐汇.高二期末)已知1F 、2F 是定点,12||6F F =.若动点M 满足12||||6M F M F +=,则动点M 的轨迹是( ) A .直线B .线段C .圆D .椭圆(2)(2019·宁波市第四中学高二期中)设p 是椭圆2212516x y+=上的点.若12F F ,是椭圆的两个焦点,则12PF PF +等于( )A .4B .5C .8D .10【答案】(1)B (2)D【解析】(1)对于在平面内,若动点M 到1F 、2F 两点的距离之和等于6,而6正好等于两定点1F 、2F 的距离,则动点M 的轨迹是以1F ,2F 为端点的线段.故选:B .(2)因为椭圆的方程为2251162x y +=,所以225a =,由椭圆的的定义知12=210PF PF a +=,故选D .【一隅三反】1.(2020·河南省鲁山县第一高级中学高二月考)若椭圆上一点P到左焦点的距离为5,则其到右焦点的距离为( ) A .5 B .3C .2D .1【答案】D【解析】由题意a=3,P 点到右焦点的距离为2a -5=12.(2020·东城.北京五十五中高二月考)若椭圆22110036x y +=上一点P 到其焦点1F 的距离为6,则P 到另一焦点2F 的距离为( ) A .4 B .194 C .94 D .14【答案】D【解析】依题意10a =,且1222622014PF PF PF a PF +=+==⇒=.故选:D 3.下列命题是真命题的是________.(将所有真命题的序号都填上)①已知定点F 1(-1,0),F 2(1,0),则满足|PF 1|+|PF 2|=2的点P 的轨迹为椭圆; ②已知定点F 1(-2,0),F 2(2,0),则满足|PF 1|+|PF 2|=4的点P 的轨迹为线段; ③到定点F 1(-3,0),F 2(3,0)的距离相等的点的轨迹为椭圆. 【答案】 ②【解析】 ①2<2,故点P 的轨迹不存在;②因为|PF 1|+|PF 2|=|F 1F 2|=4,所以点P 的轨迹是线段F 1F 2;③到定点F 1(-3,0),F 2(3,0)的距离相等的点的轨迹是线段F 1F 2的垂直平分线(y 轴).考点二 椭圆定义的运用【例2-1】(1)(2019·福建高二期末)如果222x ky +=表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ) A .(0,1)B .(0,2)C .(1,)+∞D .(0,)+∞(2)(2019·江苏省苏州实验中学高二期中)方程2214x y m+=表示椭圆,则实数m 的取值范围( )A .0m >B .4m >C .04m <<D .0m >且4m ≠【答案】(1)A (2)D【解析】(1)222x ky +=转化为椭圆的标准方程,得22122x y k+=,因为222x ky +=表示焦点在y 轴上的椭圆,所以22k>,解得01k <<.所以实数k 的取值范围是()0,1.选A. (2)方程2214x y m+=表示椭圆,若焦点在x 轴上,40m >>;若焦点在y 轴上,4m >.综上:实数m 的取值范围是0m >且4m ≠故选:D【一隅三反】1.(2020·广东高三月考(文))“35m -<<”是“方程22153x y m m +=-+表示椭圆”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】B【解析】因为方程22153x ym m +=-+表示椭圆的充要条件是503053m m m m ->⎧⎪+>⎨⎪-≠+⎩,即35m -<<且1m ≠,故“35m -<<”是“方程22153x y m m +=-+表示椭圆”的必要而不充分条件.故选:B.2.(2017·浙江东阳.高二期中)如果方程表示焦点在x 轴上的椭圆,则实数a 的取值范围是( ) A .3a > B .2a <- C .3a >或2a <- D .3a >或62a -<<-【答案】D 【解析】椭圆的焦点在x 轴上,260a a ∴>+>,解得3a >或62a -<<-,故选D.3.(2019·北京北师大实验中学高二期中)若方程2212y x m +=-表示焦点在y 轴上的椭圆,则m 的取值范围是( )A .()3-∞,B .()23,C .()2+∞,D .()3+∞, 【答案】D【解析】因为方程2212y x m +=-表示椭圆,故:20m ->,且21m -≠;又该椭圆的焦点在y 轴上,故只需21m ->,解得3m >.故选:D.【例2-2】(1)(2018·黑龙江哈尔滨三中高二期中(文))已知ABC ∆的顶点B ,C 在椭圆221169x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另一个焦点在BC 上,则ABC ∆的周长是( )A .8B .C .16D .24(2)(2019·广西田阳高中))已知P 是椭圆221259x y +=上一点,12,F F 为椭圆的两焦点,且01260F PF ∠=,则12F PF ∆面积为( )A .B .CD 【答案】(1)C【解析】(1)ABC ∆的顶点B ,C 在椭圆221169x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另一个焦点在BC 上,由椭圆的定义可得:ABC ∆的周长是44416a =⨯=.故选:C . (2)由椭圆的标准方程可得:a =5,b =3,∴c =4,设|PF 1|=t 1,|PF 2|=t 2,所以根据椭圆的定义可得:t 1+t 2=10①, 在△F 1PF 2中,∠F 1PF 2=60°,所以根据余弦定理可得:|PF 1|2+|PF 2|2﹣2|PF 1||PF 2|cos60°=|F 1F 2|2=(2c )2=64, 整理可得:t 12+t 22﹣t 1t 2=64,②把①两边平方得t 12+t 22+2t 1•t 2=100,③ 所以③﹣②得t 1t 2=12,∴121212F PF S t t sin =∠F 1PF 2=A .【一隅三反】1.(2019·黑龙江哈尔滨市第六中学校高二月考(文))已知点12,F F 分别是椭圆221259x y +=的左、右焦点,点P 在此椭圆上,则12PF F ∆的周长等于( ) A .20 B .16 C .18 D .14【答案】C【解析】根据椭圆方程可知5,4a c ==,根据椭圆的定义可知,12PF F ∆的周长为2210818a c +=+=,故选C.2.(2018·湖南高二期中(理))已知E 、F 分别为椭圆x 225+y 29=1的左、右焦点,倾斜角为60∘的直线l 过点E ,且与椭圆交于A ,B 两点,则△FAB 的周长为( ) A .10 B .12 C .16 D .20【答案】D 【解析】椭圆x 225+y 29=1,可得a =5,三角形AF 2B 的周长=|AF 2|+|BF 2|+|AB|,|AB|=|AF 1|+|BF 1|, 所以:周长=|AF 1|+|AF 2|+|BF 1|+|BF 2|,由椭圆的第一定义,|AF 1|+|AF 2|=|BF 1|+|BF 2|=2a =10,所以,周长=4a =20.故选:D .3.已知P 是椭圆2214x y +=上的一点,F 1,F 2是椭圆的两个焦点,且∠F 1PF 2=60°,则△F 1PF 2的面积是______.【解析】∵|PF 1|+|PF 2|=4,2FF =F 1PF 2=60°, 由余弦定理可得|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|cos60° 12=(|PF 1|+|PF 2|)2-2|PF 1|·|PF 2|-|PF 1|·|PF 2|,∴1243PF PF ⋅=,∴12121sin 6023PF F S PF PF ︒∆=⋅=.考点三 椭圆的标准方程【例3】(2020·四川内江,高二期末)分别求适合下列条件的方程: (1)焦点在x 轴上,长轴长为10,焦距为4的椭圆标准方程;(2)与椭圆22143x y +=具有相同的离心率且过点(2,的椭圆的标准方程(3)已知椭圆的两个焦点的坐标分别是()2,0-,()2,0,并且经过点53,22⎛⎫-⎪⎝⎭,则此椭圆的标准方程 【答案】(1)2212521x y +=;(2)22186x y+或221252534y x +=(3)221106x y +=【解析】(1)由已知条件可得21024a c =⎧⎨=⎩,可得52a c =⎧⎨=⎩,22221b ac ∴=-=,因此,所求椭圆的标准方程为2212521x y +=;(2)易知椭圆22143x y +=的离心率12e =.当所求椭圆的焦点在x 轴上时,可设椭圆的方程为22221x y a b+=,把点(2,代入方程,得22431a b+=. 又224a c =,解得28a =,26b=,所以所求椭圆的方程为22186x y +.当所求椭圆的焦点在y 轴上时,同理可设椭圆的方程为22221x y b a+=,把点(2,代入方程,得22431b a+=. 又224a c =,解得2253a =,2254b =,所以所求椭圆的方程为221252534y x +=.(2)因设椭圆的标准方程为()222210x y a b a b+=>>,因为点53,22⎛⎫- ⎪⎝⎭在椭圆上,所以22222591444a a b b a b ⎧⎧=+=⎪⎪⇒⎨⎨=⎪⎪⎩-=⎩,所以椭圆的标准方程为221106x y +=.此椭圆的标准方程是22186x y +=或221252534y x +=.【一隅三反】1.(2019·全国高二课时练习)求满足下列条件的椭圆的标准方程: (1)焦点在y 轴上,焦距是4,且经过点M (3,2);(2)c ∶a =5∶13,且椭圆上一点到两焦点的距离的和为26.(3)已知椭圆C 的中心在原点,焦点在坐标轴上,且经过两点()0,2A 和12B ⎛⎝ 【答案】(1)2211612x y += (2)221169144x y +=或221169144y x +=(3)2214y x +=【解析】(1)由焦距是4,可得c =2,且焦点坐标为(0,-2),(0,2).由椭圆的定义知,2a 8==,所以a =4,所以b 2=a 2-c 2=16-4=12.又焦点在y 轴上,所以椭圆的标准方程为22x y 11612+=.(2)由题意知,2a =26,即a =13,又因为c ∶a =5∶13,所以c =5,所以b 2=a 2-c 2=132-52=144,因为焦点所在的坐标轴不确定,所以椭圆的标准方程为22x y 1169144+=或22y x 1169144+=.(2)设椭圆的方程为221(0,0,)mx ny m n m n +=>>≠.将A ,B 两点坐标代入方程,得411314n m n =⎧⎪⎨+=⎪⎩,解得114m n =⎧⎪⎨=⎪⎩,故所求椭圆的方程为2214y x +=. 考点四 离心率【例4】(1)(2020·武威第八中学高二期末(理))已知椭圆C :2221(0)4x y a a +=>的一个焦点为(20),,则C 的离心率为 。
