费米狄拉克统计
费米-狄拉克分布实验讲义
实验六 费米—狄拉克分布实验讲义一、实验目的:(1)通过实验验证费米——狄拉克分布。
(2)学会一种实验方法及处理实验数据的技巧。
二、理论分析:近代电子理论认为金属中的电子按能量的分布是遵从费米――狄拉克的量子统计规律的,费米分布函数为[]1/)(exp 1)(+-=kT g f εεε (1)金属中的每个电子都占有一定能量的能级,这些能级相互靠得很近,形成能带。
当其温度为绝对零度时,金属中电子的平均能量并不为零。
此时金属中的电子将能量从零到能量为εf (εf 称费米能级, εf 的值随金属的不同而不同)的能级全部占据。
而高于费米能级的那些能级全部空着,没有电子去占据。
如图(1)中的实线所示,当金属的温度为1500℃,则靠近费米能级的少数电子由于热运动的加剧,其能量超过εf值,因而从低于费米能级的能带跃迁到高于费米能级的能带上去,其分布曲线如图(1)中的虚线所示。
我们的实验是在灯丝灼热(约1400℃~1500℃)的情况下进行的,因此我们实验所测的结果也只是靠近费米能级的一部分,如图(1)中矩形所包的虚线部分。
对(1)式求导可得[][]2}1/)({exp /)(exp )()(+---==kT kT kT d dg g f f εεεεεεε (2) (1)、(2)两式的理论曲线如图(1)和图(2)所示。
由于金属内部电子的能量无法测量,只能对真空中热发射电子的动能分布进行测量。
由于电子在真空中的热运动与电子在金属内部的运动情况完全不同,这是因为金属内部存在着带正电的原子核,电子不但有热运动的动能,而且还具有势能,真空中的电子就不存在势能,εf =0,不要忘记电子从金属内部逃逸到真空中时,还要消耗一部分能量用作逸出功,因此从金属内部电子的能量ε 减去逸出功A,就可得到真空中热发射电子的动能εkεf =ε-A (3)此外,在真空与金属表面附近还存在着电子气形成的偶电层,就是说逃出金属表面的电子,还要消耗一些能量穿越偶电层,根据前苏联科学院院士,Я.И符伦克尔和И.E 塔姆的理论,电子穿越偶电层所需的能量,也就是该金属的费米能级εf 。
费米狄拉克统计

费米狄拉克统计
费米-狄拉克统计是费米子所依从的统计规律。
它表示在温度T时,能级E 的一量子态上平均分布的电子数。
因量子态上最多由一个电子所占据,所以费米-狄拉克统计的物理含义是:能量为E的每个量子态上被电子所占据的几率。
又称费米统计。
这是E.费米和P.A.M.狄拉克在1926年先后提出的(见量子统计法)。
对于费米系统,Ni个不可分辨的全同粒子分布在gi个状态上(每个态上至多只能有一个粒子)的可能方式数,就是从gi个元素中选取Ni个元素的组合数,应该等于:则对应粒子数分布{Ni}的系统微观状态数。
费米统计和玻色统计
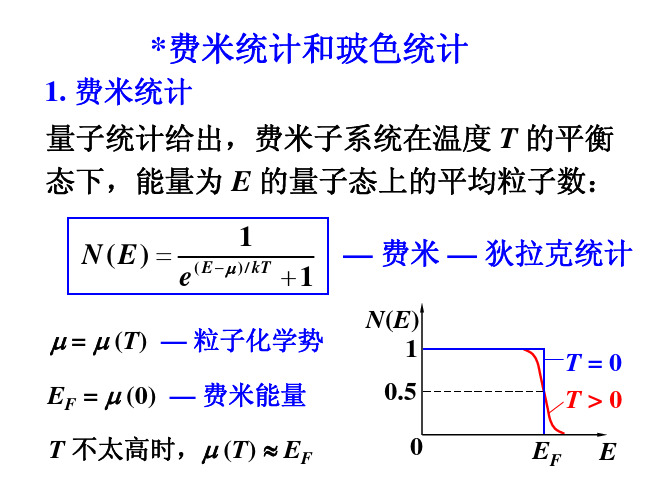
1. 费米统计 量子统计给出,费米子系统在温度 T 的平衡 态下,能量为 E 的量子态上的平均粒子数:
N (E) = 1 e
( E − μ ) / kT
+1
— 费米 — 狄拉克统计
N(E) 1 0.5 0 EF
μ = μ (T) — 粒子化学势
EF = μ (0) — 费米能量 T 不太高时,μ (T) ≈ EF
±1
≈e
− ( E − μ ) / kT
=e
μ / kT
⋅e
− E / kT
= A(T )e − E / kT
— 麦克斯韦 — 玻耳兹曼统计 所以高能态时,量子统计就过渡到经典的 麦克斯韦 — 玻耳兹曼统计。
Hale Waihona Puke 2. 玻色统计 量子统计给出,玻色子系统在温度 T 的平衡 态下,能量为 E 的量子态上的平均粒子数:
N (E) = 1 e ( E − μ ) / kT − 1
— 玻色 — 爱因斯坦统计 对所有温度 T ,N(E) 应满足 0 ≤ N(E) < ∞ , 由此可引出玻色 — 爱因斯坦凝聚的概念。
设最低能级(基态)为能量零点:E0 = 0, 1 N 0 = N ( E 0 ) = − μ / kT e −1 T → 0K 时,要求 0 ≤ N0 < ∞ , 则有 μ < 0 。
原子速度分布逐渐达到BEC的三维示意图 1995年实现了超冷原子的BEC,达到了宏观数量的 原子处于同一量子态(2001 Nobel)。 BEC实现了 原子相干,可做成原子干涉仪和量子频标等。
3. 量子统计到经典统计的过渡 当 E 很高时,(E−μ) >> kT
N (E) = 1 e
不同费米能级接触

不同费米能级接触在物理学中,费米能级是指在固体中,电子填充的最高能级。
费米能级决定了物质的电子行为和性质,而不同费米能级之间的接触则对物质的导电性和热传导性产生重要影响。
本文将就不同费米能级接触的相关内容展开讨论。
一、费米能级的概念费米能级是由意大利物理学家费米提出的,其命名来源于费米-狄拉克统计。
在固体中,费米能级可以理解为最高占据态电子能级的能量。
在零度绝对温度下,费米能级以上的能级是未被电子占据的,而费米能级以下的能级则被电子完全占据。
二、不同费米能级接触的性质1. 能带接触当两个物质的费米能级相等时,它们的能带会发生接触。
能带接触会导致电子在两个物质之间发生能量转移,从而影响物质的导电性。
如果两个能带接触的材料一个是导体而另一个是绝缘体,那么导体中的电子会流向绝缘体,使得绝缘体变为导体。
2. 能级接触当两个物质的费米能级相等时,它们的能级会发生接触。
能级接触会导致两个物质之间的电子发生能量转移,从而影响物质的热传导性。
如果一个物质的能级接触是金属而另一个是绝缘体,那么金属中的电子会传递给绝缘体,使得绝缘体的热传导性增强。
三、费米能级接触的应用1. 二维电子气体在二维电子气体中,费米能级接触会导致电子在二维材料中的传输特性发生变化。
费米能级接触可以通过调节材料的厚度和电场等因素来实现,从而实现对电子传输性质的调控。
这对于二维材料在纳电子器件中的应用具有重要意义。
2. 界面态费米能级接触在材料界面中会形成界面态。
界面态的形成会对材料的电子结构和性质产生重要影响。
界面态的性质可以通过调节费米能级的位置和界面的结构等因素来控制,从而实现对材料界面性质的调控。
这对于材料的界面工程和器件性能的提高具有重要意义。
3. 热电材料费米能级接触对热电材料的热传导性能有重要影响。
通过调节费米能级的位置和材料的结构等因素,可以实现对热电材料的热导率和电导率的调控,从而提高材料的热电性能。
这对于热电材料在能量转换和热管理等领域的应用具有重要意义。
(精编资料推荐)费米-狄拉克分布函数、解析、图像和应用

各能级被电子占据的数目服从特定的统计规律这个规律就是费米-狄拉克分布规律。
一般而言,电子占据各个能级的几率是不等的。
占据低能级的电子多而占据高能级的电子少。
统计物理学指出,电子占据能级的几率遵循费米的统计规律:在热平衡...状态下,能量为E 的能级被一个电子占据的几率为: ]/)exp[(11)(kT E E E f F -+=f(E) 称为电子的费米(费米-狄拉克)分布函数,k 、T 分别为波耳兹曼常数和绝对温度。
E fermi 称为费米能级,它与物质的特性有关。
只要知道了费米能级E fermi 的数值,在一定温度下,电子在各量子态上的统计分布就完全确定了。
费米分布函数的一些特性: 【根据f(E)公式来理解】第一, 费米能级E fermi 是一种用来描述电子的能级填充水平的假想能级...., E f 越大,表示处于高能级的电子越多;E f 越小,则表示高能级的电子越少。
(E f 反映了整体平均水平)第二,假定费米能级E f 为已知,则f(E)是能量E 与温度T 的函数。
根据f(E)式可画出 f(E) 的曲线如图所示,但要注意 因变量f(E)不像普通习惯画在纵轴,而是破天荒的画在横轴。
0 1/2 1 f(E) E E f T 0 T 1 T 2 T 3 在T 不为绝对零度前提下,若E <E f ,则 f(E) >1/2;若E = E f ,则 f(E)=1/2;若 E >E f ,则 f(E) <1/2。
上述结果文字描述,在系统的温度高于绝对零度前提下,如果某能级的能量比费米能级低E f ,则该能级(范围)被电子占据的几率大于50%;若能级的能量比费米能级E f 高,则该能级被电子占据的几率小于50%。
而当能级的能量恰等于费米能级E f 时,该能级被电子占有的几率费米分布规律不适用于非平衡状态随着温度的升高,能量略低于E f的量子态被电子占据的概率降低,而略高于E f的量子态被电子占据的概率增大。
费米能级的变化趋势

费米能级的变化趋势
费米能级是指在费米-狄拉克统计下,系统中能量最高的电子占据的能级。
费米能级的变化趋势在不同情况下可能不同,下面列举了一些情况:
1. 温度的变化:当温度增加时,费米-狄拉克分布会发生变化,费米能级的位置会发生移动。
在零温下,费米能级是一个确定的能级,但在有限温度下,费米能级会模糊化,以形成费米球,即占据概率高于一半的电子填充的一系列能级。
随着温度的增加,费米能级会逐渐向高能级移动。
2. 材料的掺杂:当将杂质或掺杂原子引入晶体中时,会引起费米能级的变化。
掺杂材料中的杂质能级可能与宿主材料的能级发生交叉或穿过费米能级,从而改变费米能级的位置。
3. 外加电场:当对材料施加外加电场时,费米能级的位置也会发生变化。
外加电场会导致电子在能带中的移动,进而改变费米能级的位置。
综上所述,费米能级的变化趋势取决于温度、材料的掺杂以及外部电场等因素。
不同情况下费米能级的变化趋势可能不同。
费米-狄拉克统计

费米-狄拉克统计在统计力学中,费米-狄拉克统计是一种由Enrico Fermi 和保罗⋅狄拉克发展起来的特殊粒子统计用来确定费米子在一个热平衡系统中各能量状态上的统计分布。
换句话说,就是在给定能级上一个费米子出现的几率。
费米子是不可分辨的并且服从泡利不相容定律,即,不会有超过一个的粒子在同时处以同一量子态。
统计热力学用来描述大量粒子的行为。
无相互作用的费米子的集合称为费米气体。
F-D 统计在1926年由Enrico Fermi 和保罗⋅狄拉克提出,并在1926年由拉尔夫⋅富勒用于描述恒星到白矮星的塌缩,在1927年由Arnold Sommerfeld 用于金属中的电子。
对于F-D 统计,处于一种能量状态i 的粒子数的期望值是1/)(+=-kT i i i e g n με 这里:n i 为粒子在状态i 的数量εi 为第i 个状态的能量g i 状态i 的简并度μ 为化学势(作为一种低温近似,有时用费米能量E F 代替)k 为玻尔斯曼常数T 为绝对温度在μ为E F 而且g i =1时,这个方程称为费米方程:11)(/)(+=-kT E F i e E F ε对于四种不同的温度,作为ε/μ的函数的费米-狄拉克分布(⎺n为n i/g i即同一能级平均每个模式(状态)上分布的粒子数,它与被占据的状态数成正比)。
温度越高曲线越光滑作为温度的函数的费米-狄拉克分布。
温度越高被占据的状态越多。
作为ε的函数的费米-狄拉克分布。
高能态对应低概率,或低能态对应高概率。
这些统计的应用费米-狄拉克和玻色-爱因斯坦统计在量子效应必须考虑以及粒子被认为是“不可分辨的”时起作用。
如果粒子的浓度(N/V)≥n q(这里n q是量子浓度)量子效应就会显现。
量子浓度是当粒子间距等于热德·布罗意波长也就是当粒子的波函数相互接触但还未重叠时的浓度。
量子浓度依赖于温度;高温会使大多数系统处在经典的限制中除非它们有非常大的密度例如白矮星。
最全费米-狄拉克分布函数概念、解析、图像和应用完整版.doc

各能级被电子占据的数目服从特定的统计规律这个规律就是费米-狄拉克分布规律。
一般而言,电子占据各个能级的几率是不等的。
占据低能级的电子多而占据高能级的电子少。
统计物理学指出,电子占据能级的几率遵循费米的统计规律:在热平衡...状态下,能量为E 的能级被一个电子占据的几率为:f(E) 称为电子的费米(费米-狄拉克)分布函数,k 、T 分别为波耳兹曼常数和绝对温度。
E fermi 称为费米能级,它与物质的特性有关。
只要知道了费米能级E fermi 的数值,在一定温度下,电子在各量子态上的统计分布就完全确定了。
费米分布函数的一些特性: 【根据f(E)公式来理解】 第一, 费米能级E fermi 是一种用来描述电子的能级填充水平的假想能级...., E f 越大,表示处于高能级的电子越多; E f 越小,则表示高能级的电子越少。
(E f 反映了整体平均水平)第二,假定费米能级E f 为已知,则f(E)根据f(E)式可画出 f(E) 的曲线如图所示,但要注意 因变量f(E)不像普通习惯画在纵轴,而是破天荒的画在横轴。
01/21E第三,费米能级E f在能级图中的位置与材料掺杂情况有关。
对于本征半导体,E f处于禁带E g的中央,在绝对零度时,在导带E c中E>E f,f(E)=0;在价带E v中E<E f,f(E)= =1,表明电子全部处于价带E v之中,因而此时半导体是完全不导电的。
第四,在T=0K处于绝对零度的前提下,若E<E f,exp→0,则f(E)=1;当T=0K时,若E>E f,则f(E)=0。
可见,在绝对零度时,能量比E f小的能级被电子占据的几率是100%,而能量比E f大的能级被电子占据的几率为零。
即所有低于E f的能级都被占满,而所有高于E f的能级都空着。
因而费米能级E f是在绝对零度时电子所具有的最大能量,是能级在绝对零度时能否被占据的一个界限,因而它是一个很重要的参数。
第五,在T≠0K时即不处于绝对零度的前提下,若E-E f>5kT,则f(E)<0.007;在T≠0K前提下,若E-E f<-5kT,则f(E)>0.993。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
费米–狄拉克统计[编辑]维基百科,自由的百科全书(重定向自费米-狄拉克统计)费米–狄拉克统计(英语:Fermi–Dirac statistics),有时也简称费米统计、FD统计,在统计力学中用来描述由大量满足泡利不相容原理的费米子组成的系统中,粒子处在不同量子态上的统计规律。
这个统计规律的命名来源于恩里科·费米和保罗·狄拉克,他们分别独立地发现了这一统计规律。
不过费米在数据定义比狄拉克稍早。
[1][2]费米–狄拉克统计的适用对象是,热平衡时自旋量子数为半奇数的粒子。
除此之外,应用此统计规律的前提是,系统中各粒子之间的相互作用可以忽略不计。
这样,就可以用粒子在不同定态的分布状况来描述大量微观粒子组成的宏观系统。
不同的粒子分处于不同的能态上,这一特点对系统许多性质会产生影响。
费米–狄拉克统计适用于自旋量子数为半奇数的粒子,这些粒子也被称为费米子。
由于电子的自旋量子数为1/2,因此它是费米–狄拉克统计最普遍的应用对象。
费米–狄拉克统计是统计力学的重要组成部分,它利用了量子力学的一些原理。
目录[隐藏]• 1 概述• 2 历史• 3 费米–狄拉克分布o 3.1 粒子的能量分布• 4 量子范畴和经典范畴• 5 参考文献• 6 相关条目概述[编辑]函数反对称,在费米子的某一个能级上,最多只能容纳一个粒子。
因而符合费米–狄拉克统计分布的粒子,当他们处于某一分布(“某一分布”指这样一种状态:即在能量为的能级上同时有个粒子存在着,不难想象,当从宏观观察体系能量一定的时候,从微观角度观察体系可能有很多种不同的分布状态,而且在这些不同的分布状态中,总有一些状态出现的几率特别的大,而其中出现几率最大的分布状态被称为最可几分布)时,体系总状态数为:费米–狄拉克统计的最可几分布的数学表达式为:由于费米-狄拉克统计在数学处理上非常困难,因此在处理实际问题时经常引入一些近似条件,使费米-狄拉克统计退化成为经典的麦克斯韦-玻尔兹曼统计。
此外,对于玻色子,也有对应的玻色-爱因斯坦统计予以处理。
历史[编辑]1926年发现费米–狄拉克统计之前,要理解电子的某些性质尚较为困难。
例如,在常温下,未施加电流的金属内部的热容比施加电流的金属少了大约100倍。
此外,在常温下给金属施加一强电场,将造成场致电子发射(Field electron emission)现象,从而产生电流流经金属。
研究发现,这个电流与温度几乎无关。
当时的理论难以解释这个现象。
[3]当时,由于人们主要根据的是经典静电学理论,因此在诸如金属电子理论等方面遇到的困难,无法得到令人满意的解答。
他们认为,金属中所有电子都是等效的。
也就是说,金属中的每个电子都以相同的程度对金属的热量做出贡献(这个量是波尔兹曼常数的一次项)。
上述问题一直困扰着科学家,直到费米–狄拉克统计的发现,才得到较好地解释。
1926年,恩里科·费米、保罗·狄拉克各自独立地在发表了有关这一统计规律的两篇学术论文。
[1][2]。
另有来源显示,P·乔丹(Pascual Jordan)在1925年也对这项统计规律进行了研究,他称之为“泡利统计”,不过他并未及时地发表他的研究成果。
[4]狄拉克称此项研究是费米完成的,他称之为“费米统计”,并将对应的粒子称为“费米子”。
1926年,拉尔夫·福勒在描述恒星向白矮星的转变过程中,首次应用了费米–狄拉克统计的原理。
[5]1927年,阿诺·索末菲将费米–狄拉克统计应用到他对于金属电子的研究中。
[6]。
1928年,福勒和L·W·诺德汉(Lothar Wolfgang Nordheim)在场致电子发射的研究中,也采用了这一统计规律。
[7]直至今日,费米–狄拉克统计仍然是物理学的一个重要部分。
费米–狄拉克分布[编辑]根据费米–狄拉克分布,给定费米子组成的系统中处于量子态上的平均粒子数可以通过下面的式子计算[8]其中是波尔兹曼常数,为绝对温度(热力学温标),为量子态上单个粒子的能量,是化学势。
当时,化学势就是系统的费米能。
半导体中电子的费米能,也被被称为费米能级。
[9][10]要应用费米–狄拉克统计,系统必须满足一定的条件:系统的费米子数量必须足够大,以至于再加入一个费米子所引起化学势的变化可以忽略不计。
[11]由于费米–狄拉克统计的推导过程中利用了泡利不相容原理,即单个量子态上最多能有一个粒子,这样的结果就是某个量子态上的平均量子数满足。
[12]•费米–狄拉克分布•平均粒子数和能量的关系,当温度较高时,平均粒子数的变化更加平缓。
当,。
不过,图中未能展现,当温度更高时,会下降。
[13]•平均粒子数和温度的关系(当)(点击图片可以获得完整尺寸)粒子的能量分布[编辑]当,温度在50开尔文与375开尔文之间取离散值时,费米函数)和能量值之间的关系曲线。
前面的章节叙述了给定费米子系统在不同量子态上的分布,一个量子态上最多只能具有一个费米子。
利用费米–狄拉克统计,还可以获得费米子系统不同能量值上的分布情况,这与分析量子态的原理略有不同,因为可能出现多个定态具有同一能量值,即出现所谓的简并能量态情况。
将费米–狄拉克统计中某个量子态上的平均粒子数与简并度(即能量值为的量子态数)相乘,就可以得到能量为的平均费米子数。
[14]当时,可能出现。
导致这个现象的原因前面提到过,即具有同一个能量值的粒子可能处于不同的定态,也就是说完全可能出现多个粒子处于同一能量值。
当一个系统的能量是准连续(quasi-continuum)的,定义其单位体积内单位能量域的量子态数为状态密度。
[14],单位能量域的平均费米子数为这里被称为费米函数,它与前面用来表达量子态上粒子数分布的函数具有相同的形式。
[15]故量子范畴和经典范畴[编辑]如果经典范畴中涉及的位移、动量之间的关系还远未达到不确定性原理所设定的极限,通常可以采用麦克斯韦-玻尔兹曼统计来代替费米–狄拉克统计,这样做可以简化数学计算的难度。
如果粒子平均间距远大于粒子的平均物质波波长,就可以采用上述经典范畴的处理方式。
[16]这里,为普朗克常数,为粒子的质量。
对于常温(约300开尔文)下金属中的电子,由于,因此该系统远离经典范畴。
这是因为电子质量较小,并且在金属中聚集程度较高。
这样,为了分析金属中的传导电子,必须采用费米–狄拉克统计。
[16]由恒星演变而来的白矮星,是另一个不属于经典范畴、必须采用费米–狄拉克统计的例子。
尽管白矮星的温度很高(其表面温度通常能达到10,000开尔文[17]),但是它内部高度聚集的电子和每个电子的低质量,使得处理这问题必须采用费米–狄拉克统计,而不能用经典的波尔兹曼统计近似处理。
[5]参考文献[编辑]1. ^ 1.01.1 Fermi, Enrico. Sulla quantizzazione del gas perfettomonoatomico. Rendiconti Lincei. 1926, 3: 145–9 (Italian)., translatedas Zannoni, Alberto (transl.). On the Quantization of the MonoatomicIdeal Gas. arXiv:cond-mat/9912229 [cond-mat.stat-mech]. 1999-12-14.2. ^ 2.02.1 Dirac, Paul A. M. On the Theory of Quantum Mechanics.Proceedings of the Royal Society, Series A. 1926, 112 (762): 661–77.Bibcode:1926RSPSA.112..661D. doi:10.1098/rspa.1926.0133.JSTOR94692.3. ^ Kittel, Charles. Introduction to Solid State Physics 4th. New York: JohnWiley & Sons. 1971. 249-250. ISBN0-471-14286-7. OCLC300039591.4. ^History of Science: The Puzzle of the Bohr–Heisenberg CopenhagenMeeting. Science-Week (Chicago).2000-05-19, 4 (20) [2009-01-20].OCLC43626035.5. ^ 5.05.1 Fowler, Ralph H. On dense matter. Monthly Notices of the RoyalAstronomical Society. 1926.December, 87: 114–22.Bibcode:1926MNRAS..87..114F.6. ^ Sommerfeld, Arnold. Zur Elektronentheorie der Metalle.Naturwissenschaften. 1927-10-14, 15 (41): 824–32.Bibcode:1927NW.....15..825S. doi:10.1007/BF01505083.7. ^ Fowler, Ralph H.; Nordheim, Lothar W. Electron Emission in IntenseElectric Fields (PDF). Proceedings of the Royal Society A.1928-05-01,119 (781): 173–81. Bibcode:1928RSPSA.119..173F.doi:10.1098/rspa.1928.0091. JSTOR95023.8. ^ Reif, F. Fundamentals of Statistical and Thermal Physics. McGraw–Hill. 1965. 341. ISBN978-0-07-051800-1.9. ^ Blakemore, J. S. Semiconductor Statistics. Dover. 2002.11. ISBN978-0-486-49502-6.10. ^ Kittel, Charles; Kroemer, Herbert. Thermal Physics 2nd. SanFrancisco: W. H. Freeman. 1980: 357. ISBN978-0-7167-1088-2.11. ^ Reif, F. Fundamentals of Statistical and Thermal Physics. McGraw–Hill. 1965. 340–2. ISBN978-0-07-051800-1.12. ^值得注意的是同时也是量子态被粒子占据的概率,由于一个量子态最多同时被一个粒子占据因此有。
