切线理论与应用共42页文档
《切线理论上》课件

02
切线的几何性质
切线的定义与性质
切线的定义
切线是一条与圆只有一个交点的 直线,这个交点叫做切点。
切线的性质
切线与半径垂直,切线与半径相 交于切点,切线在切点处与圆的 半径只有一个交点。
切线的判定定理
切线的判定定理:如果一条直线符合以下两个条件,则该直线为圆的切 线
直线过圆心;
数等,以拓展其应用领域。
针对切线理论在具体问题中的应 用,开展案例研究和实证分析, 提高其在实际问题中的可操作性
和实用性。
切线理论在其他领域的应用前景
在物理、工程、经济、金融等领 域中,探讨切线理论的应用可能 性,挖掘其潜在的价值和作用。
结合具体领域的特点和需求,开 发具有针对性的切线理论应用模 型和方法,提高其在解决实际问
切线的判定
如果直线与双曲线只有一个公 共点,则该直线为双曲线的切 线。
渐近线与切线的关系
双曲线的渐近线与切线在切点 处相交,且它们的斜率互为相
反数。
04
切线在实际问题中的应用
切线在物理问题中的应用
总结词
切线理论在物理问题中有着广泛的应用,特别是在力线表示速度的方向或加速度的方向,对于理解物体运动轨迹和变 化规律至关重要。例如,在曲线运动中,切线决定了物体的速度方向和轨迹形 状。
《切线理论上》ppt课件
目录
• 切线理论概述 • 切线的几何性质 • 切线在几何图形中的应用 • 切线在实际问题中的应用 • 切线理论的扩展与展望
01
切线理论概述
切线理论定义
切线理论是研究曲线在某一点 处的切线的几何理论。它主要 探讨曲线在某一点的切线的性 质和求法。
切线定义为曲线在某一点处与 该点处的极限相切的直线。
切线理论基本原理及实盘应用
切线理论基本原理及实盘应用
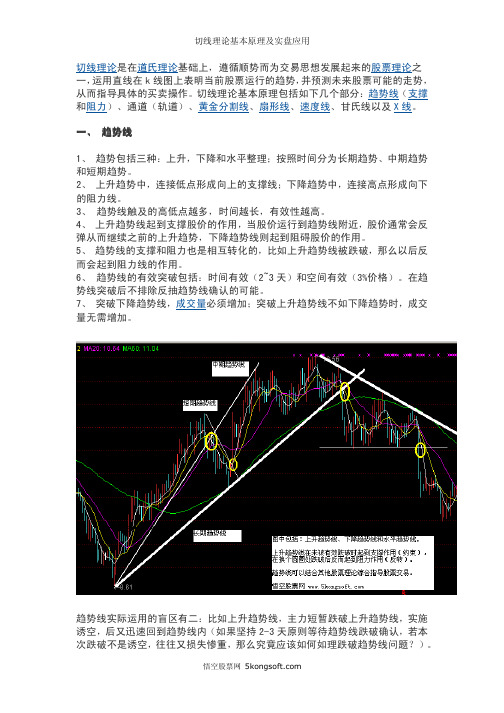
6、 甘氏线和速度线类似,是从一个点出发,依一定的角度,向后画出的多条直 线,所以,有些书上把甘氏线称为角度线。甘氏线与速度线的区别在于,速度线 通常只有三条,甘氏线有若干条帮助判断趋势。 总结:这些线的画法都比较简单,但是实际应用性不是非常强,因为他们只是表 征趋势可能的运行方式和股价走向,确定性较差,如果能够综合运用才能取得较 好效果。 五、实盘应用与图解 切线理论包括趋势线、通道、黄金分割线等,能够帮助股民认清股票趋势的延续 和逆转。下面是悟空股票网总结的切线理论的实盘应用要点和图解。 1、 单趋势线:向上突破下降趋势线时 a.应谨慎看多不宜马上介入,应等待第二个低点的产生,形成上升趋势,才是介 入良机。并且以两个低点的连线所作的上升趋势线作为止损点。 b.若突破后即行介入,应以下降压力线或前期低点或颈线作为止损价。 2、单趋势线:向下突破上升趋势线时: a.突破后立即退出,如短期内返身向上再次进入通道内部,则应在回调受到新趋 势线支撑后介入(很多股票短线诱空采取这种方式)。 b.突破后立即退出,如形成整理走势,待突破整理形态压力线时再行介入。
• 已有通道角度本身已经非常陡峭,股票短线涨幅巨大,则诱多可能很大。 • 突破发生后股价是否能保持在通道之外?如果价格突破后能保持在通道
之外,就可能出现加速运动。换句话说,价格在通道之外盘衡的时间越长, 出现衰竭的可能性越小 • 如果突破后回跌到通道内,但幅度不深,并且在短时间内,又向上突破通 道线,考虑介入。 • 三浪,说明股价将加速上升,可以介入,五浪末期,小心诱多,趋势随时 转折。 • 观察 KDJ 等其他技术指标,若已经高位钝化,诱多可能较大。
悟空股票网
切线理论基本原理及实盘应用
三、黄金分割线、百分比线 1、 黄金分割线和百分比线主要用来揭示股价高低点运行中可能存在的阻力和支 撑位。 2、 按照比率包括:0.191,0.382,0.618,0.809 以及 1/8,2/8,1/3,3/8,4/8,5/8,2/3,6/8,7/8,8/8 等。 3、 画线时,可以选择一对高点和低点,然后按照上述比率分割,比如 x,y 点 得到的比例线为 0.382*(x-y),0.618(x-y)等。也可以选取一个点(高点或低点), 然后直接分割,比如低点 z 得到的是 1.382*z,1.618*z,1.5*z 等。 4、 实际使用中牢记,所有比率线只有参考和预测作用,不能完全作为交易依据, 必须结合趋势线、通道、K 线组合、波浪理论等其他炒股理论一起作为买卖参考。
切线理论(附图)

切线理论切线理论是指按一定方法和原则在由股票价格的数据所绘制的图表上画-些直线。
然后根据这些直线的情况推测股票价格的未来趋势。
一、趋势的定义简单的说,趋势就是价格的波动方向,或者说是证券市场运动的方向。
二、趋势的方向趋势的方向有三个:(1)上升方向(2)下降方向(3)水平方向三、趋势的类型趋势分为3种类型。
1、主要趋势。
主要趋势是趋势的主要方向,是投资者极力要弄清楚的目标。
了解了主要趋势才能做到顺势而为。
主要趋势是价格波动的大方向,一般持续的时间比较长。
这是技术分析第二个假设所叙述的。
2、次要趋势。
次要趋势是在进行主要趋势的过程中进行的调整。
我们知道,趋势不会一成不变的直来直去,总要局部调整和回撤的过程,次要趋势正是完成这一使命。
3、短暂趋势。
短暂趋势是在次要趋势的过程中所进行的调整。
短暂趋势与次要趋势的关系就如同次要趋势与主要趋势的关系一样。
这三种类型的趋势的最大区别是时间的长短和波动幅度的大小上的差异。
以上三种划分可以解释绝大多数的行情。
对于更复杂的价格波动过程,以上三种划分可能还不够用。
不过这不是很大的问题,可以继续对短暂趋势进行再细分。
下图是三种趋势类型的图形说明。
四、例例1此主题相关图片如下:支撑线和压力线认清趋势是进行投资的重要步骤。
认清趋势之后,就应该采取相应的行动。
如果认清大牛市已经来临,那么就应该进入市场进行实际的投资,只是将面临一个选择入市时机的问题。
每个投资者都希望在大涨之前的低点买入,或者在涨势的中途回落的低点买入。
这些低点在哪里呢?对这些问题肯定没有十全十美的答案,但是支撑线和压力线会给我们一些帮助。
一、支撑线和压力线的含义1、支撑线。
又称抵抗线。
当价格下跌到某个价位附近时,价格停止下跌,甚至可能出现回升,这是多方在这个位置买入所造成的。
这个位置对价格的继续下跌起到了迟滞作用。
这个阻止证券价格继续下跌或者暂时阻止价格继续下跌的价格位置就是支撑线所在的位置。
2、压力线。
压力线又称阻力线。
四章节下切线理论应用

酒钢宏兴2019 年11月至2019 年4月日K线图
3×1 8×1
4×1
2×1
1× 1
1× 2 1× 3
1× 4 1×8
上证指数2000年 12月至2019年4 月周K线图
倾斜的支撑线和压力线与
水平的支撑线和压力线
倾斜的支撑线和压力线随着时间的移动,支撑 位和压力位也要不断地变化。向上斜的切线价 位会变高,向下斜的切线价位会变低。
1.预测市场波动的大概区间.
2.预测一旦市场运动打破了原有的 走势通道之后能走多远.
第二节 黄金分割线的魔力
一、黄金分割线 1.黄金分割是一个古老的数学方法. 埃及吉萨金字塔:正方形底部边长230米 高度146米 230:146=1:1.6即5:8
2.斐波那奇序列数.
1,1,2,3,5,8,13,21,34,55,89,144, ……
每条直线都有支撑和压力的功能,即当价格由 下接近一条直线时会受到压力,当价格由上而 下接近一条直线时会受到支撑。
甘氏认为,在9条角度线中,比较重要的是 1×1线(45度线)、 1×2线(26.25度线) 和 2×1线(63.25度线) 。其中又以45度线最重 要,代表着市场的一种动态平衡态势。
对水平直线来说,每个支撑位或压力位相对来 说较为固定。为了弥补它们在时间上考虑的不 周到,往往多画几条水平切线,同时提供多条 支撑线和压力线,并指望被提供的这几条中最 终确有一条能起到我们所希望的支撑和压力的 作用。水平线中最终只有一条被确认为支撑线 或压力线,对预测今后的价格趋势有帮助。
二、最重要的角度线
第四章(下) 切线理论的应用
第一节 黄金走廊----趋势通道线
一、认识趋势通道线
在市场中,价格趋势经常整个地行走 在两条平行线之间,构成一条美妙的走势 通道.在这两条线中,一条是基本的趋势线, 而另一条就是通道线.
《切线理论》课件

积分在解决实际问题中常常需要用到 切线理论,如求曲线下面积、变速直 线运动的路程等。
导数的几何意义
导数描述了函数图像在某一点的切线 斜率,是微积分中研究函数变化率的 重要工具。
切线理论在其他学科的应用
物理学中的应用
在物理学中,许多概念和公式都 涉及到切线理论,如速度、加速
度、力的方向等。
工程学科中的应用
《切线理论》ppt课 件
• 切线理论简介 • 切线理论的基本原理 • 切线理论的实践应用 • 切线理论的扩展与深化 • 总结与展望
目录
Part
01
切线理论简介
切线理论的基本概念
切线理论是一种基于几何学和 微积分的数学理论,用于描述 曲线在某一点的切线性质。
切线是曲线在某一点上的极限 方向,表示曲线在该点的斜率 或变化率。
Part
02
切线理论的基本原理
切线的几何定义
切线是一条与曲线在某一 点仅有一个公共点的直线 。
切线与曲线在该点的切点 处相切,即切线的方向与 曲线的在该点的法线方向 重合。
切线是曲线在该点的导数 或微分的几何表示。
切线的性质
STEP 01
STEP 02
STEP 03
切线与曲线在该点的切点 处相切,即切线与曲线在 该点的切点处只有一个公 共点。
切线的方向与曲线的在该 点的法线方向垂直。
切线的斜率等于曲线在该 点的导数。
切线的计算方法
利用导数求切线斜率
01
对于给定的函数,求其在某一点的导数,即为该点处切线的斜
率。
利用点斜式求切线方程
02
已知一点和斜率,利用点斜式求直线方程,即为该点处切线的
方程。
利用切线与曲线的交点求切线方程
平面曲线的切线与法线共42页文档

谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
平面曲线的切线与法线
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
切线理论与应用

7 甘氏线
甘氏线(Gann line)分上升甘氏线和下降甘 氏线两种,是由William D.Gann创立的一 套独特的理论。甘氏线就是将百分比原理 和几何角度原理结合起来的产物。甘氏线 是从一个点出发,依一定的角度,向后画 出的多条直线,所以,有些书上把甘氏线 称为角度线。
7 甘氏线
二、切线理论实战应用
切线理论与应用
讲解大纲 一、 切线理论基本原理
二、 切线理论实战应用 三、切线理论评述总结
一、切线理论基本原理
1 趋势分析
1.定义 趋势是指价格的波动方向,或者说是证券
市场运动的方向
2.方向 上升、下降、水平 3.类型 主要趋势、次要趋势、短暂趋势
2 支撑线与压力线
1.定义 2.作用 支撑线:阻止价格继续下跌 压力线:阻止价格继续上升 3.支撑线与压力线的相互转化 转化的依据:突破 4.支撑线与压力线的确认和修正
三、切线理论总结评述
切线分析究竟可不可信
这里先讲个故事:一天,庄子和他的学生在山上看见山中有一棵 参天古木因为高大无用而免遭于砍伐,于是庄子感叹说:“这棵树 恰好因为它不成材而能享有天年。” ,庄子和他的学生又到他的一位朋友的家中作客。主人殷 勤好客,便吩咐家里的仆人说:“家里有两只雁,一只会叫,一只 不会叫,将那一只不会叫的雁杀了来招待我们的客人。” ,向庄子问道:“老师,山里的巨木因 为无用而保存了下来,家里养的雁却因不会叫而丧失性命,我们该 采取什么样的态度来对待这繁杂无序的社会呢?” “还是选择有用和无用之间吧,虽然之间的分寸 太难掌握了,而且也不符合人生的规律,但已经可以避免许多争端 而足以应付人世了。”
4 百分比线
5 扇形线
当行情经过一段时间的上升,如果我们将开 始上升的低点和高位徘徊的各个低点分别 以直线连接起来,便可以画出多条上升趋 势线,就像一把扇子,作出很规则的移动 ,每一条趋势线之间形成的角度大致相等 ,我们把这些趋势线称为扇形线。下跌时 情形亦是如此。 扇形线丰富了趋势线的内容,明确给出了趋 势反转(不是局部短暂的反弹和回落)的信号。 扇形原理是依据三次突破的原则。
切线定理的证明与应用解析

切线定理的证明与应用解析切线定理,又称为切角定理,是解析几何中的一个重要定理,用于描述平面上一条曲线与其切线的关系。
本文将对切线定理的证明及其应用进行详细的解析。
一、切线定理的证明为了证明切线定理,我们首先需要了解什么是切线以及切线的性质。
在平面几何中,给定一条曲线和曲线上的一点P,过点P且与曲线仅有一个公共点的直线称为曲线在点P处的切线。
证明切线定理的关键是利用导数的概念和性质。
假设曲线的参数方程为x=f(t),y=g(t),其中f(t)和g(t)分别是x和y关于参数t的函数。
取曲线上一点P(x0,y0),并选取一条过P的切线L。
切线L的斜率可以表示为dy/dx。
由于切线仅与曲线在点P处相切,因此曲线上的其他点(x,y)也必须满足曲线方程g(x)-y=0与切线方程dy/dx(x-x0)-y+y0=0的联立条件。
通过解联立方程,我们可以得到一个关于dx和dy的方程。
对该方程进行一阶泰勒展开,可以得到一般形式的切线方程:dy/dx = [dy/dt] / [dx/dt] = g'(t) / f'(t)这个方程给出了曲线在任意一点处切线的斜率。
切线定理则是该定理的特殊情况,即当t=t0时的情况。
在切线上,有t=t0,因此切线方程简化为:dy/dx = g'(t0) / f'(t0)这个结果就是切线定理。
二、切线定理的应用切线定理在解析几何中有着广泛的应用。
下面我们将介绍切线定理在求曲线的切线、判定曲线凹凸性以及估算近似值等方面的应用。
1. 求曲线的切线通过切线定理,我们可以根据给定曲线的函数表达式,求出曲线在任意点处的切线方程。
我们只需要求出函数的导数,然后在给定点处代入即可得到切线的斜率。
再根据切线的斜率和经过给定点的条件,可以得到切线的方程。
2. 判定曲线的凹凸性对于曲线上的某一点P(x0,y0),切线定理可以用来判定该点所在的曲线的凹凸性。
如果切线的斜率dy/dx大于零,则该点位于曲线的上凸部分;若切线的斜率小于零,则该点位于曲线的下凸部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
切线理论与应用
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
13、遵守纪律的风气的培养,只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致,是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机会是不守纪律的。——雨果
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
