结构力学第2章习题及参考答案
结构力学2考试题和答案

结构力学2考试题和答案一、单项选择题(每题2分,共20分)1. 在结构力学中,下列哪一项不是结构分析的基本假设?A. 平面假设B. 小变形假设C. 材料均匀性假设D. 材料非线性假设答案:D2. 确定结构的内力时,通常采用哪种分析方法?A. 能量法B. 弯矩分配法C. 弯矩图法D. 极限平衡法答案:C3. 在结构力学中,以下哪种类型的结构是超静定结构?A. 简支梁B. 悬臂梁C. 连续梁D. 刚架答案:C4. 梁的剪力图和弯矩图的零点位置关系是什么?A. 剪力图的零点与弯矩图的极值点重合B. 弯矩图的零点与剪力图的极值点重合C. 剪力图的零点与弯矩图的零点重合D. 剪力图的极值点与弯矩图的零点重合答案:A5. 以下哪种情况下,结构的稳定性分析是必要的?A. 荷载较小B. 荷载较大C. 荷载恒定D. 荷载变化答案:B6. 确定结构的位移时,通常采用哪种方法?A. 弯矩分配法B. 弯矩图法C. 虚拟力法D. 能量法答案:C7. 在结构力学中,以下哪种结构是静定结构?A. 三铰拱B. 刚架C. 连续梁D. 悬臂梁答案:D8. 以下哪种方法可以用来求解超静定结构?A. 弯矩分配法B. 弯矩图法C. 能量法D. 所有以上方法答案:D9. 结构力学中,以下哪种荷载属于分布荷载?A. 集中荷载B. 均布荷载C. 点荷载D. 线荷载答案:B10. 在结构力学中,以下哪种情况下结构会发生屈曲?A. 荷载较小B. 荷载较大C. 荷载恒定D. 荷载变化答案:B二、填空题(每题2分,共20分)1. 结构力学中,结构的内力包括______、______和______。
答案:轴力、剪力、弯矩2. 梁的挠度计算中,通常采用的两种方法是______和______。
答案:弯矩分配法、能量法3. 结构的稳定性分析中,______是衡量结构稳定性的一个重要参数。
答案:屈曲荷载因子4. 在结构力学中,______是结构分析的基本假设之一。
结构力学课后习题答案(朱慈勉)

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m 2m2mA2m2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F两铰的位lx l lx置。
《结构力学》课后习题答案__重庆大学出版社

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学第2章习题及参考答案
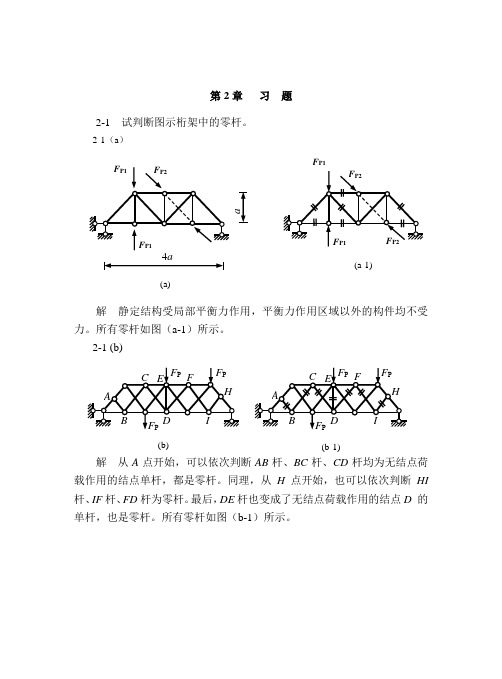
解悬臂刚架,梁部分先求杆端控制弯矩,再区段叠加。柱剪力为零,弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架,先求支座反力,再作弯矩图。注意二杆结点有外力偶作用时,杆端弯矩将产生突变,突变值等于力偶值。
2-21(c)
解(1)铰附近截面作用有集中力偶时,弯矩值等于力偶值,据此,可知顶铰左右两侧截面的弯矩为M,上侧受拉。又因为横梁上没有竖向集中力作用,弯矩图应是一条直线。考虑本题结构对称,荷载也对称,则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解:(1)确定求解顺序:EF→CDE→ABC
(2)求支座反力及各部分之间的相互作用力。结果如图(b)所示。
(3)分别画出每一部分的内力图,组合在一起就是原结构的内力图,如图(c)和(d)所示。
2-15试作图示多跨静定梁弯矩图。
解:(1)确定求解顺序。DEF→DCB→AB。
(2)二杆刚结点上,若无集中力偶作用时,则两个杆的杆端弯矩应该相等,且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构,先算上部、后算下部。两个部分均三铰刚架,分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN,FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
南京航空航天大学_结构力学_课后习题答案_第2章

第二章 薄板的弯曲(习题解答)2-1 写出2-1图所示矩形薄板的边界条件。
OA 为简支边,并作用有分布的弯矩M 。
BC 边为固支边,OC 边为简支边。
AB 边为自由边。
解:OA 边:M x w Dyw u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0;OC 边:0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ;BC 边:00=∂∂===ax a x xww ;AB 边:0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示,矩形薄板OA 边和OC 边为简支边,AB 和BC 为自由边,在点B 受向下的横向集中力P 。
试证w mxy =可作为该薄板的解答,并确定常数m 、内力及边界处反力。
解:mxy w =满足平衡微分方程0/4==∇D q wOC 边上:0)(0022220=;==∂∂+∂∂-=y y x wu y w D wOA 边上:0)(0022220=;==∂∂+∂∂-=x x y wu x w DwAB 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ;BC 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ;在B 点上:P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ;0)(2222=∂∂+∂∂-=x w u y w D M y ;2)1(2P y x w u D M xy-=∂∂∂--= ;02=∇∂∂-=w xD Q x ;02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=;)()1(222-3 如图2-3所示,半椭圆形薄板,直线边界为简支边,曲线边界ACB 为固支边,承受横向载荷0q=q xa 。
结构力学第2章习题参考答案_khdaw

2
w.
13 FN6 = 1.352 1FP
案 网
sin α =
1
cos α =
2
sin β =
2
cos β =
3
FN6 sin β + FN5 cos α − FN4 sin θ = 0
2.5Fp
Fp
Fp
∑Fy = 0
2 FP , ∑M K = 0 2 FN1 = 4 FP , ∑ Fx = 0
FN 4 = −4.5 FP
y
∑F
x
=0 FN2 = 0
FN1 = 0
取 1、2 杆相交结点为隔离体,可求得:
2-6(f) 取隔离体图(a)所示,求得支座反力。再取隔离体图(b)列方程有: G F E 0 A 1 B 2 H
答
FN3
F
w.
H FN2
案 网
da
D C 2 FN5 D Fp Fp Fp (b)隔离体图
后
FN4
Fp
kh
w.
kh
da
课
后
答
w.
案 网
Fp l=8×a
co
A D E B (d)
m
Fp
N
O
P
Q
U
V
H
课后答案网
2-2 答:
11 9 10
1 0 8
12
13 6
4 5
7 4×2.5 m
17.5 kN 依次取结点为隔离体,受力图如下所示。 10 kN FN1 FN2
32.5 kN
2×1.25 m
课后答案网
2-6(a) 答:取图(a)所示隔离体,列方程有: 80 kN 45o FN1 (a)隔离体 2 FN1 (b)隔离体 FN2 80 kN K
南京航空航天大学 结构力学 课后习题答案 第2章

第二章 薄板的弯曲(习题解答)2-1 写出2-1图所示矩形薄板的边界条件。
OA 为简支边,并作用有分布的弯矩M 。
BC 边为固支边,OC 边为简支边。
AB 边为自由边。
解:OA 边:M x w D y w u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0;OC 边:0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ;BC 边:00=∂∂===ax a x xww ;AB 边:0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示,矩形薄板OA 边和OC 边为简支边,AB 和BC 为自由边,在点B 受向下的横向集中力P 。
试证w mxy =可作为该薄板的解答,并确定常数m 、内力及边界处反力。
解:mxy w =满足平衡微分方程0/4==∇D q wOC 边上:0)(0022220=;==∂∂+∂∂-=y y x wu y w D wOA 边上:0)(0022220=;==∂∂+∂∂-=x x y wu x w D wAB 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ;BC 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ;在B 点上:P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ;0)(2222=∂∂+∂∂-=x w u y w D M y ;2)1(2P y x w u D M xy-=∂∂∂--= ;02=∇∂∂-=w xD Q x ;02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=;)()1(222-3 如图2-3所示,半椭圆形薄板,直线边界为简支边,曲线边界ACB 为固支边,承受横向载荷0q=q xa 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8 kN 20 kN
HI
J ⅠK
L
2 1
AC
D
E ⅠF
G
B
2.5m6 15m
2.5 m
(a)
K
LD
FNJK D
FN2
FNEF FD
G
B
FBy (b
)
解:(1)判断零杆。如图(a)所示。
(2)求支座反力
F x 0 , FAx 0
M A 0 , FB y 12.67 kN
F y 0 , FA y 15.33 kN
5 29
MK
M
0 K
FH yK
510 130 3 120
kN
m
FQK FQ0K cosK FH sinK 52
5 130 29
2 0 29
FNK FN0K sinK FH cosK 52
2 130 29
5 140 kN 29
2-12 图示圆弧三饺拱,求支座反力及截面 D 的 M 、FQ 、FN 值。 20kN/m
D
C
5m
5m
FH
30
A 5m
B 5m
FH
FAy
FBy
习题 2-12 图
解 (1)求支座反力。
FB y 100 kN , FA y 100 kN , FH 50 kN
(2)求等代梁 D 截面内力
M
0 D
FAy
2.5
1 2
20 2.52
187.5kNm
FQ0D FAy 20 2.5 50 kN
30 kN A 4 B 30 kN
3×2m
N 1
N
D
N
CN 2 E
N3
30 kN N
4×2mN N (b-2)反对称荷载组
30 kN N
N
解 (1)荷载分组。将荷载与支座反力分解成对称和反对称情况。
(2)求指定杆轴力。对称情况 1、2、3 杆轴力为零。反对称情况 4 杆
轴力为零。由 A 结点的平衡条件,得
(3)求三铰拱 D 截面内力
yD 5mcos30 2.5 3 m
D 30, tan D
3 3
, sin D
1 2
,cos
D
3 2
MD
M
0 D
FH yD
187.5 2.5
3 29.5 kN m
FQD FQ0D cosD FH sinD 50
3 50 1 18.8 kN
2
2
FN D
FN0D
2-11 求图示抛物线( y 4 fx(l x) / l 2 ) 三铰拱距左支座 5m 的截面内力。
y
FH A
x
FAy
20 kN/m
K
C
40 kN·m Q
4m
10 m×2=20m
习题 2-11 图
B 5m
FH
FBy
解 (1)求支座反力
FB y 48 kN , FA y 152 kN , FH 130 kN
I
3 (a-2)3
3
N
N
N
解 (1)判断零杆 ①二杆结点的情况。N、V 结点为无结点荷载作用的二杆结点,故 NA、 NO 杆件和 VI、VU 杆件都是零杆;接着,O、U 结点又变成无结点荷载作用 的二杆结点,故 OP、OJ、UT、UM 杆件也是零杆。②结点单杆的情况。BJ、 DK、QK、RE、HM、SL、LF 杆件均为无结点荷载作用的结点单杆,都是零杆; 接着,JC、CK、GM、LG 杆件又变成了无结点荷载作用的结点单杆,也都是 零杆。所有零杆如图(a-1)所示。去掉零杆后的简化体系如图(a-2)所示。
(2)求指定杆轴力。 Ⅰ-Ⅰ截面(图(b)):
F y 0 , FN3
2 2
FP
M K 0 , FN1 4FP
Fx 0 , FN4 4.5FP
Ⅱ-Ⅱ截面(图(c))
F y 0 , FN2 0.5FP
2-5 用截面法求图示桁架中指定杆的轴力。
10kN 10kN 10kN 10kN
(a)
20 kN
20 kN
(b)
解 (1)求支座反力 FAy FB y 20 kN
(2)判断零杆。去掉零杆得图(b)所示简化体系。 (3)求杆件轴力
结点 E:
FNAC FNBD 20 kN
Fy 0 , FNEC 33.33kN
结点 C
Fx 0 , FNEF 26.67 kN
由对称性可知
Ⅱ—Ⅱ截面(图(b)):将 FN 4 滑移到 B 点
M D 0 : FN4x 9 4 3 4 3 2 5 2 7 1 3 0
由比例关系
FN 4x
1 kN 3
FN4
10.52 3
32
FN 4 x
1.21kN , FN4 y
10.5 3
FN
4
x
1.17 kN
F x 0 , FN2 3.3kN
F y 0 : FN1 FN
2 2
FN 4 y
2
2
0
,
FN1
2.83 kN
2-10 选用较简捷的方法计算图示桁架中指定杆的轴力。
4m 4m
H G 1E D
4kN
4
2
A
3F C B
FAy
1kN 2kN 2kN 2kN 1kN
FBy
K 3m6 18m
习题 2-10 图
H G FN1E D
FN 2
2kN 2kN
2m 2m 3m 3m
习题 2—9 图
FN 3
FN 6
C
1kN 2kN
FN 5
(a)Ⅰ—Ⅰ截面
1kN
D
FN1
2kN 4kNFN 2
FN4 4kN
B FN4 (a)Ⅱ—Ⅱ截面
解 Ⅰ—Ⅰ截面(图(a))
F y 0 , FN5 4 kN ; M C 0 , FN3 5 kN
F x 0 , FN6 3 kN
FNOG=-FNOH 同理,G、H 结点也为“K”结点,故
(a)
FNOG=-FNGH FNHG=-FNOH 由式(a)、(b)和(c)得
(b) (c)
FNOG=FNGH=FNOH=0 同理,可判断在 TRE 三角形中
FNSK=FNKL=FNSL=0 D 结点也是“K”结点,且处于对称荷载作用下的对称轴上,故 ID、JD
FNTL FNLE 0.5 2FP , FNTS FNSR 2FP
至此已求出对称轴右侧所有杆件的轴力,对称轴左侧杆件的轴力可由
对称性很方便地得到。
2-2(b)
F GH
Fp
Fp
H Fp
aa
C
E
D
A
B
E D
A
B
l=2×a
(b)
(b-1)
(b-2)
解 (1)判断零杆。零杆如图(b-1)所示,去掉零杆后的简化体系如 图(b-2)所示。
解 Ⅰ-Ⅰ截面(图(a-1))
F x 0 , FN1 80 2 kN
Ⅱ-Ⅱ截面(图(a-2))
M K 0 , FN2 = 80 kN
2-8 (b)
60 kN
1
N
2
N
3
N 4×2 m
(b) N
3×2 m
30 kN
N 1
N
30 kN N 2
30 kN N
N3
(b-1)对称N荷载组 N
30 kN N
2-1(c) 2Fp
aa
Fp l=6×a
Fp
(c)
2Fp
N O PQ
RS T
F AG
HI
J
C Fp
D
(c-1)
M
K
L
E Fp B
解 该结构在竖向荷载下,水平反力为零。因此,本题属对称结构承受
对称荷载的情况。AC、FG、EB 和 ML 均为无结点荷载作用的结点单杆,都
是零杆。
在 NCP 三角形中,O 结点为“K”结点,所以
5kN
Ⅰ
FN1x
A
25kN
D Ⅰ FN2y
FN2x FN2
(b)
ⅡC
FN3
Ⅱ
B 10kN
(c)
解 (1)求支座反力 FAx 0 , FBy 10 kN , FAy 25kN
(2)求指定杆轴力 Ⅰ—Ⅰ截面(图(b))
MD 0 , FN1x 30kN , FN1
5 2
FN1x
15
5 kN
M A 0 , FN2y 5kN , FN2
FN 3 F C B
2kN 1kN
FBy
(a)Ⅰ—Ⅰ截面
解 (1)求支座反力
FBy
44 9
kN
4.89 kN ,
FAy
28 9
kN
3.11kN
(2)求指定杆轴力
结点 C:去掉零杆 CD
F y 0 : FN2 y 1kN , FN2
13 2
FN 2 y
1.8 kN
结点 G
F y 0 , FN4 1kN
(3)求指定杆轴力
由 I 结点的平衡条件,得
由 D 结点的平衡条件,得
FNID 8 kN
Ⅰ-Ⅰ截面(图(b))
FN1 8 2 kN
F y 0 , FN2 5FB y 28.32 kN
0.75 m 0.75m
2-7 试用对称性求图示桁架各杆轴力。
C
D
A
E
F
B
20 kN 1m8 8m
20 kN
Ⅰ—Ⅰ截面(图(a))
M F 0 : FN1 4 FN2 y 3 FBy 6 1 3 0
