4.非晶态和半晶态习题解答
第六章 非晶态与半晶态材料

高分子链的运动是以链段为单元的,是蠕动。高分 子链在分子内旋转作用下可采取各种可能的形态,如 取不同的构象,如伸直链、无规线团、折叠链、螺旋 链等。
高分子 链构象
构象是由分子内热运动引起的物理现象,是不断改变的, 具有统计性质。因此讲高分子链取某种构象是指的是它取这 种构象的几率最大。
(3)氢键
如果高分子链的分子内或分子间可以形成氢键,
氢键的影响比极性更显著,可大大增加分子链的刚
性。
(4)链的长短 如果分子链较短,内旋转产生的构象数小,刚 性大。如果分子链较长,主链所含的单键数目多, 因内旋转而产生的构象数目多,柔顺性好。 链长超过一定值后,分子链的构象服从统计规 律,链长对柔顺性的影响不大。
2.聚合物的结构
I. 高分子的链结构 高分子的二级结构: (1)高分子的大小(即分子量) (2)高分子链的形态(构象)
高分子链中的单键可内旋转,每个键的空间
i+1 i
位置受其键角的限制,但是离第一个键越远,
其空间位置的任意性越大,两者空间位置的相 互关系越小,可以想象从第i+1个键起,其空
间位置的取向与第一个键完全无关,因此高分
特点:聚合物中晶区与非晶区同时存 在,同一条高分子链可以是一部分结 晶,一部分不结晶;并且同一高分子 链可以穿透不同的晶区和非晶区。
折叠链模型
3.影响结晶度的因素
热固性聚合物不会结晶。
热塑聚合物部分结晶的能力取决于分子是否容 易移动并有效地堆垛在一起形成长程有序的难易。
影响聚合物链堆垛效率的因素: 侧基的尺寸 链分支的程度 立构规整度 重复单元的复杂性
聚合物串晶是一种类似于串珠式的多晶体。
非晶态固体物理历年试题及答案汇

非晶态固体物理历年试题及答案汇编1、 说明晶体与非晶体在结构上的区别(5分);为何制备非晶体合金需要较快冷却速度(5分)?在结构上,晶体是长程有序,原子排列有周期性;非晶体是短程有序,原子排列没有周期性。
只有在较快的冷却速度下,合金才能避免形核,即避免形成晶体,最终形成非晶体。
2、 写出非晶体的三个连续无规模型及它们各自适用的玻璃结构(10分)。
请举出其中一种模型的实例,并描述它的结构特点(10分)。
连续无规网络, 适合于共价玻璃结构;无规密堆积,适用于简单金属玻璃结构;无规线团模型,适用于聚合有机玻璃结构。
举例:α-Si 是连续无规网络结构,它的特点如下:1. z=4, 每个原子四重配位;2. 不变的键长;3. 没有悬空键;和金刚石不同的是:4. 键角有明显的分散;5. 没有长程有序。
3、 什么是分形维数(5分)?说明自迥避行走与简单无规行走的区别(5分)。
分形维数:这种维数适合于描述高分子链位的随机-几何特性,与欧几里德维数和拓扑维数不同,这个新的维数可以具有非整数值。
对于一些规则形状,从方程d N N r 1)(-=(N :一个整体分成N 个与整体相似的形状)重新得到嵌入空间的欧几里德维数d 。
对于一些非常不规则的随机形状,方程就会得出一个不同的维数,这个维数提供了非常有价值的不规则本身的测度。
这个维数在数学上称为HausdorffBescovitch 维数,我们把它叫做分形维数。
自迥避行走与简单无规行走不同的地方在于自迥避行走能记住过去曾走过些什么地方,并且不允许再回到已过去的地方。
4、 何谓波粒二象性?写出微观粒子二象性的基本公式。
(5分))/(/mu h P h ==λ,此式表明一个动量为P = mu 的电子或其它微观粒子的行为或属性宛如波长为的波的属性。
5、 什么是过渡族元素和稀土元素?(5分)凡是外层电子填充在d 轨道的元素都称为过渡族元素;外层电子填充在4f (镧系)、5f (锕系)轨道上的元素称为稀土元素。
材料物理基础习题
课后练习思考题:第一章晶体结构1-1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。
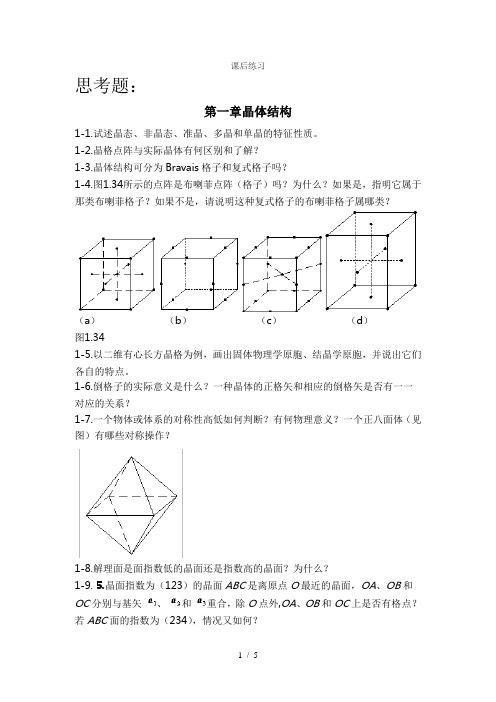
1-2.晶格点阵与实际晶体有何区别和了解?1-3.晶体结构可分为Bravais格子和复式格子吗?1-4.图1.34所示的点阵是布喇菲点阵(格子)吗?为什么?如果是,指明它属于那类布喇菲格子?如果不是,请说明这种复式格子的布喇菲格子属哪类?(a)(b)(c)(d)图1.341-5.以二维有心长方晶格为例,画出固体物理学原胞、结晶学原胞,并说出它们各自的特点。
1-6.倒格子的实际意义是什么?一种晶体的正格矢和相应的倒格矢是否有一一对应的关系?1-7.一个物体或体系的对称性高低如何判断?有何物理意义?一个正八面体(见图)有哪些对称操作?1-8.解理面是面指数低的晶面还是指数高的晶面?为什么?1-9. 5.晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、OB和OC分别与基矢、和重合,除O点外,OA、OB和OC上是否有格点?若ABC面的指数为(234),情况又如何?1-10.带轴为[001]的晶带各晶面,其面指数有何特点?1-11. 与晶列[l1l2l3]垂直的倒格面的面指数是什么?1-12. 在结晶学中,晶胞是按晶体的什么特性选取的?1-13. 六角密积属何种晶系?一个晶胞包含几个原子?1-14.体心立方元素晶体, [111]方向上的结晶学周期为多大?实际周期为多大?1-15. 面心立方元素晶体中最小的晶列周期为多大?该晶列在哪些晶面内?1-16. 在晶体衍射中,为什么不能用可见光?第二章固体的结合2-1.试述离子键、共价键、金属键、范德瓦尔斯键和氢键的基本特征.2-2.有人说“晶体的内能就是晶体的结合能”,对吗?2-3.当2个原子由相距很远而逐渐接近时,二原子间的力与势能是如何逐渐变化的?2-4.为什么金属比离子晶体、共价晶体易于进行机械加工并且导电、导热性良好?2-5.是否有与库仑力无关的晶体结合类型?2-6.如何理解库仑力是原子结合的动力?2-7.晶体的结合能,晶体的内能,原子间的相互作用势能有何区别?2-8.原子间的排斥作用取决于什么原因?2-9.原子间的排斥作用和吸引作用有何关系?起主导的范围是什么?2-10.共价结合为什么有“饱和性”和“方向性”?2-11.共价结合,两原子电子云交迭产生吸引,而原子靠近时,电子云交迭会产生巨大的排斥力,如何解释?2-12.试解释一个中性原子吸收一个电子一定要放出能量的现象.2-13.如何理解电负性可用电离能加亲和能来表征?2-14.何为杂化轨道?2-15.你认为固体的弹性强弱主要由排斥作用决定呢,还是吸引作用决定?第三章晶格振动与晶体的热学性质3-1.什么是简谐近似?3-2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线,并简要说明其意义。
高分子物理第三章习题及解答

高分子的溶解溶解与溶胀例3-1 简述聚合物的溶解过程,并解释为什么大多聚合物的溶解速度很慢解:因为聚合物分子与溶剂分子的大小相差悬殊,两者的分子运动速度差别很大,溶剂分子能比较快地渗透进入高聚物,而高分子向溶剂地扩散却非常慢。
这样,高聚物地溶解过程要经过两个阶段,先是溶剂分子渗入高聚物内部,使高聚物体积膨胀,称为“溶胀”,然后才是高分子均匀分散在溶剂中,形成完全溶解地分子分散的均相体系。
整个过程往往需要较长的时间。
高聚物的聚集态又有非晶态和晶态之分。
非晶态高聚物的分子堆砌比较松散,分子间的相互作用较弱,因而溶剂分子比较容易渗入高聚物内部使之溶胀和溶解。
晶态高聚物由于分子排列规整,堆砌紧密,分子间相互作用力很强,以致溶剂分子渗入高聚物内部非常困难,因此晶态高聚物的溶解要困难得多。
非极性的晶态高聚物(如PE)在室温很难溶解,往往要升温至其熔点附近,待晶态转变为非晶态后才可溶;而极性的晶态高聚物在室温就能溶解在极性溶剂中。
例3-2.用热力学原理解释溶解和溶胀。
解:(1)溶解:若高聚物自发地溶于溶剂中,则必须符合:上式表明溶解的可能性取决于两个因素:焓的因素()和熵的因素()。
焓的因素取决于溶剂对高聚物溶剂化作用,熵的因素决定于高聚物与溶剂体系的无序度。
对于极性高聚物前者说影响较大,对于非极性高聚物后者影响较大。
但一般来说,高聚物的溶解过程都是增加的,即>0。
显然,要使<0,则要求越小越好,最好为负值或较小的正值。
极性高聚物溶于极性溶剂,常因溶剂化作用而放热。
因此,总小于零,即<0,溶解过程自发进行。
根据晶格理论得=(3-1)式中称为Huggins参数,它反映高分子与溶剂混合时相互作用能的变化。
的物理意义表示当一个溶剂分子放到高聚物中去时所引起的能量变化(因为)。
而非极性高聚物溶于非极性溶剂,假定溶解过程没有体积的变化(即),其的计算可用Hildebrand的溶度公式:=(3-2)式中是体积分数,是溶度参数,下标1和2分别表示溶剂和溶质,是溶液的总体积。
固体物理第一章习题解答

对于面心立方结构的(111)晶面,其面积为 。在此晶面上有2个原子:面心原子 个,顶角原子 。因此,(111)晶面族的原子数面密度为
(1)底心六角的原胞为AIBKEJFL所表示,它具有一个垂直于底面的四度旋转轴,它的原胞形状如图所示,是简单格子,属于单斜晶系。
(2)底心立方如下图所示,它的底面原子的排列情况可看出每个原子的周围情况都是相同的,因而都是等价的,所以它的基元也由一个原子组成,是简单格子,属于四角晶系。
(3)底心四方如下图所示,每个原子的周围情况完全相同,基元中只有一个原子,属于简单格子,属于四角晶系。
11、在六角晶系中,晶面常用四个指数(hkil)表示,如图所示,前三个指数表示晶面族中最靠近原点的晶面族在互成1200的共面轴 上的截距为 ,第四个指数表示该晶面在六重轴c上的截距为 。
求证:
并将下列用(hkl)表示的晶面用(hkil)表示: 。
证明:
解:为清楚起见图中给出了六角格子底面的格点排列情况,假设有一晶面与底面的交线为AB,它在基矢 上的截距分别为 ,假设直线AB的法线方向为 ,则
可得EF//BD
所以∠a=∠b
△ABD中,AD=BD= AB=
由余弦定理可求得:∠a=109°28′
10、求证:任何点群中两个二重旋转轴之间的夹角只能是300、450、600、和900.
证明:设想一个群包含两个二重轴2和2’,如图所示,它们之间的夹角用 表示。
考虑先后绕2和2’转动 ,称它们为A操作和B操作。显然,与它们垂直的轴上的任意点N,先转到N’,最后又转回到原来的位置N,这表明B、A相乘得到的操作:
第一章习题

班级成绩
学号Chapter 4晶格振动与晶体的热学性质
姓名(lattice vibration and its heat characteristics)
一、简要回答下列问题(answer the following questions):
3.氢键结合4.原子的电负性
四、证明计算题
1.由N个原子(离子)所组成的晶体的体积可以写为
式中 是每个原子(离子)平均所占据的体积; 为离子间的最短距离;γ是和结构有关的常数。试求下列各种结构的γ值:
(1)简立方点阵;
(2)面心立方点阵;
(3)体心立方点阵;
(4)金刚石结构;
(5)氯化钠型结构。
2.由N个惰性气体原子结合成的具有面心立方结构的晶体,其总的相互作用能可以表示为
(2)计算衍射强度;(3)讨论 情况。
9.用波长为λ的X射线,照射晶格常数为a的金刚石结构晶体,问要得到衍射面指数为(220)的衍射斑点,对应的布拉格角应是多少?
10.试求面心立方结构、体心立方结构和金刚石结构的几何结构因子;并讨论其衍射消光条件。
11.用钯靶 X射线投射到NaCl晶体上,测得其一级反射的掠射角为5.9°,已知NaCl晶胞中Na+与Cl-的距离为 ,晶体密度为 。求:(1) X射线的波长;(2)阿伏加德罗常数。
5、格波与弹性波有何不同?
6、长声学波能否导致离子晶体的宏观极化?
7、在绝对零度时还有格波存在吗?若存在,格波间还有能量交换吗?
8、声子数代表的物理意义是什么?为什么说声子是玻色子?
9、一维双原子链中,原子的质量分别为M和m,若用一个杂质原子分别替代这两种原子,说明在何种情况下可以在晶格中产生隙模、高频模、共振模?
高聚物的非晶态

1).主链结构:主链由饱和单键所组成的聚合物,如-C-C-, -C-N-,-C-O-,-Si-O-等,柔顺性较好,一般Tg不高:
C2 HCH C3 H
Tg(oC) -18
C2 HO -50
C3 H Si O C3 H
-123
整理课件
主链中引入孤立双键,可提高分子链的柔顺性,使Tg降低,如:
C2 HCH C3 H
无规线团模型
实验证据: 1. 橡胶的弹性理论完全是建立在无规
线团模型的基础上的,实验证明, 橡胶的弹性模量和应力—温度系数 关系并不随稀释剂的加入而有反常 的改变, 2. 高能辐射使高分子发生交联的实验 结果 3. X光小角散射实验结果 4. 中子小角散射实验结果
整理课件
2. 折叠链缨状胶束粒子模型(两相球粒模型)
f rg
T Tg
fTfgfT T g
T 整理T课g件
fT fg
WLF方程定义的自由体积: WLF方程是由M.L.Williams,ndel和J.D.Ferry提出的一个半经验 方程
lo gT Tg51.1 .6 74(4(T TT Tgg))
这个方程可以从Doolittle方程出发进行推导
聚氯乙烯的△H、G、△ 和温度的关系
整理课件
5.3.2 玻璃化转变理论
1、自由体积理论
自由体积理论认为聚合物的体积是由两部分组成:高分子 链本身所占的体积和高分子链间未被占据的空隙。高分子链间 未被占据的空隙称自由体积。
自由体积是分子链进行构象转变和链段运动所需的活动空间。
当聚合物冷却时,自由体积逐渐减小,当达到某一温度时, 自由体积收缩到最低值,聚合物的链段运动因失去活动空间而 被冻结,聚合物进入玻璃态。因此自由体积理论认为玻璃化温 度就是使聚合物自由体积达到某一最低恒定临界值时的温度。 在这临界值以下,已经没有足够的空间进行分子链构象的调整 了。因而高聚物的玻璃态可视为等自由体积状态。
材料科学基础2版余永宁 (4)

在熔点时的 数值对不同材料是不同:一般的bcc 金属,大约为
0.11,一般的fcc金属,大约为0.07。
非晶态是一种过冷液态 不具有长程有序,但因为它相对于液体熔点有很大的过冷,所 以原子是定域化的。
材料科学基础
北京科技大学 材料科学与工程学院
编制
第4章 非晶态与半晶态
固态
物体可分为
液态
气态
从结构看可分为 原子的迁移性接近
晶态
非晶态
气态
刚性固体
周期性长程有序
缺少长程有序 具有短程序
原子的迁移性接近
非晶态材料
• 大多数热固性塑料 • 氧化物及非氧化物(硫属化合物及氟化物)玻璃态 • 非晶态聚合物、干凝胶 • 非晶态半导体 • 非晶态金属或合金 • 非晶态电介质 • 非晶态离子导体 • 非晶态超导体
非晶态材料具有其他状态物质所没有的特性和优异性能。 在很多新材料应用领域如:光通信材料、激光材料、光集成电 路、新型太阳能电池、高效磁性材料、输电和输能材料等其都 是研究和开发的热点。
聚合物
• 聚合物是一类由长分子组成的有机材料,通常由碳骨架与 其他元素或结构单位连接作为侧基构成。
• 聚合物不容易晶化。即使在缓慢冷却条件下,聚合物通常 只是部分结晶或完全不结晶,而形成半晶态或非晶态。
• 在20世纪已经能够人工合成聚合物,并且可通过人工调整分 子的结构获得所希望的性能,这使得聚合物成为一大类重 要的材料,在建筑、汽车、通信甚至航空工业等领域都获 得重要的应用。
本章主要讨论非晶态和半晶态的结构、它们的基本特 征和一些简单材料。
4.1 非晶态
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
33040 = 785.2 42.01 (4) 这个聚丙烯聚合度的分散性 PD 为 M 36240 = 1.097 PD = w = M n 33040 n=
4-5.什么是单体、聚合物的链节(重复单元)?它们之间有什么关系?写出以下聚合物的 链节结构式。(1)聚乙烯;(2)聚氯乙烯;(3)聚甲醛;(4)聚对苯二甲酰对苯二胺。 解: 高分子由许多相同的简单结构单元通过共价键重复连接而成, 这些重复结构单元简称重 复单元,又称链节,形成结构单元的分子称单体。 (1) 聚乙烯链节结构式是
图 x4-1 当玻璃板两侧表面激冷至室温时,因为快冷,在较高的温度转变为玻璃,即 Tg 较高,并且 比体积 V 较大。在继续冷却时,虽然表面层的比体积比内层的过冷液体大,但由于内层是 过冷液态,可以松弛因此而产生的应力。当板的中心缓慢地冷却至室温,因它的 Tg 较表面 层低,在比较低的温度转变为玻璃态,它的比体积 V 比表层的小,对表层产生平行表面的 压应力。因为这时表层已是玻璃态,不能松弛这压应力。表层这种压应力,是表层不易产生 裂纹(裂纹都是由张应力产生的) ,起到强化玻璃的作用。 4-4. 下表列出聚丙烯的相对分子质量的资料,(1)计算数均相对分子质量。(2)计算重均相对 分子质量。(3)求其聚合度。(4)求聚合度的分散性。ٛ 相对分子质量范围 (g/mol)ٛ ٛ ٛ 8000∼16000 所占数量分数 0.05
把给出聚乙烯分子链的数据代入上式,得
2 Rn = 400003 / 5 × 3.08
1 + cos109.5o nm = 1256 nm 1 − cos109.5o
4-8. 官能度与聚合物结构形态有什么关系? 解:如果聚合物单体的官能度等于 2,那么,单体只能连接成长的分子链,没有分支,是线 型结构。若官能度等于 3 或大于 3,聚合时,三官能度的一个官能度提供与另一个分子链桥 接共价交联形成网状, 是体型结构。 这样的聚合物实际上是一个整体的分子量非常巨大的分 子。 4-9. 辐照特别是高能辐照,会破坏聚合物中的共价键。高能辐照会对半晶态聚合物结晶度 有什么影响? 解:因为高能辐照破坏聚合物中的共价键,使聚合物链的规则性降低,因此,不易堆垛 4-10. 您认为普通窗玻璃的玻璃转变温度在室温以上还是以下?橡胶带聚合物的玻璃转化 温度又如何?
4-1
所占质量分数 0.02
16000∼24000 24000∼32000 32000∼40000 40000∼48000 48000∼56000 解:(1) 数均相对分子质量 M n = ∑i N i M i 子 0.20 0.07
0.10 0.20 0.30 0.27 0.11
4-1. 为什么大多数诸如窗户和饮料玻璃等商业氧化物需要把 CaO 和 Na2O 加到 SiO2 中? 解: SiO2 氧化物满足查卡里阿森规则能形成大面积的三维玻璃网络, 是玻璃的网络形成体, + + CaO 和 Na2O 氧化物在玻璃中不能形成网络。Na 只有一个官能度,Ca2 只有两个官能度, 当它们加入 SiO2 网络与氧离子连接后,必打断网络的一次键,降低了网络一次键的密度从 而降低玻璃化温度。对一般的广口瓶和窗户玻璃,他们在低温使用,它不需要过高的玻璃化 温度 Tg,低的 Tg,使产品易于操作并降低成本。 4-2. 含碳酸钠的硅氧化物玻璃放在熔盐中实现离子交换。钾离子与钠离子交换。交换结果 使玻璃转变温度升高还是降低?如果锂离子与钠离子交换又如何? 解:将碳酸钠的硅氧化物玻璃浸入钾熔盐中,玻璃的钠离子被熔盐中的钾离子置换。由于钾 离子半径(rK+=0.133 nm)比钠离子半径(rNa+=0.098 nm)大,在表面的钾离子使表面伸张, 但受到中心部分的约束而使表面受压应力。 若浸入锂的熔盐中, 玻璃的钠离子被熔盐中的锂 离子置换。由于锂离子半径(rLi+=0.078 nm)比钠离子半径小, 4-3. 氧化物玻璃常用如下的热处理来强化:熔融玻璃成为约 3 mm 厚的板,然后玻璃两侧表 面激冷至室温, 板的中心缓慢地冷却至室温。 比较靠近板表面材料与靠近板中心材料的玻璃 转变温度及比体积有何不同?说明能强化玻璃的原因。 解:玻璃化温度 Tg 与冷却速度 v 有关系,如图 x4-1 所示。当冷却速度慢时,在冷却过程结 构可以弛豫的时间比较长, 过冷液体可以维持到比较低的温度才形成玻璃, 所以玻璃化温度 低,相应的比体积 V 大;相反,冷却速度快,在冷却过程可供以弛豫的时间比较长短,过 冷液体在比较高的温度就凝结为玻璃,玻璃化温度高,相应的比体积小。
4-3
解: 普通窗玻璃的玻璃转变温度应该在室温以上。 如果在室温以下, 则它在室温时仍是液态, 虽然粘度很大,仍有流动性,原子还是非定域的。这样,不能保持在室温下的固定形状。对 于橡胶带聚合物, 它的玻璃转变温度则在室温以下。 因为橡胶带聚合物在室温有很大的弹性, 如果它在室温就是玻璃态,它不可能出现弹性,而是出现脆性。
4-11. 轻度交联的橡胶带拉长了数倍,去除作用力后橡胶带会恢复原来的长度。若拉长后的 橡胶带放置在玻璃转变温度以下,或者放置玻璃转变温度以上,这两种情况去除作用力 后,橡胶的长度会发生什么变化?为什么? 解:当拉长后的橡胶带放置在玻璃转变温度以下时,它转变为玻璃态。玻璃态转变实现了原 子从非定域性到定域性的转变(固化) ,所以去除外力后不么能恢复原来的长度。 当拉长后的橡胶带放置玻璃转变温度以上时,聚合物在拉长后会结晶,并产生热。如果 产生的热被散逸,则可以保持伸长状态。如果提供热以熔化晶体,伸长才会发生恢复。 4-12. 含人造纤维的衣服洗涤后凉干,衣服缩小了,请解释。 解: 人造纤维的衣服中的纤维聚合物都被拉长而具有一定的结晶态, 当衣服洗涤去除伸张状 态使聚合物链回复卷曲状态, 这是因为卷曲状态的熵值比伸张状态大的原故, 结果衣服缩小 了。 4-13. 一个透明的 PET 薄膜在室温慢慢地伸张,它通常保持透明。但是,如果在 130℃伸张, 它会变成不透明的,为什么? 解:PET(聚对苯二甲酸乙二醇酯)的玻璃化温度是 90°C。在 130℃伸张,即在玻璃化温度 以上伸张,在玻璃化温度以上分子链易于流动,外力伸张可以帮助聚合物结晶,因为结晶使 透明度降低,随着结晶度加大不透明度也加大。但在室温(玻璃化温度以下)慢慢地伸张, 聚合物难以结晶,所以仍保持其透明度。 4-14. 已知 PET 约在 255 ℃熔化,估计它的玻璃转变温度,将结果和表 6-4 列出的温度进行 对比。 解:Tg/Tm≈2/3 4-15. 如图 4-52 所示的二维向列相液晶的分子排列,说明取向序参数 S=2<cos2θ>−1 是恰当 的。
∫
π
0
P(θ )dθ
∫ =
π
0
cos2 θ (1 / π )dθ
∫
π
0
(1/π )dθ
=
1 1 ⎛θ ⎞ ⎜ + sin θ cos θ ⎟ = π⎝2 ⎠0 2
π
把<cos2θ>-1/2 代入取向序参数 S=2<cos2θ>−1,获得 S=0,符合 S 对完全无序的定义。
4-4
在完全有序时,只有在θ=0 时概率密度 P(θ)=1,θ等于其它值时为 0,所以<cos2θ>=1。把 <cos2θ>=1 代入取向序参数 S=2<cos2θ>−1,获得 S=1,符合 S 对完全有序的定义。
(2) 聚氯乙烯链节结构式是
(3) 聚甲醛链节结构式是
(4) 聚对苯二甲酰对苯二胺链节结构式是
4-2
4-6. 均聚合度为 25000 的聚苯乙烯,求它的重均相对分子质量。 解:聚苯乙烯的单体是[CH2–CH(C6H5)],故链节含 8 个 C 和 8 个 H。链节的分子质量为 8(12.01+1.008)=104.14 g/mol。现均聚合度为 25000,重均相对分子质量为
4-16. 指出晶体、液晶、玻璃和液体各结构中是否具有位置长程序、位置短程序和取向序。 解:答案列于下表。
位置长程序 晶体 液晶 玻璃 液体 有 无 无 无 位置短程序 有 有 有 有 取向序 有 有 无 无
4-17. 由刚性形状各向异性分子构成的固体加热后变成熔体。4 种可能的二维结构示意图如 图 4-53 所示。对于如图 4-53 所示的三维材料,回答以下问题: (1) 对 4 种结构各给出在材料科学中使用的一般名称。 (2) 对 4 种结构确定其分子三维情况下的表观平移和旋转自由度。
(2) 重均相对分子质量 M w = ∑i wi M i 量是一个范围,采用其中值计算:
Mw =
∑ w 。把上表给出的数据代入,因给出的相对分子质
i i
∑ ( w M ) = 0.02 × 12000 + 0.10 × 20000 + 0.20 × 28000 + 0.30 × 36000 + 0.27 × 44000 + 0.11 × 52000 g/mol 1 ∑w
i i i i i
= 36240 g/mol
(3) 丙烯的单体是 (CH2-CH-CH3) , 每个单体含 3 个 C 和 6 个 H, C 的相对原子质量是 12.01, H 的相对原子质量是 1.008,单体的质量是 3×12.01+6×1.008) g/mol=42.01 g/mol。其平均聚 合度 n 为
4-5
2 Rn = nl
1 + cos θ 1 − cos θ
式中θ为键角,C 的键角为 109.5°。但是,对于长分子链,重复单元的无规连接不能穿越自 身的链, 即高分子链的不同部分要相互回避, 要对上式修正。 对于三维空间中的长链修正 (近 似)为
2 Rn = n3 / 5 l
1 + cos θ 1 − cos θ
M n = 25000 × 104.14 g/mol = 2603500 g/mol
,估计分子链的长度。 4-7. 聚合度 n 为 40000 聚乙烯分子链,假设分子完全伸长(即成直线) 若假设分子链在熔融状态,估计分子链两端点间的距离(键长数据参阅例题 4-6) 。 解:首先计算一个单体的长度。聚乙烯的单体是[CH2–CH2],其结构式参见题 4-5(1),聚乙烯链 节的长度是 2 个 C—C 键长, 而键长 C—C=1.54 nm, 即聚乙烯链节的长度是 l=2×1.54 nm=3.08 nm。聚合度 n 为 40000 聚乙烯分子链完全伸长的长度 L 为 L = n × l = 40000 × 3.08 nm = 123200 nm = 0.1232 mm 若分子链在熔融状态,它的构象无规线团构象。按无规行走模型, n 个链节的分子链两端 点间的距离的均方根为
