第三章运动基础及卫星星历PPT课件
合集下载
第三章 卫星运动基础及GPS卫星星历
轨道面倾角i 轨道面倾角 升交点赤径 轨道椭圆的长半径a 轨道椭圆的长半径 轨道椭圆的偏心率e 轨道椭圆的偏心率 近地点角距ω 近地点角距 真近点角V 真近点角
V
6
卫星运动基础及GPS卫星星历 卫星运动基础及GPS卫星星历 GPS
3.3 卫星的受摄运动
各种作用力 地球引力 日、月引力 太阳辐射压力 地球潮汐作用力 大气阻力
9
卫星运动基础及GPS卫星星历 卫星运动基础及GPS卫星星历 GPS
& 轨道倾角的变化率（ 轨道倾角的变化率 弧度/ I ——轨道倾角的变化率（弧度/秒）
Cuc——纬度幅角的余弦调和项改正的振幅（弧度）， 纬度幅角的余弦调和项改正的振幅（ 纬度幅角的余弦调和项改正的振幅 弧度）， Cus——纬度幅角正弦调和项改正的振幅（弧度）， 纬度幅角正弦调和项改正的振幅（ 纬度幅角正弦调和项改正的振幅 弧度）， Crc——轨道半径的余弦调和项改正的振幅（米）， 轨道半径的余弦调和项改正的振幅（ 轨道半径的余弦调和项改正的振幅 Crs——轨道半径的正弦调和项改正的振幅（米）， 轨道半径的正弦调和项改正的振幅（ 轨道半径的正弦调和项改正的振幅 Cic——道倾角的余弦调角和项改正的振幅（弧度）， 道倾角的余弦调角和项改正的振幅（ 道倾角的余弦调角和项改正的振幅 弧度）， Cis——轨道倾角的正弦调角和项改正的振幅（弧度）， 轨道倾角的正弦调角和项改正的振幅（ 轨道倾角的正弦调角和项改正的振幅 弧度）， GPD——周数（周）， 周数（ 周数 Tgd——电离层延迟改正（秒）， 电离层延迟改正（ 电离层延迟改正 IODC——星钟的数据龄期（N）， 星钟的数据龄期（ ）， 星钟的数据龄期 卫星钟差（ 时间偏差， ɑ0——卫星钟差（秒）——时间偏差， 卫星钟差 时间偏差 卫星钟速（ 秒 频率偏差系数， ɑ1——卫星钟速（秒/秒）——频率偏差系数， 卫星钟速 频率偏差系数 卫星钟速变率（ 秒 ） 漂移系数， ɑ2——卫星钟速变率（秒/秒2）——漂移系数， 卫星钟速变率 漂移系数 卫星精度——（N）， 卫星精度 （ ）， 卫星健康——（N）。 卫星健康 （ ）。
V
6
卫星运动基础及GPS卫星星历 卫星运动基础及GPS卫星星历 GPS
3.3 卫星的受摄运动
各种作用力 地球引力 日、月引力 太阳辐射压力 地球潮汐作用力 大气阻力
9
卫星运动基础及GPS卫星星历 卫星运动基础及GPS卫星星历 GPS
& 轨道倾角的变化率（ 轨道倾角的变化率 弧度/ I ——轨道倾角的变化率（弧度/秒）
Cuc——纬度幅角的余弦调和项改正的振幅（弧度）， 纬度幅角的余弦调和项改正的振幅（ 纬度幅角的余弦调和项改正的振幅 弧度）， Cus——纬度幅角正弦调和项改正的振幅（弧度）， 纬度幅角正弦调和项改正的振幅（ 纬度幅角正弦调和项改正的振幅 弧度）， Crc——轨道半径的余弦调和项改正的振幅（米）， 轨道半径的余弦调和项改正的振幅（ 轨道半径的余弦调和项改正的振幅 Crs——轨道半径的正弦调和项改正的振幅（米）， 轨道半径的正弦调和项改正的振幅（ 轨道半径的正弦调和项改正的振幅 Cic——道倾角的余弦调角和项改正的振幅（弧度）， 道倾角的余弦调角和项改正的振幅（ 道倾角的余弦调角和项改正的振幅 弧度）， Cis——轨道倾角的正弦调角和项改正的振幅（弧度）， 轨道倾角的正弦调角和项改正的振幅（ 轨道倾角的正弦调角和项改正的振幅 弧度）， GPD——周数（周）， 周数（ 周数 Tgd——电离层延迟改正（秒）， 电离层延迟改正（ 电离层延迟改正 IODC——星钟的数据龄期（N）， 星钟的数据龄期（ ）， 星钟的数据龄期 卫星钟差（ 时间偏差， ɑ0——卫星钟差（秒）——时间偏差， 卫星钟差 时间偏差 卫星钟速（ 秒 频率偏差系数， ɑ1——卫星钟速（秒/秒）——频率偏差系数， 卫星钟速 频率偏差系数 卫星钟速变率（ 秒 ） 漂移系数， ɑ2——卫星钟速变率（秒/秒2）——漂移系数， 卫星钟速变率 漂移系数 卫星精度——（N）， 卫星精度 （ ）， 卫星健康——（N）。 卫星健康 （ ）。
第三章卫星运动的基础知识与ppt课件
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
第二节 GPS卫星星历
卫星星历是描述卫星运行轨道的参数，分
预报星历和后处理星历。
春分
1、预报星历
点
由卫星向用户播发。可用于实时定位。分
C/A码星历和P码星历。
内容：分三部分，开普勒六参数、轨道
3、偏近点角与真近点角的计算
偏近点角： E=M+e.sinE 真近点角：
1
tanV211eess
2
tanEs 2
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
4、无摄卫星位置计算
在轨道直角坐 标系中的位置：
卫星在轨道平面上的位置：真近点角V（变量）；
轨道平面与地球体之间的相对定向：升交点赤经Ω；轨道面倾角i。 辅助参数平近点角M和偏近点角E。 M=n(t-t0)…………t0为卫星过近地点时刻。
参数说明 近地点角距——近地点与升交点的地心夹角。 真近点角——卫星与近地点的地心夹角。 升交点赤经——升交点与春分点的地心夹角。 轨道面倾角——卫星轨道面与天球赤道面的夹角。 升交距角——卫星与升交点的地心夹角，即真近点角与近地点角距之
和。
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
开普勒六参数
偏近点角E
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
GPS课件第三章卫星运动基础及GPS卫星
z
卫星
赤道 地心 春分 点 轨道
v Ω ω
升交 点
近地点
i y
3.2.2 二体问题的运动方程
卫星的无摄运动—二体问题 3.2 卫星的无摄运动 二体问题
研究卫星绕地球的运动，主要是研究卫星运动状态 随时间的变化规律。根据物理学中牛顿定律确定的微 分方程（3-6）用直角坐标表示的二体问题微分方程：
ɺɺ = − x ɺɺ = y ɺɺ = z r = 加速度
卫星的无摄运动—二体问题 3.2 卫星的无摄运动 二体问题
为轨道的长半径,e a 为轨道的长半径,e 为 轨道椭圆偏心率， 轨道椭圆偏心率，这 两个参数确定了开普 勒椭圆的形状和大小。 为升交点赤经： Ω为升交点赤经：即地球 赤道面上升交点与春 分点之间的地心夹角。 为轨道面倾角： i为轨道面倾角：即卫星 轨道平面与地球赤道 面之间的夹角。这两 个参数唯一地确定了 卫星轨道平面与地球 x 体之间的相对定向。
(µ − (µ − (µ
x
2
/ r / r / r +
3 3 3
)x )y )z
:
2
（ 3 − 6）
卫星地心向径 y
+ z
2
,
: ɺ ɺ ɺ , a = (X ɺ , Y ɺ , Z ɺ )
µ
= GM
地球引力常数
.
微分方程的解为六个轨道参数。
卫星的无摄运动—二体问题 3.2 卫星的无摄运动 二体问题
卫星运动基础及GPS GPS卫星星历 第三章 卫星运动基础及GPS卫星星历
本章需学习的内容： 本章需学习的内容： 3.1 概述 卫星的无摄运动( 3.2 卫星的无摄运动(弄清二体问题的六个轨 道参数) 道参数) 3.3 卫星的受摄运动 GPS卫星星历 星历参数有哪些) 卫星星历( 3.4 GPS卫星星历(星历参数有哪些)
卫星
赤道 地心 春分 点 轨道
v Ω ω
升交 点
近地点
i y
3.2.2 二体问题的运动方程
卫星的无摄运动—二体问题 3.2 卫星的无摄运动 二体问题
研究卫星绕地球的运动，主要是研究卫星运动状态 随时间的变化规律。根据物理学中牛顿定律确定的微 分方程（3-6）用直角坐标表示的二体问题微分方程：
ɺɺ = − x ɺɺ = y ɺɺ = z r = 加速度
卫星的无摄运动—二体问题 3.2 卫星的无摄运动 二体问题
为轨道的长半径,e a 为轨道的长半径,e 为 轨道椭圆偏心率， 轨道椭圆偏心率，这 两个参数确定了开普 勒椭圆的形状和大小。 为升交点赤经： Ω为升交点赤经：即地球 赤道面上升交点与春 分点之间的地心夹角。 为轨道面倾角： i为轨道面倾角：即卫星 轨道平面与地球赤道 面之间的夹角。这两 个参数唯一地确定了 卫星轨道平面与地球 x 体之间的相对定向。
(µ − (µ − (µ
x
2
/ r / r / r +
3 3 3
)x )y )z
:
2
（ 3 − 6）
卫星地心向径 y
+ z
2
,
: ɺ ɺ ɺ , a = (X ɺ , Y ɺ , Z ɺ )
µ
= GM
地球引力常数
.
微分方程的解为六个轨道参数。
卫星的无摄运动—二体问题 3.2 卫星的无摄运动 二体问题
卫星运动基础及GPS GPS卫星星历 第三章 卫星运动基础及GPS卫星星历
本章需学习的内容： 本章需学习的内容： 3.1 概述 卫星的无摄运动( 3.2 卫星的无摄运动(弄清二体问题的六个轨 道参数) 道参数) 3.3 卫星的受摄运动 GPS卫星星历 星历参数有哪些) 卫星星历( 3.4 GPS卫星星历(星历参数有哪些)
卫星运动基础及GPS卫星星历
第1章 卫星运动基础及GPS 卫星星历卫星的无摄运动只考虑地球质心引力作用的卫星运动称为卫星的无摄运动，即作为二体问题研究两个质点在万有引力作用下的运动。
1.1.1 开普勒三定律(1) 卫星运行的轨道是一个椭圆，该椭圆的一个焦点与地球质心重合。
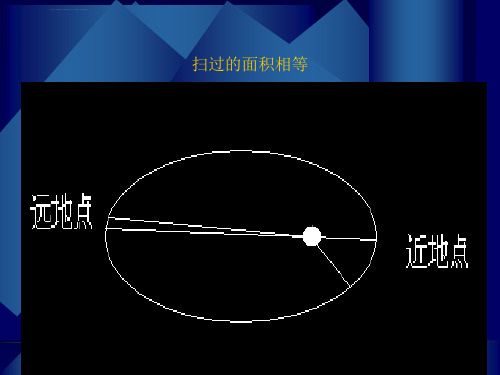
(2) 卫星的地心向径，即地球质心与卫星间的距离向量，在相同的时间里扫过的面积相等。
(3) 卫星运行周期的平方与轨道椭圆长半径的立方之比是一常量，而该常量是地球引力常数GGGG 的倒数。
TT 2aa 3=4ππ2GGGG 1.1.2 卫星运动的轨道参数（开普勒轨道参数，轨道根数）图3-1 卫星轨道参数aa ——轨道椭圆的长半径。
ee ——轨道椭圆的偏心率。
ΩΩ——升交点的赤经，即地球赤道平面上升交点NN 与春分点γγ之间的地心夹角，0°~360°。
ii ——轨道面的倾角，即卫星轨道平面与地球赤道平面夹角，0°~180°。
ωω——近地点角距，即在轨道平面上，近地点AA 与升交点NN 之间的地心角距，0°~360°。
ff ——真近点角，即轨道平面上卫星与近地点之间的地心角距。
升交点 XX ZZ 春分点γγ 卫星近地点 OO ZZ ʹ AA NN SSΩΩ ff ωω 赤道面轨道面⎩⎪⎪⎨⎪⎪⎧①aa 、ee 唯一确定了卫星轨道的形状和大小②ΩΩ、ii 确定了卫星轨道平面与地球体的相对定向③ωω确定了轨道椭圆在轨道平面内的指向④ff 确定了卫星在轨道上的瞬时位置上述6个参数一旦确定，（在二体问题下）即可唯一确定卫星的运动状态（任意时刻tt 卫星的位置和运动速度）。
1.1.3 二体问题的运动方程1.1.4 二体问题微分方程的解1.1.5 轨道空间直角坐标系OO -XX ʹYY ʹZZ ʹ，以地球质心为原点，XX ʹ指向近地点，ZZ ʹ垂直于轨道平面向上，YY ʹ在轨道平面上垂直于XX ʹ轴，构成右手系。
演示文稿卫星运动基础及GPS卫星星历PPT课件
太阳光辐射压力
卫星体反射压力
加速度 /（m/s-2）
5 × 10-6 3 × 10-7 5 × 10-6 1 × 10-9 1 × 10-9 1 × 10-7 1 × 10-8
卫星轨道受摄度/m
3小时弧段
2天弧段
2000
14000
5~80
100~1500
5~150
1000~3000
——
0.5~1.0
真近点角
符号 i Ω as es
ωs fs
意义
决定轨道平面的空间位置
决定轨道椭圆的大小 决定轨道椭圆的形状 决定近地点在轨道椭圆上的位置 卫星以角速度n0运行的瞬时位置
第13页/共43页
13
无摄运动>无摄卫星轨道的描述
选用上述6个轨道参数来描述卫星运动的轨道， 一般来说是合理而必要的。
6个轨道参数i,Ω,ω,a,e,f所构成的坐标系统，称轨 道坐标系统。
在该系统中，6个参数一经确定，卫星在任一瞬 间相对地球体的空间位置及速度便可唯一确定。
14
第14页/共43页
计算真近点角fs
• 真近点角的两个辅助参数 • 偏近点角（Es） ：卫星S在其辅助圆上的
相应点S’和轨道椭圆中心O’的连线与轨 道椭圆极轴延长线之间的夹角，叫偏近点 角。
• 平近点角（Ms）：在轨卫星从过近地点时 15 元 tp 开始，按平均角速度n0 运行到时元
35
第35页/共43页
• 导航电文中的星历参数
• t0e——参考历元
• M0——参考时刻的平近点角
• es——轨道偏心率
• as1/2——轨道长半径的平方根
• 0——参考时刻的升交点赤经
• i0——参考时刻的轨道倾角
GNSS-第3讲 卫星运动基础与位置计算
§3.1 卫星无摄运动
开普勒第一定律（轨道定律)： 卫星沿一个椭圆轨道环绕地 球运行，而地球处于椭圆的 一个焦点上
b a
m
r f
M
近地点
r a (1 e2 ) 1 e cos f
§3.1 卫星无摄运动
1、卫星运动轨道参数
m
a
b M
f
近地点
z
ω
升交点
a ：椭圆长半轴 b ：椭圆短半轴，也可以用偏心率e表示
n
(
i0 ik
x xk
xi xi
)
yk
拉格朗日多项式内插
内插精度
➢ 采用17阶多项式，精度可优于5mm
注意事项
➢ 要对某一时段的轨道内插，精密轨道数据应该完全 覆盖该时段，最好前后有9个历元的延伸
➢ 下载数据时，需要观测当天及前后各一天的数据
2、根据精密星历计算卫星位置
任意时刻 t 卫星位置的计算
➢ 原理：插值法 ➢ 方法：拉格朗日插值法、且贝雪夫插值法等
拉格朗日插值法:
已知函数y f (x)的n个结点x0 , x1,...,xn及其对应的 函数值y0 , y1,...,yn对于插值区间内的任一点x，其函数 值为
f
(x)
n k 0
X轴旋转i角、绕Z轴旋转 M
y
角，求出卫星在天球坐
i
标系下的坐标。
x 春分点
升交点
3）将天球坐标转换到地球 坐标。
起始子 午面 Z
春分点 x
z
Y
f Mω
Ω0
升交点
X
近地点 y
计算过程
1) 计算卫星运行的平均角速度（引力常数和长半轴）
n0
GM a3
第三章-卫星运动基础及GPS卫星星历PPT课件
式中，G为万有引力常数。
（3-1）
09.02.2021
-
16
3.2.3 二体问题的运动方程
设as、ae为卫星与地球在万有引力作用下产 生的加速度，则根据牛顿第二定律，可得：
as (GrM2 )•r0
ae
(GM)•r0 r2
（3-2）
09.02.2021
-
17
3.2.3 二体问题的运动方程
因牛顿第二定律只适用于惯性坐标系，若要 讨论卫星S相对于地球质心O的运动，必须 将坐标原点移至地球质心，并设a为卫星S相 对于O的加速度，则：ຫໍສະໝຸດ a(1 r2
)
•
r
0
（3-5）
09.02.2021
-
20
3.2.3 二体问题的运动方程
设以O为原点的直角坐标系为O-XYZ，s点
的坐标为（X，Y，Z），则卫星S的地心向
径r=（X，Y，Z），加速度 a(X,Y,Z),
代入（3-4）式即得：
X
X r3
Y
Y r3
式中，r X2Y2Z2
09.02.2021
09.02.2021
-
7
3.2.1 开普勒定律
开普勒第一定律
卫星运行的轨道为一椭圆，该椭圆的一个焦 点与地球质心重合。此定律阐明了卫星运行 轨道的基本形态及其与地心的关系。由万有 引力定律可得卫星绕地球质心运动的轨道方 程。r为卫星的地心距离，as为开普勒椭圆 的长半径，es为开普勒椭圆的偏心率；fs为 真近地点角，它描述了任意时刻卫星在轨道 上相对近地点的位置，是时间的函数。
表达了开普勒椭圆在轨道平面上的定向。 6、真近地点角V：即轨道平面上卫星与近地点之间的地心角距。该参
数为时间的函数，确定卫星在轨道上的瞬时位置。
（3-1）
09.02.2021
-
16
3.2.3 二体问题的运动方程
设as、ae为卫星与地球在万有引力作用下产 生的加速度，则根据牛顿第二定律，可得：
as (GrM2 )•r0
ae
(GM)•r0 r2
（3-2）
09.02.2021
-
17
3.2.3 二体问题的运动方程
因牛顿第二定律只适用于惯性坐标系，若要 讨论卫星S相对于地球质心O的运动，必须 将坐标原点移至地球质心，并设a为卫星S相 对于O的加速度，则：ຫໍສະໝຸດ a(1 r2
)
•
r
0
（3-5）
09.02.2021
-
20
3.2.3 二体问题的运动方程
设以O为原点的直角坐标系为O-XYZ，s点
的坐标为（X，Y，Z），则卫星S的地心向
径r=（X，Y，Z），加速度 a(X,Y,Z),
代入（3-4）式即得：
X
X r3
Y
Y r3
式中，r X2Y2Z2
09.02.2021
09.02.2021
-
7
3.2.1 开普勒定律
开普勒第一定律
卫星运行的轨道为一椭圆，该椭圆的一个焦 点与地球质心重合。此定律阐明了卫星运行 轨道的基本形态及其与地心的关系。由万有 引力定律可得卫星绕地球质心运动的轨道方 程。r为卫星的地心距离，as为开普勒椭圆 的长半径，es为开普勒椭圆的偏心率；fs为 真近地点角，它描述了任意时刻卫星在轨道 上相对近地点的位置，是时间的函数。
表达了开普勒椭圆在轨道平面上的定向。 6、真近地点角V：即轨道平面上卫星与近地点之间的地心角距。该参
数为时间的函数，确定卫星在轨道上的瞬时位置。
第三讲卫星运动基础及卫星星历-PPT
v 根据能量守恒定理,卫星在近地点处速度最大, 动能最大,势能最小;在远地点时速度最小,动能 最小,势能最大。
开普勒第三定律
卫星围绕地球运动周期得平方与轨道椭 球长半径得立方成正比,其比值等于地 球引力常数得GM倒数、
3、2 卫星得无摄运动
开普勒轨道参数(1/2)
确定卫星轨道形状、大小与 §a（椭圆长半径） 卫星在轨道上得瞬时位置 §e（偏心率）
3、3 卫星得受摄运动
大气阻力
对低轨道卫星影响较大
对于GPS卫星(高度为20 200km)得影 响可忽略
3、4 GPS卫星星历
§ 卫星星历:一组对应某一时刻得轨道 参数及其变率
§ 由星历可计算出任一时刻得卫星位 置及其速度
§ 预报星历(广播星历) § 后处理星历(精密星历)
3、4 GPS卫星星历
cos sin i
3、3 卫星得受摄运 动
§ 考虑了摄动力后,卫星得轨道参数随时间变化, 不再为常数。
§ 卫星在地球质心引力与各种摄动力总得影响 下得轨道参数称为瞬时轨道参数。
§ 卫星运动得真实轨道称为卫星得摄动轨道或 瞬时轨道。瞬时轨道不就是椭圆,轨道平面在 空间得方向也不就是固定不变得。
3、3 卫星得受摄运动
第三讲卫星运动基础及卫星星历
3、1 概述
为什么要研究卫星运动规律？
§相关名词
- 卫星轨道:卫星在空间运行得轨迹。 - 轨道参数:描述卫星轨道状态与位置得参数。
§ 在利用GPS进行导航与测量时,卫星就是做为 位置已知得高空观测目标,所以其轨道误差将 影响定位精度。(例子)
§ 为了制订GPS测量得观测计划与便于捕获
确定卫星受摄运动轨道的瞬时特征
3、2 卫星得无摄运 动
§ 卫星运动得开普勒定律 § 卫星运动得开普勒轨道参数
开普勒第三定律
卫星围绕地球运动周期得平方与轨道椭 球长半径得立方成正比,其比值等于地 球引力常数得GM倒数、
3、2 卫星得无摄运动
开普勒轨道参数(1/2)
确定卫星轨道形状、大小与 §a（椭圆长半径） 卫星在轨道上得瞬时位置 §e（偏心率）
3、3 卫星得受摄运动
大气阻力
对低轨道卫星影响较大
对于GPS卫星(高度为20 200km)得影 响可忽略
3、4 GPS卫星星历
§ 卫星星历:一组对应某一时刻得轨道 参数及其变率
§ 由星历可计算出任一时刻得卫星位 置及其速度
§ 预报星历(广播星历) § 后处理星历(精密星历)
3、4 GPS卫星星历
cos sin i
3、3 卫星得受摄运 动
§ 考虑了摄动力后,卫星得轨道参数随时间变化, 不再为常数。
§ 卫星在地球质心引力与各种摄动力总得影响 下得轨道参数称为瞬时轨道参数。
§ 卫星运动得真实轨道称为卫星得摄动轨道或 瞬时轨道。瞬时轨道不就是椭圆,轨道平面在 空间得方向也不就是固定不变得。
3、3 卫星得受摄运动
第三讲卫星运动基础及卫星星历
3、1 概述
为什么要研究卫星运动规律？
§相关名词
- 卫星轨道:卫星在空间运行得轨迹。 - 轨道参数:描述卫星轨道状态与位置得参数。
§ 在利用GPS进行导航与测量时,卫星就是做为 位置已知得高空观测目标,所以其轨道误差将 影响定位精度。(例子)
§ 为了制订GPS测量得观测计划与便于捕获
确定卫星受摄运动轨道的瞬时特征
3、2 卫星得无摄运 动
§ 卫星运动得开普勒定律 § 卫星运动得开普勒轨道参数
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
假设观测站至所测卫星的距离为，卫星轨道误差
为，两观测站间的基线长度为D，由 引起的基线
长度误差为D，则其间的关系可近似表示为：
D DD
D D
相对精度/ppm 卫星轨道误差 基线长度D
（m）
(km)
基线长度误 差
D（cm）
1
20
10
1
D
10- 0
10
3
1000
100
D
为什么要研究卫星运动规律？
V 轨道平面上卫星与近地点之间
的地心角距。确定卫星在轨道
上的- 瞬时位置。
10
真近点角的计算（表示为时间的函数）
在描述卫星无摄 运动的6个开普勒轨 道参数中，只有真近 点角是时间的函数， 其余均为常数。故卫 星瞬间位置的计算， 关键在于计算真近点 角。
远地点
ms
bs as
fs
近地点
M
r as(1es2) 1 es cos fs
卫星轨道在GPS定位中具有重要意义； 为了制订GPS测量的观测计划和便于捕获卫 星发射的信号，也需要知道卫星的轨道参数。
-
4
影响卫星轨道的因素及其研究方法
卫星受力：卫星受到的作用力，如果设地球引力视 为1，则其他作用力均小于10-5。
除了受地球重力场的引力作用外，还受到太阳、月 亮和其它天体的引力影响，以及太阳光压、大气阻力和 地球潮汐力等因素影响。
d 2X
dt2
r3
•
X
d 2Y
dt2
r3
•
Y
d 2Z
dt2
•Z
r3
轨道面的法线向量为
A X B Y C Z 0
h A2B2C2
n[A B C]T
-
h h h 17
轨道倾角和升交点赤经
aarrccccooss((XY,h,h))aarcrcccoos(s(A hB h))iaracrccotasn((ZY,N h))aarrccctoasn((C h)A)
中心力：假设地球为均质球体（质量集中于球心）的 所产生的引力。
非中心力：包括地球非球形对称的作用力、日月引力、 大气阻力、光辐射压力以及地球潮汐力等，也称摄动力。 摄动力使卫星的运动产生一些小的附加变化而偏离理想 轨道，同时偏离量的大小也随时间而改变。 10-3
由此出现无摄运动和受摄运动。
-
5
§ 3.2卫星的无摄运动
i为轨道面倾角
s为近地点角距 y fs为卫星的真近点角
-
9
卫星运动的轨道参数
中文名称 轨道平面倾角 升交点赤经
轨道椭圆的长 半径
轨道椭圆的偏 心率
符号 i Ω a
意义 决定轨道平面 的空间位置 决定轨道椭圆的大小
e 决定轨道椭圆的形状
近地点角距 （幅角）
真近点角
ω 轨道平面上，升交点与近地点 之间的地心夹角决定开普勒椭 圆在轨道平面上的定向。
-
14
3.2.2 二体问题
根据万有引力定律，卫星受地球的引力
G•M•m r
Fs r2
ห้องสมุดไป่ตู้
• r
按照牛顿第二定律，可写出卫星和地球的运动方程
FS
md2r dt2
GM m
r2 r
Fe
M
d2r dt2
G M r2
m
r
卫星相对地球的运动方程为
d2r dt2
G•(M r2m)•rr-
15
d 2X
第三章 卫星运动的基础及GPS卫星星 历
§ 3.1 概述 § 3.2卫星的无摄运动 § 3.3卫星的受摄运动 § 3.4 GPS卫星星历
-
1
§ 3.1 概述
为什么要研究卫星运动规律？ 卫星轨道：卫星在空间运行的轨迹； 轨道参数：描述卫星轨道位置和状态的参数；
-
2
§ 3.1 概述
已知的高空观测目标，在进行绝对定位时，卫星轨道 误差将直接影响用户接收机位置的精度；而在相对定位时， 尽管卫星轨道误差的影响将会减弱，但当基线较长或精度 要求较高时，轨道误差影响不可忽略。
dt2
•X
r3
d 2Y
dt2
r3
•
Y
d 2Z
dt2
r3 • Z
GM
二阶常数微分方程组的积分含6个积分常数，
卫星运动状态就由这6个积分常数确定，一般称
为轨道6参数。
-
16
卫星轨道6参数和开普勒三大定律
• 开普勒第一定律：卫星在通过地球质心的平面内运 动，其向径扫过的面积与所经历的时间成正比
cosfs
-
coEss es 1es coEss
13
真近点角的计算（表示为时间的函数）
• 真近点角fs • 偏近点角ES
cosfs
coEss es 1es coEss
EsM sessiE ns
• 平近点角MS Ms n(tt0)
• t0为卫星过近地点的时刻，t为观测卫星时刻。n为 卫星的平均角速度
-
7
§ 3.2卫星的无摄运动
3.2.1 开普勒轨道
参数
z
卫星轨道：卫
星在空间运行的
卫星
轨迹
轨道参数：描
赤道
fs
近地点
述卫星轨道位置 和状态的参数
真近点角的计
算
x
地心
s i
春分点 升交点
y
轨道
-
8
开普勒轨道参数示意图
z
卫星
赤道
fs
近地点
地心
s i
春分点 升交点
x
轨道
as为轨道的长半径 es为轨道椭圆偏心率 为升交点赤经
-
11
真近点角的计算（表示为时间的函数）
为了计算真近点角，引入两个辅助参数：偏近点角Es 和平近点角Ms。 Ms是一个假设量，当卫星运动的平均角 速度为n，则 Ms = n ( t - t0 )，t0为卫星过近地点的时 刻，t为观测卫星时刻。
平近点角与偏近点角间存在如下关系：Es = Ms + essinEs。 由此可得真近点角
m
cofss
coEss es 1escoEss
bs
as r
as
Es ases
- fs
近地点
12
真近点角的计算（表示为时间的函数）
m
bs
as r
as
Es ases M
fs
m
近地点
r as(1es2) 1es cosfs
M m r cf s o a s c s E s o a s e s s a s (c E s e o s ) s
开普勒轨道 卫星精密轨道的计算涉及到复杂的力学模型，为 简化问题，作下列假设： 地球为均质球体，引力场对称； 卫星质量与地球质量相比忽略不计； 忽略摄动力影响
-
6
§ 3.2卫星的无摄运动
3.2.1 开普勒轨道参数 描述卫星在轨的瞬时位置。
（表示为时间的函数）
3.2.2 二体问题：万有引力定律
3.2.3 二体问题的解
iarccos(Z,h)arccos(C) h
XN
B
轨道倾角和升交点赤经一经确定，轨道平面在 空间的位置也就完全确定了
-
18
开普勒第二定律：卫星运动的轨道为一椭 圆，地心位于此椭圆的焦点上
d 2x d t 2
r3
x
d
2
y
d t 2
r3
y
x y